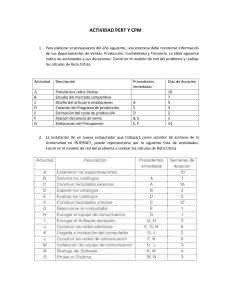
INV. OPERACIONES I 1.3 Principales aplicaciones de la investigación de operaciones. INSTITUTO TECNOLÓGICO SUPERIOR DE NARANJOS Nombre de la materia: Investigación de operaciones 1 Nombre del docente: ING. JORGE ARMANDO AVENDAÑO RODRIGUEZ Grado y grupo: 402A Carrera: INGENIERIA INDUSTRIAL Nombre del alumno: o Torres Chávez Jesús vitelio-211H0082 o González del ángel Diego Axel 211H0157 o Hernández Aguilar Ana Karen 201H0144 Nombre de la actividad: Investigación acerca del tema 1.3 Principales aplicaciones de la investigación de operaciones Número de la unidad: Unidad 1 Naranjos ver. A 17 de febrero de 2023 . Introducción………… Como se verá a continuación, la Investigación de Operaciones es la aplicación, por grupos interdisciplinarios, del método científico a problemas relacionados con el control de las organizaciones o sistemas, con el fin de que se produzcan soluciones que mejor sirvan a los objetivos de la organización. La forma convencional en que la investigación de operaciones realiza esto es construyendo un modelo matemático que represente la esencia del problema. En este tema estudiaremos cuál es la metodología que sigue la Investigación de Operaciones y cuáles son los principales modelos matemáticos que utiliza. ¿QUE ES LA INVESTIGACION DE OPERACIONES? Es una rama de la ingeniería industrial. También tiene relación con la ingeniería en sistemas y la investigación en todas sus ramas. Consiste en el uso de modelos matemáticos, estadísticos y algoritmos. Su objetivo es realizar la toma de decisiones, con la finalidad de mejorar y optimizar el funcionamiento de los procesos. Para la integración de equipos debe incluirse personal con intereses firmes en: matemáticas, estadísticas, teoría de la probabilidad, economía, administración de empresas, computación e ingeniería. Dentro de una Empresa la Investigación de Operaciones se aplica en las áreas de: producción, marketing, compras, manufactura y contabilidad. El proceso de la Investigación de Operaciones comprende las siguientes fases: ❖ ❖ ❖ ❖ ❖ Formulación y definición del problema. Construcción del modelo. Solución del modelo. Validación del modelo. Implementación de resultados. Demos una explicación de cada una de las fases: o o o Formulación y definición del problema. En esta fase del proceso se necesita una descripción de los objetivos del sistema, es decir, qué se desea optimizar; identificar las variables implicadas, ya sean controlables o no; determinar las restricciones del sistema. También hay que tener en cuenta las posibles alternativas de decisión y las restricciones para producir una solución adecuada. Construcción del modelo. En esta fase, el investigador de operaciones debe decidir el modelo a utilizar para representar el sistema. Debe ser un modelo tal que relacione a las variables de decisión con los parámetros y restricciones del sistema. Los parámetros (o cantidades conocidas) se pueden obtener, ya sea a partir de datos pasados o estimados por medio de algún método estadístico. Es recomendable determinar si el modelo es probabilístico o determinístico. El modelo puede ser matemático, de simulación o heurístico, dependiendo de la complejidad de los cálculos matemáticos que se requieran. Solución del modelo. Una vez que se tiene el modelo, se procede a derivar una solución matemática, empleando las diversas técnicas y métodos matemáticos para resolver problemas y ecuaciones. Debemos tener en cuenta que las soluciones que se obtienen en este punto del proceso, son matemáticas y debemos interpretarlas en el mundo real. Además, para la solución del modelo, se deben realizar análisis de sensibilidad, es decir, ver o o cómo se comporta el modelo a cambios en las especificaciones y parámetros del sistema. Esto se hace debido a que los parámetros no necesariamente son precisos y las restricciones pueden estar equivocadas. Validación del modelo. La validación de un modelo requiere que se determine si dicho modelo puede predecir con certeza el comportamiento del sistema. Un método común para probar la validez del modelo es someterlo a datos pasados disponibles del sistema actual y observar si reproduce las situaciones pasadas del sistema. Pero como no hay seguridad de que el comportamiento futuro del sistema continúe replicando el comportamiento pasado, entonces siempre debemos estar atentos de cambios posibles del sistema con el tiempo, para poder ajustar adecuadamente el modelo. Implementación de resultados. Una vez que hayamos obtenido la solución o soluciones del modelo, el siguiente y último paso del proceso es interpretar esos resultados y dar conclusiones y cursos de acción para la optimización del sistema. Si el modelo utilizado puede servir a otro problema, es necesario revisar, documentar y actualizar el modelo para sus nuevas aplicaciones. Principales aplicaciones de la investigación de operaciones. Esta herramienta es de gran relevancia ya que se puede obtener una solución cuantitativa a problemas de diversos tipos o enfoques para tomar una buena decisión basada en el proceso analítico, tiene aplicación en cualquier disciplina o sector de diversa dimensión, que puede ir desde un pequeño negocio o establecimiento hasta una gran empresa u organización de cualquier giro. Dentro de una empresa la IO se aplica en las áreas de producción y envasado de productos, contabilidad, logística, marketing, manufactura, asignación de costos, horarios, maquinas, puestos, así como en las rutas de embarque y transportación, entre otras más. La principal área en la que se aplica esta disciplina es en problemas relacionados al área de la matemática aplicada. No obstante, existen otras aplicaciones más prácticas como, por ejemplo, en la Ingeniería Industrial. Los procesos industriales y de fabricación relacionados con producción con recursos limitados, sistemas logísticos, asignación de tareas y responsabilidades para los empleados e, incluso, el control de los recursos financieros, materiales y humanos pueden pasar por un estudio y análisis bajo el enfoque de la investigación operativa. De modo que la investigación de operaciones puede ser aplicable en cada área de las empresas y organizaciones como lo son los recursos humanos, sector operativo y distribución de productos, y en el uso de los recursos financieros. Para ser un poco más específico y entender mejor qué es la investigación de operaciones y sus aplicaciones, detallemos algunos ejemplos más específicos. ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ Planeamiento de proyectos complejos. Diseño de circuitos de producción y fabricación. Optimización de redes y telecomunicaciones. Asignación de tareas y responsabilidades según el área departamental. Localización de instalaciones. Búsqueda de objetivos empresariales o de producción. Administración de la cadena de suministro. Transporte y gestión de almacén. Se han desarrollado muchos métodos de investigación de operaciones que se aplican a los problemas de los negocios, aunque al mismo tiempo se presentan en muchas industrias distintas. Los modelos para la solución de problemas se pueden agrupar en distintas formas, las más importantes son: Problemas estocásticos o probabilísticos: son útiles al tener que enfrentarse a un ambiente incierto, la estadística de Bayes desarrolla un método poderoso para tomar decisiones cuando se tiene información limitada. Pronósticos: es una responsabilidad ineludible de la gerencia el pronosticar, enfrentando a la incertidumbre respecto al futuro, la conducta pasada como un indicador de lo que va a venir. Dentro de los temas que ven pronósticos se tienen: ▪ Promedios simples ▪ Promedios móviles ▪ Promedios dobles ▪ Suavización exponencial ▪ Regresión ▪ Correlación ▪ Tendencia Modelos de inventarios: ayudan al control de los costos totales de inventarios, estos enfoques pueden reducir el costo total de compra, de almacenar, de llevar el inventario y quedarse sin él, también analiza y evalúa los descuentos ofrecidos por proveedores, así como la compra de artículos múltiples a un mismo proveedor. Programación lineal: es de valor cuando se debe de escoger entre alternativas numerosas para evaluarlas con los métodos convencionales. Al usar la programación lineal, se pueden determinar combinaciones óptimas de los recursos de una firma para alcanzar ciertos objetivos. Problemas de asignación y transporte: son los enfoques útiles cuando la gerencia se enfrenta a problemas que tienen que ver con la mejor alternativa de distribución o el método óptimo de asignar operarios a las máquinas, etc. Teoría de redes: permite a los gerentes hacer frente a las complejidades involucradas en los grandes proyectos, el uso de esta técnica ha disminuido notablemente el tiempo necesario para planear y producir productos complejos, las técnicas más usuales son: ▪ PERT (Técnica de Evaluación y Revisión de Proyectos). ▪ CPM (Método de la Ruta Crítica). ▪ PERT/COSTO (Técnica de programación con limitación de recursos tanto en costo como en tiempo). Teoría de colas o líneas de espera: estudia las llegadas aleatorias a una estación de servicio o proceso de capacidad limitada, los modelos le permiten a la gerencia calcular a futuro las longitudes de las líneas de espera, el tiempo promedio gastado en la línea por una persona que espera el servicio y la necesidad de agregar estaciones de servicio. Esta técnica se estudia primeramente mediante el uso de fórmulas y posteriormente por simulación con computadora. Algunas otras aplicaciones de la investigación de operaciones 1. Recursos humanos En todo caso, puede usarse para ver el impacto del proceso de la automatización y la reducción de costos, en el proceso de reclutamiento de personal, la asignación de tareas y funciones al personal. Así como el uso de incentivos para el proceso de producción. 2. Proceso de mercado y distribución También cuando una empresa espera desarrollar e introducir un nuevo producto al mercado. O bien, realizar pronósticos sobre la demanda, la ubicación de centros de distribución y analizar la situación competitiva. 3. Proceso de producción Por supuesto es usada en el proceso de planificación y el control de la producción. La combinación de los factores de producción, la localización y el tamaño de la planta de producción. De la misma forma para el control de calidad. 4. Compra de materiales Es usada para determinar las cantidades de material requeridos. Ejemplo de ello son las fuentes de suministro y sustitución de insumos, el reemplazo de equipos y máquinas, los costos fijos y variables. 5. Contabilidad y finanzas Adicionalmente se utiliza para analizar el capital requerido. Considerando las inversiones alternativas, el análisis del flujo de caja, manejo de reclamaciones y la seguridad en el manejo de los datos. Un modelo matemático comprende principalmente tres conjuntos básicos de elementos. Éstos son: ❖ Variables y parámetros de decisión. ❖ Restricciones. ❖ Función objetivo. 1. Variables y parámetros de decisión. Las variables de decisión son las incógnitas (o decisiones) que deben determinarse resolviendo el modelo. Los parámetros son los valores conocidos que relacionan las variables de decisión con las restricciones y función objetivo. Los parámetros del modelo pueden ser determinísticos o probabilísticos. 2. Restricciones. Para tener en cuenta las limitaciones tecnológicas, económicas y otras del sistema, el modelo debe incluir restricciones (implícitas o explícitas) que restrinjan las variables de decisión a un rango de valores factibles. 3. Función objetivo. La función objetivo define la medida de efectividad del sistema como una función matemática de las variables de decisión. La solución óptima será aquella que produzca el mejor valor de la función objetivo, sujeta a las restricciones. La Investigación de Operaciones intenta encontrar la solución más óptima para resolver el problema bajo consideración. En lugar de contentarse con sólo perfeccionar el estado de las cosas, la meta es identificar el mejor curso de acción posible. Aun cuando debe interpretarse con todo cuidado, esta "búsqueda de la optimización" es un aspecto muy importante dentro de la Investigación de Operaciones. Un modelo siempre debe ser menos complejo que el problema real, es una aproximación abstracta de la realidad con consideraciones y simplificaciones que hacen más manejable el problema y permiten evaluar eficientemente las alternativas de solución. Resolver un modelo consiste en encontrar los valores de las variables dependientes, asociadas a las componentes controlables del sistema con el propósito de optimizar, si es posible, o cuando menos mejorar la eficiencia o la efectividad del sistema dentro del marco de referencia que fijan los objetivos y las restricciones del problema. La selección del método de solución depende de las características del modelo. Algunas de las técnicas utilizadas en la Investigación de Operaciones son: • • • • • • • • • • • • • • Programación Lineal. Árboles de decisión. Redes (Incluye PERT/CPM). Modelos de Inventarios. Econometría, pronóstico y simulación. Programación Entera. Programación Dinámica. Programación Estocástica. Programación No Lineal. Teoría de Juegos. Control óptimo. Líneas de Espera. Ecuaciones Diferenciales. Modelo de Hoja de Cálculo Electrónica. A lo largo de este curso iremos estudiando los Árboles de Decisión, Modelos de Inventario, Redes y Programación Lineal. Conclusión... Como se alcanzó a ver a lo largo del trabajo se logro tener una idea mas clara y amplia de la importancia de esta de la investigación de operaciones y sus diferentes aplicaciones dentro de lo laboral desglosando las diferentes técnicas y metodologías requeridas para poder llevar acabo dichas aplicaciones desempeñando un valor optimo y resultados favorables. REFERENCIAS BIBLIOGRAFICAS. • • • • Taha, H. A. (2004). Investigación de operaciones. Pearson Educación. Martínez López, Y., Oquendo Ferrer, H., Caballero Mota, Y., Guerra-Rodríguez, L. E., JuncoVillegas, R., Benítez Cortés, I., ... & Madera Quintana, J. (2020). Aplicación de la investigación de operaciones a la distribución de recursos relacionados con la COVID-19. Retos de la Dirección, 14(2), 86-105. Tischer, I. (2013). La investigación de operaciones en aplicaciones a sistemas productivos: Desarrollo recientes. Investigación de Operaciones I: Unidad Uno Tema 1.3 (ioi-itstb.blogspot.com)