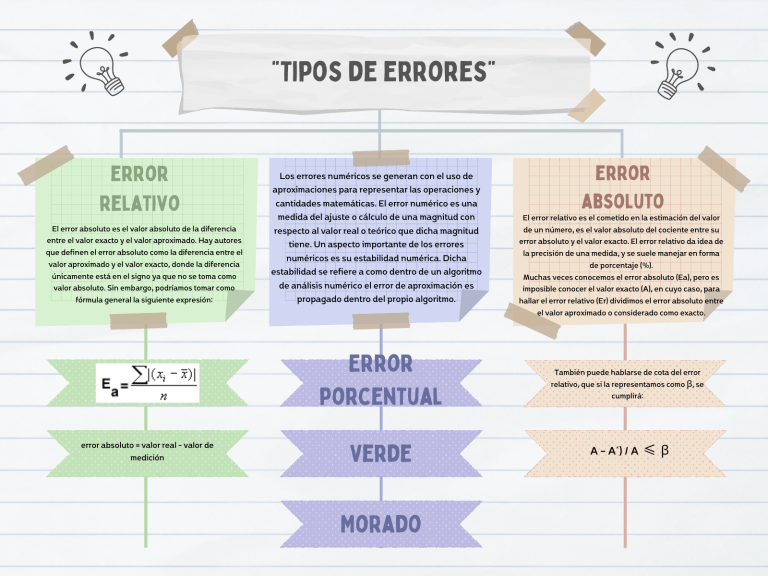
"Tipos de errores" error relativo El error absoluto es el valor absoluto de la diferencia entre el valor exacto y el valor aproximado. Hay autores que definen el error absoluto como la diferencia entre el valor aproximado y el valor exacto, donde la diferencia únicamente está en el signo ya que no se toma como valor absoluto. Sin embargo, podríamos tomar como fórmula general la siguiente expresión: Los errores numéricos se generan con el uso de aproximaciones para representar las operaciones y cantidades matemáticas. El error numérico es una medida del ajuste o cálculo de una magnitud con respecto al valor real o teórico que dicha magnitud tiene. Un aspecto importante de los errores numéricos es su estabilidad numérica. Dicha estabilidad se refiere a como dentro de un algoritmo de análisis numérico el error de aproximación es propagado dentro del propio algoritmo. Error porcentual error absoluto = valor real - valor de medición Verde Morado error absoluto El error relativo es el cometido en la estimación del valor de un número, es el valor absoluto del cociente entre su error absoluto y el valor exacto. El error relativo da idea de la precisión de una medida, y se suele manejar en forma de porcentaje (%). Muchas veces conocemos el error absoluto (Ea), pero es imposible conocer el valor exacto (A), en cuyo caso, para hallar el error relativo (Er) dividimos el error absoluto entre el valor aproximado o considerado como exacto. También puede hablarse de cota del error relativo, que si la representamos como β, se cumplirá: A – A´) / A ≤β error procentual El error porcentual es fácil de definir, es el resultado de multiplicar el error relativo por 100. ERP = ER X 100 Error de redondeo Como no es posible guardar un numero binario de longitud infinita o un numero de mas dígitos de los que posee la mantisa de la computadora que se esta empleando, se almacena sólo un numero finito de estos dígitos; como consecuencia, se comete automáticamente un pequeño error, conocido como error de redondeo, que al repetirse muchas veces puede llegar a ser considerable. Ya que la mayor parte de las computadoras tienen entre 7 y 14 cifras significativas, los errores de redondeo parecerían no ser muy importantes. Sin embargo, hay dos razones del porqué pueden resultar críticos en algunos métodos numéricos: El efecto del redondeo puede ser exagerado cuando se llevan a cabo operaciones algebraicas que emplean números muy pequeños y muy grandes al mismo tiempo. Ya que en este caso se presenta en muchos métodos numéricos, el error de redondeo puede resultar de mucha importancia. error de truncamiento Cuando una expresión matemática se remplaza por una fórmula más simple, se introduce un error, conocido como error de truncamiento. Los errores de truncamiento son aquellos que resultan al usar una aproximación en lugar de un procedimiento matemático exacto. Estos tipos de errores son evaluados con una formulación matemática: la serie de Taylor. Taylor es una formulación para predecir el valor de la función en Xi+1 en términos de la función y de sus derivadas en una vecindad del punto Xi. Siendo el término final: Rn= ((ƒ(n+1) (ξ))/(n+1)!)hn+1