PROBLEMAS DE MECÁNICA CLÁSICA
2. VECTORES
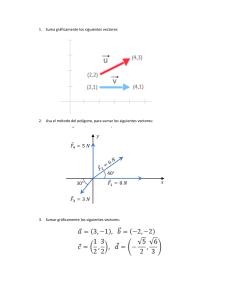
1. Dos vectores están dados por A = 3i - 2j y B
a) A + 8 y lA+ Bl
b) A- 8 y lA- 81
e) La direccion de A + B y A- B
v
o)
=- i - 4j. Calcular:
·-._..:-.._.:...._:...._,
(A+~'J=C~:-2,i)+(-Z-4j) =- ,....-..-.,.._..,.
?.Z·-bJ~}
___,.,
lA+~\~ J~ 2+ {--~ =J 4 t ;,
-) -"
bJ\ .- (A'P.>) = [ 3 Z-- 2S) - (- (. -'i
4
/A -e\::-
i4L-f 22!:!
::
~'"J
---..~
\._. -'"""---'"'- '-'--
i t
4 {) -:: 4 ; + 2
~ . . ~~
{¡+4 = 4~~
............ --..J
2. Hallar el ángulo entre los vectores A= -Si- Jj + 2k y B
4
-~
A· B
=A B ces G
~- - -
-- C. i
=- 2j- 2k
)
.....0 ...;:;¡
A~ B
-::. A.x ú::t. tA·,jiB't -t At: f1> 2.
-"-7--"9
A- B-: (-s)(.o) + (-3)(-~) +{2)(-2)::: o+(;- 4
t A1::.
ü-s} t(-3)2. t(~)'¿ -= ~ ;¡5 t ~ +L1
lB\-:..~
.,
D+l-2)2.+(-z:-,2.-:::
Su..s4ti u\\-cv1d.o
1:
~ ;2
::. 6. i b
~4+4 '~ -~ - 8"3
n L r) '1 6Í1SftJOntLo:
.~ :::.{G-i0)(.< . :.33) MS ~
1
Prof. Sergio Alvarado Alvarado
3. Dados !os vectores desplazamiento A
= 3i -
4j + 4k
y B = 2i + 3j - ?k
J
encontrar las
magnitudes de fos vectores:
a) C =A+ 8
b) D = 2A- 8
\,)
~
r?
·-7
.
•
.
... ():::~A-8 ~ ~l3c:~4J"+-4lc::)"= €-
-_ , . -: , '
i ·- g J. T" 8 \(
.r
P :: ..11 2 +c-n/·-t'sz
,
·.: :
(=<¿t3j-tt::)
,.... 2. ~ -- 3 j ..¡ :J ~ :::.
.
J;""-tl2.i.f22.5 "'::::
4; ~ ·11 J. -t- 1S k.
,---
v362::
I
'-- ..-\____ ·' -·
C!
.
~~
4. Dados los vectores A= 3i- 2j y 8 =- 4i + j, calcular:
a) El vector suma y su módulo
b) El vector diferencia y el ángulo que forma con el eje +X
e) El vector C = 2A- 38
...l
~) :- S::
"'-"'4..._........_......_...·
At B -= (3 i - zJ ) +(- 4 L-+ .n ~ -¿ -j
""'--'- ''- /'
JSI=1t +-r
2
b) .-
.:;¡
-7
--=?
2
'='
~
-~~
\r:i (
.-y.-,--r~
'--""--'-- '' -
D:? A -8 -=
{3Z -2,j)- {-4~.-+j) ~ ~~J
~ 't 2f-(_-~}-:- J4t¡ ·+ 1 =-~-..: f
1D\-=
r-v-Y'"'
-1
e-=-{d
-+=-+i (:).42-R
'1
1
\....- .'-...--- ..........\...--'
í
-=-~3·;2° t
ry---y-y"'
Prof. Sergio Alvarado Alvarado
2
5. Dados !os vectores A (2, -1, O), B (3, -2, 1) y C (0, -2, 1). Calcular:
a)(A + B}.
b) (A- 8) X
e
e
c)(A x 8). e
d) (A X 8) X e
'-\l.- (r1 L- Jt o ~<H (3i-z.i+ K)} (oí -'--.i + K) -=(:; ¡ ·3.Í +~<\·(o- z.í +~e)
'-'--''-'
= O+bJ+ ~XI::::::.. ~+}"f../';:. '+t~ 1-
I
~
(}),((
~ ~ ·-.) 1-c ~·) -e 3 z - 2J· -r ~))x e6 z- 2j· + ¡e'>
¡
A-B:: :--Z-tJ.- K
- _:::¡
(
~
\i
-7
J.
l<!.
t ·-\
-~
A-S)XC=
e
(.J :-
.....;::;>
.:.1
¡· i
j.
. . __,;'- '- '--'--·'---'---
-:::i(t-('-2.))- .)(-t-c)+~(2-o)-::3~+5-t2k_(
~" "-:-'~~
t
-2.
\(. \
A'!--fJ-;-. ~- _,
1
"
o ·::. t(-l·-e)-.)(2-c)+~(-4-C.-3)')=-i:-'2--~)o-k
3 -2
\
(-A~~J· e(-== e-~ -ZJ·- \()·(_o¿_ 2s"' \L·~::
ct') r ~m o Á y..e =- l. -2- s-- IL :
eA'/-~..:::1) "'J,C ::..
....=¡
..::¡
\i
.i
<~\
o
k: \
.-1.
_
-2
'
¡
.
.
. .
0+4j- k :::
e +4 -l
=,TI
..
:"\
:: L (- 2 -!)- J [- {~o 1 f lt-
(.
~ ~'--(>'- '-·~~
2-c J ::>-'4 L +~\ +2 il.'"'\1 ~
,...,.~ ""' ""
6. Hallar el módulo y ra dirección de A x 8 y A. 8 considerando que se tienen !os siguientes
vectores: A
4i - 7j y B 3i.- 21 :
=-
-~
=
~
A 'f..f3 :: /A 1 l €1 \
$ef>
6
~ 4 z+,_z -= ~ tf¡·t411-=- ~\
~1'\ e:: A x.B~::: _ :J. 9
:: ~== 1
lA\-:.
~
4
l~llB\
(8.o6,)(3·6)
2'
3
Prof. Sergio Alvarado Alvarado
7. Un triángulo está definido por los siguientes vértices : A (2 , 1, 3), B (2, -1 , 1} y C (0, -2 , 1).
Calcular ef área de dícho triángulo:
'.i:n ,y J;1(r:r. i
¡ lltJr~
h}q·;,¡-u. Lv
u ·n
)tn.fJ>1~J .¡.-~..ec.·
A:::.lbh
;?.,
EJJ-/c nr:_JkJ,·
fJ ~
±Jflli ;x ¡,-e¡
A~:::~-~= (~,-1, 1) -{:<
-7~
A~
~
-)
1 (,
.3) o('- t- .1· H)- (J ¿fJ. fb k:)=
~.?j -Z ~
----.. - -_____,
= ~ ·-.11
-=-(o1 .:..2 1·) ...... (·.., ¡ 3) -!. ·~ • ·) ( , .
t
-", ,.,. -LCL-2,J+k:- ~¿ +J ·f 3k)::.-2ti ..-3J..-21L
Por f o k r7 .)o:
\ ¿· u.,·
""'.;¡ ~~
AR>XI}-c:: .e - '2
-·z
·1c. \
.
_¿ ·:::
-3 -2.
I'A'P., "'j.~JTC.\ :::.1 6z. 4 z+A2'";'- ~ 4 -t/l3tf6
1
A:: _L [e,)-::-~~~~{
;;..
~--- '""~
i(4-b)-.i(o-A)+t-:lo-4)-:: ..,2Ü-t-4J~-4~
-::
\
-
v z¡;
.::. 4]
8. Usando el triple producto escalar, encontrar el volumen de un prisma rectangular definido por
los siguientes vectores: A = 3k, 8 = 4i y C = 6j.
rQ'(Q UV\
fJT ;ó 1nú. ~CrJ: ¡)l~S ~Llt ·.
'\-:: r\t{a cLt Ct. h1~ Y-.. A L.fvyz,. .
...
~~-e_::
~L
\
~vv\~nec ·¡ :
0
~
k-\~ L
t)
C'
G
t
(c))-:1 (o)+ IC-(.:24-a):::
~4
.
K
'2.
\,_./'-...'-·..._:
• \)::: [3 \C). (:¡4 JL2.) .,. 12
3
U
~
/'\.--v""f
4
Prof. Sergio Alvarado Alvarado
9. Dados los vectores A= Si +4j +6k y B= - 3i + 2j - 3k. Determinar:
a) R= A+ B, IR 1y la dirección de R
b) D=A -B, IDI y la dirección de D
e) El ángulo entre A y B
G\)
·¡_=-~ti~ (s,· +4J~+6 ~t-) +(~3[ +2j- 3 ~)-=- ;¿-:-;;¡;;:·~
~_,~~
Jl\~ {:z 2·+6 2 f3~..'--=.{4 -f3{,·tCf ='1-J
la t//rtt:cÚ:J~ cft:·
/l SC~Ti~"
f¡, ~ t ~
/OS
~
t! os ol-=.
;¡;,Jufos. rtJsft'c/o a- /c?J
fjt~
~~>L-
M if5
~7 ·~_:}~:~",~
~
ees (6 =
tos
b).--
f2.'t =.f...=
rt 1
'Ot::.1L·=
Jll
-7
..:=}
¡:).
-=~
gs t-
1-::::. e~ 428
1
-~
D= A-6-=-(S("+4J76J:.)-{-3i-t2j"~.3~)
\_.., "-- ·'---~"--"'-./ (
=8i-t2,jt<1k ~
/fJ J:: ...¡ rf:t.:i+12-' ::. -~ 6'4 ·M -t-8 ~ =/2,7~
.......,_ "\.. '\.-'-'V ··v
"'"'
'""'Y-y ....,. ......
-~
Co.s o(= lD:.
8
\......,..-''-"''......._......_..·~·
-~
ra't-:: ""/272 -
\.....--\...... '-- ' - ..__.
~
éos (3~ DI::\ :::: .L -~ 0·163
ID 1
_.. i
'
¡3=---..
&c.6r.)
...........
'..._A._-'\.._.·'-· ' -
Ces ~ ~ -~ =_j_ -:::
1 ) /2•2.
~
-~
/2.-7-
~
e),'"
;; ~_;t'-f
O. 6SS
...,
A·8~ABeos
0
,-:¡?:> 1
~=-? if:: 42-S
"l
~~-y
e
J'e c.'L.-nld..t:
A- i:: (S; +4,)+-b le). (:-3; +2J -3"') -=--!S+ S -t 8 :::._:o< SJ
2
JAt-=- -~5 + 4 2 tb 2." =1:?S+ 1b+ JC. =~.tt-J
1
....::¡.
l ~ 1~ i {-',)~+ 22. ·t(-3)2.~:: '119 +4 +q :: 4 ·1 l
A·~-:. (B·S)., (4·~) -::_41.3Cl
~~
ec~ e~ A·B _
-;;?s
A·lb - 41·~' ·::,-O.b04
~\_.-.
J e:: ;n. 18·
(
·~~-y/)'-
Prof. Sergio Alvarado Alvarado
11. Determinar el desplazamiento resultante causado por los siguientes desplazamientos:
2i +3j-3k, 3i- Sj- 2k y- 6i +2} + Bk expresándolo en términos de i, j, k, así como en términos
de su magnitud.
~
-~..,;;;."'""'
¡2_ ~ /) j- t3 f-e.
12. El vector A= 2i- Sj
+7k, si SB- 2A = 3 (A+
5/J), encontrar el vector B.
Prof. Sergio Alvarado Alvarado