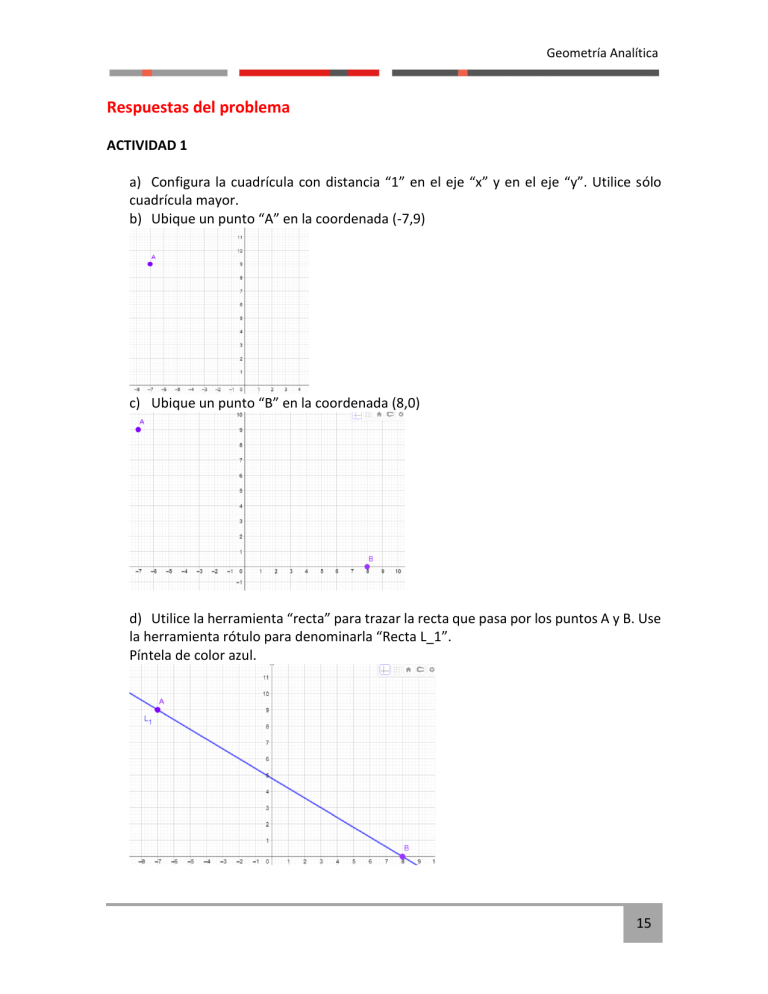
Geometría Analítica Respuestas del problema ACTIVIDAD 1 a) Configura la cuadrícula con distancia “1” en el eje “x” y en el eje “y”. Utilice sólo cuadrícula mayor. b) Ubique un punto “A” en la coordenada (-7,9) c) Ubique un punto “B” en la coordenada (8,0) d) Utilice la herramienta “recta” para trazar la recta que pasa por los puntos A y B. Use la herramienta rótulo para denominarla “Recta L_1”. Píntela de color azul. 15 Geometría Analítica e) Ubique un punto “C” en la coordenada (-9,-3) f) Ubique un punto “D” en la coordenada (9,9) g) Utilice la herramienta “recta” para trazar la recta que pasa por los puntos C y D. Use la herramienta rótulo para denominarla “Recta L_2”. Píntela de color rojo. h) Ubique el punto “P” en la intersección de las dos rectas. 16 Geometría Analítica i) Mida los cuatro ángulos en torno al punto P. ¿Qué sucede con los ángulos? Los ángulos DPA y CPB tienen igual medida (115,35°), a su vez los ángulos APC y BPD también tienen igual medida (64,65°) j) Pinte los ángulos de igual valor de un mismo color. A estos los denominaremos “ángulos opuestos por el vértice”. k) Arrastre el punto C. ¿Qué sucede con los ángulos opuestos por el vértice mientras arrastra el punto? Las medidas cambian, pero los ángulos opuestos siguen teniendo igual medida. 17 Geometría Analítica ACTIVIDAD 2 a) ¿Cuál es la ecuación que define la recta L1, entregada por GeoGebra? b) La pendiente y el coeficiente de posición de la recta L1. 𝑚 = −0,6 ; 𝑛 = 4,8 c) Determine la forma principal de la recta L1. d) Determine la forma general de la recta L1. Es importante mencionar en este punto que, a partir de la ecuación de la pregunta a, la forma general puede ser 3x+5y-24=0 y, no necesariamente la que entrega GeoGebra. El docente puede argumentar más al respecto. ACTIVIDAD 3 Siguiendo con la construcción de la actividad 1. a) Utilice la herramienta “Recta paralela” para trazar la recta que pasa por el punto B y es paralela a la Recta CD. Use la herramienta rótulo para denominarla “Recta L_3”. Píntela de color violeta. 18 Geometría Analítica b) Busque la manera de medir los cuatro ángulos en torno al punto B. c) ¿Qué sucede con los ángulos? Tienen las mismas medidas que los ángulos resultantes de la actividad anterior. d) Pinte los ángulos, manteniendo los colores para aquellos de igual valor. e) Arrastre el punto A. ¿Qué sucede con los ángulos mientras arrastra el punto? Cambian todos los ángulos, manteniéndose la igualdad de opuestos por el vértice. 19 Geometría Analítica f) Ubique un punto “H” en la coordenada (-13,4), píntelo de color naranja. f g) Ubique un punto “I” en la coordenada (2,11), píntelo de color naranja. h) Utilice la herramienta “recta” para trazar la recta que pasa por los puntos H y I. Use la herramienta rótulo para denominarla “Recta L_4”. Píntela de color verde. 20 Geometría Analítica i) Ubique el punto “Q” en la intersección de las rectas L1 y L4. j) Mida los cuatro ángulos en torno al punto Q. k) ¿Qué diferencia observa en los ángulos en torno a Q, con respecto a los observados en B y P? 21 Geometría Analítica Que, si bien todos los ángulos son opuestos por el vértice, las medidas de los ángulos del punto Q son diferentes a las obtenidas de los puntos B y P. e) Mueva el punto H hasta tener los ángulos en torno a Q igual a los observados en B y P. ACTIVIDAD 4 A partir de las construcciones anteriores: a) Deje en forma principal todas las ecuaciones de las rectas L1, L2, L3 y L4 b) Compare la pendiente de la recta L2 y L3, ¿cómo son entre ellas? Las pendiente son iguales, por lo tanto las rectas son paralelas entre sí. c) Mueva el punto A y déjelo en la coordenada (-2,15), ¿cómo son los ángulos que se forman entre las rectas L1 y L2 y entre L1 y L3? Los ángulos que se forman son perpendiculares. 22 Geometría Analítica d) ¿Cuál es el valor de la pendiente de la recta L1? 𝑚1 = −1,5 e) ¿Cuál es el valor de la pendiente de la recta L2? 𝑚2 = 0,67 f) Verifique que si dos rectas son perpendiculares el producto de sus pendientes es -1. 𝑚1 ∙ 𝑚2 = −1 −1,5 ∙ 0,67 = −1,005 El resultado es aproximadamente -1, esto ocurre por las aproximaciones de los decimales. Orientar realizar la comprobación con los valores exactos de las pendientes. 23









