Internal Friction Study of Aging Hardening and Kinetics in Low Carbon Steel

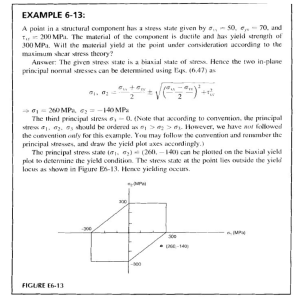
Available online at www.sciencedirect.com
Available online at www.sciencedirect.com
ScienceDirect
ScienceDirect
Procedia
Engineering 00 (2017) 000–000
Procedia Engineering 207 (2017) 645–650
www.elsevier.com/locate/procedia
International Conference on the Technology of Plasticity, ICTP 2017, 17-22 September 2017,
Cambridge, United Kingdom
Internal Friction Study of Aging Hardening and Kinetics in Low
Carbon Steel
Lin Du , Weijuan Li* , Shengshi Zhao , Shansheng Wang
School of Materials and Metallurgy, University of Science and Technology Liaoning, Anshan 114051,China
__________________________________________________________________________________________________________________
Abstract
The low carbon steel with 2% pre-strained had the strain aging treatment in different baking time at 170°C. The stress-strain
curves, bake hardening (BH) value and internal friction-temperature spectrum of tested steels were studied by tensile test and
internal friction. The Harper aging kinetic equation respectively using the parameters of BH value, yield point elongation (YPE)
or Snoek-Ke-Koster (SKK) peak height was established. The results show that with the increase of aging time, the yield point
elongation and BH value of tested steel increases, and then the stress-strain curve of the steel become from continuous yield to
discontinuous yield. In the internal friction-temperature curve, the Snoek peak height decreases, the SKK peak height
continuously increases, and peak temperature changes slightly. It indicates that the primary mechanism of age hardening is
Cottrell atmosphere hardening. The time index n in the Harper aging kinetic equation fitted by the BH value, YPE and SKK peak
height were 0.53, 0.59 and 0.59, respectively. The linear relationship of BH value and SKK peak is BH=17119•hSKK-33.
© 2017 The Authors. Published by Elsevier Ltd.
© 2017 The Authors. Published by Elsevier Ltd.
Peer-review under responsibility of the scientific committee of the International Conference on the Technology
Peer-review under responsibility of the scientific committee of the International Conference on the Technology of Plasticity.
of Plasticity.
Keywords: Kinetics of strain aging; age hardening; Cottrell atmosphere; internal friction; YPE(yield point elongation)
____________________________________________________________________________________________________________________
1. Introduction
The bake-hardening steel plate is an important material for the forming of outer panel of modern cars[1]. The
bake-hardening phenomenon is due to the Cottrell atmosphere formation and carbide precipitation in numerous
studies[2-6]. When the low carbon steels are baked at 170 °C for 20 min, carbide precipitation did not occur because
of the low carbon content[7]. So the primary hardening mechanism of steels is Cottrell atmosphere formation[8].
*Weijuan Li. Pro. Supported by the National Natural Science Foundation of China (Grant No. 51274121) Tel.: +86-412-5929528
E-mail address: [email protected]
1877-7058 © 2017 The Authors. Published by Elsevier Ltd.
Peer-review under responsibility of the scientific committee
Plasticity.
of the International Conference on the Technology of
1877-7058 © 2017 The Authors. Published by Elsevier Ltd.
Peer-review under responsibility of the scientific committee of the International Conference on the Technology of Plasticity.
10.1016/j.proeng.2017.10.1035
Lin Du et al. / Procedia Engineering 207 (2017) 645–650
646
Lin Du/ Procedia Engineering 00 (2017) 000–000
The kinetics study of the Cottrell atmosphere formation was studied initially by Cottrell and Bilby, and many
research results revealed that the time index of Cottrell atmosphere formation in the kinetic equation is 2/3[9-14].
Harper[15] further studied the aging kinetics, and proposed the kinetic equation. The relationship is following:
n
n
t
ln 1  W  
  
  kt 
 
(1)
Where W is the interstitial carbon atoms segregating to mobile dislocation in the time of t divided by and total
interstitial carbon atoms before aging, which is equal to the increase amount of yield strength divided by the
increase maximum value of yield strength(BH/BHmax). τ is the relaxation constant varying with temperature, and it
follows the relationship of Arrhenius-type. n is the time index. k=k0exp[(H/RT)], R is the gas constant, K0 is a
constant, and △H is activation energy of aging process. The n value was fitted with yield point elongation
YPE/YPEmax, which is essentially as W in the formula (1), and the n value was close to the result of fitting with
yield strength. It indicats both YPE and the change of yield strength are able to effectively reflect the formation
process of Cottrell atmosphere[16]. D.R. Mosher[17] fitted W in Harper formula with the variation of Snoek peak
height, to indicate the formation process of Cottrell atmosphere in the aging. The value of n distributes from 0.34 to
0.5, which has a large deviation from 0.66.The internal friction also has a highly sensitive for Cottrell atmosphere
formation, because interstitial carbon atoms continuously diffuse into the movable dislocations to form Cottrell
atmosphere in the aging process [18-32], which enables Snoek peak height decreased gradually and SKK peak
height(or peak temperature) changed. However, little research has been done on the Harper aging kinetic equation
using the parameters of internal friction. This paper focuses on the characterization of the aging kinetics equation
using the parameters of the Snoek-Ke-Koster (SKK) peak height, and
the microscopic phenomena of aging process and aging hardening
mechanism are also investigated.
60
50
BH/MPa
2. Experimental materials and methods
40
3. Experimental results
3.1. BH value under different aging time
After 2% pre-deformation and in different baking time at 170 ℃, the BH time curve is shown in Figure 1. As can be seen from Figure 1, BH value
with the aging time variation can be divided into two stages: t<20min, the
BH value rises rapidly to 40 MPa with the increasing of aging time; t>20min,
the growth rate slows down in the subsequent aging time and the BH value is
60MPa at 200min.
/MPa
30
The experimental materials were annealed low carbon steel and its
chemical composition (mass fraction): C 0.017%, Si 0.0076%, Mn 0.6%,
20
P 0.043%, S 0.0087%, Al 0.031%, Ti 0.015%. The samples cut from the
10
steel plate were performed the tensile testing according to the GB/T
0
228-2002 standard. The tensile testing with 2% pre-deformation was
0
50
100
150
200
carried out on a TUM5305 tensile machine at a constant strain rate of 5
t/min
mm·min-1. The aging testing was conducted in the oven at the
Fig. 1.The change of BH value with aging time
temperature of 170℃ for 0.5min-200min. The value of BH was
measured at the GB/T24147-2009 standard. The internal friction peak was
320
measured by pendulum mechanical spectroscopy under free decay mode, and
the amplitude was 30.The size of internal friction samples 50 mm x2 mm x1
mm.
300
0.5 min
1 min
2 min
5 min
8 min
15 min
20 min
100 min
200 min
280
260
1
2
 /%
3
4
Fig. 2. Stress-strain curves under different
aging time
Lin Du et al. / Procedia Engineering 207 (2017) 645–650
647
Lin Du/ Procedia Engineering 00 (2017) 000–000
YPE,%
0.03
0.02
0.01
0
50
100
t/min
150
200
Fig. 3.The change of the yield point elongation
with aging time
0.0016
350
0.0012
345
0.0008
1min
8min
20min
200min
Q-1
ultimate strength/MPa
355
340
1
10
t/min
100
0.0004
300 400 500 600 700
T/K
Fig. 5. Internal friction spectrum under
different aging time
Fig. 4. The change of tensile strength with
baking time
3.2. Stress-strain curves under different aging time
Q-1/10-4
Fig.2 shows the stress-strain curves under different aging time. The stress-strain curves are transited from
continuous yielding to discontinuous yielding with the aging time increasing. When the aging time is less than 2min,
the tested steels are under continuous yield. Moreover, if the aging time is over 2min, the tested steel under
discontinuous yield. Both the length of yield plateau and yield stress are gradually increased. There is the special
yield phenomenon at 100min and 200min. The external stress continues to increase after yield, and the yield
platform and lower yield point appear due to the large hardening and deformation. Fig.3 shows the change of yield
point elongation with different aging time. The yield point elongation is continuously growing with all the aging
time as illustrated in Fig.3. When the aging time is less than 2min, there is no yield platform in the continuous yield
process. When the aging time is from 2 min to 20min, the YPE is
increasing rapidly with the extension of aging time. While the aging
time is over 20 min, the YPE is increasing slowly and it remains stable
4 (a)
0.5 min
1 min
at 200min. The strain aging can be divided into two stages. The first
2 min
5 min
stage is mainly the formation of Cottrell atmosphere and the second
3
8 min
stage is primary the precipitation of carbon or nitride. BH value and
20 min
50 min
YPE have a similar increasing trend and the tensile strength is almost
2
100 min
unchanged. After that, the BH value is grown slowly and tensile
200 min
strength is gradually increased [32]. The curve of the tensile strength
1
with aging time is indicated in Fig.4. The tensile strength has no
significant change with the aging time increasing. According to the
0
300
400
500
behavior of BH, YPE and tensile strength, it indicates that the
T/K
formation of Cottrell atmosphere is the primary phenomenon in all
200min aging.
6 (b)
Fig.5 shows the internal friction spectrum is under different aging
time. The curve of internal friction in the spectrum shows a double
peak, and the two peaks occurred in about 320K and 500K.The formula
[34] is used to calculate every activation energy of internal friction
peak by the temperature and peak frequency. Internal friction peak at
320K is Snoek peak and at 500K is SKK peak. The internal friction
which be measured in the experiment generally consists of background
internal friction and true internal friction[35]. Background internal
friction can be attributed to grain internal process, and we use the
Q-1/10-4
3.3. Internal friction spectrum under different aging time
0.5 min
1 min
2 min
5 min
8 min
20 min
50 min
100 min
200 min
4
2
0
300
400
500
600
700
T/K
Fig. 6. Actual internal friction peak at different
aging time (a)Snoek peak (b)SKK peak
648
Lin Du et al. / Procedia Engineering 207 (2017) 645–650
Lin Du/ Procedia Engineering 00 (2017) 000–000
Damping Gauss software to have the exponential fitting of internal friction temperature curve, and
deduct
background internal friction according to the index law. Fig.6 is the true internal friction peak spectrum. It can be
attained by the deduction of background internal friction from Figure 5. Snoek peak height is continuously
decreasing with increasing time. That means interstitial carbon atoms continue to move away from the interstitial
site during aging process. Fig.6(b) is the true SKK peak. With increasing time from 0.5min to 200min, SKK peak
height gradually increases, while the peak temperature changes slightly. SKK peak height is proportional to pinned
dislocation density and pinned dislocation line length. [22] According to the analysis of 3.2 section, the
strengthening mechanism of aging process is mainly Cottrell atmosphere strengthening, and there is not too much
carbide precipitation at dislocation. The length of pinned movable dislocation line changes marginally [36], and the
rising of SKK peak height shows that the density of mobile dislocation is increasing. Table 2 shows that the
activation energy of SKK peak has not changed greatly with the aging time increase. The concentration of carbon
atoms segregated at the movable dislocations influences easily the activation energy. That means concentration do
not changed too much with the increase of aging time. Therefore, the Cottrell atmosphere continuously forms and
the number of it is increasing, the average concentration of carbon or the density of atmosphere at movable
dislocations doesn’t vary significantly.
4. Results analysis and discussion
4.1. Aging kinetics fitting of Harper model
ln(-ln(1-w))
BH/BHmax and YPE/YPEmax were used as W (after this, all W were derived from formula 1), and the
coordinate system was drawn (lnt as horizontal coordinate and ln(-ln(1-w)) as vertical coordinate) as shown in the
Fig.7. The time index n are 0.53 and 0.59 respectively, which are slightly larger than other experimental value of
0.5[15]. The Harper aging kinetic equation respectively using the parameters of BH value and yield point elongation
(YPE) was established, and then the fitting value of n was the almost same. That means the Cottrell atmosphere
formation process can be explained well through the W which is coming from yield strength variation and yield
point elongation[37].The interstitial carbon atoms, which had not time to diffuse during the aging process, still
diffused to dislocation in the increasing-temperature measurement of internal friction. Therefore, the aging time of
SKK internal friction peak formed was composed of the original aging time
and SKK internal friction measurement time. It was assumed that carbon
1 (a)
atoms begin to diffuse at 150℃ and stopped at 240℃. Carbon atoms
y=0.53x-1.4
diffusion time can be calculated (240-150) /3=30min during the
0
measurement, where 3 is the heating rate in the measurement. The Harper
aging kinetic equation using the parameters of SKK peak height was
established. The relationship curve is shown in Fig.8. It can be seen that
-1
fitting time index n is 0.59. In the comparison of BH/BHmax、YPE/YPEmax
and hSKK/hSKKmax, the different time index n are close. It indicates that the
-2
variations of SKK peak height can also fully describe Cottrell atmosphere
0
2
4
lnt
formation.
4.2. Age hardening mechanism of low carbon steel
ln(-ln(1-w))
As can be seen from three above aging kinetics Harper equations
(Figure7, Figure8), the corresponding time index n are 0.53, 0.59 and 0.59
respectively, and the values are similar. It means the change rules of BH
value, YPE and SKK peak height are similar with the variation of aging
time. All of them are able to characterize the aging degree. BH value is the
added value of overcoming the resistance when a small amount of
dislocation movement causes plastic deformation. YPE is the plastic
enhancement which be caused by mobile dislocation movement in Cottrell
atmosphere. SKK peak height is relevant to formation quantity of
atmosphere and the density of pinned dislocation. Interstitial carbon atoms
1
(b)
y=0.59x-1.99
0
-1
2
3
lnt
4
5
Fig. 7. Fitting results of Harper model
(a) BH/BHmax (b) YPE/YPEmax
Lin Du et al. / Procedia Engineering 207 (2017) 645–650
649
Lin Du/ Procedia Engineering 00 (2017) 000–000
ln(-ln(1-w))
1.2
0.8
0.4
3.6
4.0 lnt 4.4
4.8
Fig. 8. Fitting results of Harper model
(hSKK/hSKKmax)
0.0006
0.0004
40
BH Value/MPa
60
Fig. 9. The relationship between BH
value and SKK peak height
60
BH Value/MPa
5. Conclusion
(1) For 2% pre-deformation low carbon steel, it is the formation stage of
Cottrell atmosphere in 200min baking time. BH value and YPE are
increased with the formation of Cottrell atmosphere.
(2) The BH value, YPE and SKK peak height are applied to fit Harper
aging kinetics equation respectively and the corresponding time index n is
0.53, 0.59 and 0.59. The SKK peak height can explain the formation of
Cottrell atmosphere well like BH value and YPE.
(3) BH value and SKK peak height have a linear relationship, whose
relationship can be expressed BH=17119•hSKK-33
y=0.59x-1.82
hSKK/Q-1
continuously segregate at the movable dislocations to form Cottrell
atmosphere during the aging process, and the increasing of Cottrell
atmosphere number results in the increasing of SKK peak height.. After
aging process, mobile dislocation needs to overcome the large pinning
resistance to move, which makes the material yield. Because of the higher
density of pinning dislocation, the more amount of Cottrell atmosphere, the
higher overcome resistance is required, and the BH value is higher. A
small amount of movable dislocation will bring the change of stress field
around the dislocation, and enable the nearby pinned dislocation to move.
It can cause the plastic increase, and the YPE is rising. Fig.9 is the
relationship figure of BH value and SKK peak height. BH value and SKK
peak have a linear relationship at any aging time in the formation process
of Cottrell atmosphere. The relationship can be expressed as
BH=17119•hSKK-33.The relationship of BH value and YPE is shown in
Figure10. BH value and YPE is linear relationship when YPE is lower, and
BH value is slowly rising when YPE is increasing. When aging time is
short, the quantity of Cottrell atmosphere is less BH value and YPE both
are determined by pinned moveable dislocation density in the aging
process, which enables the relationship of two values is in a linear
relationship. When the aging time is long, the quantity of Cottrell
atmosphere is more and pinned moveable dislocation density is higher. A
large number of dislocations move out of pinning in the re-tensile
deformation after aging process, which makes YPE increase. At the same
time, the dislocation movement resistance is decreasing rapidly (100min
and 200min in Figure2), due to off-pin, the BH value decreased, resulting
in the value of BH increases slowly with the increase of YPE.
40
20
0
0.00
0.01 0.02
YPE,%
0.03
Fig. 10.The relationship between BH
value and YPE
References
[1]Kang Y L, Chen J P and Liu G P. China Metall,2008; 18: 14
[2]De A K, VandeputteS,and De Cooman B C. J Mater Eng Perform, 2001; 10(5): 567
[3]S. Berbenni, V. Favier, X. Lemoine, M. Berveiller. A micromechanical approach to model the bake ardening effectfor low carbon steels[J].
ScriptaMaterialia, 2004,51: 303-308
[4]J.Z. ZHAO, A.K. DE, B.C. De COOMAN. Formation of the Cottrell Atmosphere during Strain Agingof Bake-Hardenable Steels.
metallurgical and materials transactions a, volume 32a, february 2001, 417-423
[5]A.K. De, S. Vandeputte, B.C. De Cooman. Kinetics of Strain Aging in Bake Hardening Ultra LowCarbon Steel-a Comparison with Low
Carbon Steel[J]. Journal of Materials Engineering and Performance, 2001, 10(5): 567–575
[6]Cottrell A H, Bilby B A. Proc Phys Soc, 1949; A62: 49-62.
[7]De Cooman C. World Iron Steel, 2003, 1: 39
[8]Li D S, Li X F and Zhou X B. Met Form Techonl, 2001; 19(2): 14
[9]Cui Y, Ma J H and Zhang R H. stable control about the bake hardening ability of Ultra-low carbon bake hardening steel, Beijing:
Metallurgical Industry Press, 2014
650
Lin Du et al. / Procedia Engineering 207 (2017) 645–650
Lin Du/ Procedia Engineering 00 (2017) 000–000
[10]Leslie W C. Acta Metall, 1961; 9: 1004
[11]Doremus R H. Trans AIME, 1960; 218:596-605.
[12]Neife S I, Pink E, and Stuüwe H P. ScriptaMetall Mater, 1994;30:361
[13]Buono V T L, Andrade M S, and Gonzalez B M.Metall Trans A,1998;29A:1415
[14]Bullough R and Newman R C. Proc R Soc, 1959; A249: 427
[15]Harper S. Phys Rev, 1951; 83: 709-12.
[16]Rashid M S.Metall Trans, 1976; 7A: 497
[17]Mosher D R, Diercks D R, and Wert C A. Metall Trans, 1972; 3: 3077
[18]Ji J W, Liu F D, Wang D J, Che Y Y, Hua Q Z, Liu J M and Huang Z R. ActaMetall Sin, 1999; 35: 913
[19]Magalas L B. Defect Diffus Forum, 2001; 194-199: 115
[20]Magalas L B. J Phys IV, 1996; 6: 163
[21]Magalas L B and Ngai K L. In: Wolfenden A and Kinra V K, M3D Ⅲ: Mechanics and Mechanisms of Material2Damping. West
Conshohocken: ASTP 1304,1997: 189
[22]Nowick. Anelastic relaxation in crystalline solids, New York: Academic Press, 1972: 401
[23]G. Schoeck, Friccioninternadebido a la interaction entredislocaciones y atomossolutos, ActaMetallurgica11, 617-622(1963).
[24]L.B. Magalas, J.F. Dufresne, P. Moser, The Snoek-Kösterrelaxation in iron, J. de Phys. 42, 127-132 (1981).
[25]G. Schoeck, The cold work peak, Scripta Metall. 16, 233-239(1982).
[26]Seeger, The kink-pair-formation theory of the Snoek-Kösterrelaxation, Scripta Metall. 16, 241-247 (1982).
[27]G. Schoeck, On the mechanism of the Snoek-Koesterrelaxation, Scripta Metall. 22, 389-394 (1988).
[28]Seeger, A theory of the Snoek-Köster relaxation (cold-workpeak) in metals, phys. stat. sol. (a) 55, 457-468 (1979).
[29]K.L. Ngai, Y.N. Wang, L.B. Magalas, Theoretical basis andgeneral applicability of the coupling model to relaxations incoupled systems, J.
Alloy Compd. 211/212, 327-332 (1994).
[30]L.B. Magalas, The Snoek-Köster relaxation. New insights ‒New paradigms, J. de Phys. IV, 6, 163-172 (1996).
[31]L.B. Magalas, Diffusion in the Cottrell atmosphere, Defect andDiffusion Forum 194-199, 115-120 (2001).
[32]D.V. Wilson and B. Russell: Acta Metall., 1960, vol. 8, pp. 36-45.
[33]Xu W C and Xu W X. PICT(Part A: Physical Testing), 2004; 40(30): 114
[34]Weller M. Mater Sci Eng, 2006; 442(1): 23
[35]Gao Y J, Shi W，Chen C. Shanghai Metals, 2010; 32(2): 50
[36]Ji J W and Yu N. Prog Phys, 2006; 26: 296
[37]M. S. Rashid. Strain aging kinetics of vanadium or titanium strengthened high-strength low-alloy steels.Metallurgical Transactions A, 1976,
Volume 7(4), pp 497–503