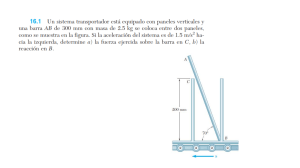
27-5-2020 Cinemática de cuerpos rígidos en movimientos planos. Resumen Edwin Sánchez ING. MECANICA - 4B1 INSTITUTO TECNOLÓGICO DE SALINA CRUZ MATERIA: DINAMICA CARRERA: INGENIERÍA MECÁNICA SEMESTRE: IV GRUPO: B1 NOMBRE DEL TRABAJO: RESUMEN ANALÍTICO DEL MOVIMIENTO PLANO DE UN CUERPO RÍGIDO. ALUMNO: SANCHEZ PEREZ EDWIN DOCENTE: ING. PONDIGO MENDOZA JORGE SALINA CRUZ OAXACA A 27 DE MAYO DE 2020 INDICE Contenido Introduccion........................................................................................................... 4 cinematica de cuerpos rigidos en movimientos planos .................................... 5 4.1. Ecuaciones de movimiento de un cuerpo rígido ......................................... 5 4.2. Movimiento angular de un cuerpo rígido en el plano.................................. 6 4.3. Movimiento plano de un cuerpo ................................................................... 7 4.4. Principio del trabajo y energía ...................................................................... 9 conclusion ........................................................................................................... 11 bibliografia ........................................................................................................... 12 INTRODUCCION Durante el trascurso de esta información demostrara el movimiento plano que presenta un cuerpo rígido. Con la ayuda de la información planteada se podrá identificar el comportamiento del movimiento de las partículas e identificar las ecuaciones para su respectivo movimiento. El presente trabajo tiene el objetivo de que el estudiante pueda comprender por medio de la lectura y análisis del tema 4 “Cinemática de cuerpos rígidos en movimientos planos” de la clase de Dinámica. En la que se debe de analizar las relaciones que existen entre las fuerzas que actúan sobre un cuerpo rígido, su efecto sobre la forma y masa, asi también sobre el movimiento que provoca. Este resumen explicara de la manera más breve la información siento este un resumen para asi lograr la comprensión de tema, además que obliga al estudiante, a investigar en otras fuentes para enriquecer aún más su conocimiento. Además, que constara con ayudas visuales (imágenes), en las que el lector pueda comprender mejor la información planteada o explicada. Este contenido fue desarrollado con el apoyo de un libro de texto en específico que lleva por nombre: “Mecánica vectorial para ingenieros: DINAMICA”, novena edición de BERR JHONSTON, en el capítulo 16 y 17, asi mismo se consultó en páginas web bajo previo análisis de estas; con la intención de evitar una confusión de información. En el proceso de aprendizaje del tema 4, el estudiante conocerá y comprenderá el movimiento plano de un cuerpo rígido, siendo que este tipo de movimiento se agrupan en 3 tipos. A. Traslación B. Rotación alrededor de un eje fijo C. Movimiento plano general Además de determinar las formulas para cada uno de estos movimientos, ya sea mediante el análisis de fuerzas y aceleraciones o por el método de la energía, asi como también conocer sus relaciones entre las fuerzas, su efecto que provoca según la forma del cuerpo, como su masa que este presenta. Se espera que este trabajo desarrollado reúna toda la información necesaria, para lograr la compresión del tema, ya que el mismo será de mucha ayuda en situaciones futuras, como, por ejemplo; cuando se vea la resolución de un problema, de un cuerpo rígido que se encuentra en movimiento plano, lograr identificar el tipo de movimiento y utilizar las ecuaciones correctas y asi hallar a la solución. 4 CINEMATICA DE CUERPOS RIGIDOS EN MOVIMIENTOS PLANOS El movimiento plano de un cuerpo rígido ocurre cuando todas sus partículas se desplazan a lo largo de trayectorias equidistantes de un plano fijo. Existen tres tipos de movimiento plano de un cuerpo rígido • • Traslación Rotación alrededor de un eje fijo • Movimiento plano general En la cual hablaremos más adelante. Continuamos con el contenido temático… 4.1. Ecuaciones de movimiento de un cuerpo rígido Considere un cuerpo rígido sobre el que actúan varias fuerzas externas F1, F2, F3. Considerando el movimiento del centro de masa G del cuerpo con respecto al sistema de referencia newtoniano Oxyz, la ecuación se escribe. ∑ 𝐹 = 𝑚ā 1 Donde: m es la masa del cuerpo ā es la aceleración del centro de masa G. Ahora considerando al movimiento del cuerpo relativo al sistema de referencia centroidal 𝐺𝑥´𝑦´𝑧´ la ecuación, se escribe. ∑ 𝑀𝐺 = 𝐻′𝐺 2 donde 𝐻′𝐺 representa la razón de cambio 𝐻𝐺 En lo subsecuente, 𝐻𝐺 hará referencia simplemente a la “cantidad de movimiento angular del cuerpo rígido en torno a su centro de masa G”. Las ecuaciones (1) y (2) expresa que el sistema de fuerzas externas es equipolente al sistema consistente. Entre el vector 𝑚ā y al par de momento 𝐻′𝐺. 5 4.2. Movimiento Angular de un cuerpo rígido en el plano Considere una placa rígida en movimiento plano. Suponiendo que la placa está integrada por un gran número n de partículas 𝑃𝑖 de masa 𝛥𝑚𝑖. La cantidad de movimiento angular 𝐻𝐺 puede calcularse considerando los momentos alrededor de G de las cantidades de movimiento de las partículas de la placa en su movimiento con respecto al sistema de referencia 𝐺𝑥´𝑦, y se escribe. 𝑛 𝐻𝐺 = ∑(𝑟´𝑖 𝛸 𝑣´𝑖 𝛥𝑚𝑖) 3 𝑖=1 Donde: 𝑟´𝑖 𝑦 𝑣´𝑖 𝛥𝑚𝑖 denotan, respectivamente, el vector de posición y la cantidad de movimiento lineal de la partícula 𝑃𝑖 En vista de que la partícula pertenece a la placa, se tiene que 𝑣´𝑖 = 𝜔 𝛸 𝑟´𝑖 Donde: ω es la velocidad angular de la placa en el instante considerado. Se escribe 𝑛 𝐻𝐺 = ∑[𝑟´𝑖 𝛸 (𝜔 𝛸 𝑟´𝑖) 𝛥𝑚𝑖] 4 𝑖=1 En la figura anterior se representa un vector de la misma dirección que ω y de 2 𝛥𝑚𝑖. magnitud igual a 𝜔 ∑ 𝑟´ 𝑖 6 Recordando que la suma ∑ 𝑟´𝑖 2 𝛥𝑚𝑖 representa el momento de inercia I, se concluye que la cantidad de movimiento angular 𝐻𝐺 de la placa en torno a su centro de masa es. 𝐻𝐺=Ī 𝜔 5 𝐻´𝐺=Ī ώ = Ī 𝛼 6 Al diferenciar se obtiene. En consecuencia, la razón de cambio de la cantidad de movimiento angular de la placa se representa mediante un vector de la misma dirección que α y de magnitud Ī 𝜶. 4.3. Movimiento plano de un cuerpo Considere una placa rígida de masa m que se mueve bajo la acción de varias fuerzas externas F1, F2, F3. Al sistituir 𝐻´𝐺 de la ecuacion 6 en la ecuacion 2, se tiene. ∑ 𝐹𝑥 = 𝑚ā𝑥 ∑ 𝐹𝑦 = 𝑚ā𝑦 ∑ 𝑀𝐺 = Ī 𝛼 Las ecuaciones (7) muestran que la aceleración del centro de masa G de la placa y su aceleración angular α se obtienen fácilmente una vez que se ha determinado la resultante de las fuerzas externas y su momento resultante alrededor de G. Puesto que el movimiento de un cuerpo rígido depende sólo de la resultante y del momento resultante de las fuerzas externas que actúan sobre él, se concluye que dos sistemas de fuerzas que son equipolentes son equivalentes; es decir tienen exactamente el mismo efecto sobre un cuerpo rígido dado. En consecuencia, es posible establecer que. “las fuerzas externas que actúan sobre un cuerpo rígido son equivalentes a las fuerzas efectivas de las diferentes partículas que lo constituyen”. “Principio de d’Alembert” 7 7 A. Traslación En el caso de un cuerpo en traslación, la aceleración angular del mismo es idénticamente igual a cero y sus fuerzas efectivas se reducen al vector 𝒎ā fijo en G. Las ecuaciones para un movimiento plano cualquiera se reduce a: ∑ 𝐹𝑥 = 𝑚ā𝐺𝑥 ∑ 𝐹𝑦 = 𝑚ā𝐺𝑦 ∑ 𝑀𝐺𝑍 = 0 B. Rotación alrededor de un eje fijo Cuando una placa o, más generalmente, un cuerpo simétrico con respecto al plano de referencia gira alrededor de un eje fijo perpendicular al plano de referencia y pasa por su centro de masa G, se afirma que el cuerpo está en rotación centroidal. Las ecuaciones para este movimiento son: ∑ 𝐹𝑥 = 𝑚ā𝐺𝑥 = 0 ∑ 𝐹𝑦 = 𝑚ā𝐺𝑦 = 0 ∑ 𝑀𝐺𝑍 = Ī𝐺𝑧 𝛼 C. Movimiento plano general Para esta ecuación podemos visualizar un cuerpo rígido como se presenta en la siguiente imagen en donde es sometido a un plano general, podemos asociar las ecuaciones anteriores, el cual determinamos que las ecuaciones que representan el plano general es la siguiente manera: Las ecuaciones para este movimiento son: ∑ 𝐹𝑥 = 𝑚(𝑎𝐺)𝑥 ∑ 𝐹𝑦 = 𝑚(𝑎𝐺)𝑦 8 ∑ 𝑀𝐺 = Ī𝐺 𝛼 4.4. Principio del trabajo y energía El principio del trabajo y la energía se utilizará ahora para analizar el movimiento plano de cuerpos rígidos. Su ventaja principal radica en el hecho de que son cantidades escalares. Para aplicar el principio del trabajo y la energía en el análisis del movimiento de un cuerpo rígido, se supondrá otra vez que el cuerpo rígido está compuesto por un gran número n de partículas de masa 𝜟𝒎𝒊, la ecuación se escribe. 𝑇1+ 𝑈1→2 = 𝑇2 Donde 𝑇1, 𝑇1 = valores inicial y final de la energía cinética total de las partículas que forman al cuerpo rígido 𝑈1→2 = trabajo de todas las fuerzas que actúan sobre las diversas partículas del cuerpo La energía cinética total 𝑛 1 𝑇 = ∑ 𝛥𝑚𝑖𝑣𝑖2 2 𝑖=1 se obtiene al sumar cantidades escalares positivas La expresión 𝑈1→2 representa el trabajo de todas las fuerzas externas e internas que actúan sobre las distintas partículas del cuerpo. Sin embargo, el trabajo total de las fuerzas internas que mantienen unidas las partículas de un cuerpo rígido es cero. Considere dos partículas A y B de un cuerpo rígido y las dos fuerzas iguales y opuestas F y - F que se ejercen entre sí Mientras los pequeños desplazamientos dr y dr´ de las partículas son diferentes, las componentes de estos desplazamientos a lo largo de AB deben ser iguales; de otra forma, las partículas no permanecerían a la misma distancia una de otra y el cuerpo no sería rígido. Entonces la expresión 𝑈1→2 se reduce al “trabajo de las fuerzas externas” que actúan sobre el cuerpo durante el desplazamiento considerado. 9 El trabajo de una fuerza F durante un desplazamiento de su punto de aplicación desde 𝐴1 hasta 𝐴2 es 𝐴2 𝑈1→2 = ∫ 𝐹 ∙ 𝑑𝑟 𝐴1 O 𝑆2 𝑈1→2 = ∫ (𝐹 cos 𝛼) 𝑑𝑠 𝑆1 Donde F es la magnitud de la fuerza α es el ángulo que forma con la dirección de movimiento de su punto de aplicación A s es la variable de integración que mide la distancia recorrida por A a lo largo de su trayectoria. 10 CONCLUSION La siguiente descripción de este trabajo da a conocer la formulación de esta, mediante el análisis de información que pudimos recopilar para lograr hacer el proyecto de manera breve y que sea agradable al momento de leerla En el que abordamos puntos claves e importantes del tema de “cinemática de cuerpos rígidos en movimientos planos”, en donde estudiaremos las ecuaciones de los mismo, y clasificarlos en tres ecuaciones de los movimientos básicos entre ellos tenemos que son. A. Traslación B. Rotación alrededor de un eje fijo C. Movimiento plano general En donde nos preguntamos ¿Por qué es importante identificar cada tipo de movimiento plano?, ¿será que existe un inconveniente si no se analiza bien? El objetivo de saber identificar cada tipo de movimiento es que nos será más fácil determinar las ecuaciones del movimiento de un cuerpo rígido, además que si se nos llegara a presentar algunos ejercicios poder saber con facilidad algunos datos que posiblemente no se presentaran en el texto, como por ejemplo esta el caso del movimiento traslacional, que se dice que no hay un movimiento angular (w = a = 0); por tanto, todas las partes del cuerpo tienen la misma aceleración lineal a. En el caso del movimiento de rotación alrededor de un eje fijo, puesto que la aceleración ā es idénticamente igual a cero, las fuerzas efectivas del cuerpo se reducen al par Īα. En un movimiento plano general podemos decir que es una combinación de traslación y rotación por lo que si asociamos las ecuaciones de A y B, podremos determinar las ecuaciones de este tipo de movimiento. Ahora para finalizar debemos recalcar que estos temas están enfocados únicamente al movimiento plano de cuerpos rígidos, esto es, a un movimiento en el que cada partícula permanece a una distancia constante de un plano de referencia fijo, y se supondrá que los cuerpos rígidos estarán compuestos sólo por las placas planas y los cuerpos que son simétricos con respecto al plano de referencia. Por lo que no se aplican en el caso de cuerpos no simétricos o en el caso de movimiento tridimensional, dado que esos puntos de hablaran en otros capítulos. Por lo que espero que esta información sea suficiente para poder cumplir el objetivo y propósito mencionados el principio de este trabajo, ya que se tiene considerado un proyecto aún mucho mayor en donde se expresara detalladamente la metodología de problemas del movimiento plano de un cuerpo rígido. Por mi parte esto es todo muchas gracias. 11 BIBLIOGRAFIA https://sites.google.com/site/dinamicadelarotacion/ecuaciones-del-movimiento-deun-cuerpo-rigido file:///C:/Users/edwin/Documents/dinamica/dinam.pdf Del libro dinámica beer Johnston 9 edición https://es.slideshare.net/marcorah/cinemtica-plana-de-un-cuerpo-rgido 12