Examen de Mecánica – 18 de febrero de 2010

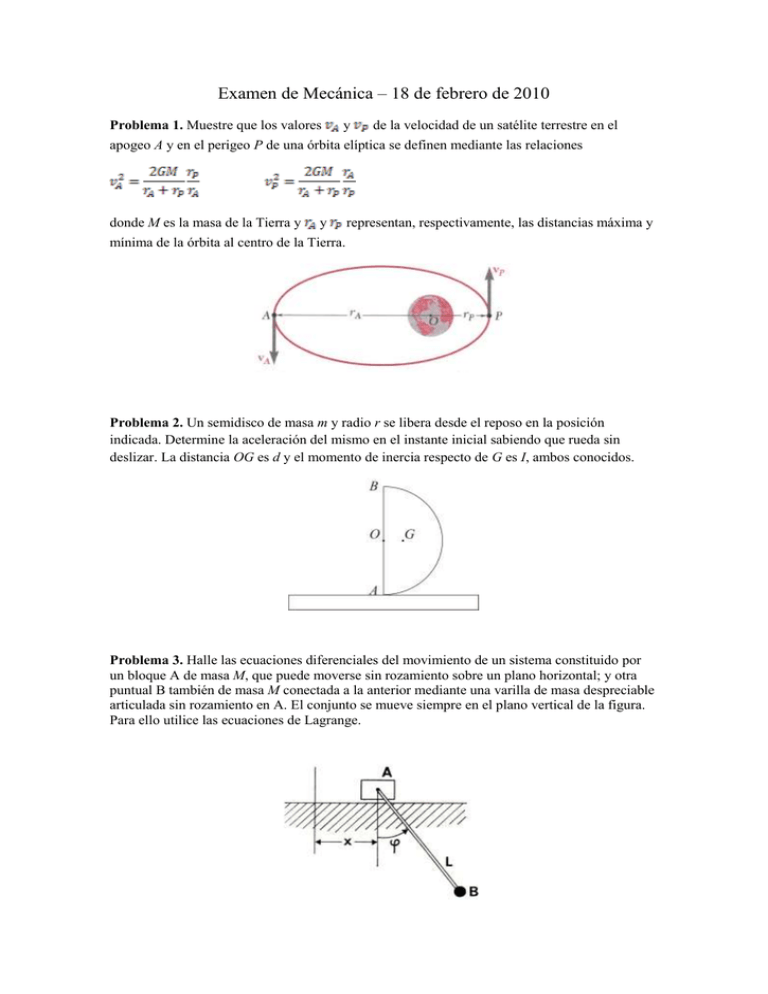
Examen de Mecánica – 18 de febrero de 2010
Problema 1. Muestre que los valores
y
de la velocidad de un satélite terrestre en el
apogeo A y en el perigeo P de una órbita elíptica se definen mediante las relaciones
donde M es la masa de la Tierra y y representan, respectivamente, las distancias máxima y
mínima de la órbita al centro de la Tierra.
Problema 2. Un semidisco de masa m y radio r se libera desde el reposo en la posición
indicada. Determine la aceleración del mismo en el instante inicial sabiendo que rueda sin
deslizar. La distancia OG es d y el momento de inercia respecto de G es I, ambos conocidos.
Problema 3. Halle las ecuaciones diferenciales del movimiento de un sistema constituido por
un bloque A de masa M, que puede moverse sin rozamiento sobre un plano horizontal; y otra
puntual B también de masa M conectada a la anterior mediante una varilla de masa despreciable
articulada sin rozamiento en A. El conjunto se mueve siempre en el plano vertical de la figura.
Para ello utilice las ecuaciones de Lagrange.
Fórmulas útiles
Movimiento circular: velocidad, aceleración centrípeta y aceleración tangencial
Ley del movimiento de Newton, energía cinética de una partícula y trabajo de una fuerza
Cantidad de movimiento y momento angular de una partícula. Cantidad de movimiento de un
sistema de partículas. Fuerza de fricción estática y dinámica
Torque respecto de un punto O de una fuerza F aplicada en un punto P
Energía potencial gravitatoria y elástica
Movimiento del centro de masa de un sistema de partículas. Variación del momento angular de
un sistema de partículas
Momento angular de un rígido respecto de un punto O solidario al mismo (G centro de masa del
rígido). IO momento de inercia en O.
Distribución de velocidades y aceleraciones de un rígido. Derivada de un vector unitario u
Fuerzas centrales: radio vector r, momento angular por unidad de masa l, tiempo t entre dos
puntos de una trayectoria y energía potencial gravitatoria
Geometría de la elipse: semieje mayor a, semieje menor b y área A