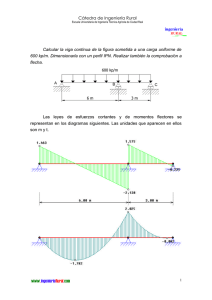
En la viga de la figura se pide :
Anuncio
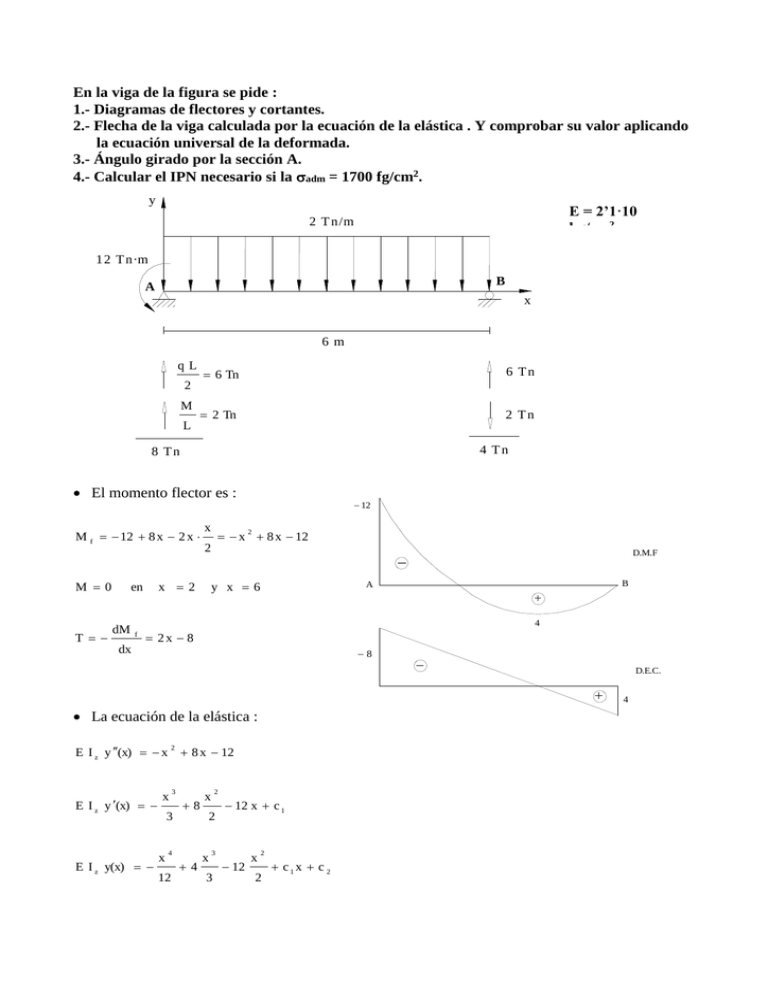
En la viga de la figura se pide : 1.- Diagramas de flectores y cortantes. 2.- Flecha de la viga calculada por la ecuación de la elástica . Y comprobar su valor aplicando la ecuación universal de la deformada. 3.- Ángulo girado por la sección A. 4.- Calcular el IPN necesario si la adm = 1700 fg/cm2. y E = 2’1·10 kg/cm2 2 T n/m 12 T n·m B A x 6m qL 6 Tn 6 Tn 2 Tn 2 Tn 2 M L 4 Tn 8 Tn El momento flector es : M f 12 8 x 2 x M 0 T x 8 x 12 2 2 x 2 en dM x 12 D.M.F y x 6 B A 4 f 2x 8 dx 8 D.E.C. La ecuación de la elástica : E I z y (x) x 8 x 12 2 E I z y (x) E I z y(x) x 3 8 3 x 2 4 12 2 x 4 x 12 x c 1 3 3 12 x 2 2 c1x c 2 4 En y(0) = 0 c2 = 0 y(6) = 0 108 + 288 216 + c1·6 = 0 c1 = 6 La ecuación de la elástica queda finalmente : E I z y(x) 4 x 4 12 x 6 x 6x 3 2 3 Para hallar la flecha tenemos que calcular donde se anula la ecuación y’ : y (x) ( x) 3 x 8 3 x 2 2 12 x c 1 0 Obtenemos tanteando 3 resultados : x10’62 m x2’83 m x37’54 m No sirve, se sale de viga. Suponiendo que en el segundo se produzca la flecha máxima tenemos : y(3'83) 8 '056 E Iz Hacemos ahora la comprobación mediante la ecuación universal : E I z y(x) E I z o (x) x E I z y o (x) En x = 6 2(x 0 ) 24 4 8(x 0 ) 6 yo(x) = 0 y(x) = 0 Entonces : E I z o (x) 6 E I z y(x) x 4 12 4 x 6 x 6x 3 2 3 El ángulo girado por el punto A será : A o (x ) 6 E Iz La flecha sale igual. 3 12(x 0 ) 2 2 1 Dimensionamos la viga según un IPN : M f max max Wz 12 10 10 3 Wz adm adm 1700 kg cm 2 2 705 '88 cm 3 1700 El IPN mayor siguiente es Wz = 782 cm3 que es IPN 320, que tiene un Iz = 12510 cm4. Entonces la flecha quedaría : f y(3'83) 8 '056 0 '3 cm E Iz Y un giro del punto A de : A 6 2 '28 10 3 rad 0'13 E Iz La viga quedaría tal que : A 0'13 0 '3 0 '62 3 '83