Edición
2ª Edición
Análisis Evolutivo
(d)
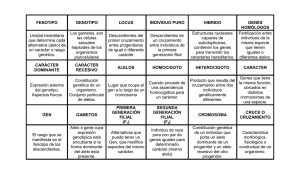
70
# Número de flores
por inflorescencia
60
50
mx
int
40
1a T1 T2 T3 A1 A2 A3 A4 A5
A6
A8
A7
30
20
3'
10
S
M
L
5'
lab
pb
Dfd Scr
Grupo Antennapedia
Antp
Ubx abdA AdbB
Grupo Bithorax
0
50
100
150
200
Área de los sépalos petalizados (mm2)
eeman
Scott Freeman
Jon C. Herron
Análisis Evolutivo
Segunda edición
Datos de catalogación bibliográfica
Freeman, S. y Herron, J. C.
Análisis Evolutivo
PEARSON EDUCACIÓN, S. A., Madrid, 2002
ISBN: 978-84-832-2774-9
Materia: Genética 525.
Formato: 215 ⫻ 270
Páginas: 720
Todos los derechos reservados.
Queda prohibida, salvo excepción prevista en la ley,
cualquier forma de reproducción, distribución,
comunicación pública y transformación de esta obra
sin contar con autorización de los titulares de propiedad
intelectual. La infracción de los derechos mencionados
puede ser constitutiva de delito contra la propiedad
intelectual (arts. 270 y sgts. del Código Penal).
DERECHOS RESERVADOS
© 2002 PEARSON EDUCACIÓN, S. A.
Núñez de Balboa, 120
28006 Madrid
PRENTICE HALL es un sello editorial autorizado de PEARSON EDUCACIÓN
Freeman, S. y Herron, J. C.
Análisis Evolutivo
ISBN: 84-205-3390-4
Depósito Legal: MTraducido de:
Evolutionary Analysis. Second edition.
Copyright © 2001, por Scott Freeman y Jon C. Herron
Published by Prentice Hall, Inc.
ISBN: 0-13-017291-X
Edición en español:
Equipo editorial:
Editora: Isabel Capella
Técnico editorial: Marta Caicoya
Equipo de producción:
Director: José Antonio Clares
Técnico: José Antonio Hernán
Equipo de diseño:
Equipo de diseño de Pearson Educación, S. A.
Composición: COPIBOOK, S. L.
Impreso por:
IMPRESO EN ESPAÑA - PRINTED IN SPAIN
Este libro ha sido impreso con papel y tintas ecológicos.
Análisis Evolutivo
Segunda edición
Scott Freeman
University of Washington
Jon C. Herron
University of Washington
Traducción
Dr. José Luis Ménsua Fernández
Catedrático de Genética
Dr. Santiago Elena Fito
Profesor Titular de Genética de Poblaciones
Universitat de València
Madrid • México • Santafé de Bogotá • Buenos Aires • Caracas • Lima
Montevideo • San Juan • San José • Santiago • São Paulo • White Plains
Resumen del contenido
PARTE I
INTRODUCCIÓN
1 Un caso para pensar evolutivamente
comprendiendo el HIV
CAPÍTULO 2 Las pruebas de la evolución
CAPÍTULO 3 Selección natural darwiniana
PARTE IV
1
CAPÍTULO
CAPÍTULO
3
21
47
PARTE II
LOS MECANISMOS
DEL CAMBIO EVOLUTIVO
CAPÍTULO
CAPÍTULO
4 Mutación y variación genética
5 Genética mendeliana en
poblaciones I: selección y mutación como
mecanismos evolutivos
CAPÍTULO 6 Genética mendeliana en
poblaciones II: migración, deriva genética
y apareamiento no aleatorio
CAPÍTULO 7 Evolución en loci múltiples:
ligamiento, sexo y genética cuantitativa
LA HISTORIA DE LA VIDA
CAPÍTULO
12 Los mecanismos de especiación
13 Reconstrucción de árboles
evolutivos
14 El origen de la vida y la evolución
precámbrica
CAPÍTULO 15 La explosión cámbrica
y más allá
CAPÍTULO 16 Evolución humana
401
403
437
CAPÍTULO
465
507
549
73
75
PARTE V
INVESTIGACIÓN ACTUAL. EJEMPLOS
109
CAPÍTULO
CAPÍTULO
CAPÍTULO
17 Desarrollo y evolución
18 Evolución molecular
19 Evolución y salud
585
587
611
639
155
197
PARTE III
ADAPTACIÓN
8 Estudiando la adaptación: el análisis
evolutivo de la forma y la función
CAPÍTULO 9 Selección sexual
CAPÍTULO 10 Selección familiar
y comportamiento social
CAPÍTULO 11 El envejecimiento y otros
caracteres de historia de vida
249
CAPÍTULO
251
289
331
359
v
Contenido
Prefacio
xiii
3.2.
1
3.3.
3.4.
3.5.
PARTE I
INTRODUCCIÓN
CAPÍTULO
1
Un caso para pensar evolutivamente:
comprendiendo al HIV
1.1.
1.2.
1.3.
1.4.
1.5.
Sumario 18 • Preguntas 18 • Explorando
la bibliografía 18 • Bibliografía 19
CAPÍTULO
2
Las pruebas de la evolución
2.1.
2.2.
2.3.
2.4.
49
52
57
62
65
Resumen 70 • Preguntas 70 • Explorando
la biliografía 71 • Bibliografía 72
3
La historia natural de la epidemia
4
¿Por qué el AZT es efectivo a corto plazo,
pero falla a largo plazo?
7
¿Por qué el VIH es mortal?
10
¿Por qué algunas personas son resistentes
a la infección por el VIH
12
¿Podrá una vacuna proporcionar protección
ante las diversas cepas del VIH?
14
La evolución de la forma del pico
de los pinzones de las Galápagos
Cuadro 3.1 Aspectos que complican la manera
de estimar la heredabilidad
La naturaleza de la selección natural
La evolución del darwinismo
El debate sobre el “creacionismo
científico”
PARTE II
LOS MECANISMOS DEL CAMBIO
EVOLUTIVO
CAPÍTULO
73
4
Mutación y variación genética
75
4.1.
4.2.
76
85
De dónde vienen los alelos nuevos
De dónde vienen los genes nuevos
21
Parentesco de las formas de vida
22
Cuadro 2.1 Homología y organismos modelo
25
Cambios con el tiempo
31
La edad de la Tierra
36
Cuadro 2.2 A Una mirada con detalle de la datación
radioactiva
40
Correspondencia entre grupos de datos
41
Resumen 44 • Preguntas 44 • Explorando
la bibliografía 45 • Bibliografía 45
CAPÍTULO
3
Selección natural darwiniana
3.1.
La selección natural: los cuatro postulados
de Darwin
47
48
vii
viii Contenido
4.3.
4.4.
Alteraciones cromosómicas
Medida de la variación genética en
poblaciones naturales
Cuadro 4.1 Electroforesis en gel
90
5.4.
94
95
Resumen 103 • Preguntas 104 • Explorando
la bibliografía 105 • Bibliografía 106
CAPÍTULO
5.1.
5.2.
5.3.
Resumen 150 • Preguntas 150 • Explorando
la bibliografía 151 • Bibliografía 152
5
Genética mendeliana en poblaciones I:
selección y mutación como
mecanismos evolutivos
Mutación
142
Cuadro 5.9 Tratamiento matemático de la mutación
como fuerza evolutiva
144
Cuadro 5.10 Frecuencias alélicas en el equilibrio
mutación-selección
146
Cuadro 5.11 Estimas de las tasas de mutación para
alelos recesivos
148
109
La genética mendeliana en las poblaciones:
el equilibrio de Hardy-Weinberg
110
Cuadro 5.1 Combinando probabilidades
113
Cuadro 5.2 El equilibrio de Hardy-Weinberg
con más de dos alelos
117
Selección
119
Cuadro 5.3 Un tratamiento general de la selección 122
Cuadro 5.4 El equilibrio de Hardy-Weinberg entre
alelos mutantes diferentes que dan lugar a
enfermedades genéticas recesivas
126
Cuadro 5.5 Análisis estadístico de las frecuencias
alélicas y genotípicas utilizando la prueba 2
(chi-cuadrado)
127
Tipos de selección
129
Cuadro 5.6 Predicción de la frecuencia del alelo
130
CCR5-⌬32 en generaciones futuras
Cuadro 5.7 Tratamiento algebraico de la selección
sobre alelos recesivos y dominantes
132
Cuadro 5.8 Equilibrio estable con superioridad
del heterozigoto y equilibrio inestable con inferioridad
del heterozigoto
136
CAPÍTULO
6
Genética mendeliana en poblaciones II:
migración, deriva genética y apareamiento
no aleatorio
155
6.1.
157
6.2.
6.3.
6.4.
Migración
Cuadro 6.1 Tratamiento algebraico de la migración
como fuerza evolutiva
Cuadro 6.2 Selección y migración en las serpientes
de agua del lago Erie
Deriva genética
Cuadro 6.3 Probabilidad de que un alelo dado
sea el que se fije por deriva
Cuadro 6.4 Tamaño poblacional efectivo
Cuadro 6.5 La tasa de sustituciones evolutivas
con deriva genética
Apareamiento no aleatorio
Cuadro 6.6 Frecuencias genotípicas en una
población consanguínea
Genética de la conservación de la gallina
grande de las parederas de Illinois
158
161
163
171
175
179
179
184
188
Resumen 191 • Preguntas 191 • Explorando
la bibliografía 193 • Bibliografía 194
CAPÍTULO
7
Evolución en loci múltiples: ligamiento,
sexo y genética cuantitativa
7.1.
197
Evolución de dos loci: equilibrio y desequilibrio
de ligamiento
198
Cuadro 7.1 El coeficiente del desequilibrio
de ligamiento
201
Cuadro 7.2 Análisis de Hardy-Weinberg
para dos loci
202
Cuadro 7.3 La reproducción sexual reduce el
desequilibrio de ligamiento
206
Contenido ix
7.2.
7.3.
Cuadro 7.4 Estima de la antigüedad de la
mutación CCR5-⌬32
El significado adaptativo del sexo
Selección sobre cuantitativos
Cuadro 7.5 Variación genética aditiva respecto
de la variación genética de la dominancia
Cuadro7.6 El gradiente de selección y el diferencial
de selección
Cuadro 7.7 Selección sobre caracteres múltiples
y caracteres correlacionados
9.3.
230
La elección de la hembra
Cuadro 9.2 Cópulas fuera de la pareja
Cuadro9.3 ¿Selección sexual de escape en las
moscas de ojos pedunculados?
Diversidad en los papeles sexuales
Selección sexual en plantas
Diformismo sexual en el tamaño corporal
humano
231
Resumen 324 • Preguntas 325 • Explorando
la bibliografía 327 • Bibliografía 327
212
213
224
227
Resumen 245 • Preguntas 246 • Explorando
la bibliografía 247 • Bibliografía 248
9.4.
9.5.
9.6.
CAPÍTULO
ADAPTACIÓN
CAPÍTULO
249
8
Estudiando la adaptación: el análisis evolutivo
de la forma y la función
251
8.1.
8.2.
8.3.
8.4.
8.5.
8.6.
8.7.
8.8.
Todas las hipótesis deben comprobarse
reconsiderando el cuello de las jirafas
252
Experimentos
255
Estudios basados en la observación
259
Cuadro 8.1 Una introducción al contraste
estadístico
260
El método comparativo
265
Plasticidad fenotípica
268
Cuadro 8.2 Calculando contrastes filogenéticamente
independientes
269
Cada carácter adaptativo evolucionó a partir
de algo distinto
271
Compromisos y restricciones
276
Estrategias para preguntar cuestiones
interesantes
283
Resumen 284 • Preguntas 284 • Explorando
la bibliografía 285 • Bibliografía 287
CAPÍTULO
9
Selección sexual
289
9.1.
9.2.
292
Asimetrías en la reproducción sexual
Competencia entre machos: selección
intrasexual
Cuadro 9.1 Estrategias alternativas para el
apareamiento en los machos
295
300
314
317
319
322
10
Selección familiar y comportamiento social
PARTE III
302
306
10.1. Selección familiar y la evolución del
altruismo
Cuadro 10.1 Cálculo de los coeficientes de
parentesco
Cuadro 10.2 Reconocimiento familiar
10.2. La evolución de la eusociabilidad
Cuadro 10.3 Evolución de la proporción de sexos
10.3. El conflicto entre padres e hijos
10.4. Altruismo recíproco
Cuadro 10.4 El dilema del prisionero: análisis
de la cooperación y del conflicto mediante la teoría
de juegos
Resumen 354 • Preguntas 355 • Explorando
la bibliografía 356 • Bibliografía 357
331
332
333
337
337
340
345
349
350
x Contenido
CAPÍTULO
11
El envejecimiento y otros caracteres
de historia de vida
11.1. Elementos básicos en el análisis de las
historias de vida
11.2. ¿Por qué los organismos envejecen
y mueren?
11.3. ¿Cuántos descendientes debe producir
un individuo en un año cualquiera
Cuadro 11.1 ¿Existe una explicación evolutiva
para la menopausia?
11.4. ¿Qué tamaño debe tener cada
descendiente?
11.5. Conflictos de intereses entre historias
de vida
11.6. Las historias de vida en un contexto
evolutivo amplio
359
12.5. La genética de la diferenciación y el
aislamiento
Cuadro 12.3 Cartografía de QTL
Resumen 432 • Preguntas 432 • Explorando
la bibliografía 433 • Bibliografía 433
361
CAPÍTULO
Reconstrucción de árboles evolutivos
437
375
13.1. Parsimonia y filogenia
Cuadro 13.1 El métidi cladista
13.2. La filogenia de las ballenas
Cuadro 13.2 Alternativas a la parsimonia:
máxima verosimilitud y distancias genéticas
13.3. Utilización de filogenias para responder
preguntas
Cuadro 13.3 El reloj molecular
438
438
441
376
382
386
390
401
12
Los mecanismos de especiación
403
12.1. Conceptos de especie
Cuadro 12.1 El concepto de espec ie en bacteriasa
12.2. Mecanismos de aislamiento
12.3. Mecanismos de divergencia
Cuadro 12.2 Especiación parapátrica
y simpática
12.4. El contacto secundario
404
405
409
414
14.1. El mundo del RNA
14.2. Mirando incluso más atrás ¿cómo se
consiguió el RNA?
Cuadro 14.1 La hipótesis de la panspermia
14.3. Mirando hacia delante: cuando la vida
se hizo celular
465
467
477
478
487
Resumen 501 • Preguntas 501 • Explorando
tla bibliografía 502 • Bibliografía 503
CAPÍTULO
417
421
450
452
14
El origen de la vida y la evolución
precámbrica
PARTE IV
448
Resumen 459 • Preguntas 460 • Explorando
la bibliografía 462 • Bibliografía 462
CAPÍTULO
CAPÍTULO
13
362
Resumen 396 • Preguntas 396 • Explorando
la bibliografía 397 • Bibliografía 398
LA HISTORIA DE LA VIDA
427
431
15
La explosión cámbrica y más allá
507
15.1.
15.2.
15.3.
15.4.
15.5.
508
511
521
527
536
La naturaleza del registro fósil
La explosión cámbrica
Patrones macroevolutivos
Extinciones
Extinciones recientes: el meteorito humano
Resumen 543 • Preguntas 543 • Explorando
la bibliografía 544 • Bibliografía 545
CAPÍTULO
16
Evolución humana
549
16.1. Las relaciones entre los humanos y los
simios actuales
16.2. Los ancestros recientes de los humanos
550
557
Contenido xi
16.3. El origen de la especie
Homo sapiens
564
16.4. La evolución de caracteres exclusivamente
humanos
572
Cuadro 16.1 Utilización del desequilibrio de
ligamiento para fechar la divergencia entre
poblaciones africanas y no africanas
573
Resumen 580 • Preguntas 580 • Explorando
la bibliografía 581 • Bibliografía 582
PARTE V
INVESTIGACIÓN ACTUAL. EJEMPLOS
CAPÍTULO
585
17
Desarrollo y evolución
587
17.1. Genes homeóticos, formación de patrones
y diversificación
17.2. La genética de la homología: extremidades
17.3. Flores
17.4. Homología profunda
588
595
601
606
Resumen 607 • Preguntas 607 • Explorando
la bibliografía 608 • Bibliografía 608
CAPÍTULO
18
Evolución molecular
18.1. La cantidad y la tasa del cambio de las
secuencias
18.2. Detección de la selección natural en las
secuencias de DNA
18.3. Elementos transponibles
18.4. Genomas de orgánulos
611
612
617
623
632
Resumen 635 • Preguntas 636 • Explorando
la bibliografía 636 • Bibliografía 637
CAPÍTULO
19
Evolución y salud
639
19.1. Evolución de patógenos: evasión de la
respuesta inmunológica del huésped
641
19.2. Evolución de los patógenos: resistencia
a los antibióticos
19.3. Evolución de los patógenos: virulencia
19.4. Los tejidos como poblaciones de células
que evolucionan
Cuadro 19.1 La genética forense resuelve un
misterio médico
19.5. El programa adaptacionista aplicado
a los humanos
19.6. Adaptación y fisiología médica: fiebre
19.7. Adaptación y comportamiento humano:
cuidado paterno
Cuadro 19.2 ¿Es darwiniana la evolución
cultural?
647
651
655
656
659
663
669
670
Resumen 677 • Preguntas 677 • Explorando
la bibliografía 679 • Bibliografía 679
Glosario
681
Índice
687
Prefacio
Los objetivos y la audiencia del Análisis evolutivo no han cambiado de la primera edición
a la segunda. Nuestro objetivo todavía es ayudar a los estudiantes a aprender a pensar como
biólogos evolutivos. La presentación está pensada para estudiantes de licenciatura que se
están especializando en ciencias biológicas, o preparándose para profesiones en medicina,
conservación, educación, periodismo científico o investigación. Suponemos que nuestros
lectores han finalizado los cursos introductorios y están preparados para explorar cómo un
curso de biología evolutiva puede enriquecer su vida personal y profesional.
Nuestro enfoque y filosofía tampoco han cambiado. Nuestro deseo es presentar los
temas que forman el núcleo de la biología evolutiva con el mismo espíritu de curiosidad
que impulsa la investigación. Siempre que sea posible, motivamos el material con los tipos de preguntas que se hacen los biólogos evolutivos. ¿Están los humanos más íntimamente emparentados con los chimpancés o con los gorilas? Si las personas con la mutación CCR5-∆32 son resistentes a la infección por el VIH, ¿aumentará la frecuencia de este
alelo en las poblaciones afectadas por la epidemia del SIDA? ¿Por qué los dinosaurios se
extinguieron súbitamente, después de ser los vertebrados terrestres dominantes durante
más de 150 millones de años? A menudo, un tratamiento teórico ayudará a enfocar estas
cuestiones, a generar hipótesis y a hacer predicciones que puedan comprobarse. Después
de introducir los experimentos y las observaciones que los biólogos han utilizado para
comprobar hipótesis rivales, analizamos los datos resultantes y consideramos qué trabajo
queda por hacerse. A lo largo del libro, nuestro objetivo es presentar la biología evolutiva como una empresa dinámica y cada vez más interdisciplinaria.
Aunque las premisas y el enfoque fundamental del libro no han cambiado, su organización sí. Para ordenar la secuencia de capítulos lo más cercanamente posible al modo en
que muchos profesores enseñan la asignatura, la hemos organizado en cinco partes:
• Parte I. Introducción: demuestra por qué la evolución es importante para resolver problemas del mundo real, establece el hecho de la evolución y presenta la selección natural como un proceso observable.
• Parte II. Mecanismos del cambio evolutivo: desarrolla los fundamentos teóricos
de la Síntesis Moderna, explorando cómo la mutación, selección, migración y deriva producen cambio evolutivo. La cobertura de la genética de poblaciones se amplía muchísimo respecto de la primera edición, pero se simplifica situando la mayoría de los tratamientos algebraicos en cuadros. Estos capítulos también se han enriquecido aumentado
la atención sobre cómo los modelos de la genética de poblaciones y de la genéticacuantitativa pueden aplicarse a problemas de la vida real en medicina y en conservación.
• Parte III. Adaptación: es una nueva unidad que comienza introduciendo métodos
para estudiar la adaptación y continúa ofreciendo investigaciones detalladas sobre selección sexual, selección familiar y selección sobre caracteres del ciclo de vida.
• Parte IV. La historia de la vida: comienza con un análisis de los métodos para deducir la especiación y la filogenia. Los capítulos siguientes se centran en la evolución
precámbrica, el Fanerozoico y la evolución humana.
• Parte V. Investigación actual-Ejemplos: incluye un capítulo que trata de temas
clásicos y recientes sobre evolución molecular. La unidad también tiene dos capí-
xiii
xiv Prefacio
tulos nuevos. Uno de éstos se centra en ideas que sobre la evolución han surgido por
los avances de la genética del desarrollo; el otro explora las aplicaciones de la biología evolutiva en epidemiología, fisiología médica, comportamiento humano y salud
pública.
Como en la primera edición, muchos capítulos incluyen cuadros que tratan temas o métodos especiales, proporcionando un análisis más detallado u ofreciendo el desarrollo de
ecuaciones. Todos los capítulos terminan con una serie de preguntas que animan al estudiante a revisar el material, aplicar conceptos a nuevos temas y explorar la bibliografía
básica.
Página web
El material complementario en Internet del Análisis evolutivo se ha revisado y ampliado.
Cada unidad incluye ahora dos casos de estudio. Estas tutorías desafían al estudiante a plantear cuestiones, formular hipótesis, diseñar experimentos, analizar datos y sacar conclusiones. Una tutoría sobre genética de poblaciones presenta problemas que los estudiantes
pueden resolver utilizando una simulación que se puede bajar de la red. El sitio de Internet también proporciona respuestas a algunas cuestiones seleccionadas del final de los capítulos, guías para explorar la bibliografía, conexiones con otros lugares relacionados con
la evolución.
El sitio de Internet para el Análisis evolutivo es accesible a través de la página principal
del libro en:
http://www.librosite.net/freeman
El compromiso de Prentice Hall con un formato a cuatro colores para esta edición del
Análisis evolutivo, nos ha permitido hacer esquemas, gráficos de datos y fotografías más
fáciles de interpretar y al conjunto de la presentación más brillantez y accesibilidad.
Agradecimientos
Nos gustaría dar las gracias más sinceras a todos los colegas que han ayudado a que este libro sirva mejor a los estudiantes,
contribuyendo con revisiones publicadas, revisiones autorizadas, sugerencias por correo electrónico, paquetes de “copias de
artículos” y conversaciones con nosotros en reuniones. En particular, los añadidos y revisiones en esta edición se inspiraron
en una serie de ideas y críticas constructivas proporcionadas por los siguientes colegas:
Leticia Avilés, University of Arizona
Loren E. Babcock, The Ohio State University
David Begun, University of Toronto
Andrew Berry, Harvard University
Keith A. Crandall, Brigham Young University
W. Ford Doolittle, Dalhousie University
Jerry F. Downhower, The Ohio State University
Scott Edwards, University of Washington
Gary M. Fortier, Delaware Valley College
Glenys Gibson, Acadia University
Lonnie J. Guralnick, Western Oregon University
Werner G. Heim, Colorado College
Joel Kingsolver, University of Washington
Andrew H. Knoll, Harvard University
Robert A. Krebs, Cleveland State University
Catherine S. McFadden, Harvey Mudd College
Andrew Martin, University of Colorado
Arnold I. Miller, University of Cincinnati
Nancy A. Moran, University of Arizona
Stephen W. Schaeffer, Pennsylvania State University
Robert Sinsabaugh, University of Toronto
Maureen Stanton, University of California, Davis
Daniel B.Thompson, University of Nevada, Las Vegas
Sara E.Via, University of Maryland, College Park
Prefacio xv
Sería difícil poner excesivo énfasis en cuánto se ha beneficiado esta edición del cuidado y
creatividad de estos críticos. En un sentido muy real, este libro es el producto de una comunidad que está apasionada por el estudio de la evolución y dedicada a su enseñanza.
Además, nos gustaría ampliar nuestras sinceras gracias a los estudiantes que han enviado correos electrónicos con sugerencias para mejorar. Especialmente útiles fueron las críticas escritas formalmente con las que contribuyó la clase del Dr. Peter Wimberger, de la
Universidad de Puget Sound, y muchos comentarios y sugerencias de nuestros propios
estudiantes de la Universidad de Washington.
Tenemos una deuda especial con tres colegas que contribuyeron a la revisión de capítulos clave y con la Dra. Kathleen Hunt, que contribuyó con versiones revisadas de las
preguntas del final de los capítulos. Somos muy afortunados por haber tenido contribuyentes de gran talento implicados en la preparación de esta edición. Concretamente, el
Dr. Michael Hart, de la Universidad de Dalhousie, revisó los capítulos de la historia de la
vida, inferencia filogenética y el Fanerozoico y dio origen al capítulo sobre evolución y
desarrollo. Su dominio de la bibliografía y su entusiasmo por la biología evolutiva fue una
tremenda ventaja durante el proceso de revisión y su ingenio y excitación por la ciencia
hacen que trabajar con él sea un placer. El Dr. Niles Lehman, de la Universidad del Estado de New York, en Albany, revisó el capítulo sobre el origen de la vida y la evolución en
el Precámbrico. Su creatividad, pasión, conocimiento y rápido hacer fueron vitales para proporcionar a los estudiantes una lectura fresca y precisa de este tema tan dinámico. El
Dr. David Begun, de la Universidad de Toronto, puso al día el capítulo sobre la evolución
humana. Su experiencia fue una contribución impagable a nuestro enfoque de este campo
que cambia tan rápidamente, y su buena voluntad para trabajar hasta el límite del tiempo
se aprecia enormemente.
Este libro no existiría sin la habilidad, la profesionalidad y la dedicación de la editorial
y del equipo de producción de Prentice Hall. El liderazgo de Paul Corey y su compromiso como Director editorial de Ciencia y Matemáticas ha sido importantísimo. La
Editora Jefe de producción, Debra Wechsler, realizó un magnífico trabajo gestionando los
miles de detalles requeridos para hacer un libro tan libre de errores y omisiones como fue
humanamente posible. La Editora artística, Karen Branson, reunió y dirigió un talentoso
grupo de artistas para crear el programa de figuras a cuatro colores. Robin S. Manasse
realizó la mayoría de las nuevas ilustraciones biológicas, incluyendo a los animales de la
cubierta. Los Directores artísticos Anne France, Joe Sengotta y Jon Boylan, hicieron un
diseño y una cubierta atractivos para el libro. Andrew Stull fue responsable de ampliar y
mejorar los sitios web. Jennifer Welchans, ejecutiva de marqueting es quien suministró el
impulso y las herramientas necesarias para asegurar que los profesores de todo el mundo
tengan la oportunidad de considerar este libro para sus cursos.
Finalmente y por encima de todo, damos las gracias al Editor Jefe de Biología, Sheri
Snavely, cuya visión y energía han sido el sostén de este libro. Su pasión por la publicación,
su instinto infalible, su humor y devoción son una constante fuente de inspiración.
Scott Freeman
Jon C. Herron
Seattle,Washington
PARTE I
El archipiélago de las Galápagos ha servido como laboratorio para estudios evolutivos durante mas de 160 años. (Frans Lanting/Mindem Pictures)
INTRODUCCIÓN
U
BIOLOGÍA EVOLUTIVA ES QUE ESTÁ
enraízada en un mecanismo organizativo único. Este mecanismo es el de la selección natural.
Por ello, profundizar en la comprensión de la selección natural es el primer reto para cualquiera que
estudie evolución. La selección natural es conceptualmente simple pero, en general, mal comprendida. La comprensión de cómo funciona el mecanismo requiere ir más allá de frases como “la supervivencia del más adaptado”.
Nuestro objetivo principal en la Parte I (Capítulos 1-3) es introducir la selección natural como
un factor de cambio evolutivo. La exploración del proceso comienza con un capítulo dedicado a la
comprensión del virus de la inmunodeficiencia humana (VIH) y de la epidemia del SIDA. El Capítulo 2 amplía esta presentación, revisando las pruebas de que todos los organismos han cambiado, o
evolucionado a lo largo del tiempo, a lo largo de la historia de la vida, al igual que el VIH ha evolucionado durante el pasado medio siglo. En el Capítulo 3 exploramos con más detalle cómo actúa la
selección natural. Esta serie de capítulos proporcionan la base para explorar, en la Parte II, los otros
mecanismos que dan lugar al cambio a lo largo del tiempo.
Nuestro segundo objetivo en estos capítulos es introducir los métodos experimentales y analíticos
utilizados por los investigadores en la ciencia de la evolución. Estos métodos son un tema destacado
a lo largo del texto. Los subrayamos para ayudar a los lectores a aprender cómo hacer preguntas, diseñar experimentos, analizar datos y revisar de manera crítica artículos científicos, además de entender a fondo los hechos. Los ejemplos detallados que presentamos no solo dejan claros los conceptos
generales de la biología evolutiva sino que también proporcionan ideas de cómo sabemos lo que
sabemos.
NO DE LOS ASPECTOS MÁS ATRACTIVOS DE LA
CAPÍTULO
1
Un caso para pensar evolutivamente:
comprendiendo al VIH
Las partículas rojas que emergen de esta célula T humana son viriones VIH. (National Institute for Biological
Standards and Control, England/Science Photo Library/Photo Researchers, Inc.)
E
N EL COMIENZO DE UN CURSO, PUEDE SER ÚTIL VOLVER ATRÁS Y HACERNOS
dos preguntas: ¿qué tipo de materia se cubrirá? y ¿de qué manera esta información me
ayudará en mi vida profesional y diaria? Para ayudar a responder a estas cuestiones, exploraremos la evolución del virus de la inmunodeficiencia humana (VIH). Este es el patógeno que da lugar al síndrome de la inmunodeficiencia adquirida (SIDA).
En este capítulo introduciremos el alcance del análisis evolutivo mediante un análisis pormenorizado de un tema muy actual. Nuestro objetivo es ilustrar las cuestiones que investigan los biólogos evolutivos, demostrar cómo una perspectiva evolutiva puede ayudar a la
investigación biológica, e introducir conceptos que se explorarán con detalle más tarde en
el texto.
El VIH es un caso de estudio obligado, porque plantea temas que, casi con toda certeza, influirán en la vida profesional y personal de todos nuestros lectores. Como virus emergente, que desarrolla rápidamente resistencia a los medicamentos, el VIH es un ejemplo
de dos de los temas más agobiantes de la salud pública. El SIDA ya es una de las epidemias
más devastadoras que haya experimentado nunca nuestra especie.
3
4 PARTE I Introducción
Las cuestiones a las que nos referimos son:
• ¿Por qué ha sido tan poco efectivo, a largo plazo, el prometedor tratamiento del SIDA
con el medicamento azotimidina (AZT)?
• ¿Por qué algunas personas son resistentes a la infección o a que la enfermedad progrese una vez que han sido infectadas?
• ¿Por qué el VIH mata a la gente?
• ¿Podría una vacuna proporcionar protección contra la diversidad de cepas de VIH que
existen en la actualidad?
Como caso de estudio, el VIH
demostrará cómo los biólogos
evolutivos estudian la
adaptación y la diversidad.
Estas cuestiones pueden sonar como si no tuvieran nada que ver con la biología evolutiva, pero la biología evolutiva es una ciencia dedicada a la comprensión de dos cosas: (1)
de qué manera las poblaciones cambian a lo largo del tiempo en respuesta a modificaciones en su ambiente y (2) cómo aparecen nuevas especies. De manera más formal, los biólogos evolutivos estudian la adaptación y la diversidad. Éstos son exactamente los temas
abordados en nuestras preguntas acerca del SIDA y del VIH. Sin embargo, antes de enfrentarnos con ellos, necesitamos profundizar en algunos aspectos biológicos básicos.
1.1. La historia natural de la epidemia
En diciembre de 1999, el programa sobre el SIDA de las Naciones Unidas estimaba que,
en todo el mundo, cerca de 40 millones de personas estaban infectadas con el VIH (Piot
1998; Figura 1.1). La epidemia ya había sido responsable de más muertes que la peste negra, que devastó a Europa en el siglo XIV. A finales de 2001, el SIDA sobrepasó a la epidemia de la gripe “española” de 1918 como epidemia responsable del mayor número de
muertes en la historia de la humanidad.
La mayoría de las infecciones con el VIH tuvieron lugar en dos procesos epidémicos relacionados, pero distintos, durante la década de 1980 y de 1990 del siglo pasado: uno entre varones y mujeres heterosexuales en el África subsahariana y en el sur y sureste asiático, y el otro entre varones homosexuales y drogadictos por vía intravenosa en los Estados
Unidos y Europa. Los dos procesos se distinguen por el número de personas implicadas y
por la forma de transmisión de la enfermedad.
En el África subsahariana, el número de casos de SIDA es casi abrumador (véase Mann
y Tarantola 1998; Piot 1998). Los epidemiólogos estiman que cerca de 23 millones de africanos están infectados con el VIH-1. En muchas ciudades subsaharianas, cerca del 75% de
las muertes entre personas adultas se deben al SIDA; si las previsiones se mantienen, la ter-
Figura 1.1 Distribución de los
infectados por el VIH Este
mapa muestra la distribución geográfica de los infectados por el
VIH-1. La conclusión más dramática que se deduce de esta figura
es que el SIDA es una enfermedad
principalmente de naciones en desarrollo. Se estima que más del
90% de las personas infectadas por
el VIH viven en países pobres del
hemisferio sur. Sólo en el África
subsahariana se encuentran los dos
tercios de éstos.
360.000
920.000
520.000
530.000
220.000
6 millones
1,7 millones
23,3 millones
12.000
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 5
cera parte de la masa laboral de algunos países puede morir finalmente de la enfermedad.
En este proceso epidémico (y en su expansión actual por la India y China) el virus se
transmite normalmente a nuevos huéspedes a través de relaciones heterosexuales.
En contraste, la epidemia del SIDA en América del Norte y en Europa se debe principalmente a la transmisión vía relación homosexual y al hecho de compartir jeringuillas entre los drogadictos por vía intravenosa. La frecuencia de la infección entre el público en
general es baja en las naciones desarrolladas: alrededor del 0,56% en América del Norte
frente al 10% o más en muchos países africanos. Además en la Figura 1.2 se muestra que,
mientras que el número de personas infectadas continúa aumentando en Asia y en África,
el esfuerzo de educadores e investigadores la está frenando en América del Norte y en
Europa: en los países industrializados el número de nuevas infecciones por el VIH está
disminuyendo.
¿Qué es el VIH?
Como cualquier virus, el VIH es un parásito intracelular obligado. Es incapaz de una vida
independiente y es altamente específico en cuanto a los tipos de células que infecta. El VIH
parasita a elementos del sistema inmunológico humano llamados macrófagos y células T.
Utiliza la maquinaria enzimática y la energía que encuentra en estas células para hacer copias de si mismo, matando a la célula huésped en el proceso.
En la Figura 1.3 se describe con mayor detalle el ciclo biológico del VIH. El paso 1
muestra la fase extracelular o infecciosa, cuando el virus se puede transmitir de un huésped a otro. En esta fase, el virus se denomina virión o partícula. Los pasos del 2 al 8 describen la fase intracelular o parasitaria, cuando el virus se replica.
En el caso del VIH, el proceso de replicación comienza cuando un virión se une a una
proteína específica, llamada CD4, que se encuentra en la superficie de ciertos macrófagos
y células T. La unión a la superficie de la célula huésped se completa cuando el VIH se une
a una segunda proteína de la superficie celular, llamada correceptor. Cuando se produce
la unión, la envoltura del virión y la membrana celular se fusionan (pasos 2 y 3) y el contenido del virión penetra en la célula (paso 3). Este contenido incluye al genoma diploide
del virus (en la forma de dos moléculas de RNA idénticas) y una proteína, llamada transcriptasa inversa, que transcribe este genoma.
El siguiente paso en el ciclo biológico se ilustra en el paso 4. La transcriptasa inversa sintetiza DNA vírico en el citoplasma de la célula huésped, utilizando ATP y nucleótidos
Número de nuevos adultos infectados
por el VIH (millones)
4
3
El VIH es un parásito que
afecta a las células del
sistema inmunitario humano.
África subsahariana
Sur y sudeste de Asia
Extremo Oriente e islas del Pacífico
América Latina y Caribe
Países industrializados
2
1
Figura 1.2 Tasas de infección por el VIH por zonas
geográficas Este gráfico muestra el número estimado,
0
1980
1985
1990
Año
1995
2000
anual, de nuevas infecciones por el VIH en cinco grandes
áreas geográficas. El número de nuevas infecciones está
disminuyendo en Norte América y Europa, pero está aumentando rápidamente en África y Asia.
6 PARTE I Introducción
Virión VIH
Genoma de RNA (2 copias)
Transcriptasa inversa
gp120 (proteína de membrana)
1) VIH extracelulares, o
estadio de virión
1
2) La proteína gp120 del VIH se
une a la CD4 y al correceptor
de la célula huésped
2
Correceptor
CD4
3
RNA del VIH
4) La transcriptasa inversa
sintetiza el DNA del VIH a partir
de un molde de RNA del VIH
4
DNA del VIH
DNA del huésped
DNA
del VIH
5) El DNA del VIH se integra
en el genoma huésped y se
transcribe mRNA del VIH
5
mRNA del VIH
Núcleo de la célula
huésped
6
Proteína del VIH
6) El mRNA del VIH se traduce
a proteína VIH por los
ribosomas de la célula huésped
7) Se ensambla una nueva
generación de viriones dentro
de la célula huésped
7
Figura 1.3
Ciclo de vida del VIH
Célula T o macrófago
(célula huésped)
3) El genoma de RNA del VIH
y la transcriptasa inversa
penetran en la célula huésped
8
8) Nuevos viriones salen de la
célula huésped por gemación
de la membrana
suministrados por la célula huésped. Luego, el DNA vírico se introduce en el núcleo, se
integra en el genoma del huésped y se transcribe por la polimerasa II del DNA de la célula
huésped (paso 5). Los mRNA víricos resultantes se traducen en proteínas por los ribosomas de la célula huésped (paso 6).
Es decir, en el VIH y en otros “retrovirus,” el flujo de la información genética es distinto al de las células y al de muchos virus con genomas de DNA. En los retrovirus, como
el VIH, la información genética no sigue la familiar ruta del DNA al mRNA y a las proteínas. En su lugar, el flujo de información va del RNA al DNA, al mRNA y a las proteínas. Es este primer paso, que revela un flujo inverso de la información, el que inspira el
prefijo “retro-” al retrovirus y el adjetivo “inverso” a la transcriptasa inversa.
Después de que se han sintetizado las proteínas víricas y las copias del genoma de RNA,
se recompone una nueva generación de viriones en el citoplasma de la célula huésped
(paso 7). El ciclo biológico concluye cuando los viriones salen por gemación de la membrana celular al exterior, como se muestra en el paso 8. Estos viriones quedan flotando en
la corriente sanguínea. Si encuentran otra célula en el mismo huésped que contenga la proteína CD4 en su superficie, el ciclo comienza de nuevo. O bien, los viriones se pueden
transmitir a un nuevo individuo huésped mediante transfusión sanguínea, al compartir una
jeringuilla o en una relación sexual.
El aspecto importante que hay que destacar del ciclo biológico es que el virus utiliza
la maquinaria enzimática de las células del huésped (sus polimerasas, ribosomas y tRNA)
en casi cada paso. Ésta es la razón por la que la enfermedad vírica es tan difícil de tratar.
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 7
Los medicamentos que interrumpen el ciclo biológico del virus, casi con toda certeza
interfieren en las funciones enzimáticas de las células del huésped y también provocan
efectos colaterales debilitantes.
¿De qué manera el VIH da lugar al SIDA?
El cuerpo humano responde a la infección del VIH de dos maneras: destruyendo viriones que flotan en la corriente sanguínea y matando a sus propias células infectadas antes
de que se ensamblen nuevos viriones y sean expulsados. Las células infectadas por el VIH
(los macrófagos y las células ayudantes T) son cruciales para los dos aspectos de la respuesta
inmunitaria. Debido a que la infección por el VIH mata a estas células, infecciones por el
VIH avanzadas comienzan a socavar la respuesta inmunitaria. El colapso final del sistema
inmunitario conduce a la situación conocida como SIDA. El síndrome se caracteriza por
infecciones oportunistas de bacterias y hongos patógenos que raramente ocasionan problemas en personas con un sistema inmunitario robusto. Una vez que un individuo infectado por el VIH comienza a desarrollar los síntomas del SIDA, la muerte ocurre normalmente a los dos años.
Teniendo en cuenta la información anterior, estamos preparados para explorar cuestiones
a cerca de la evolución del VIH. La primera ha sido frustrante para todo aquél implicado
en la lucha contra la epidemia: ¿por qué está siendo tan difícil desarrollar medicamentos
capaces de combatir el VIH? Ciertamente no es por no intentarlo; los gobiernos y las
compañías privadas han dedicado cientos de millones de dólares a la investigación del
SIDA y al desarrollo de medicamentos. La historia del AZT, uno de los primeros medicamentos contra el SIDA, se ha convertido en un caso típico. Al principio, el AZT parecía
prometedor, pero últimamente ha sido decepcionante. Para explicar el por qué, necesitamos introducir el principio de evolución por selección natural.
El SIDA comienza cuando la
infección por el VIH ha
progresado hasta el punto en
que el sistema inmunitario no
funciona adecuadamente.
1.2. ¿Por qué el AZT es efectivo a corto plazo,
pero falla a largo plazo?
Para combatir las infecciones víricas, los investigadores buscan medicamentos capaces de inhibir a las enzimas específicas del virus. Por ejemplo, un medicamento que interrumpa la
transcripción inversa mataría de manera efectiva y específicamente a los retrovirus con efectos colaterales mínimos. Ésta es exactamente la lógica en el caso de la azotimidina, o AZT.
Adviértase la timidina en el nombre del AZT: el AZT es un análogo de nucleótido, similar en su estructura a la timidina normal, que “engaña” a la transcriptasa inversa. Cuando el AZT se encuentra en la célula, la transcriptasa inversa lo añade erróneamente a la
cadena de DNA creciente allí donde debería añadir timidina 5-trifosfato. Este error
interrumpe la transcripción inversa, ya que el AZT no aceptará la adición del siguiente
nucleótido a la cadena que está creciendo.Así, el AZT interrumpe la formación de nuevas
proteínas víricas y de nuevos viriones, parando la infección.
En las primeras pruebas, el AZT funcionó. Interrumpía de manera efectiva la pérdida de
macrófagos y de células T en pacientes con SIDA. Pero debido a que también engaña en
algunos momentos a la polimerasa del DNA e interrumpe la síntesis de DNA en las células del huésped, el AZT da lugar a graves efectos colaterales. No obstante, parecía prometer la inhibición o, al menos, retardar el progreso de la enfermedad. Sin embargo, hacia
1989, tras pocos años de uso los pacientes dejaron de responder al tratamiento y los recuentos
de células con CD4 comenzaron de nuevo a disminuir. ¿Por qué?
Para responder a esta pregunta, consideremos un experimento imaginario. Si quisiéramos modificar por ingeniería genética un virión del VIH para que pudiera replicarse en
Cuando la transcriptasa
inversa añade AZT a la copia
del genoma del VIH que se está
sintetizando, en lugar de
timidina, la síntesis se
interrumpe. De este modo, el
AZT puede hacer más lenta o
parar el progreso de la
infección.
8 PARTE I Introducción
Algunas mutaciones en el
centro activo de la
transcriptasa inversa hacen
que la enzima tenga menor
probabilidad de añadir el AZT
en lugar de la timidina.
Figura 1.4 Imágenes de la
transcriptasa inversa generadas por ordenador (a) Esta
imagen muestra el gran surco de la
enzima transcriptasa inversa por
donde se une al sustrato (RNA).
(Thomas A. Steitz, Yale University)
(b) Las esferas rojas de esta imagen
indican la localización de las sustituciones de aminoácidos correlacionadas con la resistencia al AZT.
Advierta que se localizan en el surco de la enzima, o centro activo.
(Lori Kohlstaedt en Jon Cohen,
"AIDS Research: The Mood is Uncertain," Science, Vol. 260, 28 de
mayo, 1993.)
presencia del AZT, ¿qué haríamos? La respuesta más simple podría ser modificar el centro
activo de la enzima transcriptasa inversa, para que se equivoque con menor probabilidad
entre el AZT y el nucleótido normal. En la práctica, podríamos utilizar un mutágeno
químico o una radiación ionizante para producir cepas del VIH con alteración en las
secuencias nucleotídicas de sus genomas, y de esa manera alterar las secuencias de aminoácidos de sus proteínas. Si produjéramos muchos mutantes, al final tendríamos un número
limitado de éstos con un cambio en la parte de la molécula de la transcriptasa inversa que
reconoce y se une a la timidina normal (Figura 1.4a). Si una de estas secuencias alteradas
tuviera menor probabilidad de equivocarse entre el AZT y el nucleótido normal, entonces la variante mutante del VIH sería capaz de continuar replicándose en presencia del
medicamento. En poblaciones de viriones del VIH tratados con AZT, las cepas incapaces
de replicarse en presencia de AZT disminuirían en número y las nuevas formas llegarían
a ser dominantes en las poblaciones del VIH.
Los pasos dados en este experimento imaginario se han dado realmente en el interior de los pacientes con el VIH. ¿Cómo lo sabemos? Los investigadores tomaron repetidamente muestras de viriones del VIH de pacientes que tomaban el AZT a lo largo de
su tratamiento. En cada muestra del virus, los investigadores secuenciaban el gen de la
transcriptasa inversa. Encontraron que las cepas víricas presentes tardíamente en el tratamiento eran diferentes genéticamente de las cepas víricas presentes antes del tratamiento
en los mismos individuos huéspedes. La población de virus se había hecho resistente al AZT.
Las mutaciones asociadas con la resistencia fueron a menudo las mismas de un paciente
a otro (St. Clair et al. 1991; Mohri et al. 1993; Shirasaka et al. 1993), y se localizaban en
el centro activo de la transcriptasa inversa (Figura 1.4b). Los investigadores han observado directamente la evolución de la resistencia al AZT en docenas de pacientes con
SIDA. En cada individuo, las mutaciones en el genoma del VIH daban lugar a sustituciones de aminoácidos concretos del centro activo de la transcriptasa inversa. Estos cambios genéticos permitían a las cepas mutantes del virus replicarse en presencia del AZT.
Sin embargo, a diferencia de la situación en nuestro experimento imaginario, no ha habido ninguna manipulación consciente. Entonces, ¿cómo ha ocurrido el cambio en la
cepa vírica?
La clave es doble: la transcriptasa inversa es propensa al error y el genoma del VIH no
tiene instrucciones para sintetizar enzimas que corrijan los errores. (En relación con esto,
el VIH es como la mayoría de los retrovirus, pero diferente de los organismos celulares basados en DNA como nosotros mismos.) Por ello, alrededor de la mitad de los transcritos
de DNA producidos por la transcriptasa inversa tienen al menos un error o mutación
(Hübner et al. 1992;Wain-Hobson 1993). El VIH tiene la tasa más alta de mutación ob(a)
(b)
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 9
servada hasta la fecha en cualquier virus u organismo. Debido a que se producen miles de
generaciones de replicación del VIH en cada paciente durante el desarrollo de una infección, una cepa del VIH puede dar lugar, con el tiempo, a cientos de variantes diferentes
de la transcriptasa inversa.
Simplemente debido a su número, casi con certeza una o más de estas variantes contendrán una sustitución aminoacídica que disminuya la afinidad de la transcriptasa inversa
por el AZT. Si el paciente está tomando AZT, se suprimirá la replicación de las variantes
del VIH no alteradas, pero los mutantes resistentes serán capaces de sintetizar algo de DNA
y producir nuevos viriones. A medida que los viriones resistentes se reproducen y los no
resistentes decaen, la fracción de los viriones que son resistentes al AZT en el paciente aumenta con el tiempo. Además, es probable que en cada generación de viriones aparezcan
viriones con nuevas mutaciones.Algunas de éstas pueden incrementar aún más la capacidad de la transcriptasa inversa para funcionar en presencia del AZT. Debido a que su reproducción es rápida, los viriones que lleven estas nuevas mutaciones aumentarán también
en frecuencia a expensas de sus antecesores menos resistentes.
Este proceso de cambio con el tiempo en la composición de la población vírica se denomina evolución por selección natural. Se ha dado de manera tan consistente en los pacientes que tomaban AZT que se ha abandonado su uso como único medicamento en la
terapia del SIDA.Además, cuando se han utilizado otros análogos de nucleótidos, como ddI
o ddC, solos o juntamente con el AZT, las poblaciones del VIH han evolucionado resistencia múltiple a los medicamentos (Larder et al. 1993; Shirasaka et al. 1993; Mohri et al.
1993). La resistencia a medicamentos inhibidores de proteasas apareció a los dos años de
su utilización (Ala et al. 1997; Deeks et al. 1997).
Consideremos ahora una cuestión ligeramente diferente. Hemos estado siguiendo el
destino de los viriones que llevan versiones diferentes del gen de la transcriptasa inversa
cuando está presente el AZT (en las células del huésped). Las cepas mutantes del VIH, ¿son
también más eficaces al reproducirse en células sin AZT? La respuesta es no: cuando se ha
comenzado la terapia con AZT y luego se interrumpe, la proporción de viriones resistentes
al AZT en las poblaciones víricas disminuye con el tiempo, volviendo a los niveles que
había antes de comenzar el tratamiento con el AZT. La selección natural favorece las
mutaciones retrógradas que restauran la secuencia de aminoácidos de la transcriptasa
inversa a su configuración original (St. Clair et al. 1991). Advierta cuál es la dinámica de
la selección natural: en ausencia del AZT, la selección natural favorece a los viriones no
mutantes; en presencia de AZT la selección natural favorece a los viriones mutantes. ¿La
evolución por selección natural, es unidireccional e irreversible? La respuesta es, claramente, no.
Advierta que el proceso que acabamos de revisar implica cuatro pasos:
1. Los errores en la transcripción cometidos por la transcriptasa inversa dan lugar a mutaciones en el gen de la propia transcriptasa inversa.
2. Estas mutaciones producen variabilidad entre viriones en la función de la enzima.
3. Algunos viriones fueron más capaces de sobrevivir y reproducirse en un ambiente con
AZT que otros, debido a las propiedades funcionales de sus transcriptasas inversas mutantes.
4. Estas mutaciones se trasmitieron a los descendientes de los viriones resistentes al
AZT.
El resultado de este proceso es que nuevas formas víricas llegan a ser dominantes en las
poblaciones del VIH de los huéspedes. La composición genética de la población del VIH
al final del proceso fue diferente de la del comienzo. Esto es evolución por selección natural.
Cambios en la composición
genética de las poblaciones del
VIH con el tiempo tienen que
dar lugar a un aumento de la
resistencia a los
medicamentos. Este es un
ejemplo de evolución por
selección natural.
10 PARTE I Introducción
1.3. ¿Por qué el VIH es mortal?
Hay varias hipótesis
alternativas para explicar
porque el VIH es mortal. La
virulencia del VIH podría deberse
a (1) un resultado inevitable de
la infección de las células del
sistema inmunitario, (2)
ausencia de variación genética,
o (3) un carácter que permite
que ciertas cepas del VIH
prosperen en ambientes
particulares.
Una de las claves para convertirse en biólogo evolutivo es aprender a pensar como un organismo. Es decir, adoptar lo que los biólogos llaman “pensamiento selectivo”. Por ejemplo,
desde el punto de vista del VIH, la tendencia para ocasionar enfermedad en un huésped
(el carácter denominado virulencia) es en gran parte función de su tasa de reproducción.
La enfermedad del huésped es un efecto colateral por las altas tasas de reproducción. Una
tasa de reproducción extremadamente elevada puede dar lugar a la muerte del huésped. De
acuerdo con el pensamiento selectivo, la clave para comprender por qué el VIH es mortal
es comprender por qué es ventajoso para los viriones replicarse tan rápidamente como lo
hacen. Si el VIH puede evolucionar tan rápidamente en respuesta a la terapia con medicamentos, ¿por qué no ha evolucionado para tener un impacto menor sobre el huésped?
A veces, la respuesta a preguntas como ésta es porque no puede. Es decir, quizá las cepas
del VIH competidoras tendrían mas éxito (en el sentido de infectar a más personas) si se
multiplicaran más lentamente y no mataran a sus huéspedes, pero no pueden hacerlo debido a alguna propiedad invariable de la transcriptasa inversa, o debido a que las células diana CD4 inevitablemente conducen a que la infección sea mortal. Es importante reconocer que los organismos están constreñidos de una serie de modos. La selección natural no
puede optimizar cada uno de los aspectos de un ciclo biológico.
Sin embargo, la evidencia sugiere que las constricciones no son la causa de la elevada
virulencia del VIH.Varias enfermedades no letales afectan a las células CD4, como el herpes vírico 6, que parece que da lugar sólo a una leve erupción parecida a la rubéola que
se sufre en la infancia (véase Culliton 1990), o un virus llamado VIH-2, que a menudo puede no ser letal (Ewald 1994; Marlink et al. 1994). Estas observaciones sugieren que la infección de las células CD4 no es especialmente virulenta por definición.
Otra explicación de la virulencia del VIH es que no se ha producido una evolución hacia
un estado benigno, simplemente debido a la falta de variación en el grado de virulencia.
Si no hay mutaciones que alteren el nivel de virulencia, entonces la virulencia no puede
evolucionar por selección natural. Sin embargo hay tres aspectos que están en contra de
esta hipótesis. En primer lugar, las cepas VIH-1 que dominan tardíamente en una infección dada, cuando el paciente es sintomático, se multiplican más rápido en cultivo que las
cepas presentes al principio de la infección, sugiriendo que son más virulentas (véase
Goldsmith 1990; Ewald 1994). En segundo lugar, se han identificado sustituciones específicas de bases que están asociadas a un aumento de la virulencia (estas sustituciones de
bases se encuentran en el gen que codifica para la proteína gp120, que se encuentra en la
superficie de los viriones del VIH; véase Groenink et al. 1993). En tercer lugar, se han
identificado cambios genéticos específicos que están asociados a una disminución de la
virulencia (estas sustituciones de bases se encuentran en un gen que codifica para una de
las proteínas reguladoras del VIH; véase Deacon et al. 1995).
Una tercera hipótesis es que la selección natural ha favorecido a cepas muy virulentas
del VIH-1. Esto es lo que propone Paul Ewald con su hipótesis sobre la tasa de transmisión (Ewald 1994), ilustrada en la Figura 1.5. La hipótesis predice que si la transmisión de
enfermedades por vía sexual desde un huésped actual a uno nuevo es frecuente, entonces
la selección natural favorecerá el aumento de la virulencia. Pero si la transmisión a nuevos
huéspedes no es frecuente, entonces la selección favorecerá a cepas más benignas. La clave
de la hipótesis de la tasa de transmisión es el concepto de compromiso. Los biólogos evolutivos analizan los compromisos en términos de costes y beneficios de estrategias opuestas. En este caso, las estrategias son crecer rápidamente o crecer lentamente. Para un virión,
el beneficio del crecimiento rápido es aumentar su predominio en la corriente sanguínea
del huésped y por ello aumentar su probabilidad de transmitirse durante un episodio dado
de intercambio sexual. El coste del crecimiento rápido es matar a demasiadas células CD4
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 11
Fracción de pacientes muertos (%)
a) Supuesto 1: Las cepas más virulentas mantienen una concentración más elevada
de viriones VIH en la sangre de los pacientes y matan al paciente rápidamente.
Cepas más virulentas: Carga viral inicial >30.000 copias
de RNA del VIH por mililitro de sangre
100
b) Supuesto 2: Las cepas más virulentas
son las que tienen mayor probabilidad
de transmitirse en una relación sexual.
Cepas menos virulentas: Carga viral inicial <500
copias de RNA del VIH por mililitro de sangre
100
0
0
10
Carga viral medida años después
Fracción de pacientes
infectados que transmitieron
el VIH a su pareja
heterosexual durante
una relación que
duró al menos 6 meses
0
c) Hipótesis:
Cuando el huésped cambia de pareja a menudo, una cepa más virulenta tiene
mayor eficacia. Tiene la oportunidad de infectar a muchos nuevos huéspedes,
aun cuando mate con relativa rapidez a su huésped original.
Pacientes con cepas Pacientes con cepas
más virulentas
menos virulentas
(>100.000 copias de (<100.000 copias de
RNA de VIH por ml)
RNA de VIH por ml)
Cuando el huésped cambia raramente de pareja, las cepas menos virulentas
tienen mayor eficacia. Permiten a su huésped vivir lo suficiente como para darles
la oportunidad de infectar a más de un nuevo huésped.
Figura 1.5 Hipótesis de la tasa de transmisión Los esquemas de la parte superior ilustran dos supuestos importantes que apoyan la hipótesis. Los datos de la parte (a) son de J.W. Mellors, 1998. Scientific American 279 (Julio): 90; los datos de la parte (b) son de M.V. Ragni et al., Journal of
Acquired Immune Deficiency Syndromes and Human Retrovirology 17:42-45. Cuando estos supuestos se cumplen, las cepas virulentas de patógenos
que se transmiten sexualmente se extenderían por la población más eficazmente cuando las tasas de cambio de pareja sean altas, mientras que las
cepas más benignas se extenderían más eficazmente si las tasas de cambio de pareja son bajas (véase la parte c).
como para que el huésped enferme y sea menos probable que se realice un intercambio
sexual.
La lógica que subyace en la hipótesis de la tasa de transmisión queda ahora evidente: si
las personas raramente cambian de compañero sexual, un episodio dado de relación sexual
es improbable que implique a un nuevo compañero. En este ambiente, la transmisión a un
nuevo huésped es improbable durante cualquier episodio de relación sexual. Si las personas infectadas son monógamas, las formas altamente virulentas del VIH matarán a la pareja
casi con toda certeza antes de que pueda ocurrir la transmisión a un nuevo huésped. Si la
monogamia está extendida en la población huésped, entonces las formas muy virulentas
del virus serán eliminadas. En su lugar aumentará la frecuencia de las formas del VIH de
12 PARTE I Introducción
Las diferencias en el grado de
virulencia entre cepas VIH se
puede analizar como
estrategias en competencia,
cada una con costes y
beneficios. Qué estrategia
tendrá éxito depende de las
condiciones ambientales: en
este caso, del grado de
promiscuidad sexual.
reproducción lenta. ¿Por qué? Estas cepas se encuentran siempre en bajo número en la corriente sanguínea o en el semen de un huésped, pero se pueden transmitir si los individuos monógamos encuentran ocasionalmente nuevos compañeros sexuales después de un
divorcio o de la muerte del esposo/a.
Por el contrario, si prevalece la promiscuidad, entonces las cepas muy virulentas se transmitirán a nuevos huéspedes con más frecuencia que las cepas que se replican lentamente.
Por ello, aumentarán su frecuencia en la población vírica total.
La idea de Ewald es que las cepas muy virulentas llegan a ser dominantes en las poblaciones de VIH debido a las prácticas de intercambio sexual entre varones y mujeres heterosexuales en África central y oriental, y en varones homosexuales en los Estados Unidos
y Europa. Debido a las circunstancias económicas de las décadas de los 70 y de los 80,
millones de varones africanos emigraron de sus tierras, en zonas rurales, a las grandes
ciudades de Zaire, Uganda y Kenia. Como respuesta floreció una gran industria del sexo,
con prostitutas que en algunas ciudades llegaban a tener hasta 1000 relaciones sexuales
por año (véase Ewald 1994). De igual manera, la tasa de cambio de compañero entre los
varones homosexuales en los Estados Unidos y en Europa hacia finales de los 70 y principios de los 80 fue elevada: hasta 10 cada seis meses (Koblin et al. 1992). La hipótesis de
la tasa de transmisión sostiene que los cambios en la dinámica de la transmisión, ocasionados por cambios en el comportamiento de las poblaciones huésped, favorecen enormemente la evolución de cepas virulentas del VIH.
Además, la hipótesis predice que poblaciones diferentes albergarán cepas del VIH con
diferentes grados de virulencia, dependiendo de la frecuencia con la que los individuos
cambian de compañero sexual. Dos experimentos naturales que se llevan a cabo en la
actualidad nos pueden ayudar a entender la validez de esta hipótesis.
• Desde el comienzo de la epidemia, las tasas de cambio de compañero entre varones
homosexuales en los Estados Unidos y en Europa han disminuido drásticamente (Adib
et al. 1991), y la tasa de utilización del preservativo ha aumentado (Catania et al. 1992).
En contraste, la utilización del preservativo y las prácticas sexuales en África parece que
han cambiado muy poco (Editorial de la redacción 1995). La hipótesis de la tasa de
transmisión pronostica que el VIH se irá haciendo poco a poco menos dañino en América del Norte y en Europa, pero continuará matando a las personas, después de una
infección relativamente breve, en África central y oriental y quizá también en Asia.
• El VIH-2, íntimamente relacionado con el VIH-1, es similar en cuanto a su ciclo biológico y composición genética, pero es mucho más benigno (DeCock et al. 1993). El
VIH-2 se ha desplazado recientemente desde su centro histórico de incidencia en África
Occidental, donde la tasa de transmisión sexual debido al cambio de compañero es baja,
a la India, donde las tasas pueden ser mucho más elevadas (Ewald 1994). Si la investigación confirma que el VIH-2 se está transmitiendo más rápidamente en la India que en África Occidental debido a la mayor promiscuidad en las prácticas sexuales, la hipótesis de la
tasa de transmisión predice que aparecerán en Asia cepas muy virulentas del VIH-2.
¿Es correcta la hipótesis de la tasa de transmisión? Sólo el tiempo, y los datos, lo dirán.
1.4. ¿Por qué algunas personas son resistentes
a la infección por el VIH?
El principio de evolución por selección natural explica por qué cepas del VIH se han
convertido en resistentes a los medicamentos.También puede explicar por qué el virus es
mortal. ¿Puede el mismo principio aclarar por qué algunas personas que están expuestas
repetidamente al virus no quedan infectadas?
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 13
Para los investigadores y médicos que están luchando por encontrar estrategias para
controlar la epidemia del SIDA, la existencia de personas expuestas, pero no infectadas, era
un rayo de esperanza. Si existe resistencia natural al virus, y si se pudieran identificar las bases moleculares de esta resistencia, sería posible copiar el mecanismo de resistencia mediante
nuevas terapias médicas.
Los dos “sies” se han confirmado ya. A principios de la década de 1990, el trabajo de
varios laboratorios demostró que algunas personas permanecen no infectadas incluso
después de exposiciones repetidas al virus y que algunas personas que están infectadas con
el virus sobreviven muchos más años de lo esperado (véase Cao et al. 1995). Se dio un avance en el reconocimiento de las bases moleculares de la resistencia cuando el grupo dirigido por Edward Berger identificó las moléculas correceptoras que permiten al VIH entrar
en los macrófagos y en las células T (véase Feng et al. 1996; Alkhatib et al. 1996). Poco
después, Rong Liu y sus colaboradores (1996) y Michel Samson y asociados (1998), sugirieron que los individuos resistentes podrían tener formas raras de las moléculas correceptoras y que estas proteínas mutantes impedirían la entrada del VIH.
Para comprobar esta hipótesis, Samson y sus colegas secuenciaron el gen que codifica un
correceptor particularmente importante, llamado CCR5, a partir de tres individuos infectados por el VIH que habían sobrevivido largo tiempo. Uno de los individuos tenía una
forma mutante del gen, como se había pronosticado. Debido a que este alelo se diferencia
por tener una deleción de 32 pares de bases en la secuencia normal del DNA, Samsom y
sus colaboradores lo denominaron alelo ⌬32 (⌬ es la letra griega delta). Luego demostraron que el VIH no puede entrar en las células que tienen la forma ⌬32 del CCR5 en su
superficie. Este experimento confirmó que el alelo protege a los individuos de la infección.
Para comprobar este resultado, Samson y sus colaboradores tomaron muestras de DNA
de un gran número de individuos del norte de Europa, de Japón y de ascendencia africana, examinaron el gen CCR5 de cada individuo y calcularon la frecuencia de los alelos
normal y ⌬32 en cada población. Surgió una notable diferencia: el alelo mutante está presente en una frecuencia relativamente elevada del 9%, en Caucásicos, pero no se encuentra en individuos de ascendencia asiática o africana.
¿Por qué una forma de un gen es relativamente común en una población y no se encuentra en otras? Samson y sus colaboradores ofrecieron dos posibles explicaciones: o bien
el alelo ⌬32 había sido favorecido recientemente por selección natural en las poblaciones
caucásicas, o podría haber aumentado por azar debido a un proceso llamado deriva genética. Estas hipótesis contrarias están siendo comprobadas. Stephen O’Brien, por ejemplo,
favorece una explicación basada en la selección natural. Propone que la selección dio lugar a un aumento en la frecuencia del alelo ⌬32 en Europa durante la aparición de la peste negra en el siglo XIV. De acuerdo con O’Brien, el alelo ⌬32 protege a los individuos
contra la infección de la bacteria que da lugar a la peste negra, al mismo tiempo que contra la infección del VIH. Si esto es así, entonces los experimentos que se están llevando a
cabo demostrarán que las células T con la forma mutante de la proteína CCR5 resisten a
la infección de la bacteria, al igual que resisten a la infección del VIH.
Sin embargo, la historia de los “alelos de resistencia” no comienza y termina con el alelo ⌬32. Después de que se publicara el estudio de Samson y asociados, los grupos dirigidos por Luc Montagnier y Stephen O’Brien lograron encontrar dos nuevos alelos mutantes
asociados con la resistencia a la infección o a la progresión lenta del SIDA (Smith et al. 1997;
Quillent et al. 1998; véase también Carrington et al. 1999).Algunos de estos alelos se encuentran en frecuencias similares en diferentes grupos étnicos; otros varían su frecuencia
de una población a otra.
Estos descubrimientos han inspirado la continuación del trabajo en dos frentes: los
biólogos moleculares están intentando diseñar medicamentos que mimeticen los efectos
de los alelos de resistencia, mientras que los biólogos evolutivos miden lo comunes que son
Existen alelos que confieren
resistencia al VIH en distintas
frecuencias y en diferentes
poblaciones humanas. Por ello...
14 PARTE I Introducción
...la frecuencia de los alelos
para la resistencia puede
aumentar en respuesta a la
selección natural, en la forma
de epidemia de SIDA.
en distintas poblaciones y analizan cómo pueden cambiar sus frecuencias a medida que continúa la epidemia. Desde una perspectiva evolutiva, el VIH está originando selección natural en las poblaciones humanas. Debido a que los humanos presentan diferencias respecto
a la resistencia a la infección, las poblaciones humanas evolucionarán en respuesta a la
epidemia. Concretamente, como las personas con versiones normales de los genes correceptores mueren de SIDA, aumentará la frecuencia de los alelos de resistencia en las poblaciones. Si ocurre este cambio en la composición genética de las poblaciones humanas,
se convertirá en un importante ejemplo de evolución por selección natural.
1.5. ¿Podrá una vacuna proporcionar protección
ante las diversas cepas del VIH?
Los grandes éxitos históricos en el control de enfermedades víricas (desde la polio a la viruela) se han producido como consecuencia del desarrollo de las vacunas. La dificultad en
el diseño de medicamentos antivirales, junto con la tasa a la que ha evolucionado la resistencia del VIH a estos medicamentos, ha hecho del desarrollo de la vacuna una prioridad
urgente para la comunidad que investiga el SIDA. ¿Es posible diseñar una vacuna que haga
a las personas inmunes al VIH?
Un estudio reciente sobre la historia evolutiva del virus del SIDA ha reforzado un
creciente consenso acerca del desarrollo de una vacuna. Para comprender el resultado y las
implicaciones para el futuro de la epidemia, necesitamos hacer dos cosas: revisar cómo
actúan las vacunas y comprender la lógica básica que hay detrás del esfuerzo para reconstruir una historia evolutiva.
Breve resumen de cómo actúan las vacunas
Para responder a las infecciones bacterianas y víricas, las células del sistema inmunitario llamadas células T tienen que identificar a la proteína del patógeno como extraña, o como
no propia. El fragmento de la proteína extraña que es reconocida como no propia y que
desencadena una respuesta de las células T se denomina epitopo.
Las vacunas consisten en epitopos de viriones muertos o incompletos.Aunque no se dé
una infección real después de una vacunación, el sistema inmunitario responde activando
a las células que reconocen los epitopos presentes. Si más tarde comienza una auténtica infección, el sistema inmunitario está “preparado” para responder rápidamente. En casi todos los casos el invasor es eliminado antes de que la infección progrese hasta el punto de
producir una enfermedad.
En el caso del VIH, la mayoría de los epitopos reconocidos por el sistema inmunitario derivan de la proteína llamada gp120, que forma parte de la cubierta del virión. Entonces, para
ser efectiva, una vacuna tendría que contener epitopos de las proteínas gp120 que se encuentran en muchas cepas diferentes del VIH. ¿Exactamente, cuánto se han diversificado estas cepas? Para responder a esta cuestión los biólogos han analizado secuencias génicas del
VIH de todas las partes de mundo y han utilizado los datos para reconstruir la historia evolutiva del virus.
¿Cómo reconstruyen los investigadores la historia evolutiva?
De acuerdo con la teoría de la evolución por selección natural, examinada en detalle en
los Capítulos 2 y 3, todos los organismos están relacionados entre sí a partir de un antecesor común. En el caso del VIH, la teoría predice que la diversidad de cepas presentes en
la actualidad se originó a partir de una única población ancestral. ¿Cuál fue la naturaleza
de este antecesor? ¿Cuánto se ha diversificado el VIH desde entonces?
Al igual que las relaciones históricas de los individuos quedan descritas por sus genealogías, las relaciones históricas entre poblaciones o especies se describen por sus filogenias.
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 15
Una representación de estas relaciones evolutivas en la que se muestra el árbol familiar
de un grupo de especies o poblaciones se denomina cladograma o árbol filogenético.
La metodología para reconstruir filogenias es compleja (dedicamos todo el Capítulo 13 a
este tema), pero la base lógica del programa de investigación es simple: en general, especies
íntimamente emparentadas tendrán características más similares que formas más lejanamente emparentadas. En el caso del VIH los investigadores deducen las relaciones históricas entre cepas comparando las secuencias nucleotídicas de sus genes. La premisa de
trabajo es que cepas con secuencias nucleotídicas muy similares comparten un antecesor
común más reciente que cepas con secuencias nucleotídicas muy diferentes.
Para valorar las perspectivas del desarrollo de vacunas a la luz de la historia evolutiva del
VIH, examinaremos dos filogenias. La primera muestra las relaciones entre el VIH y los
virus que infectan las células del sistema inmunitario de otros primates. La segunda es más
concreta y muestra las relaciones entre las cepas del VIH.
Un árbol filogenético muestra
las relaciones históricas entre
un grupo de virus u
organismos.
El origen del VIH
Para reconstruir la historia del VIH, Feng Gao y sus colegas (1999) secuenciaron el gen
que codifica para la transcriptasa inversa en varios virus de inmunodeficiencia de simios
(VIS) y las compararon con las secuencias que se encuentran en una serie de cepas del VIH.
Los VIS son parásitos que infectan el sistema inmunitario de chimpancés y monos. Sin embargo, estos virus no parece que den lugar a enfermedades graves en sus huéspedes.
Cuando Gao y asociados utilizaron los datos de las secuencias para estimar qué virus
están mas íntimamente relacionados, el resultado fue la filogenia que se muestra en la Figura 1.6a. En este árbol, la longitud de las líneas horizontales indica el porcentaje de las
bases que son diferentes entre cepas víricas. Ramas cortas entre especies indican que sus
secuencias son similares; ramas más largas indican que sus secuencias son más divergentes.
Ya que las secuencias divergen como consecuencia de las mutaciones que se producen a
lo largo de muchos años, la longitud de las ramas horizontales en este árbol está íntimamente correlacionada con el tiempo. (Por el contrario, las longitudes de las líneas verticales del árbol son arbitrarias. Se han dibujado así para hacer al árbol más legible.)
Para leer el árbol y entender qué implica acerca de la historia del VIH, comencemos
por la flecha en la parte inferior izquierda. El punto de ramificación, o nodo, que señala
esta flecha representa el antecesor común a todos los virus del árbol.Advierta que cada uno
de los distintos grupos, o linajes, que se ramifican a partir de la población ancestral conducen a virus que infectan a monos y chimpancés. Esto sugiere que el VIH desciende de
virus que infectaban a monos y chimpancés. Las ramas dibujadas en azul van hacia virus
que infectan a una serie de primates no humanos, mientras que las ramas rojas y verdes conducen a virus que parasitan tanto a humanos como a primates no humanos.
¿De dónde vino el virus de la inmunodeficiencia humana? Encuentre en el árbol el virus designado por VIH-2 y advierta que se encuentra próximo a un virus que infecta a una
especie de mono (Cercocebus torquatus). El VIH-2 es frecuente en África Occidental, y mucho menos virulento que el VIH que causa la epidemia del SIDA. Debido a que dicho
mono se caza como alimento y se tiene como animal de compañía en África Occidental,
y puesto que sus secuencias génicas están tan íntimamente relacionadas con el VIH-2, los
investigadores concluyen que el virus probablemente se transmitió desde dicho mono a humanos en un pasado reciente. Una vez en humanos, la evolución por selección natural dio
lugar a las cepas conocidas como VIH-2.
Por el contrario, las líneas rojas en la parte superior del árbol se dirigen a cepas que infectan a humanos y a chimpancés. Estas poblaciones incluyen al VIH-1, el virus causante
de la epidemia del SIDA. Debido a que en África los chimpancés se cazan para alimento,
y puesto que sus secuencias génicas son tan parecidas al VIH-1, Gao y sus colegas propo-
Los dos tipos principales de
VIH, el VIH-2 y el VIH-1 se
transmitieron a los humanos a
partir de diversos orígenes. El
VIH-2 se originó en Cercocebus
torquatus, mientras que el
VIH-1 se originó y se transmitió
a humanos desde los
chimpancés.
16 PARTE I Introducción
VIH-1/U455: Humano
a)
b)
VIH-1/LAI: Humano
VIH-1/ELI: Humano
VIH-1, Cepas diversas
del grupo M
VIH-1/YBF30: Humano
VISchmUS: Chimpancé
VISchmCAM3: Chimpancé
VISchmGAB1: Chimpancé
VIH-1/MPV5180: Humano
*
VISchmUS
YBF30
VISchmCAM5
VISchmCAM4
VIH-1/ANT70: Humano
VISchmANT: Chimpancé
Chimpancé
VISchmCAM3
VISchmGAB1
276Ha
VISlhoest: Mono de L’Hoest
VISsun: Mono de cola dorada
VISmnd: Mandril
VISagmVerTYO: Mono verde africano
Chimpancé
VIH-1 grupo N
*
ANT70
VAU
MVP5180
VISchmANT
VIH-1 grupo O
Chimpancé
VISagmVer3: Mono verde africano
VISagmVer155: Mono verde africano
VISagmGri677: Mono verde africano
VISagmTan1: Mono verde africano
VIH-2/ROD: Humano
VIH-1 y parientes
Linajes principales del VIS
VIH-2 y parientes
VIH-2/D205: Humano
VISsmH4: Cercocebus torquatus
VIH-2/FO784: Humano
VISstm: Macaca arctoides
VISsyk: Mono
de Sykes
Tiempo
FIGURA 1.6
El "árbol familiar" de los virus VIH y relacionados (a) Este árbol muestra las relaciones evolutivas entre las formas principales del VIH,
llamadas VIH-1 y VIH-2 y los virus de la inmunodeficiencia que afectan a primates no humanos. Advierta que los virus que se ramifican cerca de la flecha en
la base del árbol parasitan monos. Basándose en este hecho, los investigadores concluyeron que las cepas de virus saltaron de los monos a los humanos. (b)
Este árbol muestra un análisis más detallado realizado por Gao et al. (1999). (El asterisco señala el mismo punto de ramificación en ambos árboles.) Las flechas indican los lugares del árbol en donde los virus de la inmunodeficiencia se transmitieron desde los chimpancés a los humanos. De acuerdo con este
árbol, cada una de las cepas principales del VIH-1 se originaron en sucesos de transmisión diferentes desde el chimpancé hospedante. Modificación de las
Figuras 1a y 3b de Gao et al. (1999). Copyright © 1999, Macmillan Magazines Ltd. Reimpreso con el permiso de Nature.
nen que el VIS que infecta a chimpancés (VISchm) se transmitió de los chimpancés a los
humanos, en donde evolucionó hacia el VIH-1.
Para analizar más profundamente este suceso de transmisión, Gao y colaboradores compararon las secuencias de genes del VIH-1 y del VISchm que codifican para proteínas que
se encuentran en la superficie de los viriones. El árbol basado en estos datos, que se reproduce en la Figura 1.6b, da una visión más detallada de las relaciones entre estos virus.
Adviértase que las cepas del VIH se agrupan en tres grupos diferentes, que los investigadores llaman subgrupos M, N y O. Cada subgrupo del VIH está íntimamente relacionado
con una cepa diferente del VISchm. Para Gao y asociados esto es una prueba de que el virus
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 17
“saltó” de los chimpancés a los humanos en tres ocasiones distintas. Proponen que el VIH1 se transmitió a los humanos desde los chimpancés, no una vez sino en varias ocasiones.
Utilidad de los árboles evolutivos para ver el bosque
Los investigadores en biomedicina, los funcionarios de la salud pública y los médicos
pueden sacar varias conclusiones generales al analizar la filogenia del VIH:
• Debido a que el VISchm está tan íntimamente relacionado con el VIH-1, los chimpancés
son animales importantes para su estudio. ¿En qué medida es común en la naturaleza el
VISchm y cómo se transmite? ¿Por qué el virus no provoca enfermedad en el chimpancé?
• Existen muchos subgrupos diferentes del VIH-1 como consecuencia de sucesos de transmisión independientes desde los chimpancés a los humanos. La diversidad de cepas del
VIH resultante plantea problemas para el desarrollo de una vacuna.Además, debido a que
la transmisión del VIS a los humanos ha ocurrido repetidamente en el pasado, es probable que continúe en el futuro.
• La longitud de las ramas de la Figura 1.6b sugiere que la divergencia en la secuencia es
alta, incluso dentro de los subgrupos del VIH-1. Para aclarar este punto,Tuofo Zhu y sus
colaboradores (1998) secuenciaron genes del VIH-1 que se encontraba en una muestra
de sangre tomada de un congoleño en 1959. Ésta es la infección por VIH más antigua
que se conoce. Su análisis demuestra que la muestra de 1959 es notablemente distinta
de las cepas actuales. Con las propias palabras de los investigadores (pág. 596), “La diversificación del VIH en los pasados 40 o 50 años pronostica incluso una mayor heterogeneidad viral en las próximas décadas.” La rápida evolución del VIH, como el cambio genético rápido que normalmente se observa en los virus de la gripe y del constipado,
hace que el diseño de una vacuna sea difícil.
¿Qué es lo que tiene que decir la biología evolutiva, si es que tiene
algo que decir, acerca del modo de vencer a la epidemia del SIDA?
La comprensión de la biología evolutiva puede ayudar a luchar contra el VIH, aunque
sólo sea en cierto modo.
Primero, muchos investigadores del campo han concluido que la búsqueda de una
vacuna para el SIDA puede ser inútil (Korber et al. 1998; Letvin 1998; Baltimores y Heilman
1998). Dado que la tasa de mutación del VIH es tan alta, el virus se diversifica rápidamente. Por ello, cepas diferentes presentan una gran variedad de epitopos al sistema
inmunitario humano, haciendo el diseño de la vacuna difícil, sino imposible.
Segundo, hay alelos resistentes que, si la epidemia continúa, aumentarán su frecuencia
en las poblaciones humanas. Las personas que carezcan de los alelos resistentes tienen un
gran riesgo de infectarse.
Tercero, si la hipótesis de la tasa de transmisión es correcta, la mejor defensa contra el
VIH es, de manera incuestionable, la educación y los cambios en el comportamiento. El
aumento del uso del preservativo, la fidelidad sexual, la abstinencia y el uso de jeringuillas
estériles no solo disminuirá directamente la tasa de transmisión sino que potencialmente
también ayudará a la detención de la epidemia, dando lugar indirectamente a la evolución
de un parásito menos virulento. La hipótesis de la tasa de transmisión arguye que las tasas
de transmisión lentas tendrán un efecto multiplicador en detener la epidemia, disminuyendo
tanto la incidencia como la gravedad de la enfermedad.
Finalmente, el VIH continuará indudablemente desarrollando resistencia a los medicamentos antivirales. En la actualidad los médicos prescriben de manera rutinaria una “combinación de terapias” (que significa varios medicamentos al mismo tiempo) en un esfuerzo por retrasar la evolución de las cepas resistentes. La intención es ganar tiempo para el
desarrollo de nuevos medicamentos.
Cada uno de los principales
subgrupos del VIH-1 se originó
por un suceso de transmisión
independiente de chimpancés a
humanos.
El VIH evoluciona tan
rápidamente que la
investigación por una vacuna
efectiva puede ser inútil.
18 PARTE I Introducción
Resumen
En este capítulo nos centramos en la adaptación y diversificación de un virus e introducimos conceptos que se utilizarán a lo largo del texto: mutación y variación, competencia,
selección natural, reconstrucción filogenética, diversificación
de linajes y aplicaciones de la teoría evolutiva a problemas
científicos y humanos. Nuestra tarea será ahora ampliar el
enfoque concreto de esta introducción e introducir la diversidad de teorías, experimentos y modelos que conforman
la biología evolutiva.
El temario comienza, en el Capítulo 2, con el hecho de
la evolución. La comprensión de que las especies cambian a
lo largo del tiempo y de que los organismos que viven en
la actualidad descienden de formas que vivieron en el pasado, es lo que motivó a Darwin para buscar un mecanismo
que lo explicara: un proceso que pudiera crear cambio con
el tiempo. Entonces, ¿cuáles son las pruebas del hecho de la
evolución?
Preguntas
1. El SIDA es, principalmente, una enfermedad de personas jóvenes. ¿De qué manera dicha enfermedad afecta al tamaño, la
distribución por edades y la tasa de crecimiento de las poblaciones humanas con el tiempo?
2. A principios de la década de 1990, los investigadores comenzaron a encontrar cepas del VIH-1 resistentes al AZT en
pacientes recientemente infectados, que nunca habían sido
tratados con AZT. ¿Cómo pudo ocurrir esto?
3. En este capítulo, hemos discutido dos tipos distintos de selección: selección de diferentes cepas de virus dentro de un
huésped y selección de aquellas cepas de virus que pueden
transmitirse de un huésped a otro. Supongamos que un asesor sobre el VIH está hablando con un paciente que está angustiado por si pudiera tener una cepa virulenta del VIH.“No
se preocupe,” dice el asesor.“Incluso si Ud. tuviera realmente una cepa virulenta, debido a que Ud. es monógamo la cepa
virulenta desaparecerá.” ¿De qué manera ha malinterpretado
el asesor la hipótesis de la tasa de transmisión?
4. Una alternativa a la hipótesis de la tasa de transmisión, sostenida tradicionalmente por investigadores en biomedicina, es
que los agentes que causan la enfermedad evolucionan de manera “natural” hacia formas más benignas a medida que el sistema inmunitario de sus huéspedes desarrolla respuestas más
eficaces contra ellos. ¿Qué predicciones haría esta “hipótesis
coevolutiva” acerca de la evolución de la virulencia del VIH
en los Estados Unidos respecto de África y del Sureste Asiático? ¿Qué datos podrían ayudarle a decidir si es correcta la
hipótesis de la tasa de transmisión o la hipótesis coevolutiva?
¿Sugieren las hipótesis modos diferentes de gastar los limitados fondos para investigación y educación sobre el VIH?
5. Responda a la siguiente cita del personaje llamado Mr. Spock
de “Star Trek”:“Un parásito realmente exitoso es un comensal, que vive en amistad con su huésped e incluso confiriéndole ciertas ventajas, como, por ejemplo, los protozoos que
viven en el sistema digestivo de sus termitas y les digieren la
madera que comen. Un parásito que de manera regular e inevitablemente mata a su huésped no puede sobrevivir largo
tiempo, en sentido evolutivo, a menos que se multiplique con
tremenda rapidez... no sobrevivirá.”
6. El texto afirma que las poblaciones humanas evolucionarán en
respuesta a la epidemia del SIDA, ya que los alelos que confieren resistencia a la infección por el VIH aumentarán en frecuencia en las poblaciones con el tiempo. ¿Está de acuerdo con
esta predicción? ¿Cómo diseñaría una investigación para comprobar esto?
7. Suponga que el VIH fue el antecesor del VIS, en lugar de lo
contrario. Si los virus de la inmunodeficiencia se transmitieron originalmente desde los humanos a los monos y chimpancés, haga un esquema de cómo sería la Figura 1.6a.
Explorando la bibliografía
8. En una gran variedad de virus, bacterias y otros parásitos se ha
desarrollado resistencia a los medicamentos. Los siguientes artículos introducen datos sobre la evolución de la resistencia a
los medicamentos en los virus de la gripe y de la hepatitis B
y en poblaciones de bacterias responsables de la tuberculosis:
Bishai, W. R., N. M. H. Graham, S. Harrington, C. Page,
K. Moore-Rice, N. Hooper, and R. E. Chaisson. 1996.
Rifampin-resistant tuberculosis in a patient receiving rifabutin prophylaxis. New England Journal of Medicine 334:15731576.
Carman,W., H.Thomas, and E. Domingo. 1993. Viral genetic variation: Hepatitis B virus as a clinical example. Lancet
341:349-353.
Capítulo 1 Un caso para pensar evolutivamente: comprendiendo al VIH 19
9. Para comprobar la hipótesis de la tasa de transmisión en otros
organismos, consúltense los siguientes artículos:
Herre, E.A. 1993. Population structure and the evolution of
virulence in nematode parasites of fig wasps. Science 259:
1442-1445.
Lipsitch, M., S. Siller, and M.A. Nowak. 1996.The evolution
of virulence in pathogens with vertical and horizontal transmission. Evolution 50:1729-1741.
Bibliografía
Adib, S. M., J. G. Joseph, D. G. Ostrow, M.Tal, and S. A. Schwartz. 1991. Relapse
in sexual behavior among homosexual men:A 2-year follow-up from the Chicago MACS/CCS. AIDS 5: 757-760.
Ala, P. J. et al. 1997. Molecular basis of HIV-1 protease drug resistance: Structural
analysis of mutant proteases complexed with cyclic urea inhibitors. Biochemistry
36: 1573-1580.
Alkhatib, G., C. Combadiere, C.C. Broder,Y. Feng, P. E. Kennedy, P. M. Murphy,
and E. A. Berger. 1996. CC CKR5: A RANTES, MIP-1␣, MIP-1 receptor
as a fusion cofactor for macrophage-tropic HIV-1. Science 272: 1955-1952.
Baltimore, D. and C. Heilman. Vacunas contra el VIH: dificultades y perspectives.
Investigación y Ciencia (Sept. 98):72-81.
Cao,Y., L. Qin, L. Zhang, J. Safrit, and D. D. Ho. 1995. Virologic and immunologic characterization of long-term survivors of human immunodeficiency virus type 1 infection. New England Journal of Medicine 332: 201-208.
Carrington, M. et al. 1999. HLA and HIV-1: Heterozygote advantage and B*35CW*04 disadvantage. Science 283: 1748-1752.
Catania, J.A.,T. J. Coates, R. Stall, H.Turner, J. Peterson, N. Hearst, M. M. Dolcini, E. Hudes, J. Gagnon, J. Wiley, and R. Groves. 1992. Prevalence of AIDSrelated risk factors and condom use in the United States. Science 258: 1101-1106.
Culliton, B. 1990. Emerging viruses, emerging threat. Science 247:279-280.
De Cock, K. M., G.Adjorlolo, E. Ekpini,T. Sibailly, J. Kouadio, M. Maran, K. Brattegaard, K. M. Vetter, R. Doorly, and H. D. Gayle. 1993. Epidemiology and
transmission of HIV-2. Journal of the American Medical Association 270: 208-2086.
Deacon, N. J., et al. 1995. Genomic structure of an attenuated quasi species of
HIV-1 from a blood transfusion donor and recipients. Science 270: 988-991.
Deeks, S. G., M. Smith, M. Holodniy, and J. O. Kahn. 1997. HIV-1 protease inhibitors. Journal of the American Medical Association 277: 145-153.
Editorial staff. 1995. Death by denial. The Lancet 345: 1519-1520.
Ewald, P.W. 1994. Evolution of Infectious Disease. Oxford: Oxford University Press.
Feng,Y., C. C. Broder, P. E. Kennedy, and E. A. Berger. 1996. HIV-1 entry cofactor: Functional cDNA cloning of a seven-transmembrane, G protein-coupled
reactor. Science 272: 872-877.
Gao, F., E. Bailes, D. L. Robertson,Y. Chen, C. M. Rodenburg, S. F. Michael, L. B.
Cummins, L. O.Arthur, M. Peeters, G. M. Shaw, P. M. Sharp, and B. H. Hahn.
1999. Origin of HIV-1 in the chimpanzee Pan troglodytes troglodytes. Nature
397: 436-441.
Goldsmith, M. F. 1990. Science ponders whether HIV acts alone or has another
microbe’s aid. Journal of the American Medical Association 264: 665-666.
Groenink, M., R. A. M. Fouchier, S. Broersen, C. H. Baker, M. Koot, A. B. van’t
Wout, H. G. Huisman, F. Miedema, M.Tersmette, and H. Schuitemaker. 1993.
Relation of phenotype evolution of HIV-1 to envelope V2 configuration.
Science 260:1513-1515.
Hübner, A., M. Kruhoffer, F. Grosse, and G. Krauss. 1992. Fidelity of human immunodeficiency virus type 1 reverse transcriptase in copying natural RNA. Journal of Molecular Biology 223: 595-600.
Koblin, B.A., J. M. Morrison, P. E.Taylor, R. L. Stoneburner, and C. E. Stevens. 1992.
Mortality trends in a cohort of homosexual men in New York City, 19781988. American Journal of Epidemiology 136: 646-656.
Korber, B., J.Theiler, and S.Wolinsky. 1998. Limitations of a molecular clock applied to considerations of the origin of HIV-1. Science 280: 1868-1870.
Larder, B. A., P. Kellam, and S. D. Kemp. 1993. Convergent combination therapy
can select viable multidrug-resistant HIV-1 in vitro. Nature 365: 451-453.
Letvin, N. L. 1998. Progress in the development of an HIV-1 vaccine. Science 280:
1875-1880.
Liu, R. et al. 1996. Homozygous defect in HIV-1 coreceptor accounts for resistance of some multiply-exposed individuals to HIV-1 infection. Cell 86: 367377.
Mann, J. M. y D. J. M. Tarantola. Panorámica del SIDA en 1998. Investigación y
Ciencia. (Sept. 98):58-59.
Marlink, R., P. Kanki, I.Thior, K.Travers, G. Eisen,T. Siby, I.Traore, C-C. Hsieh,
M. C. Dia, E-H. Gueye, J. Hellinger,A. Gueye-Ndiaye, J-L. Sankalé, I. Ndoye,
S. Mboup, and M. Essex. 1994. Reduced rate of disease development after
HIV-2 infection as compared to HIV-1. Science 265:1587-1590.
Mohri, H., M. K. Singh,W.T.W. Ching, and D. D. Ho. 1993. Quantitation of zidovudine-resistant human immunodeficiency virus type 1 in the blood of treated and untreated patients. Proceedings of the National Academy of Sciences, USA
90:25-29.
Piot, P. 1998.The science of AIDS: A tale of two worlds. Science 280: 1844-1845.
Quillent, C. et al. 1998. HIV-1-resistance phenotype conferred by combination of
two separate inherited mutations of CCR5 gene. The Lancet 351: 14-18.
St. Clair, M. H., J. L. Martin, G.Tudor-Williams, M. C. Bach, C. L.Vavro, D. M. King,
P. Kellam, S. D. Kemp, and B.A. Larder. 1991. Resistance to ddI and sensitivity
to AZT induced by a mutation in HIV-1 reverse transcriptase. Science 253:15571559.
Samson, M. et al. 1998. Resistance to HIV-1 infection in caucasian individuals bearing mutant alleles of the CCR-5 chemokine receptor gene. Nature 382: 722725.
Shirasaka,T., R.Yarchoan, M. C. O’Brien, R. N. Husson, B. D.Anderson, E. Kojima,T. Shimada, S. Broder, and H. Mitsuya. 1993. Changes in drug sensitivity
of human immunodeficiency virus type 1 during therapy with azidothymidine, didieoxycytidine, and dideoxyinosine: An in vitro comparative study. Proceedings of the National Academy of Sciences, USA 90: 562-566.
Smith, M.W. et al. 1997. Contrasting genetic influence of CCR2 and CCR5 variants on HIV-1 infection and disease progression. Science 277: 959-965.
Wain-Hobson, S. 1993.The fastest genome evolution ever described: HIV variation in situ. Current Opinion in Genetics and Development 3: 878-883.
Zhu,T., B.T. Korber, A. J. Nahmias, E. Hooper, P. M. Sharp, and D. D. Ho. 1998.
An African HIV-1 sequence from 1959 and implications for the origin of the
epidemic. Nature 391: 594-597.
CAPÍTULO
2
Las pruebas de la evolución
Estas huellas las hizo el Australopithecus afarensis, una especie relacionada con los humanos actuales. Los fósiles son de Laetoli, Tanzania y tienen
3,6 millones de años de antigüedad. Advierta que dos individuos estaban andando, uno al lado del otro. (John Reader/Science Photo Library/Photo
Researchers, Inc.)
L
BIOLOGÍA EVOLUTIVA PLANTEA PREGUNTAS FUNDAMENTALES ACERCA DEL
mundo. ¿De dónde vienen los seres vivos? ¿Por qué hay tantas clases diferentes de organismos y cómo han llegado a ser tan eficientes en tareas como encontrar alimento o pareja, combatir enfermedades o evitar depredadores?
Charles Darwin fue un naturalista inglés que dedicó su vida a responder a estas cuestiones. Cuando comenzó a estudiar seriamente biología, como estudiante de un “college” en
los primeros años de la década de 1820, la explicación admitida en Europa sobre el origen
de las especies era la Teoría de la Creación Especial. Esta teoría mantenía que todos los organismos fueron creados por Dios durante los seis días de la creación, como se describe en el
libro bíblico del Génesis 1:1-2:4. Los tipos ideales formados en este proceso especial, incluidos Adán y Eva, fueron los progenitores de todos los organismos que viven en la actualidad.
La teoría mantenía que las especies se mantuvieron sin cambio, inmutables desde su creación
y que la variación dentro de cada tipo está estrictamente limitada. Se creía también que el
suceso de la creación había sido reciente: en 1664, el arzobispo James Ussher, de la iglesia protestante irlandesa, utilizó las genealogías del Viejo Testamento para calcular que la Tierra tenía
exactamente una edad de 5.668 años. Escribió que: “Cielo y Tierra, centro y sustancia se
hicieron en el mismo instante y que las nubes llenas de agua y el hombre fueron creados por
la Trinidad el 26 de octubre del año 4.004 a.C. a las 9 en punto de la mañana.”
A
21
22 PARTE I Introducción
Las teorías científicas tienen a
menudo dos componentes.
El primero es una descripción
acerca de un patrón que existe
en la naturaleza; el segundo es
un proceso que explica dicho
patrón.
Sin embargo, en la época en la que Darwin comenzó a trabajar en el problema, en la
década de 1830, era creciente la insatisfacción con la Teoría de la Creación Especial. La
investigación en las ciencias biológicas y geológicas estaba avanzando rápidamente y los
datos se contradecían con los dogmas centrales y las predicciones del creacionismo.
Para comprender los temas en los que Darwin se interesaba, es importante advertir
que las teorías científicas frecuentemente tienen dos componentes. El primero es una
declaración de principios: la reivindicación de que existe un patrón en el mundo natural. El segundo identifica el proceso responsable de dar lugar al patrón. La Teoría de la
Creación Especial, por ejemplo, plantea tres declaraciones de principios: (1) las especies
fueron creadas independientemente unas de otras, (2) no han cambiado a lo largo del
tiempo y (3) fueron creadas recientemente. De acuerdo con la Teoría de la Creación
Especial, el proceso responsable de este patrón fue un acto especial, o sobrenatural, de
creación de Dios.
El objetivo de este capítulo es revisar las pruebas que apoyan una declaración de principios alternativa, que Darwin denominó “descendencia con modificación”, y que más
tarde se llegó a conocer como evolución. De acuerdo con Darwin, las especies han cambiado a lo largo del tiempo y están relacionadas por descendencia de un antecesor común.
En el Capítulo 3 se introduce el proceso, llamado selección natural, que Darwin propuso como el principal agente responsable de este patrón.
Las primeras tres secciones de este capítulo exploran datos que se refieren a cada una
de las declaraciones de principios presentados por la Teoría de la Creación Especial, que
las especies son independientes, inmutables y recientes. La sección final introduce grupos
de datos obtenidos de diferentes campos científicos que corroboran y apoyan todas y cada
una de las predicciones hechas por la teoría de la evolución por selección natural.
2.1.
La Teoría de la Creación
Especial sostiene que cada
especie fue creada
independientemente. En
contraste, la Teoría de la
Evolución sostiene que los
organismos están
emparentados por un
antecesor común.
Parentesco de las formas de vida
Aunque el nombre de Darwin se asocia normalmente con la Teoría de la Evolución, no
fue el primero en reconocer los componentes del patrón teórico. El hecho de la evolución ya se había propuesto por varios investigadores hacia finales del siglo XVIII y principios del XIX, entre los que se encuentran el conde de Buffon, Erasmus Darwin (abuelo
de Charles) y el gran biólogo francés Jean-Baptiste Lamark (Eiseley 1958; Desmond y
Moore 1991). Estos primeros fueron partidarios de recusar la hipótesis de que cada especie fuera creada independientemente y arguyeron que las especies estaban relacionadas por
ascendencia común. Darwin reunió y sintetizó gran parte de las pruebas de esta conclusión en su libro Sobre el origen de las especies mediante selección natural, publicado en 1859.
¿Cuáles son estas pruebas?
Homología
Como los campos de la anatomía y de la embriología comparadas, desarrollados a
principios del siglo XIX, uno de los resultados más notables que surgieron fue el de las
semejanzas fundamentales subyacentes a las obvias diferencias físicas entre especies. Los primeros investigadores llamaron al fenómeno homología; literalmente, el estudio de las
semejanzas. Por ejemplo, Richard Owen, importante anatomista británico y el barón
Georges Cuvier de París, fundador de la anatomía comparada, describieron muchas
homologías entre los esqueletos y los órganos de los vertebrados.Algunas de éstas se indican en la Figura 2.1a. Darwin (1859, p. 434) se refiere a su trabajo cuando escribe:“¿Qué
podría ser más curioso que la mano del hombre, formada para agarrar, la de un topo para
cavar, la pierna del caballo, la aleta de la marsopa y el ala del murciélago, se hubieran construido de acuerdo con el mismo patrón, e incluyendo los mismos huesos y en las mismas
Capítulo 2 Las pruebas de la evolución 23
(a)
Húmero
Radio
Cúbito
Carpales
Metacarpales
Murciélago
Falanges
Humano
Caballo
Foca
Tortuga
Ave
(b)
Tortuga
(c)
Humano
Gallina
Pétalos
(recortados)
Antera
Rostelo
Estigma
Labelo
Sépalos
(recortados)
Epipactis latifolia
Orchis mascula
Figura 2.1 Homologías estructurales (a) Estas extremidades anteriores de los vertebrados se utilizan para diversas funciones, pero tienen la
misma secuencia y disposición de los huesos. En esta ilustración, los huesos homólogos están coloreados o sombreados del mismo modo y se
designan en el brazo humano. (b) Los embriones de distintos vertebrados son similares, especialmente en los comienzos del desarrollo. Los
embriones fotografiados aquí se encuentran en el estadio de primordio de la cola. (c) Las flores de las orquídeas son diferentes en tamaño y forma,
pero están formadas por elementos similares en estructura y orientación.
posiciones relativas?” La conclusión es que el diseño subyacente de cada una de las estructuras es similar, aunque las funciones y apariencias sean muy diferentes. Basándose en esta
observación, Darwin concluyó que las estructuras no fueron creadas independientemente, sino que están relacionadas por un linaje común. Su razonamiento fue que un constructor consciente no hubiera diseñado herramientas para agarrar, cavar, correr, nadar y
24 PARTE I Introducción
Las homologías estructurales
son un producto de patrones
de desarrollo compartidos.
Secuencias similares de
desarrollo son la consecuencia
de programas genéticos
homólogos.
Programas genéticos
homólogos son la
consecuencia de linajes
compartidos.
volar utilizando el mismo grupo de elementos estructurales en la misma disposición. De
acuerdo con Darwin, la homología apoya la teoría de la evolución.
Sin embargo, los datos no se limitaban a los vertebrados o a las formas adultas. El naturalista Louis Agassiz fue uno de los muchos que observaron que los embriones de los vertebrados, desde los peces a los humanos, son notablemente similares, especialmente en las fases
tempranas del desarrollo (Figura 2.1b). El mismo Darwin (1862) analizó la anatomía de la
flor de las orquídeas y demostró que, aun cuando son distintas en la forma, están formadas
realmente por la misma serie de piezas. Como las extremidades de los vertebrados, cada una
de las flores de la Figura 2.1c tiene las mismas partes en las mismas posiciones relativas.
¿Cuál es la causa de estas semejanzas? Agassiz, Owen, Cuvier y otros estudiosos anteriores reconocieron que las estructuras homólogas en los adultos se desarrollan de grupos
de células homólogas de los embriones. Por ello, la homología se definió originalmente
como una semejanza debida a vías de desarrollo compartidas. Pero, ¿por qué compartirían algunos organismos vías de desarrollo? Darwin arguyó que la descendencia de un antecesor común era la explicación más lógica. Afirmó que los embriones de la Figura 2.1c
eran semejantes debido a que todos los vertebrados evolucionaron del mismo antecesor
común y por ello algunos estadios del desarrollo han permanecido similares aunque los
peces, anfibios, reptiles y mamíferos se hayan diferenciado con el tiempo.
En la actualidad, los biólogos reconocen que las homologías estructurales y el desarrollo se deben a las homologías genéticas. Las estructuras embrionarias y adultas son similares entre especies debido a que los genes que codifican dichas estructuras son similares.
Por ejemplo, la Figura 2.2 presenta la secuencia de aminoácidos codificada por un gen que
está implicado en el desarrollo del ojo. Cuando Rebecca Quiring y sus colegas (1994)
compararon la secuencia de esta proteína de la mosca de la fruta con la de los vertebrados, encontraron que más de un 90% de los aminoácidos eran idénticos en ciertos segmentos. Propusieron que homologías genéticas como éstas eran responsables de las semejanzas en los órganos receptores de luz de los animales.
Los avances en genética molecular han revelado otras semejanzas fundamentales entre
organismos. Entre ellas, la más importante es el código genético. Con unas pocas excepciones, todos los organismos estudiados hasta la fecha utilizan los mismos tripletes de
nucleótidos, o codones, para especificar a los mismos RNA de transferencia portadores
de aminoácidos. Los biólogos interpretan estas semejanzas como pruebas de que los organismos vivos descienden de un antecesor que utilizó el mismo código genético. En el
Cuadro 2.1 se indica que la misma lógica evolutiva subyace en la utilización de organismos modelo en investigación biomédica y en la prueba de medicamentos.
Parentesco entre especies
El reconocimiento de Darwin del parentesco por compartir antecesores se extendió a otros
aspectos distintos de la homología. Su viaje a las Islas Galápagos tuvo una enorme influencia en su idea acerca del parentesco entre las especies. Mientras estuvo a bordo del H.M.S.
Beagle durante cinco años, en una misión exploratoria y de cartografía, Darwin coleccionó y catalogó la flora y la fauna que encontraba en su viaje. Le impresionaron especialmente los sinsontes comunes que encontró durante su trabajo en las Galápagos, debido a
que varias islas tenían poblaciones diferentes. Aunque todas ellas eran similares en color,
tamaño y forma (y por ello claramente emparentadas unas con otras) cada población de
sinsontes parecía lo bastante diferente como para clasificarse como una especie distinta.
Esto lo confirmó más tarde un taxónomo, colega de Darwin, cuando volvió a Inglaterra.
Darwin y otros completaron estos resultados con estudios que demostraron el mismo
patrón en las tortugas y los pinzones de las Galápagos: las distintas islas albergaban especies diferentes, aunque muy relacionadas (véase Desmond y Moore, 1991).
Capítulo 2 Las pruebas de la evolución 25
(a)
Segunda base
Primera
base
U
C
A
G
UGU
UGC
UGA
UGG
Cisteina
Cisteina
Parada
Triptófano
C
C
W
U
C
A
G
H
H
Q
Q
CGU
CGC
CGA
CGG
Arginina
Arginina
Arginina
Arginina
R
R
R
R
U
C
A
G
Asparagina
Asparagina
Lisina
Lisina
N
N
K
K
AGU
AGC
AGA
AGG
Serina
Serina
Arginina
Arginina
S
S
R
R
U
C
A
G
Ácido Aspártico
Ácido Aspártico
Ácido Glutámico
Ácido Glutámico
D
D
E
E
GGU
GGC
GGA
GGG
Glicina
Glicina
Glicina
Glicina
G
G
G
G
U
C
A
G
UUU
UUC
UUA
UUG
Fenilalanina
Fenilalanina
Leucina
Leucina
F
F
L
L
UCU
UCC
UCA
UCG
Serina
Serina
Serina
Serina
S
S
S
S
UAU
UAC
UAA
UAG
Tisosina
Tisosina
Parada
Parada
Y
Y
C
CUU
CUC
CUA
CUG
Leucina
Leucina
Leucina
Leucina
L
L
L
L
CCU
CCC
CCA
CCG
Prolina
Prolina
Prolina
Prolina
P
P
P
P
CAU
CAC
CAA
CAG
Histidina
Histidina
Glutamina
Glutamina
A
AUU
AUC
AUA
AUG
Isoleucina
I
Isoleucina
I
Isoleucina
I
Comienzo (Metionina M)
ACU
ACC
ACA
ACG
Treonina
Treonina
Treonina
Treonina
T
T
T
T
AAU
AAC
AAA
AAG
G
GUU
GUC
GUA
GUG
Valina
Valina
Valina
Valina
V
V
V
V
GCU
GCC
GCA
GCG
Alanina
Alanina
Alanina
Alanina
A
A
A
A
GAU
GAC
GAA
GAG
Aminoácido
Abreviatura
U
Codón
Tercera
base
(b)
humano L Q R N R T S F T Q E Q I E A L E K E F E R T H Y P D V F A R E R L A A K I D L P E A R I Q VW F S N R R A KWR R E L
ratón
codorniz
pez cebra
mosca de la fruta
ND
DS
G
G
Figura 2.2 Homologías genéticas (a) En casi todos los organismos estudiados, los mismos tripletes de nucleótidos, o codones,
especifican al mismo aminoácido transportado por los RNA de transferencia. (b) Este cuadro muestra la secuencia de aminoácidos de
una parte llamada el homeodominio de una proteína implicada en el desarrollo del ojo. (Quiring et al. 1994). Los puntos indican el
mismo aminoácido que la secuencia de arriba.
CUADRO 2.1 Homología y organismos modelo
L
a homología puede parecer un concepto abstracto,
pero realmente es la principal guía de la mayor parte
de las investigaciones biomédicas. La homología es la
razón por la que los investigadores médicos pueden obtener resultados válidos cuando comprueban la seguridad
de nuevos medicamentos en ratones o cuando estudian
las bases moleculares de enfermedades en ratas. Los resultados se pueden extrapolar a la especie humana si son
homólogas las bases moleculares o celulares del fenómeno que está siendo estudiado.
Los investigadores eligen un organismo de estudio,
también llamado organismo “modelo”, basándose en el
grado de homología necesaria para estudiar un proceso
o enfermedad concretos. Por ejemplo, en psiquiatría y en
ciencias del comportamiento, los monos y los primates
son a menudo el sujeto experimental preferido, debido
a que ciertos aspectos de su comportamiento y de las
estructuras cerebrales son homólogos de las de los humanos. Debido a que alguno de los genes implicados en los
procesos más básicos, como el ciclo celular, son homólogos entre parientes muy alejados, los investigadores
pueden utilizar la levadura de panificación (Saccharomyces
cerevisiae) para estudiar por qué ciertos genes que funcionan mal producen cáncer en la especie humana. En
un nivel incluso más básico, los genes implicados en la
reparación del DNA son homólogos entre la bacteria
Escherichia coli y los humanos. Los primates, las levaduras
y las bacterias comparten estas características con la especie humana debido a que las han heredado de un antecesor común.
26 PARTE I Introducción
Las especies que son muy
similares entre sí tienden a
agruparse geográficamente.
Esto sugiere que no fueron
creadas de manera
independiente, sino que son
descendientes de un antecesor
común que vivió en la misma
zona.
Para explicar este patrón, Darwin hipotetizó que una pequeña población de sinsontes
había colonizado las Galápagos desde América del Sur hacía mucho tiempo. Su tesis era
que la población se expansionó en el nuevo hábitat y que las siguientes subpoblaciones
colonizaron distintas islas del archipiélago. De este modo, una vez que las poblaciones de
sinsontes comunes quedaron físicamente aisladas unas de otras, divergieron lo suficiente
como para convertirse en especies distintas. Al igual que las homologías estructurales, la
existencia de formas íntimamente relacionadas en grupos de islas era un resultado lógico
de la descendencia con modificación.
Por el contrario, ambos patrones no eran consistentes con la creación especial, que predecía que los organismos fueron creados independientemente. De acuerdo con la creación
especial, no era de esperar ningún tipo de patrón concreto en el diseño o en las relaciones geográficas de los organismos.
Introducción a la idea de árbol
Los datos revisados en esta sección tienen un mensaje fundamental: las especies no son
independientes, sino que están conectadas por descendencia de un antecesor común. Esto
quiere decir que las especies tienen relaciones genealógicas similares a las genealogías familiares humanas. En el Capítulo 1 señalamos que la genealogía de un grupo de especies
recibe el nombre de filogenia y que una representación gráfica de estas relaciones se denomina árbol filogenético o cladograma.
En el Capítulo 13 introduciremos las técnicas que los biólogos evolutivos utilizan para
reconstruir las relaciones evolutivas y estimar la forma de los árboles filogenéticos. En
este momento nos hacemos preguntas más básicas: ¿cómo se leen y se interpretan las
filogenias? Y, ¿cómo las utilizan los biólogos para responder cuestiones sobre la evolución?
Los árboles filogenéticos son
representaciones visuales del
hecho de que las especies
están emparentadas por
descendencia de un antecesor
común.
Leyendo un árbol
La única figura en el libro de 490 páginas de Darwin El origen de las especies es un esquema que representa su visión de cómo las especies cambian a lo largo del tiempo. La ilustración es hipotética, pero incluye los tres elementos principales que se encuentran en una
filogenia real: puntas, ramas y nodos. Las puntas representan especies extinguidas o especies vivientes. Las ramas representan poblaciones ancestrales de estas especies en el tiempo.
Los nodos indican los puntos en donde una especie se dividió en dos o más poblaciones
descendientes.
Parte del dibujo de Darwin se reproduce en la Figura 2.3.Advierta que el eje vertical
del diagrama representa al tiempo y el eje horizontal indica la divergencia morfológica.
Para leer el árbol, comience por la población marcada con una A y continúe leyendo hacia
arriba. El esquema indica que la especie A se dividió inmediatamente en seis subpoblaciones. Cuatro de éstas se extinguieron rápidamente, pero las poblaciones marcadas con
a1 y m1 sobrevivieron al tiempo I. Estas poblaciones continuaron divergiendo con el tiempo y dieron lugar a subpoblaciones. Aunque la mayoría de estas nuevas poblaciones se
extinguieron finalmente, en el tiempo X, la especie ancestral A ha dado lugar a tres nuevas especies, marcadas como a10, f 10 y m10.
Al dibujar este esquema, Darwin inventó una técnica para ilustrar cómo las especies
están relacionadas por descendencia con modificación a partir de un antecesor común. Las
filogenias publicadas en la literatura científica actual son descendientes directas de este
ingenio gráfico.
La Figura 2.4a muestra uno de los modos en que se dibujan normalmente las filogenias en la actualidad. Las puntas de este árbol se etiquetan del Taxón 1 al Taxón 6 para ilustrar un punto importante: las puntas, ramas y nodos de una filogenia pueden representar
Tiempo
(cada línea horizontal representa
1.000 generaciones)
Capítulo 2 Las pruebas de la evolución 27
Divergencia morfológica
Figura 2.3 Árbol hipotético de Darwin Véase el texto para su explicación. Reproducido
con el permiso del Presidente y de los Colegiales del Harvard College.
poblaciones de organismos a cualquier nivel taxonómico: desde poblaciones o especies
hasta fila o reinos. (Un taxón es cualquier grupo de organismos, como una población,
género o familia; el plural es taxones.)
Otra clave para leer los árboles es reconocer que se pueden orientar verticalmente, con
el origen en la base y las puntas en la parte superior, u horizontalmente, con el origen a
la izquierda y las puntas a la derecha. Las ramas se pueden representar por líneas en diagonal o perpendiculares (Figura 2.4b). Si la longitud de la rama de un árbol en concreto es proporcional al tiempo o al aumento de cambio genético que se ha acumulado
desde que divergieron los taxones, entonces se proporciona una escala o un eje rotulado. Si no, las longitudes de las ramas son arbitrarias y se dibujan sólo con objeto de que
sea más legible.
Finalmente, los árboles evolutivos pueden o no tener raíz. Debido a que en los árboles con raíz se identifica en dónde se originó el linaje en cuestión, establecen el orden en
que ocurrieron los hechos que dieron lugar a la divergencia. Por el contrario, los árboles
sin raíz presentan las relaciones entre especie, pero no indican qué nodo o rama es más
moderno o mas primitivo (véase la Figura 2.4c).
Utilizando filogenias
El esfuerzo para estimar y leer filogenias se amortiza cuando un árbol permite a los investigadores responder a cuestiones a cerca de cómo han cambiado las especies con el
tiempo. Como ejemplo de las ideas que pueden surgir de la “lectura de un árbol”, consideremos la evolución de la vejiga natatoria de los peces.
La vejiga natatoria es un órgano que ayuda a los peces a flotar. Los músculos y los huesos son más pesados que el agua, por lo que, para evitar el hundimiento constante, muchos
peces mantienen una cámara, llamada vejiga natatoria, llena de aire. Estructuralmente, estos
órganos son homólogos de los pulmones que se encuentran en peces y en tetrápodos.
28 PARTE I Introducción
(a)
Taxón 6
Taxón 5
Taxón 4
Taxón 3
Taxón 2
Taxón 1
Taxones
hermanos
Más reciente
Puntas de
los nodos
terminales
D
B
A
Raíz
(b)
A
A
Más antiguo
Nodos
Tiempo
C
Ramas
(b)
A
A
B
F
B
F
C
E
C
E
D
D
(c)
D
D
E
C
E
C
F
B
F
F
BA
F
A
E
B
E
B
D
C
D
C
C
F
C
F
B
E
B
E
A
D
A A
A
D
A
A
B
B
B
B
F
C
F
C
E
D
E
D
D
E
D
E
C
C
F
D
E
A
F
B
C
Figura 2.4 Interpretación de un árbol filogenético (a) Para entender este árbol, comience por debajo y suba hacia arriba. La población
de la bifurcación marcada con A es la antecesora común a los taxones del 1 al 6. Se divide en dos grupos. Uno de éstos evolucionó hacia el Taxón
1; el otro evolucionó hacia la población de la bifurcación B, que es la antecesora común a los taxones del 2 al 5. ¿Qué hacen las poblaciones
representadas en las bifurcaciones C y D, y cuáles son sus relaciones con la población de la bifurcación B? (b) Estos gráficos muestran seis formas
de ilustrar las mismas relaciones evolutivas. Todos los árboles están orientados verticalmente, por lo que el taxón basal está debajo y los grupos
derivados arriba. Éstos también se podrían representar horizontalmente, girados 90º (según Mayden y Wiley 1992). (c) Este árbol sin raíz muestra
las mismas relaciones entre los taxones que están esquematizados en la parte (b). Sin embargo, no tiene raíz, por lo que no indica qué
ramificaciones se dieron al principio y cuáles se dieron más tarde en la evolución.
F
Capítulo 2 Las pruebas de la evolución 29
(Los tetrápodos, o “con cuatro pies”, incluyen a los anfibios, reptiles y mamíferos.)
Desde el punto de vista del desarrollo, tanto los pulmones como las vejigas natatorias se
originan como invaginaciones del intestino.
Gracias a los esfuerzos de los primeros investigadores, Darwin se dio cuenta de la homología entre el pulmón y la vejiga natatoria.Ya que los peces aparecen en el registro fósil
mucho antes que los tetrápodos y ya que las vejigas natatorias son mucho más frecuentes
en los peces que los pulmones, concluyó que los pulmones debieron haberse derivado de
las vejigas natatorias. ¿Es esto cierto?
En la Figura 2.5a se muestra la filogenia de los tetrápodos y de los principales grupos
de peces, basada en el análisis de características distintas de los pulmones y de las vejigas
natatorias. Adviértase que los pulmones ya se encuentran presentes en la población de la
base del árbol, que representa al antecesor común de todos los grupos presentados. Karl
Liem, el biólogo que hizo este estudio, hizo esta propuesta debido a que los pulmones se
encuentran en uno de los grupos más primitivos de peces con mandíbulas, los llamados
placodermos. Especímenes de un placodermo corriente en las rocas de la península Gaspé
de Quebec, llamado Bothriolepis, presenta impresiones que indican claramente un par de
pulmones bien desarrollados que se abren a partir de la faringe (Liem 1988; Colbert y
Morales 1991).También se encuentra pulmones o vejigas natatorias en cada uno de los
grupos descendientes de la filogenia, excepto en los tiburones y las rayas (elasmobranquios). Sin embargo, las vejigas natatorias se encuentra sólo en dos grupos: los superórdenes Condrósteos (un antiguo grupo con aletas radiales) y Teleósteos (el grupo de peces con
aletas radiales que incluyen a las formas más modernas).
Para averiguar cómo han cambiado los pulmones y las vejigas natatorias en el curso de
la evolución, Liem contó con un principio lógico llamado parsimonia. Invocar la parsimonia en biología evolutiva implica que, cuando se extraen conclusiones acerca de lo que
ocurre en la evolución, los investigadores favorecen las explicaciones simples sobre las
complejas. Es decir, los investigadores prefieren interpretaciones de los datos que minimicen el número de cambios evolutivos ocurridos. Esto es adecuado cuando se estudian
sucesos que raramente ocurren. Por ejemplo, en la Figura 2.5b se ilustran hipótesis opuestas de cómo evolucionaron las vejigas natatorias. La hipótesis 1 mantiene que las vejigas
natatorias evolucionaron tempranamente y luego dieron lugar a los pulmones en cuatro
ocasiones (en los linajes que dieron lugar a los Dipnoos y otros grupos, Cladistia,
Ginglimodi y Halecomorfos). La hipótesis 2 mantiene que las vejigas natatorias se originaron tardíamente y aparecieron independientemente en dos ocasiones (en los linajes que
conducen a los Condrósteos y a los Teleósteos. De acuerdo con el principio de la parsimonia, aceptamos la hipótesis 2 como más probable debido a que requiere sólo dos cambios, en lugar de cuatro.
Entonces, el análisis filogenético muestra que los pulmones se encontraban en la base
del árbol, que se perdieron completamente en los linajes que dieron lugar a tiburones y a
rayas y que los pulmones se transformaron en vejigas natatorias en dos linajes diferentes
de peces. Esta última conclusión está reforzada por la observación de que las vejigas natatorias de los Condrósteos y Telósteos se desarrollan de forma diferente: en los primeros se
originaron como invaginaciones del estómago y en los segundos como invaginaciones del
esófago (Liem 1988).
La conclusión final del análisis es importante: los peces respiraron aire antes de ser buenos flotadores. Lo que confundió a Darwin, y a muchos otros naturalistas, al suponer que
las formas ancestrales debían de tener vejigas natatorias, es que la mayor parte de los peces
actuales y muchas formas ancestrales las tienen. No tiene que ser necesariamente cierto
el que caracteres muy corrientes sean ancestrales. La interpretación evolutiva de la vejiga
natatoria en un contexto filogenético dejó clara la dirección real del cambio. La idea del
árbol es una herramienta poderosa para entender la historia de la vida.
La Teoría de la Evolución se
considera potente porque
sugiere nuevas ideas para
comprobar y conduce a nuevas
percepciones. El análisis del
origen de la vejiga natatoria de
los peces es un ejemplo de
esto. Este análisis se basó en
el reconocimiento de que las
especies están emparentadas
por ascendencia común.
30 PARTE I Introducción
Elasmobranquiomorfos
Dipnoos
Tetrápodos
(tiburones y rayas)
(peces
pulmonados)
(anfibios,
reptiles,
mamíferos)
Actinistia
Cladistia
(peces
(celacantos
acorazados)
y
otros)
Condrósteos
(peces
primitivos con
aletas radiales)
Ginglimodia Halecomorfos
(peces
aguja)
(familia
Amidae)
Teleósteos
(peces
actuales con
aletas radiales)
digestivo
pulmón
Pulmones presentes
vejiga natatoria
(a)
Hipótesis 1: Las vejigas natatorias evolucionan tempranamente
Elasmobranquiomorfos
Dipnoos Tetrápodos Actinistia Cladistia Condrósteos Ginglimodia Halecomorfos Teleósteos
Pérdida de pulmones
Pulmones presentes
Se obtiene vejiga
natatoria
Pérdida de vejiga natatoria;
se obtienen pulmones
Hipótesis 2: Las vejigas natatorias evolucionan tardíamente
Elasmobranquiomorfos
Dipnoos Tetrápodos Actinistia Cladistia Condrósteos Ginglimodia Halecomorfos Teleósteos
Se
obtiene
vejiga natatoria
Se obtiene vejiga
natatoria
Pérdida de pulmones
Pulmones presentes
(b)
Figura 2.5 Historia evolutiva de los pulmones y de las vejigas natatorias (a) Este esquema muestra una estima de las relaciones entre los
principales grupos de vertebrados que viven actualmente. En los dibujos, encima de cada grupo, los sacos delineados con líneas gruesas son
pulmones, los sacos con líneas dobles son vejigas natatorias y los sacos más pequeños rallados representan el tracto gastro-intestinal. En cada
dibujo la parte dorsal del animal está en la parte de arriba y la parte ventral en la parte de abajo. (En el cuerpo de un animal, los lados dorsales
miran hacia arriba y los ventrales hacia abajo.) (b) Estos árboles ilustran dos hipótesis opuestas de la evolución de los pulmones y de las vejigas
natatorias. Advierta que las relaciones entre los taxones son las mismas que en la parte (a). Véase el texto para su explicación.
Capítulo 2 Las pruebas de la evolución 31
2.2.
Cambios con el tiempo
Uno de los dogmas centrales de la Teoría de la Creación Especial fue que las especies, una
vez creadas, eran inmutables. Esta pretensión se combatió con varios tipos de pruebas que
apoyaban la hipótesis alternativa de que los organismos han cambiado con el tiempo. Los
datos que revisaremos aquí provienen tanto de las especies actuales como de formas
extintas preservadas en el registro fósil.
Pruebas en especies actuales
Cuando Darwin comenzó su trabajo sobre “la cuestión de las especies”, la anatomía comparada había descrito una serie de caracteres curiosos llamados estructuras vestigiales. Una
estructura vestigial es una parte del cuerpo no funcional, o rudimentaria, que es homóloga de una parte que tiene una función importante en especies íntimamente relacionadas.
En la Figura 2.6a se presentan varios ejemplos. Algunos peces ciegos, habitantes de cavernas, tienen huecos oculares, pero sin ojos; las aves y los insectos no voladores tienen alas reducidas; algunas serpientes tienen caderas y patas traseras minúsculas; los humanos tenemos un
hueso caudal reducido. Los humanos también tenemos músculos para erizar cada cabello
del cuerpo cuando se tiene frío o se está excitado. Este fenómeno es homólogo del erizado del pelaje de otros mamíferos, que indica alarma o amenaza agresiva. En los humanos la
respuesta homóloga da lugar a un carácter vestigial llamado tener la piel de gallina.
Caracteres vestigiales que se pueden identificar a tres niveles
Como las homologías descritas en la Sección 2.1, los caracteres vestigiales se pueden
observar a los niveles estructural, de desarrollo y genético. En la Figura 2.6b se observa un
carácter vestigial que aparece durante el desarrollo de las “manos” y pies de las aves. Las
(a)
(b)
Figura 2.6 Caracteres vestigiales Las estructuras
vestigiales y los estadios del desarrollo son comunes.
(a) Los humanos tienen un hueso de la cola rudimentario,
llamado el cóccix, en la base de su columna vertebral.
(Vincent Zuber/Custom Medical Stock Photo). Muchas
criaturas ciegas cavernícolas, como esta salamandra
(Typhlotriton spelaeus), tienen bulbos de tejido no funcionales
en lugar de ojos. (Nathan W. Cohen/Visuals Unlimited)
(b) Las gallinas adultas tienen tres dedos en sus alas y cuatro
en sus patas. Pero durante el desarrollo, aparece un dedo
extra durante un tiempo breve en la “mano” (izquierda) y en
el pie (derecho). (A.C. Burke/Alan Feduccia 1997)
32 PARTE I Introducción
Las estructuras vestigiales
son una manifestación de
cambios en el tiempo.
gallinas adultas tienen tres dedos en sus alas y cuatro en sus pies. Pero cuando se tiñe un
embrión de gallina con un colorante para el tejido que inicia el desarrollo del hueso, aparece un dedo extra (marcado con una flecha en la figura) que desaparece más tarde. ¿Por
qué? Darwin arguyó que la presencia de caracteres vestigiales como éstos no es explicable en el contexto de la creación especial. Pero de acuerdo con la Teoría de la Evolución,
se interpretan fácilmente. En este caso, la observación clave es que la mayoría de los tetrápodos fósiles y vivientes tienen cinco dedos en las extremidades anteriores y posteriores.
Luego es lógico suponer que los antecesores de las aves también tenían cinco dedos en
cada extremidad. La hipótesis evolutiva sostiene que el número de dedos se redujo a tres
o cuatro durante la evolución de la aves y que todavía aparece durante un corto período
del desarrollo el “dedo vestigial perdido”.
Un fenómeno similar se presenta en el ámbito molecular, en la forma de secuencias de
DNA llamadas pseudogenes. Estos “falsos genes” no codifican un RNA funcional o un
producto proteico. Como ejemplo, consideremos los genes que codifican a las proteínas
transportadoras de oxígeno, llamadas hemoglobinas. Los humanos tenemos una gran
familia de loci que codifican subunidades polipeptídicas de la hemoglobina.Tres de estos
loci son similares en estructura y secuencia a los genes funcionales, pero no dan lugar a
un producto. Uno de éstos, llamado el locus ψα (psi-alfa), se parece al locus normal α, pero
tiene mutaciones que impiden su transcripción normal. La existencia de un pseudogen no
funcional como éste es enigmática en la Teoría de la Creación Especial, pero fácilmente
comprensible en la Teoría de la Evolución. La explicación evolutiva es que en algún
momento en el pasado, una mutación dio origen a un codón de parada en la parte central de la secuencia normal e inutilizó de manera efectiva al locus. El pseudogen ha persistido como un vestigio molecular de un carácter normal. Proporciona pruebas de que
los organismos han cambiado con el tiempo.
Observación directa de cambios en el tiempo
También se puede observar directamente el cambio en el tiempo. Durante los pasados 60
años, los biólogos han documentado cambios evolutivos en cientos de especies distintas.
Como ejemplo, consideremos el reciente trabajo sobre el chinche del jaboncillo, un
insecto oriundo del sur de los Estados Unidos.
Los chinches del jaboncillo se alimentan agujereando con sus aparatos chupadores los
frutos de la planta huésped. Como se muestra en la Figura 2.7, consiguen introducir la
cubierta de las semillas que se encuentran dentro del fruto y luego succionan el contenido de éstas. Los datos de la Figura 2.7 demuestran que en la primera parte del siglo XX,
los chinches del jaboncillo recogidos en Florida y conservados en colecciones de museos tienden a tener unos labios chupadores extraordinariamente largos. Esto es lógico, ya
que en aquellos tiempos, la planta huésped más importante para estos chinches era el farolillo de fruto grande, que se presenta en la figura. Sin embargo, hacia mediados del siglo XX,
muchas poblaciones del chinche del jaboncillo de Florida comenzaron a alimentarse de
los pequeños frutos de un arbolillo que acababa de ser importado de Asia, del género
Koelreuteria. Como muestra la figura, los chinches del jaboncillo recogidos después del
cambio de huésped tienden a tener unos aparatos chupadores más pequeños que las
poblaciones anteriores. Las características del chinche del jaboncillo no son inmutables.
Cambian drásticamente con el tiempo.
Pruebas del registro fósil
Un fósil es la traza de cualquier organismo que vivió en el pasado. El conjunto de todas
las colecciones de fósiles del mundo repartidos en miles de distintas instituciones e individuos se denomina el registro fósil.
Arbolillo del género Koelreuteria
introducido en Florida
Capítulo 2 Las pruebas de la evolución 33
Fruto del arbolillo del género Koelreuteria
Fruto del farolillo
9,0
Longitud del pico (mm)
8,5
8,0
Figura 2.7 Cambios evolutivos en los
chinches del jaboncillo Los dibujos de la
7,5
parte superior de esta figura muestran a chinches
del jaboncillo alimentándose del fruto del farolillo
(izquierda) y del arbolillo del género Koelreuteria
(derecha). El farolillo es nativo del estado de
Florida, mientras que el arbolillo del género
Koelreuteria se introdujo hacia finales de la
década de 1920 desde Asia. En el eje de
coordenadas se representa la longitud de los
picos de las hembras de los chinches del
jaboncillo de Florida de colecciones de museo
(cada punto representa a un individuo). Véase el
texto para su explicación. De las Figuras 1 y 6 de
Carroll y Boyd (1992), Copyright © 1992
Evolution. Reimpreso con permiso.
7,0
6,5
6,0
5,5
1880
1900
1920
1940
Fecha
1960
1980
El simple hecho de la existencia de los fósiles y de que la gran mayoría de las formas
fósiles son especies distintas de las que viven actualmente, argumenta que la vida ha cambiado a lo largo del tiempo. Cuatro observaciones concretas acerca del registro fósil ayudaron a Darwin y a otros científicos del siglo XIX a entender este punto.
El hecho de la extinción
En 1801, el barón Georges Cuvier, especialista en anatomía comparada, publicó una lista
de 23 especies desaparecidas. Su trabajo constituyó un desafío a la hipótesis, ampliamente aceptada, de que las raras formas del registro fósil se encontrarían finalmente como especies vivas, una vez que los científicos europeos hubieran visitado todas las partes del
globo. La lista puso en duda esta hipótesis, ya que incluía a los mastodontes y a otras enormes criaturas recuperadas de los estratos de la cuenca de París. Estas especies eran tan grandes que parecía altamente improbable que no se hubieran detectado todavía.
El hecho de la extinción deja de generar controversias después de 1812, cuando Cuvier
publicó un cuidadoso examen de fósiles del alce irlandés: el ciervo gigante de la edad de
los hielos que se muestra en la Figura 2.8. Se habían encontrado fósiles de este ciervo en
todo el norte de Europa y en las Islas Británicas. El análisis de Cuvier demostró que era
una especie extinguida y no simplemente una versión gigante de las especies que vivían
en la zona.
34 PARTE I Introducción
Figura 2.8 El alce irlandés confirma el hecho de la extinción
Cuvier confirmó que los fósiles del ciervo gigante de la era glaciar, llamado
alce irlandés, representaba a una especie extinguida (Neg. No. 22851.
Photo AMNH. Cortesía del Dept. of Library Services. American Museum of
Natural History).
Cuando Darwin escribía El origen de las especies, se habían encontrado plantas y animales
extintos en rocas que se habían formado en muchos momentos y lugares diferentes. Los
creacionistas argumentaban que estas especies habían perecido en una serie de riadas, similares al suceso bíblico del tiempo de Noé. Por el contrario, Darwin y otros biólogos interpretaban las especies extintas como parientes de organismos vivos. Señalaban el hecho de
la extinción como una prueba más de que la fauna y la flora terrestre había cambiando
con el tiempo.
La ley de la sucesión
Ya en el siglo XVIII, el paleontólogo Willian Clift fue el primero en publicar una observación, confirmada más tarde y ampliada por Darwin (Darwin 1859; Eiseley 1958): los
organismos fósiles y vivientes de la misma zona geográfica están emparentados y son claramente diferentes de los organismos encontrados en otras zonas. Clift trabajaba en la fauna
de marsupiales extintos de Australia y advirtió su íntima relación con las formas vivas;
Darwin analizó a los armadillos de Argentina y sus relaciones con los glyptodontos fósiles que él había desenterrado (Figura 2.9). Esta correspondencia entre formas fósiles y
formas vivientes se denomina ley de la sucesión. La ley mantiene que a las especies fósiles que se encuentran en un área determinada les suceden especies vivientes similares. El
resultado fue apoyado por los análisis en una amplia variedad de localizaciones y grupos
taxonómicos, y proporcionó muchas pruebas del cambio a lo largo del tiempo.
Formas de transición
Darwin mantenía que las especies habían cambiado a lo largo del tiempo y que los fósiles
eran representantes de poblaciones ancestrales a las especies actuales. Si esto era así, entonces el registro fósil debería contener formas de transición entre los grupos principales de
organismos. La predicción es que las especies de transición deberían tener tanto características de las poblaciones ancestrales como caracteres nuevos observados en las especies des-
Capítulo 2 Las pruebas de la evolución 35
Figura 2.9 La “Ley de la sucesión” Los primeros investigadores observaron una íntima relación entre especies
fósiles y actuales en las mismas zonas geográficas, y entre formas fósiles de estratos de roca adyacentes, por lo que
rutinariamente dicho patrón se conocía como la ley de la sucesión. Darwin advirtió las semejanzas entre los
armadillos pigmeos contemporáneos (Zaedyus pichiy)(izquierda) y el gliptodonto fósil (derecha) de la Argentina.
(Foto de Tom McHugh/Photo Researchers, Inc.).
cendientes. Un buen ejemplo es el ave más antigua del registro fósil, el Archaeopteryx. La presencia de plumas identifica claramente a esta especie como un ave, pero el esqueleto es tan
parecido al de los dinosaurios que un espécimen fue una vez identificado erróneamente
como el dinosaurio terópodo Compsognathus. El Archaeopteryx representa una transición
entre las poblaciones ancestrales de dinosaurios y sus descendientes, las aves.
Debido a que durante su vida se habían descubierto muy pocas formas de transición,
Darwin se esmeró en explicar aquello que era raro en el registro fósil en una sección de su
libro denominada “Dificultades de la teoría.” Sin embargo, en los años siguientes se encontraron un gran número de formas de transición. Considere el fósil de ballena dibujado en la
Figura 2.10. Debido a que los fósiles de mamífero más primitivos representan a especies
terrestres, los biólogos dedujeron que los antecesores de las ballenas también vivieron sobre
la tierra y tenían extremidades funcionales. (Como muestra la figura, algunas ballenas modernas todavía tienen extremidades vestigiales.) Luego entre estos grupos ancestrales y las ballenas modernas debería de haber formas intermedias que tendrían extremidades funcionales,
así como rasgos que les identificaran como especies habitantes del mar. Dos de tales formas
de transición se muestran en la figura. La primera, llamada Ambulocetus natans, se descubrió
y describió por J. G. M. Thewissen y sus colaboradores (1994). Este fósil se estima que tiene
unos 50 millones de años de antigüedad. El segundo es Basilosaurus isis, una especie fósil analizada por Philip Gingerich y sus colegas (1990), que vivió aproximadamente hace unos 38
millones de años. Como se había pronosticado, las especies fósiles son intermedias entre antecesores con extremidades y descendientes sin extremidades. De sus análisis de cómo articulaban la extremidad con el cuerpo,Thewissen et al. sugieren que Ambulocetus utilizaba sus
extremidades para nadar, como hacen muchas nutrias actuales. El grupo de Gingerich sostiene que las extremidades de Basilosaurus eran demasiado reducidas para ayudarle en la natación y podrían haber servido como órganos para asirse durante la cópula. Cualquiera que
sea la función de estas extremidades, los fósiles señalan una transición evolutiva importante.
Cambio ambiental
Los fósiles de ballena que se presentan en la Figura 2.10 se encontraron en los desiertos de
Egipto y en las colinas de Pakistán, juntamente con almejas, caracoles y otras especies marinas. En la época de Darwin, se habían descubierto fósiles de organismos marinos en los Andes
en América del Sur, en los Alpes en Europa y en el Gran Cañón en el árido sudoeste norteamericano. Darwin interpretó estos datos como prueba de que las condiciones ambien-
En el registro fósil, las formas
de transición indican tanto la
ganancia como la pérdida de
características prominentes
con el tiempo.
36 PARTE I Introducción
(a) Hace 50 millones de años
50 cm
(b) Hace 38 millones de años
Figura 2.10 Formas de
transición (a) Ambulocetus
natans (traducido literalmente
significa “ballena andadora que
nada”) es un fósil de hace unos 50
millones de años. Tenía
extremidades posteriores
funcionales, que probablemente
utilizaba como paletas para nadar.
De Thewissen et al. (1994).
(b) Basilosaurus isis es un fósil de
hace unos 38 millones de años.
Tenía extremidades posteriores
reducidas, que probablemente no
eran funcionales para nadar. En
su lugar, las extremidades
anteriores podrían haber sido
utilizadas como estructuras para
agarrar en la cópula. Según
Gingerich et al. (1990).
(c) Algunas ballenas actuales
tienen un fémur y una pelvis
vestigiales. Copyright © 1990,
1994, American Association for
the Advancement of Science.
Reimpreso con permiso.
~40 cm
(c) Contemporáneo
Pelvis
Femur
tales no se habían mantenido constantes. Sugirió que los hábitats habían cambiado de localización y características a lo largo del curso de la historia. Sostuvo que los hábitats y el paisaje
terrestre estaban siendo continuamente modificados, igual que lo eran las especies.
2.3.
La edad de la Tierra
En el tiempo en que Darwin comenzó a trabajar en el origen de las especies, los datos de
la joven ciencia de la Geología habían desafiado un hito de la Teoría de la Creación
Especial: que la tierra tenía sólo unos 6.000 años de antigüedad. Se fueron acumulando
pruebas de que la tierra era más antigua.
Capítulo 2 Las pruebas de la evolución 37
Gran parte de las pruebas se cimentaron en el principio del uniformismo, enunciado por James Hutton a finales del siglo XVIII. El uniformismo es la afirmación de que los
procesos geológicos que tienen lugar ahora han actuado de manera similar en el pasado.
Se propuso en directo contraste con la hipótesis denominada catastrofismo. Ésta era una
propuesta que afirmaba que las formaciones geológicas actuales son el resultado de sucesos catastróficos, como el diluvio universal de la Biblia, que ocurrió en el pasado en una
escala nunca observada en la actualidad.
Las suposiciones del uniformismo y el rechazo del catastrofismo llevaron a Hutton, y
más tarde a Charles Lyell, a deducir que la Tierra era inimaginablemente vieja en términos humanos. Esta conclusión fue apoyada por datos. Estos primeros geólogos midieron
la tasa del proceso de formación de las rocas, como la deposición de lodo, arena y grava
en las playas y deltas de los ríos y la acumulación de conchas marinas (los precursores de
la caliza). Basándose en estas observaciones, quedó claro la gran cantidad de tiempo que
se necesitaba para producir las grandes formaciones rocosas que se habían cartografiado
en las Islas Británicas y Europa por estos investigadores.
La escala de tiempo geológico
Cuando Darwin comenzó su trabajo, Hutton y sus seguidores ya se encontraban en
medio de un esfuerzo de 50 años para disponer las formaciones más importantes de rocas
y los estratos productores de fósiles de Europa en una secuencia de reciente a antigua. Su
técnica se denominó datación relativa debido a que su objetivo era determinar lo vieja
que era cada formación rocosa con relación a otros estratos. La datación relativa fue un
ejercicio de lógica basado en las siguientes suposiciones:
• Las rocas más jóvenes se depositan sobre las rocas más viejas (el llamado principio de
la superposición).
• La lava y las rocas sedimentarias, como areniscas, calizas y arcillas, se depositaron originalmente en posición horizontal. Por ello, cualquier tipo de inclinación o de pliegue
en estos tipos de roca deben de haber ocurrido después de su deposición (principio de
la horizontalidad original).
• Las rocas que penetran en grietas de otras rocas, o como diques, son más jóvenes que
las rocas huésped (principio de las relaciones cruzadas).
• Cantos rodados, guijarros u otros fragmentos que se encuentran formando una roca,
son más viejos que su roca huésped (principio de las inclusiones).
• Las formas de vida fósil más tempranas son más simples que las formas más recientes y
las formas más recientes son más similares a las formas actuales (principio de la sucesión de la fauna).
Utilizando estas reglas, los geólogos establecieron la cronología de fechas relativas conocida como la escala de tiempo geológico (Figura 2.11).También desarrollaron el concepto de columna geológica, que es una historia geológica de la Tierra basada en una
secuencia compuesta de estratos rocosos de los más viejos a los más jóvenes. (No hay ningún lugar en la Tierra en donde todos los estratos de roca que se han ido formado a lo largo
del tiempo se encuentren todavía presentes. Siempre hay huecos porque algunos estratos
han sido completamente erosionados. Los geólogos han sido capaces de reunir un registro
completo de la historia geológica combinando los datos de diferentes localizaciones.)
El principio del uniformismo, la escala de tiempo geológico y la columna geológica
proporcionaron impresionantes pruebas de la antigüedad de la Tierra. Los geólogos
comenzaron a trabajar en una escala de tiempo de decenas de millones de años, en lugar
de unos pocos miles de años, mucho antes de que Darwin publicara sus ideas sobre el
cambio a lo largo del tiempo y de la descendencia con modificación. Estos datos fueron
La joven ciencia de la Geología
confirmó que la tierra había
existido durante larguísimos
períodos de tiempo. La
evolución es un proceso que
depende del tiempo, pero la
creación especial no.
38 PARTE I Introducción
importantes para la Teoría de la Evolución. La creación especial es un proceso instantáneo, pero el cambio evolutivo requiere largos períodos de tiempo para producir la diversidad de la vida que observamos en la actualidad.
Eon
Era
Período
Época
Edad
Ma
Formas de vida
Holoceno
Neogeno
Terciario
Cenozoico
Cuaternario
Pleistoceno
Plioceno
Mioceno
Oligoceno
Paleógeno
Eoceno
Paleoceno
Cretácico
Mesozoico
Fanerozoico
Tardío
Medio
Temprano
Tardío
Triásico
55,6
Primeras margaritas
Primeros primates
Primeras praderas
Primeras ballenas
Primeros caballos
65
Extinción de dinosaurios
98,9
Primeros mamíferos
placentarios
23,8
33,5
144
160
206
228
Primeras plantas con
vasos conductores de
agua
290
Primeros mamíferos
reptilianos
Carbonífer
Paleozoico
353,7
Devónico
408,5
Primeros reptiles
Primeros anfibios
Primeras plantas leñosas
Primeros insectos
Primeras plantas vasculares
Silúrico
439
495
Primeros peces
(sin mandíbulas)
Primeras plantas terrestres
Cámbrico
Hadeico Arcaico Proterozoico
eras, períodos y épocas que se
presentan en la parte izquierda de esta
tabla se estableció mediante la técnica
de la datación relativa. Cada intervalo
de tiempo con nombre está asociado a
una fauna y flora fósil característica. El
tiempo absoluto que se incluye aquí se
añadió mucho más tarde, cuando se
dispuso de los sistemas de datación
radioactiva. La abreviatura Ma significa
hace millones de años.
Primeros mamíferos
Primeros dinosaurios
251
Ordovicico
Figura 2.11 La escala de tiempo
geológico La secuencia de eones,
Primeras aves
180
Pérmico
Misisipiense
Primeras fanerógamas
Medio
Escitiense
Pensilvaniense
Primeros Homo
5,2
Tardío
Temprano
Jurásico
1,8
543
Primeros organismos
pluricelulares
Primeros eucariotas
2.500
Primeras bacterias
3.600
¿Origen de la vida?
Rocas más antiguas
4.600
Formación de la Tierra
Capítulo 2 Las pruebas de la evolución 39
Datación radioactiva
Hacia mediados del siglo XIX, Hutton, Lyell y sus seguidores habían establecido, más allá
de toda duda razonable, que la Tierra era vieja. Pero, ¿cuánto? ¿Cuánto tiempo había pasado desde que la vida comenzó en la Tierra?
El descubrimiento de Marie Curie de la radioactividad a principios del siglo XX, dio
a los científicos un modo de contestar a estas cuestiones. Utilizando una técnica llamada
de datación radioactiva, los físicos y geólogos comenzaron a asignar edades absolutas a
los datos relativos establecidos por la escala de tiempo geológico.
La técnica de la datación radioactiva utiliza los isótopos inestables de los elementos que
se encuentran en la naturaleza. Estos isótopos se desintegran, lo que significa que se transforman en otros elementos diferentes o en isótopos diferentes del mismo elemento. Cada
isótopo se desintegra con una tasa particular y constante, que se mide con una unidad llamada vida media. La vida media es el espacio de tiempo que tarda el 50% del isótopo original en pasar al siguiente isótopo (Figura 2.12). El número de sucesos de desintegración
observados en una muestra de roca con el tiempo depende sólo del número de átomos
radioactivos que haya. Las tasas de desintegración no están afectadas por la temperatura,
la humedad o por ningún otro factor ambiental. Por ello, los isótopos radioactivos funcionan como relojes naturales. Para más detalles véase el Cuadro 2.2.
Debido a sus largas vidas medias, los sistemas potasio-argón y uranio-plomo son los
isótopos elegidos para determinar la edad de la Tierra. Usando estos sistemas, ¿qué rocas
se pueden analizar para determinar cuándo se formó la Tierra? Los modelos corrientes de la formación de la Tierra predicen que el planeta estuvo fundido durante gran
parte de su historia primitiva, lo que hace que la respuesta a esta pregunta sea difícil.
Sin embargo, si asumimos que todos los componentes de nuestro sistema solar se formaron al mismo tiempo, hay dos tipos de rocas candidatas disponibles para datar el origen de la Tierra: las rocas lunares y los meteoritos.Tanto el sistema de datación uranioplomo, como el de potasio-argón, sitúan la edad de las rocas lunares traídas por los
astronautas del Apolo en 4.530 millones de años. Además, prácticamente todo meteorito encontrado en la Tierra que ha sido datado tiene una edad de unos 4.600 millones de años. Por consiguiente, los científicos pueden deducir que el planeta tiene unos
4.600 millones de años.
100% del isótopo paterno
e
Núm
Número de átomos
75% del isótopo paterno
25% del isótopo filial
ótopo filial
os del is
m
o
t
á
ro de
50% del isótopo paterno
50% del isótopo filial
25% del isótopo paterno
75% del isótopo filial
Núm
0
1
2
12.5% del isótopo paterno
87.5% del isótopo filial
ero
de á
t o m os
del isóto
po
3
Vidas medias transcurridas
p
Figura 2.12 Desintegración radioactiva Muchos
isótopos radioactivos se desintegran a través de una serie
de intermediarios hasta que se produce un isótopo hijo
estable. Los investigadores miden la proporción de
isótopo paterno y filial en una muestra de roca, y luego
utilizan un gráfico como éste para convertir la proporción
medida al número transcurrido de vidas medias.
Multiplicando el número de vidas medias que han pasado
por el número de años que tarda para que transcurra la
vida media, se obtiene una estima de la edad absoluta de
la roca.
40 PARTE I Introducción
CUADRO 2.2 Una mirada con detalle de la datación radioactiva
L
a datación radioactiva permite a los geólogos asignar
edades absolutas a las rocas. La técnica funciona de la
siguiente manera: primero se determina la vida media de
un isótopo radioactivo poniendo una muestra en un instrumento que registre el número de desintegraciones con
el tiempo. Desde luego, para isótopos de larga vida, los investigadores deben extrapolar de los datos recogidos durante un corto intervalo de tiempo. Luego se mide en una
muestra de la roca la proporción de isótopos paternos y
filiales, a menudo con un instrumento llamado espectrómetro de masas. Una vez que se conoce la vida media del
isótopo paterno y la proporción actual de los isótopos
paterno y filial, se puede calcular el número de años que
han pasado desde que se formó la roca.
Un supuesto crítico aquí es que se conoce la proporción de isótopo paterno y filial cuando se formó la roca.
Este supuesto se puede comprobar. Por ejemplo, la datación con potasio-argón es un sistema importante para
datar rocas de origen volcánico. Se puede pronosticar
que, inicialmente, no habría nada del isótopo filial, el
argón-40. Esto se debe a que el argón-40 es un gas que
burbujearía de la roca líquida y sólo comenzaría a acumularse después de su solidificación. Las observaciones de
flujos de lava recientes confirman que esto es así: expresado como una razón de porcentajes, la razón de potasio-40
a argón-40 en basaltos, lavas y cenizas recién formados es,
como se pronosticó, 100:0 (véase Damon 1968, Faure
1986).
De los muchos isótopos radioactivos presentes en la
corteza terrestre, los isótopos enumerados en la Tabla 2.1
son los más útiles. No solo son lo bastante corrientes como
para encontrarse en cantidades mensurables, sino que también son estables en el sentido de que no migran fácilmente de o hacia las rocas después de su formación inicial.
Si las moléculas se desplazaran, tendríamos que desechar
nuestras estimas de la edad de las rocas circundantes.
Para elegir un isótopo adecuado para la datación de las
rocas y de los fósiles de una edad concreta, los geocronólogos y paleontólogos buscan isótopos de vida media lo
bastante corta como para permitir que se acumule una cantidad mensurable del isótopo filial, pero lo bastante larga
como para asegurar que todavía quede una cantidad mensurable del isótopo paterno. En muchos casos se puede utilizar más de un sistema de isótopos para las mismas rocas o
fósiles, proporcionando una comprobación independiente
de la fecha.
Tabla 2.1 Isótopos paterno y filial utilizados en la datación radioactiva
Isótopo
paterno
Isótopo
filial
Vida media del
paterno (años)
Rango de datación
efectiva (años)
Materiales normalmente
datados
Rubidioestroncio
Rb-87
Sr-87
47.000 millones
10 millones–4.600 millones
Minerales ricos en potasio,
como la biotita, potasio,
muscovita, feldespato y
hornablenda; rocas volcánicas
y metamórficas.
Uranioplomo
U-238
Pb-206
4.500 millones
10 millones–4.600 millones
Zirconio, uraninita, y ganga
de uranio, como la pecblenda;
rocas ígneas y metamórficas.
Uranioplomo
U-235
Pb-207
713 millones
10 millones–4.600 millones
Igual que antes.
Torioplomo
Th-232
Pb-208
14.100 millones
10 millones–4.600 millones
Zirconios, uraninita.
Potasioargon
K-40
Ar-40
1.300 millones
100.000–4.600 millones
Minerales ricos en potasio
como la biotita, muscovita y
feldespato potásico; rocas
volcánicas.
Carbono-14
C-14
N-14
5.730
100–100.000
Cualquier material que lleve
carbón, como huesos, madera,
conchas, carbón vegetal,
ropas, papel y excrementos de
animales.
Método
Capítulo 2 Las pruebas de la evolución 41
Esto nos lleva a la siguiente pregunta, ¿cuánto hace que evolucionó la vida sobre la
Tierra? Los organismos fósiles más antiguos descubiertos hasta el momento son impresiones de células bacterianas en rocas de unos 3.500 millones de años de Australia
Occidental (Schopf 1993). Las pruebas químicas de vida más antiguas en rocas de
Groenlandia datan de más de 3.700 millones de años. Las pruebas químicas son gránulos
de carbón que tienen una proporción característica de los isótopos del carbono 13C y
12
C. Las formas vivas absorben preferentemente 12C y el carbono que se encuentra en
las rocas de Groenlandia tiene mucho menos 13C y más 12C de lo esperado de acuerdo con la abundancia real de los dos isótopos en la naturaleza. Por ello, los investigadores deducen que los gránulos de carbón representan restos de seres vivos (Mojzsis et
al. 1996; Rosing 1999). Estos datos sugieren que la Tierra no tuvo vida durante unos
900 millones de años y que la evolución se ha producido durante unos 3.700 millones
de años.
En el siglo XIX, la datación relativa sugería que la Tierra era mucho más vieja de los
6.000 años predichos por el obispo Ussher. En el siglo XX, la datación absoluta confirma
que la vida ha existido unas 600.000 veces más del tiempo sugerido por la Teoría de la
Creación Especial.
2.4.
Correspondencia entre grupos de datos
Los datos revisados en este capítulo contradicen las propuestas de que las especies fueron
creadas independientemente, de que las especies son inmutables y de que la Tierra es joven.
Irónicamente, muchos de los datos que Darwin utilizó para refutar estas hipótesis, fueron
reunidos por ardientes creacionistas, como Cuvier,Agassiz y Owen. Estos científicos contribuyeron en observaciones sobre homologías estructurales y de desarrollo, caracteres vestigiales, extinción, la ley de la sucesión y la escala de tiempo geológico.
Sin embargo, con todo lo persuasivas que son las pruebas de la evolución, es importante advertir que no hay ningún gran experimento que haya descartado la creencia en
la Teoría de la Creación Especial y abierto un camino para una nueva teoría. Observaciones
tales como homologías estructurales y de desarrollo no refutan una creación especial. Más
bien, la evolución fue simplemente mucho más eficaz para explicar los datos.
La observación directa de la evolución ha proporcionado pruebas abrumadoras del
cambio a lo largo del tiempo. Pero hay otro tipo de datos que también apoyan los componentes del patrón de la teoría de la evolución. Es la correspondencia entre fuentes
independientes de datos sobre la historia de la Tierra y la historia de la vida. En el ejemplo que resumimos aquí, datos del análisis del campo magnético terrestre, datación
radiactiva y el registro fósil nos cuentan una historia coherente acerca del cambio a lo
largo del tiempo.
Cambio geológico y el movimiento de las placas
Los geólogos interpretan la historia de la Tierra mediante la teoría de la tectónica de
placas. Esta serie de hipótesis ha desempeñado un principio organizador central en la
ciencia geológica desde finales de la década de 1960. Las directrices de esta teoría sostienen que la corteza terrestre está fragmentada en placas y que la posición de estas placas (y por ello la localización de continentes y océanos) ha cambiado con el tiempo. El
proceso responsable de este patrón es la distribución desigual del calor en el interior
de la Tierra que dirige el movimiento de las placas debido a que ciertas rocas se dilatan (para saber más de cómo esta teoría se desarrolló y se comprobó véase Chernicoff
1995).
Capítulo 1 Las pruebas de la evolución 42
Los geólogos pueden utilizar datos sobre la historia del campo magnético terrestre para
seguir la pista del movimiento de los continentes con el tiempo. Esto es posible debido
a que los minerales magnéticos pierden su magnetismo cuando se calientan lo suficiente.
Cuando los minerales desmagnetizados alcanzan la superficie terrestre en una erupción
volcánica, se enfrían y se remagnetizan en la dirección marcada por el campo magnético terrestre. De este modo, los campos magnéticos quedan congelados en rocas volcánicas. Como la placa que contiene estas rocas se desplaza, la dirección del campo
magnético “congelado” comienza a diferir del campo magnético terrestre real. Debido
a que la dirección del campo magnético congelado no cambia, registra fehacientemente dónde se encontraba una placa concreta en un momento dado de la historia terrestre. Recogiendo rocas volcánicas que se originaron en momentos diferentes en la misma
placa y luego resolviendo dónde tenía que haber estado la placa para producir cada uno
de los campos magnéticos antiguos, los geólogos pueden reconstruir la historia del movimiento de las placas. La Figura 2.13 muestra los tipos de mapas que resultan. Los mapas
que se reproducen aquí muestran la posición de los continentes en los pasados 90 millones de años.
Historia de los mamíferos marsupiales
Para reconstruir cómo los
marsupiales se desplazaron
de un continente a otro con el
tiempo, se pueden combinar
datos de la tectónica de
placas, de la datación
radiológica y del registro fósil.
¿De qué manera los datos sobre los movimientos de las placas apoyan los componentes del
patrón de la evolución? Cuando se combinan datos geológicos con datos radioactivos y
datos del registro fósil, surge un esquema coherente de cambio a lo largo del tiempo. Por
ejemplo, consideremos la historia de un grupo de mamíferos, los marsupiales. Los marsupiales se distinguen por su forma de reproducción: después de un embarazo corto, las
madres dan a luz a diminutos hijos que, entonces, escalan a una bolsa en donde continúan el desarrollo. Los marsupiales son el tipo de mamífero dominante que se encuentra en
Australia; en América del Sur todavía se encuentran unas pocas especies y en América del
Norte vive la zarigüeya.
Sin embargo, el registro fósil demuestra que los marsupiales vivieron por todo el
mundo. Advierta, en la Figura 2.13, que los marsupiales aparecieron en América del
Norte, hace unos 80 millones de años. Unos 10 millones de años más tarde se comienzan
a encontrar en el registro fósil del norte de América del Sur. En rocas datadas en unos 56
millones de años, se encuentran fósiles marsupiales en Europa y África del Norte así como
en la Antártida.Algo más tarde se encuentran fósiles marsupiales en Australia. Hace unos
30 millones de años los marsupiales desaparecieron del registro fósil de Asia, África del
Norte, Europa y Antártida. Por aquel tiempo Australia había roto sus conexiones con la
Antártida y se había convertido en un continente isla.
El punto importante es que tres grupos independientes de datos describen los desplazamientos de las especies de marsupiales que son lógicos en términos del momento, dirección y disponibilidad de conexiones entre continentes. Los grupos de datos se combinan
para proporcionar pruebas claras que corroboran que la Tierra y sus formas de vida han
cambiado con el tiempo.
¿Cómo puede darse el cambio evolutivo? Ésta es una cuestión con la que comenzaremos el Capítulo 3.
Capítulo 2 Las pruebas de la evolución 43
80 Ma
Áreas donde vivieron los marsupiales
Tierra firme
Océano
70 Ma
Placas continentales sumergidas
50 Ma
30 Ma
Figura 2.13 La historia evolutiva de los mamíferos marsupiales Para su explicación véase el texto.
Capítulo 1 Las pruebas de la evolución 44
Resumen
Las directrices de la Teoría de la Evolución indican que las
especies han variado a lo largo del tiempo y que están relacionadas entre si por descendencia de un antecesor común.
Darwin arguyó vigorosamente su teoría en su libro Sobre el
origen de las especies, publicado en 1859. En su tiempo, una
explicación importante de la historia de la vida fue la Teoría
de la Creación Especial, que mantiene que las especies fueron creadas reciente e independientemente y que no han
cambiado a lo largo del tiempo.
Diversos argumentos sostienen que las especies no fueron creadas independientemente. Por ejemplo, entre los
organismos hay amplias homologías estructurales, de desarrollo y genéticas. Estas semejanzas se explican de manera
más lógica como consecuencia de la descendencia a partir
de un antecesor común. De igual manera, grupos de especies íntimamente relacionadas de una misma área geográfica, como los sinsontes, pinzones y tortugas que Darwin
observó en las Islas Galápagos, se interpretan fácilmente
como descendientes de poblaciones que colonizaron el área
en el pasado.
Datos sobre especies vivas y fósiles refutan la hipótesis de
que las especies no cambian con el tiempo. La presencia de
estructuras rudimentarias, de estadios del desarrollo transitorios y de secuencias de DNA vestigiales en organismos
contemporáneos se entienden fácilmente como consecuencia del cambio a lo largo de tiempo. Cambios en características importantes, como la longitud de los labios chu-
padores del chinche del jaboncillo, se han observado también directamente en cientos de especies distintas. La hipótesis del cambio a través del tiempo viene apoyada además
por las extinciones masivas, la “ley de la sucesión” y las formas de transición documentadas en el registro fósil.
Hacia mediados del siglo XIX, el principio del uniformismo y la conclusión de la escala de tiempo geológico, persuadió a muchos científicos de que la Tierra es mucho más
vieja que los pocos miles de años propuestos por la Teoría de
la Creación Especial. Este resultado fue verificado hacia principios del siglo XIX mediante datación radioactiva. Los mejores datos disponibles sugieren que la Tierra se formó hace
unos 4.600 millones de años. La primera evidencia fósil de
vida es de hace unos 3.700 millones de años.
En muchos casos, grupos de datos independientes sobre
la historia de la Tierra y la historia de la vida se combinan
para proporcionar un esquema coherente de cambio a través del tiempo. Combinando datos del registro fósil de marsupiales, datación radioactiva y mapas de los movimientos
continentales a lo largo del tiempo, los biólogos han reconstruido que el grupo se originó en América del Norte, luego
se extendió hacia el Este, hacia Europa y Asia, y hacia el Sur,
América del Sur, la Antártida y finalmente Australia.
La Teoría de la Evolución tiene éxito porque proporciona una explicación lógica a una variada serie de observaciones y porque hace predicciones que pueden comprobarse y
verificarse.
Preguntas
1. Analogía y homología son conceptos importantes, utilizados
en la comparación de especies. Los caracteres son homólogos
si tienen, desde el punto de vista evolutivo y de desarrollo, el
mismo origen estructural. Los caracteres son análogos si tienen funciones similares, pero derivan, desde el punto de vista
evolutivo y de desarrollo, de diferente origen estructural. Un
ejemplo clásico de estructuras análogas son las alas de los
insectos y de los murciélagos. ¿Cuáles de las siguientes parejas de estructuras son análogas y cuáles homólogas?
a. Las aletas dorsales de una marsopa y de un salmón.
b. La articulación de la pata de una mariquita y de un petirrojo.
c. La cola de una siamang y el cóccix humano.
d. Las brácteas rojas y brillantes (hojas modificadas) de una
poinsettia y las hojas verdes de una rosa.
e. Las brácteas rojas y brillantes de una poinsettia y los pétalos de una rosa.
2. Hacia principios del siglo XX la datación radioactiva permitió
a los geólogos asignar la antigüedad absoluta a la mayoría de los
estratos que albergan fósiles. Las fechas absolutas resultaron
completamente consistentes con las fechas relativas propuestas
en el siglo XIX. ¿Qué nos dice este resultado acerca de las suposiciones relativas a la lista de fechas indicadas en la página 38?
3. Revise las pruebas de la evolución analizadas en las Secciones
2.1-2.3. Indique las fuentes de las pruebas que Darwin disponía y las que aparecieron más tarde. Indique qué pruebas considera más sólidas y cuáles más débiles. Explique el porqué.
4. Dibuje un sencillo árbol filogenético que muestre las relaciones que podría haber entre cinco especies actuales. Luego
dibuje la genealogía de su familia o de una familia amiga,
comenzando por la generación más vieja y continuando por
las más jóvenes. Señale las partes de cada esquema. ¿En qué
son semejantes los árboles filogenéticos y las genealogías? ¿En
qué son diferentes?
5. Revise las hipótesis alternativas que se presentan en la Figura
2.5. ¿Es ciertamente más parsimónico deducir que las vejigas
natatorias evolucionaron de los pulmones y no lo contrario?
Explíquelo.
Capítulo 2 Las pruebas de la evolución 45
Suponga que no sabemos nada acerca de la biología de los
peces aguja, de Polypterus bichir (pez de agua dulce Africano)
y de Amia calva (pez de río de Norteamérica). ¿Llegaría a conclusiones diferentes acerca de si han evolucionado primero las
vejigas natatorias o los pulmones? ¿Por qué?
6. Dibuje un mapa de flujo que ilustre las relaciones entre las
homologías genéticas, de desarrollo y estructurales. Si dos organismos comparten una estructura homóloga, ¿cree que deben
compartir también el correspondiente gen (o genes) homólogo? Si comparten genes homólogos, ¿cree que deben también
compartir una estructura o proteína homóloga?
7. Basándose en la suposición de que las extinciones fueran
ocasionadas por diluvios universales catastróficos del tipo descrito en la Biblia, ¿qué predicciones hace la Teoría de la
Creación Especial acerca de la naturaleza del registro fósil?
¿Qué predicciones hace la Teoría de la Evolución acerca de
la naturaleza del registro fósil?
8. El texto mantiene que la correspondencia entre grupos de
datos independientes es una prueba particularmente sólida de
la evolución. ¿Está de acuerdo con esta afirmación? ¿En qué
sentidos son independientes el registro fósil, los datos radiométricos y los mapas de la posición de los continentes?
Explorando la bibliografía
9. Las filogenias que se han construido a partir de datos morfológicos, moleculares, datación radioactiva y registro fósil
representan otra serie de grupos de datos independientes que
se combinan para corroborar una visión evolutiva de la historia de la vida. La investigación sobre la evolución de los
tetrápodos es un buen ejemplo de grupos de datos combinados. Las siguientes citas le ayudarán a introducirse en este
tema:
Ahlberg, P. E. and Z. Johanson. 1998. Osteolepiforms and the
ancestry of tetrapods. Nature 395: 792-794.
Hedges, S. B. and L. L. Poling. 1999. A molecular phylogeny
of reptiles. Science 283: 998-1001.
Shubin, N. 1998. Evolutionary cut and paste. Nature 394:
12-13.
Zardoya, R. and A. Meyer. 1996. Evolutionary relationship of
the coelacanth, lungfishes, and tetrapods based on the 28S
ribosomal RNA gene. Proceedings of the National Academy
of Sciences, USA 93: 5449-5454.
10. Debido en gran parte a la solidez de las pruebas que Darwin
reunió, ha habido poco debate científico, si es que lo ha habido, acerca del hecho de la evolución desde 1870. Sin embargo, los biólogos continúan debatiendo las pruebas de la evolución con no científicos. Para participar en esta discusión,
explore http://www.talkorigins.org.
Bibliografía
Burke,A. C. and A, Feduccia.1997. Developmental patterns and the identification
of homologies in the avian hand. Science 278: 666-668.
Carroll, S. P. and C. Boyd.1992. Host race radiation in the soapberry bug: natural
history with the history. Evolution 46: 1052-1069.
Chernicoff, S. and R.Venkatakrishnan. 1995. Geology: An Introduction to Physical
Geology NewYork:Worth Publishers.
Colbert, E. H. and M. Morales.1991. Evolution of the Vertebrates. NewYork:
Wiley-Liss.
Damon, P. E. 1968. Potassium-argon dating of igneous and metamorphic rocks
with applications to the basin ranges of Arizona and Sonora. In Hamilton,
E. I., and R. M. Farquhar, eds. Radiometric Dating for Geologists. London:
Interscience Publishers.
Darwin, C. 1859. On the Origin of Species by Means of Natural Selection. London:
John Murray.
Darwin, C. 1862. The Various Contrivances by Which Orchids are Fertilized by Insects.
London: John Murray.
Desmond,A. and J. Moore. 1991. Darwin. New York:W.W. Norton.
Eiseley, L. 1958. Darwin’s Century Garden City, NY:Anchor Books.
Faure, G. 1986. Principles of Isotope Geology. New York: John Wiley & Sons.
Gingerich, P. D., B. H. Smith, and E. L. Simons. 1990. Hind limbs of Eocene
Basilosaurus: evidence of feet in whales. Science 249: 154-156.
Liem, K. F. 1988. Form and function of lungs: the evolution of air breathing
mechanisms. American Zoologist 28: 739-759.
Mayden, R. L. and E. O. Wiley. 1992.The fundamentals of phylogenetic systematics. Pp.114-185 in R. L. Mayden, ed. Systematics, Historical Ecology, and
North American Freshwater Fishes. Stanford, CA, Stanford Univ. Press.
Mojzsis, S. J., G.Arrhenius, K. D. McKeegan,T. M. Harrison,A. P. Nutman, and C.
R. L. Friend. 1996. Evidence for life on Earth before 3,800 million years ago.
Nature 384: 55-59.
Quiring, R., U.Walldorf, U. Kloter, and W. J. Gehring.1994. Homology of the eyeless gene of Drosophila to the small eye gene in mice and aniridia in humans.
Science 265: 785-789.
Richardson, M. K., J. Hanken, M. L. Gooneratne, C. Pieau, A. Raynaud, L.
Selwood, and G. M. Wright. 1997.There is no highly conserved embryonic
stage in the vertebrates: implications for current theories of evolution and
development. Anatomy and Embryology 196: 91-106.
Rosing, M. T. 1999. 13C-depleted carbon microparticles in >3700-Ma seafloor
sedimentary rocks from West Greenland. Science 283: 674-676.
Scotese, C. R. 1998. Paleomap project. http://www.scotese.com.
Schopf, J.W. 1993. Microfossils of the early archean apex chert: New evidence of
the antiquity of life. Science 260: 640-646.
Szalay, E. S. 1994. Evolutionary History of the Marsupials and an Analysis of Osteological Characters. New York: Cambridge University Press.
Thewissen, J. G. M. , S. T. Hussain, and M. Arif. 1994. Fossil evidence for the
origin of aquatic locomotion in archaeocete whales. Science 263: 210-212.
CAPÍTULO
3
Selección natural darwiniana
Las bandas azules de las patas de este macho de pinzón terrestre mediano se marcaron para estudiarlo. Los investigadores han observado la
selección natural en acción estudiando esta especie del Archipiélago de las Galápagos. (Peter R. Grant, Princeton University)
E
SOBRE EL ORIGEN DE LAS ESPECIES, DARWIN
(1859, p. 3) escribió que “un naturalista, al reflexionar sobre las afinidades mutuas de
los seres orgánicos, en sus relaciones embriológicas, en su distribución geográfica, en las
sucesiones geológicas y en otros hechos similares, podría llegar a la conclusión de que cada
especie no ha sido creada independientemente, sino que desciende... de otras especies. No
obstante, tal conclusión, aunque esté bien fundamentada, sería insatisfactoria a no ser que
se pudiera demostrar de qué manera han sido modificadas las innumerables especies que
habitan este mundo...” (énfasis añadido).
Con esta frase, Darwin indicaba, con toda precisión, las relaciones entre el patrón y los
procesos componentes de una teoría científica. Los primeros evolucionistas habían descubierto un fenómeno importante. Un cuerpo de datos creciente indicaba que tanto los organismos fósiles como los vivientes habían descendido de un ancestro común. La evidencia
que Darwin acumuló para apoyar esta hipótesis fue indirecta, pero lo bastante convincente como para que la controversia científica sobre el patrón de la teoría de la evolución
hubiera finalizado prácticamente hacia mediados de la década de 1870. Gracias a Darwin
y a su agudeza intelectual, la evolución llega a ser un hecho bien establecido.
Pero, ¿qué procesos pueden dar lugar al patrón llamado evolución? La comprensión de
los mecanismos que dan lugar a un patrón en la naturaleza son el corazón y el alma de la
explicación científica. El Capítulo 2 se centró en las pruebas del patrón llamado descenN LA INTRODUCCIÓN AL LIBRO
47
48 PARTE I Introducción
dencia con modificación; este capítulo introduce un proceso, llamado selección natural,
que da lugar al patrón.
3.1. La selección natural: los cuatro postulados de Darwin
La selección natural es el resultado lógico de cuatro postulados que Darwin indicó en su
introducción a Sobre el origen de las especies mediante selección natural.Al resto del libro lo consideró como “un extenso argumento” en su apoyo (Darwin 1859, p. 459). Los postulados
son los siguientes:
1.
2.
3.
4.
La selección natural es un
proceso que da lugar a
descendientes con
modificaciones, o evolución.
Una adaptación es una
característica que aumenta la
eficacia de un individuo, cuando
se la compara con individuos
sin la característica.
Los individuos que forman las especies son variables.
Algunas de estas variaciones pasan a los descendientes.
En cada generación se producen más descendientes de los que pueden sobrevivir.
La supervivencia y la reproducción de los individuos no son al azar: los individuos que
sobreviven y llegan a reproducirse, o la mayoría de los que se reproducen, son aquellos
que presentan las variaciones más favorables. Son seleccionados de manera natural.
Como consecuencia de este proceso, las características de las poblaciones cambian de
una generación a la siguiente. La lógica es clara: si hay variación entre los individuos de
una población que puede transmitirse a los descendientes, y si hay éxito diferencial entre
aquellos individuos en cuanto a la supervivencia y/o a la reproducción, entonces algunos
caracteres pasarán con mayor frecuencia que otros. Por ello, las características de la población cambiarán ligeramente en cada una de las generaciones siguientes. Esto es evolución
darwiniana: cambio gradual de la población con el tiempo. Los cambios en las poblaciones son la consecuencia de la selección natural sobre los individuos.
Para aclarar este punto, recuerde los viriones del VIH descritos en el Capítulo 1. Cada
uno de los viriones de un mismo huésped varía en cuanto a su capacidad para sintetizar
DNA en presencia de AZT, debido a las diferencias en las secuencias de aminoácidos del
lugar activo de la transcriptasa inversa. Los viriones con formas de la transcriptasa inversa que tengan menos probabilidad de unir el AZT se reproducirán más que las formas que
enlazan fácilmente el AZT. Entonces, en la generación siguiente, un mayor porcentaje de
viriones que en la generación anterior tendrán la forma modificada de la transcriptasa
inversa. Esto es evolución por selección natural.
Darwin se refirió a los individuos que ganan en esta competición (que raramente es una
lucha cuerpo a cuerpo) y a sus descendientes, que comprenden un mayor porcentaje de
la población en la generación siguiente, como a los más aptos.Al hacerlo así dio a las palabras inglesas “fit” (apto) y “fitness” (aptitud) un nuevo significado. La eficacia darwiniana
es la habilidad de los individuos para sobrevivir y reproducirse en su ambiente.
Un aspecto importante de la eficacia es su naturaleza relativa. El término se refiere a
lo bien que sobrevive un individuo y a cuántos descendientes produce en comparación
con otros individuos de su especie. Los biólogos utilizan la palabra adaptación para referirse a un carácter o característica de un organismo, como por ejemplo una forma modificada de la transcriptasa inversa, que aumenta su eficacia relativa respecto de los individuos
sin la modificación.
Por cierto, la misma teoría había sido desarrollada de forma independiente por un colega de Darwin, llamado Alfred Russel Wallace. Aunque formado en Inglaterra,Wallace se
había establecido en Malasia enviando especímenes biológicos a coleccionistas privados.
Mientras se estaba recuperando de un brote de malaria en 1858, redactó un informe en
el que explicaba la selección natural y se lo envió a Darwin. Darwin, que había escrito el
primer borrados del tema en 1842 y que no lo había publicado, se dio cuenta inmediatamente de que él y Wallace habían formulado la misma teoría de manera independiente.
Capítulo 3 Selección natural darwiniana 49
Unas breves comunicaciones de Darwin y Wallace se leyeron juntas en la Sociedad
Linneana de Londres y luego Darwin se apresuró a publicar Sobre el origen de la especies
(17 años después de haber escrito su primer borrador). En la actualidad el nombre de
Darwin está más claramente asociado con la Teoría de la Evolución por selección natural
por dos razones: claramente fue el primero en darse cuenta y su libro proporcionó una
exposición completa de la idea, con una enorme documentación.
Uno de los aspectos más atractivos de la teoría de Darwin-Wallace es que cada uno de
los cuatro postulados (y sus consecuencias lógicas) se pueden verificar independientemente. Es decir, la teoría es comprobable. No hay suposiciones ocultas ni nada que se tenga
que aceptar de manera no crítica. En la siguiente sección examinaremos cada uno de los
cuatro postulados, revisando un estudio en curso sobre los pinzones de las Islas Galápagos, frente a las costas del Ecuador. ¿Se puede comprobar rigurosamente la Teoría de la
Evolución por selección natural mediante observación directa?
La Teoría de la Evolución
por selección natural puede
comprobarse.
3.2. La evolución de la forma del pico de los pinzones
de las Galápagos
Peter Grant, Rosemary Grant y sus colegas han estado estudiando continuadamente
varias especies de pinzones de las Galápagos en las distintas islas del archipiélago desde
1973 (véase Boag y Grant 1981; Grant 1981a, 1991, 1999; Grant y Grant 1989). Las 14
especies de pinzones que se encuentran en las islas son similares en tamaño y coloración.
Su tamaño va de diez a quince centímetros y su coloración de marrón a negro. Sin
embargo, hay dos caracteres que presentan una notable variación entre especies: el tamaño y la forma de sus picos.
El pico es la principal herramienta que usan las aves para alimentarse y la enorme variación en la morfología de los picos entre los pinzones de las Galápagos refleja la diversidad
de los alimentos que toman (Figura 3.1). El pinzón curruca (Certhidea olivacea) se alimenta
de insectos, arañas y néctar; los pinzones picamaderos y del manglar (Cactospiza pallida y
Cactospiza heliobates) utilizan ramitas o espinas de cactus como herramienta para apalancar larvas de insecto o termitas en maderas muertas; varios pinzones terrestres del género
Geospiza arrancan garrapatas de iguanas y de tortugas, además de comer semillas; el pinzón vegetariano (Platyspiza crassirostris) come hojas y frutos.
Para comprobar la Teoría de la Evolución por selección natural, nos concentraremos en
los datos que Grant, Grant y sus colegas han reunido sobre el pinzón terrestre mediano,
Geospiza fortis, en la isla Daphne Major.
El tamaño y la localización de Daphne Major la hacen un estupendo laboratorio natural. La isla es diminuta.Tiene un tamaño justo por debajo de las 40 hectáreas (alrededor
de 40 campos de fútbol), con una elevación máxima de 120 m. Como todas las islas de
los Galápagos, es la cima de un volcán. El clima es estacional, aunque su localización es
ecuatorial (Figura 3.2). Una estación cálida y húmeda desde enero a mayo se alterna con
una estación más fría y seca de junio a diciembre. La vegetación consiste en un bosque
árido y monte bajo, con varias especies de cactus.
El Geospiza fortis de Daphne Major es una población de estudio ideal porque pocos pinzones migran hacia o desde la isla y la población es lo suficientemente pequeña como para
estudiarla exhaustivamente. En un año promedio, hay unos 1.200 pinzones en la isla. Hacia
1977, Grant, Grant y su equipo habían capturado y marcado casi la mitad de ellos; desde
1980, prácticamente se había marcado el 100% de la población.
El pinzón terrestre mediano se alimenta principalmente de semillas. Las aves cascan las
semillas atenazándolas con la base del pico y apretando. Grant, Grant y sus colegas han
demostrado que tanto dentro como entre especies de pinzones, el tamaño del pico está
Debido a que es el carácter
más importante utilizado para
adquirir alimento, el tamaño
y la forma del pico de un ave
tiene consecuencias
importantes para su eficacia.
50 PARTE I Introducción
(a)
Geospiza
fuliginosa
(b)
Geospiza
fortis
Geospiza
magnirostris
Geospiza
scandens
Geospiza
conirostris
Geospiza
difficilis
Camarhynchus
parvulus
Camarhynchus
psittacula
Camarhynchus
pauper
Cactospiza
pallida
Platyspiza
crassirostris
Certhidea
fusca
Pinarolaxes
inornata
Certhidea
olivacea
Figura 3.1 Los pinzones de las Galápagos y el pinzón terrestre mediano Geospiza fortis (a) Esta filogenia se dedujo de las semejanzas y
diferencias en las secuencias del DNA por Kenneth Petren y sus colegas (1999), y muestra las relaciones evolutivas entre 14 especies de los pinzones
de Darwin. Las fotos muestran la gran variación del tamaño y de la forma del pico entre especies. De Petren et al. (1999). (b) Macho (arriba) y
hembra (abajo) del pinzón terrestre mediano. (Fotos: Peter R. Grant, Princeton University)
Capítulo 3 Selección natural darwiniana 51
92° W
91°
2°
Cocos
Darwin
Wolf
Galápagos
América
del Sur
1° N
Pinta
Marchena
Genovesa
Santiago
0°
• Bartolomé
• Rocas Bainbridge
• Daphne Minor
• Cowley Daphne
Rábida Major •
Eden •
• Plazas
Santa Cruz
Pinzón
San Cristóbal
Fernandina
Isabela
• Los Hermanos
Santa Fe
Tortuga
1° S
50 km
92° W
Ecuador 0°
1° S
Champion
•• Enderby
Floreana
• Caldwell Española • Gardner
•
91°
90°
Gardner
Figura 3.2 El Archipiélago de las
Galápagos Catorce especies de pinzones
habitan las Galápagos y un pinzón reside
en Cocos. En este mapa, la isla Daphne Major
es un diminuto islote entre Santa Cruz
y Santiago.
correlacionado con el tamaño de las semillas cosechadas. En general, las aves con picos más
grandes comen semillas más grandes y las aves con picos más pequeños comen semillas
más pequeñas. Esto se debe a que las aves con picos de tamaños diferentes son capaces de
manipular semillas de tamaños diferentes de manera más eficaz (Bowman 1961; Grant et
al. 1976;Abbott et al. 1977; Grant 1981b).
Comprobación del postulado 1: ¿son variables las poblaciones?
Los investigadores marcan cada pinzón que cazan poniendo bandas coloreadas de aluminio
alrededor de cada una de sus patas. Esto les permite identificar individualmente a las aves en
el campo. Los científicos también pesan cada pinzón y miden la longitud de sus alas, cola
y anchura, altura y longitud del pico.Todos los caracteres que han investigado son variables.
Por ejemplo, cuando Grant y Grant representaron gráficamente las medidas de la altura del
pico de la población de Ceospiza fortis de la isla de Daphne Major, los datos indicaban que
la altura varía (Figura 3.3).Todas las características de los pinzones que se han medido están
claramente de acuerdo con el primer postulado de Darwin. Como veremos en el Capítulo 4, la variación entre los individuos de una población es prácticamente universal.
Comprobación del postulado 2: ¿es heredable la variación entre
los individuos?
En una población, cada uno de los pinzones puede tener una altura del pico distinta, debido a que el ambiente que han experimentado es diferente, o porque sus genotipos son
diferentes o por ambas cosas a la vez. Hay varias maneras de que la variación ambiental
pueda dar lugar a la variación de la altura del pico representada en la Figura 3.3. La variación en la cantidad de alimento que cada pájaro recibió cuando era un polluelo puede dar
Algunos Geospiza fortis tienen
picos que son sólo la mitad
de altos que el de otros
individuos.
52 PARTE I Introducción
Figura 3.3 La altura del pico en
los pinzones terrestres medianos
CUADRO 3.1
L
Número de pinzones
Este histograma muestra la distribución
de la altura del pico en los pinzones
terrestres medianos de Daphne Major
en 1976, en el comienzo del estudio
de Grant. Algunas aves tienen picos
bajos, de menos de 8 mm. Muchas
aves tienen picos medianos, entre 8 y
11 mm. Algunas aves tienen picos
altos, de más de 11 mm. (N se refiere
al tamaño de la muestra; la flecha azul
en el eje de las x indica la media.)
Cuando se representa la variación
de las características de un organismo,
es frecuente observar una curva en
campana, como la que se forma en
este histograma. La amplitud, las
causas y la naturaleza de la variación
en los caracteres es el objeto de los
Capítulos 4 y 7.
90
N = 751
60
30
6
7
8
9
10
11
12
13
14
Altura del pico (mm)
Aspectos que complican la manera de estimar la heredabilidad
a heredabilidad se estima midiendo la semejanza de
caracteres entre individuos íntimamente emparentados. Pero los parientes comparten no solo los genes sino
también el ambiente, y cualquier correlación que se deba
al ambiente compartido hincha la estima de la heredabilidad. Por ejemplo, se sabe que las aves tienden a alcanzar
un mayor tamaño cuando han tenido alimento abundante en su juventud. Pero los territorios de cría más ricos en
alimento los obtienen y defienden a menudo los adultos
de mayor tamaño de la población. En esos territorios las
crías tenderán a convertirse en los adultos más grandes en
la generación siguiente. Por ello, un investigador podría
medir una elevada relación entre el tamaño del pico y del
cuerpo entre padres e hijos y aducir una elevada heredabilidad para estos caracteres cuando en realidad no hay
ninguna. En este caso, la relación real se da entre los ambientes que los padres y sus hijos experimentaron de polluelos.
En muchas especies, este problema se puede evitar realizando lo que se denomina intercambio de padres, jardín
común o experimentos de transplante recíprocos. En las
aves estos experimentos implican sacar los huevos de sus
nidos y situarlos en nidos de padres adoptivos elegidos
aleatoriamente. Las mediciones en las crías, hechas cuando
han llegado a su máximo desarrollo, se comparan con los
datos de sus padres biológicos. Este tratamiento experimental elimina cualquier desviación en el análisis origina-
do por el hecho de que los padres y sus hijos comparten
un mismo ambiente. Desgraciadamente, mediante estos
experimentos no se pueden eliminar los efectos ambientales debidos a diferencias en los nutrientes almacenados en los huevos o en las semillas. Simplemente tenemos
que asumir que estos efectos maternos son demasiado
pequeños como para desviar seriamente los resultados.
Los experimentos de intercambio de padres en una
gran variedad de especies de aves han confirmado elevadas
heredabilidades casi en la mayoría de todos los caracteres
morfológicos analizados. Sin embargo, para Boag y Grant
(1978) no fue posible realizar este crítico experimento en
los pinzones de las Galápagos. Debido a que las Galápagos
son un parque nacional, los experimentos que manipulan
individuos más allá de la captura y marcaje están prohibidos. Para evitar esta limitación, Peter Grant (1991) comparó individuos que se criaron en territorios con escasez
de alimento respecto de territorios con riqueza de alimento para ver si una vez alcanzaran la edad adulta criaban en ambientes similares. Los datos demostraron que no
hay correlación entre la calidad del territorio en donde un
ave se crió y la calidad del territorio en donde crió a sus
descendientes. Este resultado apoya la afirmación de que las
elevadas heredabilidades estimadas en los caracteres de los
pinzones, como la dimensión del pico, son reales y no
artefactos por el hecho de que los padres y su descendencia compartan el mismo ambiente.
Capítulo 3 Selección natural darwiniana 53
Altura del pico de los descendientes
lugar a la variación en la altura del pico entre los adultos. El daño o la abrasión por semillas duras o rocas puede también afectar a la forma y tamaño del pico.
Para determinar si, al menos en parte, la variabilidad del pico entre los pinzones tiene
base genética, y por ello puede pasar de padres a hijos, un colega de Peter y Rosemary
Grant, llamado Peter Boag, estimó un parámetro conocido como heredabilidad.
La heredabilidad es la proporción de variación observada en una población que se debe
a la variación de los efectos de los genes.Ya que es una proporción, la heredabilidad varía
de 0 a 1. En el Capítulo 7 desarrollaremos mucho más ampliamente la teoría de cómo se
estima la heredabilidad. De momento, señalemos sólo que normalmente se estima midiendo la semejanza entre parejas emparentadas. Ésta es una aproximación válida, ya que las
semejanzas entre parientes está ocasionada, al menos en parte, por los alelos que comparten (para más detalles, véase el Cuadro 3.1). Normalmente se reúnen datos de grupos de
hermanos o de padres y descendientes.
Boag comparó la altura del pico de Geospiza fortis jóvenes, después de que hubieran
alcanzado el tamaño adulto, con la altura media del pico de sus padres y encontró una gran
correspondencia entre parientes. Como muestran los datos representados en la Figura 3.5,
padres con picos altos tienden a tener descendientes con picos altos y padres con picos
poco altos tienden a tener polluelos con picos poco altos. Esto es una prueba de que una
gran proporción de la variación observada de la altura del pico es genética y puede transmitirse a los descendientes (Boag y Grant 1978; Boag 1983). El resultado está de acuerdo
con cientos de estudios similares. En la mayoría de los caracteres de la mayoría de los organismos, una cantidad significativa de la variación que existe en la población se debe a variación en la composición genética de los individuos.
11,0
1978
1976
10,0
9,0
8,0
8,0
9,0
10,0
11,0
Altura media del pico de los padres
Figura 3.4 Heredabilidad de la altura del pico en Geospiza fortis Este gráfico muestra las
relaciones entre la altura de pico de los padres y de sus descendientes. El valor medio de los padres es el
promedio de las medidas paternas y maternas. La utilización de esta medida es importante ya que los
machos de Geospiza fortis son mayores que las hembras.
En el gráfico, las líneas son el resultado de un procedimiento estadístico llamado análisis de regresión.
En el tipo de regresión utilizado aquí, la línea se sitúa de tal manera que se minimizan las sumas de los
cuadrados de la distancia vertical entre cada punto y la línea. A ésta se le denomina el mejor ajuste lineal.
Si la pendiente de la línea es horizontal, ó 0, entonces no hay relación entre las dos variables representadas;
lo que indica que toda la variación entre individuos está ocasionada por las diferencias ambientales que
sufren. Si la pendiente es 1, entonces toda la variación entre los individuos está ocasionada por la variación
en sus genotipos.
La línea y los círculos rojos pertenecen a los datos de 1978 y los azules a los datos de 1976. Los
resultados de los dos años son consistentes. Ambos muestran una gran relación entre la altura del pico de
los padres y de sus descendientes. Podemos deducir que la asociación es una consecuencia de los genes
compartidos. Según Boag (1983).
En los pinzones, la altura del
pico de los padres y de los
descendientes es similar. Esta
observación sugiere que
algunos alelos tienden a
producir picos bajos, mientras
que otros tienden a producir
picos altos.
54 PARTE I Introducción
Comprobación del postulado 3: ¿hay un exceso de descendientes de tal
manera que sólo algunos individuos sobreviven y se reproducen?
Una sequía en Daphne Major
dio lugar a un suceso selectivo
espectacular.
Debido a que se censaron las poblaciones de pinzones terrestres a lo largo de varios años,
los investigadores pudieron observar un suceso importante. En 1977 hubo una grave
sequía en la zona estudiada. En lugar de los 130 mm de lluvia, habituales durante la estación húmeda, sólo cayeron 24 mm. A lo largo de 20 meses, el 84% de los pinzones
terrestres medianos de la población de Daphne Major desaparecieron (Figura 3.5a). El
grupo dedujo que la mayoría murió de inanición: había una gran correspondencia entre
el tamaño poblacional y la disponibilidad de semillas (Figura 3.5b); realmente se encontraron 38 pájaros demacrados muertos y ninguno de los pájaros desaparecidos reaparecieron el año siguiente. Estaba claro que sólo una parte de la población sobrevivió y se
reprodujo. Este tipo de mortalidad no es raro. Por ejemplo, Rosemary Grant ha demostrado que el 89% de los Geospiza conirostris mueren antes de criar (Grant 1985).Trevor
Price y sus colaboradores (1984) determinaron que un 19% y un 25% adicionales de los
Geospiza fortis de Daphne Major murieron durante posteriores sequías en 1980 y 1982
respectivamente.
De hecho, en cada población natural estudiada, se producen en cada generación más
descendientes de los que sobreviven para reproducirse. Si una población no aumenta de
tamaño, entonces cada padre dejará como promedio, a lo largo de su ciclo vital, un des-
(a)
Número de pinzones
1.400
1.000
600
200
Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene
1975
Figura 3.5 Declive de la población de pinzones terrestres y
de las semillas disponibles durante la sequía de 1977 (a) En este
gráfico se representa el número de pinzones terrestres encontrados
en Daphne Major antes, durante y después de la sequía. Las líneas
verticales de cada punto representan una cantidad llamada error típico,
que indica la cantidad de variación en las estimas del censo. En este
gráfico, las líneas de un punto a otro se han dibujado simplemente para
que se vea mas fácilmente la tendencia.
(b) En este gráfico se representa la abundancia de semillas en
Daphne Major antes, durante y después de la sequía. Reimpreso con
permiso de Boag y Grant (1981). Copyright © 1981, American
Association for the Advancement of Science.
Abundancia de semillas (g/m2)
(b)
1976
1977
1978
12,0
8,0
4,0
Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene
1975
1976
1977
1978
Capítulo 3 Selección natural darwiniana 55
cendiente que sobrevivirá para reproducirse. Pero la capacidad reproductora (o potencial
biótico) de los organismos es asombrosa (Tabla 3.1).
De igual manera, los datos demuestran que, en la mayoría de las poblaciones, algunos
individuos tienen más éxito en los apareamientos y en la producción de descendientes que
otros. La variación en el éxito reproductor representa una oportunidad para la selección,
como la variación en la supervivencia.
Comprobación del postulado 4: la supervivencia y la reproducción, ¿se
dan de manera no aleatoria?
El cuarto postulado de Darwin fue que los individuos que sobreviven y llegan a la reproducción, o los que más se reproducen, son aquellos que tienen ciertas variaciones favorables. ¿Sobrevivió a la sequía de 1977 un subgrupo seleccionado, no al azar, de las
poblaciones de pinzones terrestres? Midiendo a principios de 1978 los mismos caracteres
que se habían medido en 1976 en una muestra grande y aleatoria de aves que sobrevivieron, el grupo de Grant encontró que había sobrevivido una parte diferente de la
población, aquéllos con los picos más altos (Figura 3.6). Debido a que el superviviente promedio tenía un pico más alto que el no superviviente promedio, el tamaño promedio del
pico había cambiado en la población.
¿De qué modo era favorable la altura de los picos? ¿Podemos relacionar causas ecológicas con efectos evolutivos? La respuesta es sí: no solo el número, sino también los tipos de
semillas disponibles durante la sequía de 1977 habían cambiado drásticamente (Figura 3.7).
Concretamente, los grandes y duros frutos de una planta anual denominada Tribulus cistoides
se convirtieron en el recurso alimentario básico. En los años normales estas semillas casi siempre se ignoran, pero durante la sequía el suministro de semillas pequeñas y blandas disminuye rápidamente. Sólo las aves grandes, con picos altos y estrechos, pueden romper y
comer los frutos de Tribulus.Además, las aves grandes defienden los recursos alimentarios con
más éxito durante los conflictos. Debido a que el tamaño grande y la altura del pico están
correlacionados positivamente, los dos caracteres responden conjuntamente a la selección.
El suceso selectivo de 1977-1978, aunque fue muy importante, no fue un hecho aislado. En 1980 y en 1982 hubo sequías similares y la selección favoreció de nuevo a los indi-
Tabla 3.1 Potencial reproductivo
En esta tabla se da el número de descendientes que puede producir un solo individuo (o pareja
de individuos en especies con sexualidad) en condiciones óptimas, suponiendo que todos los
descendientes sobreviven hasta tener descendencia, en varios intervalos de tiempo. Darwin
eligió a los elefantes para sus cálculos debido a que era entonces el animal conocido de tiempo
de generación más largo.
Organismo
Potencial reproductivo
Citas
Aphis fabae (áfido)
524.000 millones al año
Gould 1977
Elefante
19 millones en 750 años
Darwin 1859
Mosca doméstica
191 ⫻ 1018 en 5 meses
Keeton 1972
Mycophila speyeri (díptero
que se alimenta de hongos)
215.000/metro cuadrado en 35 días
Gould 1977
Staphylococcus aureus
(bacteria)
En 48 horas la Tierra se cubriría con
una capa de células de 2 metros
Audesirk y
Audesirk 1993
Estrella de mar
1079 en 16 años*
Dodson 1960
*1079 es el número estimado de electrones en el universo visible.
La selección natural se
produce debido a que (1) sólo
una fracción de los
descendientes sobrevive lo
suficiente como para tener
descendencia, y (2) de los
individuos que pueden tener
descendencia, algunos tienen
mucho más éxito que otros.
Durante la sequía, los pinzones
con picos más grandes y altos
tuvieron ventaja.
56 PARTE I Introducción
Número de pinzones
90
Todas las aves de Daphne en 1976
N = 751
60
30
6
7
8
9
10
11
12
13
14
Número de pinzones
12
Figura 3.6 Altura del pico antes y
después de la selección natural En estos
histogramas se muestra la distribución de la
altura del pico de los pinzones terrestres
medianos de Daphne Major, antes y después
de la sequía de 1977 (Grant 1986).
Copyright © 1986, Princeton University Press.
Reimpreso con el permiso de Princeton
University Press.
Supervivientes en 1978
N = 90
8
4
6
7
8
9
10
11
12
13
14
Altura del pico (mm)
viduos con mayor tamaño corporal y picos más altos (Price et al. 1984). Luego, en 1983,
la influencia de la superficie cálida del agua de las costas de América del Sur, llamada El
Niño, dio lugar a una estación húmeda con 1359 mm de lluvia sobre Daphne Major. Este
espectacular cambio ambiental (casi 57 veces más lluvia que en 1977) dio lugar a una superabundancia de semillas pequeñas y blandas y, consiguientemente, a una fuerte selección a
favor de tamaños corporales pequeños (Gibbs y Grant 1987). Después de años húmedos,
sobreviven y se reproducen más aves pequeñas con picos bajos debido a que cosechan las
semillas pequeñas mucho más eficazmente que las aves grandes con picos altos. Las aves
grandes se vieron favorecidas en las condiciones de sequía, pero las aves pequeñas lo fueron en los años húmedos. La selección natural (como señalábamos en nuestro análisis de
la evolución del VIH en el Capítulo 1) es dinámica.
¿Se dio evolución?
La selección ocurre dentro de
una generación; la evolución se
da entre generaciones.
Los cambios observados en los picos de los pinzones son ejemplos de la acción de la
selección natural. Pero al principio dijimos que la evolución es una respuesta a la selección: un cambio en las características de una población de una generación a la siguiente. La selección da lugar a cambios distintos en la distribución de los caracteres en una
generación; la evolución es un cambio en la distribución de los caracteres entre generaciones. ¿Se dio evolución en los pinzones de las Galápagos? La respuesta es sí: como muestran los datos de la Tabla 3.2, los descendientes de las aves que sobrevivieron a la sequía
de 1977 fueron significativamente más grandes, en promedio, que la población que existía antes de la sequía.
Capítulo 3 Selección natural darwiniana 57
Tamaño corporal medio de los pinzones
(a)
Machos
0,8
0,4
Todas las aves
0,0
Hembras
-0,4
Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene
1975
1976
1977
1978
(b)
Grandes
y duras
Figura 3.7 Cambios en el tamaño corporal de los pinzones
terrestres y en las características de las semillas (a) Estos
Características medias
de las semillas
6,0
5,0
4,0
Pequeñas
y blandas
Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene Abr Jul Oct Ene
1975
3.3.
1976
1977
1978
gráficos muestran el tamaño corporal de los pinzones capturados
antes, durante y después de la sequía en Daphne Major. (Los ejes no
tienen unidades, ya que el tamaño corporal se calculó como una
medida compuesta, llamada medida de componentes principales.) La
línea “todas las aves” representa el promedio de hembras y machos.
Como en la Figura 3.5, los puntos representan medias poblaciones,
las líneas verticales errores típicos y se han dibujado las líneas entre
puntos simplemente para que sea más fácil ver la tendencia. (b) Este
gráfico muestra los cambios en la dureza de las semillas disponibles
en Daphne Major antes, durante y después de la sequía. El índice de
dureza, indicado en el eje de las y, es una medida especial inventada
por Boag y Grant (1981). Reimpreso con permiso. Copyright ©
1981, American Association for the Advancement of Science.
La naturaleza de la selección natural
Aunque la Teoría de la Evolución por selección natural se puede exponer de manera concisa, puede ser difícil comprobarla rigurosamente en las poblaciones naturales, validarla y
comprenderla a fondo. Una de las razones es que es esencial un proceso estadístico: el cambio de la distribución de los caracteres en las poblaciones. El razonamiento estadístico no
es fácil para mucha gente y hay un número de ideas ampliamente compartidas acerca de
la selección natural que son incorrectas. En esta sección nuestro objetivo es tratar algunos
puntos clave acerca de cómo la selección actúa y no actúa.
La selección natural actúa sobre los individuos, pero sus consecuencias
son poblacionales
Cuando se seleccionaron las cepas del VIH al exponerlas al AZT, o cuando se seleccionaron
las poblaciones de pinzones por cambios en la disponibilidad de semillas, ninguno de los
individuos seleccionados (virus o pinzones) cambió en absoluto. Simplemente unos sobrevivieron al efecto de la selección mientras que otros murieron, o se reprodujeron más
que los virus o pinzones competidores. Lo que cambió después del proceso selectivo
fueron las características de las poblaciones de virus o de pinzones, no los propios individuos afectados. Concretamente, un mayor porcentaje de virus VIH de la población fue
58 PARTE I Introducción
Tabla 3.2 Respuesta evolutiva a la selección
Estos datos resumen los cambios en las medias poblacionales de los caracteres del tamaño
corporal y del pico en Geospiza fortis antes y después de la sequía de 1976-1977. SE es la
abreviatura de “Standard Error” (error típico), que cuantifica la cantidad de variación alrededor
del valor medio. La columna delta (∆) muestra las diferencias entre generaciones.
Antes de la selección
1976
Generación siguiente
1978
Carácter
Media
SE
Media
SE
∆
Peso (g)
16,06
0,06
17,13
0,13
+1,07
Longitud del ala (mm)
67,88
0,10
68,87
0,20
+0,99
Longitud del tarso (mm)
19,08
0,03
19,29
0,07
+0,21
Longitud del pico (mm)
10,63
0,03
10,95
0,06
+0,32
9,21
0,03
9,70
0,06
+0,49
8,58
0,02
8,83
0,05
+0,25
Altura del pico (mm)
Anchura del pico (mm)
Tamaño de muestra
634
135
Fuente: Grant y Grant 1995
La selección natural no
cambia las características de
los individuos. Cambia
las características de las
poblaciones.
capaz de replicar en presencia del AZT, y una mayor proporción de pinzones tenía los
picos más altos.
Dicho de otra manera, el esfuerzo por romper las semillas de Tribulus no hizo que los
picos de los pinzones fueran más altos y que sus cuerpos fueran más grandes, y la necesidad de transcribir RNA en presencia del AZT no cambió la composición de aminoácidos del lugar activo de la transcriptasa inversa. Lo que ocurrió es que aumentó el tamaño
promedio del pico y del cuerpo en la población de pinzones debido a que los pinzones
más pequeños murieron con mayor probabilidad que los más grandes y la secuencia promedio del lugar activo de la transcriptasa inversa cambió debido a que ciertos mutantes
tuvieron una mejor oportunidad de fabricar nuevos virus.
La selección natural actúa sobre los fenotipos, pero la evolución
consiste en cambios en las frecuencias alélicas
Los pinzones de tamaño grande y picos altos habrían sido favorecidos durante el período
de sequía, incluso si toda la variación de la población hubiera sido ambiental en su origen (es decir, si la heredabilidad hubiera sido cero). Pero no se habría dado evolución. La
frecuencia de los fenotipos observados antes y después de la selección habría cambiado,
pero en la generación siguiente la distribución de los fenotipos tendría que volver a lo que
fue antes de la selección.
Ya que la evolución es la respuesta a la selección, sólo se da cuando los caracteres seleccionados tienen una base genética. La variación en el fenotipo de los pinzones, sobre la
que actuó la selección natural, tenía una base genética. Por ello, la distribución de los fenotipos cambió en la generación siguiente.
La selección natural se observa mirando hacia atrás, no hacia delante
Cada generación es el producto de la selección por las condiciones ambientales que prevalecieron en la generación anterior. Los descendientes de los virus VIH y de los pinzones que sufrieron la selección natural están mejor adaptados al ambiente dominado por
Capítulo 3 Selección natural darwiniana 59
el AZT o por las condiciones de sequía, respectivamente, que lo estuvo la generación
paterna. Sin embargo, si el ambiente cambia de nuevo durante la vida de estos descendientes, no estarían necesariamente adaptados a las nuevas condiciones.
Un error corriente es pensar que los organismos se pueden adaptar a condiciones futuras o que la selección puede mirar hacia delante en el sentido de anticiparse a los cambios ambientales en generaciones futuras. Esto es imposible. La evolución se da siempre
una generación después de cualquier cambio en el ambiente.
La selección natural puede producir nuevos caracteres, aun cuando
actúa sobre caracteres ya existentes
La selección natural adapta a
las poblaciones a condiciones
que prevalecían en el pasado,
no a condiciones que podrían
darse en el futuro.
La selección natural puede actuar sólo a partir de la variación que ya existe en la población. Por ejemplo, la selección no puede crear de manera instantánea un pico nuevo y
óptimo para romper los frutos de Tribulus. Únicamente selecciona a partir del rango de
los picos que existen en la población.
Sin embargo, con el tiempo, la selección natural puede dar lugar a caracteres nuevos. La
evolución de nuevos caracteres es posible porque, en cada generación, las mutaciones dan
lugar a nuevas variantes y por ello una nueva serie de caracteres sobre los que la selección
puede actuar. Para entender por qué esto es importante, consideremos los resultados de
un experimento de selección natural llevado a cabo en la Universidad de Illinois (Leng
1962). Un grupo de investigadores comenzó con 163 mazorcas de maíz, en las que se
comprobó el contenido en aceite de los granos, encontrándose que la cantidad variaba del
4 al 6%. Seleccionaron las 24 mazorcas con mayor contenido de aceite como padres de la
siguiente generación, obtuvieron los descendientes, comprobaron el contenido en aceite
de los granos y seleccionaron de nuevo a los individuos con mayor contenido en aceite
como padres de la siguiente generación. Continuando este régimen de selección durante 60 años, los investigadores lograron producir plantas de maíz cuyos granos tenían un
contenido en aceite alrededor del 16% (Figura 3.8). No hay solape entre la distribución
del contenido de aceite en las poblaciones ancestral y descendiente. La evolución ha dado
lugar a un nuevo valor del carácter.
La selección natural puede dar lugar también a características novedosas. Esto es posible debido a que la selección es capaz de “reorientar” comportamientos, estructuras o
Contenido en aceite de los granos de maíz (%)
16
14
12
10
8
6
Rango de la población original
4
2
0
0
10
20
30
40
50
Generaciones seleccionadas
60
Figura 3.8 La selección continuada puede dar lugar a
cambios espectaculares en los caracteres Véase el texto para
su explicación. Modificado de Leng (1962). Reimpreso con permiso
de Blackwell Wissenschafts-Verlag GmbH.
60 PARTE I Introducción
genes ya existentes hacia funciones nuevas. El pulgar del panda gigante es un buen ejemplo (Gould 1980). Los pandas utilizan dicha estructura como un sexto dedo cuando se alimentan de su comida favorita, el bambú. Como se muestra en la Figura 3.9, pasan los tallos
por el hueco entre el pulgar y los otros cinco dedos para arrancar las hojas y alcanzar los
vástagos que se comen. Pero este sexto dedo no es un auténtico pulgar. Anatómicamente, el hueso que forma el “pulgar” es un hueso sesamoideo radial muy modificado, que en
especies íntimamente relacionadas forma parte de la muñeca. Sabiendo de qué manera
actúa la selección natural en poblaciones contemporáneas, suponemos que cuando las primeras poblaciones del panda comenzaron a explotar el bambú, habría variación individual
en cuanto a la longitud del hueso sesamoideo radial. Como consecuencia de una selección continuada y potente, durante muchas generaciones, la longitud promedio del hueso
aumentó hasta alcanzar sus proporciones actuales.
Un carácter que se utiliza de un modo novedoso y que se transforma finalmente por
selección en una estructura completamente nueva, como el sesamoideo radial de los
ancestros del panda, se conoce como preadaptación. Un punto importante acerca de las
preadaptaciones es que son una casualidad. Una preadaptación mejora la eficacia de un
individuo por accidente, no porque la selección natural sea consciente o vea el futuro.
La selección natural no es “perfecta”
Los párrafos anteriores subrayan que la selección natural está continuamente mejorando
la adaptación.Aunque esto es cierto, es igualmente importante constatar que la evolución
no da lugar a caracteres “perfectos”.
Para entender este punto, consideremos que cuando Boag y Grant analizaron sus datos
sobre la supervivencia de los pinzones después de la sequía de 1977, advirtieron que también habían sobrevivido mejor individuos con picos relativamente estrechos. Esto tiene
sentido porque los pinzones aprietan por ambos lados cuando rompen los frutos de Tribulus, y los picos más estrechos concentran la fuerza de manera más efectiva a ambos lados.
(a)
(b)
5 dedos
"Pulgar"
Caña de bambú
"Pulgar"
Sesamoide radial
Figura 3.9 El pulgar del panda (a) Los pandas gigantes arrancan las hojas de bambú haciendo pasar el tallo por sus manos.
(Bill Kamin/Visuals Unlimited) (b) En este dibujo se muestra como el “pulgar” del panda forma una ranura por la que pasa el tallo del
bambú. Según Endo et al. 1999.
Capítulo 3 Selección natural darwiniana 61
Pero los picos más anchos están correlacionados positivamente con picos más altos y con
un mayor tamaño corporal. Por ello, las aves con picos más altos, que son adecuados para
aplicar la presión hacia abajo, tienden también a tener picos más anchos, que son menos
efectivos para aplicar la fuerza por los lados. Probablemente, existe esta correlación debido
a que los mismos genes afectan a la altura y a la anchura del pico y al tamaño corporal,
haciendo que todos los caracteres sean más grandes, o más pequeños, de manera conjunta. La conclusión es que la selección por tamaño más grande y picos más altos produce
picos más anchos, aun cuando deberían favorecerse picos más estrechos
Este es un punto importante. Debido a la correlación genética entre caracteres, la selección natural no optimiza todos los caracteres implicados. La selección natural da lugar a
la adaptación, pero no a la perfección.
La selección natural no es ni aleatoria ni progresiva
La evolución por selección natural se caracteriza a veces como un proceso aleatorio, pero
nada puede estar más lejos de la realidad. La evolución por selección natural no es aleatoria, ya que aumenta la adaptación al ambiente.
Sin embargo, como los ejemplos del VIH, de los pinzones y del panda demuestran, el
proceso de selección no aleatoria está completamente libre de cualquier intencionalidad
consciente. Realmente Darwin llegó a rechazar la frase acuñada “seleccionada naturalmente” porque la gente creía que la palabra selección implicaba un acto consciente o la
elección por algún ser. No ocurre nada de esto.
Además, aunque la evolución tiende con el tiempo a aumentar la complejidad, el
grado de organización y la especialización de los organismos, no es progresiva en el sentido de conducir hacia algún objetivo predeterminado. La evolución hace organismos
“mejores” sólo en el sentido de aumentar la adaptación a su ambiente. No hay una tendencia inevitable hacia formas más avanzadas de vida. Por ejemplo, las tenias actuales no
tienen sistema digestivo y han evolucionado realmente para ser más simples que sus antecesores. Las serpientes evolucionaron a partir de antecesores que tenían extremidades. Las
aves más primitivas del registro fósil tenían dientes.
Desgraciadamente, una visión finalista de la evolución tardará en desaparecer. Incluso
Darwin tenía que recordarse a sí mismo lo de “nunca usar las palabras superior o inferior” cuando se discutían relaciones evolutivas. Es cierto que algunos organismos descienden de linajes antiguos y otros de linajes más recientes, pero todos los organismos del
registro fósil y los que viven en la actualidad fueron adaptados a sus ambientes.Todos ellos
son capaces de sobrevivir y reproducirse. Ninguno es “superior” o “inferior” respecto de
cualquier otro.
La eficacia no es circular
La Teoría de la Evolución por selección natural se critica a menudo (no por biólogos) de
tautológica, o circular en su razonamiento. Es decir, después de revisar los cuatro postulados de Darwin, se podría decir “Desde luego, los individuos con variaciones favorables
son los únicos que sobreviven y se reproducen, debido a que la teoría define como favorable la capacidad para sobrevivir y reproducirse.”
La clave para resolver el problema es darse cuenta de que la palabra “favorable”, aunque es una abreviatura cómoda, es falsa. El único requerimiento para la selección natural
es que ciertas variantes lo hagan mejor que otras, como opuesto a las aleatorias. Siempre
que un grupo no aleatorio de la población sobreviva mejor y deje más descendientes, se
producirá selección natural. En los ejemplos que hemos analizado, la investigación no solo
determinó qué grupos no aleatorios sobrevivieron a un hecho selectivo, sino también descubrió por qué se favoreció a dichos grupos.
No hay plantas o animales
superiores o inferiores.
62 PARTE I Introducción
En el presente también debería tener sentido que la eficacia darwiniana no es un valor
abstracto. La eficacia se puede medir en la naturaleza. Se hace contando los descendientes que producen los individuos durante su vida u observando la capacidad de los individuos para sobrevivir a un suceso selectivo y comparando la actuación de cada individuo
respecto de otros individuos de la población. Éstos son criterios objetivos, independientes y mensurables para estimar la eficacia.
La selección natural actúa sobre individuos, no sobre grupos
Los individuos no hacen cosas
por el bien de la especie.
Se comportan de modo tal que
maximizan su propia eficacia.
Uno de los errores más persistentes sobre la selección natural, especialmente la selección en
el comportamiento animal, es que los individuos realizan acciones por el bien de la especie.
El autosacrificio, o comportamiento altruista, se da en la naturaleza. Los perritos de las praderas hacen llamadas de alarma cuando se aproximan los predadores, lo que dirige la atención
hacia ellos mismos. Las leonas a veces cuidan cachorros que no son suyos. Pero la selección
no puede favorecer caracteres a menos que incrementen la eficacia de sus portadores en
relación con la competencia individual. Si hay un alelo que produce un comportamiento
realmente altruista, es decir, un comportamiento que reduce la eficacia del portador y
aumenta la eficacia de otros, sería seleccionado fuertemente en contra. Como veremos en
el Capítulo 10, se ha encontrado que todo comportamiento altruista que ha sido estudiado
en detalle aumenta la eficacia del altruista, bien porque los beneficiarios del comportamiento
son parientes genéticos muy próximos (como en los perritos de las praderas) o porque los
beneficios con recíprocos (como en el cuidado de la crías en los leones).
Sin embargo, la idea de que los animales harán cosas para el bien de la especie está tan
arraigada que consideraremos este punto una segunda vez. Consideremos de nuevo a los
leones. Los leones viven en grupos sociales llamados manadas. Coaliciones de machos
luchan para tomar posesión de la manada. Si un nuevo grupo de machos derrota en combate a los machos de la manada, los recién llegados matarán rápidamente a todas las crías.
Estas crías no están emparentadas con ellos. Matar a las crías aumenta la eficacia de los nuevos machos, ya que las hembras volverán a ser fértiles de nuevo muy pronto y concebirán descendientes para los nuevos machos (Packer y Pusey 1983, 1984). El infanticidio está
muy extendido entre los animales. Claramente, un comportamiento de este tipo no existe por el bien de la especie. El infanticidio existe, más bien, porque en ciertas circunstancias aumenta la eficacia de los individuos que lo realizan frente a los que no lo realizan.
3.4.
La evolución del darwinismo
Ya que la evolución por selección natural es un rasgo de organización general de los sistemas vivientes, la teoría de Darwin se sitúa como una de las grandes ideas en la historia del
intelecto. Su impacto en la Biología es análogo al que tuvieron las leyes de Newton sobre
la Física, la teoría de Copérnico sobre el Sol como centro del Universo en la Astronomía y
la Teoría de las Placas Tectónicas en Geología. En palabras del genético evolutivo Theodosius Dobzhansky (1973):“Nada en Biología tiene sentido si no es a la luz de la evolución.”
No obstante, a pesar de su fuerza, la Teoría de la Evolución por selección natural no fue
aceptada universalmente por los biólogos hasta 70 años después de su propuesta inicial.
Había tres problemas serios con la teoría, tal como fue formulada originalmente por Darwin, que había que resolver.
1. Ya que Darwin no sabía nada acerca de la mutación, no tenía idea de
cómo se generaba la variabilidad en las poblaciones. Por ello, no pudo responder
a las críticas que mantenían que la cantidad de variabilidad en las poblaciones era estrictamente limitada, y que la selección natural la pulverizaría hasta detenerse cuando la variabilidad se agotase. No fue hasta principios del siglo XX, cuando genéticos como Thomas
Capítulo 3 Selección natural darwiniana 63
Hunt Morgan comenzaron a experimentar con las moscas de la fruta, cuando los biólogos
comenzaron a entender la naturaleza continua y universal de la mutación. Morgan y sus
colegas demostraron que se producen mutaciones en cada carácter y en cada generación.
2. Ya que Darwin no sabía nada acerca de la genética, no tenía idea de cómo
pasaba la variación a los descendientes. No fue hasta el redescubrimiento y verificación de los experimentos de Mendel con guisantes, 35 años después de su publicación,
cuando los biólogos comprendieron cómo los caracteres paternos pasan a los descendientes. Las leyes de la segregación y de la transmisión independiente de Mendel confirmaban el mecanismo del postulado 2, que afirma que algo de la variación observada en
las poblaciones es heredable.
Hasta entonces, muchos biólogos proponían que los genes actuaban como los pigmentos en la pintura. Los abogados de esta hipótesis, llamada herencia de las mezclas, argüían
que las mutaciones favorables simplemente se mezclarían gradualmente con los caracteres
existentes y se perderían. En 1867, el ingeniero escocés Fleeming Jenkin publicó un tratamiento matemático de la herencia de las mezclas, en un famoso y cuidado experimento relativo a los descendientes de personas con piel clara y piel oscura. Por ejemplo, si un marino
de piel oscura quedara embarrancado en una isla ecuatorial habitada por personas de piel
clara, el modelo de Jenkins predice que, independientemente de lo ventajosa que pudiera
ser la piel oscura (por ejemplo, por reducir el cáncer de piel), la población nunca llegaría
a ser de piel oscura debido a que caracteres como el color de la piel se mezclan. Si el ma
rinero de piel oscura tuviera hijos con una mujer de piel clara, éstos serían de piel morena.
Si éstos tuvieran a su vez hijos con personas de piel clara, sus hijos tendrían la piel morena
clara y así sucesivamente. De manera inversa, si un marinero de piel clara embarrancara en
una isla septentrional habitada por personas de piel oscura, la herencia de las mezclas indicaba que, independientemente de lo ventajosa que fuera la piel clara (por ejemplo, al facilitar la
síntesis de la vitamina D por la luz UV), la población nunca llegaría a tener la piel clara. En
la herencia de las mezclas las nuevas variantes se empantanan, y las nuevas mutaciones se diluyen, hasta que dejan de tener efectos mensurables. Para que la selección natural actúe, las nuevas variantes favorables deben de pasar a los descendientes intactas y permanecer discretas.
Desde luego, ahora comprendemos que los fenotipos se mezclan en algunos caracteres, como en el color de la piel, pero los genotipos nunca lo hacen. De hecho, la hipotética población de Jenkins se convertiría gradualmente de piel más oscura o más clara si la
selección fuera fuerte y la mutación añadiera continuamente en las poblaciones variantes
para piel oscura o para piel clara a través de cambios en los genes implicados en la producción de melanina (Figura 3.10).
El mismo Darwin batalló con el problema de la herencia, adoptando finalmente una
hipótesis totalmente incorrecta, basada en el trabajo de Jean-Baptiste Lamarck. Lamarck
fue un gran biólogo francés de principios del siglo XIX que propuso que las especies evolucionan por la herencia de los cambios producidos en los individuos1. La idea de Lamarck
fue rompedora por dos razones: reconoce que las especies han cambiado con el tiempo y
propone un mecanismo para que se produzca dicho cambio. Sin embargo, su teoría fue
errónea porque los descendientes no heredan los cambios fenotípicos adquiridos por sus
padres. Si una persona desarrolla su musculatura elevando pesas, sus descendientes no serán
más musculosos; si las jirafas estiran sus cuellos para alcanzar las hojas más altas de los árboles, esto no tiene consecuencias para la longitud de los cuellos de sus descendientes.
3. Lord Kelvin, el más famoso físico del siglo XIX, publicó una serie de trabajos importantes hacia 1860, calculando la edad de la Tierra en un máximo
de unos 15 a 20 millones de años. El análisis de Kelvin se basaba en la medida del calor
1
Nota del traductor. La idea básica de Lamarck fue que los organismos “sentían” el impulso por evolucionar, por
progresar. La idea de que los caracteres adquiridos se heredan no repugnaba a Darwin.
64 PARTE I Introducción
CH2
HO
CH2
H-C-COOH
HO
H2N
H-C-COOH
HO
H2N
Tirosina
Figura 3.10 Por qué no se produce la
herencia de mezcla En este esquema se
muestra la vía metabólica de la melanina, el
pigmento oscuro de la piel humana. La vía
implica una serie de pasos que comienzan con
la fenilalanina o tirosina, que son aminoácidos
frecuentes en la dieta. Las enzimas
responsables para catalizar cada una de las
reacciones presentadas, están codificadas por
varios genes distintos. Debido a que los
diferentes alelos de estos genes tienen
diferentes niveles de actividad, y debido a que
la vía hacia la melanina implica numerosos
pasos, el color de la piel es consecuencia de la
actividad de muchos genes y alelos. En este
sentido, la acción de los genes se mezcla para
dar lugar al fenotipo. Sin embargo, ya que
cada alelo es diferente, cada efecto de las
enzimas sobre la vía metabólica pasa a los
descendientes intacto. Ésta es la razón por la
que no hay herencia de mezcla.
O
O
CH2
H-C-COOH
O
N
H
HO
HO
COOH
O
H2 N
O
N
H
O
N
H
Polimerización
Melanina
(sustancia compleja de
elevado peso molecular)
del Sol y en las temperaturas actuales de la Tierra. Debido a que el fuego era la única fuente de calor conocida en aquel tiempo, Kelvin supuso que el Sol estaba quemándose como
un enorme conjunto de carbón. Esto tenía que significar que el Sol se estaba consumiendo
gradualmente, irradiando progresivamente menos calor con el paso de los milenios. Por
ello, tanto geólogos como físicos llegaron al convencimiento de que la superficie de la
Tierra se estaba enfriando gradualmente. Esto se basaba en la suposición de que la Tierra
estuviera cambiando de un estado fundido a un estado sólido por radiación de calor a la
atmósfera. Esta suposición parecía estar apoyada por la medida de la temperatura, progresivamente mayor, en pozos profundos de las minas. Estos datos permitieron a Kelvin
calcular el ritmo de enfriamiento por radiación.
Lo importante de los cálculos de Kelvin fue que la transición de caliente a frío del Sol
y de la Tierra proporcionaba un estrecho margen de tiempo para que la vida sobre la Tierra
fuera posible. Este margen era claramente demasiado estrecho para permitir que se acumularan los cambios graduales que propugnaba el darwinismo y proporcionaba un sólido apoyo a la creación instantánea y especial para explicar la adaptación y la diversidad.
El descubrimiento de los isótopos radioactivos a principios del siglo XX cambió todo
esto. Los cálculos de Kelvin eran inatacables, pero sus suposiciones eran completamente
equivocadas. Los geólogos y los físicos confirmaron que el calor de la Tierra es un subproducto de la desintegración radioactiva y no del enfriamiento por radiación y que la
energía solar es consecuencia de la fusión nuclear y no de la combustión.
La síntesis moderna resuelve
décadas de controversia sobre
la validez de la evolución por
selección natural.
La síntesis moderna
La comprensión de la variabilidad, la herencia y el tiempo fue tan difícil que los primeros
70 años de la biología evolutiva se caracterizaron por su turbulencia (véase Provine 1971;
Capítulo 3 Selección natural darwiniana 65
Mayr 1980, 1991). Pero entre 1932 y 1953 se publicaron una serie de libros importantes que
integraron con éxito la genética con los cuatro postulados de Darwin y condujeron a la
reformulación de la Teoría de la Evolución. Esta reformulación, conocida como la síntesis
moderna de la Teoría de la Evolución, fue una teoría consenso basada en dos propuestas:
• La evolución gradual es consecuencia de pequeños cambios genéticos sobre los que
actúa la selección natural.
• El origen de las especies y de los taxones superiores, o macroevolución, se puede explicar en términos de la selección natural que actúa sobre los individuos, o microevolución.
Con la síntesis, los cuatro postulados originales de Darwin, y sus consecuencias, pudieron
reformularse de la siguiente manera:
1. Como consecuencia de la mutación, que da lugar a nuevos alelos, y de la segregación
y transmisión independientes de éstos, que los barajan dando lugar a combinaciones
nuevas, los individuos de las poblaciones son variables para casi todos los caracteres.
2. Los individuos pasan a sus descendientes sus alelos intactos.
3. En muchas generaciones se producen más descendientes de los que pueden sobrevivir.
4. Los individuos que sobreviven y llegan a reproducirse, o aquellos que tienen más descendientes, son los que tienen alelos y combinaciones alélicas que los adaptan mejor a
su ambiente.
El resultado es que los alelos asociados con mayores eficacias aumentan en frecuencia
de generación en generación.
Esta idea de la vida
Darwin terminó la introducción de la primera edición de Sobre el origen de las especies con
una frase que todavía representa la visión consensuada de los biólogos evolutivos (Darwin
1859, p. 6): “La selección natural ha sido el principal, aunque no el exclusivo, medio de
modificación.” Nosotros pensamos ahora en las modificaciones en términos de cambios
en las frecuencias de los alelos responsables de caracteres, como la altura del pico y la resistencia al AZT. Somos mas finamente conscientes de otros procesos que dan lugar a
cambios evolutivos, además de la selección natural. (Los Capítulos del 4 al 6 exploran estos
procesos en detalle.) Pero la visión darwiniana de la vida, como una competición entre
individuos con capacidades diferentes para sobrevivir y reproducirse, se ha demostrado
correcta casi en todos los detalles.
Como Darwin escribió en su frase final (1859, p. 490): ”Hay grandeza en esta idea de
que la vida, con sus diversas energías, fue originalmente alentada en contadas formas, o
acaso en una sola; y que, mientras este planeta ha ido girando de acuerdo con las leyes fijas
de la gravedad, desde aquel principio tan sencillo se han desarrollado y están evolucionando, incontables formas de lo más hermosas y maravillosas.”
Los creacionistas quieren que
3.5.
El debate sobre el “creacionismo científico”
La controversia científica sobre el hecho de la evolución terminó hacia finales el siglo XIX,
cuando las pruebas revisadas en el Capítulo 2 sobrepasaron a las críticas.Todavía se discutió
hasta finales de los años 1930 si la selección natural era el proceso primario responsable
tanto de la adaptación como de la diversidad, cuando los trabajos de la síntesis moderna
proporcionaron una base mecanicista a los cuatro postulados de Darwin y unificaron la
micro- y la macroevolución. La evolución por selección natural se considera en la actualidad la gran idea unificadora de la biología.Aunque el discurso científico acerca de la vali-
la Teoría de la Creación
Especial sea enseñada en las
escuelas públicas, aun cuando
fue rechazada como
alternativa viable a la Teoría de
la Evolución por selección
natural hace un siglo.
66 PARTE I Introducción
dez de la evolución por selección natural terminó hace más de medio siglo, en Estados
Unidos y en Europa todavía continua una controversia política y filosófica (Holden 1995;
Kaiser 1995). ¿Cuál es este debate y por qué se mantiene?
Historia de la controversia
El juicio de los monos contra Scopes en 1925 es quizá el suceso más conocido de un debate religioso que ha durado desde la primera publicación de Darwin (véase Gould 1983,
ensayo 20). John Scopes fue un maestro de biología que enseñaba darwinismo en violación de la Ley Butler del Estado de Tennessee, que prohibía la enseñanza de la evolución
en las escuelas públicas.William Jennings Bryan, un famoso político y orador fundamentalista, fue el fiscal; Clarence Darrow, el más renombrado abogado defensor de su generación, representó a Scopes.Aunque Scopes fue declarado culpable y multado con 100 dólares, el juicio se percibió ampliamente como un gran triunfo de la evolución ya que Bryan
había sugerido, en el estrado de los testigos, que los seis días de la creación descritos en el
Génesis 1:1-2:4, podrían haber sido días de más de 24 horas. Esto se consideró una inconsistencia grave y un revés a la integridad del punto de vista creacionista. Pero lejos de terminar el debate sobre la enseñanza de la evolución en las escuelas de los Estados Unidos,
el juicio de Scope fue simplemente un paso intermedio.
De hecho, la Ley Butler permaneció vigente hasta 1967; no fue hasta 1968, con el juicio de Epperson contra Arkansas, en que la Corte Suprema de los Estados Unidos anuló las
leyes que prohibían la enseñanza de la evolución. Los argumentos de la Corte se basaron
en la separación de la Iglesia y del Estado en la Constitución de los Estados Unidos. En
respuesta, los grupos religiosos fundamentalistas de los Estados Unidos reformularon sus
argumentos como “ciencia de la creación” y pidieron el mismo tiempo para la que para
ellos era, insistían, una teoría alternativa al origen de las especies. Hacia finales de 1970,
26 legislaturas estatales debatieron la legislación del “tiempo igual” (Scott 1994). Arkansas y Louisiana aprobaron tales leyes sólo para tener que derribarlas en las cortes estatales.
Entonces se apeló ante la Corte Suprema de los Estados Unidos la Ley de Louisiana en
todos sus términos, que decidió en 1987 (Edwards contra Aquillard) que debido a que el
creacionismo es esencialmente una idea religiosa, enseñarla en las escuelas públicas era una
violación de la primera enmienda. Sin embargo, dos jueces escribieron formalmente que,
no obstante, sería aceptable que los maestros presentasen teorías alternativas a la evolución
(Scott 1994).
Una respuesta de los oponentes a la evolución ha sido eliminar las palabras creación y
creador de sus escritos y pedir o bien igual tiempo para enseñar que no ha ocurrido evolución o para enseñar una propuesta llamada Teoría del Diseño Inteligente, que se refiere
a la presencia de un creador de la perfección y de la adaptación de los organismos actuales (Scott 1994; Schmidt 1996). La complejidad y perfección de los organismos es realmente una objeción largamente aducida contra la evolución por selección natural. Darwin
fue consciente de esto; en su Origen dedicó una sección del capítulo titulado “Dificultades de la teoría” a los “órganos de gran perfección.” ¿Cómo puede la selección natural,
escogiendo cambios aleatorios del genoma, producir caracteres complejos e integrados
como el ojo de los vertebrados?
Perfección y complejidad en la naturaleza
El clérigo inglés William Paley escribió en 1802, en apoyo a la Teoría de la Creación Especial, un argumento ahora clásico. Si una persona encuentra un reloj y descubre que fue
un instrumento especialmente complejo y preciso, debería deducir, lógicamente, que
habría sido construido por un relojero altamente cualificado. Entonces Paley hizo un paralelismo entre el reloj y la perfección del ojo de los vertebrados y pidió a sus lectores que
Capítulo 3 Selección natural darwiniana 67
dedujeran la existencia de un Creador perfecto y con propósito. Argumentaban que los
organismos están tan bien construidos que tienen que haber sido el trabajo de un diseñador consciente. Esta lógica, todavía utilizada por los creacionistas en la actualidad, recibe el nombre del argumento del diseño (Dawkins 1986).
Ya que percibimos la perfección y la complejidad del mundo natural, parece que la evolución por selección natural desafía la credulidad.Aquí hay, realmente, dos asuntos. El primero es cómo cambios al azar pueden dar lugar a un orden. Las mutaciones son sucesos
aleatorios, por lo que la producción de variación en una población se da al azar. Pero la
selección de dichas variantes, o mutantes, no es al azar: está dirigida en el sentido de
aumentar la eficacia biológica.Y lo que nosotros percibimos como altamente ordenado,
complejo o incluso perfecto en el mundo natural son las adaptaciones: estructuras o comportamientos que aumentan la eficacia. Pero no hay nada consciente o inteligente debajo del proceso. El biólogo Richard Dawkins captó este punto refiriéndose a la selección
natural como a un “relojero ciego.”
Un segundo asunto, íntimamente relacionado, es ¿cómo han podido evolucionar,
mediante el proceso darwiniano de acumulación gradual de pequeños cambios, estructuras tan complejas y altamente integradas, como el ojo de los vertebrados? Cada etapa
evolutiva tendría que incrementar la eficacia de los individuos de la población. Por ejemplo, un creacionista, llamado Michael Behe (1996), reclama que los sistemas biológicos,
como las vías metabólicas, son “de una complejidad irreducible,” y que no es posible que
sean el resultado de la selección natural. En contraste, el darwinismo propone que las
estructuras complejas han evolucionado a través de una serie de estados intermedios o
formas graduales. ¿Es esto cierto? Por ejemplo, cuando consideramos una estructura
como la del ojo, ¿encontramos realmente una serie de formas, algunas más complejas que
otras?
La respuesta a estas cuestiones es sí. En algunas especies unicelulares hay realmente
orgánulos celulares con funciones análogas a las del ojo. Por ejemplo, las manchas oculares de una serie de protozoos llamados euglenoides, contienen moléculas que absorben
la luz, que están oscurecidas por un lado por pigmento. Cuando estas moléculas absorben luz, sufren cambios estructurales.Ya que la luz les puede llegar sólo por un lado, un
cambio en la molécula que absorbe luz tiene información útil acerca de dónde viene la
luz. Incluso algunos dinoflagelados tienen un orgánulo, parecido a una lente, que puede
concentrar la luz sobre la capa de pigmento. Sin embargo, es improbable que estos protistas unicelulares puedan formar una imagen, ya que no son capaces de un proceso nervioso. Más bien, sus ojos funcionan, probablemente, transmitiendo información acerca de
la profundidad de la célula en la columna de agua, lo que ayuda a ésta a orientarse y a
nadar hacia la luz.
Los ojos más complejos tienen una unidad básica llamada fotorreceptor. Es una célula que tiene pigmento capaz de absorber la luz. El tipo más simple de ojo pluricelular consta de unas pocas células fotorreceptoras en un hueco o dispuestas en copa, y se presenta
en las Figuras 3.11a y 3.11b. Este tipo de ojo se encuentra en una gran variedad de taxones, como los platelmintos, poliquetos (gusanos segmentados del filum de los anélidos),
algunos crustáceos (camarones, cangrejos y similares) y algunos vertebrados. Estos órganos se utilizan para orientación y para el control de la longitud del día (Willson 1984;
Brusca y Brusca 1990). Ojos ligeramente más complejos, como los presentados en la Figura 3.11c, tienen cálices ópticos, con una estrecha abertura que actúa como lente y
pueden formar imágenes, al menos en algunas especies. Se encuentran en unos pocos
nemertinos (gusanos cinta) y anélidos (gusanos segmentados), copépodos, moluscos
primitivos y nautiloideos. Los ojos más complejos (Figura 3.11d) se clasifican en dos categorías funcionales que se basan en si las células fotorreceptoras están dispuestas en una
lámina cóncava, como una retina, como los ojos de los vertebrados y pulpos, o convexa,
El argumento del diseño
sostiene que las adaptaciones
deben producirse por la acción
de una entidad consciente.
68 PARTE I Introducción
(a)
Células pigmentadas
Células epiteliales
Fibras nerviosas
(b)
Células
pigmentadas
(c)
Cavidad llena
de agua
Epitelio
Capa pigmentada
(retina)
Fibras nerviosas
Nervio óptico
(d)
Córnea
Cristalino
Córnea
Iris
Figura 3.11 Variación en los ojos de los moluscos (a) Mancha
pigmentaria; (b) copa simple con pigmento; (c) copa óptica simple que
se encuentra en gasterópodos primitivos; (d) los ojos complejos con
lentes de un caracol marino llamado Littorina y de un pulpo. Las células
pigmentarias se muestran en color.
Cristalino
Retina
Nervio óptico
como el ojo compuesto de los insectos y otros artrópodos (Goldsmith 1990). Estos ojos
tienen lentes y en la mayoría de los casos pueden formar imágenes.
Sin embargo, es importante reconocer que los ojos más simples que hemos revisado no
representan formas intermedias en el camino hacia estructuras más avanzadas. Las manchas
oculares, las copas y fosas pigmentadas que se encuentran en los seres vivos son adaptaciones
actuales al problema de la sensibilidad a la luz. No son formas ancestrales. Sin embargo, se
puede argumentar que los tipos de ojos discutidos aquí forman un sendero evolutivo
(Gould 1983, ensayo 1). Es decir, es concebible que ojos como estos constituyan estadios
intermedios en la evolución de los ojos complejos que se encuentran en los vertebrados,
pulpos e insectos. Esto es exactamente lo que Darwin argüía en su sección sobre “órganos
de extremada perfección.” (Para profundizar más acerca de la evolución de los ojos, véase
Salvini-Plawen y Mayr 1977; Nilsson y Pelger 1994; Quiring et al. 1994; Dawkins 1994.)
Otras objeciones
Hemos encontrado otros cuatro argumentos que los creacionistas utilizan regularmente
y hemos aportado respuestas desde una perspectiva evolutiva (véase Gish 1978; Kitcher
1982; Futuyma 1983; Gould 1983 ensayos 19, 20 y 21; Dawkins 1986; Swinney 1994).
1. La evolución por selección natural no es científica ya que no se puede
probar que no es cierta y porque hace predicciones no comprobables. Cada uno
de los cuatro postulados de Darwin es comprobable independientemente, por lo que la
teoría cumple el criterio clásico de que las ideas deben poder comprobarse y que no son
ciertas para considerarse científicas. Además, decir que los biólogos evolutivos no hacen
predicciones no es cierto. Los paleontólogos predicen rutinariamente (y correctamente)
qué estratos tendrán fósiles y de qué tipo (un ejemplo espectacular fue que en la Antártida
se encontrarían mamíferos marsupiales fósiles); Peter y Rosemary Grant han utilizado técnicas estadísticas basadas en la teoría evolutiva para predecir correctamente la cantidad y
Capítulo 3 Selección natural darwiniana 69
la dirección del cambio en las características de los pinzones durante los períodos selectivos de finales de 1980 y principios de 1990 (Grant y Grant 1993, 1995). El creacionismo
científico, por otro lado, llega a una incongruencia; en palabras de uno de sus líderes, el
Dr. Duane Gish (1978, p. 42): “No podemos descubrir por métodos científicos nada
acerca del proceso creador utilizado por Dios.”
2. Ya que la Tierra fue creada hace unos 6.000 a 8.000 años, no ha habido
tiempo suficiente para que la evolución darwiniana produzca la adaptación
y la diversidad observada en los seres vivos. Los científicos de la Creación presentan teorías sobre una Tierra joven y arguyen que la mayoría de las formas geológicas y de los estratos resultaron del diluvio universal del tiempo de Noé. (Por ejemplo,
véase Gish 1978 y Swinney 1994.) Muchos simplemente no creen en las suposiciones
que hay detrás de la datación radiactiva y niegan la validez de los datos. La suposición
del uniformismo en la evolución de la vida y de las formas terrestres también es rechazada por los científicos de la creación. De nuevo citamos a Gish (1978, p.42):“No sabemos cómo creó Dios, qué procesos utilizó, Dios utilizó procesos que ya no son operativos en
el universo natural” (énfasis original).
Sin embargo, las bases de la datación radioactiva se han comprobado y se ha demostrado que son correctas. La datación radioactiva ha demostrado que los estratos rocosos
difieren en edad, y que la Tierra tiene unos 4.600 millones de años.
3. Ya que los organismos progresan desde formas más simples a más complejas, se viola la segunda ley de la termodinámica. Aunque la segunda ley ha sido
enunciada de varios modos desde su formulación hacia finales del siglo XIX, la versión más
general es: “Los procesos naturales tienden a moverse hacia un estadio de mayor desorden” (Giancoli 1955). La segunda ley se centra en el concepto de entropía. Es una cantidad que mide el estado de desorden de un sistema. La segunda ley, redactada en términos
de entropía, es que:“La entropía de un sistema aislado nunca disminuye. Sólo puede mantenerse sin cambio o aumentar” (Giancoli 1995).
La clave para entender la relevancia de la segunda ley para la evolución es la palabra “aislado.” La segunda ley es cierta sólo en sistemas cerrados. Sin embargo, los organismos vivos
son sistemas abiertos: la Tierra, en donde formas de vida fotosintéticas captan la energía
solar y la convierten en energía química que ellos y otros organismos pueden consumir.
Debido a que continuamente se está añadiendo energía a los sistemas vivos, la segunda ley
no es aplicable a su evolución.
4. Nadie ha visto formarse una nueva especie, por lo que la evolución es
indemostrable.Y debido a que los evolucionistas dicen que la especiación es
tan lenta como para no poderse observar directamente, la evolución es indemostrable y se basa en la fe. Aunque la especiación es un proceso lento, va marchando
y se puede estudiar. En el Capítulo 12 exploraremos uno de los ejemplos mejor estudiados: la divergencia de la mosca del manzano en dos razas huésped distintas. Las dos formas de estas moscas dejan sus huevos en frutos distintos, que servirán de alimento a sus
orugas. Como consecuencia de patrones distintos de selección natural sobre caracteres,
como las preferencias por el alimento y el momento del apareamiento, están comenzando a surgir marcadas diferencias genéticas entre las dos poblaciones. La investigación en
estos organismos está documentando sucesos clave en el comienzo de un proceso de escisión de una especie en dos.
Ya que hay decenas de millones de especies de insectos y debido a que muchos insectos están especializados en comer plantas, lo que está sucediendo con la mosca cresa del
manzano es de interés general: puede estar sufriendo un proceso que ha ocurrido muchas
veces en el curso de la evolución. El Capítulo 12 introduce también otros estudios experimentales y observaciones sobre la “especiación en acción.”
70 PARTE I Introducción
¿Qué es lo que motiva la controversia?
Durante décadas, la evolución por selección natural se ha considerado una de las teorías
mejor documentadas y con más éxito en las ciencias biológicas. Muchos científicos no
ven conflicto entre la evolución y la fe religiosa (Easterbrook 1997; Scott 1998) y
muchos cristianos están de acuerdo. Por ejemplo, en 1996 el Papa Juan Pablo II reconoció que la evolución darwinista es un resultado científico firmemente establecido y
afirmó que la aceptación del darwinismo es compatible con la tradicional comprensión
cristiana de Dios.
Si el hecho de la evolución y de la validez de la selección natural no son controvertidos y si la creencia en la evolución es compatible con la creencia en Dios, entonces, ¿por
qué continúa el debate creacionista?
En la discusión acerca de si la materia de la evolución debería incluirse en los textos
de enseñanza, un miembro de la Junta escolar del estado de Alabama, llamado David Byers,
dijo:“Es idiota e ingenuo creer que lo que se enseña a los niños acerca de lo que ellos son,
y de cómo tienen que ser, no tiene nada que ver con lo que deducen acerca de por qué
están aquí y cuáles son sus obligaciones, si, de hecho, tienen alguna obligación, y de cómo
deberían vivir” (Radio Pública Nacional 1995). Esta frase sugiere que, para algunos
creacionistas, la controversia no es acerca de la validez de las pruebas científicas o de su
compatibilidad con la religión. Más bien se refiere a lo que la evolución significa para la
moralidad y el comportamiento humanos.
Los creacionistas y los evolucionistas comparten el deseo de que los niños crezcan y
lleguen a ser adultos moralmente responsables. Los creacionistas luchan contra la evolución porque creen que es moralmente peligrosa. Los biólogos evolutivos, por otro lado,
creen que los niños deberían aprender lo que la ciencia dice acerca de cómo los seres
vivos llegaron a ser y les dejan que escojan las implicaciones morales, si es que las hay,
por sí mismos.
Resumen
Antes de que Darwin comenzara su trabajo sobre el origen
de las especies, muchos científicos estaban convencidos de
que las especies cambian con el tiempo. La singular contribución realizada por Darwin y Wallace fue darse cuenta de
que el proceso de selección natural proporcionaba un mecanismo para esta pauta, que Darwin denominó descendencia
con modificación.
La evolución por selección natural es el resultado lógico
de cuatro hechos: (1) los individuos varían en la mayoría de
sus caracteres; (2) algo de esta variación tiene base genética
y puede pasar a los descendientes; (3) se producen más descendientes de los que pueden sobrevivir hasta la edad reproductora, y de aquellos que llegan, algunos tienen más éxito
que otros; y (4) los individuos que más se reproducen constituyen un subgrupo de la población general no al azar, o
más adaptado. Este proceso de selección da lugar a cambios
en la constitución genética de las poblaciones con el tiempo o evolución.
Preguntas
1. En inglés corriente, la palabra adaptación significa “un ajuste a las condiciones ambientales.” ¿En qué sentido es diferente
la definición evolutiva de adaptación del sentido vulgar?
2. Razone cómo los datos sobre el pico de los pinzones demuestran los postulados de Darwin.
• ¿A qué se parecería la Figura 3.3 si la altura del pico no
fuera variable?
• ¿A qué se parecerían los datos de la Tabla 3.2 si la altura
del pico fuera variable, pero la variación no fuera heredable?
• ¿Por qué en la Figura 3.4 la línea dibujada a partir de los
datos de 1978, después de la sequía, está por enzima de la
línea dibujada a partir de los datos de 1976, antes de la
sequía?
Capítulo 3 Selección natural darwiniana 71
3. De acuerdo con el texto, es correcto decir que la mayoría de
los pinzones que murieron de hambre durante la sequía de
1977 lo hicieron porque “había una gran correspondencia
entre el tamaño poblacional y la disponibilidad de semillas.”
¿Acepta esta hipótesis? Si la acepta, ¿por qué no presentan los
datos de la Figura 3.5 una correspondencia perfecta entre el
momento en que comenzó el declive en la disponibilidad de
semillas y el momento en el que el tamaño de la población
comenzó a declinar?
4. Suponga que está comenzando un estudio a largo plazo de
una población de plantas con flores anuales, aisladas en una
pequeña isla. La lectura de ciertos trabajos recientes le han
convencido de que el calentamiento global es real y que
dará lugar a cambios significativos a largo plazo en la cantidad de lluvia que la isla recibe. Describa las observaciones
y experimentos que necesitaría hacer a fin de documentar
si se da selección natural en su población de estudio a lo
largo de su investigación. ¿Qué caracteres mediría y por qué?
5. Al final de un artículo acerca de cómo las mutaciones en el
número variable de secuencias de DNA repetidas en tandem
(VNTR) están asociadas con enfermedades, Krontiris (1995,
p. 1683) escribe:“El proceso mutacional en las VNTR, realmente puede seleccionarse positivamente; escogiendo a aquellos de nosotros con edad media y mayores, la evolución lleva
a nuestra especie a un combate engañoso.” Este investigador
propone que la selección natural sobre la especie humana
favorece a los individuos que mueren relativamente pronto.
Su lógica es que morir a causa de mutaciones VNTR es
beneficioso y se extenderá, ya que, como consecuencia, el
conjunto de la población se hará mas joven y saludable.
¿Puede ser cierta esta hipótesis, dado que la selección actúa
sobre los individuos? Explíquelo.
6. Muchos científicos en activo están relativamente poco interesados en la historia de su campo. El desarrollo histórico del
darwinismo, revisado en la Sección 3.4, ¿le ayuda a comprender mejor la teoría? ¿Por qué sí o por qué no? ¿Cree que
es importante para la práctica científica emplear cierto tiempo estudiando la historia?
7. Recientemente, la Junta escolar de Alabama, después de revisar los textos de Biología de las escuelas, votaron pedir que se
pusiera este aviso en el interior de la contraportada del libro
aprobado (Radio Pública Nacional 1995):
Este libro de texto discute la evolución, una teoría controvertida que algunos científicos presentan como explicación
científica del origen de seres vivos como los vegetales, los
animales y los humanos. Nadie estuvo presente cuando la
vida apareció por primera vez en la Tierra; por consiguiente, cualquier declaración acerca del origen de la vida
debe considerarse como teoría, no como un hecho.
¿Acepta esta última sentencia en esta declaración? ¿El punto
de vista del inserto, se refiere a otras teorías científicas, como
la teoría celular, la teoría atómica, la teoría de la tectónica de
placas y la teoría bacteriana de las enfermedades?
8. En 1991, una encuesta de Gallup entre adultos de los Estados
Unidos, encontró que el 47% creía que Dios había creado al
hombre en los últimos 10.000 años (Root-Bernstein, 1995).
Dadas las pruebas de la evolución por selección natural,
comente por qué tan pocas personas en los Estados Unidos
la aceptan.
Explorando la bibliografía
9. En los pasados 50 años, cientos de virus, bacterias, hongos e
insectos han desarrollado resistencia a medicamentos, herbicidas, funguicidas o insecticidas. Éstos son ejemplos notables
de la evolución en acción. En algunos de estos casos conocemos el mecanismo molecular del cambio evolutivo implicado. Para explorar en mayor profundidad este tema, lea los
siguientes trabajos. Piense acerca de cómo las pruebas de
estos estudios se equiparan con las pruebas de la evolución de
los pinzones de Darwin y del VIH.
Anthony, R. G.,T. R.Waldin, J. A. Ray, S.W. J. Bright, and P.
J. Hussey. 1998. Herbicide resistance caused by spontaneous mutation of the cytoskeletal protein tubulin.
Nature 393: 260-263.
Cohen, M. L. 1992. Epidemiology of drug resistance: Implications for a post-antimicrobial era. Science 257: 1050-1055.
Davies, J. 1994. Inactivation of antibiotics and the dissemination of resistance genes. Science 264: 375-382.
Van Rie, J.,W. H. McGaughey, D. E. Johnson, B. D. Barnett,
and H.Van Melleart. 1990. Mechanism of insect resistance
to the microbial insecticide Bacillus thuringiensis. Science
247: 72-74.
10 Parece improbable que pueda darse la selección de caracteres
“por el bien del grupo”. Sin embargo, algunos biólogos evolutivos sostienen que en ciertas condiciones, la selección de
grupo de comportamientos altruistas puede ser posible de
hecho. Lea los siguientes trabajos para aprender más acerca
de este tema:
Avilés, L., and P.Tufino. 1998. Colony size and individual fitness in the social spider Anelosimus eximius.American Naturalist 152: 403-418.
Morell,V. 1996. Genes vs. Teams: Weighing group tactics in
evolution. Science 273: 739-740. (News perspective.)
Wilson, D. F., and E. Sober.1994. Reintroducing group selection to the human behavioral sciences. Behavioral Brain
Sciences 17: 585-609.
Wilson, D. S., and L. A. Dugatkin.1997. Group selection and
assortative interactions. American Naturalist 149: 336-351.
72 PARTE I Introducción
Bibliografía
Abbott, I., L. K. Abbott, and P. R. Grant. 1977. Comparative ecology of Galápagos ground finches (Geospiza Gould): Evaluation of the importance of floristic diversity and interspecific competition. Ecological Monographs 47: 151–184.
Audesirk, G., and T. Audesirk. 1993. Biology: Life on Earth. New York:
Macmillan.
Behe, M. 1996. Darwin’s Black Box:The Biochemical Challenge to Evolution. New
York: Free Press/Simon and Schuster.
Boag, P.T. 1983.The heritability of external morphology in Darwin’s ground finches (Geospiza) on Isla Daphne Major, Galápagos. Evolution 37: 877–894.
Boag, P.T., and P. R. Grant. 1978. Heritability of external morphology in Darwin’s finches. Nature 274: 793–794.
Boag, P.T., and P. R. Grant. 1981. Intense natural selection in a population of Darwin’s finches (Geospizinae) in the Galápagos. Science 214: 82–85.
Bowman, R. I. 1961. Morphological differentiation and adaptation in the Galápagos finches. University of California Publications in Zoology 58: 1–302.
Brusca, R. C., and G. J. Brusca. 1990. Invertebrates. Sunderland, MA: Sinauer.
Darwin, C. 1859. On the Origin of Species by Means of Natural Selection. London:
John Murray.
Dawkins, R. 1986. The Blind Watchmaker. Essex: Longman Scientific.
Dawkins, R. 1994.The eye in a twinkling. Nature 368: 690–691.
Dobzhansky,T. 1973. Nothing in biology makes sense except in the light of evolution. American Biology Teacher 35: 125–129.
Dodson, E. O. 1960. Evolution: Process and Product. New York: Reinhold
Publishing.
Easterbrook, G. 1997. Science and God:A warming trend? Science 277: 890–893.
Endo, H., D.Yamagiwa,Y. Hayashi, H. Koie,Y.Yamaya, and J. Kimura. 1999. Role
of the giant panda’s ‘pseudo-thumb.’ Nature 397: 309–310.
Futuyma, D. J. 1983. Science on Trial:The Case for Evolution. New York: Pantheon.
Giancoli, D. C. 1995. Physics: Principles with Applications. Englewood Cliffs, NJ:
Prentice Hall.
Gibbs, H. L., and P. R. Grant. 1987. Oscillating selection on Darwin’s finches. Nature 327: 511–513.
Gish, D.T. 1978. Evolution:The Fossils Say No! San Diego: Creation-Life Publishers.
Goldsmith,T. H. 1990. Optimization, constraint, and history in the evolution of
eyes. Quarterly Review of Biology 65: 281–322.
Gould, S. J. 1977. Ever Since Darwin: Reflections in Natural History. New York:W.W.
Norton.
Gould, S. J. 1980. The Panda’s Thumb. New York:W.W. Norton.
Gould, S. J. 1983. Hen’s Teeth and Horse’s Toes. New York:W.W. Norton.
Grant, B. R. 1985. Selection on bill characters in a population of Darwin’s finches:
Geospiza conirostris on Isla Genovesa, Galápagos. Evolution 39: 523–532.
Grant, B. R., and P. R. Grant. 1989. Evolutionary Dynamics of a Natural Population.
Chicago: University of Chicago Press.
Grant, B. R., and P. R. Grant. 1993. Evolution of Darwin’s finches caused by a rare
climatic event. Proceedings of the Royal Society of London, Series B 251: 111–117.
Grant, P. R. 1981a. Speciation and adaptive radiation on Darwin’s finches. American Scientist 69: 653–663.
Grant, P. R. 1981b.The feeding of Darwin’s finches on Tribulus cistoides (L.) seeds.
Animal Behavior 29: 785–793.
Grant, P. R. 1991. Natural selection and Darwin’s finches. Scientific American October: 82–87.
Grant, P. R. 1999. Ecology and Evolution of Darwin’s Finches, 2nd ed. Princeton:
Princeton University Press.
Grant, P. R., and B. R. Grant. 1995. Predicting microevolutionary responses to
directional selection on heritable variation. Evolution 49: 241–251.
Grant, P. R., B. R. Grant, J. N. M. Smith, I. J.Abbott, and L. K.Abbott. 1976. Darwin’s finches: Population variation and natural selection. Proceedings of the National Academy of Sciences, USA 73: 257–261.
Holden, C. 1995.Alabama schools disclaim evolution. Science 270: 1305.
Kaiser, J. 1995. Dutch debate tests on evolution. Science 269: 911.
Keeton,W.T. 1972. Biological Science. New York:W.W. Norton.
Kitcher, P. 1982. Abusing Science:The Case Against Creationism. Cambridge, MA: MIT
Press.
Krontiris,T. G. 1995. Minisatellites and human disease. Science 269: 1682–1683.
Leng, E. R. 1962. Results of long-term selection for chemical composition in
maize and their significance in evaluating breeding systems. Zeitschrift für Pflanzenzüchtung 47: 67–91.
Mayr, E. 1980. Prologue. In Mayr, E., and W. B. Provine, eds., The Evolutionary
Synthesis. Cambridge, MA: Harvard University Press.
Mayr, E. 1991. One Long Argument: Charles Darwin and the Genesis of Modern Evolutionary Thought. Cambridge, MA: Harvard University Press.
National Public Radio. 1995. Evolution disclaimer to be placed in Alabama textbooks. Morning Edition,Transcript #1747, Segment #13.
Nilsson, D. E., and S. Pelger. 1994. A pessimistic estimate of the time required for
an eye to evolve. Proceedings of the Royal Academy of London, Series B 256: 53–58.
Packer, C., and A. E. Pusey. 1983.Adaptations of female lions to infanticide by incoming males. American Naturalist 121: 716–728.
Packer, C., and A. E. Pusey. 1984. Infanticide in carnivores. Pp. 31–42 in G. Hausfater and S. B. Hardy, eds. Infanticide. New York:Aldine Publishing Company.
Petren, K., B. R. Grant, and P. R. Grant. 1999. A phylogeny of Darwin's finches
based on microsatellite DNA length variation. Proceedings of the Royal Society
of London, Series B 266: 321–329.
Price,T. D., P. R. Grant, H. L. Gibbs, and P.T. Boag. 1984. Recurrent patterns of
natural selection in a population of Darwin’s finches. Nature 309: 787–789.
Provine,W. B. 1971. The Origins of Theoretical Population Genetics. Chicago: University
of Chicago Press.
Quiring, R., U.Walldorf, U. Kloter, and W. J. Gehring. 1994. Homology of the eyeless gene of Drosophila to the small eye gene in mice and aniridia in humans.
Science 265: 785–789.
Root-Bernstein, R. S. 1995.“Darwin’s Rib.” Discover (September) 38–41.
Salvini-Plawen, L. v., and E. Mayr. 1977. On the evolution of photoreceptors and
eyes. Evolutionary Biology 10: 207–263.
Schmidt, K. 1996. Creationists evolve new strategy. Science 273: 420–422.
Scott, E. C. 1994.The struggle for the schools. Natural History 7: 10–13.
Scott, E. C. 1998.Two kinds of materialism. Free Inquiry 18: 20.
Swinney, S. 1994.“Evolution: Fact or Fiction.” Kansas City, MO: 1994 Staley Lecture Series, KLJC Audio Services.
Willson, M. F. 1984. Vertebrate Natural History. Philadelphia: Saunders.
PARTE II
Aunque varían en color, la mayoría de las estrellas de mar de esta fotografía pertenecen a la misma especie. Los capítulos de
esta unidad exploran cómo actúa el proceso evolutivo sobre la variación genética para dar lugar a cambios en las características
de las poblaciones a lo largo del tiempo. (Carr Clifton/Minden Pictures)
LOS MECANISMOS
DEL CAMBIO EVOLUTIVO
A
LO LARGO DE LA PARTE
I NOS HEMOS REFERIDO A LA SELECCIÓN NATURAL COMO UN
mecanismo de cambio evolutivo. Hacia el final del Capítulo 3, habíamos definido la evolución
como un cambio de las frecuencias alélicas en las poblaciones y probamos como funciona la selección natural como agente del cambio evolutivo.
Sin embargo, la selección natural no es el único proceso que altera las frecuencias alélicas. Hay otros
tres mecanismos evolutivos adicionales: la mutación, la migración y la deriva genética.
Debido a que ninguna de las cuatro fuerzas de la evolución pueden actuar a menos que exista variación genética, comenzamos la Parte II con un capítulo dedicado a la mutación: proceso que introduce continuamente nuevos alelos, y ocasionalmente nuevos genes, en las poblaciones. Utilizando una
combinación de modelos algebraicos y pruebas experimentales, los Capítulos 5 y 6 demuestran cómo
la selección, mutación, migración y deriva actúan sobre esta variación para producir cambio evolutivo. El Capítulo 6 investiga también de qué manera la consanguinidad y otras formas de apareamiento no aleatorio afectan al destino de los alelos en las poblaciones. El Capítulo 7 completa la unidad,
tratando las interacciones que se dan entre loci cuando actúan las cuatro fuerzas y explorando cómo
los biólogos estudian el cambio evolutivo en caracteres determinados por un gran número de genes.
El objetivo global de esta parte es ofrecer una amplia perspectiva de los procesos evolutivos. Los
cuatro capítulos proporcionarán una sólida comprensión de cómo y por qué ocurre la evolución, y
sentarán las bases para un profundo análisis del resultado de la evolución: la adaptación y el cambio
a lo largo del tiempo. Éstos son los objetivos de las Partes III y IV.
CAPÍTULO
4
Mutación y variación genética
Este individuo tiene una mutación que da lugar al desarrollo de seis dedos en cada mano. (Science Photo Library/Photo Researchers, Inc.)
L
AS MUTACIONES SON LA MATERIA PRIMA DE LA EVOLUCIÓN. SIN MUTACIÓN NO
hay nuevos genes, nuevos alelos y finalmente no hay evolución. La mutación es la última fuente de variación heredable sobre la que actúa la selección natural y otros procesos
evolutivos.
Este capítulo tiene dos objetivos: investigar los mecanismos responsables de la generación
de nuevos alelos y genes y explorar cómo los biólogos cuantifican la cantidad de variación
genética que existe en las poblaciones naturales. Comenzamos revisando cómo se producen las mutaciones en una sola base y otros tipos de cambios a pequeña escala en las
secuencias del DNA. Estos procesos dan lugar a nuevos alelos. Más tarde, consideramos
cambios a gran escala que pueden dar lugar a nuevos genes, cambios en la organización
de los cromosomas o en la alteración del número de dotaciones cromosómicas de una
especie. El capítulo termina considerando cómo los investigadores analizan la variación
genética intraespecífica.
No obstante, el capítulo no pretende una revisión exhaustiva de todas las mutaciones
que pueden afectar a la secuencia y organización de los genes. La lista de tipos de mutación, especialmente en el ámbito cromosómico, es simplemente demasiado grande. En su
lugar, dedicamos nuestra atención al subgrupo de mutaciones que tienen el mayor impacto evolutivo (Tabla 4.1).
75
76 PARTE II Los mecanismos del cambio evolutivo
Tabla 4.1 Tipos de mutación con impacto evolutivo importante
Esta tabla resume los tipos de mutaciones revisados en este capítulo.
Nombre
Descripción
Causa
Significado
Mutatión puntual
Sustituciones
de pares de bases
en secuencia
de DNA
Errores en la
síntesis del DNA
o durante la
reparación de
daños en el DNA
Da lugar a nuevos alelos
Inversión
cromosómica
Inversión de un
segmento
cromosómico, de
tal manera que
se altera el orden
de los genes en el
cromosoma
Roturas en el DNA
por radiación
Los alelos del interior
de la inversión están
“bloqueados” formando
una unidad
Duplicación génica
Duplicación de
un segmento corto
de DNA, originando
una copia adicional
de un gen
Entrecruzamiento
desigual en la
meiosis
(véase Figura 4.3)
El gen “extra”
es libre para mutar
y quizá adquiera una
nueva función
Poliploidía
Adición de una
dotación completa
de cromosomas
Errores en la meiosis
o en la mitosis
(en plantas)
Puede dar lugar
a especies nuevas
4.1.
De dónde vienen los alelos nuevos
Las instrucciones para construir y organizar un organismo están codificadas en su material hereditario: la molécula llamada ácido desoxirribonucleico o DNA. Como se muestra
en la Figura 4.1a, el DNA está formado por pequeñas moléculas llamadas desoxirribonucleótidos: cada uno de ellos contiene un azúcar de 5 carbonos, llamado desoxirribosa, un
grupo fosfato y una base nitrogenada diferente. Las cuatro bases del DNA pertenecen a
dos grupos químicos diferentes: la citosina y la timina son pirimidinas, mientras que la adenina y la guanina son purinas. Los cuatro desoxirribonucleótidos se abrevian habitualmente
como C,T,A y G.
En la Figura 4.1b se muestra cómo estas moléculas están unidas formando largas cadenas mediante enlaces fosfodiéster, que se forman entre el carbono 5 de un desoxirribonucleótido y el carbono 3 de otro. Por ello, una cadena sencilla de DNA consta de una
secuencia de bases unidas a una “columna vertebral” de azúcar-fosfato. Sin embargo, en
las células el DNA consta normalmente de dos de tales cadenas. Éstas están enrolladas una
alrededor de la otra en una doble hélice, esquematizada en la Figura 4.1c. Esta estructura
está estabilizada por puentes de hidrógeno que se forman entre las bases de cada cadena.
Debido a la geometría de las bases y a la cantidad de espacio disponible dentro de la hélice, los puentes de hidrógeno se forman sólo cuando las bases adenina y timina (A-T) o
guanina y citosina (G-C) se enfrentan en cadenas opuestas. Éstas combinaciones, purina-pirimidina, se denominan pares de bases complementarias. Como se muestra en la
Figura 4.1d, entre G y C se forman tres puentes de hidrógeno, pero sólo dos entre A y T.
La naturaleza de la mutación
Después de que James Watson y Francis Crick (1953) hubieron deducido la estructura en
doble hélice del DNA, tal y como se muestra en la Figura 4.1c, advirtieron de inmediato que
Capítulo 4 Mutación y variación genética 77
Purinas
(a)
O
NH2
N
N
Grupo
fosfato
Base
nitrogenada
–O
P O
5
Pirimidinas
1
3
N
H
N
Guanina
O
4
O–
H2N
N
H
Adenina
N
O
N
HN
2
O
NH2
N
Carbono 5 del azúcar
O
CH2
HN
O
N
H
Citosina
N
H
Timina
3'
(b)
(c)
O
3'
5'
Base
CH2
O
4
G
C
T
1
3
(d)
A
2
5'
Adenina
Timina
O
–O
O
P O
N
T
O
Base
CH2
O
4
A
1
3
G
A
Enlace
fosfodiester
HN
H N
N H
O
CH3
2
Esqueleto de
azúcar-fosfato
H
N H
P O
A
O
4
3
N
G
N H
C
A
1
T
N
O
O
3'
P O
T
5'
A
N
N
H N
H
2
O
O
N
T
Base
CH2
O
–O
N
N
T
O
–O
N
C
3'
Citosina
Guanina
5'
Puente de
hidrógeno
3'
5'
Figura 4.1 La estructura del material genético (a) El esquema de la izquierda muestra la forma tipo de un nucleótido. Advierta que cada
átomo de carbono del azúcar está numerado y que no se muestran los átomos de hidrógeno y oxígeno unidos a estos carbonos. El esquema de la
derecha muestra la estructura de las cuatro bases nitrogenadas. (b) Los nucleótidos están unidos por enlaces fosfodiester entre el carbono 5’ de un
nucleótido y el carbono 3’ de otro, formando largas cadenas. (c) Cuando las bases complementarias de las cadenas de DNA opuestas forman
enlaces de hidrógeno, la molécula gira formando una doble hélice, como la que se muestra aquí. (d) La adenina y la timina forman dos enlaces de
hidrógeno; la citosina y la guanina forman tres.
la complementariedad en el apareamiento de las bases proporcionaba un mecanismo para la copia del material hereditario. Como
se ilustra en la Figura 4.2, una cadena sirve de molde para hacer la copia de la otra cadena. En 1960,Arthur Kornberg logró
aislar la primera de una serie de proteínas, llamadas polimerasas del DNA, responsables de la copia del DNA en las células.
78 PARTE II Los mecanismos del cambio evolutivo
Una mutación es un cambio en
la secuencia de bases del DNA.
Hacia finales de 1950 y principios de 1960, se realizaron una serie de experimentos para
clarificar cómo la secuencia de bases del DNA codifica información y cómo la información genética se transforma en proteínas que construyen y organizan las células. El resultado final fue que el DNA se transcribe en RNA mensajero (mRNA) que posteriormente
se traduce a una proteína (Figura 4.3a). Los investigadores establecieron que el código
genético se lee en tripletes, llamados codones.También descifraron qué aminoácidos están
codificados por cada uno de los 64 codones distintos (Figura 4.3b). Debido a que los 64
codones sólo necesitan especificar a 20 aminoácidos, el código genético es altamente
redundante; que quiere decir que el mismo aminoácido puede estar especificado por más
de un codón.
Estos resultados inspiraron y explicitaron la visión molecular del gen y de la mutación.
Los genes quedaron definidos como fragmentos de DNA que codifican para distintos
RNA o productos proteicos. Los alelos quedaron definidos como versiones del mismo gen
que difieren en su secuencia de bases. Las mutaciones se entendieron como cambios en
la secuencia de bases del DNA.
Para aclarar este punto, consideremos la primera mutación que se caracterizó en el ámbito molecular: el cambio en la hemoglobina humana que da lugar a la anemia falciforme,
enfermedad a veces mortal. La hemoglobina es una proteína que transporta oxígeno y que
se encuentra en los glóbulos rojos. En 1949, el laboratorio de Linus Pauling comunicó que
las personas que sufrían de anemia falciforme tenían una forma de hemoglobina diferente de la de las personas sanas. En 1958,Vernon Ingram demostró que la diferencia entre la
hemoglobina normal y la falciforme se debía al cambio en un solo aminoácido en la posición 6 de la cadena proteica, que tiene 146 aminoácidos. En lugar de tener el ácido glutámico en dicha posición, el alelo falciforme tiene valina. Posteriormente se estableció que
la sustitución del aminoácido está motivada por la sustitución de una sola base en el gen
de la hemoglobina. El alelo mutante tiene una adenina en lugar de una timina en el nucleótido 2 del codón para el aminoácido 6. Este tipo de cambio se denomina mutación puntual, ya que altera un solo punto en la secuencia de bases de un gen.
Hélices desenrolladas
Síntesis en marcha
Síntesis completa
A
T
A
T
A
T
A
T
A
T
C
G
C
G
C
G
C
G
C
G
G
C
G
C
A
C
G
C
A
C
T
A
T
A
T
A
T
A
T
A
T
A
T
A
T
A
T
A
T
A
A
T
A
G
C
A
T
T
A
G
T
A
T
A
T
A
T
C
G
C
G
C
G
C
A
T
A
T
A
T
T
A
T
A
T
A
Figura 4.2 El DNA forma un molde para su síntesis Debido a que las bases complementarias se
aparean, cada cadena de una molécula de DNA forma un molde para la síntesis de una cadena
complementaria. Si la polimerasa del DNA inserta una base errónea, como en la cadena del extremo
derecho, se produce un par desemparejado que tiene que repararse.
Capítulo 4 Mutación y variación genética 79
(a)
Flujo de la información Ejemplo
DNA
C A A C G T C C G A C A A G T
mRNA
G U U G C A G G C U G U U C A
Proteína
Valina Alanina Glicina Cisteina Serina
(b)
Segunda base
Primera
base
U
A
C
G
Tercera
base
U
UUU
UUC
UUA
UUG
Fenilalanina
Fenilalanina
Leucina
Leucina
UCU
UCC
UCA
UCG
Serina
Serina
Serina
Serina
UAU
UAC
UAA
UAG
Tisosina
Tisosina
Parada
Parada
UGU
UGC
UGA
UGG
Cisteina
Cisteina
Parada
Triptófano
U
C
A
G
C
CUU
CUC
CUA
CUG
Leucina
Leucina
Leucina
Leucina
CCU
CCC
CCA
CCG
Prolina
Prolina
Prolina
Prolina
CAU
CAC
CAA
CAG
Histidina
Histidina
Glutamina
Glutamina
CGU
CGC
CGA
CGG
Arginina
Arginina
Arginina
Arginina
U
C
A
G
A
AUU
AUC
AUA
AUG
Isoleucina
Isoleucina
Isoleucina
Comienzo (Metionina)
ACU
ACC
ACA
ACG
Treonina
Treonina
Treonina
Treonina
AAU
AAC
AAA
AAG
Asparagina
Asparagina
Lisina
Lisina
AGU
AGC
AGA
AGG
Serina
Serina
Arginina
Arginina
U
C
A
G
G
GUU
GUC
GUA
GUG
Valina
Valina
Valina
Valina
GCU
GCC
GCA
GCG
Alanina
Alanina
Alanina
Alanina
GAU
GAC
GAA
GAG
Ácido Aspártico
Ácido Aspártico
Ácido Glutámico
Ácido Glutámico
GGU
GGC
GGA
GGG
Glicina
Glicina
Glicina
Glicina
U
C
A
G
Codón
Aminoácido
Figura 4.3 En los organismos, la información fluye del DNA al RNA y a las proteínas (a) En las células, la secuencia de bases del DNA se
transcribe a una secuencia de bases de una cadena de RNA mensajero (mRNA), que se traduce a una secuencia de aminoácidos de la proteína.
Advierta que el RNA tiene una base nitrogenada llamada uracilo en lugar de timina. Una adenina en el DNA especifica a una uracilo en el RNA.
(b) Éste es el código genético. Cada uno de los 64 codones del mRNA que se presentan aquí, especifica a un aminoácido, o el comienzo o el final
de la unidad de transcripción. Advierta que en muchos casos, el cambio de la tercera base de un codón no cambia el mensaje.
Mutaciones puntuales
Las mutaciones puntuales son sustituciones de una sola base en el DNA a causa de alguno
de estos dos procesos: errores aleatorios en la síntesis del DNA o errores aleatorios en la
reparación de los lugares dañados por agentes químicos o radiación de alta energía.Ambos
tipos de cambios se producen por reacciones catalizadas por la polimerasa del DNA.
Si la polimerasa del DNA sustituye erróneamente a una purina (A o G) por otra, o a
una pirimidina (T o C) por otra durante la síntesis normal, o la que se da durante la reparación, la mutación puntual se denomina transición (Figura 4.4). Si se sustituye una
purina por una pirimidina, o a la inversa, la mutación se denomina transversión. De los
dos tipos de mutación puntual, la transición es mucho más frecuente. Normalmente
sobrepasan a las transversiones al menos en una proporción de 2:1. La hipótesis más aceptada para explicar este hecho es que la transición da lugar a una desorganización mucho
menor de la hélice del DNA durante la síntesis, por lo que es mucho menos probable
que sea reconocida como error y por consiguiente menos probable que sea corregida de
manera inmediata.
80 PARTE II Los mecanismos del cambio evolutivo
Pirimidinas
Purinas
A
Transversiones
Transiciones
Transiciones
G
Figura 4.4 Transiciones y transversiones
Las mutaciones puntuales son
sustituciones de una sola
base en el DNA. Se clasifican
de dos maneras: como
transiciones o transversiones
y como sustituciones
sinónimas o no sinónimas.
C
T
Transversiones
Si cualquiera de estos tipos de sustitución de bases se da en las regiones codificadoras
de un gen, la mutación cambia el codón leído por la proteína, llamada polimerasa del
RNA, que sintetiza RNA a partir de un molde de DNA. Por ejemplo, la sustitución de
una A por una T en el gen de la hemoglobina es una tranversión que cambia el mensaje
del codón número 6. Mirando al código genético en la Figura 4.3b advertiremos que cambios en la primera o segunda posición de un codón casi siempre cambian el aminoácido
especificado por el mRNA resultante. No obstante, debido a la redundancia del código
genético, cambios en la tercera posición no dan lugar normalmente a ningún cambio.
Las mutaciones puntuales que dan lugar al cambio de un aminoácido, se llaman sustituciones no sinónimas (o de reemplazamiento); las que no dan lugar a un cambio
se denominan sustituciones sinónimas (o silenciosas). Ambos tipos de mutaciones
puntuales dan lugar a nuevos alelos. La pregunta que surge ahora es, ¿de qué manera estos
nuevos alelos afectan a la eficacia del organismo?
Los efectos de las mutaciones sobre la eficacia
La sustitución silenciosa de un lugar en el DNA no afecta al fenotipo del organismo debido a que no modifica los productos génicos. Por ello, las mutaciones silenciosas no están
sujetas a la selección natural basada en la función de las proteínas o del RNA. Los alelos
que no tienen efecto sobre la eficacia se dice que son neutros.
¿Pero qué ocurre con las sustituciones no sinónimas, que sí dan lugar a un cambio en
la estructura de la proteína? Debido a que cambian el fenotipo del organismo, las sustituciones no sinónimas están expuestas a la selección natural. Por ejemplo, la mutación falciforme da lugar a un cambio muy importante en el fenotipo. Las moléculas mutantes de
hemoglobina tienden a cristalizar, formando largas fibras. La hemoglobina se encuentra
dentro de los glóbulos rojos y cuando la molécula cristaliza distorsiona la forma normal
en disco de las células en células falciformes como las descritas en la Figura 4.5. Las células falciformes tienden a adherirse en los capilares. Esto bloquea el flujo sanguíneo, priva
a los tejidos de oxígeno y ocasiona graves daños. Las células falciformes son también más
frágiles y se destruyen más rápidamente que las células normales. Esta continua pérdida de
glóbulos rojos da lugar a la anemia.
La falcemia y la anemia son más graves en las personas homozigóticas para el alelo
mutante debido a que todas sus moléculas de hemoglobina tienden a cristalizar. Las personas heterozigóticas presentan algo de falcemia, especialmente cuando la concentración
del oxígeno disuelto en sus glóbulos rojos es baja. Entonces, parecería que el alelo tiene
Capítulo 4 Mutación y variación genética 81
TGG
Treonina
TCT
Prolina
GAC
GAC
Ácido
glutámico
Ácido
glutámico
TGG
Treonina
TCT
Prolina
GCC
Valina
GAC
Ácido
glutámico
Figura 4.5 Formas normal y falciforme de glóbulos rojos humanos El diagrama de la izquierda muestra una
pequeña sección cerca del comienzo del DNA y de la secuencia proteica de la hemoglobina normal; la foto de la izquierda
muestra glóbulos rojos normales. El esquema de la derecha muestra la misma sección del DNA y de la secuencia proteica
de una hemoglobina mutante; la foto de la derecha muestra los glóbulos rojos falciformes consecuencia de dicha
mutación. (Fotos de Photo Researchers, Inc.)
un fuerte efecto adverso sobre la eficacia de los individuos. La selección natural eliminaría rápidamente a los alelos mutantes de la población.
Sin embargo, la situación no es tan simple. Las personas que tienen una copia del alelo
normal y una copia del alelo mutante tienen una ventaja inesperada: son resistentes a la
malaria. La resistencia se debe, aparentemente, a que en los heterozigotos, los glóbulos
rojos que tienen parásitos de la malaria son mucho más propensos a ser falcémicos que
los que no los tienen. Esto implica que los glóbulos rojos que tienen parásitos son destruidos selectivamente. En ambientes en donde la malaria es endémica, la resistencia a
la malaria es tan valiosa que los heterozigotos tienen mayor eficacia que cualquiera de
los dos tipos de homozigotos. Por ello el alelo mutante es beneficioso en ambientes en
donde la malaria es endémica, pero es perjudicial en ambientes en donde la malaria es
rara. Las bases genéticas de la anemia falciforme proporcionan un ejemplo de superioridad de los heterozigotos. En el Capítulo 5 discutiremos con mayor detalle la superioridad del heterozigoto.
Resumiendo, la mutación falciforme origina un nuevo alelo que es beneficioso en algunos ambientes y deletéreo en otros. Esto no es corriente, ya que la gran mayoría de las sustituciones no sinónimas dan lugar a nuevos alelos que tienen poco o ningún efecto sobre
la eficacia (Keightley y Caballero 1997; García-Dorado 1997). No es sorprendente que
muchos de los cambios aleatorios en las secuencias de aminoácidos de las proteínas no
mejoren su función, ya que la mayor parte de las proteínas han estado sometidas a la selección durante millones de años. No esperaríamos que un cambio aleatorio mejorase la función de la proteína, al igual que no esperaríamos que un cambio aleatorio en el circuito
de un ordenador mejorase el funcionamiento del procesador. No obstante, es importante reconocer que tanto las sustituciones sinónimas como las no sinónimas dan lugar a un
amplio rango de efectos sobre la eficacia (desde altamente deletéreas a neutras hasta beneficiosas) y que los efectos de los alelos sobre la eficacia dependen del ambiente.Volveremos a estos temas en los Capítulos 5 y 18.
En secuencias codificantes,
los efectos sobre la eficacia de
las sustituciones no
sinónimas van desde
altamente deletéreos en unos
hasta beneficiosos en otros.
La mayoría de las mutaciones
tienen muy poco efecto sobre
la eficacia.
82 PARTE II Los mecanismos del cambio evolutivo
Tasas de mutación
¿Con qué frecuencia se forman nuevos alelos? Muchos de nuestros mejores datos sobre
las tasas de mutación se refieren a una clase de cambios conocidos con el nombre de
mutaciones de pérdida de función. En estos tipos de mutaciones, la pérdida de un producto proteico normal da lugar a un fenotipo fácilmente reconocible. Por ejemplo, los
investigadores pueden rastrear una amplia población humana y contabilizar la incidencia
de un síndrome autosómico dominante como la acondroplasia (enanismo) o de una
enfermedad recesiva ligada al X como la hemofilia A (en la que la coagulación sanguínea
está alterada). La idea es elegir un carácter que sea fácil de detectar y cuya transmisión
genética permita a los investigadores detectar nuevas mutaciones. Por ejemplo, un individuo con acondroplasia, en el que ninguno de sus padres presenta la anomalía, debe de tener
una mutación nueva. De datos similares, un investigador puede deducir tasas de mutación
en unidades por gen y por generación.
El problema de este método es que las mutaciones de pérdida de función se producen
por cualquier proceso que inactive a un gen. Como se muestra en la Figura 4.6, los genes
pueden perder su función por la sustitución de un par de bases, que dé lugar a un codón
de terminación de cadena o a una secuencia aminoacídica no funcional.También pueden
perder su función por la inserción de un elemento genético móvil, por una reordenación
cromosómica o por la alteración de la pauta de lectura de los codones, ocasionada por la
adición o deleción de una o dos pares de bases (éstas se denominan mutaciones del corrimiento de la pauta de lectura).Además, muchas mutaciones interesantes (la mayoría de las
sustituciones no sinónimas, por ejemplo) no son detectables cuando los investigadores
determinan los fenotipos de los descendientes, ya que sus efectos son menos aparentes que
los de pérdida de función. Debido a estas dificultades, la mayor parte de los datos actuales son estimas muy por debajo de la tasa real a la que ocurren las mutaciones.
Secuencia de DNA
Normal
ACAATGGTACGACAA
codón
Inserción
de 1 base
ACAGATGGTACGACAA
Deleción
de 1 base
ACAATGTACGACAA
Mutación a
codón de
parada
ACAATTGTACGACAA
Inserción de
un elemento
genético móvil
ACAATGAGGGGGCTACGCGTACGA
Secuencia proteica
Cisteina
Tirosina
Histidina
Cisteina
Leucina
Prolina
Cisteina
Tirosina
Metionina
Tirosina
Serina
Alanina
Valina
Valina
Cisteina
Leucina
Cisteina
Cisteina
Prolina
Ácido aspártico
Alanina
Histidina
Alanina
Figura 4.6 Mutaciones de pérdida de función Cualquier causa que inactive a un gen da lugar a mutantes “knock-out”. Advierta que la
inserción o la deleción de una sola base cambia todos los codones siguientes del gen, dando lugar a una proteína no funcional.
Capítulo 4 Mutación y variación genética 83
Incluso con estas limitaciones, todavía podemos decir algunas cosas interesantes acerca de las tasas de mutación. Por ejemplo, consideremos los datos de la Tabla 4.2 sobre tasas
y frecuencias de mutaciones de pérdida de función y otros cambios con efectos importantes. Las tasas de mutación indicadas son muy bajas considerando como base el gen. Pero
hay tantos loci en los organismos (al menos 60.0001 en los humanos, por ejemplo) que
Tabla 4.2 Variación en las tasas de mutación de genes y especies
(a) Tasas de mutación a fenotipo recesivo en genes del maíz. L. J. Stadler (1942) cultivó un gran número de plantas de maíz y analizó
a los descendientes para una serie de caracteres recesivos.
Gen
Número de
gametos examinados
Número de
mutaciones encontradas
Número medio
de mutaciones
por millón de gametos
Tasa de mutación
(frecuencia por
gameto)
R3r
554.786
273
492,0
4,9 104
I3i
265.391
28
106,0
1,1 104
Pr 3 pr
647.102
7
11,0
1,1 105
Su 3 su
1.678.736
4
2,4
2,4 106
Y3y
1.745.280
4
2,2
2,2 106
Sh 3 sh
2.469.285
3
1,2
1,2 106
Wx 3 wx
1.503.744
0
0,0
0,0
(b) Estos datos, que resumen las tasas de mutación de una serie de genes y especies, están tomados de R. Sager y F. J. Ryan,
Heredity. New York: John Wiley, 1961.
Organismo
Mutación
Valor
Bacteriofago T2 (virus bacteriano)
Inhibidor de la lisis r 3 r
Amplitud de huésped h 3 h
1 10
3 109
Tasa: genes mutantes
por replicación génica
Escherichia coli (bacteria)
Fermentación de la lactosa lac 3 lac
Requerimiento de histidina his 3 his
his 3 his
2 107
4 108
2 106
Tasa: células mutantes
por división celular
Chlamydomonas reinhardtii (alga)
Sensibilidad a la estreptomicina strs 3 strr
1 106
Neurospora crassa (hongo)
Requerimiento de inositol inos 3 inos
Requerimiento de adenina ad 3 ad
8 108
4 108
Unidades
8
Drosophila melanogaster (mosca de la fruta) Color del ojo W 3 w
4 105
Ratón
3 105
Humanos
a dominantes autosómicos
a recesivos ligados al X
en células de cultivo de médula ósea
1
Dilución D 3 d
Corea de Huntington
Síndrome uña-rótula
Epiloia (predisposición a cierto tipo
de tumor cerebral)
Poliposis múltiple del intestino delgado
Acondroplasia (enanismo)
Neurofibromatosis (predisposición a
tumores del sistema nervioso)
Hemofilia A
Distrofia muscular de Duchene
Normal 3 resistencia a azaguanina
1 106
2 106
4–8 106
Frecuencia: por espora
asexual
Frecuencia: por gameto
1–3 10
4–12 105
3–25 105
5
2–4 105
4–10 105
7 104
Nota del traductor. Datos recientes publicados en Nature (15/02/2001) indican que en la especie humana debe de
haber unos 30.000 genes.
Tasa: células mutantes
por división celular
84 PARTE II Los mecanismos del cambio evolutivo
quizá el 10% de los gametos lleven una mutación detectable fenotípicamente. Éste es un
porcentaje alto, teniendo en cuenta que las tasas publicadas subestiman el número de
sustituciones no sinónimas y por ello de nuevos alelos. Una idea que surge de este conjunto de datos es que es posible, e incluso probable, que la mayoría de los descendientes
lleven al menos un nuevo alelo en alguna parte de su genoma.
Una segunda idea se refiere a la variación de las tasas de mutación. Las tasas de mutación detectables fenotípicamente varían en un rango de 500 veces entre los genes de una
especie (Tabla 4.2a) y hasta 5 órdenes de magnitud, unas 100.000 veces, entre especies
(Tabla 4.2b). Una pregunta obvia es ¿por qué?
¿Por qué las tasas de mutación son variables?
La tasa a la que se producen nuevos alelos varía a tres niveles: entre los individuos dentro
de una población, entre los genes de un individuo y entre las especies. De acuerdo con
las investigaciones realizadas hasta la fecha, parece que puede haber mecanismos diferentes responsables de la variación observada en cada nivel.
Las tasas de mutación varían
entre individuos debido
a variaciones en la secuencia
de bases de la polimerasa
del DNA y de los loci que
reparan el DNA.
Variación entre individuos
La tasa de mutación varía entre individuos por dos razones: los alelos de la polimerasa del
DNA pueden variar en su tasa de error y los alelos implicados en la reparación del daño
en el DNA pueden variar en su eficiencia.
Frances Gillin y Nancy Nossal (1976a,b) comprobaron que las polimerasas del DNA
varían en su precisión. Lo hicieron al investigar sustituciones de una sola base en la polimerasa del DNA del bacteriófago T4 (un virus que parasita bacterias).Algunas de las mutaciones aisladas por Gillin y Nossal disminuían la tasa de errores de la polimerasa durante
la replicación del DNA y reducían la tasa global de mutación. Otras mutaciones en la polimerasa aumentaban la tasa de error y elevaban la tasa de mutación global. Un hallazgo clave
fue determinar que los mutantes de la polimerasa propensos a cometer más errores eran
significativamente más rápidos que la forma de la enzima más precisa. Esto implica que
hay un compromiso entre la velocidad y la precisión de la replicación del DNA.
Las tasas de mutación puntual también dependen de la eficacia en la corrección de los
errores. La reparación de las bases mal emparejadas con las de la cadena complementaria
pueden tener lugar después de la síntesis o después de que el DNA haya sido dañado por
radiación o agentes químicos. La investigación sobre la reparación de emparejamientos erróneos ha sido intensa debido a que las mutaciones en los genes responsables de la reparación están implicados en el envejecimiento y en el desarrollo de ciertos tipos de cáncer. Hay
varios sistemas diferentes de reparación de los emparejamientos erróneos y en los mamíferos están implicadas al menos 30 proteínas diferentes (Mellon et al. 1996).Al menos, algunos de los sistemas de reparación están muy conservados; los genes de reparación de
emparejamientos erróneos se identificaron en humanos mediante su homología con genes
de levadura y de la bacteria Escherichia coli (Friedberg et al. 1995). En Escherichia coli y en
Salmonella enteritidis, las mutaciones en estos loci dan lugar a cepas con tasas de mutación
de 100 a 1000 veces superiores a lo normal (LeClerc et al. 1996). Lo que se deduce de estos
estudios es que la eficacia en la reparación de emparejamientos erróneos en el DNA, como
la tasa de error de la polimerasa del DNA, son caracteres con variación heredable.
Variación entre especies
Los datos de la Tabla 4.2b sugieren que las tasas de mutación varían de unas especies a otras.
Por ejemplo, parece que la mosca de la fruta, los ratones y los humanos, tienen tasas de
mutación más bajas que las de virus y bacterias. John Drake (1991) ha publicado datos
similares que indican que las tasas de mutación varían mucho entre virus, bacterias y leva-
Capítulo 4 Mutación y variación genética 85
duras. Sin embargo, un problema en estos estudios es que no comparan directamente las
tasas de mutación de genes homólogos. Por ello, no está claro si las diferencias observadas
se deben a la tasa de variación entre genes o entre especies.
Edward Klekowski y Paul Godfrey (1989) resolvieron este problema estudiando la tasa
de mutación del albinismo en el mangle Rhizophora mangle, y comparándola con la tasa de
mutación al albinismo de especies cultivadas bien estudiadas, como la cebada o el trigo negro.
En las plantas, el albinismo se produce por una mutación de pérdida de función en los genes
responsables de la síntesis de la clorofila. Klekowski y Godfrey eligieron el mangle como
organismo experimental debido a que es un árbol longevo, con un carácter especial: sus semillas germinan sobre el padre. Entonces, para estimar la tasa de mutación los investigadores
pudieron contar el número de descendencia albina que germinaba sobre padres normales.
Sus datos demuestran que la tasa fue 25 veces mayor en el mangle que la tasa de mutaciones al albinismo que se había calculado con anterioridad en la cebada y en el trigo negro.
¿Por qué esta diferencia? La explicación de Klekowski y Godfrey se basó en la constatación de que, en plantas, las células de la línea germinal se diferencian tarde en el desarrollo. (En los animales, las células germinales y somáticas se separan pronto en el desarrollo.
Por ello, las mutaciones que se dan en el tejido somático de los animales no pasa a los descendientes.) En plantas grandes y longevas, como el mangle, las células somáticas de tallos
y vástagos acumulan mutaciones a lo largo de muchas divisiones celulares somáticas antes
de diferenciarse como tejido germinal y sufrir la meiosis. Por ello, las plantas longevas deberían tener mayores tasas de mutación por generación que las plantas de vida corta. Los datos
de Klekowski y Godfrey están de acuerdo con esta predicción, ya que la cebada y el trigo
negro son plantas anuales y de pequeño tamaño. El resultado sugiere una interesante generalización: el tiempo de generación puede ser un factor clave que influya en la variación
de las tasas de mutación entre especies.
Variación entre genes
Comparada con la variación entre individuos y especies, sabemos mucho menos acerca
de por qué las tasas de mutación varían entre genes. No obstante, del estudio de los sistemas de reparación del DNA han surgido dos importantes generalizaciones: las regiones
codificantes se reparan de manera más eficaz que las regiones no codificantes (Bohr et al.
1985) y varios de los sistemas de reparación actúan sólo en genes activos transcripcionalmente. Por ello, la precisión parece ser mayor en aquellos casos en que las mutaciones pueden ser más perjudiciales.
4.2.
De dónde vienen los genes nuevos
El origen de nuevos alelos es bastante directo, pero, ¿de dónde vienen los genes nuevos?
Como con los alelos nuevos, varios tipos de mutaciones pueden dar lugar a genes nuevos. Revisaremos sólo un subgrupo. La duplicación génica es, probablemente, la fuente más importante de genes nuevos. Las duplicaciones se producen como consecuencia de
un fenómeno conocido con el nombre de entrecruzamiento desigual, esquematizado en
la Figura 4.7. El entrecruzamiento desigual es un error aleatorio, ocasionado por las
proteínas implicadas en dirigir la recombinación (entrecruzamiento) durante la meiosis.
Como muestra la Figura 4.7, uno de los productos del entrecruzamiento desigual es un
tramo de DNA redundante. El genoma tiene ahora una copia extra de la secuencia localizada en el segmento duplicado. Debido a que la copia original produce un producto normal, la secuencia redundante puede acumular mutaciones libremente sin consecuencias
para el fenotipo. La nueva secuencia podría incluso cambiar de función con el tiempo y
convertirse por ello en un nuevo locus. Éste es un punto importante. Debido a que la
duplicación génica da lugar a DNA extra, es el primer mecanismo que hemos encontra-
Las tasas de mutación
pueden variar entre especies
debido a diferencias en el
número de divisiones celulares
que tienen lugar antes de la
formación de los gametos.
Las tasas de mutación varían
entre loci debido a que los
genes más activos
transcripcionalmente se
reparan de manera más eficaz.
86 PARTE II Los mecanismos del cambio evolutivo
1
2
3
4
A
B
C
D
E
A
B
C
D
E
A
B C
A
B
C
D
E
D
E
1
2
3
4
A
B
C
D
E
A
B
D
E
A
B
C
C
D
A
B
C
D
E
E
Figura 4.7 Entrecruzamiento desigual y origen de las duplicaciones génicas Las letras y las barras de cada cromosoma del
esquema indican la localización de loci; los círculos indican la localización del centrómero. Los cromosomas de la izquierda están en
sinapsis, pero se produce entrecruzamiento entre puntos no homólogos. La consecuencia es que uno de los productos del entrecruzamiento
tiene una duplicación del gen C y otro una deleción del gen C. Se cree que fenómenos parecidos de entrecruzamiento desigual
constituyen el mecanismo más frecuente que da lugar a las duplicaciones génicas.
do que da lugar a unas posibilidades totalmente nuevas para la función génica. La familia
génica de la globina proporciona un estupendo ejemplo de cómo la duplicación génica
permite la divergencia de función.
Duplicaciones génicas en la familia génica de la globina
En la especie humana, la familia génica de la globina consta de dos agrupaciones principales de loci que codifican las subunidades proteicas de la hemoglobina. Los grupos son
la familia α en el cromosoma 16 y la familia β en el cromosoma 11 (α y β son las letras
griegas alfa y beta). Una molécula completa de hemoglobina está formada por un grupo
hemo que se une al hierro, rodeado por cuatro subunidades proteicas: dos codificadas por
los loci de la familia α y dos codificadas por los loci de la familia β.
Los datos representados en la Figura 4.8 demuestran que cada locus de las familias α y
β se expresan en diferentes momentos del desarrollo. Por ejemplo, en el primer trimestre
α
La familia α– incluye
tres loci funcionales:
50
Porcentaje total de la
síntesis de globina
γ
β
40
α, α2, ξ (zeta)
30
La familia β– incluye
5 loci funcionales:
20
10
ξ
ε
β
β, ε (Épsilon), δ (Delta)
Gγ (Gamma G),
Aγ (Gamma A)
γ
δ
6
12 18 24 30 36
6
Nacimiento
Edad después de la
concepción (semanas)
12
18 24 30 36
Edad después del
nacimiento (semanas)
42
48
Figura 4.8 El momento de la expresión difiere entre miembros de la familia génica de las globinas Este
gráfico muestra cambios en la expresión de los genes humanos de la globina de las familias α y β durante el embarazo y
después del nacimiento. En los embriones, la hemoglobina se forma con la globina ζ de la familia α y la globina ⑀ de la
familia β. En el feto, la hemoglobina se forma con la globina α de la familia α y la globina δ de la familia β. En los adultos,
la hemoglobina se forma con la globina α de la familia α y la globina β de la familia β. Cada una de estas hemoglobinas
tienen diferencias funcionales importantes.
Capítulo 4 Mutación y variación genética 87
del embrión la hemoglobina está formada por dos cadenas ζ (zeta) y dos ⑀ (epsilon), mientras que en los adultos está formada por dos cadenas α y dos cadenas β (recuerde que la
mutación falciforme se da en una de las cadenas β). Combinaciones diferentes de polipéptidos de las globinas dan lugar a moléculas de hemoglobina con importantes diferencias
funcionales. Por ejemplo, la hemoglobina fetal tiene una mayor afinidad por las moléculas del oxígeno que la hemoglobina del adulto. Esto incrementa la transferencia de oxígeno
de la madre al embrión.
Se cree que los loci de la familia globina son un producto de sucesos de duplicación
génica. La hipótesis viene apoyada por la gran semejanza estructural de las unidades de
transcripción entre los loci, incluyendo la notable correspondencia en la longitud y posición de sus intrones y exones, que se esquematizan en la Figura 4.9. La lógica de esta hipótesis es que es extremadamente improbable que semejanza estructural tan alta pueda darse
entre loci que no comparten un antecesor común reciente. La hipótesis de la duplicación
también viene apoyada por la observación de la gran semejanza en la secuencia entre los
loci de las globinas así como en su función similar.
Entonces, el modelo completo es que una secuencia ancestral se duplicó varias veces
durante el curso de la evolución de los vertebrados. En varios de estos nuevos loci, las
mutaciones cambiaron la función del producto proteico de un modo que la selección
natural lo favoreció, dando lugar a la formación de una familia génica. Debido a que las
familias α y β también contienen loci no funcionales llamados pseudogenes, que no se
transcriben, los biólogos deducen que algunos loci duplicados se volvieron no funcionales por mutación.
Lugar de la
Caperuza AUG
Globinas
humanas
31–104
1–30
122
222
850
126
(94)
118
Aγ
53
93
122
222
866
126
(58)
87
Gγ
53
93
122
222
886
126
(58)
87
δ
49
93
128
222
886
126
(103)
128
β
50
93
130
222
850
126
(107)
132
α
37
1–31
93
32–99
113
1–30
51
93
204
51
96
100–141
141
129
31–104
116
1–31
α
originales y proporcionar una
copia adicional del locus
paterno, (2) adquirir una nueva
función mediante mutación y
selección, o (3) convertirse en
pseudogenes no funcionales.
105–146
93
Globinas
de ratón
β
mantener sus funciones
Lugar
Poli-A
5355
ε
Los loci duplicados pueden (1)
105–146
222
646
32–99
122
Secuencia codificante
Secuencia
Intrón
no traducida
codificante traducida
204
(91)
112
126
(108)
135
100–142
135
126
(71)
105
Figura 4.9 Unidades de
transcripción de la familia génica
de las globinas En estos esquemas,
los cuadros anaranjados representan
secuencias codificadoras que no se
traducen, los cuadros verdosos se
refieren a secuencias codificantes que
se traducen y las zonas blancas indican
intrones. Los números dentro de cada
cuadro se refieren al número de
nucleótidos presentes en el transcrito
primario, mientras que los números
que están encima de los cuadros
indican las posiciones de los
aminoácidos en el polipéptido
resultante. AUG es el codón de inicio,
La longitud y la posición de los
intrones y de los exones de los loci de
las familias α y a β es prácticamente
idéntica.
88 PARTE II Los mecanismos del cambio evolutivo
Las familias génicas indicadas en la Tabla 4.3 comparten varios rasgos importantes con
los loci de la globina: tienen genes estructuralmente homólogos, con funciones similares,
agrupados juntos en el mismo cromosoma y acompañados ocasionalmente por algún
pseudogen. Sin embargo, es importante advertir que no todas las duplicaciones génicas dan
lugar a loci con funciones diferentes. En algunos casos notables, como el de los genes del
rRNA, una serie de copias múltiples del mismo gen tienen una secuencia de bases idéntica o casi idéntica, y producen un producto con la misma función.
Otros mecanismos para originar genes nuevos
Además de la duplicación, hay otros mecanismos que pueden originar genes nuevos, o funciones radicalmente nuevas para genes duplicados. Un ejemplo, llamado sobreimpresión,
se produce por mutaciones puntuales que dan lugar a nuevos codones de inicio y a nuevas pautas de lectura para la traducción. Paul Keese y Adrian Gibbs (1992) investigaron este
fenómeno en los timovirus, los cuales provocan enfermedades de tipo mosaico en ciertos
vegetales. El pequeño genoma de un timovirus, el virus del mosaico amarillo del nabo,
consta de tres genes. Dos de ellos se solapan, lo que indica que se traducen a partir de diferentes pautas de lectura en el mismo fragmento de nucleótidos. Keese y Gibbs estimaron
la filogenia de cinco timovirus y nueve virus íntimamente relacionados basándose en las
secuencias de aminoácidos de las replicasas (Figura 4.10), encontrando que los timovirus
forman su propia rama en la filogenia. Los timovirus son también los únicos de la filogenia con un gen solapado sobreimpreso en el gen de la replicasa.
Tabla 4.3 Algunas familias génicas
En esta tabla, la columna “número de genes duplicados” se refiere al número de loci en varias
familias génicas. Se supone que estos loci son el resultado de duplicaciones. Tienen una elevada
homología de secuencia, codifican sustancias con funciones muy relacionadas y a menudo se
encuentran agrupados uno al lado del otro en el mismo cromosoma.
Familia
Número de genes duplicados
Loci que se encuentran en muchos organismos
Actinas
5–30
Tubulinas (a y b)
5–15
Miosina, cadena pesada
5–10
Histonas
Queratinas
Proteínas del choque térmico
100–1000
⬎ 20
3
Insectos
Proteinas de la cubierta del huevo
⬎ 50
(gusano de la seda y mosca de la fruta)
Vertebrados
Globinas (muchas especies)
Familia ␣
1–5
Familia 
ⱖ 50
Ovoalbumina (gallina)
3
Vitelogenina (rana, gallina)
5
Inmunoglobulinas, regiones variables (muchas especies)
Antígenos de trasplante (ratón y humano)
⬎ 500
50–100
Capítulo 4 Mutación y variación genética 89
Virus del mosaico amarillo del nabo
Timovirus del mosaico amarillo de las Kennedya
Timovirus del mosaico de la berenjena
Timovirus del mosaico amarillo de las Ononis
Timovirus latente de Erysinum
Potexvirus X de la patata
Potexvirus del mosaico del trébol
Potexvirus del mosaico del narciso
Closterovirus del manchado clorótico de las hojas del manzano
Carlavirus M de la patata
Alfamovirus del mosaico de la alfalfa
Sindbis
Tobamovirus del mosaico del tabaco
Furovirus del necrosado amarillo de los nervios de la remolacha
Basándose en estos datos, Keese y Gibbs proponen que el gen de la replicasa es ancestral
y que el gen que se solapa se originó en el antecesor común a los timovirus. Su hipótesis es que una mutación dio lugar a un nuevo codón de inicio, con una pauta de lectura
diferente, en el fragmento de nucleótidos que codifica a la proteína replicasa. Advierten
que la evolución en el nuevo locus está, probablemente, altamente constreñida debido a
que cualquier mutación que mejore la función de la proteína solapante, probablemente
sería deletérea para la función de la replicasa. Basándose en su revisión de los trabajos sobre
genomas virales, también proponen que la sobreimpresión ha sido un mecanismo corriente para crear genes nuevos durante la evolución de los virus.
Charles Langley y sus colegas han investigado el origen de genes nuevos por otro mecanismo. El gen ancestral que estudiaron, que se encuentra en moscas de la fruta del género
Drosophila, codifica a la enzima alcohol deshidrogenasa (Adh). Este locus está localizado en
el cromosoma 2. Langley et al. (1982) descubrieron un locus similar en el cromosoma 3 en
dos (y sólo en dos) especies de moscas, D. teissieri y D. yakuba. Jeffs y Ashburner (1991)
secuenciaron este locus del cromosoma 3 y encontraron que carece de los intrones que se
encuentran en el gen Adh del cromosoma 2. Jeffs y Ashburner proponen que el nuevo locus
del cromosoma 3 se originó cuando un RNA mensajero del gen Adh se transcribió inversamente y el DNA complementario (cDNA) resultante se insertó en el cromosoma 3.
Como veremos en el Capítulo 18, este mecanismo de duplicación génica no es raro. La
transcriptasa inversa es corriente en los núcleos de las células eucariotas.
La cuestión que ahora surge es, ¿tiene este nuevo locus alguna función o es simplemente
un pseudogen? Long y Langley (1993) secuenciaron el DNA del locus del cromosoma 3
de un cierto número de individuos, tanto de D. teissieri como de D. yakuba con el propósito de analizar alelos del nuevo locus que hubieran surgido por mutación puntual. Descubrieron que la mayoría de los alelos diferían entre si sólo en las sustituciones silenciosas. Esto implica que la selección natural está actuando para conservar la secuencia de
aminoácidos de la proteína codificada por el nuevo locus. En contraste, el patrón común
de los pseudogenes es que las sustituciones no sinónimas sean tan frecuentes como las sinónimas. Por ello, Long y Langley concluyeron que el nuevo locus es un gen funcional. Lo
denominaron jingwei, por el protagonista de un mito de reencarnación chino.
Long y Langley aislaron el mRNA transcrito del gen jingwei. Después de secuenciar el
mRNA, encontraron que el gen contenía exones adicionales que no se encontraban en
su antecesor Adh. Estos exones adicionales aparentemente se habían anexionado de una
región flanqueante del cromosoma 3, después de que la transcripción inversa del Adh se
hubiera insertado. Jingwei es pues un locus híbrido, formado por trozos de genes de dos
cromosomas distintos. Aunque este mecanismo de duplicación génica parece exótico, es
Figura 4.10 Filogenia
estimada de los timovirus y
sus parientes De las especies
representadas en esta figura, sólo
los timovirus tienen genes
sobreimpresos. Esto implica que la
mutación que dio lugar a un gen
sobreimpreso ocurrió en algún
momento a lo largo de la rama
señalada por la flecha. Según
Keese y Gibbs (1992).
En muchos genomas,
la transcripción inversa de
mRNA y la inserción del DNA
resultante en una localización
nueva es una fuente
importante de genes nuevos.
90 PARTE II Los mecanismos del cambio evolutivo
un ejemplo de algo muy general: los genomas son dinámicos. La cantidad, localización y
formación del material genético cambia con el tiempo.
4.3
Alteraciones cromosómicas
En la morfología de los cromosomas se puede producir una amplia variedad de cambios.
Algunas de estas mutaciones afectan sólo al orden y organización de los genes; otras dan
lugar a duplicaciones o deleciones que afectan a la cantidad global de material genético.
Pueden también implicar a toda la molécula de DNA o sólo a una parte. Aquí nos centraremos en dos tipos de alteraciones cromosómicas que son particularmente importantes en la evolución.
Inversiones
Las inversiones cromosómicas implican a fragmentos de DNA más largos que los tipos de
mutación revisados en las Secciones 4.1 y 4.2.También dan lugar a consecuencias muy distintas. Las inversiones se producen como consecuencia de un proceso en varios pasos, que
comienza cuando una radiación ionizante da lugar a una doble rotura de la doble cadena en un cromosoma. Después de la rotura un segmento del cromosoma puede separarse, darse la vuelta y reasociarse en su localización original. Como muestra la Figura 4.11,
el orden de los genes del cromosoma queda invertido.
¿Cuáles son las consecuencias evolutivas? Las inversiones afectan a un fenómeno conocido como ligamiento genético. El ligamiento es la tendencia de alelos de diferentes
genes de segregarse juntos en la meiosis. Por razones obvias, los genes situados en el mismo
cromosoma tienden a estar mas íntimamente ligados (es decir, es más probable que se hereden juntos) que los genes que se encuentran en cromosomas no homólogos. De igual
manera, cuanto más juntos estén los genes en el mismo cromosoma, más fuerte será el ligamiento. Por otro lado, el entrecruzamiento en la meiosis rompe las combinaciones de alelos y reduce el ligamiento (véase el Capítulo 7).
Debido a que las secuencias invertidas no se pueden alinear adecuadamente en la sinapsis con las homólogas no invertidas,un entrecruzamiento que tenga lugar dentro de una inversión da lugar a la duplicación o a la pérdida de segmentos cromosómicos y a la producción
de gametos no funcionales. Cuando las inversiones están en heterozigosis es extremadamente raro que un entrecruzamiento tenga éxito. La consecuencia es que los alelos situados dentro de la inversión están unidos tan íntimamente que se heredan como un único “supergen”.
Roturas
A
B
C
D
A
E
B
E
D
C
F
B
E
F
D
C
A
Figura 4.11 Inversión cromosómica Las inversiones se producen cuando un segmento cromosómico se rompe por dos sitios,
gira y se vuelve a unir. Advierta que después del hecho, el orden de los genes indicados como C, D y E se ha invertido.
F
Capítulo 4 Mutación y variación genética 91
Las inversiones son frecuentes en Drosophila: el insecto más cuidadosamente estudiado
de todos. ¿Son importantes en la evolución? Consideremos una serie de inversiones que
se encuentran en Drosophila subobscura. Esta mosca se encuentra en Europa Occidental,
África del Norte y Oriente Medio, y tiene seis cromosomas. Cinco de estos cromosomas
son polimórficos para al menos una inversión (Prevosti et al. 1988), lo que significa que
hay cromosomas con y sin inversión. Desde los años 60 del siglo pasado los biólogos saben
que la frecuencia de estas inversiones varía regularmente con la latitud y con el clima. Este
tipo de cambio regular en frecuencia de un alelo o de una inversión en un área geográfica se denomina clina.Varios autores han propuesto que inversiones distintas deben contener combinaciones específicas de alelos que funcionan juntos, bien en condiciones
ambientales frías o calientes, húmedas o secas. Pero la clina, ¿es realmente el resultado de
la selección natural sobre los supergenes? ¿O puede ser un accidente histórico, ocasionado por diferencias en las poblaciones fundadoras tiempo atrás?
Un experimento natural ha resuelto el problema. En 1978 se encontró por primera vez
D. subobscura en el Nuevo Mundo, inicialmente en Puerto Montt, Chile, y luego, cuatro años
más tarde, en Port Angeles,Washington, USA.Varias pruebas apoyan que la población de
América del Norte proviene de la de América del Sur. Por ejemplo, de las 80 inversiones
que se encuentran en las poblaciones del Viejo Mundo, exactamente el mismo subgrupo
de 19 se encontró tanto en Chile como en el estado de Washington.Además, Drosophila es
frugívora, Chile es uno de los principales exportadores de frutas y Port Angeles es un puerto de mar. En pocos años, después de su llegada a cada continente, las poblaciones de
D. subobscura se han expansionado enormemente a lo largo de cada una de las costas y han
desarrollado las mismas clinas en las frecuencias de inversiones que se encuentran en el Viejo
Mundo (Figura 4.12). Incluso las clinas están correlacionadas con los mismos cambios climáticos: desde ambientes marinos húmedos, pasando por climas mediterráneos, hasta desiertos y estepas secas (Prevosti et al. 1988; Ayala et al. 1989). Ésta es una prueba sólida de
que las clinas se forman por selección natural y no se deben a accidentes históricos.
¿Qué genes están bloqueados en la inversión y cómo afectan a la adaptación a los cambios climáticos? En el laboratorio, líneas de D. subobscura seleccionadas para menor tamaño corporal tienden a ser homozigóticas para la inversión que se encuentra en la parte más
seca y cálida del rango (Prevosti 1967). Investigaciones recientes han confirmado que existen clinas pronunciadas y paralelas en el tamaño corporal en poblaciones de moscas de
América del Norte y de Europa (Huey et al. 2000). Estos resultados indican que los alelos que se encuentran en las inversiones afectan al tamaño corporal, favoreciendo la selección natural moscas grandes en climas húmedos y fríos, y moscas pequeñas en zonas secas
y cálidas. La investigación en este experimento natural continua. Mientras tanto, el estudio de la mosca ilustra un punto clave sobre las inversiones: son una clase importante de
mutaciones, ya que afectan a la selección de grupos de alelos.Volveremos a este tema sobre
selección en alelos múltiples en el Capítulo 7.
América del Sur
orden de los genes y
disminuyen la frecuencia de
entrecruzamiento...
...como consecuencia, los
alelos que se encuentran
dentro de las inversiones
tienden a heredarse como una
unidad.
América del Norte
75
75
Frecuencia de la
Inversión Est
Las inversiones cambian el
65
65
55
55
Figura 4.12 Las frecuencias
de las inversiones forman
clinas en Drosophila subobscura
45
45
30
40
Latitud Sur
50
30
40
Latitud Norte
50
Estos gráficos muestran la
frecuencia de una inversión,
llamada Est, en poblaciones de
Drosophila subobscura de América
del Sur y de America del Norte.
De datos de Prevosti et al. 1988.
92 PARTE II Los mecanismos del cambio evolutivo
Poliploidía
A menudo, las poblaciones de
individuos poliploides están
aisladas genéticamente de
sus especies parentales.
El último tipo de mutación que examinaremos, se da a la mayor escala posible: dotaciones completas de cromosomas. En lugar de ser haploide (n) o diploide (2n), un organismo poliploide puede ser tetraploide (4n), octoploide (8n) o mayor.
La poliploidía es frecuente en vegetales y rara en animales. Casi la mitad de las especies de angiospermas (plantas con flores) son poliploides, como también la mayoría de los
helechos. Pero en animales la poliploidía es rara. Se da en grupos como en las lombrices
de tierra y en algunos platelmintos, en donde los individuos tienen tanto gónadas masculinas como femeninas y pueden autofecundarse (estas especies se denominan hermafroditas autocompatibles). También se encuentra en grupos que pueden dar lugar a
descendientes sin fecundación, mediante un proceso llamado partenogénesis. En algunas
especies de escarabajos, cochinillas, polillas, camarones, carpas doradas y salamandras, se
puede dar cierto tipo de partenogénesis que dé lugar a la duplicación de los cromosomas.
En los vegetales, la poliploidía puede originarse a partir de varios fenómenos distintos.
Quizá los más frecuentes sean los errores en la meiosis, que dan lugar a gametos diploides
(Ramsey y Schemske 1998). Cuando los vegetales producen gametos diploides, pueden
suceder dos cosas. Si los individuos que producen gametos diploides tienen estructuras
reproductivas tanto masculinas como femeninas y se autofecundan, puede aparecer descendencia tetraploide (4n)(véase la Figura 4.13a). Si este descendiente se autofecunda
cuando alcanza la madurez, o si se cruza con un hermano tetraploide que produce gametos diploides, puede quedar establecida una población tetraploide.
Alternativamente, los individuos que producen gametos diploides pueden cruzarse con
individuos normales que producen gametos haploides. Como se muestra en la Figura 4.13b,
este tipo de cruce da lugar a descendencia triploide. Sin embargo, los individuos triploides
tienen poca fertilidad. Debido a que sus cromosomas homólogos están presentes en número impar, no pueden realizar la sinapsis correctamente en la meiosis. Por ello, la mayoría de
los gametos que producen los triploides terminan con un número erróneo de cromosomas
(véase el histograma superior de la Figura 4.13b). Pero el histograma inferior de la Figura
4.13b muestra que si un individuo triploide se autofecunda, la mayoría de la descendencia
resultante es tetraploide. Estos datos demuestran que los pocos descendientes que escapan
del “bloqueo triploide” pueden dar lugar a poblaciones viables de tetraploides.
La poliploidía es importante porque puede dar lugar a que se formen especies nuevas.
Para entender el porqué, imaginemos la descendencia de los cruces entre individuos de
una población tetraploide, establecida por uno de los mecanismos descritos más arriba, y
la población diploide de donde procede. Si los individuos de las dos poblaciones se cruzan, su descendencia triploide será semiestéril. Pero si los individuos tetraploides continúan
autofecundándose o se cruzan entre ellos, se producirá descendencia tetraploide totalmente
fértil. De este modo, la selección natural favorecerá a los poliploides que quedan reproductivamente aislados de sus poblaciones parentales. Si las poblaciones diploides y tetraploides quedan genéticamente aisladas, se deberán considerar como especies distintas.
Es también importante reconocer que las dotaciones cromosómicas duplicadas, como
la duplicación de genes concretos que analizamos anteriormente en este capítulo, quedan
libres para obtener nuevas funciones como consecuencia de la mutación y de la selección.
La poliploidía es una fuente importante de variación genética, ya que da lugar a cientos
o miles de loci duplicados.
¿Cuál es la tasa de mutación para la poliploidía en vegetales? Justin Ramsey y Douglas Schemske (1998) han respondido a esta cuestión calculando la frecuencia de los dos
mecanismos principales de formación de tetraploides. Para estimar la frecuencia con la
que se combinan gametos diploides para formar descendencia tetraploide (la ruta hacia
la poliploidía, esquematizada en la Figura 4.13a), revisaron estudios publicados sobre la
Capítulo 4 Mutación y variación genética 93
(a) "Ruta directa" hacia la tetraploidía
Progenitor
(b) Tetraploidía pasando por
el "bloqueo triploide"
Progenitores
2n
Autofecundación,
cruzamiento
con igual o
"cruce retrógrado"
con el progenitor
Descendientes de la
primera generación
4n
Gametos
Gametos
2n
+
2n
4n
1n
Descendientes de la
primera generación
3n
2n
Descendientes
de la segunda
generación
+
2n
?
Gametos
+
?
4n
30
20
10
0
7* 8 9 10 11 12 13 14
Número de cromosomas del polen
Descendientes
de la segunda
generación
4n
Porcentaje de polen
+
2n
?
?
?
*Los datos de las gráficas pertenecen a
plantas columbinas, en las que los
gametos haploides normales tienen n = 7
cromosomas y los descendientes
diploide normales tienen n = 14
Porcentaje de descendientes
Gametos
2n
2n
80
60
40
20
0
28
14* 16
Número de cromosomas
en los descendientes
Figura 4.13 Mecanismos que dan lugar a individuos tetraploides en plantas Véase el texto para su explicación.
tasa de formación de gametos diploides en fanerógamas.Ya que los datos de la literatura sugieren que los gametos diploides se producen en la mayoría de las fanerógamas a una
frecuencia promedio de 0,00465, la frecuencia de los tetraploides producidos por esta vía
debería ser 0,00465 0,00465 = 2,16 10-5. Luego, en cada generación, este mecanismo de formación de poliploides dará lugar a 2 de cada 10.000 descendientes que se
producen en una fanerógama típica. Ramsey y Schemske emplearon la misma estrategia
para estimar la frecuencia con la que surge descendencia triploide y llega a producir descendientes tetraploides. (Ésta es la ruta hacia la poliploidía esquematizada en la Figura
4.13b.) Utilizando las series de datos publicadas sobre la frecuencia de cada paso en la
secuencia que conduce de hecho a la formación de poliploides por este mecanismo, calcularon que los tetraploides se producen con una frecuencia de al menos 1,16 10-5
por generación.
Lo que se deduce del estudio de Ramsey y Schemske es importante: en las fanerógamas, la formación de poliploides se da a una frecuencia parecida a la de las mutaciones
puntuales en loci concretos. Junto con las sustituciones no sinónimas, las duplicaciones
génicas y las inversiones cromosómicas, la poliploidía es una fuente importante de variación genética en poblaciones naturales.
En las plantas, la poliploidía se
da lo bastante a menudo
como para considerarla un
tipo importante de mutación.
94 PARTE II Los mecanismos del cambio evolutivo
4.4 Medida de la variación genética en poblaciones
naturales
Tradicionalmente, los biólogos
creían que la variación alélica
de las poblaciones sería
limitada...
...pero la investigación ha
revelado que es realmente
abundante.
En las tres secciones anteriores de este capítulo, hemos discutidos los procesos que dan
lugar a nueves alelos, genes o cromosomas. Estos procesos producen variabilidad genética, que es la base de la evolución. En esta última sección volveremos a los métodos que
los biólogos utilizan para medir la cantidad de variación genética presente en las poblaciones naturales.
Nos centraremos en la medida de la variación alélica en loci concretos. Sin embargo,
antes de considerar los datos sobre la variación genética en poblaciones, es importante considerar cuánta variación genética podríamos encontrar. El punto de vista clásico era que
en las poblaciones había poca variación genética. El razonamiento para afirmar esto era
que entre los posibles alelos de un locus dado, uno de ellos tendría que ser mejor que todos
los demás. La selección natural conservaría al alelo más ventajoso para la supervivencia y
la reproducción y eliminaría al resto. El mejor alelo se denominó el de tipo silvestre; cualquier otro alelo presente se consideraba mutante.
Como veremos, los métodos actuales para comprobar la variación genética han revelado que el punto de vista clásico era erróneo. Comenzando con los primeros trabajos
de Harris (1966) y Lewontin y Hubby (1966), los biólogos evolutivos han analizado las
proteínas codificadas por los alelos y el DNA de estos mismos alelos. Cuanto más profundo ha sido su análisis, más variación genética se ha encontrado. En la actualidad, los
biólogos evolutivos reconocen que las poblaciones naturales albergan mucha variación
genética.
Determinando genotipos
Para medir la diversidad de alelos de un locus concreto, debemos determinar los genotipos de los individuos. Para algunos loci, es posible deducir los genotipos de los individuos
por sus fenotipos. Por ejemplo, la esquistosomiasis intestinal es una enfermedad humana
ocasionada por la infección del platelminto parásito Schistosoma mansoni. Diversos datos
indican que la susceptibilidad a la infección por Schistosoma mansoni está fuertemente
influenciada por un solo locus del cromosoma 5, llamado SM1.(Para una revisión véase
Online Mendelian Inheritance in Man 1999.) Laurent Abel y sus colegas (1991) analizaron las genealogías de 20 familias brasileñas, y encontraron que sus datos estaban de
acuerdo con un modelo en el que SM1 tiene dos alelos codominantes. Los individuos
homozigotos para uno de los alelos son susceptibles, mientras que los homozigotos para
el otro alelo son resistentes. Los heterozigotos tienen una resistencia intermedia. En zonas
en donde todo el mundo está expuesto a agua contaminada por Schistosoma mansoni, es
posible, con razonable exactitud, deducir el genotipo de una persona por la intensidad de
la infección.Abel y sus colegas estimaron que en las poblaciones brasileñas estudiadas, cerca
del 60% de las personas era homozigótica resistente, alrededor del 5% era homozigótica
susceptible y el restante 35% era heterozigótica.
En contraste con el SM1, para muchos loci es difícil o imposible deducir el genotipo
de los individuos simplemente observando sus fenotipos. Por ello, la mayoría de los biólogos que estudian la diversidad alélica observan directamente las proteínas codificadas por
los alelos, o al DNA de éstos. Hay una serie de métodos para hacerlo, muchos de los cuales se basan en la electroforesis en gel. La electroforesis en gel utiliza una lámina de material similar a la gelatina y un campo eléctrico para separar las moléculas por tamaños, masa
y carga eléctrica. (Véase el Cuadro 4.1.)
Nuestro ejemplo de cómo los investigadores utilizan la electroforesis para determinar genotipos se refiere al gen humano CC-CKR-5. Este gen, localizado en el cromo-
Capítulo 4 Mutación y variación genética 95
CUADRO 4.1 Electroforesis en gel
L
a electroforesis en gel es una técnica ampliamente utilizada para estimar la cantidad de variación genética en
las poblaciones. En esencia, la electroforesis es simplemente un método para separar moléculas. En la Figura 4.14a se
presenta un aparato básico de electroforesis. El gel es una
plancha porosa de material gelatinoso, fabricado a partir
de un cierto número de ingredientes, como almidón, agarosa o poliacrilamida. En un extremo del gel, o a veces en
(a)
Fuente de energía
Electrodo (-)
Muestra
Pocillo para la muestra
Electrodo (+)
Gel
Recipiente con el gel (lleno con una solución tampón)
(b)
(c)
Figura 4.14 Electroforesis en gel (a) El esquema muestra el equipo mínimo necesario
para la electroforesis. En la estructura presentada, el suministro de energía consiste
simplemente en cinco baterías de 9 voltios conectadas para lograr una sola batería de 45
voltios. Los investigadores normalmente utilizan fuentes de energía comerciales con voltaje
variable, cronómetros, etc. (b) Esta fotografía muestra el resultado de la electroforesis de
proteínas. El gel de la foto se ha teñido para la enzima PGM. Si un individuo tiene dos formas
de la enzima, aparecerán dos bandas en la misma carrera. Ya que asumimos que las formas
alternativas son producto de alelos distintos (Feder et al. 1989a), podemos deducir que un
individuo con dos bandas es heterozigoto. Este gel indica que hay tres alelos distintos y que
8 de las 20 moscas de la muestra son heterozigóticas para el locus PGM (Jeff Feder, University
of Notre Dame) (c) Esta fotografía muestra el resultado de la electroforesis de fragmentos de
DNA. Los fragmentos de DNA de este gel se han teñido con bromuro de etidio, que los hace
visibles a la luz ultravioleta. Los fragmentos más pequeños están próximos al comienzo del gel
(National Institutes of Health/Custom Medical Stock Photo Inc.)
96 PARTE II Los mecanismos del cambio evolutivo
CUADRO 4.1
Continuación
el centro, hay una serie de ranuras o pocillos. El investigador llena cada uno de estos pocillos con una solución que
contiene una mezcla de las moléculas que quiere separar.
El gel se sumerge en una solución tamponada, que mantiene húmedo el gel y permite el paso de la electricidad.
Un suministro de corriente se conecta a los electrodos para
originar un campo eléctrico a lo largo del gel.
Muchas moléculas biológicas, como las proteínas y el
DNA, están cargadas eléctricamente cuando están en solución. Debido a que están cargadas, se desplazan por el gel
por la influencia del campo eléctrico. Por ejemplo, las
moléculas cargadas negativamente se mueven hacia el electrodo positivo. La velocidad a la que una molécula se desplaza a través del gel viene determinada por una serie de
factores, incluyendo estos:
1. La razón entre la carga eléctrica de la molécula y su
masa. Las moléculas con mayor carga y menor masa se
desplazan más rápidamente.
2. El tamaño físico de la molécula. Las moléculas más
pequeñas pasan más fácilmente a través de los poros del
gel y por consiguiente se desplazan más rápidamente.
Si la mezcla situada en un pocillo tiene moléculas con
razón de carga y masa diferentes o de distinto tamaño, estas
moléculas se separaran a medida que se desplazan a velocidades distintas a través del gel.
Electroforesis de proteínas
Suponga que hay dos alelos en un locus que codifica a una
enzima. Recuerde que las enzimas son proteínas y que las
proteínas son cadenas de aminoácidos. Imagine que nuestros
dos alelos codifican versiones de la enzima que tienen aminoácidos diferentes en algunas posiciones. Estas versiones
distintas de la enzima, codificadas por alelos del mismo locus,
se llaman alozimas. Si una alozima tiene un aminoácido cargado negativamente en donde la otra tiene uno neutro o
cargado positivamente, entonces las dos versiones de la proteína tendrán cargas eléctricas diferentes. Se desplazarán a
diferente velocidad a través del gel de electroforesis.
Para determinar en un individuo el genotipo de nuestro locus enzimático, podemos tomar una muestra de las
proteínas del individuo y separarlas en un gel de electroforesis. Luego situaremos el gel en un baño que contenga
un sustrato para una reacción química catalizada por la
enzima en cuestión y un colorante que se una a un producto de la reacción química. Este baño teñirá el gel sólo
en los lugares a donde haya llegado la enzima que estamos
estudiando. Si en el gel se produce una sola mancha, entonces nuestro individuo tendrá una sola versión de la enzima.
Por consiguiente el individuo tiene que ser homozigoto.
Si en el gel aparecen dos manchas, entonces el individuo
tiene dos versiones de la enzima y por consiguiente será
heterozigoto. Podemos hacer correr muestras de proteínas
de varios individuos, unas al lado de otras en el mismo gel
y luego comparar el patrón de manchas, o bandas, en cada
carril (Figura 4.14b).
Electroforesis de DNA
Suponga que hay dos alelos en un locus. Por definición,
los alelos tienen diferente secuencia en su DNA. Hay
una gran variedad de métodos basados en la electroforesis que nos permitirán distinguir a individuos con genotipos diferentes. Todos ellos se basan en procedimientos
para preparar el DNA en donde alelos con secuencias distintas dan lugar a fragmentos de DNA con tamaños distintos.
Las moléculas de DNA en solución están cargadas negativamente, principalmente debido a los grupos fosfato de
cada nucleótido.Todas las moléculas de DNA tienen, aproximadamente, la misma razón de carga a masa, independientemente de su longitud. Sin embargo, las moléculas de
DNA más pequeñas se mueven más rápidamente en un gel
de electroforesis. Si hiciéramos correr una mezcla de fragmentos de DNA en un gel, los fragmentos se ordenarían
por tamaños. Si hiciéramos visibles los fragmentos, quizá
tiñéndolos o marcándolos con fluorescencia, entonces veríamos una banda en el gel correspondiente al tamaño de
cada uno de los fragmentos (Figura 4.14c). Podemos hacer
correr DNA preparado de varios individuos en un gel,
unos al lado de otros. Los individuos con genotipos diferentes darán patrones de bandas diferentes.Véase el texto
para un ejemplo.
soma 3, codifica para una proteína llamada receptor 5 de la quimioquina C-C, abreviado normalmente como CCR5. El CCR5 es una proteína de la superficie de membrana que se encuentra en los glóbulos blancos. Como su nombre sugiere, la función del
CCR5 es unirse a las quimioquinas, que son moléculas producidas como señal por otras
Cálculo de las frecuencias alélicas
Ya hemos advertido que una cuestión importante respecto del alelo CCR5-∆32 es, ¿en
qué medida es frecuente? Para contestar a dicha pregunta de manera precisa, necesitamos
utilizar los datos de los genotipos de la Tabla 4.4 para calcular la frecuencia del alelo ∆32
+/∆32
∆32/∆32
células del sistema inmunitario. Cuando un leucocito se estimula por la unión de las quimioquinas a sus receptores, las células se desplazan hacia los tejidos inflamados para ayudar en la lucha contra la infección. Lo que hace particularmente interesante al CCR5
es que es utilizado también como correceptor por la mayoría de las cepas del VIH-1
transmitidas por vía sexual.
Como mencionamos en el Capítulo 1, los viriones VIH-1 utilizan una proteína propia, llamada Env, para introducirse en las células del huésped. Env parece actuar uniéndose primero a una proteína de superficie celular, llamada CD4, y luego uniéndose a CCR5.
Cuando Env se une a CCR5, se inicia la fusión de la cubierta viral con la membrana de
la célula huésped. Esta fusión libera al material genético del virus en el citoplasma de la
célula huésped.
En 1996, Rong Liu y sus colegas descubrieron variantes alélicas del locus CCR5 que
influían en la susceptibilidad a la infección por cepas del VIH-1 transmitidas por vía sexual.
Liu y sus colegas estaban estudiando a dos individuos sanos a pesar de los múltiples
encuentros sexuales no protegidos con parejas que se sabía eran VIH positivas. Los investigadores descubrieron que estos individuos eran homozigotos para una deleción de 32
pares de bases en la región codificadora del gen para la CCR5. Como consecuencia de la
deleción, la proteína codificada se acortaba mucho y no era funcional. Al carecer de la
CCR5 en su superficie, las células de los homozigotos por deleción no ofrecían puntos
de unión a los VIH-1 que debían unirse a la CCR5 para iniciar la infección.
Llamaremos al alelo funcional CCR5+, o sólo +, y al alelo con una deleción de 32 pares
de bases CCR5-∆32, o simplemente ∆32. Los individuos con genotipo +/+ son susceptibles a la infección por el VIH-1, los individuos con genotipo +/∆32 son susceptibles,
pero el SIDA puede progresar más lentamente y los individuos ∆32/∆32 son resistentes
a la mayoría de las cepas de virus transmitidas sexualmente.
Al estudiar el alelo CCR5-∆32, los investigadores del SIDA intentaron inmediatamente
saber cuál era su frecuencia. Michel Samson y sus colegas (1996), que descubrieron el alelo
independientemente, desarrollaron un ensayo que funciona como sigue. Los investigadores extraían primero DNA de una muestra de células del sujeto. Luego utilizando la reacción en cadena de la polimerasa (PCR) hicieron muchas copias de una región del gen,
de una longitud de varios cientos de pares de bases, que contenía el lugar de la deleción
de 32 pares de bases. (La PCR duplica muchas veces una secuencia diana, utilizando un
sistema de replicación del DNA en tubo de ensayo, en combinación con secuencias cebadoras sintetizadas específicamente, que dirigen a la polimerasa del DNA a copiar exactamente el locus de interés.) Finalmente, los investigadores cortaron las secuencias duplicadas
del DNA con una enzima de restricción y corrieron los fragmentos resultantes en una
electroforesis en gel.
Los resultados aparecen en la Figura 4.15. Ambos alelos dan lugar a dos fragmentos
de DNA. Los fragmentos del alelo CCR5+ tienen una longitud de 332 y 403 pares de
bases. Los fragmentos del alelo CCR5-∆32 tienen una longitud de 332 y 371 pares de bases. Los homozigotos presentan dos bandas, mientras que los heterozigotos tienen tres
bandas.
Varios laboratorios han completado estudios de los genotipos CCR5 en varias poblaciones nativas de todo el mundo. Datos recogidos en una investigación de Jeremy Martinson y sus colegas (1997) aparecen en la Tabla 4.4.
+/+
Capítulo 4 Mutación y variación genética 97
403 pb
371 pb
332 pb
Figura 4.15 Determinación
de los genotipos CCR5
mediante electroforesis del
DNA Cada carrera de este gel
tiene fragmentos de DNA
preparados a partir de alelos CCR5
de un solo individuo. La posición
en el gel de las manchas negras, o
bandas, indica el tamaño de los
fragmentos. Cada genotipo da
lugar a un patrón único de
bandas. Según Samson et al.
(1996). Reimpreso con permiso de
Nature. © 1996, Macmillan
Magazines Ltd.
98 PARTE II Los mecanismos del cambio evolutivo
Tabla 4.4 Diversidad de genotipos CCR5 en diversas poblaciones
Número de cada genotipo
Población
Frecuencia alélica (%)
Número
de personas
analizadas
ⴙ/ⴙ
ⴙ/⌬32
⌬32/⌬32
CCR5-ⴙ
CCR5-⌬32
43
102
283
29
91
44
63
26
75
223
24
81
40
60
16
24
57
5
10
4
3
1
3
3
0
0
0
0
79,1
85,3
20,9
14,7
110
241
34
96
231
34
14
10
0
0
0
0
46
34
34
25
50
26
59
101
151
38
32
33
25
50
26
59
100
151
7
2
1
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
111
52
80
87
96
36
110
52
80
87
96
36
1
0
0
0
0
0
0
0
0
0
0
0
96
94
98
59
17
96
94
96
58
17
0
0
2
1
0
0
0
0
0
0
38
52
98
119
37
52
98
119
1
0
0
0
0
0
0
0
Europa
Ashkenazi
Islandia
Gran Bretaña
España:Vascos
Italia
Irlanda
Grecia
Cercano Oriente
Caucaso: Daghestan
Arabia Saudí
Yemen
Asia
Rusia: Udmurtia
Pakistán
Punjab
Bengala
Hong Kong
Filipinas
Mongolia
Tailandia
Borneo
África
Nigeria
República Central Africana
Kenia
Costa de Marfil
Zambia
Kalahari San
Oceanía
Costa de Nueva Guinea
Polinesia Francesa
Aborígenes Australianos
Guam
Fiji
Americas
Nuu-Chah-Nulth
México (Huicholes)
Brasil (Amerindios)
Jamaica
Extraída de Martison et al. 1997. Copyright © 1997, Nature Genetics. Reimpreso con permiso del Nature Publishing Group, New York, NY.
Capítulo 4 Mutación y variación genética 99
en las distintas poblaciones analizadas. La frecuencia de un alelo es su representación fraccionaria entre todos los alelos presentes en la población.
Como ejemplo, calculemos la frecuencia del alelo ∆32 en la población Ashkenazi
europea, a partir de los datos de la primera columna de la Tabla 4.4. El modo más simple
para calcular las frecuencias alélicas es contar los alelos presentes. Martinson y sus colegas
analizaron 43 individuos. Cada individuo lleva dos alelos, por lo que los investigadores
comprobaron un total de 86 alelos. De estos 86 alelos, 18 eran alelos ∆32: uno de cada uno
de los 16 heterozigotos y 2 del único homozigoto. Por ello, la frecuencia del alelo ∆32 en
la muestra Ashkenazi es
18
ᎏᎏ ⫽ 0,209
86
Para estimar la cantidad de
variación genética de una
población, los investigadores
calculan la frecuencia de cada
alelo presente.
o el 20,9%. Podemos realizar una comprobación calculando la frecuencia del alelo +,
que es
(52 ⫹ 16)
ᎏᎏ ⫽ 0,791
86
o el 79,1%. Si nuestros cálculos son correctos, la frecuencia de los dos alelos debería sumar
uno, que es lo que ocurre.
Un método alternativo para calcular las frecuencias en la población Ashkenazi es partir de las frecuencias genotípicas. Martinson y sus colegas analizaron 43 individuos, por lo
que las frecuencias genotípicas son:
+/+
+/∆32
16
ᎏᎏ ⫽ 0,372
43
∆32/∆32
26
1
ᎏᎏ ⫽ 0,605
ᎏᎏ ⫽ 0,023
43
43
La frecuencia del alelo ∆32 es la frecuencia de ∆32/∆32 mas la mitad de la frecuencia de
+/∆32:
1
0,023 ⫹ ᎏᎏ (0,372) ⫽ 0,209
2
que es el mismo valor que obtuvimos con el primer método.
Hemos calculado las frecuencias alélicas de las dos primeras filas de la Tabla 4.4.
Dejamos a los lectores que calculen las frecuencias alélicas del resto de las poblaciones
de la tabla y que sitúen en un mapamundi las distintas poblaciones. Los lectores que lo
hagan encontrarán una distribución intrigante. El alelo CCR5-∆32 es corriente en las
poblaciones originales del Norte de Europa, con frecuencias de hasta el 21%. A medida
que nos desplazamos desde el norte de Europa, tanto hacia el este como hacia el sur, la
frecuencia del alelo ∆32 disminuye. Fuera de Europa, de Oriente Medio y de Asia occidental, el alelo ∆32 es prácticamente ausente.Volveremos a esta distribución en los Capítulos 5 y 7.
¿Cuánta diversidad genética existe en una población típica?
Desde mediados de 1960, los biólogos evolutivos han utilizado la electroforesis en gel para
enzimas como estima de la diversidad genética en poblaciones de cientos de especies vegetales y animales. En la Figura 4.16 aparecen datos de dos de estos estudios.
J. G. Oakeshott y sus colegas (1982) estudiaron la variabilidad alélica del locus de la alcohol deshidrogenasa de la mosca de la fruta. La alcohol deshidrogenasa, o Adh, degrada el
etanol, el ingrediente tóxico activo en el vino, la cerveza y, lo más importante para las moscas de la fruta, en los frutos en descomposición. Hay dos alozimas de la Adh que se distinguen electroforéticamente: AdhF y AdhS. F y S son abreviaturas de “fast” (rápido) y
“slow” (lento), la velocidad a la que los alelos enzimáticos se mueven en el gel de elec-
Documentar las frecuencias
alélicas en una serie de
poblaciones puede revelar
patrones interesantes.
100 PARTE II Los mecanismos del cambio evolutivo
Si hay más de un alelo en un
locus dado, se dice que la
población es polimórfica para
dicho locus.
troforesis. Oakeshott y sus colegas determinaron la frecuencia de los dos alelos de la Adh
en 34 poblaciones de moscas australianas (Figura 4.16a). Este análisis demostró que casi
todas las poblaciones eran polimórficas para el locus Adh. Es decir, en casi todas las poblaciones se encontraban los dos alelos. El mapa de la Figura 4.16a también revela un patrón
que se repite en Europa y en América del Norte: en general, AdhS se encuentra en frecuencias más elevadas en las latitudes bajas (es decir, más cercanas al ecuador), mientras que
AdhF se encuentra en mayor frecuencia en las latitudes altas. El significado de esta distribución no está claro, aunque puede estar relacionado con el hecho de que AdhS es más
estable a temperaturas elevadas.
(a)
AdhF
Frecuencia de: AdhS
10°
20°
30°
N
40°S
115°E
125°
135°
145°
155°
Figura 4.16 La electroforesis en gel de enzimas revela
diversidad alélica en poblaciones naturales (a) Los diagramas en
círculo de este mapa muestran las frecuencias de dos alelos de la
alcohol deshidrogenasa en poblaciones australianas de la mosca de la
fruta: AdhF (negro) y AdhS (blanco). Según Oakeshott et al. (1982),
Copyright © 1991, Evolution. Reimpreso con permiso. (b) En esta
gráfica se muestra la frecuencia del alelo Ldh-Bb en función de la latitud
en poblaciones del ciprinodóntido (Fundulus heteroclitus) a lo largo de
la costa este de los Estados Unidos. Ldh-Bb es uno de los dos alelos de la
lactato deshidrogenasa-B que se distinguen electroforéticamente; el
otro alelo es el Ldh-Ba. Reimpreso con permiso de Powers et al. (1991).
© 1991, por Annual Reviews. www.AnnualReviews.org.
Frecuencia del alelo LDH-Bb
(b)
1,0
0,8
0,6
0,4
0,2
44
Norte
Frío (6°C)
42
40
38
36
Latitud (grados Norte)
34
32
30
Sur
Cálido (21ºC)
Capítulo 4 Mutación y variación genética 101
Dennis Powers y sus colegas (1991, 1998) estudiaron la diversidad alélica del locus de
la lactato deshidrogenasa B en poblaciones de un ciprinodóntido (Fundulus heteroclitus), un
pez de unos 5 a 10 cm de longitud que vive en ensenadas, bahías y estuarios a lo largo de
las costas atlánticas de América del Norte. La lactato deshidrogenasa B, o Ldh-B, es una
enzima que convierte la lactosa en piruvato; es importante tanto en la producción de glucosa como en el metabolismo aerobio. Hay dos alelos enzimáticos de la Ldh-B, diferenciables electroforéticamente: Ldh-Ba y Ldh-Bb. Powers y sus colegas determinaron las frecuencias de los dos alelos de la Ldh-B en poblaciones de dicho ciprinodóntido desde
Maine a Georgia. Este análisis demostró que la mayoría de las poblaciones eran polimórficas.Además, como muestra la gráfica de la Figura 4.16b, hay un patrón muy influenciado geográficamente: Ldh-Bb está en elevada frecuencia en las poblaciones del norte,
mientras que Ldh-Ba lo está en las poblaciones del sur. Esta distribución tiene sentido porque Ldh-Bb tiene mayor eficacia catalítica a temperatura baja, mientras que Ldh-Ba la tiene
a temperatura elevada.
Para deducir conclusiones generales de estudios parecidos a los revisados en los dos
párrafos anteriores, necesitamos resumir los datos sobre diversidad alélica de loci en poblaciones. Hay dos estadísticos que se usan normalmente: la heterozigosidad media y el porcentaje de loci polimórficos. La heterozigosidad media se puede interpretar de dos maneras equivalentes: como la frecuencia promedio de los heterozigotos en el conjunto de los
loci, o como la fracción de loci que son heterozigotos en el genotipo del individuo promedio. El porcentaje de loci polimórficos es la fracción de loci de una población que tiene
al menos dos alelos.
Los estudios electroforéticos de enzimas han demostrado que la mayor parte de las
poblaciones naturales albergan sustancial variación genética. La Figura 4.17 resume datos
sobre heterozigosidades medias de invertebrados, vertebrados y plantas. Como caso general, en una población natural típica, entre el 33 y el 50% de los loci enzimáticos son polimórficos y el individuo promedio es heterozigoto para el 4 al 15% de sus loci (Mitton
1997).
Los métodos que examinan directamente el DNA de los alelos son incluso más eficaces para revelar la diversidad genética. Esto es así porque no cualquier cambio en las
secuencias del DNA de un locus da lugar a una proteína detectable electroforéticamente.
Entre los loci más intensamente estudiados hasta la fecha se encuentra el gen responsable
de la fibrosis quística en humanos. Este locus, en el cromosoma 7, codifica una proteína
llamada el regulador de la conductancia transmembrana de la fibrosis quística (CFTR). La
CFTR es una proteína de la superficie celular que se expresa en el revestimiento mucoso
de la membrana de los intestinos y pulmones. Gerald Pier y sus colegas (1997) demostraron que una de las funciones clave de la CFTR es capacitar a las células de la superficie
pulmonar para ingerir y destruir a la bacteria Pseudomonas aeruginosa. Los individuos
homozigotos para mutaciones de pérdida de función del gen de la CFTR tienen fibrosis
quística. Sufren una infección crónica por Pseudomonas aeruginosa, lo que finalmente produce graves daños en los pulmones. Los genéticos moleculares han examinado la secuencia del DNA de los alelos de la CFTR en más de 15.000 pacientes con fibrosis quística,
con un total de más de 30.000 copias de alelos para la enfermedad. Han descubierto unas
500 mutaciones diferentes de pérdida de función en este locus (Figura 4.18).Volveremos
al gen de la CFTR en el Capítulo 5.
¿Porqué hay poblaciones diferentes genéticamente?
Como advertimos al comienzo de esta sección, el punto de vista clásico de la diversidad
genética, que esperaba poca diversidad en la mayoría de las poblaciones, era claramente erróneo. ¿Cómo podemos explicar la sustancial diversidad presente en la mayoría de
Los análisis de la variación
proteica sugieren que en una
población tipo, entre la tercera
parte y la mitad de todos los
loci codificantes son
polimórficos...
... mientras que los primeros
análisis de la variación de las
secuencias del DNA sugieren
que dicho polimorfismo puede
ser incluso más amplio.
102 PARTE II Los mecanismos del cambio evolutivo
Frecuencia (%)
30
Vertebrados
(648 especies)
20
10
0
Frecuencia (%)
15
10
Invertebrados
(370 especies)
5
0
Figura 4.17 La electroforesis de enzimas revela
que muchas poblaciones albergan considerable
diversidad genética Estos histogramas muestran la
distribución de la heterozigosidad de enzimas en especies
de animales y vegetales. Por ejemplo, alrededor del 7% de
todas las especies vegetales tienen una heterozigosidad
entre 0,08 y 0,10. La heterozigosidad se puede interpretar
de dos modos: como el porcentaje medio de individuos
heterozigotos para un locus, o como el porcentaje medio
de loci heterozigóticos por individuo. De la Figura 2.2,
p. 19, de Avise (1994). © 1994, Chapman y Hall.
Reimpreso con el permiso de Kluwer Academic Publishers.
Frecuencia (%)
18
Plantas
(785 especies)
12
6
0
0
0,10
0,20
0,30
0,40
>0,40
Heterozigosidad (H)
las poblaciones? Dos explicaciones han reemplazado en la actualidad a la teoría clásica.
De acuerdo con la teoría del equilibrio, o seleccionista, la diversidad genética se mantiene por selección natural, favoreciendo a los individuos raros, a los heterozigotos o a
alelos diferentes en diferentes sitios y momentos. De acuerdo con la teoría neutralista,
la mayoría de los alelos de muchos loci polimórficos son funcional y selectivamente
equivalentes. En efecto, la diversidad genética se mantiene debido a que no es eliminada por selección. Consideraremos las teorías seleccionista y neutralista con mayor detalle en los Capítulos 5, 7 y 18.
Capítulo 4 Mutación y variación genética 103
Número de cromosomas
10.000
1.000
100
10
1
5'
3'
1 2 3
4
5 6a 6b
Dominio de unión
a la membrana
7
8
9
10
11 12
Unión a ATP
13
14a 14b 15 16 17a 17b 18
Dominio R
Dominio de unión
a la membrana
19
20 21 22 23 24
Unión a ATP
Figura 4.18 Los estudios de secuenciación han revelado una enorme diversidad genética en el locus de la fibrosis quística humana
Este gráfico muestra la abundancia y localización de las mutaciones de pérdida de función descubiertas al examinar unos 30.000 alelos causantes
de la enfermedad en el locus de la fibrosis quística. En el histograma se indica el número de copias que se encontraron de cada mutación. El mapa
del locus está debajo, en el que las cajas representan exones, y muestra la localización de cada mutación dentro del gen CFTR. Las cajas en la parte
inferior del gráfico indican las funciones de las regiones codificadoras del gen. De la Figura 2, p. 395, en Tsui (1992). Copyright © 1992, Elsevier
Science. Reimpreso con el permiso de Elsevier Science.
Resumen
Las mutaciones van desde la sustitución de un solo par de
bases a la duplicación de dotaciones completas de cromosomas y su impacto varía desde ningún cambio en la
secuencia de aminoácidos a cambios en un solo aminoácido hasta la creación de genes y la duplicación de genomas.
Las mutaciones puntuales se producen por errores de la
polimerasa del DNA en las síntesis de éste, o por errores de
las enzimas de reparación del DNA después de que las
secuencias se han dañado por mutágenos químicos o por
radiación. Las mutaciones puntuales en la primera y en la
segunda posición de los codones dan lugar frecuentemente a sustituciones no sinónimas que dan lugar a cambios en
la secuencia de aminoácidos de las proteínas. Las mutaciones puntuales en la tercera posición de los codones dan
lugar normalmente a sustituciones silenciosas que no producen cambios en la secuencia de aminoácidos de las proteínas. Las mutaciones puntuales dan lugar a nuevos alelos.
Las tasas de mutación varían tanto entre los genes de un
genoma como entre especies.Tanto la polimerasa del DNA
como los muchos loci implicados en la reparación de los
emparejamientos erróneos, presentan variabilidad heredable.
Por ello, la tasa de mutación es un carácter que puede responder a la selección natural y a otros procesos evolutivos.
La fuente más común de nuevos genes son las duplicaciones, que se producen por errores en el entrecruzamiento.
Un gen duplicado puede divergir de su secuencia paterna
y convertirse en un nuevo locus, con una función diferente, o en un pseudogen no funcional. También pueden
aparecer nuevos genes cuando un mRNA se transcribe
inversamente y se inserta en el genoma en una localización
diferente.
Las alteraciones de los cromosomas forman una clase
numerosa de mutaciones. Las inversiones cromosómicas tienen interesantes implicaciones evolutivas porque reducen la
104 PARTE II Los mecanismos del cambio evolutivo
frecuencia de la recombinación entre los loci dentro de la
inversión. Por ello, los alelos que se encuentran dentro de
ésta tienden a heredarse juntos en lugar de independientemente. La poliploidía se caracteriza por la duplicación de
una dotación completa de cromosomas. Es frecuente en
vegetales y es importante porque los individuos poliploides
están aislados genéticamente de la población en la que se
originaron.
Los biólogos evolutivos normalmente miden la diversidad alélica de las poblaciones utilizando la electroforesis en
gel para observar directamente las proteínas codificadas por
los alelos o al DNA de los alelos mismos.Tales estudios han
revelado que la mayoría de las poblaciones naturales tienen
diversidad genética sustancial.
Ahora que conocemos algo acerca del origen de los alelos y genes, y acerca de la diversidad genética presente en
muchas poblaciones, estamos listos para desviar nuestra atención y hacernos preguntas distintas: ¿qué es lo que determina el destino de los nuevos alelos y de los genes en una
población? Esto será el objeto de los Capítulos 5 y 6.
Preguntas
1. El biólogo evolutivo Graham Bell (1997) ha dicho que:
“Muchas mutaciones no son muy deletéreas. El acometer la
adaptación no es función exclusiva de una tormenta de mutaciones que matan o mutilan, sino más bien de un goteo estable de mutaciones con efectos ligeros o inapreciables sobre la
salud o el vigor” (Bell 1997). Esta frase se apoya en experimentos clásicos en la mosca de la fruta y en otros organismos.
No obstante, en la especie humana muchas mutaciones dan
lugar a graves enfermedades (por ejemplo, véase la Tabla
4.2b). ¿Es posible que las mutaciones en humanos sean cualitativamente diferentes que las mutaciones en otros organismos? ¿O nuestra percepción tradicional de las mutaciones
como altamente deletéreas ha sido exagerada por los intensos estudios sobre un pequeño subgrupo de mutaciones
humanas? Para un gen como el de la β-globina, ¿cómo haría
para determinar la frecuencia con la que se producen mutaciones con pequeños efectos?
2. Schlager & Dickie (1971) se dispusieron a determinar la tasa
de mutación en el color del pelaje de los ratones. Durante seis
años estudiaron cinco genes del color del pelaje en unos siete
millones de ratones, examinando miles de cruces hermano
por hermana de 28 cepas consanguíneas. Para cada gen estudiaron dos tasas de mutación: (1) la tasa a la que un gen normal muta a una forma que da lugar a la pérdida de la función
y (2) la tasa a la que un gen mutante mutaría retrógradamente
a la forma normal. Por ejemplo, en 67.395 cruces comprobados, el gen “albino” mutó a partir del normal (con color)
a no funcional (albino) exactamente tres veces, con una tasa
de mutación de 44,5 10-6. Es interesante señalar que en
todos los genes para el color del pelaje, las tasa de mutación
retrógrada (es decir, de albino a coloreado) fue alrededor de
2,5 10-6, tasa que siempre fue menor que las de pérdida de
función. Reflexione acerca de las mutaciones distintas que
pueden dar lugar a la pérdida de función de un gen y las
mutaciones que pueden ocasionar una ganancia de función.
¿Porqué las tasas de mutación de pérdida de función son
siempre más altas que las retrógradas de ganancia de función?
3. Voelker, Schaffer & Mukai (1980) estudiaron 1.000 líneas de
moscas durante 220 generaciones para estimar la tasa de
mutación de cierta proteína. En 3.111.598 cruces encontraron 16 moscas con mutaciones nuevas de sustitución no sinónima en dicha proteína (detectadas por un ligero cambio en
su carga eléctrica), una tasa de mutación de 5,1 10-6. Sin
embargo, sólo cuatro de dichas mutaciones alteraban realmente la función proteica; las otras doce no la afectaban de
manera detectable. Si Voelker et al. hubieran medido simplemente la pérdida de función, ¿hubiera sido la tasa de mutación estimada más alta o más baja? Si hubieran podido medir
también las sustituciones silenciosas, ¿hubieran sido sus estimas de la tasa de mutación más alta o más baja? ¿Cree que
midiendo los cambios en la carga de la proteína hubieran sido
capaces de medir todas las sustituciones no sinónimas que se
producen? ¿Cuál cree que es la medida más informativa de la
tasa de mutación?
4. En este capítulo introdujimos las consecuencias de las mutaciones en dos tipos de caracteres: cambios en los caracteres
fenotípicos, como la estructura de la hemoglobina, y cambios
en la misma tasa de mutación. Para aclarar las diferencias
entre estos dos tipos de caracteres, examine la siguiente lista.
¿Cuáles de estas proteínas pueden afectar a la misma tasa de
mutación? ¿Cuáles no afectan a la tasa de mutación, pero en
su lugar afectan a algún otro carácter del organismo?
Proteína
• β-globina
• Proteínas que
reparan errores
de emparejamiento
• Melanina (proteína
del color del pelaje)
• Hormona del
crecimiento
• Polimerasa del DNA
Ejemplo de mutación en la proteína
• Aumenta la tendencia falciforme
• Mayor tasa de reparación del
daño en el DNA
• Pelaje rojo en lugar de negro
• Enanismo o gigantismo
• Mayor velocidad y menor
fidelidad en la replicación del
DNA
5. El descubrimiento de la “sobreimpresión” demuestra que es
posible para un segmento de DNA codificar dos proteínas
funcionales y completamente diferentes. Examinemos este
Capítulo 4 Mutación y variación genética 105
raro fenómeno un poco más. Supongamos que descubrimos
un diminuto gen, de 12 pares de bases de longitud, que codifica un diminuto polipéptido de sólo 3 aminoácidos:
• DNA
• Aminoácidos
ACU GCU GUC UAA
thr-ala-val-Parada
Supongamos ahora que este organismo se beneficiaría enormemente si tuviera otro pequeño polipéptido compuesto
por leu-leu-ser. ¿Sería esto posible si el organismo comenzara
a transcribir el gen desde el segundo par de bases? Consulte
el código genético en la Figura 4.3b para comprobarlo.
Suponga, además, que el organismo se beneficiaría aun más
si en lugar de leu-leu-ser tuviera pro-leu-ser. ¿Qué mutaciones serían necesarias para lograr esto, y, se destruiría la
secuencia de aminoácidos de la proteína original presentada
más arriba? En general, ¿qué tipo de mutaciones pueden
darse que no alteren a la proteína original, pero que permitan cambios en los aminoácidos de las proteínas “sobreimpresas”?
6. Las secuencias de aminoácidos codificadas por los genes de
los pigmentos visuales rojo y verde de la especie humana son
idénticas en un 96% (Nathans et al. 1986). Estos dos loci se
encuentran juntos en el cromosoma X, mientras que el locus
para el pigmento azul se localiza en el cromosoma 7. Entre
los primates, sólo los monos del Viejo Mundo, los grandes
antropoides y los humanos tienen un tercer gen para pigmento; los monos del Nuevo Mundo sólo tienen un gen
para pigmento ligado al X. Comente las tres hipótesis siguientes:
• Uno de los dos loci para pigmentos visuales del cromosoma X se ha originado por duplicación génica.
• La duplicación génica ocurrió después de que divergieran
de un antecesor común los monos del Nuevo Mundo y
del Viejo Mundo, que tenían dos genes para pigmentos
visuales.
• Los varones con uno de los genes para pigmento rojo o para
pigmento verde mutado tienen la misma visión del color
que los machos de nuestros antecesores primates.
7. El número de cromosomas puede evolucionar por cambios a
pequeña escala, distintos de la duplicación de dotaciones completas de cromosomas. Por ejemplo, los caballos domésticos
tienen 64 cromosomas por dotación diploide, mientras que los
caballos de Przewalski, una subespecie asiática, tienen 66. Se
cree que los caballos de Przewalski han evolucionado de un
antecesor con 2n = 64. La cuestión es, ¿cómo se originó este
par de cromosomas extra? Parece improbable que se formara de novo un nuevo par cromosómico en el caballo de Przewalski. Para dar una hipótesis que explique el origen del
nuevo cromosoma en el caballo de Przewalski, examine la
figura adjunta. El dibujo muestra cómo ciertos cromosomas
realizan la sinapsis en los descendientes híbridos del cruce
entre un caballo doméstico y un caballo de Przewalski (Short
et al. 1974). Los restantes cromosomas presentan un apareamiento normal 1:1.
¿Cree que este tipo de cambio gradual en el número de
cromosomas implica un cambio en el número real de los
genes presentes, o simplemente se trata de una reordenación
del mismo número de genes?
8. Si no lo ha hecho ya, complete la Tabla 4.4 calculando las
frecuencias de los alelos CCR5+ y CCR5-⌬32 de cada
población. ¿Puede sugerir alguna hipótesis para explicar la
distribución global del alelo CCR5-⌬32? ¿Qué preguntas
adicionales surgen de los datos presentados en la tabla? Haga
una lista tan amplia como pueda. Luego, elija una y describa
un proyecto de investigación que pudiera contestarla.
9. Hemos visto que en los vegetales, el tiempo de generación
puede afectar al número de mutaciones que se observan en
los descendientes: las plantas que tienen mayor longevidad
tienen frutos con más mutaciones que las plantas de corta
duración. Esto se debe, probablemente, a que en los vegetales, hay muchas divisiones celulares somáticas antes de la producción de los gametos.
a. ¿Cree que lo mismo podría ser cierto para los animales
(podría el tiempo de generación afectar a la acumulación
de mutaciones en los gametos de los individuos)? ¿Podría el
tiempo de generación afectar a la acumulación de mutaciones por año en una población de animales? ¿Por qué sí o
por qué no?
b. En los mamíferos, los espermatozoides los producen células paternas (espermatogonias) que sufren constantes divisiones celulares toda la vida, mientras que los óvulos se
producen sólo durante el desarrollo fetal. ¿Cree que el
número promedio de mutaciones por gameto podría diferir en machos respecto de las hembras? ¿Por qué sí o por
qué no? ¿Cómo podría comprobar esta teoría? Vea
Shimmin, L. C., B. H.-J. Chang, W.-H. Li. 1993. Maledriven evolution of DNA sequences. Nature 362: 745747.
Explorando la bibliografía
10. La hipótesis de la mutación dirigida ha sido una de las ideas
más controvertidas en la investigación reciente sobre la mutación. Esta hipótesis, inspirada en trabajos experimentales con
la bacteria Escherichia coli, mantiene que los organismos pueden producir tipos específicos de mutación en respuesta al
desafío de ambientes concretos. Por ejemplo, si el ambiente
se hace más cálido con el tiempo, la hipótesis mantiene que
los organismos responderían mediante mutaciones generadas
específicamente en genes implicados en competir en temperaturas elevadas. Esto implica que las mutaciones no ocurren
106 PARTE II Los mecanismos del cambio evolutivo
al azar, sino que son dirigidas por el ambiente. Lea los siguientes trabajos para profundizar más en esta controversia:
Cairns, J., J. Overbaugh, and S. Miller. 1988. The origin of
mutants. Nature 335: 142-145.
Foster, P. L., and J. M.Trimarchi. 1994.Adaptive reversion of
a frameshift mutation in Escherichia coli by simple base deletions in homopolymeric runs. Science 265: 407-409.
Galitski, T., and J. R. Roth. 1995. Evidence that F plasmid
transfer replication underlies apparent adaptive mutation.
Science 268: 421-423.
Radicella, J. P., P. U. Park, and M. S. Fox. 1995.Adaptive mutation in Escherichia coli: A role for conjugation. Science 268:
418-420.
Rosenberg, S. M., S. Longerich, P. Gee, and R. S. Harris. 1994.
Adaptive mutations by deletions in small mononucleotide
repeats. Science 265: 405-407.
Sniegowski, P. D., and R. E. Lenski. 1995. Mutation and adaptation: The directed mutation controversy in evolutionary
perspective. Annual Review of Ecology and Systematics 26: 553578.
11. Algunos genéticos evolutivos han sugerido que el código
genético ha sido modelado por selección natural para minimizar las consecuencias deletéreas de las mutaciones. Para
introducirse en este aspecto, véase:
Knight, R. D., S. J. Freeland, and L. F. Landweber. 1999. Selection, history and chemistry:The three faces of the genetic code. Trends in Biochemical Sciences 24: 241-247.
Freeland S. J., and L. D. Hurst. 1998. Load minimization of the
genetic code: History does not explain the pattern. Proceedings of the Royal Society London, Series B 265: 2111-2119.
Freeland S. J., and L. D. Hurst. 1998.The genetic code is one in
a million. Journal of Molecular Evolution 47: 238-248.
Bibliografía
Abel, L., F. Demenais, et al. 1991. Evidence for the segregation of a major gene in
human susceptibility/resistance to infection by Schistosoma mansoni.American
Journal of Human Genetics 48: 959-970.
Avise, John C. 1994. Molecular Markers, Natural History and Evolution. New York:
Chapman & Hall.
Ayala, F. J., L. Serra, and A. Prevosti. 1989. A grand experiment in evolution:The
Drosophila subobscura colonization of the Americas. Genome 31: 246-255.
Bell, G. 1997. Selection:The Mechanism of Evolution. New York: Chapman & Hall.
Bohr,V.A., C.A. Smith, D. S. Okumoto, and P. C. Hanawalt. 1985. DNA repair in
an active gene: Removal of pyrimidine dimers from the DHRF gene of CHO
cells is much more efficient than in the genome overall. Cell 40: 359-369.
Drake, J.W. 1991.A constant of rate of spontaneous mutation in DNA-based microbes. Proceedings of the National Academy of Sciences, USA 88: 7160-7164.
Feder, J. L., C. A. Chilcote, and G. L. Bush. 1989. Inheritance and linkage relationships of allozymes in the apple maggot fly. Journal of Heredity 80: 277-283.
Friedberg, E. C., G. C.Walker, and W. Siede. 1995. DNA Repair and Mutagenesis.
Washington D.C.:ASM Press.
García-Dorado,A. 1997.The rate and effects distribution of viability mutation in
Drosophila: minimum distance estimation. Evolution 51: 1130-1139.
Gillin, F. D., and N. G. Nossal. 1976a. Control of mutation frequency by bacteriophage T4 DNA polymerase I.The ts CB120 antimutator DNA polymerase is defective in strand displacement. Journal of Biological Chemistry 251:
5219-5224.
Gillin, F. D., and N. G. Nossal. 1976b. Control of mutation frequency by bacteriophage T4 DNA polymerase II.Accuracy of nucleotide selection by L8 mutator, CB120 antimutator, and wild type phage T4 DNA polymerases. Journal
of Biological Chemistry 251: 5225-5232.
Harris, H. 1966. Enzyme polymorphisms in man. Proceedings of the Royal Society
London, Series B 164: 298-310.
Huey, R. B., G.W. Gilchrist, M. L. Carlson, D. Berrigan, and L. Serra. 2000. Rapid
evolution of a geographic cline in size in an introduced fly. Science 287: 308-309
Ingram,V. M. 1958. How do genes act? Scientific American 198: 68-76.
Jeffs, P., and M.Ashburner. 1991. Processed pseudogenes in Drosophila. Proceedings
of the Royal Society of London, Series B 244: 151-159.
Keese, P. K., and A. Gibbs. 1992. Origins of genes:“Big bang” or continuous creation? Proceedings of the National Academy of Sciences, USA 89: 9489-9493.
Keightley, P. D., and A. Caballero. 1997. Genomic mutation rates for lifetime reproductive output and lifespan in Caenorhabditis elegans. Proceedings of the National Academy of Sciences, USA 94: 3823-3827.
Klekowski, E. J., Jr., and P. J. Godfrey. 1989.Aging and mutation in plants. Nature
340: 389-391.
Langley, C.H., E. Montgomery, and W.F. Quattlebaum. 1982. Restriction map variation in the Adh region of Drosophila. Proceedings of the National Academy of
Sciences, USA 78: 5631-5635.
LeClerc, J. E., B. Li,W. L. Payne, and T.A. Cebula. 1996. High mutation frequencies among Escherichia coli and Salmonella pathogens. Science 274: 1209-1211.
Lewontin, R. C., and J. L. Hubby. 1966.A molecular approach to the study of genetic heterozygosity in natural populations. II. Amount of variation and degree of heterozygosity in natural populations of Drosophila pseudoobscura. Genetics 54: 595-609.
Liu, R.,W. A. Paxton, et al. 1996. Homozygous defect in HIV-1 coreceptor accounts for resistance in some multiply-exposed individuals to HIV-1 infection.
Cell 86: 367-377.
Long, M., and C. H. Langley. 1993. Natural selection and the origin of jingwei, a
chimeric processed functional gene in Drosophila. Science 260: 91-95.
Martinson, J. J., N. H. Chapman, et al. 1997. Global distribution of the CCR5
gene 32-base-pair deletion. Nature Genetics 16: 100-103.
Mellon, I., D. K. Rajpal, M. Koi, C. R. Boland, and G. N. Champe. 1996.Transcription-coupled repair deficiency and mutations in the human mismatch repair genes. Science 272: 557-560.
Mitton, J. B. 1997. Selection in Natural Populations. Oxford: Oxford University Press.
Nathans, J., D. Thomas, and D. S. Hogness. 1986. Molecular genetics of human
color vision:The genes encoding blue, green, and red pigments. Science 232:
193-202.
Oakeshott, J. G., J. B. Gibson, et al. 1982.Alcohol dehydrogenase and glycerol-3phosphate dehydrogenase clines in Drosophila melanogaster on different continents. Evolution 36: 86-96.
Online Mendelian Inheritance in Man, OMIM(TM). 1999. Johns Hopkins University, Baltimore, MD. MIM Number: 181460. World Wide Web URL:
http://www.ncbi.nlm.nih.gov/omim/
Pauling, L., H.A. Itano, S. J. Singer, and I. C.Wells. 1949. Sickle-cell anemia, a molecular disease. Science 110: 543-548.
Pier, G. B., M. Grout , and T. S. Zaidi. 1997. Cystic fibrosis transmembrane conductance regulator is an epithelial cell receptor for clearance of Pseudomonas
aeruginosa from the lung. Proceedings of the National Academy of Science, U.S.A.
94: 12088-12093.
Powers, D. A., T. Lauerman, et al. 1991. Genetic mechanisms for adapting to a
changing environment. Annual Review of Genetics 25: 629-659.
Capítulo 4 Mutación y variación genética 107
Powers, D. A., P. M. Schulte, D. Crawford, and L. DiMichele. 1998. Evolutionary
adaptations of gene structure and expression in natural populations in relation
to a changing environment:A multidisciplinary approach to address the millionyear saga of a small fish. The Journal of Experimental Zoology 282: 71-94.
Prevosti, A. 1967. Inversion heterozygosity and selection for wing length in Drosophila subobscura. Genetical Research Cambridge 10: 81-93.
Prevosti, A., G. Ribo, L. Serra, M. Aguade, J. Balaña, M. Monclus, and F. Mestres.
1988. Colonization of America by Drosophila subobscura: Experiment in natural populations that supports the adaptive role of chromosomal-inversion polymorphism. Proceedings of the National Academy of Sciences, USA 85: 5597-5600.
Ramsey, J., and D.W. Schemske. 1998. Pathways, mechanisms, and rates of polyploid formation in flowering plants. Annual Review of Ecology and Systematics
29: 467-501.
Samson, M., F. Libert, et al. 1996. Resistance to HIV-1 infection in caucasian individuals bearing mutant alleles of the CCR5 chemokine receptor gene. Nature 382: 722-725.
Schlager, G., and M.M. Dickie. 1971. Natural mutation rates in the house mouse. Estimates for 5 specific loci and dominant mutations. Mutation Research 11:
89-96.
Short, R.V.,A.C. Chandley, R. C. Jones, and W. R.Allen. 1974. Meiosis in interspecific equine hybrids. II.The Przewalski horse/domestic horse hybrid. Cytogenetics and Cell Genetics 13: 465-478.
Stadler, L. J. 1942. Some observations on gene variability and spontaneous mutation.
Spragg Memorial Lectures. East Lansing: Michigan State College.
Tsui, L.-C. 1992.The spectrum of cystic fibrosis mutations. Trends in Genetics 8:
392-398.
Voelker, R. A., H. E. Schaffer, and T. Mukai. 1980. Spontaneous allozyme mutations in Drosophila melanogaster: Rate of occurrence and nature of the mutants. Genetics 94: 961-968.
Watson, J. D., and F. H. C. Crick 1953. A structure for deoxyribose nucleic acid.
Nature 171: 737-738
CAPÍTULO
5
Genética mendeliana en poblaciones I:
selección y mutación como
mecanismos evolutivos
Población de ratones, con recién nacidos, formas juveniles y adultos (C.C. Lockwood/Animals Animals/Earth Scenes)
L
A MAYORÍA DE LAS PERSONAS SON SUSCEPTIBLES AL VIH. SU MEJOR PROBAbilidad de evitar la infección es evitar el contacto con el virus. Sin embargo, hay algunos individuos que permanecen sanos a pesar de su exposición repetida. En 1996, los
investigadores del SIDA descubrieron que al menos algunas de las variaciones en la susceptibilidad al VIH tienen base genética (véanse los Capítulos 1 y 4). El gen responsable
codifica una proteína de la superficie celular llamada CCR5. La CCR5 es utilizada por la
mayoría de las cepas de transmisión sexual del VIH-1 como medio para infiltrarse en los
leucocitos sanguíneos. Hay un alelo mutante del gen CCR5, llamado CCR5-∆32, con una
deleción de 32 pares de bases que destruye la funcionalidad de la proteína. Los individuos
que heredan dos copias de este alelo no tienen CCR5 en la superficie de sus leucocitos y
por consiguiente son altamente resistentes al VIH-1. El hecho de que los individuos
homozigóticos para el CCR5-∆32 tengan muchas menos probabilidades es de contraer el
SIDA, plantea una cuestión: la epidemia del SIDA ¿dará lugar a un incremento en la frecuencia del alelo ∆32 en las poblaciones humanas?
Consideremos también esta cuestión. En el caso de 1927 de Buck contra Bell, la Corte
Suprema de los Estados Unidos apoyó con una votación de ocho contra uno el estatu-
109
110 PARTE II Mecanismos del cambio evolutivo
to de esterilización del estado de Virginia. Redactado con el informe de eugenicistas,
la ley intentaba mejorar la calidad genética de generaciones futuras permitiendo las esterilizaciones forzosas de individuos afectados con formas hereditarias de locura, imbecilidad y otros defectos mentales. La decisión de la corte en el caso de Buck contra Bell
revigorizó un movimiento por la esterilización obligatoria que databa del año 1907
(Kevles 1995). Hacia 1940, treinta estados habían promulgado leyes sobre la esterilización y hacia 1960 cerca de 60.000 personas habían sido esterilizadas sin su consentimiento (Reilly 1991; Lane 1992). En retrospectiva, las pruebas de que dichos individuos
sufrieran enfermedades hereditarias eran débiles. Si las suposiciones genéticas hubieran
sido correctas, ¿hubiera sido la esterilización una forma efectiva para reducir la incidencia de caracteres no deseables?
Y, finalmente, consideremos esta otra cuestión. La fibrosis quística es una de las enfermedades genéticas más graves y frecuentes entre personas de ascendencia europea, afectando aproximadamente a un recién nacido de cada 2.500. La fibrosis quística se hereda
como un carácter recesivo autosómico (véase el Capítulo 4). Los individuos afectados
padecen infecciones crónicas por la bacteria Pseudomona aeruginosa y finalmente sufren graves daños pulmonares (Pier et al. 1997). En la actualidad, la mayor parte de los individuos
con fibrosis quística viven hasta los treinta o cuarenta años (Elias et al. 1992), pero hasta
hace poco, pocos sobrevivían hasta la edad reproductiva.A pesar del hecho de que la fibrosis quística fue letal en la mayor parte de la historia de la humanidad, en algunas poblaciones hay hasta un 4% de individuos portadores. ¿Cómo pueden ser tan frecuentes alelos
que dan lugar a enfermedades genéticas letales?
Las cuestiones planteadas en los párrafos anteriores se refieren a las fuerzas que cambian las frecuencias de los alelos en las poblaciones.Tales cuestiones se pueden resolver utilizando las herramientas de la genética de poblaciones. La genética de poblaciones, que
es el objeto de los Capítulos 5 y 6, integra la teoría de Darwin de la evolución por selección natural con la genética mendeliana (para una revisión histórica, véase Provine 1971).
La idea más importante en genética de poblaciones es que los cambios en la abundancia
relativa de los caracteres en una población se pueden relacionar con cambios en la abundancia relativa de los alelos que los regulan. Desde el punto de vista de la genética de
poblaciones, la evolución es el cambio de las frecuencias alélicas a lo largo de las generaciones. La genética de poblaciones proporciona las bases teóricas para gran parte de nuestra comprensión actual de la evolución.
5.1. La genética mendeliana en las poblaciones:
el equilibrio de Hardy-Weinberg
La genética de poblaciones
comienza con un modelo de lo
que sucede a las frecuencias
alélicas y genotípicas en una
población ideal. Una vez que
sepamos cómo se comportan
los genes mendelianos en una
población ideal, podremos
explorar cómo se comportan
en las poblaciones reales.
Antes de que podamos predecir si la epidemia del SIDA dará lugar a un aumento en la
frecuencia del alelo CCR5-∆32 en las poblaciones humanas, necesitamos comprender
cómo se comportaría el alelo en ausencia de la epidemia del SIDA. En otras palabras, necesitamos desarrollar un modelo nulo del comportamiento de los genes en las poblaciones.
Este modelo nulo especificará, en las condiciones más simples posible, qué le pasaría, a lo
largo de las generaciones, a la frecuencia de los alelos y de los genotipos. El modelo se
podrá aplicar no solo a los humanos, sino también a cualquier población de organismos
que sean diploides con reproducción sexual.
Una población es un grupo de individuos y de sus descendientes que se cruzan entre
sí (Figura 5.1). Los acontecimientos más importantes en el ciclo vital de una población son
los siguientes: los adultos producen gametos, los gametos se combinan dando lugar a zigotos y los zigotos se desarrollan para dar lugar a la siguiente generación de adultos. Deseamos rastrear el destino, a lo largo de las generaciones, de genes mendelianos en tales
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 111
Adultos
Población
Zigotos
Gametos
Conjunto de genes
Figura 5.1 El ciclo de vida de una población ideal de ratones,
destacando los estadios que serán importantes en nuestro
desarrollo de la genética de poblaciones.
poblaciones. Deseamos saber si un alelo o genotipo concreto se convertirá en más o menos
frecuente con el tiempo, y por qué.
Imaginemos que los ratones de la Figura 5.1 tienen en sus genomas un locus concreto,
el locus A, con dos alelos: A y a. Podemos comenzar a rastrear a estos alelos en cualquier
momento del ciclo vital. Sigámoslos durante una vuelta completa, de una generación a la
siguiente, para ver si sus frecuencias cambian.
Ejemplo numérico
La tarea de seguir a los alelos será más sencilla si comenzamos con los gametos que producen los adultos cuando se cruzan. Supondremos que los adultos eligen a sus parejas
al azar. Una idea útil es considerar que el proceso de apareamiento al azar ocurre de la
siguiente manera: tomamos todos los óvulos y esperma que producen todos los adultos
de la población y los mezclamos en un barril. A este barril se le conoce como el conjunto de los genes. Cada espermatozoide se desplaza hasta colisionar al azar con un
óvulo para producir un zigoto. Algo parecido a esto ocurre realmente en los erizos de
mar y otros organismos marinos que simplemente desprenden sus gametos en la
corriente. Para otros organismos, como los ratones o los humanos, esto es, obviamente,
una simplificación.
Los adultos de nuestra población de ratones son diploides, por lo que cada uno tiene
en el locus A dos alelos. Pero los adultos producen sus óvulos y esperma por meiosis.
Siguiendo la ley de la segregación de Mendel, cada gameto recibe exactamente un alelo
del locus A. Imagine que el 60% de los óvulos y del esperma reciben el alelo A y que el
40% recibe el alelo a. En otras palabras, la frecuencia del alelo A en el conjunto de genes
es de 0,6 y la del alelo a de 0,4 (Figura 5.2).
¿Qué sucede cuando un espermatozoide encuentra a un óvulo? Por ejemplo, ¿qué fracción de zigotos se producirán con el genotipo AA? En la Figura 5.2 se muestran las cuatro
combinaciones posibles de óvulos y esperma, los zigotos que se producen y un cálculo
especificando la probabilidad de cada uno de ellos. Por ejemplo, si tomamos un óvulo al
azar, hay una probabilidad del 60% de que tenga el genotipo A. Cuando un espermato-
Comenzando con óvulos y
esperma que constituyen
el conjunto de genes, nuestro
modelo sigue a los alelos a
través de los zigotos y
adultos hasta el conjunto de
genes de la generación
siguiente.
112 PARTE II Mecanismos del cambio evolutivo
Figura 5.2 La unión al azar en el
conjunto de genes de nuestra
población ideal de ratones da lugar
a zigotos con frecuencias
genotípicas predecibles.
Un conjunto de genes con
frecuencias alélicas de 0,6 y 0,4...
a
A
A
A
a
A
A
A
A
a
A
...produce zigotos con
frecuencias genotípicas
de 0,36, 0,48 y 0,16
a
a
a
A
a
A
A
A
a
Óvulo
Esperma
Zigoto
Probabilidad
A
&
A
AA
0,6 x 0,6 = 0,36
A
&
a
Aa
0,6 x 0,4 = 0,24
a
&
A
aA
0,4 x 0,6 = 0,24
a
&
a
aa
0,4 x 0,4 = 0,16
= 0,48
Esperma
0,4 a
0,6 A
0,36 AA
0,24 Aa
0,4 a
0,24 aA
0,16 aa
Óvulos
0,6 A
Zigotos
AA
Aa
Total
aa
0,36 + 0,48 + 0,16 =
+
+
1,0
=
Figura 5.3 Representación
geométrica de las frecuencias
genotípicas producidas por
apareamiento al azar Las
fracciones en los bordes izquierdo
y superior del cuadrado
representan las frecuencias de A y
a de óvulos y esperma en el
conjunto de genes. Las fracciones
en el interior del cuadrado
representan las frecuencias
genotípicas de los zigotos
formados por encuentros al azar
de los gametos del conjunto de
genes.
zoide va a fertilizar a un óvulo, hay un 60% de probabilidad de que el esperma tenga el
genotipo A. La probabilidad de que presenciemos la producción de un zigoto AA será,
por consiguiente,
0,6 ⫻ 0,6 = 0,36
(véase el Cuadro 5.1)
Si observamos la formación de todos los zigotos, el 36% tendrá el genotipo AA. Los cálculos de la Figura 5.2 muestran que el apareamiento al azar en el conjunto de genes dará
lugar a las siguientes proporciones de zigotos:
AA
0,36
Aa
0,48
aa
0,16
(La categoría Aa incluye a los heterozigotos producidos por la combinación bien de un
óvulo A y un espermatozoide a, o de un óvulo a con un espermatozoide A.) Advierta que,
0,36 0,48 0,16 1
Esto confirma que hemos tenido en cuenta a todos los zigotos. La Figura 5.3 muestra una
representación geométrica de los mismos cálculos.
Dejemos ahora que los zigotos se desarrollen hasta adultos y que los adultos produzcan gametos para obtener el conjunto de genes de la siguiente generación. ¿Será diferente
la frecuencia de los alelos A y a en el conjunto de genes de lo que fue en la generación
anterior?
En el nuevo conjunto de genes, podemos calcular la frecuencia del alelo A de la
siguiente manera.Ya que los adultos de genotipo AA constituyen el 36% de la población,
producirán el 36% de los gametos.Todos estos gametos llevarán el alelo A.Así mismo, los
adultos de genotipo Aa constituyen el 48% de la población, y producirán el 48% de los
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 113
CUADRO 5.1 Combinando probabilidades
L
a probabilidad de que dos sucesos independientes se
den al mismo tiempo es igual al producto de las probabilidades de cada uno de los sucesos. Por ejemplo, la
probabilidad de que al echar una moneda salga cara es
1/2. La probabilidad de que al echar otra moneda salga cara
es también 1/2. Si echamos las dos monedas juntas, lo que
salga en una es independiente de los que salga en la otra.
Por ello, la probabilidad de que salga cara en las dos
monedas es
1
1
1
2
2
4
La probabilidad combinada de dos sucesos cualesquiera mutuamente excluyentes será igual a la suma de
cada una de sus probabilidades. Cuando echamos un dado
puede salir o un uno o un dos (entre otras posibilidades),
pero no pueden salir los dos números a la vez. Por ello,
la probabilidad de que salga o bien un uno o bien un dos
es
1
1
1
6
6
3
gametos. La mitad de estos gametos llevarán el alelo A. Por ello, la fracción de gametos del
conjunto de genes que lleva el alelo A es,
1
0,36 0,48 0,6
2
()
En la Figura 5.4 se presenta este cálculo gráficamente. La figura también muestra un cálculo que establece que la fracción de gametos del conjunto de genes que llevan el alelo
a es 0,4.Advierta que
0,6 + 0,4 = 1
Esto confirma que hemos tenido en cuenta a todos los gametos. En la Figura 5.5 se muestra una representación geométrica de los mismos cálculos.
Una población con
frecuencias genotípicas
de 0,36, 048 y 0,16...
Aa
Aa
AA
AA
AA
Aa
Aa
Aa
AA
AA
AA
Aa
Aa
Aa
aa
aa
AA
AA
AA
Aa
Aa
Aa
aa
aa
...produce gametos...
...con frecuencias
de 0,6 y 0,4
Aa
A
a
A
a
A
a
A
A
A
A
A
A
A
a
A
a
A
a
A
A
A
A
A
A
A
a
A
a
A
a
a
a
a
a
A
A
A
A
A
A
A
a
A
a
A
a
a
a
a
a
A
0,36 +
1
(0,48) = 0,6
2
a
1
(0,48) + 0,16 = 0,4
2
Figura 5.4 Cuando los adultos de nuestra población ideal de ratones producen gametos, dan lugar a un conjunto
de genes en el que las frecuencias alélicas son idénticas a las que comenzamos en la generación anterior.
114 PARTE II Mecanismos del cambio evolutivo
AA
0,36
Los ejemplos numéricos
demuestran que en nuestra
población ideal, las frecuencias
alélicas permanecen
constantes generación tras
generación.
Total
0,48
+ 0,16 =
1,0
+
=
+
Gametos
El área de cada cuadro representa la frecuencia genotípica de un adulto o de un
gameto. Advierta que la mitad de los gametos producidos por los adultos Aa llevan
el alelo A y la otra mitad el alelo a.
aa
+
Adultos
Figura 5.5 Representación geométrica de las frecuencias alélicas que se
producen cuando los adultos de nuestra población ideal forman gametos
+
Aa
0,24
+ 0,16
0,36
+ 0,24
0,6
A
=
+
0,4 =
a
1,0
Total
Hemos cerrado el círculo y hemos llegado exactamente a donde comenzamos. Comenzamos con frecuencias alélicas del 60% para A y del 40% para a en el conjunto de genes
de la población. Seguimos a los alelos a través de los zigotos y de los adultos y en el conjunto de genes de la siguiente generación. Las frecuencias alélicas en el nuevo conjunto
de genes es también el 60% y el 40%. Por ello, las frecuencias alélicas de A y de a se
encuentran en equilibrio en nuestra población: no cambian de una generación a la
siguiente. La población no evoluciona.
El primer biólogo que abordó un ejemplo numérico, siguiendo las frecuencias de los
alelos mendelianos de una generación a la siguiente en una población ideal, fue G. Udny
Yule en 1902. Comenzó con un conjunto de genes en el que las frecuencias de los dos
alelos eran 0,5 y 0,5 y demostró que en el conjunto de genes de la siguiente generación
las frecuencias alélicas eran todavía 0,5 y 0,5. (Los lectores podrían reproducir sus cálculos como un ejercicio.)
Como nosotros,Yule concluyó que las frecuencias de los alelos en su población ideal estaban en equilibrio. La conclusión de Yule fue tanto novedosa como correcta, pero la tomó
de una forma demasiado literal. Había desarrollado un único ejemplo, y creyó que las frecuencias alélicas de 0,5 y 0,5 representaban el único estado de equilibrio posible para un sistema de dos alelos. Por ejemplo,Yule creía que si aparecía un alelo A por mutación en una
población cuyo conjunto de genes era sólo de a, entonces la frecuencia del alelo A aumentaría automáticamente hasta constituir la mitad del conjunto de genes.Yule arguyó esta idea
durante la discusión que siguió a una charla dada en 1908 por R. C. Punnett (el famoso Punnett del cuadrado). Punnet creía que Yule no tenía razón, pero no supo cómo probarlo.
Desde luego, ya hemos demostrado que Punnet estaba en lo cierto al rechazar la idea
de Yule. Nuestros cálculos demuestran que una población con frecuencias alélicas de 0,6
y 0,4 también está en equilibrio. Sin embargo, lo que Punnet deseaba era una prueba generalizada. Esta prueba demostraría que cualesquiera frecuencias alélicas, siempre que sumaran 1, permanecerán sin cambio de una generación a la siguiente.
Punnett planteó el problema a su amigo matemático G. H. Hardy, que obtuvo la prueba en corto tiempo (Hardy 1908). Hardy simplemente repitió los cálculos que Yule había
realizado, pero utilizando variables en lugar de frecuencias alélicas específicas tal como Yule
había hecho. Los cálculos de Hardy para un caso general demostraron realmente que cualesquiera frecuencias alélicas estarán en equilibrio1.
1
Nota del traductor. Quienes realmente estarán en equilibrio o no son las frecuencias genotípicas, como se verá
más adelante. Las frecuencias alélicas son las que son. Con unas frecuencias alélicas dadas se pueden formar tanto
genotipos cuyas frecuencias estén en equilibrio, como genotipos cuyas frecuencias NO estén en equilibrio.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 115
Óvulo
Esperma
Zigoto
Probabilidad
A1
&
A1
A1A1
p x p = p2
A1
&
A2
A1A2
p x q = pq
A2
&
A1
A2A1
q x p = qp
A2
&
A2
A2A2
q x q = q2
= 2pq
Figura 5.6 Caso general de la unión aleatoria del conjunto de genes
de nuestra población ideal de ratones.
El caso general
En nuestra versión del caso general de Hardy, trataremos de nuevo con una población
ideal. Estamos interesados en un único locus con dos alelos: A1 y A2. Utilizamos mayúsculas con subíndices debido a que queremos que nuestros cálculos abarquen tanto casos
en los que los alelos son codominantes como en los que hay un dominante y un recesivo. Los tres genotipos diploides posibles son A1A1,A1A2 y A2A2.
Como en nuestro ejemplo numérico, comenzaremos con el conjunto de genes y
seguiremos a los alelos a lo largo de una vuelta completa del ciclo de vida. El conjunto
de genes tendrá una frecuencia dada de gametos A1 y de gametos A2. Denominaremos a
la frecuencia de A1 en el conjunto de genes p y a la frecuencia de A2 q. Hay sólo dos alelos en la población, por lo que
pq1
El primer paso es permitir que los gametos del conjunto de genes se combinen para
producir zigotos. En la Figura 5.6 se muestran las cuatro combinaciones posibles de óvulos y esperma, los zigotos que se producen y el cálculo que especifica la probabilidad de
cada caso. Por ejemplo, si cogemos un óvulo al azar, la probabilidad de que sea de genotipo A1 es p. Cuando un espermatozoide fertiliza al óvulo, la probabilidad de que sea de
genotipo A1 es p. Por consiguiente, la probabilidad de que presenciemos la producción de
un zigoto A1A1 es
p p p2
Si observamos la formación de todos los zigotos, p2 de ellos tendrán genotipo A1A1. Los
cálculos de la Figura 5.6 muestran que el apareamiento al azar en nuestro conjunto de
genes da lugar a zigotos en las siguientes proporciones:
A1A1
p2
A1A2
2pq
A2A2
q2
La Figura 5.7 muestra una representación geométrica de los mismos cálculos. La figura
también demuestra que
p2 2pq q2 1
Esto confirma que hemos tenido en cuenta a todos los zigotos. El mismo resultado se
puede demostrar algebraicamente sustituyendo q por (1 – p) en la expresión p2 2pq q2
y simplificando.
Hemos ido de las frecuencias alélicas en el conjunto de genes a las frecuencias genotípicas de los zigotos. Ahora dejaremos que los zigotos lleguen a adultos y que los adultos
produzcan gametos para formar el conjunto de genes de la siguiente generación.
Podemos calcular la frecuencia del alelo A1 en el nuevo conjunto de genes como sigue.
Ya que los adultos de genotipo A1A1 constituyen una proporción p2 de la población, pro-
El reto ahora es probar
algebraicamente que no hubo
nada especial en nuestros
ejemplos numéricos.
Cualesquiera frecuencias
alélicas permanecerán
constantes de generación en
generación.
116 PARTE II Mecanismos del cambio evolutivo
Esperma
fr(A1) = p fr(A2) = q
fr(A1) = p
fr(A1A1)
= p2
fr(A1A2)
= pq
fr(A2A1)
= qp
fr(A2A2)
= q2
Óvulos
fr(A2) = q
Figura 5.7 Representación geométrica del caso general de las frecuencias
genotípicas producidas por apareamiento aleatorio Las variables a lo largo de los bordes
izquierdo y superior del cuadro representan las frecuencias de A y a, de óvulos y esperma, del
conjunto de genes. Las expresiones dentro de la caja representan las frecuencias genotípicas de
los zigotos formados por la unión al azar de los gametos del conjunto de genes.
Zigotos
A1A1
A1A2
p2
+
Total
A2A2
2pq
q2
+
+
+
=
1,0
=
ducirán p2 gametos.Todos estos gametos llevarán el alelo A1. De igual manera, los adultos de genotipo A1A2 constituyen una proporción 2pq de la población, y producirán 2pq
gametos. La mitad de estos gametos llevarán el alelo A1. Por ello, la fracción total de gametos del conjunto de genes que llevarán el alelo A1 es
1
p2 2pq p2 pq
2
()
Podemos simplificar esta expresión sustituyendo q por (1 – p) en la parte derecha. Esto da
p2 pq p2 p (1 p)
p2 + p p2
p
Nuestro modelo ha
demostrado que nuestra
población ideal no evoluciona.
Esta conclusión se conoce
como el equilibrio de
Hardy-Weinberg.
En la Figura 5.8 se presenta gráficamente este cálculo. La figura también muestra un cálculo que establece que la fracción de gametos del conjunto de genes que llevan el alelo A2
es q. Asumimos por principio que p y q suman 1, por lo que sabemos que hemos tenido
en cuenta a todos los gametos.
De nuevo hemos completado el círculo y vuelto a donde habíamos comenzado.
Comenzamos con frecuencias alélicas p y q en nuestro conjunto de genes de la población.
Seguimos a los alelos a través de los zigotos y los adultos y hasta el conjunto de genes de
la siguiente generación. Las frecuencias alélicas en el nuevo conjunto de genes sigue siendo p y q. Las frecuencias alélicas p y q pueden presentar cualquier valor entre 0 y 1, siempre y cuando sumen 1. En otras palabras, cualesquiera frecuencias alélicas se mantendrán en
equilibrio, no sólo p = q = 0,5 como creía Yule.
A1A1
p2
Adultos
o de un gameto.
2pq
+
Gametos
Figura 5.8 Representación geométrica del caso general de las frecuencias
alélicas producidas cuando los adultos de nuestra población ideal producen
gametos El área de cada caja representa la frecuencia genotípica de un adulto
A1A2
+
q2
+
p
A1
=
1,0
=
+
p2
+ 1/2(2pq)
Total
A2A2
+
=
1/ (2pq)
2
+ q2
+
q =
A2
1,0
Total
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 117
Éste es un resultado importante. Al comienzo del capítulo definimos la evolución
como el cambio de las frecuencias alélicas en las poblaciones. Los cálculos que acabamos
de realizar demuestran que, dados supuestos simples, en poblaciones que siguen las reglas
de la genética mendeliana, las frecuencias alélicas no cambian.
Hemos presentado este resultado como el trabajo de Hardy (1908). Independientemente fue deducido por Wilhelm Weinberg (1908) y se conoce como el equilibrio
de Hardy-Weinberg. (Algunos biólogos evolutivos se refieren a él como el equilibrio de
Hardy-Weinberg-Castle, debido a que William Castle [1903] planteó un ejemplo numérico y constató el equilibrio de manera no matemática cinco años antes de que Hardy y
Weinberg explícitamente demostraran el caso general [véase Provine 1971].) El equilibrio
de Hardy-Weinberg da lugar a dos conclusiones fundamentales:
• Conclusión 1: las frecuencias alélicas de una población se mantendrán constantes
generación tras generación.
• Conclusión 2: si las frecuencias alélicas de una población son p y q, las frecuencias
genotípicas serán p2, 2pq y q2.
Llegamos a resultados análogos si generalizamos el análisis del caso de dos alelos al caso
normal en una población que tiene muchos alelos en un locus (véase Cuadro 5.2).
¿Cuál es la utilidad del equilibrio Hardy-Weinberg?
Puede ser sorprendente que en un libro sobre evolución hayamos dedicado tanto espacio
a una prueba que aparentemente demuestra que no se produce evolución. Lo que hace
útil al equilibrio de Hardy-Weinberg es que descansa en una serie de condiciones simples. Cuando se viola una o más de una de estas condiciones, las conclusiones de HardyWeinberg no se cumplen.
Cuando desarrollamos nuestra hipótesis nula de cómo se comportan los alelos mendelianos en las poblaciones, dejamos la mayoría de las condiciones sin especificar. Podemos ahora comentarlas explícitamente. Las condiciones más importantes son:
1. No hay selección. Todos los miembros de nuestra población ideal sobreviven con la
misma tasa y contribuyen con igual número de gametos al conjunto de genes. Cuando no se cumple este supuesto (cuando individuos con determinados genotipos sobreviven y se reproducen a mayor tasa que otros) las frecuencias de los alelos pueden cambiar de una generación a la siguiente.
El equilibrio de Hardy-Weinberg
se convierte en útil cuando
enumeramos los supuestos que
hicimos acerca de nuestra
población ideal. Al proporcionar
una serie de condiciones
explícitas bajo las cuales no hay
evolución, el análisis de HardyWeinberg identifica las fuerzas
que pueden dar lugar a evolución
en las poblaciones reales.
CUADRO 5.2 El equilibrio de Hardy-Weinberg con más de dos alelos
I
magine un locus con varios alelos. Podemos denominar
a los alelos Ai, Aj, Ak y así sucesivamente y podemos
representar sus frecuencias en el conjunto de genes con las
variables pi, pj, pk y así sucesivamente. La formación de un
zigoto con genotipo AiAi precisa de la unión de un óvulo
Ai y un espermatozoide Ai.Así, la frecuencia de cualquier
genotipo homozigoto AiAi será pi2.
La formación de un zigoto con genotipo AiAj requiere
bien la unión de un óvulo Ai con un esperma Aj, o de un
óvulo Aj con un esperma Ai.Así, la frecuencia de cualquier
genotipo heterozigoto AiAj es 2pipj.
Por ejemplo, si hay tres alelos con frecuencias p1, p2 y p3,
de tal manera que
p1 p2 p3 1
entonces, las frecuencias genotípicas serán
(p1 p2 p3)2 p12 p22 p32
2p1 p2 2p1 p3 2p2 p3
y las frecuencias alélicas no cambiaran de generación en
generación.
118 PARTE II Mecanismos del cambio evolutivo
2. No hay mutación. En la población ideal, ninguno de los alelos existentes se convierte
por mutación en otro de los alelos existentes y no se originan nuevos alelos. Cuando
no se cumple esta condición y, por ejemplo, cuando algunos alelos tienen tasas de mutación mayores que otros, las frecuencias alélicas pueden variar de una generación a la
siguiente.
3. No hay migración. Ningún individuo sale o entra en la población ideal. Cuando esto
no se cumple, e individuos con ciertos alelos entran o salen de la población a una tasa
más elevada que individuos con otros alelos, las frecuencias alélicas pueden cambiar de
una generación a la siguiente.
4. No se producen fenómenos aleatorios que dan lugar a que algunos individuos
pasen más alelos a la siguiente generación que otros. Evitamos este tipo de suceso aleatorio suponiendo que los óvulos y el esperma del conjunto de genes colisionan entre
sí de acuerdo con sus frecuencias reales, p y q, sin que se produzcan desviaciones ocasionadas por azar. Otra forma de exponer este supuesto es que la población ideal sea
de tamaño infinito. Cuando no se cumple esta condición y por azar algunos individuos
contribuyen con mas alelos que otros a la generación siguiente, las frecuencias alélicas
pueden variar de una generación a la siguiente. Este tipo de cambio de las frecuencias
alélicas se denomina deriva genética.
5. Los individuos eligen a su pareja al azar. Explícitamente formamos el conjunto
de genes para permitir que los gametos se encuentren al azar. En contraste con las condiciones de la 1 a la 4, cuando esto no se cumple (cuando, por ejemplo, hay individuos
que prefieren como pareja a otros individuos del mismo genotipo) las frecuencias alélicas no varían de una generación a la siguiente. Sin embargo, las frecuencias genotípicas pueden cambiar.Tales desviaciones en las frecuencias genotípicas, en combinación
con la falta de cumplimiento de una u otra de las cuatro condiciones, pueden influir
en la evolución de las poblaciones.
Al confeccionar una lista con las condiciones específicas ideales bajo las que las poblaciones no evolucionarán, el equilibrio de Hardy-Weinberg identifica una serie de factores que pueden dar lugar a evolución en el mundo real. Éste es el sentido en el que el
equilibrio de Hardy-Weinberg sirve como modelo nulo. Los biólogos pueden medir las
frecuencias alélicas y genotípicas en la naturaleza y determinar si se mantienen las conclusiones de Hardy-Weinberg. Una población en la que las conclusiones 1 y 2 se mantengan se dice que está en equilibrio de Hardy-Weinberg. Si una población no se
encuentra en equilibrio de Hardy-Weinberg (si las frecuencias alélicas cambian de generación en generación, o si las frecuencias genotípicas no pueden, de hecho, predecirse multiplicando las frecuencias alélicas) entonces una o más de las condiciones del modelo no
se cumple.Tal constatación, por sí misma, no nos dice nada acerca de cuál de las condiciones no se cumple, pero nos dice que una investigación más profunda puede recompensarnos con descubrimientos interesantes.
En las siguientes secciones del Capítulo 5 consideraremos de qué manera la falta de
cumplimiento de las condiciones 1 y 2 afectan a las dos conclusiones de Hardy-Weinberg y
exploraremos, con investigación experimental, el papel de la selección y la mutación como
fuerzas evolutivas. En el Capítulo 6 consideraremos las violaciones de las condiciones 3, 4 y 5.
Cambios en las frecuencias del alelo CCR5-⌬32
Comenzamos este capítulo preguntándonos si podíamos esperar que la frecuencia del alelo
CCR5-⌬32 cambie en las poblaciones humanas.Ahora que hemos desarrollado un modelo nulo de cómo se comportan los alelos mendelianos en las poblaciones, podemos dar una
respuesta parcial. Siempre y cuando todos los individuos de genotipo CCR5 sobrevivan
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 119
y se reproduzcan con las mismas tasas, que no haya mutaciones que conviertan a algunos
alelos CCR5 en otros, que ninguno se desplace de una población a otra, que las poblaciones sean infinitamente grandes y que las personas elijan a sus parejas al azar, entonces
la frecuencia del alelo CCR5-⌬32 no cambiará.
Desde luego, esta respuesta es totalmente insatisfactoria. Es insatisfactoria porque
ninguna de las condiciones se cumple en ninguna población real. No hacemos esta pregunta en primer lugar precisamente porque esperamos que los individuos ⌬32/⌬32
sobrevivan a la epidemia del SIDA a una tasa superior que los individuos con cualesquiera de los otros dos genotipos. En las siguientes dos secciones veremos que nuestro modelo nulo, el equilibrio de Hardy-Weinberg, proporciona un marco que nos permitirá estimar con precisión la importancia de las diferencias en supervivencia.
5.2
Selección
Cuando trabajamos con una población ideal para deducir el equilibrio de Hardy-Weinberg, el primer supuesto de nuestra lista fue que todos los individuos sobrevivían con igual
tasa y contribuían con igual número de gametos al conjunto de genes. Las violaciones sistemáticas de este supuesto son ejemplos de selección. Hay selección cuando los individuos con un genotipo dado sobreviven hasta la edad reproductiva a una tasa superior a la
de los individuos con otros fenotipos, o cuando los individuos con un fenotipo concreto
producen más descendientes que los individuos con otros fenotipos. La base en ambos
tipos de selección es el éxito reproductivo diferencial: algunos individuos tienen más descendientes que otros. La selección puede dar lugar a evolución cuando los fenotipos que
presentan diferencias en el éxito reproductivo son heredables, es decir, cuando ciertos fenotipos están asociados a ciertos genotipos.
Los genéticos de poblaciones suponen a menudo que los fenotipos están estrictamente determinados por los genotipos. Podrían pensar, por ejemplo, en plantas de guisante que
siendo altas o enanas, las plantas con genotipo TT y Tt son altas, y con genotipo tt son enanas.Tal punto de vista es bastante exacto para algunos caracteres, incluidos los ejemplos
que utilizamos en este capítulo.
Cuando los fenotipos se agrupan en clases discretas que parecen estar determinadas
estrictamente por genotipos, podemos pensar en la selección como si actuase directamente
sobre los genotipos. Entonces podemos asignar un nivel concreto de éxito reproductivo
a cada genotipo. En realidad, la mayoría de los caracteres no están, de hecho, estrictamente
determinados por el genotipo. Las plantas de guisante con genotipo TT, por ejemplo, varían en altura. Esta variación se debe a diferencias genéticas en otros loci y a diferencias en
los ambientes en donde crecen los guisantes. Consideraremos tales complicaciones en el
Capítulo 7. Sin embargo, de momento adoptaremos el modelo más simple.
Cuando pensamos en la selección como si actuase directamente sobre los genotipos,
su aspecto definitorio es que algunos genotipos contribuyen con más alelos a generaciones futuras que otros. En otras palabras, hay diferencias entre genotipos y eficacia.
Nuestra tarea en esta sección es incorporar la selección al análisis de Hardy-Weinberg.
Comenzaremos preguntándonos si la selección puede cambiar las frecuencias alélicas del
conjunto de genes de una generación a la siguiente. En otras palabras, ¿puede la selección
hacer que no se cumpla la conclusión 1 del equilibrio de Hardy-Weinberg?
Añadiendo la selección al análisis de Hardy-Weinberg:
cambios en las frecuencias alélicas
Comenzaremos con un ejemplo numérico que demuestra que la selección puede realmente cambiar las frecuencias alélicas. Imaginemos que en nuestra población de ratones
La primera de las suposiciones
acerca de nuestra población
ideal fue que los individuos
sobreviven con igual
probabilidad y que tienen el
mismo éxito reproductivo.
Ahora exploramos qué sucede
con las frecuencias alélicas
cuando estas condiciones no
se cumplen.
120 PARTE II Mecanismos del cambio evolutivo
hay un locus, el locus B, que afecta a la probabilidad de supervivencia. Supongamos, como
hicimos con el locus A de la Figura 5.2, que la frecuencia del alelo B1 en el conjunto de
genes es 0,6 y la frecuencia del alelo B2 es 0,4 (Figura 5.9). Después del apareamiento al
azar, obtenemos unas frecuencias genotípicas para B1B1, B1B2 y B2B2 de 0,36, 0,48 y 0,16.
El resto de nuestros cálculos serán más simples si damos a la población de zigotos un tamaño definido, por lo que imaginemos que hay 1.000 zigotos:
B1B1
360
B1B2
480
B2B2
160
Estos zigotos están representados por un gráfico de barras en la figura. Seguiremos a los
individuos que se desarrollen a partir de estos zigotos hasta que lleguen a adultos. Aquéllos que sobrevivan se cruzarán para producir el conjunto de genes de la generación
siguiente.
Incorporamos la selección estipulando que los genotipos difieren en sus tasas de supervivencia.Todos los individuos B1B1 sobreviven, y también lo hacen el 75% de los individuos B1B2 y el 50% de los B2B2. Como se muestra en la Figura 5.9, en la población hay
ahora 800 adultos:
B1B2
B2B2
B1B1
360
360
80
En los adultos, las frecuencias de los tres genotipos serán:
B1B1
360/800 = 0,45
B1B2
360/800 = 0,45
B2B2
80/800 = 0,1
Cuando estos adultos produzcan gametos, la frecuencia del alelo B1 en el nuevo conjunto de genes será igual a la frecuencia de B1B1 entre los adultos que sobreviven más la
Número de
individuos
Selección
Número de
individuos
25% muere
360
360
80
50% muere
B 1 B1
B1B2 B2B2
Genotipo
B1B1
B1B2
B2B2
Genotipo
Frecuencias alélicas
resultantes
Figura 5.9 La selección puede dar lugar
a cambios en las frecuencias alélicas a lo
largo de generaciones Esta figura sigue a
480
Número de
individuos
nuestra población ideal de ratones desde
el conjunto de genes de una generación al
conjunto de genes de la generación
siguiente. Los gráficos de barras muestran el
número de individuos de cada genotipo de la
población en cualquier momento dado. La
selección, en forma de diferencias en la
supervivencia de las formas juveniles, da
lugar a que el alelo B1 aumente.
B1
B2
0,675
0,325
360
160
Frecuencias alélicas iniciales
B1B1 B1B2 B2B2
B1
B2
Genotipo
0,6
0,4
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 121
mitad de la frecuencia de B1B2. Este cálculo y el de la frecuencia para el alelo B2 son como
sigue:
B1
B2
1
1
0,45 0,45
0,45 0,1
2
2
0,675
0,325
()
()
La frecuencia del alelo B1 ha aumentado en un porcentaje del 7,5. La frecuencia del alelo
B2 ha disminuido en la misma cantidad.
La selección ha dado lugar a que no se cumpla la conclusión 1 del análisis de HardyWeinberg. La población ha evolucionado en respuesta a la selección.
Utilizamos una selección fuerte para insistir en nuestro ejemplo numérico. En la
naturaleza, las diferencias en supervivencia raramente son tan elevadas como para ocasionar cambios importantes en las frecuencias alélicas en una sola generación. Sin embargo, si la selección continúa actuando durante muchas generaciones, incluso pequeños
cambios en las frecuencias alélicas por generación pueden acumularse en cambios sustanciales después de un largo período. En la Figura 5.10 se presentan cambios acumulativos en frecuencias alélicas que se pueden obtener por selección. La figura se basa en un
modelo poblacional similar al utilizado en los ejemplos numéricos precedentes, excepto en que las frecuencias alélicas iniciales son 0,01 para B1 y 0,99 para B2. La línea amarilla presenta el cambio en frecuencias alélicas cuando las tasas de supervivencia son del
100% para B1B1, del 90% para B1B2 y del 80% para B2B2. La frecuencia del alelo B1 pasa
en menos de 100 generaciones de 0,01 a 0,99. Con esquemas de selección más débiles,
la frecuencia de B1 varía más lentamente, pero de manera inevitable. (Véase el Cuadro
5.3 para un tratamiento algebraico general que incorpora la selección en el análisis de
Hardy-Weinberg.)
Un ejemplo numérico
demuestra que cuando los
individuos con ciertos
genotipos sobreviven con
mayor probabilidad que
individuos con otros
genotipos, las frecuencias
alélicas pueden cambiar de
una generación a la siguiente.
En otras palabras, nuestro
modelo demuestra que la
selección natural da lugar a
evolución.
Investigaciones experimentales sobre el cambio de las frecuencias
alélicas por selección
Douglas Cavener y Michael Clegg (1981) documentaron el cambio acumulativo en frecuencias alélicas a lo largo de muchas generaciones en un experimento de selección natural en el laboratorio con la mosca de la fruta (Drosophila melanogaster). La mosca de la fruta,
como muchos otros animales, sintetiza una enzima que degrada el etanol, el ingrediente
activo venenoso de la cerveza, del vino y de la fruta en putrefacción. Esta enzima se denomina alcohol deshidrogenasa, o ADH. Cavener y Clegg trabajaron con poblaciones de moscas que en el locus de la ADH tenían dos alelos: el AdhF y el AdhS. (La F y la S se refieren
Frecuencia del alelo B1
1,0
Esquema de selección
0,8
Fuerte
0,6
0,4
0,2
0,0
0
200
400
600
Generación
800
1000
Débil
% de supervivientes
B1B1 B1B2 B2B2
100
90,0
80,0
100
98,0
96,0
100
99,0
98,0
100
99,5
99,0
100
99,8
99,6
Figura 5.10 La selección
continuada puede dar lugar a
cambios sustanciales en las
frecuencias alélicas con el tiempo
Cada curva muestra el cambio en
frecuencia alélica con el tiempo bajo
una intensidad de selección dada.
122 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.3
Un tratamiento general de la selección
D
esarrollaremos aquí las ecuaciones que predicen las
frecuencias alélicas en la generación siguiente, dadas
las frecuencias alélicas en esta generación y las eficacias de
los distintos genotipos. Comenzaremos con una población que tiene un conjunto de genes en el que el alelo A1
tiene una frecuencia p y el alelo A2 una frecuencia q. Permitimos que los gametos se unan al azar para formar los
zigotos, con genotipos A1A1, A1A2 y A2A2, y en las frecuencias p2, 2pq y q2 respectivamente.
Incorporamos la selección imaginando que los zigotos
A1A1 sobreviven hasta la madurez con una tasa w11, los
zigotos A1A2 sobreviven con una tasa w12 y los zigotos
A2A2 sobreviven con una tasa w22. Todos los individuos
que sobreviven dan lugar al mismo número de descendientes. Por consiguiente, la tasa de supervivencia de un
genotipo es proporcional al éxito reproductivo durante la
vida del genotipo, o eficacia. Por ello nos referiremos a la
tasa de supervivencia como de eficacia. La eficacia media
–, se obtiene por la
para el conjunto de la población, w
expresión:
– ⫽ p2w 2pqw q2w
w
11
12
22
[Para ver esto, advierta que podemos calcular el prome(1 2 2 3)
dio de los números 1, 2, 2 y 3 como 4, o como
1
1
1
( 4 1) ( 2 2) ( 4 3). Nuestra expresión para la
eficacia promedio es del segundo tipo: multiplicamos la
eficacia de cada genotipo por su frecuencia en la población
y luego sumamos los resultados.]
Calculemos ahora las frecuencias genotípicas de los
adultos que sobreviven (justo antes de que sus gametos
vayan al conjunto de genes). Las nuevas frecuencias genotípicas serán:
A1A1
p2w11
–
w
A1A2
2pqw12
–
w
A2A2
q2w22
–
w
(En cada caso hemos dividido por la eficacia media para
asegurarnos que las nuevas frecuencias todavía sumen 1.)
Finalmente, dejamos que los adultos se crucen y calculamos las frecuencias alélicas en el conjunto de genes:
• Para el alelo A1: los individuos A1A1 contribuyen con
p2w11
– gametos, los cuales son todos A1; los individuos A1A2
w
2pqw12
contribuyen con w–
gametos, de los cuales la mitad
son A1.Así, la nueva frecuencia de A1 es
p2w11 pqw12
–
w
• Para el alelo A2: los individuos A2A2 contribuyen con
2pqw12
– gametos, todos los cuales son A2; los individuos
w
q2w22
gametos, la mitad de los
A1A2 contribuyen con w–
cuales son A2. Por ello, la nueva frecuencia de A2 es
pqw12 q2w22
–
w
El lector puede confirmar que las nuevas frecuencias de A1
y A2 suman 1.
Es instructivo calcular el cambio en la frecuencia del
alelo A1 de una generación a la siguiente. Este valor, ∆p, es
igual a la nueva frecuencia del alelo A1 menos su frecuencia anterior:
p2w11 pqw12
∆p – p
w
–
2
p w11 pqw12
pw
– –
w
w
–
2
p w11 pqw12 pw
–
w
p
–)
– (pw11 qw12 w
w
La expresión final es útil porque muestra que el cambio en la
–).
frecuencia del alelo A1 es proporcional a (pw11 qw12 w
–
La expresión (pw11 qw12 w) es igual a la eficacia media
del alelo A1 cuando se une al azar con otros alelos (pw11 – ). En otras
qw12) menos la eficacia media de la población (w
palabras, si los individuos que llevan A1 tienen una eficacia
superior a la media, entonces el alelo A1 aumentara en frecuencia.
El cambio en la frecuencia del alelo A2 de una generación a la siguiente es
pqw12 q2w22
∆q – p
w
p
–)
– (pw12 qw22 w
w
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 123
a si la proteína codificada por el alelo se mueve rápidamente [en inglés, fast] o lentamente [en inglés, slow] en el gel de electroforesis [véase el Cuadro 4.1 del Capítulo 4].)
Los científicos mantuvieron dos poblaciones experimentales de moscas con alimento
rociado con etanol y dos poblaciones control con alimento normal. Los investigadores
eligieron los padres de cada generación al azar. Ésta es la razón por la que llamamos al proyecto un experimento de selección natural: Cavener y Clegg utilizaron ambientes distintos para sus diferentes poblaciones, pero los investigadores no manipularon directamente
la supervivencia o el éxito reproductivo de las moscas.
En algunas generaciones, Cavener y Clegg tomaron muestras de moscas al azar de cada
población, determinaron sus genotipos ADH y calcularon las frecuencias alélicas. Los
resultados se muestran en la Figura 5.11. Las poblaciones control no muestran grandes
cambios o cambios consistentes a largo plazo, en cuanto a la frecuencia del alelo AdhS. Por
el contrario, las poblaciones experimentales presentaron un declive rápido y muy consistente de la frecuencia de AdhS (y, desde luego, un aumento correspondiente de la frecuencia de AdhF). La conclusión 1 de Hardy-Weinberg parece que se mantiene en las
poblaciones control, pero claramente no se cumple en las poblaciones experimentales.
¿Podemos identificar con certeza cuál de las condiciones del análisis de Hardy-Weinberg
no se cumple? La única diferencia entre los dos tipos de población es que las experimentales tienen etanol en su alimento. Esto sugiere que es la ausencia de selección la condición
que no se cumple en las poblaciones experimentales. Las moscas con el alelo AdhF parece
que tienen mayor éxito reproductivo (mayor eficacia) que las moscas con el alelo AdhS
cuando hay etanol en el alimento. Cavener y Clegg advirtieron que este resultado está de
acuerdo con el hecho de que extractos del alcohol deshidrogenasa de homozigotos AdhF
degradan el etanol dos veces más rápido que los extractos del alcohol deshidrogenasa de
homozigotos AdhS. No está claro si las moscas con el alelo AdhF tiene una mayor eficacia porque tiene una mayor tasa de supervivencia o porque dan lugar a más descendencia.
La investigación experimental
con las moscas de la fruta es
consistente con nuestra
conclusión de que la selección
natural puede dar lugar a
cambios en las frecuencias
alélicas.
Añadiendo la selección al análisis de Hardy-Weinberg:
cálculo de las frecuencias genotípicas
Los cálculos y el ejemplo que acabamos de discutir demuestran que la selección puede dar
lugar a que las frecuencias alélicas cambien a lo largo de las generaciones. La selección invalida la conclusión 1 del análisis de Hardy-Weinberg. Consideremos ahora de qué manera la selección afecta a la conclusión 2 del análisis de Hardy-Weinberg. En una población
sometida a selección, ¿podemos todavía calcular las frecuencias genotípicas multiplicando las frecuencias alélicas?
.9
Frecuencia de Adhs
.8
.7
.6
.5
.4
.3
.2
.1
0
C1
C2
E1
E1
5 10 15 20 25 30 35 40 45 50
Generación
Figura 5.11 Frecuencias del alelo AdhS en
cuatro poblaciones de moscas de la fruta durante
50 generaciones Los puntos y las líneas rojos y amarillos
representan a la población control que vive en alimento
normal; los puntos y las líneas azules y verdes representan a
poblaciones experimentales que viven en alimento rociado con
etanol. Según Cavener y Clegg (1981). Copyright © Evolution.
Reimpreso con permiso.
124 PARTE II Mecanismos del cambio evolutivo
A menudo no podemos hacerlo. Como antes, usamos una población con dos alelos en
un locus que afecta a la supervivencia: B1 y B2. Supongamos que las frecuencias iniciales
de cada alelo en el conjunto de genes es 0,5 (Figura 5.12). Después del apareamiento al
azar, las frecuencias genotípicas de B1B1, B1B2 y B2B2 son 0,25, 0,5 y 0,25 respectivamente. El resto de nuestros cálculos serán más simples si damos a la población de zigotos
un tamaño dado, por lo que imaginemos que hay 1000 zigotos:
B1B1
250
B1B2
500
B2B2
250
Estos zigotos están representados en un gráfico de barras en la figura. Seguiremos a los
individuos que se desarrollan de estos zigotos hasta el estado adulto.Aquellos que sobrevivan se cruzarán para producir el conjunto de genes de la siguiente generación.
Incorporamos la selección estipulando que los genotipos se diferencian en sus tasas de
supervivencia. El 50% de los individuos B1B1 sobrevive, todos los individuos B1B2 sobreviven y el 50% de los B2B2 sobrevive. Como se muestra en la Figura 5.12, ahora habrá 750
adultos en la población:
B1B2
B2B2
B1B1
125
500
125
La frecuencia de los tres genotipos será la siguiente:
B1B1
125/750 = 0,167
B1B2
500/750 = 0,667
B2B2
125/750 = 0,167
Cuando estos adultos produzcan gametos, las frecuencias de los dos alelos en el nuevo conjunto de genes será:
B1
B2
1
1
0,167 0,667
0,667 0,167
2
2
0,5
0,5
()
()
Número de
individuos
50%
muere
50%
muere
Número de
individuos
500
Selección
125
125
B1B1 B1B2 B2B2
Genotipo
B1B1 B1B2 B2B2
Genotipo
Frecuencias alélicas
resultantes
B2
B1
población muere, las frecuencias alélicas no cambian. Pero
entre los supervivientes hay más heterozigotos que los
predichos por el equilibrio de Hardy-Weinberg.
Número de
individuos
500
Figura 5.12 La selección puede cambiar las
frecuencias genotípicas de tal manera que no
puedan ser calculadas multiplicando las frecuencias
alélicas Cuando la mitad de los homozigotos de esta
250
0,5
250
Frecuencias alélicas iniciales
B1B1 B1B2 B2B2
B1
B2
Genotipo
0,5
0,5
0,5
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 125
A pesar de la fuerte selección en contra de los homozigotos, la frecuencia de los alelos no
ha cambiado; la población no ha evolucionado.
Sin embargo, advierta que la selección ha dado lugar a que no se cumpla la conclusión
2 del análisis de Hardy-Weinberg.Ya no podemos calcular las frecuencias genotípicas de
los adultos supervivientes multiplicando las frecuencias de los alelos. Por ejemplo:
Frecuencia de B1B1
0,167
⫽
(Frecuencia de B1)2
(0,5)2 = 0,25
En nuestro ejemplo numérico utilizamos una selección fuerte para que se vea claro. De
hecho, la selección rara vez es lo suficientemente enérgica como para producir un cambio tan drástico en una sola generación. Incluso si lo produce, una sola generación de
apareamiento al azar devolverá inmediatamente a los genotipos al equilibrio de HardyWeinberg. No obstante, los investigadores encuentran a veces violaciones de la conclusión
2 de Hardy-Weinberg que parecen ser el resultado de la selección.
Investigaciones experimentales sobre selección y frecuencias
genotípicas
Nuestro ejemplo se basa en la investigación sobre una grave enfermedad genética humana llamada síndrome de Jaeken (también conocida como síndrome de glicoproteínas
deficientes en carbohidratos de tipo 1). Los pacientes con el síndrome de Jaeken tienen
graves problemas de desarrollo, con deformidades de los huesos y distribución anormal de
la grasa subcutánea (Matthijs et al. 1998). Sus funciones hepáticas no son normales y el 20%
de ellos muere antes de los cinco años.
El síndrome de Jaeken se hereda de manera autosómica recesiva. La mayoría de los casos
se deben a mutaciones de pérdida de función en un gen del cromosoma 16. El gen, llamado PMM2, codifica para una enzima llamada fosfomanomutasa (PMM). Bioquímicamente, una actividad reducida de la PMM da lugar a una disminución en la capacidad de
unir hidratos de carbono a proteínas para fabricar glicoproteinas.
Hay al menos 24 mutaciones de pérdida de función diferentes en el gen PMM2 que
pueden dar lugar al síndrome de Jaeken. La mayoría son mutaciones no sinónimas; una
es la deleción de una sola base. Gert Matthijs y sus colegas (1998), en una investigación
dirigida por Jaak Jaeken, investigaron si algunas de estas mutaciones de pérdida de función son más graves que otras. Los investigadores supusieron que algunas mutaciones
disminuyen más la actividad catalítica de la PMM que otras y por ello son especialmente
graves.
Los investigadores llevaron a cabo una comprobación de su hipótesis, que se basaba
en el equilibrio de Hardy-Weinberg. La lógica de la comprobación se basa en lo
siguiente.Todos los individuos con el síndrome de Jaeken son homozigotos, es decir, llevan los dos alelos mutantes. Sin embargo, muchos llevan dos mutaciones de pérdida de
función diferentes. Podemos pensar en los individuos afectados como homozigotos o
heterozigotos respecto de los alelos mutantes específicos que llevan. En una población,
entre los individuos afectados, los diferentes alelos para la enfermedad deberían estar en
equilibrio de Hardy-Weinberg (véase el Cuadro 5.4). Si un alelo dado para la enfermedad da lugar a una pérdida de función especialmente grave, entonces los homozigotos para dicho alelo deberían tener también poca actividad PMM por lo que serían incapaces de sobrevivir.Ya que la selección eliminaría a tales homozigotos de la población
de afectados, habría menos de ellos que los esperados al multiplicar las frecuencias de
los diferentes alelos.
Los investigadores determinaron la identidad de estos alelos para la enfermedad en 54
pacientes blancos con el síndrome de Jaeken. La mutación más frecuente que encontra-
La selección natural puede
también alejar las frecuencias
genotípicas lejos de los
valores pronosticados por el
equilibrio de Hardy-Weinberg.
126 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.4 El equilibrio de Hardy-Weinberg entre alelos mutantes diferentes que dan
lugar a enfermedades genéticas recesivas.
C
onsideremos una enfermedad genética recesiva autosómica. En un primer nivel de análisis hay dos alelos,
que denominaremos D y d. Los individuos con genotipo
DD o Dd son fenotípicamente normales; los individuos dd
manifiestan la enfermedad.
Sea p la frecuencia del alelo D y z la frecuencia del alelo
d, de tal manera que p + z = 1. En una población que está
de acuerdo con los supuestos de Hardy-Weinberg, las frecuencias genotípicas son
DD
P2
Dd
2pz
dd
z2
Imaginemos ahora que, de hecho, hay dos alelos diferentes para la enfermedad, d1 y d2. Con otras palabras, los
individuos dd pueden tener los genotipos d1d1, d1d2 y
d2d2. Sea q la frecuencia de d1 y r la frecuencia de d2.
Debido a que d1 y d2 son las dos posibles versiones de d,
sabemos que
z=qr
Así, la frecuencia de los individuos afectados se puede
expresar como
Frecuencia de dd z2
(q r)2
q2 2qr r2
Los términos de esta expresión son las frecuencias que
pronosticaríamos de acuerdo con el equilibrio de HardyWeinberg, simplemente multiplicando las frecuencias de d1
y d2. En otras palabras, dentro de la población de individuos afectados, los diferentes alelos para la enfermedad
están entre sí en equilibrio de Hardy-Weinberg.
ron, llamada R141H, fue la sustitución de un aminoácido. Si clasificamos a los alelos para
la enfermedad como aquellos que tienen la mutación R141H y los que tienen otras mutaciones, las frecuencias alélicas en la población de los 54 afectados serán:
Otras
0,6
R141H
0,4
A partir de estas frecuencias alélicas podemos calcular que si la población estuviera en
equilibrio de Hardy-Weinberg, las frecuencias genotípicas serían:
Otras/Otras
0,36
El descubrimiento de que las
frecuencias genotípicas de
una población no están en
equilibrio de Hardy-Weinberg
puede ser una pista de que la
selección natural está
actuando.
Otras/R141H
0,48
R141H/R141H
0,16
De hecho, las frecuencias genotípicas reales entre los individuos afectados son
Otras/Otras
Otras/R141H
R141H/R141H
11
0,2
54
43
0,8
54
0
Las frecuencias alélicas y genotípicas entre los individuos afectados no están de acuerdo
con la conclusión 2 del análisis de Hardy-Weinberg. Hay un notable déficit de homozigotos, especialmente de homozigotos R141H. El déficit de homozigotos es estadísticamente significativo (véase el Cuadro 5.5).
Jeaken y su equipo creen que la interpretación mas lógica de la ausencia de homozigotos R141H es que la R141H es una mutación de pérdida de función especialmente
grave. De acuerdo con esta hipótesis, los genotipos R141H/R141H se producen en la frecuencia que predice el equilibrio de Hardy-Weinberg, pero los individuos que se desarrollan a partir de estos zigotos mueren antes o inmediatamente después del nacimiento. El déficit en homozigotos Otras/Otras puede deberse a otras mutaciones de pérdida de
función graves entre los otros alelos de la enfermedad.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 127
CUADRO 5.5 Análisis estadístico de las frecuencias alélicas y genotípicas utilizando la prueba
de 2 (chi-cuadrado)
U
tilizaremos aquí los datos de Matthijs y sus colegas
(1998) para ilustrar un método para determinar si las
frecuencias genotípicas se desvían significativamente de las
esperadas de acuerdo con el equilibrio de Hardy-Weinberg. Los investigadores analizaron una población de 54
individuos afectados con el síndrome de Jaeken. El número de individuos para cada genotipo fue el siguiente:
Otros/Otros
11
Otros/R141H
43
R141H/R141H
0
A partir de estos números, calcularemos las frecuencias
alélicas de Otros y de R141H, y determinaremos si las frecuencias genotípicas observadas están de acuerdo con las
esperadas conforme el equilibrio de Hardy-Weinberg. Hay
cinco etapas:
1. Calcule las frecuencias alélicas. La muestra de 54 individuos es también una muestra de 108 alelos. Los 22 alelos que se encuentran en los 11 individuos Otros/Otros,
son Otros, como los 43 alelos que llevan los 43 individuos
Otros/R141H.Así la frecuencia de los Otros alelos es
(22 43)
0,6
108
(43 0)
0,4
108
2. Calcule las frecuencias genotípicas esperadas de acuerdo con el principio de Hardy-Weinberg, dadas las frecuencias alélicas calculadas en la etapa 1. De acuerdo
con el equilibrio de Hardy-Weinberg, si las frecuencias
de los dos alelos son p y q, entonces las frecuencias de
los genotipos serán p2, 2pq y q2. Así, las frecuencias
esperadas de los genotipos en una población de individuos con el síndrome de Jaeken serán
Otros/R141H
2(0,6)(0,4)
= 0,48
Otros/R141H
(0,48)(54)
= 25,92
R141H/R141H
(0,16)(54)
= 8,64
El número de individuos esperado es distinto del
número de individuos realmente observado (11, 43 y
0). La muestra real contiene más heterozigotos y menos
homozigotos que lo esperado. ¿Es posible que esta gran
diferencia entre lo esperado y lo observado pueda surgir por azar? ¿O es la diferencia estadísticamente significativa? Nuestra hipótesis nula es que la diferencia se
debe simplemente al azar.
4. Calcule una prueba estadística. Utilizaremos una prueba
estadística diseñada en 1900 por Karl Pearson. Es la llamada chi-cuadrado (2). El chi-cuadrado se define como
(observado esperado)2
2 Σ
esperado
en donde el símbolo Σ indica una suma de todas las clases consideradas. En nuestros datos hay tres clases: los
tres genotipos. Para nuestro grupo de datos:
(11 19,44)2
(43 25,92)2
2 19,44
25,92
(0 8,64)2
23,56
8,64
y la frecuencia del alelo R141H es
Otros/Otros
(0,6)2
= 0,36
Otros/Otros
(0,36)(54)
= 19,44
R141H/R141H
(0,4)2
= 0,16
3. Calcule el número esperado de individuos de cada
genotipo de acuerdo con el equilibrio de Hardy-Weinberg. Éstas son simplemente las frecuencias esperadas de
cada genotipo multiplicadas por el número de individuos de la muestra, 54. Los valores esperados son
5. Determine si el valor de la prueba estadística es significativo. El chi-cuadrado está definido de tal modo que
su valor se hace más grande cuando las diferencias entre
los valores observado y esperado se hacen grandes.
¿Qué probabilidad hay de obtener un valor de chicuadrado más grande de 23,56 por azar? La mayoría de
los libros de texto de estadística tienen una tabla que da
la respuesta. En Zar (1996) esta tabla se denomina
“Valores críticos de la distribución de chi-cuadrado.”
Para usar esta tabla necesitamos calcular un número
llamado los grados de libertad para la prueba estadística.
El número de grados de libertad para el chi-cuadrado es
igual al número de clases menos el número de valores
independientes que calculamos de los datos para utilizarlos en determinar los valores esperados. En nuestro
chi-cuadrado hay tres clases: los tres genotipos.A partir de
los datos calculamos dos valores para utilizarlos en la
determinación de los valores esperados: el número total
de individuos y la frecuencia del alelo R141H. (También
128 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.5
Continuación
calculamos la frecuencia de los Otros alelos, pero ésta no
es independiente de la frecuencia del alelo R141H, ya
que la frecuencia de los Otros es 1 menos la frecuencia de
R141H.) Así, el número de grados de libertad es 1. (Otra
fórmula para calcular los grados de libertad en pruebas de
chi-cuadrado para el equilibrio de Hardy-Weinberg es
df = k – 1 – m
donde k es el número de clases y m el número de frecuencias alélicas independientes estimadas de los datos.)
De acuerdo con la tabla del libro de estadística, el
valor crítico de chi-cuadrado para un grado de libertad
y una P = 0,05 es 3,841. Esto quiere decir que hay un
5% de probabilidad, de acuerdo con la hipótesis nula, de
obtener un 2 ⱖ 3,841. La probabilidad bajo la hipótesis nula, de obtener un 2 ⱖ 23,56 es, por consiguiente, considerablemente menor al 5%. Rechazamos la
hipótesis nula y afirmamos que nuestro valor de chicuadrado es estadísticamente significativo con una P
0,05. (De hecho, en este caso la P 0,00001.)
La prueba de chi-cuadrado nos dice que los alelos del
locus PMM2 de la población de individuos con el síndrome de Jaeken no están en equilibrio de Hardy-Weinberg.
Esto indica que una o más de las condiciones del análisis
de Hardy-Weinberg no se cumplen. Sin embargo, en sí
misma, no nos dice nada acerca de qué condiciones no se
cumplen, o cómo.
Este estudio del síndrome de Jaeken es un caso en el que el análisis genético-poblacional dio lugar a un descubrimiento médico potencialmente importante. El análisis
sugiere que para vivir es necesario algo de la actividad del PMM. Más aún, indica que
padres que son ambos portadores del R141H pueden esperar una distribución diferente de fenotipos entre sus hijos que padres que son portadores de dos alelos diferentes para
la enfermedad.
De vuelta con los cambios en la frecuencia del alelo CCR5-∆32
Nuestra investigación sobre la
selección natural nos ha
proporcionado herramientas
que podemos utilizar para
predecir el futuro de las
poblaciones humanas.
Ahora estamos preparados para dar una respuesta más satisfactoria a las preguntas médicas que surgieron al principio del capítulo: ¿la epidemia del SIDA dará lugar a un aumento en la frecuencia del alelo CCR5-∆32 en las poblaciones humanas? La epidemia del
SIDA podría dar lugar, en principio, a un rápido aumento de la frecuencia del alelo, pero
en la actualidad parece que no ocurrirá así en ninguna población. Esto se basa en las tres
poblaciones ideales presentadas en la Figura 5.13 (véase el Cuadro 5.6 para las operaciones matemáticas). Cada modelo se basa en suposiciones diferentes acerca de la frecuencia
inicial del alelo CCR5-∆32 y en la prevalencia de la infección por el VIH. Cada gráfico
muestra los cambios pronosticados en la frecuencia del alelo ∆32 durante 40 generaciones, aproximadamente unos 1000 años de evolución.
La población ideal, representada en la Figura 5.13a, proporciona un escenario en el que
la frecuencia del alelo ∆32 podría aumentar rápidamente. En este escenario la frecuencia
inicial del alelo CCR5-∆32 es del 20%. Una cuarta parte de los individuos con genotipo
+/+ y +/∆32 contrae el SIDA y muere sin reproducirse, mientras que todos los individuos ∆32/∆32 sobreviven. La frecuencia inicial del 20% del ∆32 es aproximadamente
igual a la mayor frecuencia publicada para cualquier población, una muestra de Judíos
Ashkenazi estudiada por Martinson et al. (1997). Las tasas de mortalidad se aproximan a
las de Botswana, Namibia, Swazilandia y Zimbabwe, en donde más del 25% de los individuos con edades entre los 15 y los 49 años están infectados con el VIH (UNAIDS 1998).
En este modelo poblacional, la frecuencia del alelo ∆32 aumenta un poco en cada generación. Después de 40 generaciones, el alelo tiene una frecuencia prácticamente del 100%.
Así, en una población humana que combine las más altas frecuencias publicadas para el
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 129
5.3
Tipos de selección
Al comienzo del capítulo nos preguntamos si una ley de esterilización obligatoria podría
lograr sus objetivos eugenésicos de reducir la incidencia de una enfermedad genética.
Antes de intentar dar una respuesta, será útil considerar de qué manera los detalles de la
genética mendeliana de un locus dado podrían afectar al curso de la evolución. Por ejemplo, ¿la tasa de evolución en respuesta a la selección contra un alelo dado depende de si
el alelo es dominante o recesivo? ¿La tasa de evolución depende de si los alelos son frecuentes o raros?
Selección sobre alelos recesivos y dominantes
Los datos recogidos por Peter Dawson (1970) son un ejemplo de cómo la recesividad y
la dominancia afectan al curso de la evolución. Dawson había estado estudiando una colonia de laboratorio del gorgojo del trigo (Tribolium castaneaum), y había identificado un gen,
que llamaremos locus 1. Este locus tenía dos alelos: y l. Los individuos con genotipos
/ y /l eran fenotípicamente normales, mientras que los individuos con genotipo l/l
no sobrevivían. En otras palabras, l es un alelo letal recesivo.
Dawson recogió heterozigotos de su colonia de gorgojos del trigo y los utilizó para
establecer dos nuevas poblaciones experimentales.Ya que todos los fundadores eran heterozigotos, la frecuencia inicial de los dos alelos era 0,5 en las dos poblaciones.Ya que los
(a)
Frecuencia inicial: 0,2
Fracción superviviente:
+/+ +/∆32 ∆32/∆32
0,75 0,75
1,0
1,0
0,6
0,2
0
(b)
Frecuencia del
alelo CCR5-∆32
alelo ∆32 con las tasas más altas de infección, la epidemia del SIDA podría dar lugar a que
la frecuencia del alelo aumentase rápidamente.
Sin embargo, en la actualidad no se conocen poblaciones que combinen altas frecuencias del alelo ∆32 con altas tasas de infección por el VIH. En el norte de Europa muchas
poblaciones tienen frecuencias del ∆32 entre 0,1 y 0,2 (Martinson et al. 1997; Stephens
et al. 1998), pero las tasas de infección por el VIH están muy por debajo del 1% (UNAIDS
1998). En la Figura 5.13b se representa un modelo poblacional que refleja estas últimas
condiciones. La frecuencia inicial del alelo ∆32 es 0,2 y la frecuencia de los individuos
/ y /∆32 que contraen el SIDA y mueren antes de reproducirse es del 0,5%. La frecuencia del alelo ∆32 prácticamente no varía. La selección es demasiado débil como para
ocasionar una evolución apreciable en tan corto tiempo.
En ciertas zonas del África subsahariana, casi una cuarta parte de los individuos en edad
reproductiva están infectados por el VIH. Sin embargo, el alelo ∆32 está prácticamente
ausente (Martinson et al. 1997). En la Figura 5.13c se representa un modelo de población
que refleja esta situación. La frecuencia inicial del alelo ∆32 es 0,01 y el 25% de los individuos / y /∆32 contraen el SIDA y mueren sin reproducirse. De nuevo, la frecuencia del alelo ∆32 prácticamente no cambia. Cuando la frecuencia del alelo ∆32 es
baja, la mayoría de las copias se encuentran en heterozigosis. Debido a que los heterozigotos son susceptibles a la infección, estas copias estarán ocultas a la selección.
El análisis que acabamos de describir se basa en ciertas suposiciones simplificadas. Por
ejemplo, hemos asumido que los individuos infectados por el VIH mueren sin reproducirse y que la tasa de mortalidad es la misma en heterozigotos que en homozigotos /.
En realidad, aunque los heterozigotos son susceptibles a la infección por el VIH, parece que
el SIDA progresa más lentamente (Dean et al. 1996). Por ello, la eficacia de los heterozigotos puede ser realmente mayor que la de los homozigotos /. Desafiamos a nuestros
lectores a explorar la evolución de las poblaciones humanas en diversas situaciones de
selección, para comprobar lo fuertemente que afectan nuestras suposiciones simplificadas
al curso predicho de la evolución.
(c)
10
20
30
40
Frecuencia inicial: 0,2
Fracción superviviente:
+/+ +/∆32 ∆32/∆32
0,995 0,995
1,0
1,0
0,6
0,2
0
10
20
30
40
Frecuencia inicial: 0,1
Fracción superviviente:
+/+ +/∆32 ∆32/∆32
0,75 0,75
1,0
1,0
0,6
0,2
0
10 20 30
Generación
40
Figura 5.13 Cambios
pronosticados en las
frecuencias alélicas del locus
CCR5 debido a la epidemia del
SIDA en tres situaciones
diferentes (a) Cuando
la frecuencia inicial del alelo
CCR5-∆32 es alta y una gran parte
de la población queda infectada
con el VIH, las frecuencias alélicas
pueden cambiar rápidamente. Sin
embargo, ninguna población real
combina estas características.
(b) En las poblaciones europeas la
frecuencia alélica es alta, pero sólo
una pequeña parte de los
individuos queda infectado.
(c) En ciertas zonas de África hay
tasas de infección elevadas, pero
las frecuencias alélicas son bajas.
130 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.6
Predicción de la frecuencia del alelo CCR5-32 en generaciones futuras
S
ea qg la frecuencia del alelo CCR5-∆32 en la generación actual. Basándonos en el Cuadro 5.3 podemos
escribir una ecuación que prediga la frecuencia del alelo en
la generación siguiente, dadas las estimas de la tasa de supervivencia (eficacia) de los individuos con cada genotipo.
La ecuación es
qg + 1 (1 qg)qgw+∆ qg2w∆ ∆
(1 qg)2w++ 2(1 qg)qgw+∆ qg2w∆ ∆
en donde qg+1 es la frecuencia del alelo ∆32 en la generación siguiente, w++ es la eficacia de los individuos homo-
La investigación experimental
sobre los escarabajos de la
harina demuestra que las
zigotos para el alelo normal, w+∆ es la eficacia de los heterozigotos y w∆ ∆ la de los homozigotos para el alelo
CCR5-∆32.
Después de elegir un valor de inicio para la frecuencia del alelo ∆32, lo sustituimos junto con las eficacias
estimadas en la ecuación para generar la frecuencia del
alelo ∆32 después de una generación. Luego sustituimos
el valor resultante en la ecuación para obtener la frecuencia del alelo después de dos generaciones y así sucesivamente.
individuos l/l tienen una eficacia cero, Dawson esperaba que su población evolucionara
hacia frecuencias cada vez más bajas del alelo l y más altas del alelo . Dawson utilizó las
ecuaciones derivadas en el Cuadro 5.3 y el método descrito en el Cuadro 5.6 para hacer
predicciones cuantitativas del curso de la evolución. Luego dejó que sus poblaciones evolucionaran durante unas doce generaciones, midiendo en cada generación las frecuencias
de los dos alelos.
Los resultados aparecen en la Figura 5.14. Los datos de Dawson están muy de acuerdo
con sus predicciones teóricas. Al principio, la frecuencia del alelo letal recesivo disminuye rápidamente (Figura 5.14a). En la segunda generación ya ha bajado del 0,5 a, aproxi-
predicciones que hicimos con
los modelos genético
0,5
menos en las condiciones de
0,4
laboratorio.
Frecuencia del alelo
letal recesivo
poblacionales son exactas, al
0,3
0,2
0,1
0
0
2
4
6
8
1
1
0
2
0
2
4
6
8
1
1
0
2
Figura 5.14 Evolución en poblaciones de laboratorio del gorgojo de la
harina (a) El declive en frecuencia de un alelo letal recesivo (símbolos rojos)
concuerda casi exactamente con la predicción teórica (línea gris). Cuando el alelo
llega a ser raro, la tasa de evolución se hace espectacularmente lenta. (b) Este
gráfico muestra el incremento en frecuencia del alelo dominante correspondiente.
Modificado de Dawson (1970).
Frecuencia del alelo
viable dominante
1,0
0,9
0,8
0,7
0,6
0,5
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 131
madamente, el 0,25. Sin embargo, a medida que la evolución progresaba, la reducción en
frecuencia del alelo letal se hizo más lenta. Entre las generaciones 10 y 12 la frecuencia
no disminuyó en absoluto. El experimento de Dawson demuestra que la teoría de la genética de poblaciones, a pesar de sus suposiciones simplificadas, nos permite predecir con
mucha exactitud el curso de la evolución, al menos en las condiciones controladas del
laboratorio.
El experimento también demuestra que la dominancia y la frecuencia alélica interactúan para determinar la tasa de evolución. Cuando el alelo recesivo es frecuente (y el alelo
dominante raro), la evolución por selección natural es rápida. Por el contrario, cuando el
alelo recesivo es raro y el alelo dominante abundante, la evolución por selección natural
es lenta.
El equilibrio de Hardy-Weinberg explica el porqué. Imagine primero un alelo recesivo que es frecuente: su frecuencia es, por ejemplo, 0,95.Así, el alelo dominante tiene una
frecuencia del 0,05. Multiplicando las frecuencias alélicas podremos calcular las frecuencias genotípicas:
AA
(0,05)2
= 0,0025
Aa
2(0,05)(0,95)
= 0,095
aa
(0,95)2
= 0,9025
Casi un 10% de los individuos de la población tienen fenotipo dominante, mientras que
el 90% restante tienen fenotipo recesivo. Ambos fenotipos están razonablemente bien
representados y si se diferencian en eficacia, las frecuencias alélicas de la siguiente generación pueden ser sustancialmente distintas. Imaginemos ahora que el alelo recesivo es raro:
su frecuencia es 0,05. Así, el alelo dominante tiene una frecuencia de 0,95. Las frecuencias genotípicas son
AA
(0,95)2
= 0,9025
Aa
2(0,95)(0,05)
= 0,095
aa
(0,05)2
= 0,0025
Prácticamente el 100% de la población tiene el fenotipo dominante, mientras que el fenotipo recesivo está casi ausente.Aunque los fenotipos se diferencien mucho en eficacia, hay
tan pocos de los fenotipos minoritarios que habrá muy poco cambio en frecuencias alélicas en la generación siguiente. En una población con apareamiento al azar, la mayoría de
las copias del alelo recesivo raro se encuentran escondidas fenotípicamente en los individuos heterozigotos. Para un tratamiento algebraico de la selección sobre los alelos recesivos y dominantes véase el Cuadro 5.7.
Selección sobre homozigotos y heterozigotos
Cuando un alelo es recesivo y el otro es dominante, la eficacia de los heterozigotos es igual
a la de uno de los dos homozigotos. Desde luego hay otras situaciones posibles.A menudo la eficacia de los heterozigotos se encuentra entre la de los dos homozigotos. Esto puede
cambiar la tasa de evolución, pero no altera el resultado final.Al final, en la población queda
fijado un alelo y el otro se pierde. En la Figura 5.10 se muestran varios ejemplos.
También es posible que la eficacia de los heterozigotos sea superior o inferior a la de
los dos homozigotos. La superioridad y la inferioridad de los heterozigotos dan lugar a
resultados completamente distintos.
Nuestro primer ejemplo viene de la investigación en poblaciones de laboratorio de la
mosca de la fruta (Drosophila melanogaster) realizada por Terumi Mukai y Allan Burdick
(1959). Al igual que Dawson, Mukai y Burdick estudiaron la evolución de un locus con
dos alelos. Los homozigotos para un alelo eran viables mientras que los homozigotos para
La selección natural es más
potente como fuerza evolutiva
cuando actúa sobre alelos
recesivos frecuentes (y alelos
dominantes raros).
132 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.7
Tratamiento algebraico de la selección sobre alelos recesivos y dominantes
D
esarrollaremos aquí las ecuaciones que destacan las
diferencias entre la selección sobre un alelo recesivo
y sobre un alelo dominante. Imaginemos un locus con
dos alelos. Sea p la frecuencia del alelo dominante A y q la
frecuencia del alelo recesivo a.
Selección sobre el alelo recesivo
Sea la eficacia de los genotipos:
wAA
1
wAa
1
waa
1s
en donde s, el llamado coeficiente de selección, indica
la fuerza de la selección sobre los homozigotos recesivos
relativa a los otros genotipos. Los valores positivos de s
indican selección a favor del alelo recesivo; los valores negativos de s indican selección en contra del alelo recesivo.
Basándonos en el Cuadro 5.3, las ecuaciones siguientes
dan la frecuencia del alelo a, q’, en la generación siguiente, dada la frecuencia de a en esta generación y la eficacia
de los tres genotipos:
pqwAa q2waa
pqwAa q2waa
q – p2wAA 2pqwAa q2waa
w
Sustituyendo los valores de eficacia de la tabla anterior,
y (1 – q) por p y simplificando, obtendremos
q(1 sq)
q 1 sq2
Si a es un letal recesivo, entonces s es igual a –1. Sustituyendo este valor en la ecuación anterior tendremos
q(1 q)
q(1 q)
q
q 2 1q
(1 q)(1 q)
(1 q)
Una breve experimentación demuestra que una vez
que un alelo letal recesivo se hace raro, las subsiguientes
disminuciones en frecuencia se hacen lentamente. Por
ejemplo, si la frecuencia del alelo a es 0,01, entonces en la
generación siguiente su frecuencia será aproximadamente
0,0099.
Selección sobre el alelo dominante
Sea la eficacia de los genotipos:
wAA
1s
wAa
1s
waa
1
donde s, el coeficiente de selección, indica la fuerza de la
selección sobre los genotipos que llevan el alelo dominan-
te relativa a los homozigotos recesivos. Los valores positivos de s indican selección a favor del alelo dominante; los
valores negativos de s indican selección en contra del alelo
dominante.
Basándonos en el Cuadro 5.3, podemos obtener una
ecuación que prediga la frecuencia del alelo A, p’, en la
generación siguiente, dada la frecuencia de A en esta generación y la eficacia de los tres genotipos:
p2wAA pqwAa
p2wAA pqwAa
p – p2wAA 2pqwAa q2waa
w
Sustituyendo los valores de eficacia de la tabla, y q por
(1 – p) y simplificando, obtendremos
p(1 s)
p 1 2sp sp2
Si A es letal dominante, s es igual a –1. Sustituyendo este
valor en la ecuación anterior se ve que el letal dominante
se elimina de la población en una sola generación.
Selección sobre los alelos recesivos en
comparación con la selección sobre los alelos
dominantes
La selección sobre los alelos recesivos y la selección sobre
los alelos dominantes son lados opuestos de la misma
moneda. La selección en contra de un alelo recesivo es
selección a favor del alelo dominante y viceversa.
En la Figura 5.15a (izquierda) se muestran 100 generaciones de evolución en una población ideal sometida a
selección contra un alelo recesivo y a favor del alelo dominante.Al principio, la frecuencia de los alelos cambia rápidamente. Sin embargo, a medida que el alelo recesivo se
hace más raro, la tasa de evolución disminuye drásticamente. Cuando el alelo recesivo es raro, la mayoría de las
copias se encuentran en los individuos heterozigotos de la
población, en donde se encuentran realmente ocultos al
efecto de la selección.
La figura también muestra (derecha) la eficacia media
de la población (véase el Cuadro 5.3) en función de la
frecuencia del alelo dominante. A medida que el alelo
dominante se va haciendo más frecuente, la eficacia media
de la población aumenta. La eficacia media se maximiza
cuando el alelo favorecido alcanza una frecuencia del
100%. Las gráficas de la eficacia media en función de la
frecuencia alélica se denominan a menudo paisajes adaptativos.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 133
CUADRO 5.7 Continuación
La Figura 5.15b (izquierda) muestra 100 generaciones
de evolución en una población ideal sometida a selección
a favor del alelo recesivo y en contra del alelo dominante.
Al principio la frecuencia de los alelos cambia lentamente. El alelo recesivo es raro, la mayoría de las copias presentes se encuentran en los heterozigotos y la selección no
puede verlos. Sin embargo, a medida que los alelos recesivos se hacen lo bastante frecuentes como para que aparezca una fracción sustancial de homozigotos, la tasa de
evolución aumenta espectacularmente. Una vez se acelera
el ritmo de la evolución, los alelos recesivos favorables
alcanzan rápidamente una frecuencia del 100%. Es decir, el
alelo recesivo queda fijado en la población.
La figura también muestra (derecha) la eficacia media de
la población (véase el Cuadro 5.3) en función de la frecuencia del alelo recesivo. A medida que el alelo recesivo
se va haciendo más frecuente, la eficacia media de la población aumenta. La eficacia media se maximiza cuando el
alelo favorecido alcanza una frecuencia del 100%.
1,0
1,0
Fracción que sobrevive:
AA
1,0
0,5
Aa aa
1,0 0,5
0,0
0
20
40
60
80
100
Eficacia media
Frecuencia de A
Frecuencia de a
(a) Selección en contra de un alelo recesivo y a favor de un alelo dominante
0,5
0
Generación
0,5
1,0
Frecuencia de A
1,0
Figura 5.15 Evolución en
poblaciones ideales sometidas a
selección contra alelos recesivos y
dominantes Los gráficos de la izquierda
1,0
Fracción que
sobrevive:
AA Aa aa
0,4 0,4 1,0
0,5
Eficacia media
Frecuencia de A
Frecuencia de a
(b) Selección a favor de un alelo recesivo y en contra de un alelo dominante
0,0
0
20
40
60
Generación
80
100
0,4
0
0,5
Frecuencia de a
1,0
muestran cambios en las frecuencias
alélicas con el tiempo. Los gráficos de la
derecha muestran los paisajes adaptativos:
cambios en la eficacia media de la
población en función de las frecuencias
alélicas.
el otro alelo no lo eran. Los investigadores utilizaron heterozigotos como fundadores para
establecer dos poblaciones experimentales con frecuencias alélicas iniciales de 0,5. Permitieron que las poblaciones evolucionaran durante 15 generaciones, midiendo en cada
generación la frecuencia del alelo viable.
Los resultados de Mukai y Burdick aparecen en la Figura 5.16, representados por los
símbolos rojos. Como se esperaba, la frecuencia del alelo viable aumentó rápidamente en
las primeras generaciones. Sin embargo, la tasa de evolución disminuyó mucho antes de
que el alelo viable se aproximara a la frecuencia de 1,0. Por el contrario, parecía que el alelo
viable alcanzaba un equilibrio, o un estado sin cambios, a una frecuencia de 0,79.
Para profundizar más, Mukai y Burdick fundaron dos nuevas poblaciones experimentales, esta vez con una frecuencia inicial del alelo viable de 0,975. La evolución de
estas poblaciones se representa en la Figura 5.16 por los símbolos azules. En lugar de
134 PARTE II Mecanismos del cambio evolutivo
Figura 5.16 Evolución en cuatro poblaciones de laboratorio de la mosca
de la fruta En homozigosis, un alelo es viable y el otro letal. No obstante, las
cuatro poblaciones evolucionan hacia un equilibrio en el que se mantienen ambos
alelos. La explicación más probable es que el heterozigoto goza de una eficacia
mayor que la de los dos homozigotos. Dibujo a partir de datos publicados por
Mukai y Burdick (1958).
Las investigaciones con la
mosca de la fruta demuestran
que la selección natural puede
actuar para mantener dos
alelos en equilibrio estable.
Una manera de que esto
suceda es cuando el
heterozigoto tiene una eficacia
superior.
el heterozigoto tenga una
eficacia inferior.
0,9
0,8
0,7
0,6
0,5
0
5
10
15
Generación
aumentar hacia 1,0, la frecuencia del alelo viable bajo, alcanzando de nuevo un equilibrio cercano al 0,79.
Adviértase que una frecuencia de equilibrio de 0,79 para el alelo viable significa que
el alelo letal tiene una frecuencia de equilibrio de 0,21. ¿Cómo puede mantener la selección natural un alelo letal a tan elevada frecuencia en esta población? Mukai y Burdick
arguyeron que la explicación más probable era la superioridad del heterozigoto, también conocida como superdominancia. De acuerdo con esta hipótesis, los heterozigotos tienen mayor eficacia que cualquiera de los homozigotos. En el equilibrio, la ventaja
selectiva que posee el alelo letal cuando está en heterozigosis se equilibra exactamente con
la desventaja obvia que sufre cuando está en homozigosis. Las curvas roja y azul de la Figura 5.16 representan la evolución en una población ideal en la que la eficacia de los tres
genotipos son las siguientes (V representa el alelo viable y L el alelo letal):
VV
0,735
También es posible que
Frecuencia del alelo viable
1,0
VL
1,0
LL
0
Las curvas teóricas se ajustan mucho a los datos. Manteniendo una población en un
equilibrio en el que ambos alelos se encuentren presentes, la superioridad del heterozigoto puede mantener diversidad genética. Para un tratamiento algebraico de la superioridad del heterozigoto, véase el Cuadro 5.8.
Nuestro segundo ejemplo, del trabajo de G. G. Foster y sus colegas (1972), demuestra
cómo evolucionan las poblaciones cuando los heterozigotos tienen menor eficacia que
cualquiera de los dos homozigotos. Foster y sus colegas utilizaron moscas de la fruta con
cromosomas compuestos. Los cromosomas compuestos son cromosomas homólogos que
han permutado brazos completos, de tal manera que un homólogo tiene dos copias de un
brazo y el otro homólogo tiene las dos copias del otro brazo (Figura 5.17a,b). En la meiosis, los cromosomas compuestos pueden segregar o no. Por ello se producen cuatro tipos
de gametos en igual número: gametos con ambos cromosomas homólogos, gametos con
sólo uno de los brazos del par, gametos con sólo el otro brazo del par y gametos sin cromosomas del par (Figura 5.17c). Cuando se cruzan dos moscas con cromosomas compuestos, la cuarta parte de sus zigotos tiene cada uno de los brazos cromosómicos en la
dosis correcta y son viables. Los otros tres cuartos tienen o demasiadas copias o demasiado pocas de uno o de los dos brazos cromosómicos y son inviables (Figura 5.17d). Cuando una mosca con cromosomas compuestos se cruza con una mosca con cromosomas normales, ninguno de los zigotos que se forma es viable (Figura 5.17e).
Foster y sus colegas establecieron poblaciones de laboratorio en las que algunos de los
fundadores tenían cromosomas segundos compuestos [C(2)] y otros tenían cromosomas
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 135
(a) Pareja de cromosomas
homólogos normales (cada
uno tiene un brazo azul y
un brazo gris).
(b) Pareja de cromosomas
compuestos (uno tiene dos
brazos azules y el otro dos
brazos verdes).
(d) Cuando se cruzan individuos con
cromosomas compuestos, la cuarta parte
de sus zigotos son viables.
Esperma
(c) Los gametos formados por un
individuo con cromosomas
compuestos pueden llevar ambos
cromosomas, uno o ninguno.
(e) Cuando un individuo con cromosomas
compuestos se cruza con un individuo
con cromosomas normales, ninguno de
sus zigotos es viable.
Óvulos
Gametos del padre
con cromosomas
normales
Gametos del padre con
cromosomas compuestos
Zigotos
(f) Evolución en 13 poblaciones de Drosophila melanogaster que tienen una mezcla de
segundos cromosomas compuestos [C(2)] y segundos cromosomas normales [N(2)]. La
frecuencia inicial de C(2) va de 0,71 a 0,96.
1,0
Frecuencia de C(2)
0,8
0,6
Tasas de supervivencia de los zigotos:
C(2)C(2)
0,4
0,25
C(2)N(2)
N(2)N(2)
0
1,0
El diseño experimental hace un
uso inteligente de los cromosomas
compuestos. Modificado con el
permiso de Foster et al. (1972).
Copyright © 1972, American
Association for the Advancement
of Science.
0,2
0
0
1
2
Generación
3
4
segundos normales [N(2)]. Para el análisis podemos tratar cada cromosoma como si fuera
un único alelo. Así, los fundadores son homozigotos C(2)C(2) y homozigotos N(2)N(2).
Basándonos en la viabilidad de los homozigotos que acabamos de describir, las eficacias
de los genotipos en la población mezcla son
C(2)C(2)
0,25
C(2)N(2)
0
Figura 5.17 Experimento
diseñado para demostrar
cómo evolucionan las
poblaciones cuando los
heterozigotos tienen menor
eficacia que los homozigotos
N(2)N(2)
1
En otras palabras, los genotipos presentan una fuerte desventaja del heterozigoto (infradominancia).
136 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.8 Equilibrio estable con superioridad del heterozigoto y equilibrio inestable con
inferioridad del heterozigoto
D
esarrollaremos aquí métodos algebraicos y gráficos
para analizar la evolución de loci con superioridad
del heterozigoto o con inferioridad del heterozigoto.
Imaginemos una población en la que el alelo A1 tiene una
frecuencia p y el A2 una frecuencia q. En el Cuadro 5.3
desarrollamos una ecuación que describe el cambio de p
por selección de una generación a la siguiente:
p
∆p ⫽ – (pw11 qw12 w–)
w
p
– (pw11 qw12 p2w11 2pqw12 q2w22)
w
Sustituyendo p por (1 – q) en los términos primero y tercero de la expresión entre paréntesis, tendremos,
p
∆p – [(1 q)w11 qw12
w
(1 q)2w11 2pqw12 q2w22]
después de simplificar y despejar q, tendremos,
pq
∆p – (w12 w11 qw11 2pw12 qw22)
w
Por definición, la frecuencia del alelo ∆1 estará en equilibrio cuando ∆p = 0. En la ecuación anterior se ve que
∆p = 0 cuando p = 0 o q = 0. Estos dos equilibrios son triviales. Se dan cuando uno u otro alelo desaparece de la
población. La ecuación también tiene una tercera situación
de equilibrio, que es cuando,
w12 w11 qw11 2pw12 qw22 0
sustituyendo q por (1 – p) y despejando p tendremos,
w22 w12
p^ w11 2w12 w22
en donde p^ es la frecuencia del alelo A1 en el equilibrio.
Finalmente, sea la eficacia de los genotipos la siguiente:
A1A1
1s
A1A2
1
A2A2
1t
Los valores positivos de los coeficientes de selección s y t
representan selección en contra del heterozigoto y los
valores negativos selección a favor del heterozigoto. Sustituyendo en las ecuaciones anteriores las eficacias y simplificando, tendremos:
t
p^ st
Por ejemplo, cuando s = –0,4 y t = –0,6, los heterozigotos tienen una mayor eficacia, y la frecuencia en el equilibrio para el alelo A1 es 0,6. Cuando s = 0,4 y t = 0,6, los
heterozigotos tienen una menor eficacia y la frecuencia en
el equilibrio para el alelo A1 es también 0,6.
Otro método útil para analizar el equilibrio es representar el ∆p en función de p. En la Figura 5.18a se muestra tal representación para los dos ejemplos numéricos que
acabamos de calcular. En ambas representaciones se demuestra que el ∆p = 0 cuando p = 0, p = 1 ó p = 0,6.
Las curvas de la Figura 5.18a también nos permiten
determinar si un equilibrio es estable o inestable. Observemos la curva roja; se refiere a un locus con superioridad
del heterozigoto. Advierta que cuando p es mayor de 0,6,
el ∆p es negativo. Esto quiere decir que cuando la frecuencia del alelo A1 sea superior a su valor de equilibrio,
la población retrocederá hacia el equilibrio en la generación siguiente. De igual manera, cuando p sea menor que
0,6, el ∆p será positivo. Cuando la frecuencia del alelo A1
se encuentra por debajo de su valor de equilibrio volverá
hacia el equilibrio en la generación siguiente. El equilibrio
“interno” de un locus con superioridad del heterozigoto
es estable.
La Figura 5.18b muestra un paisaje adaptativo para un
locus con superioridad del heterozigoto. El gráfico representa la eficacia media poblacional en función de la frecuencia del alelo A1. La eficacia media es baja cuando no
está A1 y relativamente baja cuando A1 se ha fijado. A
medida que la frecuencia del alelo se desplaza desde ambos
extremos hacia su equilibrio estable, la eficacia media
poblacional aumenta hasta un máximo.
Miremos ahora a la curva azul de la Figura 5.18a. Se
refiere a un locus con inferioridad del heterozigoto. Si p
aumenta, aunque sólo sea ligeramente, por enzima de 0,6,
seguirá aumentado hasta 1,0 en las generaciones siguientes; si p disminuye, aunque sólo sea ligeramente por debajo
de 0,6, continuará disminuyendo hasta 0 en las generaciones siguientes. El equilibrio interno para un locus con
inferioridad del heterozigoto es inestable.
La Figura 5.18c muestra el paisaje adaptativo para un
locus con inferioridad del heterozigoto. La eficacia media
poblacional es mínima cuando la frecuencia del alelo A1
coincide con el equilibrio interno inestable. Cuando la fre-
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 137
CUADRO 5.8 Continuación
(a) ∆p en función de p
0,12
s = -0,4; t = -0,6
s = 0,4; t = 0,6
∆p
0,06
0,00
-0,06
0,0
0,2
0,4
0,6
0,8
1,0
0,8
1,0
p
(b) Eficacia media en función de p
con superdominancia
0,8
Eficacia media
cuencia del alelo se aleja de este equilibrio en ambas direcciones, la eficacia media aumenta.
Una comparación del paisaje adaptativo de la Figura
5.18c con los de las Figuras 5.18b y 5.15 ofrece una conclusión importante. Cuando una población evoluciona
en respuesta a la selección, la eficacia media de los individuos de la población tiende a elevarse. Sin embargo, la
selección no siempre maximiza la eficacia media en un
sentido global. Dependiendo de las frecuencias alélicas
iniciales, la población representada en la Figura 5.18c
puede evolucionar bien hacia la fijación, bien hacia la
pérdida del alelo A1. Si el alelo queda fijado, la población
se situará en un equilibrio estable, pero la eficacia media
de la población será sustancialmente menor que si el alelo
se hubiera perdido.
0,7
0,6
0,5
0,4
0,0
0,2
0,4
0,6
p
(c) Eficacia media en función de p con
selección en contra del heterozigoto
Eficacia media
1,6
Figura 5.18 Análisis gráfico de los equilibrios estable e inestable
para loci con superioridad y con inferioridad del heterozigoto
(a) Representación del ∆p en función de p. (b) y (c) Paisajes adpatativos.
1,5
1,4
1,3
1,2
0,0
0,2
El análisis algebraico, descrito en el Cuadro 5.8, predice que una población mezclada
estará en equilibrio, con los dos alelos presentes, cuando la frecuencia de C(2) sea exactamente 0,8. Sin embargo, este equilibrio es inestable. Si la frecuencia de C(2) sube ligeramente por encima de 0,8, entonces aumentará rápidamente hasta 1,0. De igual manera,
si la frecuencia de C(2) baja ligeramente de 0,8, rápidamente caerá hasta cero.
Intuitivamente, la razón de esta predicción es la siguiente. Los heterozigotos son inviables, por lo que los adultos de la población serán todos homozigotos. Imaginemos primero
que los individuos C(2)C(2) son corrientes y los N(2)N(2) raros. Si las moscas se cruzan
al azar, casi todos los cruces se darán entre moscas C(2)C(2), o entre moscas C(2)C(2) y
N(2)N(2). Sólo raramente se cruzarán moscas N(2)N(2) entre si. Por ello, la mayoría de las
moscas N(2)N(2) tendrán un éxito reproductivo nulo, y la frecuencia de C(2) subirá hasta
1,0. Imaginemos ahora que hay bastantes moscas N(2)N(2) y que un número apreciable
de ellas se cruza entre sí. Estos cruces producirán cuatro veces más descendientes que los
0,4
0,6
p
0,8
1,0
138 PARTE II Mecanismos del cambio evolutivo
Cuando los heterozigotos
tienen una eficacia inferior, un
alelo tiende a fijarse mientras
que el otro se pierde. Sin
embargo, poblaciones
distintas pueden perder alelos
diferentes.
cruces entre moscas C(2)C(2). Por ello la frecuencia de N(2) subirá hasta 1,0 y la frecuencia
de C(2) caerá hasta cero.
Foster y sus colegas fundaron 13 poblaciones mezcladas, con frecuencias de C(2) entre
0,71 y 0,96, y luego siguieron su evolución durante cuatro generaciones. Los resultados
aparecen en la Figura 5.17f. Cuantitativamente, el resultado está perfectamente de acuerdo con las predicciones teóricas. En las poblaciones con las frecuencias iniciales de C(2)
más elevadas, aumenta rápidamente hasta la fijación, mientras que en poblaciones con frecuencias iniciales bajas, C(2) se pierde rápidamente. La situación exacta del punto de equilibrio inestable es, aproximadamente 0,9 en lugar de 0,8. Foster y sus colegas advierten que
sus moscas C(2)C(2) llevaban marcadores genéticos recesivos que los biólogos introducen
para permitir una fácil identificación. Sugieren que estos marcadores reducen la eficacia
relativa de las moscas C(2)C(2) por debajo del valor de 0,25, deducido exclusivamente en
función de sus cromosomas compuestos. El experimento de Foster y colegas demuestra
que la inferioridad de los heterozigotos da lugar a la perdida de diversidad genética en las
poblaciones. Sin embargo, llevando a la fijación a alelos diferentes en poblaciones distintas, la inferioridad del heterozigoto puede ayudar a mantener la diversidad genética en el
conjunto de las poblaciones.
Selección dependiente de frecuencias
Figura 5.19 Peces comedores
de escamas (Perissodus
microlepis) del lago Tanganika
(arriba) Pez diestro, del que se
muestran ambos lados. La boca de
este pez gira hacia el lado derecho
del pez. (abajo) Pez zurdo del que
se muestran ambos lados. La boca
de este pez gira hacia el lado
izquierdo del pez. Estos dos
individuos pertenecen a la misma
especie y son miembros de la
misma población (Dr. Michio Hori,
Kyoto University, Kyoto, Japón)
Hasta el momento hemos visto ejemplos en los que el patrón de selección es constante a
lo largo del tiempo. Cuando la selección favorece insistentemente a un alelo concreto, la
población evoluciona de manera inexorable hacia la fijación de dicho alelo y a la pérdida
de los otros. Cuando la selección favorece insistentemente a los heterozigotos, la población evoluciona hacia un equilibrio estable en el que se encuentran ambos alelos. El último
escenario que examinaremos es aquel en el que las frecuencias alélicas de una población
permanecen casi en equilibrio, pero la razón de dicho equilibrio es que la dirección de la
selección fluctúa. La selección favorece primero a un alelo, luego al otro. Este escenario
se denomina selección dependiente de frecuencias.
El ejemplo de selección dependiente de frecuencias proviene de la investigación de
Michio Hori (1993) sobre el pez comedor de escamas, Perissodus microlepis, del lago Tanganika en África. Como su nombre sugiere, el pez comedor de escamas vive arrancando
a mordiscos las escamas de otros peces. El comedor de escamas ataca por detrás, coge las
escamas del flanco de la víctima y luego escapa lejos.Todavía más raro es que entre los individuos de la especie P. microlepis, hay peces diestros, cuyas bocas están torcidas hacia la derecha, y peces zurdos, cuyas bocas están torcidas hacia la izquierda (Figura 5.19). Hori
demostró, en una primera aproximación, que esta característica está determinada por un
solo locus con dos alelos. Diestro es dominante sobre zurdo.
Hori observó los ataques sobre peces presa utilizados como señuelos y además examinó las escamas recuperadas del estómago del pez comedor de escamas. Estas observaciones demuestran que los peces diestros siempre atacan a su víctima por el flanco
izquierdo y los zurdos por el flanco derecho. (El lector puede visualizar la razón de esto
torciendo primero sus labios hacia la derecha, o hacia la izquierda, e imaginando
después que intenta morder escamas en los flancos de un pez.) Las especies presa son
cautas y vigilantes y los comedores de escamas sólo tienen éxito en el 20% de sus
ataques.
Hori razonó que si los comedores de escamas diestros fueran más abundantes que los
zurdos, las especies atacadas estarían más vigilantes de ataques desde la izquierda. Esto daría
a los comedores de escamas zurdos, que atacan por la derecha, una ventaja en sus esfuerzos por coger desprevenidas a sus presas. Los comedores de escamas zurdos obtendrían más
alimento que los diestros, tendrían más descendientes y transmitirían un mayor número
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 139
de sus genes zurdos. Esto daría lugar a un aumento de los comedores de escamas zurdos
en la población.
Cuando los comedores de escamas zurdos se hicieran más abundantes que los diestros,
los peces atacados comenzarían a estar más vigilantes de los ataques por la izquierda. Esto
daría ventaja a los comedores de escamas diestros, que atacan por la izquierda. Los diestros obtendrían más alimento y tendrían más descendientes y las frecuencias de los diestros aumentarían en la población.
El resultado sería que los peces diestros y zurdos se encontrarían en la población en
frecuencias parecidas en cualquier momento. El alelo diestro, dominante, se mantendría
en una frecuencia justo por debajo de 0,3 y el alelo zurdo, recesivo, a una frecuencia justo
por encima de 0,7; de acuerdo con el equilibrio de Hardy-Weinberg, estas frecuencias
alélicas dan unas frecuencias fenotípicas de 0,5 y 0,5. Este fenómeno, en el que el fenotipo raro es favorecido por selección natural, es un ejemplo de selección dependiente de
frecuencias.
La historia del pez de Hori es una hipótesis elegante, pero ¿es cierta? Para comprobarla, Hori utilizó una red de trasmallo para tomar una muestra de peces comedores de escamas en el lago Tanganika, cada uno o dos años durante 11 años. Las frecuencias de los dos
fenotipos realmente parecen oscilar alrededor de 0,5 (Figura 5.20). En pocos años, un poco
más de la mitad de los peces eran zurdos. Invariablemente, uno o dos años después, el péndulo había vuelto hacia atrás y una proporción ligeramente mayor de la mitad de los peces
era diestra.
¿Es posible que la frecuencia de las dos formas estuviera oscilando al azar, en lugar de
mantenerse alrededor de 0,5 por efecto de la selección? En tres años distintos Hori examinó peces adultos que se sabía estaban criando, ya que se capturaron en el momento de
la puesta de sus crías por científicos buceadores. Las frecuencias en estas muestras de
diestros-zurdos oscilaban también, pero los más abundantes entre los que criaban eran
siempre las formas contrarías a la más abundante en el conjunto de la población. (En la
Figura 5.20 los padres están indicados por un cuadrado.) En otras palabras, en cualquier
momento, la forma menos frecuente parece estar siendo más producida. Esto está de acuerdo con la hipótesis de Hori de selección dependiente de frecuencias.
Además, Hori tiene pruebas que apoyan esta hipótesis acerca del mecanismo de selección. En 1980 examinó las heridas por mordiscos en las especies presa, cuando los comedores de escamas zurdos eran más frecuentes, y en 1983, cuando los más frecuentes eran
La selección también puede
mantener dos alelos en una
población si cada alelo es
ventajoso cuando es raro.
Frecuencia de individuos zurdos
1,0
n = 147
n = 114
n = 26
n = 27
0,5
n = 25
n = 98
n = 47
n = 104
n = 29
n = 153
n = 99
n = 33
n = 18
0
'80
'81
'82
'83
'84 '85 '86 '87
Año de la muestra
'88
'89
'90
Figura 5.20 Frecuencia de peces zurdos a lo
largo del tiempo Los círculos representan peces
comedores de escamas capturados con una red de
trasmallo; los círculos rojos respecto de los azules
representan peces capturados en localidades diferentes.
Los cuadros (en 1981, 1987 y 1990) representan
adultos en edad de reproducción, capturados
selectivamente por científicos con escafandras de
buceo. Los números (n) indican el tamaño de las
muestras. Reimpreso con el permiso de Hori (1993).
Copyright © 1993, American Association for the
Advancement of Science.
140 PARTE II Mecanismos del cambio evolutivo
los diestros. En los dos años las presas tenían más marcas de mordiscos por aquellas formas que eran menos frecuentes en ese momento. Esto está de acuerdo con la idea de que
la presa está realmente más vigilante de ataques de aquellos comedores de escamas que sean
más abundantes en un momento dado. Parece que la hipótesis de Hori es correcta y que
a largo plazo las frecuencias alélicas, genotípicas y fenotípicas de los peces comedores de
escamas se mantendrán constantes por selección dependiente de frecuencias. La selección
dependiente de frecuencias, como la superioridad del heterozigoto, mantiene la diversidad genética en las poblaciones.
Esterilización obligatoria
Podemos utilizar modelos
genético-poblacionales para
evaluar si la esterilización
eugenésica pudiera llevar a
cabo los objetivos de sus
proponentes, si sus
suposiciones acerca de la
heredabilidad de los
caracteres han sido correctas.
La respuesta depende de la
frecuencia de los alelos
en cuestión y de los criterios
Frecuencia de
individuos afectados
del éxito.
0,01
0,005
0,0
0
2
4 6 8 1
Generación
Figura 5.21 Cambio
pronosticado en la frecuencia
de homozigotos para un
supuesto alelo para debilidad
mental bajo un programa de
esterilización eugenésica que
evita que los individuos
homozigotos recesivos se
reproduzcan.
0
Habiendo discutido una cierta variedad de modelos de selección, podemos considerar
ahora las consecuencias evolutivas del programa de esterilización obligatoria eugenésica.
Los que proponían la esterilización eugenésica buscaban reducir la eficacia de genotipos
concretos hasta cero, y por consiguiente reducir la frecuencia de los alelos responsables de
fenotipos no deseados.
Un fenotipo que llamó la atención de los eugenistas, quizá más que ningún otro, fue
la debilidad mental. El Real Colegio de Médicos de Inglaterra definió a un individuo débil
mental como:“Aquel que puede ganarse la vida en circunstancias favorables, pero que es
incapaz, por defectos mentales desde el nacimiento o desde la edad temprana, de (a) competir en un nivel de igual con personas normales o (b) arreglárselas por sí mismo en sus
asuntos con la prudencia normal” (véase Goddard 1914). Las pruebas presentadas por
Henry G. Goddard en 1914, que fue el director de investigación de la Escuela de adiestramiento para niñas y niños débiles mentales en Vineland, New Jersey, convenció a
muchos eugenistas que el vigor mental se comportaba como un carácter mendeliano simple (véase Paul y Spencer 1995). Se creía que la normalidad era dominante y la debilidad
mental recesiva.
Una enfermedad genética recesiva no es un objetivo prometedor para un programa que
la eliminaría mediante esterilización de los individuos afectados. Como muestran las
Figuras 5.14 y 5.15, los alelos recesivos raros disminuyen lentamente en frecuencia, incluso sometidos a una selección intensa. Por otro lado, los eugenistas no creían que la debilidad mental fuera especialmente rara (Paul y Spencer 1995). Realmente creían que la
debilidad mental era alarmantemente corriente y que aumentaba su frecuencia. Edward
M. East (1917) estimó la frecuencia de la debilidad mental en el tres por mil. Henry H.
Goddard publicó que la frecuencia entre los escolares de Nueva York era del 2%. Pruebas
en soldados americanos durante la Primera Guerra Mundial sugirieron una frecuencia cercana al 5% entre los reclutas blancos.
Asumiremos una frecuencia del 1% para la debilidad mental y reproduciremos los cálculos publicados por R. C. Punnett (1917) y revisados por R. A. Fisher (1924). Sea f el
supuesto alelo para la debilidad mental, con una frecuencia q. Si el 1% de la población tiene
el genotipo ff, entonces, de acuerdo con el equilibrio de Hardy-Weinberg, la frecuencia
inicial de f es,
苶01
苶 ⫽ 0,1
q ⫽ 兹0,
Si se esteriliza a todos los individuos afectados, entonces la eficacia del genotipo ff sería
cero (o, lo que es igual, el coeficiente de selección para el genotipo ff sería –1). Utilizando la ecuación obtenida en el Cuadro 5.7, podemos calcular el valor de q en generaciones sucesivas y, a partir de q, podemos calcular la frecuencia del genotipo ff.
El resultado aparece en la Figura 5.21. En 10 generaciones, unos 250 años, la frecuencia de los individuos afectados disminuye de 0,01 a 0,0025.
El que un genético vea estos cálculos como alentadores o desalentadores depende de
si él o ella miran a un vaso como parcialmente vacío o parcialmente lleno. Algunos, al
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 141
mirar estas cifras verán que se tardaría un tiempo muy largo en eliminar completamente
a la debilidad mental y argüirían que la esterilización obligatoria sería una solución tan
desesperadamente lenta que no vale la pena el esfuerzo. Otros, como Fisher, desechan
este argumento como “propaganda anti-eugenésica”. Fisher advirtió que después de una
sola generación, la frecuencia de los individuos afectados bajaría del 100 por diez mil al
82,6 por diez mil.“En una sola generación,” escribió,“el gasto público y la miseria personal ocasionada por la debilidad mental... se reduciría por encima del 17 por ciento.”
Fisher advirtió también que la mayoría de las copias del alelo para la debilidad mental
se encuentran en heterozigotos portadores más que en individuos afectados. Junto con
East, Punnet y otros, Fisher apeló por la investigación de métodos para identificar a los
portadores.
No es muy justo utilizar criterios actuales para criticar la investigación de Goddard
sobre la genética de la debilidad mental. La genética mendeliana estaba en su infancia. No
obstante, mirando hace casi un siglo atrás, las pruebas de Goddard eran profundamente
erróneas.
Primero, los individuos que indicó como casos estudiados pertenecían a un grupo muy
diverso. Algunos tenían el síndrome de Down, otros tenían otras formas de retraso mental.Al menos uno era sordo y parece que fue víctima de una educación totalmente funesta e inadecuada. Otros parece que habían sido confiados a la Escuela de adiestramiento de
Goddard por padres viudos que sentían que los hijos de matrimonios anteriores eran un
estorbo para encontrar una nueva esposa. Otros puede que se comportaran de manera diferente a como los directores de la escuela pensaban que deberían comportarse. Al acabar
con el primer caso que comenta en su libro, Goddard escribió de una muchacha de 16
años que había estado en la escuela durante siete años:
“Gertrudis es un buen ejemplo de aquel tipo de muchacha que, libre en el mundo, se
enfrentaría con muchas dificultades. Su belleza y simpatía y su relativamente elevada
[inteligencia], la incapacitaría para pasar frente a cualquiera como una joven normal ya
que es completamente incapaz de controlarse a sí misma, lo que le conduciría muy fácilmente al mal camino. Es un bien para la sociedad que sea cuidada como lo es”.
Segundo, los métodos de Goddard para recoger datos eran propensos a distorsión.
Envió a encuestadores a recoger genealogías de las familias de los estudiantes de su
escuela. Los encuestadores confiaban en rumores y juicios subjetivos para estimar la fortaleza de la mente de los miembros de la familia, muchos de los cuales habían fallecido
hacia tiempo.
Tercero, el método de análisis de Goddard favorecía sus conclusiones. Primero clasificó sus 327 casos en una serie de categorías: casos de herencia segura, casos de herencia probable, casos ocasionados por accidente y casos sin causa aparente. Aparentemente situó
casos en sus grupos de “herencia segura” sólo cuando tenían hermanos, antecesores recientes u otros parientes próximos clasificados también como débiles mentales. Cuando más
tarde analizó los datos para determinar si la debilidad mental era un carácter mendeliano,
Goddard analizó sólo los datos de su grupo de “herencia segura.” Teniendo en cuenta
cómo había filtrado los datos por anticipado, no es sorprendente que concluyera que la
debilidad mental era mendeliana.
Aunque la debilidad mental no se encuentra entre ellas, se sabe ahora que muchas
enfermedades genéticas se heredan como caracteres mendeliano simples. No obstante, la
esterilización eugenésica tiene pocos abogados. Una razón es que la mayoría de las
enfermedades genéticas graves son recesivas y muy raras; la esterilización de los individuos afectados tendría muy poco impacto sobre la frecuencia de nacimientos de nuevos
individuos afectados. Una segunda razón es que el pensamiento actual acerca de los derechos a la reproducción ha cambiado a favor de los derechos individuales frente a los socia-
142 PARTE II Mecanismos del cambio evolutivo
les (Paul y Spencer 1995). Una tercera razón es que, como discutiremos en la sección
siguiente, hay una creciente lista de alelos de enfermedad que se sospecha, o se sabe, que
se mantienen en la población por superioridad del heterozigoto. Sería inútil, y posiblemente desencaminado, intentar reducir la frecuencia de tales alelos evitando la reproducción de los individuos afectados.
5.4
La segunda en la lista de las
condiciones del equilibrio de
Hardy-Weinberg fue que no
hubiera mutación. Exploramos
ahora qué les sucede a las
frecuencias alélicas cuando no
se cumple esta condición.
Mutación
La última de las tres preguntas planteadas al principio del capítulo fue cómo un alelo altamente deletéreo, como el que causa la fibrosis quística, puede permanecer en frecuencias
relativamente altas en la población. Nuestras consideraciones sobre la superioridad de los
heterozigotos en secciones anteriores sugieren una posible respuesta. Otra posible respuesta
es que en las poblaciones están apareciendo constantemente por mutación nuevos alelos
para enfermedades. Antes de poder evaluar las virtudes de estas dos hipótesis para explicar la persistencia de cualesquiera de los alelos para la enfermedad, necesitamos discutir
con mayor detalle la mutación.
En el Capítulo 4 presentamos la mutación como el origen de todos los nuevos alelos
y genes. En su calidad de fuente última de toda la variación genética, la mutación proporciona la materia prima para la evolución. Consideraremos aquí la importancia de la
mutación como mecanismo evolutivo. ¿En qué medida la mutación es efectiva para cambiar las frecuencias alélicas con el tiempo? ¿De qué manera afecta la mutación a las conclusiones del análisis de Hardy-Weinberg?
Añadiendo la mutación al análisis de Hardy-Weinberg:
La mutación como mecanismo evolutivo.
Por si misma, la mutación no es en general un mecanismo evolutivo potente. Para ver
el porqué, volvamos a nuestro modelo de la población de ratones. Imaginemos un
locus con dos alelos, A y a, con frecuencias iniciales de 0,9 y 0,1. A es el alelo de tipo
silvestre y a es una mutación recesiva de pérdida de función. Además, imaginemos que
las copias de A se convierten por mutación en copias nuevas de a, a un ritmo de 1 copia
cada 10.000 por generación. Ésta es una tasa de mutación muy elevada, pero se encuentra dentro del rango de tasas de mutación conocidas (véase la Tabla 4.2 en el Capítulo
4). Las mutaciones retrógradas, que restauran la función, son mucho menos frecuentes
que las mutaciones directas de pérdida de función, por lo que ignoraremos las mutaciones que convierten las copias de a en nuevas copias de A. Finalmente imaginemos
que todas las mutaciones ocurren cuando los gametos se encuentran en el conjunto de
genes.
La Figura 5.22 sigue las frecuencias genotípicas y alélicas desde los adultos de una generación a través del conjunto de genes hasta los zigotos de la generación siguiente. Los
genotipos de los adultos se encuentran en las proporciones de Hardy-Weinberg:
AA
0,81
Aa
0,18
aa
0,01
Cuando los adultos producen gametos, las frecuencias alélicas en el conjunto de genes son
las siguientes:
A
a
0,9
0,1
Ahora, una de cada diez mil copias del alelo A se convierte en una nueva copia del alelo
a. La nueva frecuencia de A se obtiene a partir de la frecuencia anterior menos la fracción
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 143
Frecuencias genotípicas iniciales
AA Aa
aa
0,81 0,18 0,01
Frecuencias alélicas iniciales
A
0,9
Frecuencias genotípicas finales
AA
0,80984
Aa
0,18014
aa
0,01002
Frecuencias alélicas finales
A
0,89991
a
0,1
La mutación convierte
a copias de A en copias
nuevas de a, a un ritmo
de 1 cada 10.000
a
0,10009
Figura 5.22 La mutación es una fuerza
evolutiva débil En nuestra población ideal, en
una sola generación la mutación prácticamente
no da lugar a cambios en las frecuencias alélicas y
genotípicas.
que se pierde por mutación; la nueva frecuencia de a resulta de la frecuencia anterior más
la fracción que se gana por mutación. Es decir,
A
0,9 – (0,0001)(0,9)
= 0,89991
a
0,1 + (0,0001)(0,9)
= 0,10009
Finalmente, cuando los gametos se combinen al azar para producir los zigotos, los genotipos de los zigotos se encontrarán en las nuevas proporciones de Hardy-Weinberg:
Aa
0,18014
aa
0,01002
Advierta que las nuevas frecuencias alélicas y genotípicas son casi idénticas a las anteriores. Como fuerza evolutiva, la mutación no tiene prácticamente efecto.
Pero no tener prácticamente efecto no es lo mismo que no tener ningún efecto.
¿Podría la mutación de A hacia a, dándose a un ritmo de 1 copia cada 10.000 en cada
generación durante muchas generaciones, dar lugar finalmente a un cambio apreciable en
las frecuencias alélicas? El gráfico de la Figura 5.23 nos proporciona la respuesta (véase el
Cuadro 5.9 para su tratamiento matemático). Después de mil generaciones, la frecuencia
del alelo A de nuestra población ideal será alrededor de 0,81. La mutación puede dar lugar
a cambios sustanciales en las frecuencias alélicas, pero lo hace muy lentamente.
Como tasa de mutación, el valor que usamos en nuestro modelo, de 1 por 10.000 por
generación, es muy alto. Para la mayoría de los genes, la mutación es un mecanismo inclusive menos eficaz en el cambio de la frecuencia alélica.
Mutación y selección
Aunque la mutación sola normalmente no puede dar lugar a cambios apreciables en las
frecuencias alélicas, esto no quiere decir que la mutación no sea importante en la evolución. En combinación con la selección, la mutación se convierte en una potente fuerza
evolutiva. Este punto se demuestra por un experimento realizado en el laboratorio de
Richard Lenski (Lenski y Traviano 1994; Elena et al. 1996). Lenski y sus colaboradores
estudiaron la evolución de una cepa de Escherichia coli incapaz de recombinar (aquí,
recombinación se refiere a conjugación e intercambio de DNA entre células). Para las
El análisis de Hardy-Weinberg
demuestra que la mutación es
una fuerza evolutiva débil.
Frecuencia de A
AA
0,80984
1,0
0,8
0,6
0,4
0,2
0,0
0 200 400 600 800 1.000
Generación
Figura 5.23 Durante períodos
muy largos de tiempo, la
mutación puede dar lugar
finalmente a cambios
apreciables en las frecuencias
alélicas.
144 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.9
Tratamiento matemático de la mutación como fuerza evolutiva
I
magine un locus con dos alelos: un alelo silvestre, A y
una mutación de pérdida de función recesiva a. Sea µ la
tasa de mutación de A a a. Supongamos que la tasa de
mutación retrógrada de a a A es despreciable. Si la frecuencia de A en una generación es p, entonces su frecuencia después de una generación será,
p p µp
en donde pn es la frecuencia de A en la generación n, p0 es
la frecuencia de A en la generación 0 y e es la base de los
logaritmos naturales.
El lector familiarizado con el cálculo puede derivar la
última ecuación como sigue. Primero, suponga que una
generación es una cantidad infinitesimal de tiempo, por lo
que podemos rescribir la ecuación ∆p µp como
Si la frecuencia de a es q, entonces su frecuencia en la
generación siguiente es,
dp
µp
dg
q q µp
Ahora se dividen ambos términos por p y se multiplican
por dg para obtener,
La variación de p de una generación a la siguiente es,
∆p p p
que simplificando es,
∆p µp
Después de n generaciones, la frecuencia de A es aproximadamente,
pn p0 e–µn
()
1
dp µdg
p
Finalmente integramos el lado izquierdo por la frecuencia
de p0 a pn y el lado derecho de la generación 0 a la n, y
resolvemos luego para pn.
poblaciones de Escherichia coli de esta cepa, la única fuente de variación genética es la mutación. Los investigadores iniciaron 12 poblaciones repetidas, cada una a partir de una sola
célula, en un medio mínimo con sales minerales y glucosa; un ambiente exigente para estas
bacterias. Después de permitir que cada cultivo creciese hasta unas 5 ⫻ 108 células, Lenski
y sus colegas tomaron una alícuota (con aproximadamente 5 millones de células) y la transfirieron a un medio nuevo. Estas transferencias se realizaron diariamente durante 1.500
días, unas 10.000 generaciones.
A lo largo del experimento, en ciertos momentos, los investigadores congelaron muestras de las células transferidas para su posterior análisis.Ya que Escherichia coli se conserva
congelada, pero no muere, Lenski y sus colegas pudieron extraer antecesores de las congeladas y cultivarlas en un frasco con un número equivalente de células de la población
hija. Estos experimentos permitieron al grupo medir directamente la eficacia relativa de
las poblaciones ancestral y descendiente, así como la tasa de crecimiento de cada una en
competencia.Además de monitorizar de este modo los cambios en la eficacia con el tiempo, el grupo de Lenski midió el tamaño celular.
A lo largo del estudio, tanto la eficacia como el tamaño celular aumentaron muchísimo en respuesta a la selección natural. El punto clave para nuestro objetivo es que estos
incrementos se dieron de forma escalonada (Figura 5.24). El patrón en escalera se produjo por un simple proceso: la aparición de mutaciones beneficiosas que se expandieron rápidamente por la población. Cada una de las nuevas mutaciones permitían a las bacterias que
las portaban dividirse a un ritmo más rápido. La frecuencia de los mutantes aumentó rápidamente ya que se reproducían más rápido que los otros miembros de la población.
Finalmente, cada nueva mutación quedó fijada en la población. El período desde la aparición de cada mutación hasta su fijación en la población fue tan breve que no se puede
representar en la figura. Muchas de las mutaciones beneficiosas dieron lugar a un aumen-
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 145
0,70
Tamaño celular (fl)
0,65
0,60
0,55
0,50
0,45
Figura 5.24 Cambios con el tiempo del tamaño celular en
poblaciones experimentales de Escherichia coli Cada punto representa
0,40
0,35
0,30
0
500
1500
2000
1000
Tiempo (generaciones)
2500
3000
el tamaño celular promedio de las 12 poblaciones repetidas. Las líneas
verticales son barras de error; el 95% de las observaciones caen dentro del
rango indicado por las barras. Reimpreso con permiso de Elena et al. (1996).
Copyright © 1996, American Association for the Advancement of Science.
to del tamaño celular.Así, la representación del tamaño celular respecto del tiempo también muestra saltos bruscos. Entre la aparición de una mutación beneficiosa y la siguiente, se mantuvieron las 12 réplicas de la población. El porqué células más grandes eran beneficiosas en el medio pobre en nutrientes del laboratorio es un objetivo de investigación
inmediato (Mongold y Lenski, 1996; Lenski et al. 1998).
Los experimentos de Lenski y sus colegas apoyan uno de los mensajes del Capítulo 4.
Sin mutación, la evolución llegaría finalmente a un callejón sin salida. La mutación es la
última fuente de variación genética.
Investigaciones con bacterias
ilustran que aunque la
mutación sólo es una fuerza
evolutiva débil, no obstante
suministra la materia prima
sobre la que actúa la selección
natural.
Equilibrio mutación-selección
A diferencia de la minoría de las mutaciones que dan lugar a un aumento del tamaño celular y a una mayor eficacia en las poblaciones de Escherichia coli de Lenski et al., la mayoría
de las mutaciones son deletéreas. La selección actúa eliminando a tales mutaciones de las
poblaciones. Sin embargo, los alelos deletéreos perduran porque se están originando de
nuevo continuamente. Cuando la tasa a la que las copias de un alelo deletéreo está siendo eliminada por selección es exactamente igual a la tasa de aparición de nuevos alelos por
mutación, la frecuencia del alelo se encontrará en equilibrio. La situación se denomina
equilibrio mutación-selección.
¿Cuál es la frecuencia en el equilibrio de un alelo deletéreo? Si el alelo es recesivo, su
^ será
frecuencia de equilibrio, q,
µ
q^ ⫽ s
冪莦
en donde µ es la tasa de mutación y s el coeficiente de selección, un número entre 0 y 1
que expresa la fuerza de la selección contra el alelo (véase el Cuadro 5.10 para su deducción). Esta ecuación capta con economía lo que la intuición nos dice acerca del equilibrio
mutación-selección. Si el coeficiente de selección es pequeño (el alelo sólo es suavemente deletéreo) y la tasa de mutación es elevada, entonces la frecuencia del alelo en el equilibrio será relativamente elevada. Si el coeficiente de selección es grande (el alelo es muy
deletéreo) y la tasa de mutación baja, entonces la frecuencia del alelo en el equilibrio será
baja.
La investigación de Brunhilde Wirth y sus colegas (1997) en pacientes con atrofia muscular espinosa proporciona un ejemplo. La atrofia muscular espinosa es una enfermedad
neurodegenerativa que se caracteriza por la debilidad y desgaste de los músculos que controlan los movimientos voluntarios. Se produce por deleciones en un locus del cromosoma 5 llamado el gen de la supervivencia telomérica de la neurona motora (telSMN). En
algunos casos la enfermedad puede agravarse por otras mutaciones en un gen cercano. La
Al mismo tiempo que la
selección elimina alelos
deletéreos de una población, la
mutación suministra
constantemente nuevas
copias. En algunos casos, este
equilibrio entre la mutación y
la selección puede explicar la
persistencia de alelos
deletéreos en las poblaciones.
146 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.10
Frecuencias alélicas en el equilibrio mutación-selección
A
quí deduciremos las ecuaciones para predecir las frecuencias de equilibrio de alelos deletéreos en el equilibrio mutación-selección. Imaginemos un locus con dos
alelos, A1 y A2, con frecuencias p y q. A1 es el tipo silvestre y A2 es el deletéreo. Sea µ la tasa a la que las copias de
A1 se convierten en A2 por mutación. Supongamos que la
tasa de mutación retrógrada es despreciable.
La selección eliminará continuamente copias de A2 de
la población, mientras que la mutación dará lugar continuamente a nuevas copias. Deseamos calcular la frecuencia
de A2 cuando estos dos procesos se compensan mutuamente. Siguiendo a Felsenstein (1997), realizaremos nuestros cálculos de un modo circular. Desarrollaremos una
ecuación en función de p que describa el equilibrio mutación-selección para el alelo A1. Luego resolveremos la
ecuación para q a fin de obtener la frecuencia en el equilibrio de A2. Esta aproximación puede parecer contradictoria, pero simplifica enormemente el cálculo.
Equilibrio mutación-selección para un alelo
recesivo deletéreo
Imagine que A2 es un alelo recesivo deletéreo, de tal
manera que la eficacia de los genotipos viene dada por
w11
1
w12
1
w22
1⫺s
en donde el coeficiente de selección s indica la fuerza de
la selección contra A2.
En primer lugar escribiremos la ecuación para p*, la frecuencia del alelo A1 después de haber actuado la selección,
pero antes de que ocurra la mutación. Del Cuadro 5.3,
sabemos que esta ecuación es
p2w11 pqw12
p* ⫽ 2
p w11 2pqw12 q2w22
Sustituyendo la eficacia en la tabla anterior y q por (1 – p)
y simplificando, obtendremos,
p
p* ⫽ 1 s (1 p)2
A continuación escribiremos una ecuación para p , la
frecuencia del alelo A1 después de que ocurra la mutación.
La mutación convierte una fracción µ de las copias de A1
en copias de A2, dejando una fracción (1 - µ).Así,
(1 – µ)p
p (1 – µ)p* 1 s ( 1 p)2
Finalmente, cuando la mutación y la selección están en
equilibrio, p es igual a p, la frecuencia del alelo A1 que iniciamos con:
(1 – µ)p
p
1 s ( 1 p)2
Esto se puede simplificar a
µ
(1 p)2 s
Sustituyendo (1 – p) por q y despejando q obtendremos
^ la frecuencia en el equilibrio del alelo
una ecuación para q,
A2 en el equilibrio mutación-selección.
q^ 冪莦
s
µ
Si A2 es un letal recesivo, entonces s = 1, y la frecuencia en el equilibrio de A2 es igual a la raíz cuadrada de la
tasa de mutación.
Equilibrio mutación-selección para un alelo
letal dominante
Imaginemos que A2 es un alelo letal dominante, de tal
manera que la eficacia de los genotipos viene dada por
w11
1
w12
0
w22
0
La expresión para p* se simplifica hasta
p* = 1
lo que tiene sentido porque, por definición, la selección
elimina a todas las copias del alelo letal dominante A2 de
la población.Ahora la expresión para p es
p =1µ
y la condición de equilibrio es
1µp
Sustituyendo p por (1 q) y simplificando, tendremos:
q^ µ
En otras palabras, la frecuencia en el equilibrio de A2 es
igual a la tasa de mutación.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 147
atrofia muscular espinosa es, después de la fibrosis quística, la segunda enfermedad autosómica recesiva letal más común en la raza blanca (McKusick et al. 1999).
En conjunto, los alelos de pérdida de función del telSMN tienen una frecuencia alrededor de 0,01 en poblaciones blancas.Wirth y sus colegas estiman que el coeficiente de
selección es alrededor de 0,9. Con tan fuerte selección en contra, esperaríamos que los
alelos que causan la enfermedad desaparecieran de la población lenta, pero inexorablemente. Entonces, ¿por qué persisten a una frecuencia del 1 por 100?
Una posibilidad es que los alelos para la enfermedad se estén manteniendo en la
población por el equilibrio entre la mutación y la selección. Si sustituimos la frecuencia alélica y el coeficiente de selección por q^ y s en la ecuación de la página 145 y
despejamos µ, encontramos que este escenario requiere de una tasa de mutación de
0,9 ⫻ 10–4 mutaciones del alelo telSMN por generación.Wirth et al. analizaron los cromosomas de 340 individuos con atrofia muscular espinosa y los cromosomas de sus
padres y de otros miembros de la familia. Encontraron que 7 de los 340 individuos afectados llevaban una mutación nueva que no se encontraba en ninguno de sus padres. Este
dato permitió a los científicos estimar directamente la tasa de mutación del locus
telSMN (véase el Cuadro 5.11). Su estima fue de 1,1 ⫻ 10–4. Esta medida directa de la
tasa de mutación está bastante de acuerdo con la tasa pronosticada de acuerdo con la
hipótesis del equilibrio mutación-selección.Wirth et al. concluyeron que el equilibrio
mutación-selección proporciona una explicación suficiente de la persistencia de los alelos para la atrofia muscular espinosa.
Los alelos que dan lugar a la fibrosis quística, ¿se mantienen
por el equilibrio entre la mutación y la selección?
La fibrosis quística está ocasionada por mutaciones recesivas de pérdida de función en un
locus del cromosoma 7, que codifica a una proteína llamada el regulador de la conductancia transmembrana de la fibrosis quística (CFTR). La CFTR es una proteína de la
superficie celular que se expresa en el mucus de la membrana que tapiza los intestinos y
pulmones. Gerald Pier y sus colegas (1997) demostraron que una de las funciones clave
de la CFTR es capacitar a las células de la superficie pulmonar a ingerir y destruir a la bacteria Pseudomonas aeruginosa. Estas bacterias dan lugar a infecciones pulmonares crónicas
en individuos con fibrosis quística, lo que finalmente provoca graves daños en el pulmón
(Figura 5.25). La selección en contra de los alelos que dan lugar a la fibrosis quística parece que es muy fuerte. Hasta hace poco, muy pocos individuos afectados sobrevivían hasta
la pubertad; aquellos que sobrevivían eran a menudo estériles. No obstante, los alelos que
Figura 5.25 Un pulmón normal
(izquierda) comparado con un pulmón
asolado por infecciones bacterianas
que acompañan a la fibrosis quística
(derecha) (Fotos por G. Allan Johnson,
Duke University Medical Center; Scientific
American Junio de 1999, pág. 34).
148 PARTE II Mecanismos del cambio evolutivo
CUADRO 5.11
Estimas de las tasas de mutación para alelos recesivos
P
resentamos aquí el método utilizado por Brunhilde
Wirth y sus colegas (1997) para estimar las tasas de
mutación de alelos recesivos. La información clave requerida es la fracción de individuos afectados que llevan un
alelo mutante de nuevo cuño. Con técnicas moleculares
actuales, se puede averiguar esta fracción examinando
directamente los cromosomas de los individuos afectados
y de sus parientes.
Sea q la frecuencia del alelo recesivo a de pérdida de
función. Ignorando los individuos extremadamente raros
con dos copias mutantes nuevas, hay dos modos de nacer
con el genotipo aa:
1. Un individuo puede ser hijo de dos portadores. La probabilidad de que esto ocurra en un nacimiento dado es
el producto de: (a) la probabilidad de que un descendiente de dos portadores sea afectado; (b) la probabilidad de que la madre sea portadora; y (c) la probabilidad
de que el padre sea portador. Esta probabilidad viene
dada por
冤冥
1
[2q(1 q)] [2q(1 q)]
4
2. Un individuo puede ser el descendiente de un portador y de un padre homozigoto dominante y puede
recibir un alelo a del padre portador y una copia
mutante nueva del padre no portador. La probabilidad
de este suceso para un nacimiento dado es el producto
de (a) la probabilidad de que un descendiente de un
portador reciba el alelo mutante de éste; (b) la probabilidad de que la madre sea portadora; (c) la probabilidad de que el padre sea homozigoto dominante; y (d)
la tasa de mutación más la misma probabilidad para la
situación contraria, en la que el padre es portador y la
madre homozigota dominante:
冦冤 冥
冧
1
[2q(1 q)] [(1 q)2] [µ]
2
1
[2q(1 q)] [(1 q)2] [µ ]
2
冦冤 冥
冧
[2q(1 q)] [(1 q)2] [µ ]
Con estas probabilidades, podemos escribir una expresión para r, la fracción de individuos afectados que llevan
un alelo mutante nuevo. Ésta es la probabilidad segunda
dividida por la suma de la probabilidad segunda y de la primera. Simplificando un poco, tendremos:
r
2q(1 q)(1 q)2µ
2q(1 q)(1 q)2µ q(1 q)q (1 q)
simplificando un poco más, tendremos:
2(1 q)µ
r 2(1 q)µ q
Finalmente, asumimos que q es pequeño, por lo que (1 q)
es aproximadamente igual a 1. Esto nos da
2µ
r 2µ q
despejando µ tendremos:
rg
µ 2 2r
La tasa de mutación para la atrofia muscular
espinosa
En poblaciones de raza blanca, la atrofia muscular espinosa afecta a un bebé cada 10.000, lo que implica que la frecuencia del alelo mutante es
苶00
苶01
苶 0,01
q 兹0,
Wirth y sus colegas examinaron los cromosomas de 340
pacientes afectados y a miembros de sus familias. Los investigadores descubrieron que 7 de sus pacientes tenían un
nuevo alelo mutante que no se encontraba en sus padres.
Por ello,
7
r 0,021
340
Sustituyendo estos valores de q y de r en la ecuación para
µ obtenemos la estima
(0,021)(0,01)
µ 0,00011
2 2(0,021)
La tasa de mutación para la fibrosis quística
En poblaciones de raza blanca, la fibrosis quística afecta a
1 bebé cada 2.500.Wirth y sus colegas citan datos de otros
autores para establecer que sólo 2 de unos 30.000 pacientes con fibrosis quística estudiados demostraron tener un
alelo mutante nuevo no presente en ninguno de sus padres.
Estos números dan una estima de una tasa de mutación de
µ = 6,7 10–7
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 149
Número de bacterias infiltradas por gramo
de intestino de ratón (escala logarítmica)
dan lugar a la fibrosis quística tienen una frecuencia conjunta aproximadamente de 0,02
entre personas con antecedentes europeos.
Los alelos de la fibrosis quística, ¿podrían mantenerse en una frecuencia de 0,02 por
el equilibrio mutación-selección? Si asumimos un coeficiente de selección de 1 y utilizamos la ecuación deducida en el cuadro 5.10, la tasa de mutación para dar lugar a
nuevos alelos debería ser de 4 ⫻ 10–4. La tasa real de mutación de alelos de la fibrosis
quística parece ser considerablemente menor: aproximadamente 6,7 ⫻ 10–7 (véase el
Cuadro 5.11). Podemos concluir que el suministro estable por nuevas mutaciones no
puede, por si mismo, explicar el mantenimiento de los alelos de la fibrosis quística en una
frecuencia del 0,02.
Nuestra discusión sobre la superioridad de los heterozigotos sugiere una explicación
alternativa (Figura 5.16 y Cuadro 5.8). Quizá el coste en eficacia que sufren los alelos de
la fibrosis quística cuando se encuentran en homozigosis viene equilibrado por la ventaja en eficacia que tienen cuando se encuentran en heterozigosis.
Gerald Pier y sus colegas (1998) hipotetizaron que los heterozigotos para la fibrosis quística podrían ser más resistentes a fiebres tifoideas y por ello tener una mayor eficacia. Las
fiebres tifoideas las produce la bacteria Salmonella typhi. La bacteria inicia la infección cruzando la capa de células epiteliales que tapizan el tubo digestivo. Pier y sus colegas sugirieron que la bacteria Salmonella typhi se infiltra en el tubo digestivo utilizando la proteína CFTR como punto de entrada. Si esto es así, los heterozigotos, que tienen menos copias
de la CFTR en la superficie de sus células, deberían ser menos vulnerables a la invasión.
Pier y sus colegas comprobaron su hipótesis construyendo células de ratón con tres
genotipos CFTR diferentes: células homozigóticas de tipo silvestre; heterozigóticas, con un
alelo funcional para la CFTR, siendo el otro alelo el mutante para la fibrosis quística más
común en la especie humana, llamado ∆F508, que consiste en la deleción de un par de
bases; y células homozigóticas para el ∆F508. Los investigadores expusieron estas células a
Salmonella typhi y luego midieron el número de bacterias que habían entrado en cada tipo
de célula. Los resultados fueron espectaculares (Figura 5.26). Como los investigadores
habían pronosticado, las células homozigóticas para el ∆F508 fueron casi totalmente resistentes a la invasión por Salmonella typhi, mientras que las células homozigóticas de tipo silvestre fueron altamente vulnerables. Las células heterozigóticas fueron parcialmente resistentes; acumularon un 86% menos de bacterias que las células de tipo silvestre. Estos
resultados están de acuerdo con la hipótesis de que los alelos mutantes para la fibrosis quística se mantienen en las poblaciones humanas debido a que los heterozigotos tienen una
mayor eficacia en epidemias de fiebre tifoidea. La investigación de Pier et al. sirve como otro
ejemplo en el que un análisis evolutivo es provechoso en la investigación biomédica.
6
En otros casos, la frecuencia
de un alelo deletéreo puede ser
demasiado elevada como para
explicarla por el equilibrio
mutación-selección. Esto
puede ser una pista de que el
heterozigoto tiene una eficacia
superior.
569.000
77.500
5
4
3
2
1
1,3
0
Tipo silvestre Hetero(+/+)
zigotos
(+/∆F508)
Homozigotos
mutantes
(∆F508/∆F508)
Genotipo CFTR del ratón
Figura 5.26 Células cultivadas de ratón, heterozigóticas para la fibrosis quística,
muestran una gran resistencia a la infiltración de bacterias que dan lugar a la fiebre
tifoidea Las células homozigóticas para el alelo más corriente de la enfermedad humana
son casi totalmente resistentes. De Pier et al. (1998). Reimpreso con el permiso de Nature
393:79-82. © 1998, Macmillan Magazines Ltd.
150 PARTE II Mecanismos del cambio evolutivo
Resumen
La genética de poblaciones es una síntesis de la genética
mendeliana y de la evolución darwiniana, y trata de los
mecanismos que dan lugar a que las frecuencias alélicas
cambien de generación en generación. El equilibrio de
Hardy-Weinberg es un modelo nulo que proporciona el
marco conceptual para la genética de poblaciones. Demuestra que, bajo suposiciones simples (ausencia de selección, de
mutación, de migración, de deriva genética y con apareamiento al azar) las frecuencias alélicas no cambian.Además,
las frecuencias genotípicas se pueden calcular a partir de las
frecuencias alélicas.
Cuando alguna de las cuatro primeras suposiciones no
se cumple, las frecuencias alélicas pueden cambiar con las
generaciones. Por ello, la selección, la mutación, la migración y la deriva genética2 son cuatro mecanismos evolutivos. El apareamiento no aleatorio no da lugar a que las frecuencias alélicas varíen y por ello no es un mecanismo
evolutivo. Sin embargo, se pueden alterar las frecuencias
genotípicas y por consiguiente afectar al curso de la evolución.
Los genéticos de poblaciones pueden estimar las frecuencias alélicas y genotípicas en las poblaciones reales. Por
ello, los biólogos pueden comprobar si las frecuencias alélicas son estables a lo largo de las generaciones y si las frecuencias genotípicas están de acuerdo con lo esperado por
Hardy-Weinberg. Si no se cumple alguna de las conclusiones del análisis de Hardy-Weinberg, ello significa que no se
mantiene una o más de las condiciones. La naturaleza de la
desviación respecto de lo esperado por Hardy-Weinberg
no indica, por sí misma, el fallo de las condiciones. Sin
embargo, a menudo podemos deducir qué mecanismo evolutivo está actuando basándonos en otras características de la
población en estudio.
La selección se da cuando individuos con genotipos diferentes difieren en su éxito en transmitir copias de sus genes
a las generaciones futuras. Es una poderosa fuerza evolutiva.
La selección puede dar lugar a cambios en las frecuencias alélicas de una generación a la siguiente y puede desplazar a las
frecuencias genotípicas lejos del equilibrio de Hardy-Weinberg. Algunos patrones de selección tienden a conducir a
algunos alelos hacia su fijación y a otros a su eliminación;
otros tipos de selección sirven para mantener la diversidad
alélica en las poblaciones.
La mutación por si sola es una fuerza evolutiva débil. Sin
embargo, la mutación proporciona la variación genética que
es la materia prima de la evolución. En algunos casos la aparición constante de nuevos alelos mutantes puede equilibrarse por la selección en contra de esos mismos alelos, y por
consiguiente actuar manteniendo a las frecuencias alélicas en
equilibrio.
Preguntas
1. El color negro en los caballos está gobernado principalmente por un alelo recesivo del locus A. Los caballos AA y Aa no
son de color negro, como el bayo, mientras que los caballos
aa son totalmente negros. (Otros loci pueden anular el efecto del locus A, pero ignoraremos esta complicación.) Hace
algunos años, un lector del grupo de noticias de Internet
“rec.equestrian” preguntó por qué hay relativamente pocos
caballos negros de raza árabe. Una respuesta fue:“Negro es un
color raro, porque es recesivo. La mayoría de los caballos árabes son bayos o grises debido a que son colores dominantes.”
¿Qué es lo incorrecto en esta explicación? (Suponga que los
alelos A y a están en equilibrio de Hardy-Weinberg, lo que
probablemente era cierto en el momento de la discusión.) En
general, ¿qué es lo que el modelo de Hardy-Weinberg nos
muestra acerca del impacto de la dominancia o de la recesividad de un alelo sobre su frecuencia? ¿Llegaría a ser un alelo
más corriente (o menos corriente) simplemente porque es
dominante (o recesivo)?
2. En los humanos, el locus COL1A1 codifica para una cierta
proteína colágena que se encuentra en los huesos. El alelo
normal de este locus se indica por S. Un alelo recesivo s está
relacionado con la reducción en la densidad ósea y el mayor
riesgo de fractura en mujeres tanto Ss como ss. Un estudio
reciente en 1778 mujeres ha demostrado que 1194 eran SS,
526 Ss y 58 ss (Uitterlinden et al. 1998).
En esta población, ¿se encuentran en equilibrio de HardyWeinberg estos dos alelos? ¿Cómo puede averiguarlo? ¿Qué
información necesitaría para averiguar si los alelos estarán en
equilibrio de Hardy-Weinberg en la generación siguiente?
3. Utilizamos la Figura 5.11 como ejemplo de cómo la frecuencia de un alelo (AdhS en las moscas de la fruta) no cam-
2
Nota del traductor. La deriva genética cambia las frecuencias alélicas en una población, hasta llegar a la fijación o a la pérdida de un alelo dado, pero NO
cambia las frecuencias alélicas en el conjunto de las poblaciones, sólo las frecuencias genotípicas.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 151
bia en poblaciones (control) no seleccionadas, pero sí que lo
hace en respuesta a la selección. Sin embargo, mire de nuevo
las líneas de control no seleccionadas de la Figura 5.11. La frecuencia del alelo AdhS en las dos poblaciones control cambia
un poco, subiendo y bajando con el tiempo. ¿Cuál de las
condiciones del modelo de Hardy-Weinberg no se está cumpliendo con más probabilidad? Si este experimento se repitiera, ¿qué cambios en el diseño experimental reducirían esta
desviación del equilibrio de Hardy-Weinberg?
4. La mayoría de las poblaciones animales tienen una proporción
de machos y hembras de 50:50. Esto no tiene por qué ser así;
es teóricamente posible para los padres producir preferentemente descendencia masculina o predominantemente femenina. Imagine una población monógama, con una proporción
de sexos desplazada hacia los machos, por ejemplo, 70% de
macho y 30% de hembras. ¿Qué sexo tendrá mas facilidad en
encontrar una pareja? En consecuencia, ¿qué sexo tendrá probablemente una eficacia media superior? ¿Qué padres tendrán
una mayor eficacia, aquellos que produzcan más machos o
aquellos que produzcan más hembras? Imagine ahora la misma
población con una proporción sexual desplazada hacia las
hembras y conteste a las mismas preguntas. ¿Qué tipo de selección está manteniendo probablemente la proporción sexual
50:50 que se observa en la mayoría de las poblaciones?
5. Discuta de qué manera puede afectar a la frecuencia de los
alelos que dan lugar a la fibrosis quística (FQ) las siguientes
novedades recientes.
a. Muchas mujeres con FQ sobreviven ahora lo bastante
como para tener hijos. (La FQ causa problemas con los
conductos de la reproducción, sin embargo muchas mujeres con FQ pueden parir hijos. Los varones con FQ son,
normalmente, estériles.)
b. En las naciones desarrolladas la fiebre tifoidea ha disminuido a niveles muy bajos desde 1900.
c. En algunas poblaciones, las parejas que planifican tener
hijos son analizadas de manera rutinaria para los alelos
más frecuentes de la FQ.
d. En algunas naciones desarrolladas ha aparecido recientemente fiebre tifoidea resistente a los antibióticos.
6. Considere lo que hace a un nuevo alelo dominante o recesivo. Para guiarle, imagine una enzima que cambia la sustancia
A a la sustancia B. Si B es un nutriente que es necesario sólo
en cantidades mínimas, la mutación de pérdida de función
¿será dominante o recesiva? Si A es una toxina que debe ser
completamente degradada, una mutación de pérdida de función ¿será dominante o recesiva? ¿Qué pasa con nuevos alelos mutantes que dan lugar a una forma de la proteína que
puede catalizar una reacción totalmente nueva (por ejemplo,
de A a una nueva sustancia C)? ¿Puede pensar en otros ejemplos de función proteica que condicionen si un nuevo alelo
es dominante o recesivo?
7. Hay dos alelos frecuentes de la enzima muscular humana
ACE (enzima que convierte a la angiostensina): un alelo
más corto, “D”, y un alelo más largo, “I”, que tiene una
inserción de 287 pares de bases. La ACE codificada por el
alelo I tiene menos actividad, pero está también asociado a
un rendimiento muscular superior después del entrenamiento físico. Un estudio (Williams et al. 2000) de 35 varones II y 23 DD encontró que aunque no diferían en
eficacia muscular antes del entrenamiento, los homozigotos
II tenían después de 11 semanas de ejercicios aeróbicos un
8% más de eficacia muscular. El alelo I está también asociado a una mayor resistencia y crecimiento muscular después de un vigoroso entrenamiento. Especule por qué el
alelo D permanece todavía en las poblaciones humanas
con frecuencias relativamente elevadas. ¿Cómo podría
comprobar sus ideas?
8. En nuestra discusión sobre el síndrome de Jaeken, en la Sección 5.2, afirmamos que los padres que son ambos portadores del alelo R141H pueden esperar una distribución diferente de fenotipos entre sus hijos que los padres que son
portadores de dos alelos mutantes diferentes. Explique el porqué de esta afirmación. ¿Qué genotipos y fenotipos, y en qué
proporciones, esperaríamos de las siguientes parejas entre sus
hijos nacidos vivos? ¿Qué le diría a esos padres si fuera un
consejero genético?
Genotipo de la madre: +/R141H; Genotipo del padre:
+/R141H
Genotipo de la madre: +/R141H; Genotipo del padre:
+/Otros
Genotipo de la madre: +/Otros; Genotipo del padre: +/Otros
Explorando la bibliografía
9. En el ejemplo de los peces comedores de escamas, vimos que
la selección dependiente de frecuencias tiende a mantener
una proporción igual de peces zurdos y de peces diestros.Vea
las siguientes referencias para algunos casos interesantes de
posible selección dependiente de frecuencias en otras especies. ¿En qué medida encuentra lógico cada escenario?
Raymond, M., D. Pontier,A. B. Dufour, and A. P. Møller. 1996.
Frequency-dependent maintenance of left-handedness in
humans. Proceedings of the Royal Society of London, Series B
263: 1627-1633.
Sinervo, B., and C. M. Lively. 1996. The rock-paper-scissors
game and the evolution of alternative male strategies. Nature 380: 240-243.
Smithson, A., and M. R. MacNair. 1996. Frequencydependent selection by pollinators: Mechanisms and consequences with regard to behaviour of bumblebees Bombus
152 PARTE II Mecanismos del cambio evolutivo
terrestris (L.) (Hymenoptera: Apidae). Journal of Evolutionary
Biology 9: 571-588.
10. La versión del paisaje adaptativo presentado en los Cuadros
5.7 y 5.8, en los que el paisaje es una representación de la eficacia media en función de la frecuencia alélica, es realmente
algo diferente de la versión original del concepto que presentó Sewall Wright en 1932. Además, hay incluso una tercera interpretación frecuente de la idea del paisaje adaptativo.
Para una discusión sobre las diferencias de las tres versiones,
véase el Capítulo 9 en:
Provine, W. B. 1986. Sewall Wright and Evolutionary Biology.
Chicago: University of Chicago Press.
Para la respuesta de Sewall Wright a la historia de Provine, véase:
Wright, S. 1988. Surfaces of selective value revisited. The American Naturalist 131: 115-123.
El trabajo original de Wright de 1932 está reimpreso en el Capítulo 11 de:
Wright, S. 1986. Evolution: Selected Papers, William B. Provine, ed. Chicago: University of Chicago Press.
11. Si en su hemeroteca se encuentran los primeros volúmenes
del Journal of Heredity, lea:
Bell,Alexander Graham. 1914. How to improve the race. Journal of Heredity 5: 1-7.
Recuerde lo que la genética de poblaciones fue en su infancia; el mendelismo todavía tenía que integrarse con el
concepto de selección natural. ¿Qué era lo acertado y lo
erróneo en la visión de Bell sobre los mecanismos evolutivos? El plan de actuación propuesto por Bell, ¿habría conseguido realmente sus objetivos? ¿Por qué sí o por qué no?
Si la respuesta fuera sí, ¿se habría conseguido por las razones
que pensaba Bell?
12. Para un ejemplo en el que la selección natural fuerte dio lugar
a un cambio rápido en las frecuencias alélicas de una población silvestre, véase:
Johannesson, K., B. Johannesson, and U. Lundgren. 1995.
Strong natural selection causes microscale allozyme variation
in a marine snail. Proceedings of the National Academy of Sciences, USA 92: 2602-2606.
Bibliografía
Gran parte del material sobre genética de poblaciones de este capítulo está modelizado, después de su presentación, en los siguientes:
Crow, J. F. 1983. Genetics Notes. Minneapolis, MN: Burgess Publishing.
Felsenstein, J. 1997. Theoretical Evolutionary Genetics. Seattle,WA:ASUW Publishing,
University of Washington.
Griffiths, A. J. F., J. H. Miller, D. T. Suzuki, R. C. Lewontin, and W. M. Gelbert.
1993. An Introduction to Genetic Analysis. New York:W.H. Freeman.
Templeton,A. R. 1982.Adaptation and the integration of evolutionary forces. In
R. Milkman, ed., Perspectives on Evolution. Sunderland, MA: Sinauer, 15-31.
Aquí está la lista de todas las otras citas de este capítulo:
Castle,W. E. 1903.The laws of heredity of Galton and Mendel, and some laws governing race improvement by selection. Proceedings of the American Academy of
Arts and Sciences 39: 223-242.
Cavener, D. R., and M.T. Clegg. 1981. Multigenic response to ethanol in Drosophila melanogaster. Evolution 35: 1-10.
Dawson, P. S. 1970. Linkage and the elimination of deleterious mutant genes from
experimental populations. Genetica 41: 147-169.
Dean, M., M. Carrington, et al. 1996. Genetic restriction of HIV-1 infection and
progression to AIDS by a deletion allele of the CKR5 structural gene. Science
273: 1856-1862.
East, E. M. 1917. Hidden feeblemindedness. Journal of Heredity 8: 215-217.
Elena, S. F.,V. S. Cooper, and R. E. Lenski. 1996. Punctuated evolution caused by
selection of rare beneficial mutations. Science 272: 1802-1804.
Elias, S., M. M. Kaback, et al. 1992. Statement of The American Society of Human Genetics on cystic fibrosis carrier screening. American Journal of Human
Genetics 51: 1443-1444.
Fisher,R.A.1924.The elimination of mental defect. The Eugenics Review 16:114-116.
Foster, G. G., M. J.Whitten,T. Prout, and R. Gill. 1972. Chromosome rearrangements for the control of insect pests. Science 176: 875-880.
Goddard, H. H. 1914. Feeblemindedness: Its Causes and Consequences. New York:The
Macmillan Company.
Hardy, G. H. 1908. Mendelian proportions in a mixed population. Science 28: 49-50.
Hori, M. 1993. Frequency-dependent natural selection in the handedness of scale-eating cichlid fish. Science 260: 216-219.
Kevles, D. J. 1995. In the Name of Eugenics: Genetics and the Uses of Human Heredity.
Cambridge, MA: Harvard University Press.
Lane, H. 1992. The Mask of Benevolence: Disabling the Deaf Community. New York:
Vintage Books.
Lenski, R. E., and M.Travisano. 1994. Dynamics of adaptation and diversification:
A 10,000-generation experiment with bacterial populations. Proceedings of the
National Academy of Sciences, USA 91: 6808-6814.
Lenski, R. E., J.A. Mongold, et al. 1998. Evolution of competitive fitness in experimental populations of E. coli: What makes one genotype a better competitor than another? Antonie Van Leeuwenhoek International Journal of General and
Molecular Microbiology 73: 35-47.
Martinson, J. J., N. H. Chapman, et al. 1997. Global distribution of the CCR5
gene 32-base-pair deletion. Nature Genetics 16: 100-103.
Matthijs, G., E. Schollen, E.Van Schaftingen, J.-J. Cassiman, and J. Jaeken. 1998. Lack
of homozygotes for the most frequent disease allele in carbohydrate-deficientglycoprotein syndrome type 1A. American Journal of Human Genetics 62: 542-550.
McKusick, Victor A., et al. 1999. Spinal muscular atrophy I. Record #253300 in
Online Mendelian Inheritance in Man. Center for Medical Genetics, Johns
Hopkins University (Baltimore, MD) and National Center for Biotechnology
Information, National Library of Medicine (Bethesda, MD).World Wide Web
URL: http://www.ncbi.nlm.nih.gov/omim/
Mongold, J. A., and R. E. Lenski. 1996. Experimental rejection of a nonadaptive
explanation for increased cell size in Escherichia coli. Journal of Bacteriology 178:
5333-5334.
Mukai,T., and A. B. Burdick. 1959. Single gene heterosis associated with a second
chromosome recessive lethal in Drosophila melanogaster. Genetics 44: 211-232.
Paul, D. B., and H. G. Spencer. 1995.The hidden science of eugenics. Nature 374:
302-304.
Pier, G. B., M. Grout, and T. S. Zaidi. 1997. Cystic fibrosis transmembrane conductance regulator is an epithelial cell receptor for clearance of Pseudomonas
aeruginosa from the lung. Proceedings of the National Academy of Sciences, USA 94:
12088-12093.
Capítulo 5 Genética mendeliana en poblaciones I: selección y mutación como mecanismos evolutivos 153
Pier, G. B., M. Grout, et al. 1998. Salmonella typhi uses CFTR to enter intestinal
epithelial cells. Nature 393: 79-82.
Provine, W. B. 1971. The Origins of Theoretical Population Genetics. Chicago: The
University of Chicago Press.
Punnett, R. C. 1917. Eliminating feeblemindedness. Journal of Heredity 8: 464-465.
Reilly, P. 1991. The Surgical Solution:A History of Involuntary Sterilization in the United States. Baltimore: Johns Hopkins University Press.
Stephens, J. C., D. E. Reich, et al. 1998. Dating the origin of the CCR5-⌬32 AIDSresistance allele by the coalescence of haplotypes. American Journal of Human
Genetics 62: 1507-1515.
Uitterlinden A. G., H. Burger, et al. 1998. Relation of alleles of the collagen type
IA1 gene to bone density and the risk of osteoporotic fractures in postmenopausal women. New England Journal of Medicine 338: 1016-21.
UNAIDS. 1998.AIDS epidemic update: December 1998. (Geneva, Switzerland).
World Wide Web URL:http://www.unaids.org
United States Supreme Court. 1927. Buck v. Bell, 274 U.S. 200.
Weinberg,W. 1908. Ueber den nachweis der vererbung beim menschen. Jahreshefte
des Vereins für Vaterländische Naturkunde in Württemburg 64: 368-382. English
translation in Boyer, S. H. 1963. Papers on Human Genetics. Englewood Cliffs,
NJ: Prentice Hall.
Williams,A. G., M. P. Rayson, et al. 2000.The ACE gene and muscle performance. Nature 403: 614.
Wirth, B.,T. Schmidt, et al. 1997. De novo rearrangements found in 2% of index
patients with spinal muscular atrophy: Mutational mechanisms, parental origin, mutation rate, and implications for genetic counseling. American Journal of
Human Genetics 61: 1102-1111.
Yule, G. U. 1902. Mendel’s laws and their probable relations to intra-racial heredity. New Phytologist 1: 193-207; 222-238.
Zar, J. H. 1996. Biostatistical Analysis, 3rd ed. Upper Saddle, NJ: Prentice Hall.
CAPÍTULO
6
Genética mendeliana en poblaciones II:
migración, deriva genética
y apareamiento no aleatorio
Machos de la gallina grande de las praderas exhibiéndose para buscar pareja. (Richard Day/Daybreak Imagery)
L
A GALLINA GRANDE DE LAS PRADERAS, TYMPANUCHUS CUPIDO PINNATUS, ES
un ave de unos 900 gramos con un exuberante cortejo de apareamiento (Figura 6.1).
Cada primavera, los machos se congregan en zonas comunales de apareamiento, llamadas
“leks”, en donde demarcan pequeños territorios y avisan a las parejas. Extienden las plumas de sus colas, patean con sus patas y llenan de aire los sacos naranja brillante de sus gargantas. Cuando las aves introducen aire en los sacos hacen un ruido retumbante que es
audible en kilómetros: como el sonido que se hace cuando una persona insufla aire por la
boca de una botella grande vacía, pero mucho más ruidoso (Thomas 1998). Las hembras
visitan el “lek,” inspeccionan a los machos que se exhiben y eligen pareja.
Hace doscientos años, el estado de Illinois estaba casi totalmente cubierto por praderas
(Figura 6.2a) habitadas por millones de estas gallinas. Sin embargo, en 1837 se introdujo el
arado de acero (Thomas 1998). Con las primeras cuchillas que permitieron destrozar las
densas raíces de las plantas de pradera, el arado de acero permitió la conversión de la pradera en terrenos de cultivo.A medida que la pradera de Illinois se reducía, el ámbito de la
gallina grande de las praderas se reducía también (Figura 6.2b-d).Y a medida que el área de
distribución se redujo, su número se desplomó: de 25.000 en 1933, 2000 en 1962, 500 en
155
156 PARTE II Los mecanismos del cambio evolutivo
Figura 6.1 Una gallina grande de las praderas
Este macho ha hinchado su saco aéreo y desplegado
sus plumas como parte de su exhibición de cortejo.
(Richard Day/Daybreak Imagery)
Los esfuerzos para salvar las
poblaciones que quedaban de
la gallina grande de las
praderas, restaurando el
hábitat de pradera, parecieron
tener éxito al principio.
Sin embargo, muy pronto, los
tamaños poblacionales
reanudaron su declive.
¿Por qué?
1972 a 76 en 1990 (Westemeier et al. 1991; Bouzat et al. 1998). En 1994 quedaban menos
de 50 gallinas de las praderas en Illinois (Westemeier et al. 1998). Estas aves pertenecían a
dos poblaciones residuales, una en el condado de Marion y otra en el condado de Jasper.
Los esfuerzos por salvar a la gallina grande de las praderas comenzaron por prohibir su
caza en 1933 (Thomas 1998). En 1962 y 1967, respectivamente, los hábitats ocupados por
las poblaciones de los condados de Jasper y Marion se establecieron como santuarios y
como lugares para la restauración y gestión de las praderas (Westemeier et al. 1998). En la
Figura 6.3 se muestra el número de machos que se exhibieron en los “leks” del condado
de Jasper desde 1963 hasta 1997. Desde mediados de la década de los 60 hasta principios
de la década de los 70, el número de aves aumentó constantemente. Parecía que las medidas de conservación estaban funcionando. Sin embargo, hacia mediados de 1970, la población comenzó de nuevo a menguar. La población llegó a su punto más bajo, con cinco o
seis machos, en 1994, a pesar del hecho de que ahora había más praderas gestionadas disponibles para las aves que las que había en 1963.
¿Por qué la población de gallinas de la pradera del Condado de Jasper siguió disminuyendo desde mediados de 1960 a mediados de 1990, aun cuando la cantidad de hábitat
disponible estaba aumentando? ¿Y por qué los que gestionaban la vida salvaje invirtieron
finalmente el declive?
La respuesta a estas preguntas implica tres fenómenos presentados en el Capítulo 5, pero
no discutidos allí: la migración, la deriva genética y el apareamiento no aleatorio. Identificamos estos procesos como factores potencialmente importantes en la evolución de las
poblaciones cuando desarrollamos el equilibrio de Hardy-Weinberg. Cuando una población ideal no sufre selección, ni mutación, ni migración y es infinitamente grande, y
cuando los individuos eligen a sus parejas al azar, entonces (1) las frecuencias alélicas no
Figura 6.2 Destrucción del hábitat y contracción del rango de
la gallina grande de las praderas de Illinois El mapa (a) muestra
la extensión de la pradera en Illinois antes de la introducción del arado
de acero. Los mapas (b), (c) y (d) muestran la distribución de la gallina
grande de las praderas en 1940, 1962 y 1994. Fuentes: de la Figura 1
de Westemeier et al. (1998). Derivado de R.C. Anderson, Transactions of
the Illinois State Academy of Science 63, 214 (1970). Reimpreso con el
permiso de la Illinois State Academy of Science.
1810–1820
1940
1962
1994
Número de gallos de las praderas
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 157
200
150
100
Figura 6.3 Población de la gallina de la pradera en peligro de
extinción En este gráfico se representa el número de machos de la
50
0
1963
1970
1980
Año
1990
1997
gallina de las praderas que cada año se exhibían en lugares de
apareamiento en el Condado de Jasper, Illinois, desde 1963 a 1997.
Modificado con el permiso de Westemeier et al. (1998). Copyright ©
1998, American Association for the Advancement of Science.
cambian de una generación a la siguiente y (2) las frecuencias genotípicas se pueden calcular multiplicando las frecuencias alélicas. En el Capítulo 5 vimos lo que sucede cuando
relajamos las condiciones de ausencia de selección y de mutación. En este capítulo exploraremos lo que sucede cuando hay migración, el tamaño de la población es finito y el
apareamiento no es al azar.Volveremos luego al caso de las gallinas grandes de la pradera
de Illinois y contestaremos las cuestiones que plantea.
6.1.
Migración
La migración, en un sentido evolutivo, es el movimiento de alelos entre poblaciones. Este
uso del término migración es diferente de su significado más familiar, que se refiere al desplazamiento estacional de los individuos. Para un biólogo evolutivo, la migración implica
flujo de genes: la transferencia de alelos del conjunto de genes de una población al conjunto de genes de otra población. La migración puede estar ocasionada por cualquier causa
que desplace alelos lo bastante lejos como para ir de una población a otra. Los mecanismos de flujo génico van desde una dispersión ocasional de animales juveniles a gran distancia hasta el transporte de polen, semillas o esporas por el viento, el agua o los animales.
La tasa real de migración entre poblaciones en especies distintas varía enormemente,
dependiendo de lo móviles que sean los individuos o propágulos en los distintos estadios
del ciclo de vida.
Añadiendo la migración al análisis de Hardy-Weinberg:
la migración como fuerza evolutiva
Para investigar los efectos de la migración sobre las dos conclusiones del análisis de HardyWeinberg, consideremos un modelo de migración simple, el llamado modelo de una isla.
Imaginemos dos poblaciones, una en un continente y otra en una pequeña isla costera
(Figura 6.4). Debido a que la población de la isla es relativamente pequeña en relación con
la población continental, cualquier suceso migratorio desde la isla al continente no tendrá consecuencias en las frecuencias alélicas y genotípicas del continente. Por ello la
migración, y el flujo génico correspondiente, será efectiva sólo en una dirección, del continente a la isla. Como siempre, consideremos un locus con dos alelos A1 y A2. ¿Puede la
migración del continente a la isla desplazar las frecuencias alélicas y genotípicas de la isla
lejos del equilibrio de Hardy-Weinberg?
Para ver que la respuesta es sí, imagine que antes de la migración la frecuencia de A1
en la isla era 1,0 (es decir, A1 estaba fijado en la población de la isla; véase la Figura 6.5).
Isla
Continente
Figura 6.4 Modelo de
migración isla-continente Las
flechas del dibujo representan la
cantidad relativa de flujo génico
entre las poblaciones insulares y
continentales. Los alelos que
llegan a la isla desde el continente
representan una fracción
relativamente grande del conjunto
de genes de la isla, mientras que
los alelos que llegan al continente
desde la isla representan una
fracción relativamente muy
pequeña del conjunto de genes
continentales.
200 individuos A2A2
migran desde el continente
Número de
individuos
158 PARTE II Los mecanismos del cambio evolutivo
800
200
A1A1 A1A2 A2A2
Genotipos
Figura 6.5 La migración puede alterar las
frecuencias alélicas y genotípicas En este esquema
Frecuencias alélicas finales
A2
A1
Número de
individuos
se sigue a una imaginaria población insular de ratones
desde el conjunto de genes de una generación
(frecuencias alélicas iniciales) al conjunto de genes de la
generación siguiente (frecuencias alélicas finales). Los
gráficos de barras muestran el número de individuos de
cada genotipo de la población en un momento dado. La
migración, en forma de individuos que llegan de una
población continental, fijados para el alelo A2, aumenta la
frecuencia de dicho alelo en la población insular.
0,8
800
A1A1 A1A2 A2A2
Genotipos
0,2
Frecuencias alélicas iniciales
A1 A2
1,0
0
Cuando los gametos de un conjunto de genes en donde está fijado A1 se combinan al azar
para formar zigotos, las frecuencias genotípicas de estos zigotos serán 1,0 para A1A1, 0 para
A1A2 y 0 para A2A2. Nuestros cálculos serán más simples si damos a nuestra población
un tamaño dado, por lo que imaginemos que había 800 zigotos, que dejaremos que crezcan y se conviertan en adultos.
CUADRO 6.1
Tratamiento algebraico de la migración como fuerza evolutiva
S
ea pI la frecuencia del alelo A1 en una población de una
isla. Y pC la frecuencia del alelo A1 en la población
continental. Imagine que en cada generación un grupo de
individuos se desplaza de la población continental a la isla,
en donde constituyen la fracción m de la población de la
isla. Queremos conocer cómo cambia la frecuencia del
alelo A1 de la isla como consecuencia de la migración, y
si hay una frecuencia de equilibrio para A1 que no cambie más incluso si continúa la migración.
Primero obtendremos la expresión para pI, la frecuencia de A1 en la isla en la generación siguiente. Una fracción
(1 – m) de los individuos de la generación siguiente ya está
en la isla. En estos individuos, la frecuencia de A1 es pI. Una
fracción m de los individuos de la generación siguiente
viene del continente. En ellos la frecuencia de A1 es pC.
Así, la nueva frecuencia de A1 en la población de la isla es
el promedio ponderado de la frecuencia entre los residentes y la de los inmigrantes.
pI⬘ ⫽ (1 ⫺ m)(pI) ⫹ (m)(pC)
Podemos obtener una expresión para el ∆pI, que es el
cambio en frecuencia alélica en la isla de una generación
a la siguiente:
∆pI ⫽ pI⬘ ⫺ pI
Sustituyendo pI⬘ por nuestra expresión anterior y simplificando, tendremos:
∆pI ⫽ (1 ⫺ m)(pI) + (m)(pC) ⫺ pI ⫽ m(pC ⫺ pI)
Finalmente, podemos determinar la frecuencia en el equilibrio del alelo A1 en la isla. La condición de equilibrio es
que no cambie pI. Es decir,
∆pI ⫽ 0
si resolvemos la ecuación para ∆pI igual a cero, tendremos:
m(pC ⫺ pI) ⫽ 0
Esta expresión muestra que la frecuencia de A1 permanecerá constante en la isla si no hay migración (m = 0), o si
la frecuencia de A1 en la isla es idéntica a su frecuencia en
el continente (pC = pI). En otras palabras, sin ninguna
fuerza que se oponga, la migración igualará finalmente las
frecuencias de las poblaciones de la isla y del continente.
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 159
Supongamos ahora que en la población continental está fijado el alelo A2, y que antes
de que los individuos de la isla alcancen la madurez, migraron 200 individuos del continente a la isla. Después del proceso migratorio, el 80% de la población de la isla es nativa
y el 20% continental. Las nuevas frecuencias genotípicas serán 0,8 para A1A1, 0 para A1A2
y 0,2 para A2A2. Cuando los individuos de la isla se reproduzcan, su conjunto de genes
tendrá las frecuencias alélicas de 0,8 para A1 y 0,2 para A2.
La migración ha cambiado las frecuencias alélicas de la población de la isla, violando
la conclusión 1 de Hardy-Weinberg. Antes de la migración la frecuencia de A1 en la isla
era de 1,0; después de la migración la frecuencia de A1 es 0,8. La población de la isla ha
cambiado como consecuencia de la migración. (Para un tratamiento algebraico de la
migración, como mecanismo del cambio de las frecuencias alélicas, véase el Cuadro 6.1.)
La migración también da lugar a frecuencias genotípicas en los adultos que no están
de acuerdo con la conclusión 2 de Hardy-Weinberg. De acuerdo con el equilibrio de
Hardy-Weinberg, una población con frecuencias alélicas de 0,8 y 0,2 tendría unas frecuencias genotípicas de 0,64, 0,32 y 0,04. Comparados con estos valores esperados, la
población de la isla tiene, después de la migración, un exceso de homozigotos y un déficit de heterozigotos. Desde luego, con una sola generación de apareamiento aleatorio la
población volverá a las frecuencias genotípicas del equilibrio de Hardy-Weinberg.
La migración es una fuerza
evolutiva potente. En la
práctica, la migración es lo
más importante para evitar la
divergencia de las poblaciones.
Investigación experimental sobre la migración como mecanismo
evolutivo
Las serpientes de agua del lago Erie (Figura 6.6) proporcionan un ejemplo de migración
desde una población continental a una isla. Estas serpientes (Nerodia sipedon) viven en los
(a)
(b)
ONTARIO
Ontario
Mich
Lago
Lake Erie
Ohio
NY
Penn
Isla
Pelee
Isla
North
Bass
Isla
Middle
Bass
Isla
Middle
Isla
Rattlesnake
Isla
South
Bass
Isla
Kelleys
Figura 6.6 Serpientes de agua y los lugares en donde viven El mapa de
OHIO
(a) muestra las islas del lago Erie y las áreas continentales que las rodean, en
donde Richard King y sus colegas estudiaron la migración como fuerza evolutiva
en las serpientes de agua. Según King and Lawson (1995). Copyright © 1995
Evolution. Reimpreso con permiso. La foto de (b) muestra formas con bandas, sin
bandas e intermedias de las serpientes de agua del lago Erie (Nerodia sipedon).
(Richard B. King)
160 PARTE II Los mecanismos del cambio evolutivo
Figura 6.7 Variaciones en el patrón de color
dentro y entre poblaciones Estos histogramas
muestran la frecuencia de diferentes patrones de
color en diversas poblaciones. Categoría A,
serpientes sin bandas; categoría B y C, serpientes
intermedias; categoría D, serpientes con bandas
fuertes. Las serpientes del continente suelen
tener bandas; las serpientes de las islas suelen
no tener bandas o presentar un patrón
intermedio. De Camin and Erlich (1958).
Copyright © 1958 Evolution. Reimpreso con
permiso.
La migración de individuos
desde el continente a las islas
parece que evita la divergencia
de las serpientes de agua de
las islas del Lago Erie
respecto de las poblaciones
continentales.
100
90
80
70
60
50
40
30
20
10
N = 63
A B C D
Ontario
100
90
80
70
60
50
40
30
20
10
N = 64
A B C D
Continente
peninsular
100
90
80
70
60
50
40
30
20
10
N = 16
A B C D
Isla Kelleys
100
90
80
70
60
50
40
30
20
10
N = 214
A B C D
Complejo de
islas Bass
100
90
80
70
60
50
40
30
20
10
N = 188
A B C D
Islas Middle
y Pelee
alrededores del lago Erie y en las islas del lago. Los individuos tienen diferentes aspectos,
desde un bandeado fuerte hasta otro sin bandas. En una aproximación grosera, el patrón
de color viene determinado por un solo locus con dos alelos, siendo el alelo para bandas
dominante sobre el alelo sin bandas (King 1993a).
En el continente prácticamente todas las serpientes de agua son bandeadas, mientras que
en las islas muchas serpientes no tienen bandas (Figura 6.7). La diferencia en la composición de las poblaciones del continente respecto de las de las islas parece que es consecuencia de la selección natural promovida por los predadores. En las islas, las serpientes
toman el sol sobre rocas calizas en la orilla del agua. Siguiendo un primer trabajo de Camin
y Ehrlich (1958), Richard B. King (1993b) demostró que entre las serpientes más jóvenes, los individuos sin bandas son más crípticos sobre las rocas de las islas que los que tienen
bandas. Las serpientes más jóvenes y pequeñas son probablemente más vulnerables a los
predadores. King (1993b) utilizó estudios de marcaje y recaptura, entre otros métodos, para
demostrar que en las islas, las serpientes sin bandas tienen realmente una mayor tasa de
supervivencia que las serpientes con bandas.
Si la selección favorece a las serpientes sin bandas en las islas, entonces se esperaría que
las poblaciones isleñas estuvieran formadas sólo por serpientes sin bandas. ¿Por qué no es
así? La respuesta, al menos en parte, es que en cada generación varias serpientes con bandas se desplazan del continente a las islas. Los migrantes traen consigo alelos para el
patrón a bandas. Cuando las serpientes migrantes se cruzan con las serpientes de la isla contribuyen con copias del alelo para bandas al conjunto de genes de la isla. En este ejemplo
la migración actúa como fuerza evolutiva en oposición a la selección natural, evitando que
en las poblaciones de las islas quede fijado el alelo sin bandas. (Para un tratamiento algebraico de la influencia de las fuerzas opuestas de la selección y la migración en las serpientes de agua del lago Erie, véase el Cuadro 6.2.)
La migración como una fuerza evolutiva homogeneizadora
entre las poblaciones
La migración de las serpientes de agua, desde el continente a las islas, hace que las poblaciones de las islas sean más similares a la población continental de lo que serían de otra
manera. Éste es el efecto general de la migración: tiende a homogeneizar las frecuencias
alélicas a lo largo de las poblaciones. En las serpientes de agua, a esta homogeneización se
opone la selección natural.
¿Hasta dónde iría la homogeneización si no se opusiera la selección? El modelo algebraico desarrollado en el Cuadro 6.1 demuestra que el flujo génico desde un continente
a una isla, llevará finalmente las frecuencias alélicas de la isla a un valor exactamente igual
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 161
CUADRO 6.2 Selección y migración en las serpientes de agua del lago Erie
C
omo se describe en el texto, la genética del patrón
del color de las serpientes de agua del lago Erie
puede depender, aproximadamente, de un solo locus, con
un alelo dominante para el patrón de bandas y otro recesivo para el patrón sin bandas (King 1993a). La selección
por los predadores en las islas favorece a las serpientes sin
bandas. Si la eficacia de los individuos sin bandas la definimos como 1, entonces la eficacia relativa de las serpientes con bandas se encuentra entre 0,78 y 0,90 (King
and Lawson 1995) Entonces, ¿por qué la selección no ha
eliminado a las serpientes con bandas de las islas? Aquí
calculamos el efecto que tiene la migración cuando se
introducen en cada generación nuevos alelos para bandas
en las poblaciones de las islas.
King y Lawson (1995) agruparon a todas las serpientes
de las islas en una sola población, ya que parece que las
serpientes se mueven entre las islas mucho más frecuentemente que del continente a las islas. King y Lawson utilizaron técnicas genéticas para estimar que en cada generación
se desplaza una media de 12,8 serpientes desde el continente a las islas. Los científicos estimaron que la población
total de serpientes de las islas estaba entre 523 y 4.064 individuos, con una mejor estima de 1.262. Esto indica que los
migrantes representan una fracción entre el 0,024 y el
0,003 de la población cada generación, con una mejor
estima de 0,01.
Con las estimas de King y Lawson sobre selección y
migración, podemos calcular el equilibrio de las frecuencias alélicas en la población de las islas, en el que los efectos de la migración y la selección se compensarán exactamente uno con otro. Sea A1 el alelo dominante para el
patrón de bandas y A2 el alelo recesivo para el patrón sin
bandas. Sea p la frecuencia de A1 y q la frecuencia de A2.
De acuerdo con el Cuadro 5.3, formamos individuos con
cruzamientos al azar y luego dejamos que la selección
actúe. Después de la selección (pero antes de la migración),
la frecuencia nueva del alelo A2 es:
pqw12 ⫹ q2w22
q* ⫽ ᎏ
ᎏ
–
w
en donde w12 es la eficacia de los heterozigotos
_ A1A2, w22
es la eficacia de los homozigotos A2A2 y w es la eficacia
media de todos los individuos de la población, que viene
dada por (p2w11 ⫹ 2pqw12 ⫹ q2w22).
Para nuestro primer cálculo utilizaremos w11 = w12 =
= 0,84, y w22 = 1. Una eficacia relativa de 0,84 para las serpientes con bandas es el punto medio del rango dentro del
que King y Lawson (1995) estimaron que se encontraba el
valor real. Esto da:
pq(0,84) ⫹ q2
q* ⫽ ᎏᎏᎏᎏ
[p2(0,84) ⫹ 2pq(0,84) ⫹ q2]
Sustituyendo p por (1 – q) tendremos:
(1 ⫺ q)q(0,84) ⫹ q2
q* ⫽ ᎏᎏᎏᎏᎏ
[(1 ⫺ q)2(0,84) ⫹ 2(1 ⫺ q)q(0,84) ⫹ q2]
0,84q ⫹ 0,16q2
⫽ ᎏᎏ
0,84 ⫹ 0,16q2
Ahora permitimos migración, representando en este
primer cálculo a los nuevos migrantes por una fracción de
0,01 de la población de la isla (la mejor estima de King y
Lawson). Ninguno de los nuevos migrantes lleva el alelo
A2, por lo que la nueva frecuencia de A2 será,
0,84q ⫹ 0,16q2
q⬘ ⫽ (0,99) ᎏᎏ
0,84 ⫹ 0,16q2
La variación de q de una generación a la siguiente es,
0,84q ⫹ 0,16q2
∆q ⫽ q⬘ ⫺ q ⫽ (0,99) ᎏᎏ
⫺q
0,84 ⫹ 0,16q2
En la Figura 6.8 se representa el ∆q en función de q.
Observe primero la curva verde (b). Esta curva representa
exactamente la función que hemos calculado. Muestra que
si q es mayor de 0,05 y menor de 0,94 en una generación
dada, entonces q aumentará en la generación siguiente (el
∆q será positivo). Si q es menor que 0,05 y mayor que 0,94
en una generación dada, entonces q disminuirá en la generación siguiente (el ∆q será negativo). Los puntos donde la
curva corta al eje horizontal, donde el ∆q = 0, son puntos
de equilibrio. El punto de equilibrio superior es estable: si
q es menor a 0,94, entonces q aumentará en la generación
siguiente; si q es mayor que 0,94, entonces q disminuirá en
la generación siguiente. Así, una predicción intermedia,
dadas las estimas de King y Lawson de selección y flujo
génico, es que la frecuencia en el equilibrio del alelo sin
bandas de la población de la isla será 0,94.
La curva (a) es una estima por exceso; utiliza las eficacias de 0,78 para A1A1, 0,78 para A1A2 y 1 para A2A2, y
una tasa de migración de 0,003 (el 0,3% de la población
son migrantes cada generación). Predice un equilibrio para
q = 0,99. La curva (c) es una estima por defecto; utiliza las
eficacias de 0,90 para A1A1, 0,90 para A1A2 y 1 para
162 PARTE II Los mecanismos del cambio evolutivo
CUADRO 6.2
Continuación
A2A2, y una tasa de migración de 0,024 (el 2,4% de la
población son migrantes cada generación). Predice un
equilibrio para q = 0,64.
La mejor estima de King y Lawson de la frecuencia real
de A2 es 0,73. Dicho valor se encuentra hacia el extremo
más bajo de nuestro rango de predicción. Nuestro cálculo
es relativamente simple y omite muchos factores, incluidos
los cambios recientes en los tamaños poblacionales, tanto
de las serpientes de agua como de sus predadores, así como
cambios recientes en las frecuencias de las serpientes con
bandas respecto de las de sin bandas. Para un tratamiento
detallado de este ejemplo, véase King y Lawson (1995).
∆q
(cambio en la frecuencia de A2
desde esta generación a la siguiente)
0,04
0,03
0,02
(a) Selección fuerte, poca migración
0,01
0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
(b) Selección y migración
moderadas
-0,01
-0,02
-0,03
q
(frecuencia de A2
en esta generación)
(c) Selección débil, mucha migración
Figura 6.8 Efectos combinados de la
migración y de la selección sobre las
frecuencias alélicas de las serpientes de agua
insulares Las curvas muestran el ∆q en función
de q para combinaciones diferentes de migración y
selección. Para los detalles véase el texto.
al que hay en el continente. En otras palabras, si se permite que prosiga la migración sin
oposición de cualquier otra fuerza evolutiva, finalmente homogeneizará totalmente las frecuencias alélicas en las poblaciones.
Barbara Giles y Jérôme Goudet (1997) documentaron el efecto homogeneizador del
flujo génico en poblaciones de Silene dioica, la coronaria de bolsa roja. La coronaria de bolsa
roja es una flor silvestre perenne, polinizada por insectos (Figura 6.9a). Las poblaciones que
Giles y Goudet estudiaron se encuentran en las islas del archipiélago de Skeppsvik, en
Suecia. Estas islas son montones de materiales depositados por los glaciares en el último
período glaciar y sumergidos bajo el agua cuando el hielo se fundió. El área sobre la que
descansan las islas se está elevando a un ritmo de 0,9 centímetros por año. Como consecuencia de este levantamiento geológico, están emergiendo constantemente nuevas islas
del agua. El archipiélago de Skeppsvik tiene docenas de islas de edades diferentes.
Las semillas de la coronaria de bolsa roja son dispersadas por el viento y por el agua y
la planta es de las primeras que colonizan las nuevas islas. Las poblaciones de coronaria crecen hasta tamaños de varios miles de individuos. Entre las islas hay flujo génico como consecuencia tanto de la dispersión de las semillas como del transporte del polen por insectos.
Siglos después, las poblaciones de coronaria son invadidas por otras especies de plantas y por
una enfermedad traída por los polinizadores. El establecimiento de nuevas plantas cesa y las
poblaciones menguan a medida que los individuos mueren.
Giles y Goudet pronosticaron que las poblaciones jóvenes, al haber sido fundadas por
el transporte al azar de unas pocas semillas, variarían en las frecuencias alélicas de varios
loci. (Consideraremos el porqué con mayor detalle en la sección 6.2.) Las poblaciones con edades intermedias deberían ser más homogéneas en sus frecuencias alélicas
como consecuencia de la migración, es decir, como consecuencia del flujo génico entre
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 163
(a)
Variación en frecuencias alélicas
entre poblaciones (FST)
(b)
0,09
0,08
0,07
0,06
Poblaciones
0,05
viejas
0,04
(N = 30)
0,03
0,02
Poblaciones
0,01
intermedias
0
(N = 30)
Poblaciones
jóvenes
(N = 13)
Figura 6.9 Variación de las frecuencias alélicas en poblaciones de
la coronaria de bolsa roja, Silene dioica (a) La coronaria de bolsa roja,
una flor silvestre perenne. (b) Medida de la variación de las frecuencias
alélicas entre poblaciones, según Giles and Goudet (1997). Los puntos rojos
representan valores de FST (véase el texto); las líneas grises verticales
representan los errores típicos (errores típicos grandes indican estimas de
FST menos exactas). Hay menos variación en frecuencias alélicas entre
poblaciones con edades intermedias que entre poblaciones jóvenes
(P ⫽ 0,05). Hay más variación en frecuencias alélicas entre poblaciones
viejas que entre poblaciones intermedias (P ⫽ 0,04). Según Giles and
Goudet (1997).
poblaciones vía dispersión de semillas y transporte de polen. Finalmente, las poblaciones más viejas, estructuradas principalmente por la supervivencia fortuita de unos
pocos individuos restantes, se convertirían de nuevo en más variables en sus frecuencias
alélicas.
Los investigadores comprobaron sus predicciones recogiendo hojas de muchas plantas
en 52 islas de edades diferentes.Analizando las proteínas de las hojas, Giles y Goudet determinaron el genotipo de cada planta para seis loci enzimáticos. Dividieron sus poblaciones
por edades en tres grupos: jóvenes, intermedias y viejas. Para cada uno de estos grupos calcularon el estadístico llamado FST. Un valor de FST se refiere a un grupo de poblaciones
y refleja la variación en frecuencias alélicas entre las poblaciones del grupo. El valor de FST
varía de 0 a 1. Los valores mayores representan más variación en frecuencias alélicas entre
poblaciones.
Los resultados confirman las predicciones de Giles y Goudet (Figura 6.9b). Hay menos
variación en frecuencias alélicas entre poblaciones de edad intermedia que entre poblaciones jóvenes o poblaciones viejas. La baja diversidad en las poblaciones intermedias probablemente refleja la influencia homogeneizadora del flujo génico. La mayor diversidad
de las poblaciones jóvenes y viejas probablemente indica deriva genética, que estudiaremos en la sección siguiente.
En resumen, la migración consiste en el movimiento de alelos de una población a
otra. En una población dada, la migración puede dar lugar a cambios en las frecuencias
alélicas de una generación a la siguiente. En poblaciones pequeñas, que reciben inmigrantes de poblaciones grandes, la migración puede ser un potente mecanismo evolutivo. A lo largo de grupos de poblaciones, el flujo génico tiende a homogeneizar las
frecuencias alélicas. Por eso la migración tiende a evitar la divergencia evolutiva de las poblaciones.
6.2.
Deriva genética
En el Capítulo 2 refutamos el error de que la evolución por selección natural es un proceso
aleatorio. Es seguro que el mecanismo de la evolución de Darwin depende de la aparición de variaciones aleatorias por mutación. La variación generada por mutación es aleatoria en el sentido de que cuando la mutación sustituye un aminoácido por otro en una
proteína, lo hace sin considerar si el cambio mejorará la funcionalidad de la proteína. Pero
164 PARTE II Los mecanismos del cambio evolutivo
la selección natural en si misma no se produce al azar. Es precisamente la no aleatoriedad
de la selección al escoger las mutaciones lo que da lugar a la adaptación.
Nos encontramos ahora en una posición adecuada para volver a estudiar el papel del azar
en la evolución. Se puede argumentar que la idea más importante de la genética de poblaciones es que la selección natural no es el único mecanismo de la evolución. Entre los mecanismos no selectivos de la evolución hay uno que es absolutamente aleatorio. Dicho
mecanismo es la deriva genética. La deriva genética no da lugar a adaptación, pero da lugar
a cambios en las frecuencias alélicas1. En el modelo de Hardy-Weinberg, la deriva genética se produce como consecuencia de que el tamaño de población infinito no se cumple.
Un modelo de deriva genética
Para ver cómo actúa la deriva genética, imaginemos una población ideal, similar a las que
hemos trabajado antes, pero de tamaño finito, de hecho, de pequeño tamaño. Como siempre, nos fijamos en un solo locus con dos alelos, A1 y A2. Imaginemos que en el conjunto de genes de la generación actual, el alelo A1 tiene una frecuencia de 0,6 y el alelo
A2 de 0,4 (Figura 6.10). Dejemos que los gametos de este conjunto de genes se combinen al azar para dar lugar exactamente a 10 zigotos. Estos diez zigotos constituirán toda
la población de la siguiente generación.
Podemos simular la producción de diez zigotos de nuestro conjunto de genes mediante un modelo físico. Una bolsa con 100 alubias representa el conjunto de genes. Sesenta
de las alubias son negras y representan al alelo A1; cuarenta son blancas y representan al
alelo A2. Construiremos cada zigoto agitando la bolsa, cerrando los ojos y sacando alubias. Primero sacaremos una alubia que represente al óvulo, anotaremos su genotipo y la
devolveremos a la bolsa. Luego sacaremos otra alubia, que represente al esperma, anotaremos su genotipo y la devolveremos a la bolsa. Sacamos alubias de la bolsa y las vamos
anotando. Los genotipos de los diez zigotos son:
A2A1
A1A1
A1A1
A2A2
A1A1
A1A2
A1A1
A1A1
A2A2
A1A1
Número de
individuos
6
2
2
A1A1 A1A2 A2A2
Genotipos
Figura 6.10 Sucesos aleatorios pueden alterar las
frecuencias alélicas y genotípicas En este dibujo se sigue
1
Frecuencias alélicas finales
A1
A2
6
Número de
individuos
a una población imaginaria de diez ratones desde el conjunto
de genes de una generación (frecuencias alélicas iniciales) al
conjunto de genes de la generación siguiente (frecuencias
alélicas finales). Los gráficos de barras muestran el número de
individuos de cada genotipo de la población en un momento
dado. La deriva genética, en la forma de error de muestreo al
extraer gametos del conjunto de genes inicial para formar los
zigotos, aumenta la frecuencia del alelo A1. Advierta que
también son posibles otros muchos resultados.
0,7
2
0,3
2
A1A1 A1A2 A2A2
Genotipos
Nota del traductor. Véase la nota 2 del Capítulo 5.
Frecuencias alélicas iniciales
A1 A2
0,6
0,4
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 165
Contando los genotipos, tenemos que A1A1 tiene una frecuencia de 0,6, A1A2 una frecuencia de 0,2 y A2A2 una frecuencia de 0,2 (Figura 6.10). Contando los alelos vemos
que cuando estos zigotos crezcan y se reproduzcan, la frecuencia del alelo A1 en el nuevo
conjunto de genes será 0,7 y la frecuencia del alelo A2 será 0,3 (Figura 6.10).
Hemos completado una generación en el ciclo de vida de nuestra población modelo.
No parece que haya sucedido gran cosa, pero advierta que no se cumplen las dos conclusiones del equilibrio de Hardy-Weinberg. Las frecuencias alélicas han cambiado de una
generación a la siguiente y no podemos calcular las frecuencias genotípicas multiplicando las frecuencias alélicas. La razón de que nuestra población no haya cumplido el principio de Hardy-Weinberg es simplemente porque es pequeña.
En una población pequeña, el azar da lugar a resultados que difieren de las esperanzas
teóricas. El azar en nuestra población simulada fue la extracción de alubias de la bolsa para
formar los zigotos. Cogimos alubias negras y alubias blancas no en la proporción exacta
predicha de 0,6 y 0,4, sino en una proporción que resultó ser un poco mayor en alubias
negras y un poco menor en alubias blancas. Este tipo de discrepancias aleatorias entre lo
esperado teóricamente y los resultados reales se denominan errores de muestreo. El error
de muestreo en la formación de zigotos a partir de un conjunto de genes se denomina
deriva genética. Debido a que se trata sólo del efecto acumulativo de sucesos aleatorios,
la deriva genética no puede dar lugar a adaptación. Pero puede dar lugar, como hemos
visto, a que las frecuencias alélicas cambien. La suerte ciega es, por sí misma, un mecanismo evolutivo.
A veces es difícil ver la diferencia entre deriva genética y selección natural. En nuestro
modelo de población pequeña, las copias del alelo A1 tuvieron más éxito en pasar a la
siguiente generación que las copias del alelo A2. El éxito reproductivo diferencial es
selección, ¿o no lo es? En este caso no lo es. Si hubiera sido selección, el éxito diferencial
de los alelos de nuestra población modelo hubiera sido explicable en términos de los fenotipos que los alelos confieren a los individuos que los llevan. Los individuos con una o dos
copias del alelo A1 deberían haber sido mejores en supervivencia, en encontrar alimento
o en atraer a la pareja. Sin embargo, los individuos que llevan copias del alelo A1 no fueron
de hecho ninguna de esas cosas. Sólo tuvieron suerte; dio la casualidad de que sus alelos
se extrajeron del conjunto de genes más a menudo. La selección es éxito reproductivo diferencial que sucede por alguna razón. La deriva genética es éxito reproductivo diferencial
que simplemente sucede.
Otra forma de ver que la deriva genética es diferente de la selección es reconocer que
las frecuencias alélicas y genotípicas en nuestros diez zigotos fácilmente podrían haber
sido diferentes de lo que fueron. Para probarlo, podemos repetir el ejercicio extrayendo alubias de nuestra bolsa para formar diez zigotos. Esta vez, los genotipos de los zigotos son:
A1A1
A2A2
A1A1
A1A2
A1A1
A1A1
A2A1
A2A1
A1A2
A2A2
En este conjunto de zigotos las frecuencias genotípicas son 0,4 para A1A1, 0,4 para A1A2
y 0,2 y para A2A2. Las frecuencias alélicas son 0,6 para A1 y 0,4 para A2.
Repitiendo el ejercicio una tercera vez se producen estos zigotos:
A1A1
A1A2
A1A1
A2A1
A1A1
A2A2
A1A2
A2A2
A1A1
A2A2
Ahora las frecuencias genotípicas son 0,4 para A1A1, 0,3 para A1A2 y 0,3 y para A2A2, y
las frecuencias alélicas son 0,55 para A1 y 0,45 para A2.
En poblaciones de tamaño
finito, sucesos aleatorios
(en la forma de errores de
muestreo en la extracción de
gametos del conjunto de
genes) pueden producir
evolución.
La selección es éxito
reproductivo diferencial que
ocurre por una razón; la deriva
genética es éxito reproductivo
diferencial que sucede por azar.
166 PARTE II Los mecanismos del cambio evolutivo
La probabilidad de que la
nueva frecuencia sea
exactamente 0,6 es
aproximadamente del 18%
Figura 6.11 Rango de resultados posibles en nuestra
población modelo de diez ratones Este gráfico muestra los
resultados posibles, con su probabilidad, cuando formamos 10
zigotos extrayendo alelos de un conjunto de genes en los que los
alelos A1 y A2 tienen unas frecuencias de 0,6 y 0,4 respectivamente.
El resultado más probable es que las frecuencias alélicas no cambien.
Sin embargo, la probabilidad de que esto suceda es sólo del 18%.
Probabilidad
0,16
La probabilidad de que
la nueva frecuencia sea
mayor a 0,6 es
aproximadamente del
41,5 %
0,12
La probabilidad de que
la nueva frecuencia sea
menor a 0,6 es
aproximadamente del
40,5 %
0,08
0,04
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
Frecuencia nueva del alelo A1
Frecuencia del alelo A1
Resumimos aquí los resultados de nuestra población modelo:
En el conjunto de genes
En el primer grupo de 10 zigotos
En el segundo grupo de 10 zigotos
En el tercer grupo de 10 zigotos
1
0,8
0,6
0,4
0,2
0
Los tres conjuntos de zigotos nos demuestran que si comenzamos con un conjunto
de genes en el que el alelo A1 está a una frecuencia de 0,6 y formamos exactamente una
población de diez zigotos, la frecuencia de A1 puede aumentar, mantenerse o disminuir.
De hecho, la nueva frecuencia de A1 en un conjunto de diez zigotos extraídos de nuestro conjunto de genes puede ser cualquiera entre 0 y 1,0, aunque dentro de este rango
los resultados extremos no son probables. La gráfica de la Figura 6.11 muestra la probabilidad teórica de cada uno de los resultados posibles. En conjunto, hay alrededor de un
18% de probabilidad de que la frecuencia del alelo A1 quede en 0,6, alrededor del
40,5% de probabilidad de que caiga a un valor menor y alrededor del 41,5% de que
aumente a un valor mayor. Los lectores no deberían aceptar tal cual lo que decimos; deberían proporcionarse su propia bolsa de alubias y formar una serie de conjuntos de zigotos. Insistimos, el tema es que la deriva genética es evolución que simplemente sucede
por azar.
1
0,8
0,6
0,4
0,2
0
1
0,8
0,6
0,4
0,2
0
Frecuencia de A1
0,6
0,7
0,6
0,55
0
100
200
Número acumulado de
zigotos producidos
Figura 6.12 Simulación de
extracción de alelos de un
conjunto de genes, realizada
tres veces Al principio, las
frecuencias del alelo A1 fluctúan
considerablemente, en una
trayectoria única en cada caso.
Sin embargo, cuando el número
de zigotos formados aumenta,
la frecuencia de A1 se va
aproximando al valor esperado
de 0,6.
Deriva genética y tamaño poblacional
La deriva genética es fundamentalmente la consecuencia del tamaño finito de las poblaciones. Si extraemos alubias de nuestro saco para formar una población de más de diez
zigotos, las frecuencias alélicas en éstos se aproximarán a los valores que predice el equilibrio de Hardy-Weinberg. Extraer alubias de un saco se convierte rápidamente en aburrido, por lo que utilizaremos un ordenador para simular la extracción de gametos para
formar, no exactamente 10, sino 250 zigotos, por ejemplo (Figura 6.12a). A medida que
el ordenador extrae cada gameto, comunica la frecuencia de A1 entre los zigotos que ha
construido hasta el momento.Al principio la frecuencia alélica fluctúa mucho. Por ejemplo, el primer zigoto resultó tener el genotipo A2A2, por lo que la frecuencia del alelo A1
comenzó en cero.Varios zigotos que siguieron fueron en su mayoría A1A1 y A1A2, que
hizo que la frecuencia del alelo A1 subiera rápidamente a 0,75.A medida que se iba acumulando el número de zigotos, la frecuencia del alelo A1 en las nuevas generaciones osci-
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 167
ló cada vez menos, estabilizándose gradualmente en el valor esperado de 0,6. Las desviaciones respecto de lo esperado con un gran número de zigotos fueron aleatorias, como se
observa en los gráficos de la Figura 6.12b y c. Estos gráficos muestran dos series más de
extracciones para formar 250 zigotos. En cada una, la frecuencia alélica de la nueva generación fluctúa mucho al principio, pero de un modo similar. Sin embargo, como en el primer gráfico, la frecuencia alélica en las nuevas generaciones siempre se estabiliza finalmente
alrededor del valor teórico pronosticado de 0,6.
Nuestras simulaciones demuestran que los errores del muestreo disminuyen a medida
que aumenta el tamaño de la muestra. Si seguimos extrayendo gametos indefinidamente
para formar una población de zigotos de tamaño infinito, la frecuencia del alelo A1 en los
zigotos será exactamente 0,6. La deriva genética es un mecanismo evolutivo potente en
poblaciones pequeñas, pero su potencia disminuye en poblaciones grandes.Volveremos a
este punto en secciones posteriores.
Investigaciones experimentales sobre el error de muestreo
como mecanismo evolutivo: efecto fundador
Si queremos observar deriva genética en la naturaleza, el mejor sitio donde buscarla es
en las poblaciones pequeñas. Las poblaciones son a menudo pequeñas cuando se acaban
de fundar por un pequeño grupo de individuos, que se han desplazado, o han sido desplazados, a una nueva localidad. Las frecuencias alélicas en la nueva población son, probablemente, diferentes de las de la población de origen, simplemente por azar. A esto se
denomina efecto fundador.
El efecto fundador es el resultado directo del error de muestreo. Por ejemplo, si en una
población continental de insectos hay 25 alelos diferentes en un locus, pero en un madero de una balsa que llega a una remota isla sólo se encuentran 10 individuos, hay una probabilidad cero de que la nueva población de la isla tenga todos los alelos presentes en el
continente. Si por azar, algunos de los individuos fundadores son homozigotos, las frecuencias alélicas de la nueva población se diferenciarán incluso mucho más. En cualquier
suceso fundador, es casi seguro que se producirá algún grado de diferenciación genética
aleatoria entre las poblaciones nueva y vieja. En otras palabras, la fundación de una población por un pequeño grupo de individuos representa típicamente no solo el establecimiento de una nueva población sino también la evolución instantánea de diferencias entre
la nueva y la vieja población.
Peter Grant y Rosemary Grant (1995) observaron el establecimiento de una nueva
población de grandes pinzones terrestres (Geospiza magnirostris) en el Archipiélago de las
Galápagos. Grant y Grant han estado trabajando en la isla Daphne Major desde 1973.
Cada año grandes pinzones terrestres visitaban la isla, entre 10 y 50 formas juveniles llegaban después de la estación de cría y se quedaban durante los meses secos. Durante los
primeros años que Grant y Grant estuvieron allí, todos los pájaros visitantes dejaban la
isla antes de que comenzara la siguiente estación de cría. Los pinzones visitantes eran
miembros de alguna población de otra isla. Luego, en el otoño de 1982, tres machos y
dos hembras, aparentemente atraídos por las primeras lluvias, se quedaron en Daphne
Major para criar. Estas cinco aves formaron parejas (una hembra se cruzó con dos machos
distintos), construyeron ocho nidos durante la estación de cría y tuvieron 17 crías a principios de 1983.
Los cinco pájaros fundaron una nueva población en 1982-1983. Desde 1983, grandes
pinzones terrestres han criado en Daphne Major cada año, con la excepción de tres años
de sequía. En 1993, la población que criaba en Daphne Major se componía de 23 machos
y 23 hembras.Al menos hasta 1992, la mayoría de los que criaban en Daphne Major habían
nacido en la isla. Eran nativos de la nueva población.
La deriva genética es muy
importante en poblaciones
pequeñas.
168 PARTE II Los mecanismos del cambio evolutivo
Cuando se funda una
población nueva por un
pequeño número de individuos,
es probable que sólo por azar
las frecuencias alélicas en la
nueva población sean
diferentes de las de la
población de origen. A esto se
le denomina efecto fundador.
La nueva población de pinzones, ¿es genéticamente diferente de la población de origen? Aunque Grant y Grant no tienen datos directos sobre frecuencias alélicas en loci concretos, habían realizado muchas mediciones anatómicas de los 238 pinzones terrestres que
visitaron Daphne Major antes del suceso fundacional, de los cinco pinzones iniciales y de
22 de sus descendientes. Grant y Grant asumieron que los 238 visitantes que no criaron
representaban a la población de origen y los compararon con los miembros de la nueva
población. Al menos en dos caracteres morfológicos, la anchura del pico y su tamaño en
relación con el tamaño corporal, los miembros de la nueva población los tenían significativamente más grandes que la población de origen. La investigación en la población
nueva de grandes pinzones terrestres y en otros pinzones de Darwin, sugiere que estos
caracteres son heredables.Así parece que el suceso fundador creó una población nueva que
es métricamente diferente de la población de origen. Se produjo evolución, no mediante la selección sino por error aleatorio del muestreo. Esto es deriva genética en forma de
efecto fundador.
A menudo se observan efectos fundadores en poblaciones humanas genéticamente aisladas. Por ejemplo, la población Amish de Pensilvania oriental desciende de un grupo de
unos 200 colonos europeos que llegaron a los Estados Unidos en el siglo XVIII. Uno
de los fundadores, bien el marido o la esposa (o ambos) de un matrimonio llamado King,
fue portador del síndrome de Ellis-van Creveld. El síndrome de Ellis-van Creveld es una
forma rara de enanismo ocasionada por un alelo recesivo en el cromosoma 4 (Bodmer
and McKie 1995). La frecuencia de este alelo en la mayoría de las poblaciones se encuentra alrededor de 0,001, pero en la actualidad, en los Amish es alrededor de 0,07 (Postlethwait and Hopson 1992). La elevada frecuencia del alelo en la población Amish, probablemente no se debe a ninguna ventaja selectiva conferida por el alelo en heterozigosis
u homozigosis. Más bien, la elevada frecuencia del alelo se debe al azar. El alelo se
encontraba en frecuencia elevada en la pequeña población de fundadores y ha continuado
oscilando hacia arriba en las generaciones siguientes. En la sección siguiente consideraremos con detalle el efecto acumulativo de la deriva genética en el curso de muchas generaciones.
Fijación al azar de alelos y pérdida de heterozigosidad
Hemos visto que la deriva genética puede dar lugar a cambios sustanciales en las frecuencias alélicas en una sola generación. La deriva es incluso un mecanismo evolutivo más
poderoso cuando sus efectos abarcan a muchas generaciones. Podemos investigar los efectos acumulativos de la deriva genética con el mismo modelo físico que utilizamos antes:
una bolsa con alubias negras y blancas. De nuevo, iniciemos la bolsa con 60 alubias negras
y 40 blancas, que representa un conjunto de genes en el que los alelos A1 y A2 se encuentran en las frecuencias de 0,6 y 0,4. A los padres que dan lugar a este conjunto de genes
los llamaremos generación cero. Como hicimos antes, extraemos alubias de la bolsa para
simular la producción de diez zigotos por apareamiento al azar. En ese momento, las frecuencias alélicas entre los zigotos recién formados resultó ser 0,5 para A1 y 0,5 para A2.
Llamamos a estos zigotos generación uno.
Para continuar la simulación en otra generación, necesitamos iniciar una nueva bolsa
con 50 alubias negras y 50 alubias blancas, que representa el conjunto de genes de la generación uno. Extrayendo alubias de este conjunto de genes, obtenemos los zigotos de la
generación dos. Resulta que las frecuencias alélicas de la generación dos fueron 0,4 para
A1 y 0,6 para A2.
Iniciamos ahora una bolsa con 40 alubias negras y 60 blancas y formamos zigotos para
obtener la generación tres. Las frecuencias alélicas en la generación tres son 0,45 para A1
y 0,55 para A2.
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 169
Ahora necesitamos una bolsa con 45 alubias negras y 55 blancas, y así sucesivamente.
La ventaja de utilizar un computador para simular la extracción de las alubias queda clara
enseguida.
Los gráficos (a), (b) y (c) de la Figura 6.13 muestran los resultados de 100 generaciones sucesivas de deriva genética en poblaciones simuladas de tamaños distintos. En cada
(d) Tamaño poblacional = 4
(a) Tamaño poblacional = 4
0,5
Heterozigosidad promedio
Frecuencia del alelo A1
1,0
0,8
0,6
0,4
0,2
0,0
0
20
40
60
80
Heterozigosidad promedio
Frecuencia del alelo A1
0,8
0,6
0,4
0,2
0
20
40
60
80
0,1
0
20
40
60
80
100
40
60
80
100
60
80
100
0,4
0,3
0,2
0,1
0,0
100
0
20
(f) Tamaño poblacional = 400
(c) Tamaño poblacional = 400
0,5
Heterozigosidad promedio
1,0
Frecuencia del alelo A1
Frecuencia del alelo A1 [=p]
0,2
0,5
1,0
0,8
0,6
0,4
0,2
0,0
0,3
(e) Tamaño poblacional = 40
(b) Tamaño poblacional = 40
0,0
0,4
0,0
100
0,5
0,4
Frecuencia de los
0,3
heterozigotos
0,2
[=2(p)(1-p)]
0,1
0,0
0,0 0,2 0,4 0,6 0,8 1,0
0
20
40
60
Generación
80
100
0,4
0,3
0,2
0,1
0,0
0
20
40
Generación
Figura 6.13 Simulaciones de deriva genética en poblaciones de tamaños distintos Los gráficos (a), (b) y (c) muestran la
frecuencia del alelo A1 durante 100 generaciones. En cada gráfico están representadas ocho poblaciones, con una población dibujada
en rojo. Los gráficos (d), (e) y (f) muestran la frecuencia media de los heterozigotos a lo largo de 100 generaciones, en las mismas
series de poblaciones simuladas. Las curvas grises representan la tasa de disminución pronosticada por la teoría. El inserto en la gráfica
(d) muestra la frecuencia de los heterozigotos de una población, calculada como 2(p)(1 ⫺ p), en función de p, que es la frecuencia del
alelo A1. En conjunto, los gráficos de esta figura muestran que la deriva genética da lugar a la fijación aleatoria de alelos y a la pérdida
de heterozigosidad y que la deriva genética es una fuerza muy poderosa en poblaciones pequeñas.
170 PARTE II Los mecanismos del cambio evolutivo
gráfica se representan las frecuencias alélicas de ocho poblaciones. Cada población
comienza con las frecuencias alélicas de 0,5 para A1 y de 0,5 para A2. Las poblaciones
representadas en la gráfica (a) tienen exactamente cuatro individuos cada una, las poblaciones representadas en la gráfica (b) tienen 40 individuos y las poblaciones de la gráfica
(c) tienen 400 individuos. Son evidentes tres patrones:
Con deriva genética, cada
población sigue una vía
evolutiva única. La deriva
genética es rápida en
poblaciones pequeñas y lenta
en poblaciones grandes.
1. Debido a que las fluctuaciones en la frecuencia alélica de una generación a la siguiente están ocasionadas por el error de muestreo al azar, cada población sigue un camino
evolutivo único.
2. La deriva genética tiene un efecto más rápido y drástico sobre las frecuencias alélicas
en las poblaciones pequeñas que en las poblaciones grandes.
3. Dado un tiempo suficiente, la deriva genética puede dar lugar a cambios sustanciales
en las frecuencias alélicas, incluso en poblaciones que sean bastante grandes.
Advierta que si la deriva genética es la única fuerza evolutiva que actúa en la población (si no hay selección, ni mutación, ni migración) entonces el error de muestreo hace
que las frecuencias alélicas oscilen entre 0 y 1. Esta oscilación es particularmente aparente en las poblaciones cuya evolución se destaca en el gráfico de la Figura 6.13b. Durante
las primeras 25 generaciones la frecuencia del alelo A1 aumenta de 0,5 a más de 0,9. Entre
las generaciones 25 y 40 baja a 0,5. Entre las generaciones 40 y 80 la frecuencia oscila entre
0,5 y 0,8. Luego la frecuencia de A1 disminuye rápidamente, de tal manera que hacia la
generación 85 A1 alcanza cero y por consiguiente desaparece de la población. La oscilación de las frecuencias alélicas da lugar a dos efectos relacionados importantes: (1) el que
los alelos derivan finalmente hacia la fijación o hacia la pérdida, y (2) que la frecuencia de
los heterozigotos disminuye.
Si la deriva genética es la
única fuerza evolutiva que está
actuando, uno de los alelos
llegará finalmente a la
frecuencia de 1 (es decir, se
fijará) y todos los otros alelos
se perderán.
Fijación al azar de alelos
Como la frecuencia de cualquier alelo oscila entre 0 y 1, tarde o temprano el alelo encontrará un destino inevitable: su frecuencia alcanzará un extremo u otro. Si la frecuencia del
alelo llega a 0, entonces el alelo se perderá para siempre (suponiendo que la mutación o
la migración no lo reintroduzcan). Si la frecuencia del alelo alcanza 1, entonces se dice que
el alelo se ha fijado, también para siempre. Entre las ocho poblaciones representadas en la
Figura 6.13a, el alelo A1 se fija por deriva en cinco y se pierde en tres. Entre las ocho
poblaciones representadas en la Figura 6.13b, el alelo A1 se fija por deriva en una y se pierde en tres. Es sólo cuestión de tiempo que el alelo A1 quede también fijado o perdido en
las otras poblaciones. A medida que algunos alelos se fijan y otros se pierden por deriva,
la variabilidad alélica de cada población disminuye.
Imaginemos ahora una población finita en la que hay varios alelos presentes en un locus
dado: A1, A2, A3, A4, y así sucesivamente. Si la deriva genética es el único mecanismo
evolutivo que actúa, entonces finalmente uno de los alelos se fijará por deriva. En el mismo
momento en que un alelo quede fijado, los otros alelos se perderán.
Nos gustaría poder predecir qué destino alcanzará cada alelo. No podemos hacerlo con
certeza, pero podemos dar probabilidades. Sewall Wright (1931) demostró que la probabilidad de que cualquier alelo de una población sea el que se fije por deriva es igual a la
frecuencia inicial de dicho alelo (véase el Cuadro 6.3). Por ejemplo, si comenzamos con
una población finita en la que A1, tiene una frecuencia de 0,73 y A2 una frecuencia de
0,27, hay un 73% de probabilidad de que el alelo que se fije por deriva sea el A1.
Pérdida de heterozigosidad
En una población finita, a medida que las frecuencias de los alelos se fija o se pierde por
deriva, la frecuencia de los heterozigotos en la población disminuye. Los gráficos (d), (e)
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 171
CUADRO 6.3 Probabilidad de que un alelo dado sea el que se fije por deriva
S
ewall Wright (1931) desarrolló una teoría detallada
de la deriva genética. Entre muchos otros resultados,
demostró que la probabilidad de que un alelo dado sea
el único que se fije por deriva es igual a la frecuencia inicial del alelo. El modelo de Wright de deriva genética
está más allá del alcance de este libro, pero podemos proporcionar una explicación intuitiva de la probabilidad de
fijación.
Imaginemos a una población con N individuos. Dicha
población contiene un total de 2N alelos. Imaginemos que
cada uno de estos alelos es único. Supongamos que la deriva genética es el único mecanismo evolutivo que actúa.
En algún momento en el futuro, uno de los 2N alelos
se habrá fijado por deriva y todos los demás se habrán
perdido. Cada alelo debe tener la misma probabilidad de
ser el que se fije por deriva; esto es lo que queremos decir
con nuestra suposición de que la deriva genética es el
único mecanismo evolutivo que está actuando. Así pues,
tenemos 2N alelos, cada uno con igual probabilidad de
quedar fijado. Por consiguiente, la probabilidad para cada
ᎏ.
alelo de quedar fijado es ᎏ21N
Imaginemos ahora que en lugar de que cada alelo sea
único, hay x copias del alelo A1, y copias del alelo A2 y z
copias del alelo A3. Cada copia del alelo A1 tiene una
probabilidad de ser el alelo que se fije por deriva igual a
1
ᎏᎏ. Por consiguiente, la probabilidad de que una de las
2N
copias del alelo A1 sea el alelo que se fije por deriva es:
1
x
x ⫻ ᎏᎏ ⫽ ᎏᎏ
2N
2N
De igual manera, la probabilidad de que una copia del
y
ᎏ, y la proalelo A2 sea el alelo que se fije por deriva es ᎏ2N
babilidad de que una copia del alelo A3 sea el alelo que se
ᎏ.
fije por deriva es ᎏ2zN
y
z
ᎏ, ᎏᎏ y ᎏᎏ son también las frecuencias
Advierta que ᎏ2xN
2N 2N
iniciales de los alelos A1, A2 y A3 en la población. Hemos
demostrado que la probabilidad de que un alelo dado sea
el que se fije por deriva es igual a la frecuencia inicial de
dicho alelo.
y (f) de la Figura 6.13 muestran la disminución de la frecuencia de los heterozigotos en
nuestras poblaciones simuladas.
Para ver por qué la frecuencia de los heterozigotos disminuye, observe primero el inserto del gráfico (d). En el inserto se representa la frecuencia de los heterozigotos, calculada
como 2(p)(1 – p), en una población con apareamiento al azar en función de p, que es la
frecuencia del alelo A1. La frecuencia de los heterozigotos tiene su valor más alto, 0,5,
cuando A1 está en la frecuencia de 0,5. Como la frecuencia de A1 disminuye hacia 0 ó
aumenta hacia 1, la frecuencia de los heterozigotos disminuirá.Y, desde luego, si la frecuencia de A1 alcanza 0 ó 1, la frecuencia de los heterozigotos caerá hasta 0.
Miremos ahora los gráficos (a), (b) y (c). En cualquier generación, la frecuencia de A1
puede desplazarse hacia o lejos de 0,5 en una población dada (siempre y cuando A1 no
se haya fijado o perdido). Así, la frecuencia de los heterozigotos de cualquier población
puede aumentar o disminuir. Sin embargo, la tendencia global, en el conjunto de las poblaciones, es que las frecuencias alélicas se alejen por deriva de valores intermedios y hacia 0
ó 1. Por ello, la frecuencia promedio de los heterozigotos, en el conjunto de las poblaciones, tenderá a disminuir. Miremos ahora a los gráficos (d), (e) y (f). La línea gruesa azul
de cada gráfico representa la frecuencia promedio de los heterozigotos a lo largo de las
ocho poblaciones en cuestión. La frecuencia de los heterozigotos realmente tiende a disminuir, rápidamente en poblaciones pequeñas y lentamente en poblaciones grandes.
Finalmente, uno u otro alelo quedará fijado en cada población y la frecuencia promedio
de los heterozigotos caerá hasta 0.
La frecuencia de los heterozigotos de una población se denomina a veces como la heterozigosidad poblacional. Nos gustaría poder predecir lo rápido que puede esperarse
que disminuya la heterozigosidad en poblaciones finitas. Sewall Wright (1931) demostró
172 PARTE II Los mecanismos del cambio evolutivo
Como los alelos tienden a
fijarse o perderse por deriva,
la frecuencia de los
heterozigotos en la población
disminuirá.
que, promediando muchas poblaciones, la frecuencia de los heterozigotos obedece a la
relación
1
Hg ⫹1 ⫽ Hg 1 ⫺ ᎏᎏ
2N
冤
冥
donde Hg ⫺1 es la heterozigosidad de la generación siguiente, Hg es la heterozigosiᎏ冥 se encuentra
dad actual y N el número de individuos de la población. El valor de 冤1 ⫺ ᎏ21N
1
siempre entre ᎏ2ᎏ y 1, por lo que la frecuencia esperada de heterozigotos de la generación
siguiente es siempre menor que la frecuencia de heterozigotos en la generación anterior.
Las curvas grises de las Figuras 6.13d, (e) y (f) muestran la disminución de la heterozigosidad pronosticada por la ecuación de Wright.
Para apreciar una de las implicaciones de la inevitable pérdida de heterozigosidad en
las poblaciones finitas, imagine que es el responsable de la gestión de una población cautiva de una especie en peligro de extinción. Suponga que hay exactamente 50 adultos
reproductores en los zoológicos de todo el mundo. Aunque pudiera disponer del traslado de los adultos o del semen para llevar a cabo un apareamiento aleatorio, todavía
apreciaría una pérdida de heterozigosidad del 1% por generación debido a la deriva
genética.
Estudio experimental de la fijación o pérdida aleatoria
de heterozigosidad
Nuestra discusión sobre la fijación o pérdida aleatoria de heterozigosidad se ha basado
hasta el momento en poblaciones simuladas y en ecuaciones matemáticas. Peter Buri
(1956) estudió este fenómeno experimentalmente, en poblaciones pequeñas de laboratorio de la mosca de la fruta Drosophila melanogaster.Adoptando un esquema que había sido
utilizado por Kerr y Wright (1954), Buri fundó 107 poblaciones de moscas, cada una de
ellas a partir de ocho hembras y ocho machos.Todas las moscas fundadoras eran heterozigóticas para alelos de un gen para el color de los ojos llamado “brown”.Todas las moscas
tenían el mismo genotipo: bw75/bw. Así, en las 107 poblaciones, la frecuencia inicial del
alelo bw75 fue de 0,5. Buri mantuvo estas poblaciones durante 19 generaciones. En cada
población y en cada generación, Buri mantuvo el tamaño poblacional en 16, extrayendo
ocho hembras y ocho machos al azar como padres de la generación siguiente.
¿Qué resultados esperaríamos? Si ninguno de los dos alelos, bw75 y bw, confiere ventaja selectiva, entonces esperaríamos que la frecuencia del alelo bw75 oscilara al azar por deriva genética en cada generación. Diecinueve generaciones serían suficientes, en poblaciones con 16 individuos, para que muchas poblaciones quedaran fijadas para uno u otro alelo.
Debido a que el alelo bw75 tiene una frecuencia inicial de 0,5 esperaríamos que este alelo
se perdiera tan a menudo como se fijase.A medida que el alelo bw75 se fija o se pierde por
deriva en cada población, esperaríamos la disminución de la heterozigosidad en el conjunto de las poblaciones. La tasa de disminución de la heterozigosidad seguirá la ecuación
de Wright, dada en la sección anterior.
Los resultados de Buri confirman estas predicciones. Cada uno de los pequeños gráficos de la Figura 6.14 son histogramas que resumen las frecuencias alélicas de las 107 poblaciones en una generación concreta. El eje horizontal representa la frecuencia del alelo
bw75, y el eje vertical representa el número de poblaciones en cada una de las frecuencias.
La frecuencia del alelo bw75 era 0,5 en la generación cero de todas las poblaciones, que
no se muestran en la figura. Después de una generación de deriva genética, muchas
poblaciones todavía presentan una frecuencia cercana a 0,5, aunque una de las poblaciones tenía una frecuencia alélica de 0,22 y otra de 0,69.A medida que la frecuencia del alelo
bw75 aumenta en unas poblaciones y disminuye en otras, la distribución de las frecuencias
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 173
Generación
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
0 2 4 6 8 101214161820222426283032
1
2
3
4
5
6
7
8
9
0 2 4 6 8 101214161820222426283032
10
11
12
13
14
15
16
17
18
Número de 30
poblaciones 0
19
,00 ,13 ,25 ,38 ,50 ,63 ,75 ,88 1,00
Frecuencia del alelo bw75
Figura 6.14 Diecinueve generaciones de deriva
genética en 107 poblaciones de 16 moscas de la
fruta Cada línea es un histograma que reúne las
frecuencias alélicas de las 107 poblaciones en una
generación dada. El eje horizontal representa la
frecuencia del alelo bw 75, y el eje vertical el número de
poblaciones que hay de cada frecuencia. La frecuencia de
bw 75 fue de 0,5 en la generación cero de todas las
poblaciones (no mostrada). Al final del experimento, 30
poblaciones se habían fijado en la frecuencia 0 y 28 en la
frecuencia 1 (línea inferior). Sin embargo, a lo largo del
experimento la distribución de las frecuencias alélicas
permaneció simétrica alrededor de 0,5. De datos de Buri
(1956), según Ayala and Kiger (1984).
alélicas se ensancha rápidamente. En la generación cuarta, la frecuencia de bw75 alcanza
1 por primera vez en una población. En la generación sexta la frecuencia de bw75 alcanza 0 por primera vez en una población.A medida que la frecuencia alcanza 0 ó 1 en más
y más poblaciones, la distribución de las frecuencias adquiere una forma en U. Hacia el
final del experimento, bw75 se había perdido en 30 poblaciones y se había fijado en 28.
La proporción 30:28 de pérdida y fijaciones está muy próxima a la proporción 1:1 que
174 PARTE II Los mecanismos del cambio evolutivo
Figura 6.15 En las poblaciones experimentales de Buri, la
frecuencia de los heterozigotos disminuye con el tiempo Los
puntos rojos representan las frecuencias de los heterozigotos en cada
generación, promedio de las 107 poblaciones. La curva gris a trazos muestra
la predicción teórica para una población de 16 moscas. La curva gris
continua muestra la predicción teórica para una población de 9 moscas.
El gráfico demuestra que (1) la heterozigosidad disminuye a lo largo de las
generaciones en poblaciones pequeñas y (2) aunque todas las poblaciones
tenían un tamaño real de 16 moscas, su tamaño poblacional efectivo era
aproximadamente de 9. Representación a partir de datos de Buri (1956),
según Hartl (1981).
Estudios experimentales
confirman que con deriva
genética los alelos tienden a
fijase o perderse y la
frecuencia de los
heterozigotos disminuye.
Realmente, estos procesos
suceden a menudo más rápido
de lo previsto.
Heterozigosidad (promediada
de las 107 poblaciones)
0,5
0,4
0,3
0,2
0,1
0,0
0
5
10
15
20
Generación
habíamos predicho con deriva genética. Durante el experimento de Buri, hubo una evolución espectacular en casi todas las 107 poblaciones de moscas de la fruta, pero la selección natural no tuvo nada que ver con esto.
Las propiedades genéticas del locus “brown” eran tales que Buri podía identificar a los
tres genotipos por sus fenotipos. Así pudo comprobar directamente la frecuencia de los
heterozigotos de cada población. La frecuencia de los heterozigotos en la generación cero
fue 1, por lo que la heterozigosidad en la generación uno fue 0,5.A partir de ese momento, Buri anotó en cada generación la frecuencia de los heterozigotos de cada población,
obteniendo posteriormente la heterozigosidad media de las 107 poblaciones. En la Figura 6.15 se representan estos valores de heterozigosidad media a lo largo de las 19 generaciones del experimento. Observe primero los puntos rojos que representan los datos
reales. De acuerdo con nuestras predicciones teóricas, la frecuencia promedio de los heterozigotos disminuye lentamente.
Sin embargo, la concordancia entre la teoría y los resultados no es perfecta. La curva
gris a trazos de la figura muestra la disminución en heterozigosidad pronosticada, utilizando
la ecuación de Wright y una población de tamaño 16. La disminución real en heterozigosidad fue más rápida de lo esperado. La curva gris continua muestra la disminución pronosticada para una población de tamaño 9; encaja bien con los datos. Las poblaciones de
Buri pierden heterozigosidad como si tuvieran sólo 9 individuos en lugar de 16. En otras
palabras, el tamaño poblacional efectivo del experimento de Buri fue 9 (véase el Cuadro 6.4). Una de las explicaciones es que alguna de las moscas de cada población pudo
haber muerto por accidente antes de reproducirse, o las hembras pudieron rechazar a algunos machos como pareja.
El experimento de Buri con moscas de la fruta demuestra que la teoría de la deriva
genética nos permite hacer predicciones cualitativamente exactas y predicciones cuantitativas razonablemente exactas, acerca del comportamiento de los alelos en poblaciones
finitas, al menos en el laboratorio. En la sección siguiente consideraremos pruebas sobre
la fijación al azar de alelos y pérdida de heterozigosidad en poblaciones naturales.
Fijación o pérdida aleatoria de heterozigosidad
en poblaciones naturales
Alan Templeton y sus colegas (1990) comprobaron las predicciones acerca de la fijación al
azar de alelos analizando los resultados de un experimento natural en las montañas de Ozark
de Missouri. Aunque cubiertas en la actualidad por un bosque de enzimas y nogales, la
región de los Ozarks fue parte de un desierto durante un extenso período de clima cálido
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 175
CUADRO 6.4 Tamaño poblacional efectivo
E
l tamaño poblacional efectivo es el tamaño de una
población ideal que perdería heterozigosidad al
mismo ritmo que una población real de interés. El tamaño poblacional efectivo es siempre menor prácticamente que el tamaño poblacional real. En el experimento de
Buri, dos posibles razones de la diferencia entre el tamaño poblacional efectivo y el real es que (1) algunas de las
moscas murieron en las botellas (accidentalmente) antes
de reproducirse y (2) las moscas de la fruta presentan
selección sexual tanto en la competencia entre machos
como en la elección de la hembra (véase el Capítulo 9);
ambos podrían haber evitado la reproducción de algunos
machos.
El tamaño poblacional efectivo es particularmente sensible a diferencias en el número de hembras reproductivamente activas respecto de los machos. Cuando hay un
número distinto de cada sexo en una población, el tamaño poblacional efectivo Ne se puede estimar como,
4NmNf
Ne ⫽ ᎏᎏ
(Nm ⫹ N f )
donde Nm es el número de machos y Nh el número de
hembras.
Para ver cuanto puede reducir el tamaño poblacional
efectivo una proporción sexual desequilibrada, utilice la
fórmula para demostrar que: cuando hay 5 machos y 5
hembras, Ne = 10; cuando hay 1 macho y 9 hembras, Ne
= 3,6; y cuando hay 1 macho y 1000 hembras, Ne =
4.Considere los problemas logísticos implicados en el mantenimiento de un programa de cruce de animales cautivos
de una especie en la que los machos son extremadamente
agresivos y no tolerarán la presencia de otros.
y seco que abarcó entre hace 8.000 años hasta hace 4.000 años. El desierto que engulló a
los Ozarks estaba junto al desierto del sudoeste de Norteamérica. Muchas especies del desierto del sudoeste ampliaron su distribución hacia el este en los Ozarks. Entre éstas se
encuentra la lagartija con collar (Crotaphytus collaris). Cuando finalizó el período cálido, la
distribución de la lagartija con collar se retrajo de nuevo hacia el oeste y el bosque de encinas y nogales volvió a invadir los Ozarks. Sin embargo, en este bosque, en afloramientos rocosos, hay pequeños restos de hábitat desértico llamados claros.Viviendo en algunos de estos
claros hay poblaciones reliquia de lagartijas con collar. La mayoría de las poblaciones están
lo suficientemente aisladas entre sí que hay poco o ningún flujo génico entre ellas. Las poblaciones reliquia son pequeñas; la mayoría tienen no más de unas docenas de individuos.
Debido al pequeño tamaño de las poblaciones de los claros,Templeton y sus colegas
predijeron que las lagartijas con collar de los Ozarks presentarían fuertes huellas de deriva genética. En cada población, la mayoría de los loci se habrían fijado para un solo alelo
y la variación genética sería muy baja. Sin embargo, qué alelo se hubiera fijado en cada
población en concreto sería una cuestión de azar, por lo que habría una considerable diversidad genética entre poblaciones.
Templeton y sus colegas analizaron la variabilidad genética de varias poblaciones de los
claros. Los investigadores examinaron los genotipos de las lagartijas de una serie de loci
enzimáticos, de sus genotipos del DNA ribosómico y de sus genotipos de DNA mitocondrial. Entre las lagartijas identificaron siete genotipos multilocus distintos. Confirmando
las consecuencias pronosticadas por el aislamiento y por el pequeño tamaño poblacional,
la mayoría de las poblaciones de los claros estaban fijadas para un único genotipo multilocus, con genotipos diferentes fijados en distintas poblaciones (Figura 6.16).
Andrew Young y sus colegas (1996) comprobaron las predicciones acerca del efecto del
tamaño poblacional sobre la heterozigosidad con un estudio comparativo en plantas. Los
investigadores reunieron datos de la bibliografía y representaron dos medidas de la diversidad genética global frente al tamaño poblacional en tres fanerógamas herbáceas y un
árbol. La primera medida de variación genética fue de polimorfismo genético, el porcentaje de loci del genoma que tienen al menos dos alelos con frecuencia superior a 0,01. La
176 PARTE II Los mecanismos del cambio evolutivo
Figura 6.16 Variación genética en
las poblaciones de la lagartija con
collar de los claros de los Ozarks
(a)
(a) El esquema en tarta da la
correspondencia de los siete genotipos
multilocus distintos que Templeton et al.
(1990) encontraron en las lagartijas con
collar de los Ozarks. Cada genotipo
multilocus se caracterizaba por el
genotipo de una malato deshidrogenasa
(MDH) [los dos alelos son “lento” (S)
y “rápido” (F)], un haplotipo del DNA
mitocondrial (designado A-D) y un
genotipo del DNA ribosómico (designado
I-III ). (b) Mapa del sur de Missouri,
mostrando la localización y composición
genética de nueve poblaciones de los
claros. El sombreado de cada esquema en
tarta representa la frecuencia en una
población de cada uno de los genotipos
multilocus presentes. (c) Ampliación de
una pequeña parte del mapa de (b). Da la
localización y composición genética de
otras cinco poblaciones de los claros. De
Templeton et al. (1990). Copyright ©
1990 Alan R. Templeton. Reimpreso con
permiso del autor.
MDH: S & F
FDI
FAI
S/F A I
F A II
mtDNA: A–D
rDNA: I–III
FCI
F A III
F B II
(b)
Crotaphytus collaris
(c)
1600
1700
1000
1100
1700
1600
1200
1300
1400
1500
1600
1500
1300
1400
1300
1200
1100
1000
900
1500
1400
1200 1300
m
Tau
uk
Sa
ek
Cre
1 Milla
1 Km
segunda fue la riqueza de alelos, el número medio de alelos por locus.Ambas medidas están
relacionadas con la heterozigosidad. Si un locus dado tiene más de un alelo, y si un sustancial número de individuos de la población son heterozigotos, entonces el locus contribuye mucho al polimorfismo y a la riqueza alélica. Por el contrario, si el locus está fijado
para un único alelo y en la población no hay heterozigotos, entonces el locus empobrece el polimorfismo poblacional y la riqueza alélica. Debido a que la deriva genética es más
pronunciada en las poblaciones pequeñas que en las grandes y debido a que da lugar a la
pérdida de heterozigosidad,Young y sus colegas predijeron que las poblaciones pequeñas
tendrían un menor nivel de polimorfismo y de riqueza alélica. Las representaciones de
Young et al. aparecen en la Figura 6.17. De acuerdo con sus predicciones, en casi todos
los casos las poblaciones pequeñas albergan realmente menos diversidad genética.
Los estudios de Templeton et al. y de Young et al. demuestran que, al menos en algunas
poblaciones naturales, la deriva genética da lugar, de acuerdo con lo predicho, a fijación al
azar y a reducción de heterozigosidad. La pérdida de diversidad genética en poblaciones
pequeñas es de particular interés para los biólogos conservacionistas por dos razones. Primero, la diversidad genética es la materia prima para la evolución adaptativa. Suponga una
especie reducida a unas pocas poblaciones remanentes por destrucción del hábitat o por
algún otro cambio ambiental. La deriva genética puede privar a las poblaciones remanentes de su potencial para evolucionar en respuesta a un cambio ambiental, precisamente en
los momentos en que el ambiente cambie más drásticamente. Segundo, la pérdida de heterozigosidad conlleva un aumento de la homozigosidad. Un aumento en homozigosidad
conduce a menudo a una eficacia menor en poblaciones experimentales (véase, por ejemplo, Polans and Allard 1989; Barrett and Charlesworth 1991). Probablemente esto implica
el mismo mecanismo que la depresión por consanguinidad: expone alelos deletéreos a la
selección. Consideraremos la depresión consanguínea en la Sección 6.3.
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 177
(a) Salvia pratensis
0,60
1,60
0,45
1,45
0,30
0
1,30
r = 0,54
P< 0,05 1,15
r = 0,62
P< 0,01
0,15
1
102
10
103
104
1
102
10
103
1,0
104
(b) Scabiosa columbaria
0,60
1,60
0,45
1,45
Polimorfismo
0
1,30
r = 0,71
P< 0,005
0,15
10
102
103
104
105
r = 0,82
P< 0,001 1,15
10
102
103
104
1,0
105
(c) Eucalyptus albens
1,00
0,90
0,80
0,60
r = 0,52
P< 0,05
r = 0,56
P< 0,01
0,70
102
10
103
104
102
10
103
3,2
3,0
2,8
2,6
2,4
2,2
104
(d) Gentiana pneumonanthe
0,35
0,30
0,25
0,20
0,15
0,10
r = 0,49
P< 0,05
1
10
102 103 104 105
1
10
102
1,30
1,25
1,20
1,15
r = 0,33 1,10
P< 0,11 1,05
1,00
103 104 105
Tamaño poblacional
Riqueza alélica (A)
0,30
Figura 6.17 Tamaño poblacional y diversidad genética Cada
punto de estos cuadros representa a una población de fanerógamas. El
polimorfismo, situado en el eje vertical de la izquierda de los cuadros, es
la proporción de loci alozímicos cuando la frecuencia del alelo más
frecuente de la población es menor a 0.99. En otras palabras, el
polimorfismo es el porcentaje de alelos que son substancialmente
polimórficos. La riqueza alélica, situada en el eje vertical de la derecha de
los cuadros, es el número medio de alelos por locus. El estadístico r es
una medida de asociación, llamado coeficiente de correlación de
Pearson, que varía de 0 (no hay asociación entre las variables) a 1
(correlación perfecta). P se refiere a la probabilidad de que el coeficiente
de correlación sea significativamente diferente de cero. Salvia pratensis,
Scabiosa columbaria y Gentiana pneumonanthe son fanerógamas
herbáceas; Eucalyptus albens es un árbol. Reimpreso de Young et al.
(1996) Copyright © 1996 Elsevier Science. Reimpreso con el permiso de
Elsevier Science.
La tasa de evolución por deriva genética
La teoría y los experimentos que hemos discutido en esta sección establecen que el error
de muestreo puede ser un mecanismo importante de evolución. El último aspecto de la
deriva que consideraremos aquí es la tasa de evolución cuando la deriva genética es la
única fuerza que actúa.
Primero, necesitamos definir qué significa la tasa de evolución en un locus dado. Definiremos la tasa de evolución como la tasa a la que los nuevos alelos originados por mutación son sustituidos por otros alelos ya presentes. En la Figura 6.18 se ilustra el proceso
de sustitución y se distingue la sustitución de la mutación. La figura muestra un conjunto
de genes de 10 alelos durante 20 generaciones. Inicialmente, todos los alelos son idénticos (círculos blancos). En la cuarta generación aparece un nuevo alelo (círculo naranja
claro) por la mutación de uno de los alelos originales. Durante varias generaciones este
alelo fluctúa hacia una frecuencia elevada. En la generación quince aparece un segundo
alelo nuevo (círculo azul), originado por la mutación de un descendiente del primer alelo
naranja claro. En la generación diecinueve se pierde el último de los alelos blancos. En este
punto podemos decir que el alelo blanco ha sido sustituido por el alelo naranja claro.Así
pues, por sustitución evolutiva queremos indicar la fijación de una mutación nueva con
o sin cambio mutacional adicional.
Cuando el único mecanismo evolutivo que actúa es la deriva genética, la tasa de sustitución es simplemente igual a la tasa de mutación (véase el Cuadro 6.5). Esto es así independientemente del tamaño poblacional, ya que los dos efectos asociados con el tamaño
178 PARTE II Los mecanismos del cambio evolutivo
Figura 6.18 La mutación es el origen de un nuevo alelo; la
substitución es la fijación del nuevo alelo, con o sin cambio
mutacional adicional Este gráfico muestra los 10 alelos presentes en cada
una de 20 generaciones sucesivas, en una población hipotética de cinco
individuos. Durante el tiempo que cubre el gráfico el alelo naranja claro
sustituyó al alelo blanco. El alelo azul puede sustituir finalmente al alelo
naranja claro o puede perderse.
Cuando interactúan la
mutación, la deriva genética y
la selección, se dan tres
procesos: (1) aparecen alelos
deletéreos y son eliminados
por selección; (2) aparecen
mutaciones neutras y se fijan
o se pierden por azar; y (3)
aparecen alelos ventajosos y
son llevados hasta la fijación
por selección. La importancia
relativa de (2) y (3) en
determinar la tasa global de
sustitución es un asunto de
debate.
poblacional se cancelan entre sí: en poblaciones grandes se producen más mutaciones, pero
en una población grande cada nueva mutación tiene una menor probabilidad de fijarse por
deriva. Con deriva genética las poblaciones grandes generan y mantienen más variación
genética que las poblaciones pequeñas, pero todas las poblaciones, independientemente de
su tamaño, acumulan sustituciones al mismo ritmo.
Por supuesto, a menudo están actuando otros mecanismos evolutivos distintos de la
deriva. Podemos permitir algo de selección natural en nuestro modelo y obtener todavía
resultados similares. Imaginemos que algunas mutaciones son deletéreas mientras que
otras son selectivamente neutras. Las mutaciones deletéreas serán eliminadas por selección
natural y nunca llegarán a fijarse. La tasa de sustitución será entonces igual a la tasa a la que
se producen las mutaciones neutras.
Los biólogos evolutivos están divididos por la relevancia de estos cálculos en las poblaciones reales.Todos están de acuerdo en que se ha omitido un tipo de mutación y un tipo
de selección (véase el Cuadro 6.5).Algunas mutaciones son ventajosas selectivamente y se
han fijado por selección natural con mayor seguridad y mucho más rápidamente que
nunca lo hubieran hecho por deriva. Sin embargo, los biólogos evolutivos piensan de dos
maneras sobre la frecuencia con la que sucede esto.
Los que apoyan la teoría neutralista, largo tiempo liderada por Motoo Kimura
(1983), mantienen que las mutaciones ventajosas son muy raras y que la mayor parte de
los alelos de la mayoría de los genes son selectivamente neutros. Los neutralistas predicen
que para la mayoría de los genes en la mayoría de las poblaciones, la tasa de evolución será
realmente igual a la tasa de mutación neutra.
Los que apoyan la teoría seleccionista, principalmente liderada por John Gillespie
(1991), mantienen que las mutaciones ventajosas son lo bastante corrientes como para que
puedan ignorarse. Los seleccionistas predicen que para muchos genes en la mayoría de las
poblaciones, la tasa de sustitución reflejará la acción de la selección natural sobre las
mutaciones ventajosas.
La disputa entre neutralistas y seleccionistas no está resuelta y aplazaremos la presentación de pruebas experimentales hasta el Capítulo 18. Sin embargo, la teoría neutralista es
básica en muchos aspectos de la biología evolutiva actual. Proporciona un modelo nulo
para la detección de selección al nivel de las secuencias del DNA y de las proteínas (véanse los Capítulos 18 y 19).También proporciona la base teórica del reloj molecular utilizado para deducir la edad de antecesores comunes a partir de datos de secuencias (véase
el Capítulo 13).
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 179
CUADRO 6.5 La tasa de sustituciones evolutivas con deriva genética
V
amos a mostrar cálculos que demuestran que cuando actúa la deriva genética como único mecanismo
evolutivo, la tasa de sustituciones evolutivas es igual a la
tasa de mutación (Kimura 1968).
Imagine una población diploide de tamaño N. En esta
población hay 2N alelos del locus de interés, en donde por
“alelo” indicamos las copias del gen, independientemente
de si son o no idénticas. Sea v la tasa de mutación selectivamente neutra por alelo y por generación, y supongamos
que cada mutación da lugar a un alelo que no se encontraba anteriormente en la población. Entonces, en cada
generación habrá:
2Nv
alelos nuevos originados por mutación.Ya que suponemos
que todos los alelos nuevos son selectivamente neutros, la
deriva genética será la única fuerza que actúe. Cada uno de
los alelos nuevos tiene la misma probabilidad que cualquier
otro alelo de la población de fijarse por deriva. Esta probabilidad es igual a la frecuencia del alelo nuevo, que es:
1
ᎏᎏ
2N
Por consiguiente, en cada generación, el número de alelos
nuevos que se originan por mutación y que se fijan por
deriva es:
1
2Nv ⫻ ᎏᎏ ⫽ v
2N
El mismo argumento se aplica en cada generación. Por
consiguiente, la tasa de evolución en el locus de interés es
de v sustituciones por generación.
Esto será útil para la discusión en otros capítulos, donde
se explorará con mayor detalle qué significa v, la tasa de
mutación neutra. Suponga que el locus de interés es un
gen que codifica para una proteína que tiene L aminoácidos de longitud. Sea u la tasa de mutación por codón y por
generación. La tasa global de mutación para nuestro locus
viene dada por:
µ ⫽ uL(d ⫹ a ⫹ f ) ⫽ uLd ⫹ uLa ⫹ uLf
donde d es el porcentaje de cambios de codón que son
deletéreos, a es el porcentaje de los que tienen ventaja
selectiva, f es el porcentaje de los que son selectivamente
neutros y d + a + f = 1.Advierta que el término de la derecha, uLf, es igual a nuestra v.
Al demostrar que la tasa de sustitución es igual a v, asumimos que d y a son iguales a cero. Desde luego, en cualquier población real muchas mutaciones son deletéreas y
d no es cero. Esto no modifica nuestro cálculo de la tasa de
sustitución. Los alelos deletéreos son eliminados por selección natural y no contribuyen a la tasa de sustituciones
evolutivas.
Los que apoyan la teoría neutralista mantienen que a es
aproximadamente igual a cero y que f es mucho mayor que
a. Por consiguiente predicen que las sustituciones evolutivas serán dominadas por las mutaciones neutras y la deriva,
y esto se dará con una tasa v = uLf, como hemos calculado.
Los que apoyan la teoría seleccionista mantienen que a
es demasiado grande como para ignorarlo y que la tasa de
sustituciones evolutivas estará influenciada de manera significativa por la selección natural en favor de alelos beneficiosos.
En resumen, la deriva genética no es un mecanismo adaptativo de evolución. Simplemente, como consecuencia del error de muestreo, las frecuencias alélicas pueden cambiar
de una generación a la siguiente. La deriva genética es muy potente en poblaciones
pequeñas y cuando actúa sobre muchas generaciones. Finalmente, la deriva genética da
lugar a la fijación de algunos alelos y a que otros se pierdan, y a una disminución global
de la diversidad genética.
6.3.
Apareamiento no aleatorio
El último supuesto del análisis de Hardy-Weinberg es que los individuos de la población
se aparean al azar. En esta sección relajaremos este supuesto y permitiremos que los individuos se apareen de manera no aleatoria. En sí mismo, el apareamiento no aleatorio no
es causa de evolución. No obstante, el apareamiento no aleatorio puede tener profundos
efectos indirectos sobre la evolución.
180 PARTE II Los mecanismos del cambio evolutivo
La consanguinidad disminuye
la frecuencia de los
heterozigotos y aumenta la
frecuencia de los homozigotos
comparando con las
previsiones bajo los supuestos
de Hardy-Weinberg.
El tipo más corriente de apareamiento no aleatorio, y en el que nos fijaremos aquí, es
la consanguinidad. La consanguinidad es el apareamiento entre parientes genéticos. El
efecto de la consanguinidad sobre la genética de una población es aumentar la frecuencia de homozigotos en comparación con lo esperado según Hardy-Weinberg.
Para mostrar cómo se produce consideremos el ejemplo más extremo de consanguinidad: la autofecundación. Imaginemos una población en equilibrio de Hardy-Weinberg,
con los alelos A1 y A2 con una frecuencia inicial de 0,5 para cada uno. La frecuencia de
los individuos A1A1 es 0,25, la de los individuos A1A2 es 0,5 y la de los individuos A2A2
es 0,25 (Figura 6.19a). Imaginemos que hay 1.000 individuos en la población: 250 A1A1,
500 A1A2 y 250 A2A2. Si todos los individuos de la población se reproducen por autofecundación, los padres homozigotos darán lugar a descendientes homozigotos, mientras
que los padres heterozigotos producirán la mitad de los descendientes homozigotos y la
otra mitad heterozigotos. En los 1.000 descendientes de nuestra población habrá 375
A1A1, 250 A1A2 y 375 A2A2. Si la población continúa autofecundándose durante dos
generaciones más, entonces entre los 1.000 individuos de la última generación habrá
468,75 homozigotos de cada tipo y 62,5 heterozigotos (Figura 6.19b). La frecuencia de
los heterozigotos se habrá reducido a la mitad en cada generación y la frecuencia de los
homozigotos se habrá incrementado.
La conclusión 2 del análisis de Hardy-Weinberg no se cumple cuando los individuos
se autofecundan: no podemos predecir las frecuencias genotípicas multiplicando las frecuencias alélicas.Advierta que en la generación tercera, en la Figura 6.19b, las frecuencias
alélicas para A1 y A2 son todavía 0,5. No obstante, la frecuencia de los heterozigotos está
lejos de 2(0,5)(0,5). Comparando con las previsiones de Hardy-Weinberg, hay un déficit
de heterozigotos y un exceso de homozigotos. El caso general con autofecundación se presenta algebraicamente en la Tabla 6.1.
Genotipos: A1A1
(a)
Número de individuos: 250
Figura 6.19 La consanguinidad
altera las frecuencias
genotípicas (a) En esta figura se
siguen las frecuencias genotípicas
en una población imaginaria de
1.000 caracoles desde los adultos
de una generación (arriba) a los
zigotos de la generación siguiente
(abajo a la izquierda). La frecuencia
de los alelos A1 y A2 es 0,5. Las
barras coloreadas indican el número
de individuos de cada genotipo.
Cada individuo se reproduce por
autofecundación. Los homozigotos
producen descendientes
homozigotos y los heterozigotos
producen descendientes tanto
homozigotos como heterozigotos,
por lo que la frecuencia de los
homozigotos aumenta y la de los
heterozigotos disminuye. (b) Estas
barras muestran lo que sucede a las
frecuencias genotípicas si esta
población continuara
autofecundándose durante dos
generaciones más.
A1A2
A2A2
500
250
Cada individuo produce descendientes
por autofecundación:
A1A1
A1A2
A2A2
375
250
375
Los individuos A1A1 producen descendientes A1A1
Los individuos A1A2 producen descendientes A1A1,
A1A2, y A2A2 en la proporción 1:2:1
Los individuos A2A2 producen descendientes A2A2
(b)
Genotipos: A1A1
A1A2
A2A2
Número de individuos: 250
500
250
Generación 0
375
250
375
Generación 1
437,5
125
437,5
Generación 2
468,75
62,5
468,75
Generación 3
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 181
Tabla 6.1 Cambios en las frecuencias genotípicas en generaciones sucesivas
de autofecundación
La frecuencia del alelo A1 es p y la frecuencia del alelo A2 es q. Advierta que las frecuencias
alélicas no cambian de generación en generación, sólo las frecuencias genotípicas. Según Crow
(1983).
Generación
A1A1
0
p2
1
2
2
Frecuencia de
A1A2
A2A2
2pq
q2
p ⫹ (pq/2)
pq
q2 ⫹ (pq/2)
p2 ⫹ (3 pq/4)
pq/2
q2 ⫹ (3 pq/4)
2
3
p ⫹ (7 pq/8)
pq/4
q2 ⫹ (7 pq/8)
4
p2 ⫹ (15 pq/16)
pq/8
q2 ⫹ (15 pq/16)
¿Qué pasa con la conclusión 1 de Hardy-Weinberg? ¿Han cambiado las frecuencias alélicas de una generación a la siguiente con consanguinidad? En nuestro ejemplo numérico no ha ocurrido. Podemos comprobar el caso general calculando la frecuencia del alelo
A1 en el conjunto de genes producidos por la población y que se muestra en la última fila
de la Tabla 6.1. La frecuencia del alelo A1 en el conjunto de genes es igual a la frecuen15pq
cia de los adultos A1A1 de la población ( ⫽ p2 ⫹ ᎏᎏ ) más la mitad de la frecuencia de
16
1 pq
A1A2 ( ⫽ ᎏᎏ ᎏᎏ ), lo que da:
[ ]
2 8
冤 冥
15pq
1 pq
15pq
pq
p2 ⫹ ᎏᎏ ⫹ ᎏᎏ ᎏᎏ ⫹ ᎏᎏ ⫹ ᎏᎏ ⫽ p2 ⫹ pq
16
2 8
16
16
Sustituyendo ahora q por (1 – p) obtendremos p2 + p(1 – p) = p. Ésta es la misma frecuencia que tenía el alelo A1 al principio, en la parte superior de la Tabla 6.1. Aunque la
consanguinidad da lugar al cambio de las frecuencias genotípicas de generación en generación, no da lugar al cambio de las frecuencias alélicas. Por consiguiente, la consanguinidad
en si misma no es un mecanismo evolutivo. Sin embargo, como veremos, la consanguinidad puede tener consecuencias evolutivas importantes.
Investigación experimental sobre la consanguinidad:
el parásito de la malaria
Ya que la consanguinidad puede dar lugar a un gran exceso de homozigotos, se puede utilizar el análisis de Hardy-Weinberg para detectar consanguinidad en la naturaleza. Como
ejemplo, consideremos la investigación sobre el parásito de la malaria en Nueva Guinea
(Paul et al. 1995). El ciclo de vida de este protozoo, Plamodium falciparum, alterna entre estadios que viven en los mosquitos y estadios que viven en los humanos (Figura 6.20). La
única fase diploide del ciclo de vida del parásito se da en el mosquito; en él, un estadio
llamado ooquiste, se localiza en la pared del intestino medio. La otra fase, que infecta al
hígado y a los glóbulos rojos humanos, e incluye a las células que se transmiten a los mosquitos, es haploide.
La biología del parásito de la malaria, P. falciparum, sugiere que la consanguinidad puede
ser normal en esta especie. El argumento es el siguiente: hace años,W. D. Hamilton (1967)
observó que cuando un solo parásito o parasitoide hembra coloniza a un nuevo huésped
son frecuentes proporciones sexuales anormales. Por ejemplo, en la avispa de la higuera que
estaba estudiando Hamilton, las hembras aisladas que colonizan los higos tienden a pro-
182 PARTE II Los mecanismos del cambio evolutivo
Se multiplican
las células masculinas
Unión de
gametos
Ooquiste
Meiosis
En el mosquito
Anopheles
En humanos
Estadio
infeccioso
En el
hígado y
en el
sistema
linfático
Figura 6.20 Ciclo de vida del parásito de la malaria
Plamodium falciparum El ooquiste (naranja) es diploide; los otros
Infección en
glóbulos rojos
estadios del ciclo de vida del parásito (azul, rojo y verde) son
haploides.
ducir muchas más jóvenes hembras que machos. Hamilton llegó a desarrollar las fórmulas que demuestran por qué evolucionó esta estrategia y predijo que se daría en cualquier
parásito en los que fueran corrientes las fundaciones aisladas (Hamilton 1967, 1979; véase
también Read et al. 1992). La esencia del argumento es ésta: en especies en las que el apareamiento entre hermanos es la regla, las hembras tendrán más nietos si producen sólo los
machos suficientes para asegurar que todas sus hijas serán fecundadas2.
¿Qué tiene que ver esto con el parásito de la malaria? R. E. L. Paul y sus colegas (1995),
trabajando en el laboratorio de Karen Day, observaron una proporción sexual desplazada
hacia las hembras (más hembras que machos) en las fases infecciosas de P. falciparum. Los
investigadores hipotetizaron que el fenómeno que Hamilton descubrió estaba actuando
en la población de parásitos que estudiaban. Aunque la malaria es endémica en Nueva
Guinea, la tasa de transmisión es relativamente baja. Esto significa que cada uno de los
humanos infectados tiende a tener sólo un único genotipo de P. falciparum o unos pocos.
Además, parece que en cada ciclo de infección en una célula sanguínea humana, que da
lugar al tipo de células de Plasmodium que toman los mosquitos, puede estar restringida a
células de un único genotipo. El resultado es que cada mosquito tiende a quedar infectado por uno, o como mucho por dos, genotipos de células de P. falciparum. En efecto, todas
las células que el mosquito toma son descendientes de una sola hembra. En esta fase de
infección es en la que Paul et al. encuentran la proporción sexual desplazada hacia las hembras. Las pocas células masculinas que se encuentran se multiplican dentro del mosquito
2
Nota del traductor. A igual número de descendientes, si éstos se han de cruzar entre sí (no han de buscar
pareja), será más eficaz producir un exceso de hembras.
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 183
Tabla 6.2 Frecuencias alélicas de tres genes polimórficos del parásito
de la malaria Plasmodium falciparum
MSP-2
MSP-1
GLURP
Alelo
Frecuencia
observada
Alelo
Frecuencia
observada
Alelo
Frecuencia
observada
A1
0,02
A1
0,02
A1
0,07
A2
0,06
A2
0,26
A2
0,42
A3
0,18
A3
0,19
A3
0,28
A4
0,27
A4
0,32
A4
0,08
A5
0,12
A5
0,12
A5
0,15
A6
0,08
A6
0,09
A7
0,05
A8
0,07
A9
0,09
A10
0,06
Fuente: calculado de la Figura 1 de Paul et al. (1995).
y luego se fusionan con las células femeninas (a menudo sus propias hermanas) para formar ooquistes diploides. Si esta hipótesis es correcta, entonces los ooquistes deberían ser
muy consanguíneos y presentarían un gran exceso de homozigotos.
Paul y sus colegas estimaron en los ooquistes las frecuencias alélicas y genotípicas de
tres proteínas de P. falciparum que codifican a los genes MSP-1, MSP-2 y GLURP. Los científicos diseccionaron primero hembras de mosquito y aislaron ooquistes de malaria englobados en su tejido estomacal. Luego los investigadores extrajeron DNA de los ooquistes
y analizaron directamente su variación alélica. Estos tres loci eran polimórficos, es decir,
cada uno de ellos tenía más de un alelo. Los datos proporcionaron una estima de la frecuencia de los diferentes alelos en la población (Tabla 6.2) y un cálculo del número de
homozigotos y heterozigotos de la muestra (Tabla 6.3).
¿Están las frecuencias alélicas y genotípicas que los investigadores estimaron de acuerdo
con lo esperado según las condiciones de Hardy-Weinberg? La respuesta es, rotundamente,
no (Tabla 6.3). De acuerdo con la predicción de Paul y sus colegas, hay un enorme exceso
de homozigotos en la población de parásitos y un correspondiente déficit de heterozigotos.
Estrictamente hablando, el exceso de homozigotos demuestra sólo que uno o más de los
supuestos de Hardy-Weinberg no se cumple en la población de malaria. Sin embargo, sólo
Tabla 6.3 Número observado de homozigotos y heterozigotos en tres loci de Plasmodium falciparum
En cada caso, el número de individuos observados con un tipo particular de genotipo se compara con el número esperado de acuerdo
con las condiciones de Hardy-Weinberg de apareamiento al azar, en ausencia de mutación, selección, migración y deriva genética. En
los tres casos, las diferencias son estadísticamente significativas (P < 0,01; véase el Cuadro 5.5).
(a) MSP-2
(b) MSP-1
Observado
Esperado
Observado
Homozigotos
55
10
38
Heterozigotos
9
54
1
(c) GLURP
Esperado
Observado
Esperado
9
40
12
30
1
29
184 PARTE II Los mecanismos del cambio evolutivo
CUADRO 6.6
Frecuencias genotípicas en una población consanguínea
A
quí añadimos la consanguinidad al análisis de HardyWeinberg. Imaginemos una población con dos alelos
en un locus dado: A1 y A2, con frecuencias p y q. Podemos
calcular las frecuencias genotípicas en la generación siguiente dejando que los gametos se encuentren en el conjunto de
genes, como haríamos en una población con apareamiento
al azar. La peculiaridad añadida por la consanguinidad es que
el conjunto de genes no está mezclado enteramente. Por
ejemplo, una vez que hemos escogido un óvulo para examinarlo, podemos pensar en el esperma del conjunto de
genes formando dos fracciones: una fracción (1 – F ) que
lleva alelos que no son idénticos por ascendencia al del
óvulo; y la fracción F que lleva alelos que son idénticos por
ascendencia al del óvulo (debido a que se produjeron por
parientes de la hembra de donde procede el óvulo). Los cálculos de las frecuencias genotípicas son como sigue:
• Homozigotos A1A1: hay dos vías por las que podríamos
esperar la formación de un homozigoto A1A1. La primera es que cojamos un óvulo que sea A1 (un suceso
con probabilidad p) y veamos que sea fecundado por
azar por un esperma que sea A1, en lugar de por ascendencia común. La frecuencia en el conjunto de genes de
un esperma A1 no emparentado es p(1 – F), por lo que
la probabilidad de obtener un homozigoto por azar es:
p ⫻ p(1 ⫺ F) ⫽ p2(1 ⫺ F)
La segunda vía para conseguir un homozigoto es coger
un óvulo que sea A1 (un suceso con probabilidad p) y
que sea fecundado por azar por un esperma que sea A1
por ascendencia común (un suceso con probabilidad F).
La probabilidad de obtener un homozigoto por esta vía
es pF. La probabilidad de obtener un homozigoto A1A1
por cualquiera de las dos vías es la suma de las probabilidades de cada una:
p2(1 ⫺ F ) ⫹ pF
• Heterozigotos A1A2: hay dos maneras de obtener un
heterozigoto A1A2. La primera es coger un óvulo que
sea A1 (un suceso con probabilidad p) y que sea fecundado por un espermatozoide no emparentado que sea
A2. La frecuencia del esperma no emparentado A2 es
q(1 – F), por lo que la probabilidad de obtener un heterozigoto por esta primera vía es pq(1 – F). La segunda es
coger un óvulo que sea A2 (probabilidad: q) y que sea
fecundado por un espermatozoide no emparentado A1
[probabilidad: p(1-F)]. La probabilidad de obtener un
heterozigoto por esta segunda vía es qp(1-F). La probabilidad de obtener un heterozigoto de ambos modos es
la suma de las probabilidades de cada una:
pq(1 ⫺ F) ⫹ qp(1 ⫺ F) ⫽ 2pq(1 ⫺ F)
• Homozigotos A2A2: podemos obtener un homozigoto
A2A2, bien cogiendo un óvulo A2 (probabilidad: q) y
que sea fecundado por un espermatozoide no emparentado A2 [probabilidad: q(1-F)], o cogiendo un óvulo A2
(probabilidad: q) y que sea fecundado por un espermatozoide A2 de ascendencia común (probabilidad: F). La
probabilidad global de obtener un homozigoto A2A2 es:
q2(1 ⫺ F ) ⫹ qF
Los lectores pueden verificar que las frecuencias genotípicas suman 1.
el apareamiento no aleatorio puede dar lugar fácilmente a un exceso de homozigotos tan
grande como el encontrado por Paul et al. En combinación con las observaciones de los
investigadores sobre la biología reproductiva del parásito, los datos de las Tablas 6.2 y 6.3 apoyan, de manera convincente, que P. falciparum en Nueva Guinea es realmente consanguíneo.
Análisis general de la consanguinidad
Hasta el momento hemos limitado el tratamiento de la consanguinidad a la autofecundación y al cruzamiento entre hermanos. Pero también se puede producir consanguinidad con
cruzamientos entre parientes más distantes, como se da entre primos. La consanguinidad, que
es menos extrema que la autofecundación, da lugar al mismo efecto que ésta (aumenta la
proporción de homozigotos) pero a un ritmo más lento. Para un tratamiento matemático
generalizado de la consanguinidad, los genéticos de poblaciones utilizan una herramienta
conceptual llamada coeficiente de consanguinidad. Este coeficiente viene simbolizado
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 185
por F, y se define como la probabilidad de que los dos alelos de un individuo sean idénticos por ascendencia (es decir, que ambos alelos provengan del mismo alelo de un antecesor
de una generación anterior). El Cuadro 6.6 muestra que en una población consanguínea,
que por lo demás obedece a la ley de Hardy-Weinberg, las frecuencias genotípicas son:
A1A1
p2(1 ⫺ F ) + pF
A1A2
2 pq(1 ⫺ F )
A2A2
q2(1 ⫺ F ) ⫹ qF
Los lectores pueden verificar estas expresiones sustituyendo los valores de F = 0, que da las
proporciones genotípicas originales de Hardy-Weinberg, y de F = 0,5, que representa la
autofecundación y que da las proporciones mostradas en la Tabla 6.1 para la generación 1.
La misma lógica se aplica cuando hay muchos alelos en el conjunto de genes. Entonces la frecuencia de cualquier homozigoto AiAi viene dada por
pi2(1 ⫺ F) + piF
y la frecuencia de cualquier heterozigoto AiAj viene dada por
2pi pj (1 ⫺ F)
donde pi es la frecuencia del alelo Ai y pj la frecuencia del alelo Aj.
La última expresión indica que el porcentaje de individuos de una población que son
heterozigotos (es decir, la heterozigosidad de la población) es proporcional a (1 – F). Si
comparamos la heterozigosidad de una población consanguínea, HF, con la de una población con apareamiento aleatorio, H0, entonces la relación será:
HF ⫽ H0 (1 ⫺ F)
Siempre que F sea mayor que 0, la frecuencia de los heterozigotos será menor en una
población consanguínea que en una población con apareamiento aleatorio.
Cálculo de F
Para medir el grado de consanguinidad en poblaciones reales, necesitamos un modo de
calcular F. Hacerlo directamente requiere de una genealogía: un esquema que muestre
las relaciones de parentesco de los individuos. La Figura 6.21 muestra una genealogía que
(a)
(b)
1
2
1
2
1
2
1
2
1
2
Probabilidad = 1 x 1 x 1 x 1
2
= 1
16
2
1
2
1
2
2
1
2
Probabilidad = 1 x 1 x 1 x 1
2
2
= 1
16
F = Probabilidad de [(a) o (b)]
= 1 + 1
16
= 1
8
16
2
2
2
Figura 6.21 Cálculo de F a partir de una
genealogía En las partes (a) y (b), los cuadrados
representan machos y los círculos hembras; las
flechas indican el paso de los alelos de padres a hijos
a través de los gametos. Los triángulos verdes y los
rombos azules representan alelos de un locus dado.
186 PARTE II Los mecanismos del cambio evolutivo
llega a una hembra que es hija de medios hermanos. Hay dos vías por las que esta hembra puede recibir alelos que son idénticos por ascendencia. Una es que reciba dos copias
del alelo “triángulo verde” de su abuela (Figura 6.21a). Esto sucederá si la abuela pasa el
alelo triángulo tanto a su hija como a su hijo y tanto la hija como el hijo lo pasen a la nieta.
La probabilidad total de esto es ᎏ11ᎏ6 . La segunda vía es que pueda recibir las dos copias
del alelo “diamante azul” de su abuela (Figura 6.21b). La probabilidad total de esto es ᎏ11ᎏ6 .
La probabilidad de que la hija de medios hermanos reciba dos alelos idénticos por ascendencia en cualquiera de los dos casos es ᎏ11ᎏ6 ⫹ ᎏ11ᎏ6 ⫽ ᎏ18ᎏ. Así, la F para un descendiente de
medios hermanos es ᎏ18ᎏ.
La consanguinidad puede
reducir la eficacia media si da
lugar a descendencia
homozigótica para alelos
deletéreos.
Depresión consanguínea
Aunque la consanguinidad no cambia por sí misma las frecuencias alélicas, no obstante
puede afectar a la evolución de una población. Entre las consecuencias más importantes
de la consanguinidad se encuentra la depresión consanguínea.
La depresión consanguínea normalmente se produce por la exposición de alelos
recesivos deletéreos a la selección. Para ver cómo funciona, consideremos el caso extremo ejemplificado por mutaciones de pérdida de función. Estos alelos son a menudo
recesivos, ya que un solo alelo de tipo silvestre puede producir, en muchos casos, suficiente proteína funcional como para dar lugar al fenotipo normal.Aun cuando en heterozigosis puedan no tener en absoluto consecuencias en la eficacia, las mutaciones de
pérdida de función pueden ser letales en homozigosis. Al aumentar la proporción de
individuos homozigotos en una población, la consanguinidad aumenta la frecuencia
de aquellos recesivos deletéreos que afectan al fenotipo. La depresión consanguínea se
refiere al efecto que estos alelos tienen sobre la eficacia media de los descendientes en
una población.
Estudios en la especie humana han demostrado que la consanguinidad expone, de
hecho, alelos recesivos deletéreos; datos de numerosos estudios demuestran consistentemente que los hijos de primos hermanos tienen una tasa de mortalidad mayor que la de
los hijos de padres no emparentados (Figura 6.22).También se ha observado frecuentemente una elevada depresión consanguínea en poblaciones de animales en cautividad (por
ejemplo, Hill 1974; Ralls et al. 1979).
Quizá los estudios más amplios sobre la depresión consanguínea en poblaciones naturales se refieren a las fanerógamas, en las que la consanguinidad se puede estudiar experi-
Figura 6.22 Depresión consanguínea en humanos Cada punto de este
gráfico representa la tasa de mortalidad infantil en una población humana. El eje
horizontal representa la tasa de mortalidad de hijos de padres no emparentados; el eje
vertical representa la tasa de mortalidad de hijos de primos hermanos. La línea gris
indica dónde caerían los puntos si las tasas de mortalidad en los dos tipos de hijos
fueran iguales. Aunque las tasas de mortalidad infantil varían mucho entre
poblaciones, la tasa de mortalidad de hijos de primos es casi siempre más alta que la
tasa de hijos de padres no emparentados, normalmente alrededor de un cuatro por
ciento. Representación de datos de Bittles and Neel (1994).
Tasa de mortalidad entre
hijos de primos hermanos
50
40
30
20
10
0
0
10
20
30
40
Tasa de mortalidad entre hijos
de padres no emparentados
50
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 187
mentalmente. En muchas angiospermas se pueden obtener descendientes por autofecundación y por fecundación cruzada de los mismos padres mediante polinización manual.
En experimentos similares, la depresión consanguínea se puede definir como
ws
␦ ⫽ 1 ⫺ ᎏᎏ
wo
donde ws y wo son las eficacias de la descendencia por autofecundación y por fecundación
cruzada, respectivamente. Esta definición permite comparar los niveles de depresión consanguínea entre especies. De los estudios experimentales surgen tres patrones.
Primero, los efectos de la consanguinidad se detectan a menudo más fácilmente cuando las plantas sufren algún tipo de estrés ambiental. Por ejemplo, cuando Michele Dudash
(1990) comparó el desarrollo y la reproducción de rosicler (Sabatia angularis) autofecundadas y por fecundación cruzada, las plantas mostraban algo de depresión consanguínea cuando se cultivaban en el invernadero o en el jardín, pero su producción divergía
mucho cuando se cultivaban en el campo. Lorne Wolfe (1993) obtuvo resultados similares con una planta acuática (Hydrophyllum appendiculatum): individuos obtenidos por autofecundación o por fecundación cruzada tenían igual eficacia cuando se cultivaban solas,
pero diferían significativamente cuando se cultivaban en competencia. Y en la planta
anual llamada hierba de Santa Catalina (Impatiens capensis), McCall et al. (1994) observaron un efecto de la consanguinidad sobre la supervivencia más pronunciado cuando se
producía un ataque de insectos no planeado en el curso de sus experimentos.
Segundo, es mucho más probable que los efectos de la consanguinidad se presenten tardíamente en el ciclo de vida (por ejemplo, no durante la germinación o el estadio de plántula). Este patrón es notable (Figura 6.23). ¿Por qué se da? Wolfe (1993) sugiere que los
efectos maternos (concretamente, la influencia de la semilla materna en el fenotipo de los
descendientes a través de los elementos nutritivos de las semillas) pueden enmascarar la
influencia de recesivos deletéreos hasta más avanzado el ciclo de vida.
Tercero, la depresión consanguínea varía entre linajes familiares. Michele Dudash y sus
colegas (1997) compararon el desarrollo y la reproducción de individuos consanguíneos
respecto de no consanguíneos de varias familias en dos ciclos anuales de la hierba Mimulus guttatus. Algunas familias presentaron depresión consanguínea; otras no presentaron
efectos apreciables del tipo de apareamiento; incluso otras mostraron una mayor producción en consanguinidad.
La depresión consanguínea también se ha observado en poblaciones naturales de animales. Estudios a largo plazo en dos poblaciones aisladas de un pájaro llamado carbonero
común (Parus major) han demostrado que la depresión consanguínea puede tener graves
consecuencias en el éxito reproductivo. Cuando Paul Greenwood y sus colaboradores
(1978) definieron los cruces consanguíneos como aquellos entre primos hermanos o indi-
Figura 6.23 La depresión consanguínea en
fanerógamas aumenta cuando los individuos
envejecen Este gráfico compara el número de flores
Número de flores
de los supervivientes
50
40
30
20
10
0
0
1
2
Edad (años)
3
producidas (como medida de la eficacia) en función
del momento en que los individuos se cruzan
(cuadrados azules) respecto de los que se
autofecundan (cuadrados rojos) en Lobelia cardinalis,
una planta perenne de la familia de los jacintos azules.
La disparidad en la producción aumenta con el tiempo,
indicando que la depresión consanguínea llega a ser
más pronunciada con la edad. De Johnston (1992).
Copyright © 1992 Evolution. Reimpreso con permiso.
Número de huevos
que no eclosionan
188 PARTE II Los mecanismos del cambio evolutivo
2
1
1
64
1
16
1
4
Coeficiente de consanguinidad
Figura 6.24 La
consanguinidad aumenta el
fallo en la eclosión del
carbonero común De van
Noordwijk y Scharloo (1981).
Copyright © 1992 Evolution.
Reimpreso con permiso.
viduos más íntimamente emparentados, encontraron que la supervivencia de las nidadas
consanguíneas era mucho menor que la de individuos no consanguíneos. De manera similar, A. J. van Noordwijk y W. Scharloo (1981) demostraron que en una población isleña
de herrerillos había una fuerte correlación entre el nivel de consanguinidad de la pareja
y el número de huevos que no eclosionaban de una puesta (Figura 6.24). Recientemente, Keller et al. (1994) encontraron que individuos no consanguíneos de una población de
gorriones cantores de la Columbia Británica, Canadá, tenían muchas más probabilidades
de sobrevivir a un invierno crudo que los individuos consanguíneos.
Dada la teoría y los datos que hemos revisado sobre la depresión consanguínea, no es
sorprendente que tanto los animales como los vegetales hayan desarrollado mecanismos
para evitarla. Entre los mecanismos para evitar la consanguinidad se encuentran la elección de pareja, la autoincompatibilidad genéticamente controlada y la dispersión. Pero en
ciertas circunstancias, la consanguinidad puede ser inevitable. Por ejemplo, en poblaciones pequeñas el número potencial de parejas para cualquier individuo concreto es limitado. Si una población es pequeña y permanece pequeña durante muchas generaciones y
si la población no recibe inmigrantes de otras poblaciones, entonces a la larga todos los
individuos de la población estarán emparentados, incluso si el apareamiento es al azar.Así,
las pequeñas poblaciones se convertirán finalmente en consanguíneas y los individuos de
las mismas podrán sufrir depresión consanguínea. Éste puede ser un problema para especies raras y en peligro de extinción y plantea un reto a los responsables de programas de
cruzamientos de animales cautivos, como veremos en la Sección 6.4.
En resumen, los apareamientos no aleatorios no alteran por sí mismos las frecuencias
alélicas. Por consiguiente, no es un mecanismo evolutivo. Sin embargo, los apareamientos
no aleatorios alteran las frecuencias genotípicas. Por ello pueden cambiar la distribución
de fenotipos en una población y alterar el patrón de selección natural y de evolución de
la población. Por ejemplo, la consanguinidad aumenta la frecuencia de homozigotos y disminuye la de heterozigotos. Esto puede exponer a alelos recesivos deletéreos a la selección, dando lugar a la depresión consanguínea.
6.4. Genética de la conservación de la gallina grande
de las praderas de Illinois
Abrimos este capítulo con el caso de la gallina grande de las praderas de Illinois (Figura 6.1),
un ave abundante con anterioridad pero que hacia mediados de 1990 parecía destinada a su
extinción. Como otras muchas especies vulnerables en peligro de extinción, el peor enemigo
de la gallina de las praderas es la destrucción de su hábitat (Figura 6.2). Antes de la introducción del arado de acero, la pradera cubría más del 90% de Illinois; en la actualidad queda
menos del uno por ciento de pradera (Westemeier et al. 1998). No obstante, para la gallina
de las praderas la destrucción del hábitat no es el único problema.A comienzos de 1960, los
conservacionistas establecieron reservas de pradera para las gallinas y trabajaron en la restauración y mantenimiento del hábitat de la pradera. Desde finales de 1960 hasta principios de
1970, sus esfuerzos parecieron tener éxito, ya que el número de gallinas de la pradera comenzó a aumentar. Pero el éxito aparente tuvo corta vida: hacia mediados de 1970, las poblaciones
de la gallina de las praderas comenzaron a disminuir de modo constante (Figura 6.3).Algo
estaba amenazando a la supervivencia de la gallina grande de la pradera de Illinois, ¿pero qué?
Nuestra discusión sobre migración, deriva genética y apareamiento no aleatorio nos da las
herramientas para comprender la respuesta probable.
Ronald Westemeier y sus colegas (1998) plantearon la siguiente hipótesis: la destrucción de la pradera ocasionó dos problemas a la población de gallinas de la pradera. Primero, redujo directamente el tamaño de las poblaciones de las aves. Segundo, fragmentó
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 189
la población que quedaba. Hacia 1980 se capturaron las pocas gallinas de la pradera que
sobrevivían en Illinois y se reunieron en pequeñas islas de pradera rodeadas de un mar de
granjas. Cada isla tenía su pequeña población de aves propia. Estas poblaciones pequeñas
quedaron aisladas geográficamente entre sí y de las poblaciones de otros estados.
Poblaciones pequeñas con poco o ningún flujo génico son precisamente el marco en
el que la deriva genética actúa con mayor fuerza.Y la deriva genética da lugar a fijación
al azar y a disminución de la heterozigosidad. Si algunos de los alelos que han quedado
fijados son recesivos deletéreos, entonces se reducirá la eficacia media de los individuos.
Una reducción de eficacia debida a deriva genética se parece a la depresión consanguínea. De hecho, es depresión consanguínea. La reducción de heterozigosis debida a deriva
y el aumento de homozigosis debido a consanguinidad son dos caras de la misma moneda. En poblaciones pequeñas todos los individuos están emparentados y no hay otra elección que cruzarse con un pariente.
Michael Lynch y Wilfried Gabriel (1990) han propuesto que la acumulación de alelos
recesivos deletéreos (fenómeno conocido como lastre genético) puede dar lugar a la
extinción de poblaciones pequeñas.Advirtieron que cuando la manifestación de las mutaciones deletéreas da lugar a una reducción del tamaño poblacional, la efectividad de la
deriva aumenta. Por consiguiente aumenta la velocidad y la proporción de las mutaciones deletéreas que se fijan, lo que de nuevo disminuye el tamaño poblacional. Lynch y
Gabriel denominaron a esta interacción sinergística entre mutación, tamaño poblacional
y deriva “disolución (fusión) mutacional”.
Westemeier y sus colegas sugirieron que las poblaciones remanentes de la gallina grande de las praderas de Illinois habían quedado atrapadas exactamente en tal escenario. A
medida que las poblaciones pierden su diversidad genética, las aves comienzan a sufrir
depresión consanguínea. Dicha depresión consanguínea reduce el éxito reproductivo
individual y da lugar a que las poblaciones remanentes continúen su declive incluso
cuando el hábitat disponible aumente. El continuo declive del tamaño poblacional da lugar
a más deriva, que a su vez da lugar a una mayor depresión consanguínea y así sucesivamente. Las aves han caído en un “vórtice de extinción” (véase Soulé y Mills 1998).
Para comprobar su hipótesis, los investigadores utilizaron primero los datos de un
amplio estudio sobre la población del Condado de Jasper para buscar pruebas de depresión consanguínea. Los investigadores representaron el éxito en la eclosión de los huevos
de las gallinas de la pradera, una medida de la eficacia individual, en función del tiempo
(Figura 6.25). A lo largo de 1960, cerca del 90% de los huevos de la gallina de las praderas del Condado de Jasper eclosionaron. Esta tasa es comparable con el porcentaje en 1930
y con el de la actualidad de las poblaciones más grandes de gallinas de las praderas en otros
Los primeros esfuerzos
por conservar las poblaciones
remanentes de la gallina
grande de las praderas
fallaron, aparentemente,
porque las aves estaban
sufriendo depresión
consanguínea.
1
Huevos eclosionados (%)
100
2
65
80
13
13
28 30
5
13
6 11
28
15 10
15
6
9
7
2
9
7
60
10
8
8
8
6
4
6
3
40
3
7
20
1963
1970
1980
Año
1990
1997
Figura 6.25 Declive en el éxito de la eclosión en poblaciones
de la gallina grande de las praderas En esta gráfica se representa
el porcentaje de huevos que eclosionaron cada año, desde 1963 a
1997, de la gallina grande de las praderas en el Condado de Jasper,
Illinois. El pequeño número que hay debajo de cada punto indica el
número de nidos que se contabilizaron; las líneas grises verticales
indican el error típico ⫾1 (una medida estadística de la imprecisión en
la estima de las tasas de eclosión). El declive en el éxito de la eclosión
desde mediados de la década de 1960 hasta principios de 1990 parece
reflejar depresión consanguínea. Dibujado con permiso de Westemeier
et al. (1998). Copyright © 1998, American Association for the
Advancement of Science.
190 PARTE II Los mecanismos del cambio evolutivo
La depresión consanguínea en
poblaciones remanentes de la
gallina grande de las praderas
estaba ocasionada por una
pérdida de diversidad alélica
por deriva genética.
estados. Sin embargo, hacia 1970 comenzó un constante declive en el éxito de la eclosión.
Hacia finales de 1980 la tasa de eclosión disminuyó por debajo del 80%. La disminución
llegó en 1990 a menos del 40% de huevos eclosionados. El declive en el éxito de la eclosión es significativo estadísticamente y representa una reducción sustancial en la eficacia
individual. En otras palabras, se asemeja a una depresión consanguínea.
Si el declive en el éxito de la eclosión en la gallina grande de las praderas del Condado
de Jasper se debió de hecho a depresión consanguínea ocasionada por deriva genética,
entonces debería estar acompañada por una señal genética. La población del Condado de
Jasper presentaría menos diversidad genética que las grandes poblaciones de otros estados
y menos diversidad genética ahora que la que tenía en el pasado. Juan Bouzat y sus colegas
(1998) analizaron el DNA de cierto número de gallinas de las praderas de Illinois, Kansas,
Minnesota y Nebraska, y determinaron el genotipo de cada ave para seis loci selectivamente
neutros (eran regiones no codificantes, con un número variable de cortas repeticiones en
tándem).Tal como se suponía, las aves de Illinois tenían una media de 3,67 alelos por locus,
significativamente menos que los 5,33 a 5,83 alelos por locus que presentaban las otras
poblaciones (Tabla 6.4). Los investigadores pudieron incluso tomar muestras de DNA de
10 especímenes de museo, que habían sido capturados en el Condado de Jasper en la década
de 1930, más 5 de 1960. Como se muestra en la última columna de la Tabla 6.4, Bouzat y
sus colegas utilizaron los datos de los especímenes de museo para estimar que la población
del Condado de Jasper había tenido anteriormente una media de al menos 5,12 alelos por
locus. De acuerdo con la hipótesis del vórtice de extinción, las gallinas de las praderas del
Condado de Jasper están genéticamente empobrecidas cuando se comparan tanto con su
propia población ancestral como con poblaciones actuales.
La prueba final de la hipótesis del vórtice de extinción fue utilizarla para desarrollar una
estrategia práctica de conservación. Si el problema de las poblaciones de la gallina de las
praderas del Condado de Jasper es su reducida diversidad genética, entonces la solución
Tabla 6.4 Número de alelos por locus encontrados en cada una de las
poblaciones actuales de Illinois, Kansas, Minnesota y Nebraska y
en la población estimada antes del cuello de botella de Illinois
Locus
Illinois
Kansas
Minnesota
Nebraska
Illinois antes
del cuello de botella*
ADL42
3
4
4
4
3
ADL23
4
5
4
5
5
ADL44
4
7
8
8
4
ADL146
3
5
4
4
4
ADL162
2
5
4
4
6
ADL230
6
9
8
10
9
Medida
3,67
5,83
5,33
5,83
5,12
SE
0,56
0,75
0,84
1,05
0,87
Tamaño de muestra
32
37
38
20
15
Nota: SE indica el error típico del número medio de alelos por locus. La población de Illinois de la columna 1 presenta, significativamente, menos diversidad alélica que el resto de las poblaciones (P < 0,05).
*El número de alelos de la población de Illinois antes del cuello de botella incluye tanto los alelos existentes que
están compartidos con las otras poblaciones como los alelos detectados en las colecciones de museo.
Fuente: de Bouzat et al. (1998).
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 191
es el flujo génico. Los migrantes de otras poblaciones tendrían los alelos que se han perdido en el Condado de Jasper. La reintroducción de estos alelos invertiría los efectos de
la deriva y eliminaría la depresión consanguínea. La migración natural de la gallina grande de las praderas al Condado de Jasper cesó hace mucho. Pero en 1992, biólogos conservacionistas comenzaron a capturar gallinas en Minnesota, Kansas y Nebraska y las
introdujeron en el Condado de Jasper. El plan parece estar funcionando.Westemeier y sus
colegas (1998) publicaron que la tasa de eclosión en el Condado de Jasper en 1993, 1994
y 1997 estaba por encima del 90%, mayor de lo que había sido en 25 años (Figura 6.25).
Y la población del Condado de Jasper está creciendo (Figura 6.3).
Todos los datos que hemos presentado sobre la gallina grande de la pradera de Illinois
provienen de la observación, por lo que siempre es posible que alguna variable ambiental no controlada y desconocida sea responsable de la variación en el éxito de la eclosión.
Sin embargo, con las pruebas disponibles, la hipótesis del vórtice de extinción de Westemeier et al. (implicando a la migración, la deriva genética y el apareamiento no aleatorio)
parece ser la mejor explicación.
La migración, en forma de aves
introducidas por los biólogos,
parece que restauró la
diversidad genética en las
poblaciones remanentes,
aliviando los efectos de la
depresión consanguínea.
Resumen
Una de las más importantes implicaciones del equilibrio de
Hardy-Weinberg es que la selección natural no es el único mecanismo evolutivo. En este capítulo examinamos las
violaciones de tres de las condiciones del análisis de HardyWeinberg que introdujimos por primera vez en el Capítulo 5 y consideramos sus efectos sobre las frecuencias
alélicas y genotípicas.
La migración, en su sentido evolutivo, es el paso de alelos de una población a otra. Cuando las frecuencias alélicas
son diferentes en la población de origen respecto de la
receptora, la migración da lugar a que la población receptora evolucione. Como mecanismo evolutivo, la migración
tiende a homogeneizar las frecuencias alélicas a lo largo de
las poblaciones. Al actuar así, puede dar lugar a la eliminación de las diferencias adaptativas entre poblaciones que se
han producido por selección natural.
La deriva genética es evolución que se produce como
consecuencia del error de muestreo en la producción de un
número finito de zigotos a partir de un conjunto de genes.
Por azar, las frecuencias alélicas cambian de una generación a
la siguiente. La deriva genética es más efectiva en las poblaciones pequeñas que en las grandes. A lo largo de muchas
generaciones, la deriva da lugar de manera inexorable a una
pérdida de diversidad genética. Si algunos de los alelos que se
han fijado son recesivos deletéreos, la deriva genética da lugar
a la reducción de la eficacia de los individuos de la población.
El apareamiento no aleatorio no modifica por sí mismo
las frecuencias alélicas y por ello no es, estrictamente hablando, un mecanismo evolutivo. Sin embargo, el apareamiento
no aleatorio tiene influencia sobre las frecuencias genotípicas. Por ejemplo, las poblaciones consanguíneas tienen más
homozigotos y menos heterozigotos que poblaciones de
tamaño comparable en las que el apareamiento es aleatorio.
Un aumento de la homozigosis da lugar a menudo a que los
alelos recesivos deletéreos queden expuestos, lo que da lugar
a una reducción de la eficacia conocida como depresión
consanguínea.
Tal como se ejemplifica en el caso de la gallina grande de
las praderas de Illinois, los fenómenos discutidos en este
capítulo encuentran su aplicación práctica en las tareas conservacionistas. La deriva puede eliminar de las pequeñas
poblaciones remanentes la diversidad genética, dando lugar
a la depresión consanguínea y al grave riesgo de la extinción.
La migración puede a veces restaurar la pérdida en diversidad genética, mejorando la probabilidad de que la población
sobreviva a largo plazo.
Preguntas
1. Los especialistas en conservación intentan a menudo habilitar
corredores de hábitats sin desarrollar para que las grandes
reservas queden unidas en una red. ¿Por qué? ¿Qué objetivos
genéticos cree que persiguen los especialistas en conservación?
2. En el gráfico de la Figura 6.26 se representa FST, una medida de la diferenciación genética entre poblaciones, en función
de la distancia geográfica. Los datos son de poblaciones humanas europeas. La diferenciación genética se ha calculado
192 PARTE II Los mecanismos del cambio evolutivo
Cromosoma Y
mtDNA
Autosomas
0,12
0,08
FST
0,04
Figura 6.26 Distancia genética entre poblaciones humanas en
función de la distancia geográfica La distancia genética (FST) es
0
una medida de diferenciación genética entre poblaciones. Aquí se ha
calculado basándose en loci autosómicos (azul), mitocondriales (verde)
y del cromosoma Y (rojo). De Seielstad et al. (1998). Copyright © 1998
Nature Genetics. Reimpreso con el permiso de Nature Publishing
Group, New York, NY, y de M. T. Seielstad, Ph.D.
0
200
400
600
Distancia (kilómetros)
800
1000
basándose en loci autosómicos (heredados de ambos padres),
mitocondriales (heredados sólo de la madre) y del cromosoma Y (heredados sólo del padre).Advierta que los patrones son
diferentes para los tres tipos de loci. Recuerde que la migración tiende a homogeneizar las frecuencias alélicas entre las
poblaciones. Desarrolle una hipótesis que explique por qué las
frecuencias alélicas son más homogéneas entre las poblaciones para los loci autosómicos y mitocondriales que para los
del cromosoma Y. Luego vaya a la hemeroteca y lea el siguiente artículo para ver si su hipótesis es similar a la propuesta por
los biólogos que prepararon el gráfico:
Seielstad, M. T., E. Minch, and L. L. Cavalli-Sforza. 1998.
Genetic evidence for […] in humans. Nature Genetics
20:278-280. [Se ha eliminado parte del título para animar
a los lectores a desarrollar sus propias hipótesis.]
3. La pérdida de heterozigosidad puede ser especialmente nociva en los loci MHC, ya que la variabilidad alélica de estos loci
aumenta la resistencia a las enfermedades. Análisis de loci
microsatélites demuestran que los lobos de la Isla Royale,
Michigan, son altamente consanguíneos (Wayne et al. 1991).
Esta población de lobos se desplomó durante una infección
del parvovirus canino en la década de 1980. ¿Cómo podrían
unirse estos dos datos dispares?¿Cómo podría comprobar sus
ideas?
4. Si fuera encargado de la conservación de las lagartijas con
collar de los Ozarks, una de sus tareas podría ser reintroducir
las lagartijas en los claros donde se hubieran extinguido.
Cuando reintroduzca las lagartijas en un claro, tendrá que elegir entre utilizar individuos sólo de una de las poblaciones de
los claros existentes, o de varias poblaciones. ¿Cuáles serían las
consecuencias evolutivas de cada alternativa, tanto para las
poblaciones donantes como para las receptores? ¿Qué estrategia seguiría y por qué?
5. Recuerde el síndrome de Ellis-van Creveld, una enfermedad
genética que es anormalmente frecuente entre los Amish. La
población Amish de Pennsylvania tiene ahora unas 10.000
personas.
a. ¿Qué fuerzas evolutivas están actuando en la actualidad
sobre el alelo del síndrome de Ellis-van Creveld en esta
población? ¿Por qué cree que el alelo se mantiene en frecuencias relativamente elevadas? ¿Cómo podría comprobar sus ideas?
b. Suponga que cientos de personas que no pertenecen a la
población Amish se casan con personas Amish cada año y
que sus hijos quedan dentro de la comunidad Amish. ¿Qué
sucedería con la frecuencia del síndrome de Ellis-van Creveld y por qué?
6. Bodmer y McKie (1995) revisaron varios casos, además del
síndrome de Ellis-van Creveld de los Amish, en los que las
enfermedades genéticas se dan con una frecuencia anormalmente alta en poblaciones que están, o estuvieron, relativamente aisladas. Por ejemplo, una deficiencia enzimática
llamada tirosinemia hereditaria se da con una frecuencia anormalmente elevada en la región de Chicoutimi al norte de la
ciudad de Québec en Canadá. Una anomalía llamada porfiria es poco corriente en surafricanos de ascendencia holandesa. ¿Por qué hay enfermedades genéticas tan corrientes en
poblaciones aisladas? ¿Qué es lo que estas poblaciones tienen
en común?
7. Las islas oceánicas son famosas por sus especies endémicas :
formas únicas que no se dan en ningún otro lugar (véase
Quammen 1996 para una narración impresionante y muy
amena). Considere los papeles de la migración y de la deriva genética en la formación de nuevas especies en islas
remotas.
a. ¿Cómo se establecen en islas remotas especies animales y
vegetales? ¿Cree que los endemismos de las islas es más
probable que evolucionen en ciertos grupos de animales
y vegetales que en otros?
b. Considere una población nueva que acaba de llegar a una
isla remota. ¿Es probable que la población sea grande o
pequeña? Los efectos fundadores, la deriva genética y las
olas adicionales de migración a partir del continente,
¿jugarán un papel relativamente grande o pequeño en la
evolución de la nueva población de la isla (comparada
con una población similar en una isla cercana al continente)? ¿ Necesita ayuda su respuesta para explicar por
qué las especies raras endémicas son más frecuentes en
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 193
islas remotas (oceánicas) que en islas próximas al continente?
8. Como hemos visto, la consanguinidad puede reducir la eficacia de los descendientes al exponerse alelos recesivos deletéreos. Sin embargo, algunos criadores de animales practican
generaciones de cuidadosa consanguinidad en una familia, o
“línea de cría”, y sorprendentemente muchos de los animales de la línea, desde perros campeones a vacas premiadas, tienen salud y fertilidad normales. ¿Cómo es posible que la
consanguinidad continúe durante muchas generaciones sin
que se presente la depresión consanguínea debida a los alelos
recesivos? (Sugerencia: los criadores de animales responsables
no utilizan animales para cruces que se sepa lleven caracteres
deletéreos.) En general, si en una pequeña población se continúa generando consanguinidad durante muchas generaciones, ¿qué sucederá con la frecuencia de los alelos recesivos
deletéreos con el tiempo?
9. Hacia mediados de la década de 1980, los biólogos conservacionistas recomendaban de mala gana que los zoológicos
no deberían intentar conservar poblaciones en cautividad de
todas las especies de los grandes felinos en peligro de extinción. Por ejemplo, algunos biólogos recomendaban interrumpir los esfuerzos para criar al extremadamente raro león
asiático, la hermosa especie que se observa en los gravados
chinos. En lugar del león asiático, los biólogos recomendaban
aumentar las poblaciones en cautividad de otros felinos en
peligro de extinción, como el tigre siberiano o el leopardo
del Amur. Reduciendo el número de especies mantenidas en
cautividad, los biólogos esperaban aumentar el tamaño de las
poblaciones en cautividad de cada especie hasta varios cientos, preferiblemente hasta al menos 500. ¿Por qué los biólogos
conservacionistas pensaban que esto era tan importante como
para arriesgarse a perder para siempre al león asiático?
10. En este capítulo vimos que en muchos casos, las frecuencias
génicas de las pequeñas poblaciones cambian a un ritmo distinto que el de las poblaciones grandes. Como revisión, indique si los siguientes procesos tendrán normalmente efectos
mayores, menores o parecidos sobre la evolución de las pequeñas poblaciones comparando con las grandes poblaciones.
Selección.
Migración.
Deriva genética.
Consanguinidad.
Mutaciones nuevas por individuos.
Mutaciones nuevas por generación en el conjunto de la
población.
Sustitución de alelos viejos por mutaciones nuevas.
Fijación de una mutación nueva.
Explorando la bibliografía
11. Para un trabajo que explore la migración como mecanismo
homogeneizador de las frecuencias alélicas en poblaciones
humanas, véase:
Parra, E. J., Marcini,A., et al. 1998. Estimating African-American admixture proportions by use of population-specific
alleles. American Journal of Human Genetics 63: 1839-1851.
12. Para otro ejemplo similar al de la investigación de Templeton
y sus colegas (1990) sobre las lagartijas con collar, en el que
los biólogos se aprovecharon de un experimento natural para
comprobar predicciones acerca de los efectos de la deriva
genética sobre la diversidad genética, véase:
Eldridge, M. D. B., King, J. M., et al. 1999. Unprecedented
low levels of genetic variation and inbreeding depression in
an island population of the black-footed rock-wallaby. Conservation Biology 13: 531-541.
13. En la Sección 6.3 mencionamos que la depresión consanguínea es de interés para los biólogos que intentan conservar
organismos en peligro de extinción con tamaños poblacionales pequeños. Los genéticos han descubierto recientemente que la depresión consanguínea varía según ambientes y
familias. Para trabajos que exploran las implicaciones de este
descubrimiento para los esfuerzos de la conservación, véase:
Pray, L. A., J. M. Schwartz, C. J. Goodnight, and L. Stevens.
1994. Environmental dependency of inbreeding depression:
Implications for conservation biology. Conservation Biology 8:
562-568.
Pray, L.A., and C J. Goodnight. 1995. Genetic variation in inbreeding depression in the red flour beetle Tribolium castaneum. Evolution 49: 176-188.
14. Determine el tamaño poblacional mínimo necesario para
hacer improbable la extinción de una especie por un largo
período es un área activa de investigación en la genética de
la conservación. Los siguientes trabajos exploran este asunto:
Lande, R. 1995. Mutation and conservation. Conservation Biology 9: 782-791.
Lynch, M. 1996.A quantitative genetic perspective on conservation issues. In J. C.Avise and J. Hamrick, eds. Conservation
Genetics: Case Histories from Nature. New York: Chapman
and Hall, 471-501.
15. Durante largo tiempo se han utilizado a los guepardos como
ejemplo clásico de una especie cuya baja diversidad genética
les pone en un mayor riesgo de extinción. Otros investigadores han debatido la validez de este punto de vista. Para
comenzar con el tema, véase:
Menotti-Raymond, M., and S. J. O’Brien. 1993. Dating the
genetic bottleneck of the African cheetah. Proceedings of the
National Academy of Sciences, USA 90: 3172-3176.
194 PARTE II Los mecanismos del cambio evolutivo
Merola, M. 1994.A reassessment of homozygosity and the case
for inbreeding depression in the cheetah, Acinonyx jubatus:
Implications for conservation. Conservation Biology 8: 961-971.
16. Para otros intentos en determinar si la poca diversidad genética amenaza la supervivencia de las poblaciones, véase:
Ledberg, P. L. 1993. Strategies for population reintroduction:
Effects of genetic variability on population growth and size.
Conservation Biology 7: 194-199.
Jimenez, J. A., K. A. Hughes, G. Alaks, L. Graham, and R. C.
Lacy. 1994.An experimental study of inbreeding depression
in a natural habitat. Science 266: 271-273.
Sanjayan, M. A., K. Crooks, G. Zegers, and D. Foran. 1996.
Genetic variation and the immune response in natural
populations of pocket gophers. Conservation Biology 10:
1519-1527.
Bibliografía
Gran parte del material en genética de poblaciones de este capítulo viene modelizado después de su presentación en los siguientes:
Crow, J. F. 1983. Genetics Notes. Minneapolis, MN: Burgess Publishing.
Felsenstein, J. 1997. Theoretical Evolutionary Genetics. Seattle,WA:ASUW Publishing,
University of Washington.
Griffiths, A. J. F., J. H. Miller, D. T. Suzuki, R. C. Lewontin, and W. M. Gelbert.
1993. An Introduction to Genetic Analysis. New York:W. H. Freeman.
Maynard Smith, J. 1998. Evolutionary Genetics. Oxford University Press, Oxford.
Roughgarden, J. 1979. Theory of Population Genetics and Evolutionary Ecology:An Introduction. MacMillan Publishing, New York.
Templeton,A. R. 1982.Adaptation and the integration of evolutionary forces. In R.
Milkman, ed., Perspectives on Evolution. Sunderland, MA: Sinauer, 15-31.
Aquí está la lista de todas las otras citas de este capítulo:
Ayala, F. J., and J. A. Kiger, Jr. 1984. Modern Genetics. Menlo Park, CA: Benjamin/Cummings.
Barrett, S. C. H., and D. Charlesworth. 1991. Effects of a change in the level of inbreeding on the genetic load. Nature 352: 522-524.
Bittles, A. H. , and J.V. Neel. 1994.The costs of human inbreeding and their implications for variations at the DNA level. Nature Genetics 8: 117-121.
Bodmer,W., and R. McKie. 1995. The Book of Man. New York: Scribner.
Bouzat, J. L., H.A. Lewin, and K. N. Paige. 1998.The ghost of genetic diversity past:
Historical DNA analysis of the greater prairie chicken. American Naturalist
152: 1-6.
Buri, P. 1956. Gene frequency in small populations of mutant Drosophila. Evolution 10: 367-402.
Camin, J. H., and P. R. Ehrlich. 1958. Natural selection in water snakes (Natrix sipedon L.) on islands in Lake Erie. Evolution 12: 504-511.
Dudash, M. R. 1990. Relative fitness of selfed and outcrossed progeny in a selfcompatible, protandrous species, Sabatia angularis L. (Gentianaceae):A comparison in three environments. Evolution 44: 1129-1139.
Dudash, M. R., D. E. Carr, and C. B. Fenster. 1997. Five generations of enforced
selfing and outcrossing in Mimulus guttatus: Inbreeding depression variation at
the population and family level. Evolution 51: 54-65.
Giles, B. E., and J. Goudet. 1997. Genetic differentiation in Silene dioica metapopulations: Estimation of spatiotemporal effects in a successional plant species.
American Naturalist 149: 507-526.
Gillespie, J. H. 1991. The Causes of Molecular Evolution. New York: Oxford University
Press.
Grant, P. R., and B. R. Grant. 1995.The founding of a new population of Darwin’s finches. Evolution 49: 229-240.
Greenwood, P. J., P. H. Harvey, and C. M. Perrins. 1978. Inbreeding and dispersal
in the great tit. Nature 271: 52-54.
Hamilton,W. D. 1967. Extraordinary sex ratios. Science 156: 477-488.
Hamilton,W. D. 1979.Wingless and fighting males in fig wasps and other insects.
In M. S. Blum and N.A. Blum, eds., Sexual Selection and Reproductive Competition in Insects. New York:Academic Press, 167-220.
Hartl, D. L. 1981. A Primer of Population Genetics. Sunderland, MA: Sinauer.
Hill, J. L. 1974. Peromyscus: Effect of early pairing on reproduction. Science 186:
1042-1044.
Johnston, M. 1992. Effects of cross and self-fertilization on progeny fitness in Lobelia cardinalis and L. siphilitica. Evolution 46: 688-702.
Keller, L., P.Arcese, J. N. M. Smith,W. M. Hochachka, and S. C. Stearns. 1994. Selection against inbred song sparrows during a natural population bottleneck.
Nature 372: 356-357.
Kerr,W. E., and S.Wright. 1954. Experimental studies of the distribution of gene
frequencies in very small populations of Drosophila melanogaster. I. Forked. Evolution 8: 172-177.
Kimura, M. 1968. Evolutionary rate at the molecular level. Nature 217: 624-626.
Kimura, M. 1983. The Neutral Theory of Molecular Evolution. New York: Cambridge University Press.
King, R. B. 1987. Color pattern polymorphism in the Lake Erie water snake, Nerodia sipedon insularum. Evolution 41: 241-255.
King, R. B. 1993a. Color pattern variation in Lake Erie water snakes: Inheritance. Canadian Journal of Zoology 71: 1985-1990.
King, R. B. 1993b. Color-pattern variation in Lake Erie water snakes: Prediction
and measurement of natural selection. Evolution 47: 1819-1833.
King, R. B., and R. Lawson. 1995. Color-pattern variation in Lake Erie water
snakes:The role of gene flow. Evolution 49: 885-896.
King, R. B., and R. Lawson. 1997. Microevolution in island water snakes. BioScience 47: 279-286.
Lynch, M., and W. Gabriel. 1990. Mutation load and the survival of small populations. Evolution 44: 1725-1737.
McCall, C., D. M.Waller, and T. Mitchell-Olds. 1994. Effects of serial inbreeding
on fitness components in Impatiens capensis. Evolution 48: 818-827.
Paul, R. E. L., M. J. Packer, M.Walmsley, M. Lagog, L. C. Ranford-Cartwright, R.
Paru, and K. P. Day. 1995. Mating patterns in malaria parasite populations of
Papua, New Guinea. Science 269: 1709-1711.
Polans, N. O., and R.W. Allard. 1989.An experimental evaluation of the recovery
potential of ryegrass populations from genetic stress resulting from restriction
of population size. Evolution 43: 1320-1324.
Postlethwait, J. H., and J. L. Hopson. 1992. The Nature of Life, 2nd ed. New York:
McGraw-Hill.
Quammen, D. 1996. The Song of the Dodo. New York:Touchstone.
Ralls, K., K. Brugger, and J. Ballou. 1979. Inbreeding and juvenile mortality in
small populations of ungulates. Science 206: 1101-1103.
Read,A. F.,A. Narara, S. Nee,A. E. Keymer, and K. P. Day. 1992. Gametocyte sex
ratios as indirect measures of outcrossing rates in malaria. Parasitology 104: 387395.
Seielstad, M.T., E. Minch, and L. L. Cavalli-Sforza. 1998. Genetic evidence for a
higher female migration rate in humans. Nature Genetics 20: 278-280.
Soulé, M. E., and L. S. Mills. 1998. No need to isolate genetics. Science 282: 16581659.
Templeton, A. R., K. Shaw, E. Routman, and S. K. Davis. 1990.The genetic consequences of habitat fragmentation. Annals of the Missouri Botanical Garden 77:13-27.
Thomas, J. 1998. A bird’s race toward extinction is halted. The New York Times 29
December: D3.
van Noordwijk, A. J., and W. Scharloo. 1981. Inbreeding in an island population
of the great tit. Evolution 35: 674-688.
Wayne, R. K., N. Lehman, D. Girman, P. J. P. Gogan, D. A. Gilbert, K. Hansen, R.
O. Peterson, U. S. Seal,A. Eisenhawer, L. D. Mech, and R. J. Krumenaker. 1991.
Capítulo 6 Genética mendeliana en poblaciones II: migración, deriva genética y apareamiento no aleatorio 195
Conservation genetics of the endangered Isle Royale gray wolf. Conservation
Biology 5: 41-51.
Wright, S. 1931. Evolution in Mendelian populations. Genetics 16: 97-159.
Westemeier, R. L., S.A. Simpson, and D.A. Cooper. 1991. Successful exchange of
prairie-chicken eggs between nests in two remnant populations. Wilson Bulletin
103:717-720.
Westemeier, R. L., J. D. Brawn, et al. 1998.Tracking the long-term decline and recovery of an isolated population. Science 282: 1695-1698.
Wolfe, L. M. 1993. Inbreeding depression in Hydrophyllum appendiculatum: Role of
maternal effects, crowding, and parental mating history. Evolution 47: 374-386.
Young,A.,T. Boyle, and T. Brown. 1996.The population genetic consequences of
habitat fragmentation for plants. Trends in Ecology and Evolution 11: 413-418.
CAPÍTULO
7
Evolución en loci múltiples:
ligamiento, sexo y genética cuantitativa
Un histograma vivo. Estos estudiantes de la Universidad de Connecticut se han distribuido en columnas de acuerdo con su estatura
(Petern Morenus, University of Connecticut)
E
N LOS CAPÍTULOS 5 Y 6 INTRODUJIMOS LA GENÉTICA DE POBLACIONES BÁSICA,
apoyándonos en el equilibrio de Hardy-Weinberg. Los modelos que hemos discutidos son elegantes y potentes. Por ejemplo, la Figura 5.14 (página 130) documenta un caso
en el que un investigador utilizó la genética de poblaciones para predecir de manera precisa el curso de la evolución en las siguientes 12 generaciones. En términos humanos, esto
es equivalente a predecir con precisión lo que sucederá dentro de 300 años. ¡Qué teoría!
Sin embargo, como con muchas teorías, la genética de poblaciones básica adquiere su
elegancia al precio de la simplificación. Los modelos que hemos utilizado hasta ahora
siguen la pista de la frecuencia de los alelos de un locus cada vez. Sólo somos capaces de
considerar la evolución de caracteres que están (o parecen estar) controlados por un solo
gen. Desde luego, los genomas de los organismos tienen cientos o miles de loci.Y muchos
caracteres vienen determinados por la influencia combinada de numerosos genes.
En el Capítulo 7 construiremos nuestros modelos de los mecanismos evolutivos más
próximos a organismos reales considerando dos o más loci simultáneamente. El primer paso
en dicha dirección será una ampliación del análisis de Hardy-Weinberg simultáneamente
para dos loci. El modelo para dos loci nos dirá cuándo podemos usar los modelos para un
solo locus, desarrollados en los Capítulos 5 y 6, para hacer predicciones y cuándo debemos tener en cuenta la confusa influencia de la selección en otros loci.
197
198 PARTE II Los mecanismos del cambio evolutivo
Nuestra discusión de la versión del análisis de Hardy-Weinberg para dos loci, que usa
términos como “desequilibrio de ligamiento,” puede parecer al principio desesperanzadoramente abstracta. Pero el esfuerzo invertido en comprender dará lugar a dos sorprendentes recompensas. La primera es que el modelo para dos loci proporciona herramientas
con las que reconstruir la historia de los genes y de las poblaciones. Utilizaremos dichas
herramientas para aplicarlas a una cuestión no resuelta en la discusión de los Capítulos 4
y 5 sobre el CCR5-∆32, el alelo que protege contra el VIH: ¿De dónde viene el alelo ∆32
y por qué sólo se encuentra en Europa? La segunda es que el modelo para dos loci proporciona ideas sobre el significado adaptativo de una de las características más notables y
desconcertantes de los organismos: la reproducción sexual.
El modelo para dos loci es más realista que el modelo para un locus, pero todavía es
inadecuado para analizar la evolución de caracteres determinados por la combinación de
los efectos de alelos de muchos loci. Cuando estudiamos tales caracteres, no sabemos a
menudo la identidad de los loci implicados. La última sección de este capítulo introduce
la genética cuantitativa, la rama de la biología evolutiva que proporciona herramientas para
analizar los caracteres multilocus. De nuevo recibiremos una sorprendente recompensa. La
discusión de la genética cuantitativa nos permitirá derribar ideas erróneas sobre las diferencias en el IQ entre grupos étnicos.
7.1. Evolución de dos loci: equilibrio y desequilibrio
de ligamiento
Locus A,
con alelos A y a
Locus B,
con alelos B y b
Figura 7.1 Un par de loci
ligados
En esta sección ampliaremos el análisis de la versión para un locus de Hardy-Weinberg
para considerar simultáneamente dos loci. Sin embargo, nuestra discusión se comprenderá más fácilmente si nos fijamos en un par de loci situados en el mismo cromosoma. Es
decir, consideraremos dos loci físicamente ligados (Figura 7.1). Imaginaremos que el locus
A tiene dos alelos, A y a, y que el locus B tiene dos alelos, B y b.
En el análisis de Hardy-Weinberg para un solo locus, estuvimos interesados principalmente en seguir las frecuencias alélicas. En la versión para dos loci, nos interesará seguir
tanto las frecuencias alélicas como las cromosómicas.Advierta que las suposiciones hechas
en los párrafos anteriores, nos permiten cuatro genotipos cromosómicos diferentes: AB,
Ab, aB y ab.A veces se denomina al genotipo multilocus de un cromosoma o gameto como
su haplotipo (término que viene de la contracción de “haploide” y “genotipo”).
Nuestro objetivo principal será determinar si la selección sobre el locus A interferirá
en nuestra capacidad para utilizar los modelos de los Capítulos 5 y 6, y hacer predicciones acerca de la evolución del locus B. La respuesta será:“A veces, dependiendo de si los
loci están en equilibrio o en desequilibrio de ligamiento.” Pronto definiremos el equilibrio y el desequilibrio de ligamiento.
Cuando utilizamos modelos
Ejemplo numérico
genético-poblacionales para
Un ejemplo numérico nos ilustrará sobre los conceptos clave y nos ayudará a definir términos. En la Figura 7.2 se muestran dos poblaciones hipotéticas, cada una con un conjunto genómico de 25 cromosomas.Al estudiar la estructura genética de estas poblaciones,
lo primero que podríamos hacer es calcular las frecuencias alélicas. En la población de arriba, por ejemplo, 15 de los 25 cromosomas llevan el alelo A en el locus A. Por ello la frecuencia del alelo es 15/25 = 0,6. Lo mismo es cierto para la población de abajo. De hecho
las frecuencias alélicas en los dos loci son idénticas en las dos poblaciones. Si sólo estuviéramos estudiando el locus A, o sólo el locus B, concluiríamos que las dos poblaciones
son idénticas.
analizar la evolución de un
locus dado, ¿necesitamos
preocuparnos de los efectos
de la selección sobre otros
loci? Sólo si el locus de interés
y los otros loci están en
desequilibrio de ligamiento.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 199
(a) Población en equilibrio de ligamiento
Cromosomas
A
Cromosomas
a
1,0
A
B
A
B
A
b
A
b
A
b
a
B
a
B
a
B
a
b
a
b
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
0,8
Frecuencia
A
B
a
B
a
B
a
B
a
B
0,6
AB
aB
Cromosomas
B
Ab
ab
Cromosomas
b
0,4
0,2
a
B
0
0
0,2
0,4
0,6
0
0,2
0,4
Frecuencia
Cálculo de las frecuencias
Cromosoma AB: 12 ÷ 25 = 0,48
Ab: 3 ÷ 25 = 0,12
aB: 8 ÷ 25 = 0,32
ab: 2 ÷ 25 = 0,08
Alelo A: 15 ÷ 25 = 0,6
a: 10 ÷ 25 = 0,4
B: 20 ÷ 25 = 0,8
b: 5 ÷ 25 = 0,2
Alelo B en cromosomas A: 12 ÷ 15 = 0,8
B en cromosomas a: 8 ÷ 10 = 0,8
(b) Población en desequilibrio de ligamiento
Cromosomas
A
Cromosomas
a
1,0
A
B
A
B
A
B
A
b
A
b
A
b
A
b
a
B
a
B
a
B
a
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
0,8
Frecuencia
A
B
a
B
a
B
a
B
a
B
a
B
AB
0,6
aB
Cromosomas
B
ab
Cromosomas
b
0,4
0,2
Ab
0
0
a
b
0,2
0,4
0,6
0
0,2
0,4
Frecuencia
Cálculo de las frecuencias
Alelo A: 15 ÷ 25 = 0,6
a: 10 ÷ 25 = 0,4
B: 20 ÷ 25 = 0,8
b: 5 ÷ 25 = 0,2
Cromosoma AB: 11 ÷ 25 = 0,44
Ab: 4 ÷ 25 = 0,16
aB: 9 ÷ 25 = 0,36
ab: 1 ÷ 25 = 0,04
Alelo B en cromosomas A: 11 ÷ 15 = 0,73
B en cromosomas a: 9 ÷ 10 = 0,9
Figura 7.2 Dos poblaciones: una en equilibrio de ligamiento y otra en desequilibrio de ligamiento.
Pero las dos poblaciones no son idénticas. Esto lo descubrimos cuando calculamos las
frecuencias cromosómicas. Por ejemplo, en la población de arriba 12 de los 25 cromosomas lleva el haplotipo AB, con una frecuencia de 0,48. Por otro lado, en la población de
abajo la frecuencia de los cromosomas AB es 11 de 25, o el 0,44. Ésta es la primera lección del análisis de Hardy-Weinberg para dos loci: un par de poblaciones pueden tener
frecuencias alélicas idénticas pero frecuencias cromosómicas diferentes.
200 PARTE II Los mecanismos del cambio evolutivo
Para entender el desequilibrio
de ligamiento, es útil
reconocer que cuando
consideramos al mismo
tiempo dos loci ligados, las
poblaciones pueden tener
frecuencias alélicas idénticas,
pero frecuencias
cromosómicas (es decir,
haplotipos) distintas.
Otra forma de ver las diferencias entre las dos poblaciones de la Figura 7.2 es calculando
la frecuencia del alelo B en cromosomas que llevan el alelo A respecto de los que llevan
el alelo a. En la población de arriba hay 15 cromosomas que llevan el alelo A, 12 de los
cuales llevan el alelo B. La frecuencia de B en cromosomas A es así 12/15 = 0,8. En la
misma población hay 10 cromosomas que llevan el alelo a, 8 de las cuales llevan el alelo
B. La frecuencia de B en cromosomas a es 8/10 = 0,8. Por ello, en la población de arriba,
la frecuencia del alelo B es la misma en cromosomas que llevan A que en los que llevan
a. No ocurre lo mismo en la población de abajo. Allí la frecuencia de B es 0,73 en cromosomas A, pero 0,9 en cromosomas a.
Los gráficos de barras de la Figura 7.2 proporcionan una representación visual de la
diferencia entre las dos poblaciones. La anchura de las dos barras en cada gráfico representa la frecuencia de los cromosomas que llevan A respecto de los cromosomas que llevan a. Advierta que la anchura combinada de las dos barras debe de ser igual a 1, por lo
que si una barra se hace más ancha la otra debe hacerse más estrecha. La parte sombreada respecto de la no sombreada de cada barra representa la frecuencia del alelo B respecto
del alelo b en los cromosomas en cuestión. El gráfico de barras nos permite ver a simple
vista lo que descubrimos mediante el cálculo en los párrafos anteriores. En la población
de arriba la frecuencia de B es la misma en cromosomas A y en cromosomas a; en las dos
barras está sombreada la misma fracción. En la población de abajo la frecuencia de B es
menor en cromosomas A que en cromosomas a.
Definición del desequilibrio de ligamiento
En la población de arriba de la Figura 7.2, los loci A y B se encuentran en equilibrio
de ligamiento. En la población de abajo, los loci se encuentran en desequilibrio de ligamiento. En una población, dos loci se encuentran en equilibrio de ligamiento cuando el genotipo de un cromosoma en un locus es independiente de su genotipo en el
otro locus. Esto significa que, conociendo el genotipo del cromosoma para un locus
no nos dice nada sobre cuál es el genotipo en el otro locus. Dos loci se encuentran en
desequilibrio de ligamiento cuando no hay una asociación aleatoria entre el genotipo de un cromosoma para un locus y su genotipo en el otro locus. Si conocemos el
genotipo de un cromosoma en un locus, esto nos da una clave acerca del genotipo en
el otro.
Estas definiciones son bastante abstractas. Más concretamente, las siguientes condiciones son ciertas para un par de loci y sólo lo son si están en equilibrio de ligamiento:
Cuando los genotipos de un
locus son independientes de
los genotipos del otro locus,
los dos loci se encuentran en
equilibrio de ligamiento. Si no
es así, los dos loci se
encuentran en desequilibrio de
ligamiento.
1. La frecuencia de B en los cromosomas que lleven el alelo A es la misma que la frecuencia de B en los cromosomas que lleven el alelo a.
2. La frecuencia de cualquier haplotipo cromosómico se puede calcular multiplicando las
frecuencias de los alelos constituyentes. Por ejemplo, se puede calcular la frecuencia de
los cromosomas AB multiplicando la frecuencia del alelo A por la del alelo B.
3. La cantidad D, conocida como el coeficiente del desequilibrio de ligamiento, es igual
a cero. D se calcula como
gABgab – gAbgaB
donde gAB, gab, gAb y gaB son las frecuencias de los cromosomas AB, ab,Ab y aB (véase
el Cuadro 7.1).
Ya hemos establecido, mediante cálculo y con gráficos de barras, que la primera condición es cierta para la población de arriba de la Figura 7.2, pero falsa para la población de
abajo. El lector puede verificar que las condiciones segunda y tercera son igualmente ciertas para la población de arriba y falsas para la de abajo.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 201
La versión del análisis de Hardy-Weinberg para dos locus
Podemos realizar la versión del análisis de Hardy-Weinberg para dos loci, que es análoga
a la versión que desarrollamos en el Capítulo 5 para un solo locus. Asumimos las condiciones de Hardy-Weinberg de ausencia de selección, de mutación, de migración, población de tamaño infinito y apareamiento aleatorio, y seguimos las frecuencias cromosómicas
durante una generación completa en el ciclo de vida de nuestra población, desde gametos en el conjunto de genes, a zigotos, a adultos y de nuevo a gametos. Estos cálculos se
presentan en el Cuadro 7.2. Proporciona nuestra primera evidencia de que el equilibrio
de ligamiento es importante en la evolución. Si los dos loci de nuestra población ideal están
en equilibrio de ligamiento, entonces, en las condiciones de Hardy-Weinberg, las frecuencias cromosómicas no cambiarán de una generación a la siguiente. Si por el contrario los loci se encuentran en desequilibrio de ligamiento, entonces las frecuencias cromosómicas cambiarán.
¿Cómo se produce el desequilibrio de ligamiento en una población?
En las condiciones de HardyWeinberg, las frecuencias
cromosómicas permanecen sin
cambio de una generación a la
siguiente, pero sólo si los loci
en cuestión se encuentran en
equilibrio de ligamiento. Si los
loci están en desequilibrio de
ligamiento, las frecuencias
cromosómicas se desplazan
hacia el equilibrio de
ligamiento en cada generación.
Tres mecanismos pueden dar origen al desequilibrio de ligamiento en una población con
apareamiento al azar: la selección sobre genotipos multilocus, la deriva genética y la mezcla de poblaciones. Consideraremos cada uno de estos mecanismos por turnos.
Para ver cómo la selección sobre genotipos multilocus puede dar lugar a desequilibrio
de ligamiento, comencemos con una población cuyo conjunto de genes se muestra en la
Figura 7.2a. Los locus A y B se encuentran en equilibrio de ligamiento. Imagine que los
gametos en este conjunto de genes se combinan al azar para producir los zigotos. En la parrilla de la Figura 7.3a aparecen los 10 tipos de zigotos producidos y sus respectivas frecuencias esperadas. Por ejemplo, ya que el 32% de los óvulos y el 32% de los espermatozoides
son aB, predecimos que la frecuencia de los zigotos aB/aB será 0,32 ⫻ 0,32 ⫽ 0,1024. Dejemos ahora que los zigotos se desarrollen hasta adultos y asignemos fenotipos como sigue:
los individuos con genotipo ab/ab tienen un tamaño de 10. En los otros genotipos, cada alelo
A o B añade una unidad al tamaño del individuo. Por ejemplo, los individuos aB/aB tienen
un tamaño de 12 y los individuos AB/Ab un tamaño de 13. Imagine, finalmente, que los
predadores capturan y se comen a todos los individuos cuyo tamaño es menor que 13. Los
CUADRO 7.1 El coeficiente del desequilibrio de ligamiento
E
l coeficiente del desequilibrio de ligamiento, que se
simboliza por D, se define como
gAB gab – gAb gaB
donde gAB, gab, gAb y gaB son las frecuencias de los cromosomas AB, ab,Ab y aB.
Para ver por qué D simboliza al coeficiente del desequilibrio de ligamiento, recuerde que cuando dos loci se encuentran en equilibrio de ligamiento, las frecuencias alélicas
de un locus son independientes de las frecuencias alélicas del otro locus. Sean p y q las frecuencias de A y a y
sean s y t las frecuencias de B y b. Si una población se
encuentra en equilibrio de ligamiento, entonces gAB = ps,
gAb = pt, gaB = qs y gab = qt. Y además,
D = psqt – ptqs = 0
Por otro lado, si la población se encuentra en desequilibrio de ligamiento, entonces gAB ≠ ps, gAb ≠ pt, gaB ≠ qs
y gab ≠ qt.Y D ≠ 0.
El valor máximo que puede alcanzar D es 0,25, cuando AB y ab son los únicos cromosomas presentes y cada
uno tiene una frecuencia de 0,5. El valor mínimo que
puede alcanzar D es –0,25, cuando Ab y aB son los únicos cromosomas presentes y cada uno en la frecuencia de
0,5. Por ello el cálculo de D es una forma útil de cuantificar el grado de desequilibrio de ligamiento de una
población.
202 PARTE II Los mecanismos del cambio evolutivo
CUADRO 7.2
Análisis de Hardy-Weinberg para dos loci
A
quí desarrollaremos la versión del equilibrio de
Hardy-Weinberg para dos loci. Demostraremos que
cuando una población ideal se encuentra en equilibrio
de ligamiento, las frecuencias cromosómicas no cambian
de una generación a la siguiente.
En la versión para un solo locus del análisis de HardyWeinberg, que introdujimos en el Capítulo 5, seguimos a
las frecuencias alélicas a lo largo de una generación completa del ciclo de vida de una población, del conjunto de
genes de una generación a los zigotos, de los zigotos a
adultos y de los adultos al conjunto de genes de la generación siguiente. Utilizaremos aquí una estrategia similar,
excepto en que no seguiremos a las frecuencias alélicas
sino a las cromosómicas. Los cromosomas de nuestros
organismos tienen dos loci: el locus A, con los alelos A y
a y el locus B con los alelos B y b. (Con estos símbolos no
intentamos necesariamente implicar una relación de
dominancia y recesividad entre alelos. Los utilizamos sólo
porque permiten una lectura más fácil de las ecuaciones
que notaciones alternativas.) Hay cuatro tipos de cromosomas: AB, Ab, aB y ab.
Imagine una población ideal en la que el conjunto de
cromosomas AB, Ab, aB y ab se encuentran en las frecuencias gAB, gAb, gaB y gab, respectivamente. Si los gametos del
conjunto de genes se combinan al azar para formar los zigotos, entre los genotipos posibles se encuentra el AB/AB.
Su frecuencia será igual a la probabilidad de que un óvulo
elegido al azar tenga un cromosoma AB, multiplicado por
la probabilidad de que un espermatozoide elegido al azar
tenga también el cromosoma AB, o gAB ⫻ gAB. Otro genotipo posible entre los zigotos es AB/Ab. Su frecuencia
será 2 ⫻ gAB ⫻ gAb. Esta expresión tiene un 2 debido a
que hay dos maneras de construir un zigoto AB/Ab: un
óvulo AB puede ser fecundado por un espermatozoide
Ab, o un óvulo Ab por un espermatozoide AB. En conjunto hay 10 posibles zigotos. Los zigotos y sus frecuencias
son los siguientes:
AB/AB
gAB gAB
Ab/Ab
gAb gAb
aB/aB
gaB gaB
ab/ab
gab gab
AB/Ab
2gAB gAb
AB/aB
2gAB gaB
AB/ab
2gAB gab
Ab/aB
2gAb gaB
Ab/ab
2gAb gab
aB/ab
2gaB gab
Si permitimos que estos zigotos se desarrollen sin selección, entonces las frecuencias genotípicas en los adultos
serán las mismas que en los zigotos.
Hemos seguido a las frecuencias cromosómicas desde
el conjunto de genes de los zigotos a adultos.Ahora pode-
mos calcular las frecuencias cromosómicas en el conjunto de genes de la siguiente generación. Consideremos el
cromosoma AB. Cinco de los 10 genotipos adultos pueden producir gametos que tengan cromosomas AB. Los
adultos que pueden producir gametos AB, junto con la
porción de gametos AB que contribuyen al nuevo conjunto de genes, son:
Adulto
Porción de
gametos AB
aportados
AB/AB
gAB gAB
AB/aB
( )(2g
( )(2g
AB/ab
(1 – r)
Ab/aB
(r)
1
ᎏᎏ
2
1
ᎏᎏ
2
AB/Ab
Notas
AB gAb)
AB gaB)
( )(2g
1
ᎏᎏ
2
( )(2g
1
ᎏᎏ
2
AB gab)
Ab gaB)
Donde r ⫽ frecuencia de
recombinación
Donde r ⫽ frecuencia de
recombinación
La primera fila de esta tabla es directa: los adultos
AB/AB constituyen una fracción gABgAb de la población, y por ello contribuyen con los gAB gAb gametos del
conjunto de genes, todos ellos AB. La segunda fila es
también directa: los adultos AB/Ab constituyen una fracción gAB gAb de la población y por ello contribuyen con
los gABgAb gametos del conjunto de genes, la mitad de
ellos AB. Las últimas dos filas de la tabla requieren explicación.
Los adultos de genotipo AB/ab producirán gametos
con cromosomas AB sólo cuando se produzca meiosis sin
entrecruzamiento entre el locus A y el B. Cuando no
ocurra entrecruzamiento, la mitad de los gametos producidos por los adultos AB/ab llevarán cromosomas AB. Si
r es la frecuencia de entrecruzamiento, o recombinación,
entre el locus A y el locus B, entonces los individuos
AB/ab contribuirán al conjunto de genes con la porción
1
(1 ⫺ r) ᎏ2ᎏ (2gABgab) de gametos AB.
Los adultos de genotipo Ab/aB producirán gametos
con cromosomas AB sólo cuando en la meiosis haya entrecruzamiento entre los locus A y B. Cuando hay entrecruzamiento, la mitad de los gametos producidos por los adultos Ab/aB llevan cromosomas AB. Si r es la frecuencia de
entrecruzamiento, entonces los individuos Ab/aB contri1
buirán al conjunto de genes con la porción (r) ᎏ2ᎏ (2gAb gaB)
de gametos AB.
Podemos ahora escribir una expresión para gAB⬘, la frecuencia de los cromosomas AB en el nuevo conjunto de
genes:
()
()
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 203
CUADRO 7.2 Continuación
gAB⬘ ⫽ gAB gAB ⫹
( )(2gAB gAb) ⫹ ( )(2gAB gaB) ⫹
(1 ⫺ r)( )(2gAB gab) ⫹ (r)( )(2gAb gaB)
1
ᎏᎏ
2
Las expresiones para gAB⬘, gAb⬘, gaB⬘ y gab⬘ demuestran
que cuando una población se encuentra en equilibrio de
ligamiento (cuando D = 0) las frecuencias cromosómicas
no cambian de una generación a la siguiente. Por otro
lado, cuando la población se encuentra en desequilibrio de
ligamiento (cuando D ⫽ 0) las frecuencias cromosómicas
cambian de una generación a la siguiente. El primer genético de poblaciones que comunicó este resultado fue H. S.
Jennings (1917).
Tenemos que advertir que las frecuencias alélicas de un
par de loci pueden estar en desequilibrio de ligamiento
aun cuando los loci se encuentren en cromosomas distintos. Para loci en cromosomas distintos es adecuado hablar
de frecuencias gaméticas en lugar de frecuencias cromosómicas. El análisis de Hardy-Weinberg para tal situación
es idéntica a la que hemos desarrollado aquí, excepto en
1
que r es siempre exactamente igual a ᎏ2ᎏ .
1
ᎏᎏ
2
1
ᎏᎏ
2
1
ᎏᎏ
2
⫽ gAB gAB ⫹ gAB gAb ⫹ gAB gaB ⫹
gAB gab ⫺ rgAB gab ⫹ rgAb gaB
⫽ gAB( gAB ⫹ gAb ⫹ gaB ⫹ gab) ⫺
r(gAB gab ⫺ gAb gaB)
Podemos simplificar esta expresión un poco más advirtiendo que (gAB ⫹ gAb ⫹ gaB ⫹ gab) ⫽ 1 y que gAB gab ⫺
⫺ gAb gaB es D, definida en el texto y en el Cuadro 7.1.
Esto nos da:
gAB⬘ = gAB ⫺ rD
Dejemos al lector que derive las expresiones para las
otras tres frecuencias cromosómicas, que son:
gAb⬘ = gAb + rD
gaB⬘ = gaB + rD
()
gab⬘ = gab – rD
supervivientes, que representan el 65,28% de la población original, aparecen en la parrilla
de la Figura 7.3b.
En el conjunto de los supervivientes, los loci A y B están en desequilibrio de ligamiento. Quizá la manera más fácil de verlo es calculando la frecuencia del alelo a y del
b. Un modo de calcular la frecuencia de a es la siguiente: los individuos que llevan el alelo
(a)
(b)
Supervivientes a la predación
0,48 AB
Fr(AB/AB)
= 0,2304
0,1536
0,12 Ab
0,0576
0,32 aB
0,1536
0,08 ab
0,0384
0,0096
0,0384
0,1024
0,0256
01
0,
0,0384
Óvulos
0,08 ab
0,0256
0,0096
AB
Ab
aB
AB
AB/AB
0,2304
AB/Ab 0,0576
0,32 aB
0,0384
0,12 Ab
44
0,48 AB
0,0576
Esperma
AB/aB
0,1536
Ab
Ab/AB
0,0576
aB
aB/AB
0,1536
0,0064
Zigotos
Figura 7.3 La selección en genotipos multilocus puede dar lugar a desequilibrio de ligamiento En el cuadro (a) se muestran las
frecuencias esperadas de los zigotos producidos por apareamiento al azar en la población en equilibrio de ligamiento de la Figura 7.2a. En el
cuadro (b) se muestran los genotipos que sobreviven después de que los predadores hayan matado a todos los individuos con menos de tres alelos
en mayúscula en sus genotipos. La población de supervivientes se encuentra en desequilibrio de ligamiento.
204 PARTE II Los mecanismos del cambio evolutivo
(a)
Cromosomas
A
Frecuencia
Cromosomas Cromosomas
B
b
1,0
0,8
0,6
AB
0,4
0,2
Ab
0
0
0,2 0,4 0,6 0,8 1,0
Mutación en un
cromosoma Ab
A
b
a
b
convierte a A en a
(b)
Cromosomas Cromosomas
A
a
0,8
AB
0,6
ab
Frecuencia
1,0
0,4
0,2
Ab
0
0
0,2 0,4 0,6 0,8
0
La selección aumenta
la frecuencia de a
(c)
Cromosomas Cromosomas
A
a
Frecuencia
1,0
0,8
0,6
AB
ab
0,4
0,2
Ab
0
0
0,2 0,4 0,6
0
0,2 0,4
Frecuencia
Figura 7.4 La deriva genética
puede dar lugar a
desequilibrio de ligamiento
(a) Frecuencias cromosómicas en
una población finita en la que sólo
está presente un alelo, el A, en el
locus A; (b) frecuencias
cromosómicas después de que
una mutación da lugar a una sola
copia del alelo a; (c) después de la
selección a favor de a, aumenta la
frecuencia cromosómica de ab. La
población en (c) está en
desequilibrio de ligamiento. La
deriva es un mecanismo crucial
que da lugar al desequilibrio, ya
que este caso únicamente podrá
darse en una población finita.
a constituyen una fracción (0,1536 + 0,1536)/0,6528 ⬇ 0,47 de los supervivientes. Así
pues llevan el 47% de los alelos del locus A. La mitad de estos alelos serán a. Por consiguiente, la frecuencia de a entre los supervivientes es 0,5 ⫻ 0,47 ⬇ 0,24. La frecuencia
de b es, aproximadamente, 0,09. Si nuestros dos loci estuvieran en equilibrio de ligamiento, entonces, de acuerdo con el criterio 2 de nuestra lista, la frecuencia de los cromosomas ab sería 0,24 ⫻ 0,09 ⬇ 0,02. De hecho, la frecuencia de los cromosomas ab es
0. Nuestros dos loci se encuentran en desequilibrio de ligamiento. Como ejercicio, el lector podría demostrar que los loci también se encuentran en desequilibrio de ligamiento de acuerdo con los criterios 1 y 3.
Para ver cómo la deriva genética puede dar lugar a desequilibrio de ligamiento, observe el escenario esquematizado en la Figura 7.4. Este escenario comienza con un conjunto de genes en el que los únicos cromosomas presentes son el AB y el Ab (Figura 7.4a). En
otras palabras, en esta población no hay copias del alelo a. Los locus A y B se encuentran
en equilibrio de ligamiento. Imaginemos ahora que en un cromosoma Ab, una mutación
convierte al alelo A en a. Esto da lugar a un único cromosoma ab (Figura 7.4b). Esto sitúa
también a la población en desequilibrio de ligamiento, ya que hay un posible haplotipo cromosómico, el aB, que no existe. Imaginemos, finalmente, que la selección favorece al alelo
a frente al A, de tal manera que la frecuencia de a aumenta y la de A disminuye (Figura
7.4c). Esto aumenta el grado de desequilibrio de ligamiento entre el locus A y el B.
El lector puede sorprenderse de por qué atribuimos a la deriva genética el desequilibrio de ligamiento generado en este escenario, cuando los sucesos clave parece que son
la mutación y la selección. La razón es que el escenario, tal como lo describimos, sólo
podría darse en una población finita. En una población infinita, la mutación que convierte
al alelo A en el a se produciría no una sola vez, sino muchas veces en cada generación,
tanto sobre los cromosomas AB como Ab. En ningún momento habría ausencia de cromosomas aB. La selección que favorece a a sobre A aumentaría simultáneamente la frecuencia de los cromosomas ab y aB. Los locus A y B nunca estarían en desequilibrio de
ligamiento. Debido a que en nuestro escenario sólo se puede generar desequilibrio de ligamiento en una población finita, el mecanismo evolutivo decisivo que actúa es la deriva
genética. Fue a causa de un error de muestreo lo que ocasionó que la mutación que dio
lugar al alelo a, sucediera una sola vez y en un cromosoma Ab.
Finalmente, para ver cómo la mezcla de poblaciones puede dar lugar a desequilibrio
de ligamiento, imagine dos conjuntos de genes (Figura 7.5). En uno hay 60 cromosomas
AB, 20 Ab, 15 aB y 5 ab. En el otro hay 10 cromosomas AB, 40 Ab, 10 aB y 40 ab. Los
locus A y B se encuentran en equilibrio de ligamiento en cada conjunto génico, como se
demuestra por los dos gráficos de barras superiores de la Figura 7.5. Ahora combine los
dos conjuntos de genes. Esto da lugar a un nuevo conjunto de genes donde hay 70 cromosomas AB, 60 Ab, 25 aB y 45 ab. En este nuevo conjunto de genes los loci A y B se
encuentran en desequilibrio de ligamiento.
La selección sobre genotipos multilocus, la deriva genética y la mezcla de poblaciones
pueden dar lugar a desequilibrio de ligamiento debido a que pueden dar lugar a poblaciones en las que algunos haplotipos cromosómicos estén poco representados y otros
demasiado representados, cuando se compara con lo que deberían ser sus frecuencias en
equilibrio de ligamiento. Por ejemplo, en nuestro esquema de selección multilocus, la
selección actuaba con más fuerza contra ab que contra cualquier otro haplotipo, ya que
no sobrevivía ningún individuo que tuviera un cromosoma ab. En nuestro escenario de
deriva, un suceso aleatorio dio lugar a un cromosoma ab, pero no a un cromosoma aB.
En nuestro ejemplo de mezcla poblacional, una simple combinación de poblaciones con
frecuencias alélicas y cromosómicas diferentes dio lugar a una nueva población con un
exceso de cromosomas AB y ab.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 205
¿Qué elimina el desequilibrio de ligamiento de una población?
Coeficiente de desequilibrio
de ligamiento (D)
Frecuencia
0,8
0,6
0,4
0,2
0
0
60
AB
15
aB
20
Ab
5
ab
0,2 0,4 0,6 0,8 0
0,2
+
Frecuencia
1,0
0,8
0,6
0,4
10 AB
10 aB
40
Ab
40
ab
Cromosomas Cromosomas
B
b
1,0
0,2
0
0
0,2 0,4
0
0,2 0,4
=
1,0
Frecuencia
Al mismo tiempo que la selección, la deriva y la mezcla de poblaciones puede dar lugar
a desequilibrio de ligamiento en una población, la reproducción sexual lo reduce inexorablemente. Por reproducción sexual queremos indicar a la meiosis con entrecruzamiento
y fecundación cruzada. La unión de gametos de padres no emparentados reúne cromosomas con haplotipos diferentes. Cuando los zigotos llegan a adultos y se reproducen, el
entrecruzamiento en la meiosis rompe las viejas combinaciones de alelos y da lugar a nuevas combinaciones. La formación de nuevas combinaciones de alelos durante la reproducción sexual se denomina recombinación genética. Debido a que la recombinación
genética tiende a aleatorizar los genotipos de un locus respecto de los genotipos de otro
locus, tiende a reducir las frecuencias de los haplotipos cromosómicos representados en
exceso y a aumentar la frecuencia de los haplotipos representados en defecto. En otras palabras, la recombinación genética reduce el desequilibrio de ligamiento.
El papel de la reproducción sexual en reducir el desequilibrio de ligamiento se demuestra algebraicamente en el Cuadro 7.3. El análisis demuestra que en las condiciones de
Hardy-Weinberg la tasa de la disminución del desequilibrio de ligamiento entre un par
de loci es proporcional a la frecuencia de recombinación entre ellos. En la Figura 7.6 aparecen las predicciones de la disminución del desequilibrio para varias frecuencias de
recombinación.
Michael Clegg y sus colegas (1980) documentaron la disminución del desequilibrio de
ligamiento en poblaciones experimentales de la mosca de la fruta. Cada población que
estudiaron albergaba dos alelos en dos de los loci del cromosoma 3. Un locus codificaba
a la enzima esterasa-c, al que llamaremos locus A, con sus alelos A y a. El otro locus codificaba a la enzima esterasa-6, al que llamaremos locus B, con sus alelos B y b.
Clegg y sus colegas fundaron poblaciones únicamente con cromosomas AB y ab, cada
uno de ellos en una frecuencia de 0,5. Los investigadores también fundaron poblaciones
con cromosomas Ab y aB, cada uno de ellos en una frecuencia de 0,5.Así, cada población
se encontraba inicialmente en completo desequilibrio de ligamiento, con una D = 0,25
o una D = –0,25.
Los investigadores mantuvieron sus poblaciones de moscas de 48 a 50 generaciones,
con tamaños aproximadamente de 1.000 individuos y dejaron que las moscas se cruzaran al azar. Cada una o dos generaciones se tomaron muestras de cada población para
determinar las frecuencias de los cuatro haplotipos cromosómicos y calcular el nivel de
desequilibrio de ligamiento entre los dos loci. Por razones que están más allá del alcance de este libro, los investigadores midieron el desequilibrio de ligamiento no con D, sino
con un estadístico relacionado denominado la correlación del estado alélico. No hay una
relación perfecta entre los valores de D y la correlación del estado alélico, pero como regla
Cromosomas Cromosomas
A
a
0,8
25
aB
70
AB
0,6
0,4
45
ab
60
Ab
0,2
0
0
0,2 0,4 0,6
0
0,2
Frecuencia
Figura 7.5 La mezcla de
poblaciones puede dar lugar a
desequilibrio de ligamiento
Las columnas de la parte superior
representan las frecuencias
cromosómicas en dos poblaciones
distintas, las dos en equilibrio de
ligamiento. Cuando se mezclan,
estas dos poblaciones dan lugar a
la población que se muestra en las
columnas inferiores; está en
desequilibrio de ligamiento.
r=0
0,25
0,2
r = 0,01
0,15
0,1
r = 0,05
0,05
0
0
5
10
15
Generación
20
25
r = 0,1
r = 0,5
Figura 7.6 Con la reproducción sexual y el apareamiento aleatorio,
el desequilibrio de ligamiento disminuye con el tiempo Este gráfico
muestra el nivel de desequilibrio de ligamiento entre dos loci durante 25
generaciones en una población con apareamiento aleatorio. La población
comienza con el máximo valor posible de desequilibrio de ligamiento, 0,25.
Cada una de las curvas muestra el declive del desequilibrio de ligamiento, de
acuerdo con la ecuación D’ = D(1 ⫺ r), para diferentes valores de r.
Con r ⫽ 0,5, que corresponde a la transmisión independiente de loci en
cromosomas distintos, la población alcanza el equilibrio de ligamiento en
menos de 10 generaciones. Con r = 0,01, que corresponde a loci
íntimamente ligados, el desequilibrio de ligamiento persiste durante muchas
generaciones. Según Hedrick (1983).
206 PARTE II Los mecanismos del cambio evolutivo
CUADRO 7.3
La reproducción sexual reduce el desequilibrio de ligamiento
A
quí demostraremos que el nivel de desequilibrio de
ligamiento disminuye inexorablemente en una población con apareamiento sexual aleatorio. Lo haremos comenzando con la definición de D dada en el texto y en el Cuadro 7.1, y derivando una expresión para D⬘, el coeficiente de
desequilibrio de ligamiento en la generación siguiente.
De acuerdo con la definición de D,
D⬘ ⫽ gAB⬘gab⬘ ⫺ gAb⬘gaB⬘
Sustituyendo gAB⬘, gab⬘, gAb⬘ y gaB⬘ por las expresiones
que deducimos en el Cuadro 7.2, tendremos:
D⬘ ⫽ [( gAB ⫺ rD)( gab ⫺ rD)] ⫺
⫺ [( gAb ⫹ rD)( gaB ⫹ rD)]
⫽ [gAB gab ⫺ gABrD ⫺ gabrD ⫹ (rD)2] ⫺
⫺ [ gAb gaB ⫹ gAbrD ⫹ gaB rD ⫹ (rD)2]
⫽ gAB gab ⫺ gABrD ⫺ gabrD ⫹ (rD)2 ⫺
⫺ gAb gaB ⫺ gAbrD ⫺ gaB rD ⫺ (rD)2
En poblaciones con
apareamiento al azar, hay tres
causas que provocan
desequilibrio de ligamiento: la
selección sobre genotipos
multilocus, la deriva genética y
la mezcla de poblaciones. Una
causa reduce el desequilibrio
de ligamiento: la
recombinación genética
resultante de la meiosis y del
cruzamiento no consanguíneo
(es decir, el sexo).
Suprimiendo términos y reordenando tendremos
D⬘ ⫽ gAB gab ⫺ gAb gaB ⫺ gABrD ⫺
⫺ gabrD ⫺ gAbrD ⫺ gaBrD
⫽ ( gAB gab ⫺ gAb gaB) ⫺
⫺ rD( gAB ⫹ gab ⫹ gAb ⫹ gaB)
Finalmente, la expresión ( gABgab ⫺ gAbgaB ) es igual a D
y la expresión ( gAB ⫹ gab ⫹ gAb ⫹ gaB ) es igual a 1, por
lo que tendremos:
D⬘ ⫽ D ⫺ rD ⫽ D(1 ⫺ r)
Recuerde que r es la frecuencia de recombinación en la
1
meiosis, que siempre se encuentra entre 0 y ᎏ2ᎏ. Esto impli1
ca que (1 – r) siempre está entre ᎏ2ᎏ y 1. Por ello, a no ser que
no haya recombinación entre un par de loci, el desequilibrio de ligamiento entre ellos se desplazará cercano a 0
en cada generación. Cuanto mayor sea la frecuencia de
recombinación entre dos loci, más pronto alcanzará la
población el equilibrio de ligamiento.
general podemos decir que cuando disminuye el desequilibrio de ligamiento en una
población y D va de 0,25 o de –0,25 hacia 0, la correlación del estado alélico también
disminuye, desplazándose hacia 0 desde 1,0 ó –1,0. Clegg y sus colegas predijeron que
esto sería exactamente lo que tendrían que observar en sus poblaciones de moscas con
apareamiento aleatorio.
Los resultados aparecen en la Figura 7.7. Las curvas grises muestran el patrón de disminución pronosticado; las líneas de color dentadas corresponden a los datos.Tal como
se pronosticó, el entrecruzamiento en la meiosis dio lugar a nuevos haplotipos cromosómicos y disminuyó el desequilibrio de ligamiento entre los loci. Realmente, el desequilibrio de ligamiento disminuyó algo más rápido de lo pronosticado. Clegg y sus colegas
creen que el declive fue más rápido de lo esperado como consecuencia de la superioridad del heterozigoto en los loci enzimáticos que estaban estudiando. La superioridad del
heterozigoto aumentaría la frecuencia de los individuos heterozigotos para ambos loci,
proporcionando así más oportunidades de entrecruzamiento para romper las asociaciones
no aleatorias entre los alelos de un locus con los del otro.
¿Por qué es importante el desequilibrio de ligamiento?
Hemos definido el desequilibrio de ligamiento como una asociación no aleatoria entre
genotipos de loci distintos. Hemos identificado a la selección multilocus, a la deriva
genética y a la mezcla de poblaciones como mecanismos evolutivos que la producen.
Hemos visto que la reproducción sexual la reduce, devolviendo a la población a una
situación de equilibrio de ligamiento.Y hemos demostrado que en una población ideal
de Hardy-Weinberg que se encuentre en equilibrio de ligamiento, las frecuencias cromosómicas no cambian de una generación a la siguiente. Sin embargo, no nos hemos
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 207
Frecuencias iniciales
de los cromosomas
para las dos poblaciones
Esterasa-c: A, a
Esterasa-6: B, b
A
B = 0,5
a
B =0
A
b =0
a
b = 0,5
A
a
AB
ab
B
1,0
b
0,8
Desequilibrio de ligamiento
(correlación con el estado alélico)
Frecuencia de:
0,6
Frecuencias cromosómicas
finales promedio de
todas las poblaciones
0,4
0,2
0
a
Ab
aB
B
b
a
AB
aB
Ab
ab
B
b
-0,2
-0,4
Frecuencias iniciales
de los cromosomas
para otras dos poblaciones -0,6
A
A
a
B = 0,17
A
b = 0,36
a
b = 0,09
Predicción
Datos
-0,8
-1,0
A
Frecuencia de: B = 0,38
0
10
20
30
40
50
Generación
Frecuencia de:
A
B =0
a
B = 0,5
A
b = 0,5
a
b =0
Figura 7.7 Demostración experimental de que la reproducción sexual reduce el desequilibrio de ligamiento Cada una de las
distintas poblaciones de moscas de la fruta comenzaron en completo desequilibrio de ligamiento (gráficos en barras superior e inferior de la
izquierda). Durante 50 generaciones todas las poblaciones se aproximaron, al equilibrio de ligamiento (gráfico en barras de la derecha). Modificado
de Clegg et al. (1980), con frecuencias en el gráfico de barras de la derecha deducidas de los datos presentados.
referido a lo que al principio dijimos fue nuestra cuestión principal: ¿puede la selección
sobre un locus interferir en nuestra capacidad para utilizar modelos para un solo locus
y predecir el curso de la evolución en otros loci? Ahora estamos listos para tratar esta
cuestión.
La mala noticia es que si el locus A y el locus B se encuentran en desequilibrio de ligamiento, entonces la selección sobre el locus A cambiará las frecuencias de los alelos del
locus B. Esto implica que en un modelo genético poblacional para un único locus, si
observamos sólo al locus B haremos predicciones inexactas acerca de su evolución.
La Figura 7.8a ilustra cómo la selección sobre el locus A puede cambiar las frecuencias alélicas del locus B.Antes de que actúe la selección el alelo B esta en frecuencia ele-
208 PARTE II Los mecanismos del cambio evolutivo
Cuando un par de loci se
encuentran en desequilibrio de
ligamiento, la selección sobre
un locus puede cambiar las
frecuencias alélicas del otro
locus. Es decir, los modelos
para un solo locus pueden
ofrecer predicciones inexactas.
vada. La mayoría de las copias de B se encuentran en los cromosomas aB. La selección a
favor del alelo A disminuye la frecuencia de los cromosomas aB. A medida que desaparecen los cromosomas aB, se llevan copias de B. Debido a que la frecuencia de B es
mucho más baja entre los cromosomas que llevan A que entre los que llevan a, muchas
de las copias de B serán reemplazadas por copias de b. El resultado final es que la frecuencia de B disminuirá.
Advierta que en el escenario que acabamos de describir, la selección actuaba sólo sobre
el locus A y no sobre el locus B. Los genotipos del locus B no tenían efecto sobre la eficacia. En su lugar, la frecuencia del alelo B descendía simplemente arrastrada. Pero si estuviéramos analizando sólo el locus B y viéramos que la frecuencia del alelo B disminuía con
el tiempo, podríamos concluir erróneamente que el objeto de la selección era el mismo
locus B. Ésta es la lección más desalentadora de la versión para dos locus del análisis de
Hardy-Weinberg: los estudios de un solo locus pueden descarrilar por desequilibrio de
ligamiento.
La buena noticia es que si el locus A y el locus B se encuentran en equilibrio de ligamiento, la selección sobre el locus A no tiene efecto, cualesquiera que sean las frecuencias
alélicas del locus B. Observe la Figura 7.8b. La selección a favor del alelo A elimina de
nuevo muchos cromosomas aB. Pero debido a que la frecuencia de B es la misma entre
los cromosomas que llevan A que entre los que llevan a, cada copia del alelo B que se
pierde es sustituida por otra copia de B. Si la selección sobre el locus A no tiene efecto
sobre las frecuencias alélicas en el locus B, entonces, al analizar la evolución del locus B,
no aparecerán interferencias por el uso de modelos para un solo locus.
Una mejor noticia es que en una población con apareamiento al azar, el sexo es tan
bueno para eliminar el desequilibrio de ligamiento que la mayoría de los pares de loci
se encuentran en equilibrio de ligamiento la mayor parte del tiempo. El trabajo de Gavin
Huttley y sus colegas (1999) ilustra esta afirmación. Huttley y sus colegas analizaron el
genoma humano buscando desequilibrio de ligamiento entre loci de repeticiones cortas
en tándem. Un locus de una repetición corta en tándem es un sitio en un cromosoma
donde una corta secuencia de nucleótidos está repetida varias veces; tales loci tienen
típicamente varios alelos. Huttley y sus colegas realizaron unas 200.000 comprobaciones del desequilibrio de ligamiento por parejas de unos 5.000 loci localizados en los
22 autosomas.
(a) Población en desequilibrio de ligamiento
AB
AB
aB
aB
Ab
ab
Selección
sobre A
Ab
ab
(b) Población en equilibrio de ligamiento
Figura 7.8 Equilibrio de ligamiento, selección en un
locus y frecuencias alélicas en un locus ligado En una
población con desequilibrio de ligamiento, como se muestra
en (a), la selección a favor del alelo A del locus A da lugar a un
declive de la frecuencia del alelo B en el locus B. En una
población en equilibrio de ligamiento, como se muestra en
(b), la selección a favor del alelo A no tiene efecto sobre la
frecuencia del alelo B.
AB
aB
Ab
ab
Selección
sobre A
AB
aB
Ab
ab
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 209
Huttley y sus colegas realmente encontraron varios lugares del genoma humano donde
loci vecinos presentaban un sustancial desequilibrio de ligamiento. Una región con gran
desequilibrio de ligamiento, ya conocida por estudios anteriores, es una zona del cromosoma 6 que contiene los loci del antígeno leucocitario humano (HLA). Los loci HLA
codifican para proteínas que el sistema celular inmunológico utiliza para el reconocimiento
de invasores extraños. Los loci HLA se encuentran sometidos a fuerte selección, y el desequilibrio de ligamiento entre ellos es probable que sea el resultado de la selección sobre
genotipos multilocus.
Sin embargo, los pares de loci que presentaban desequilibrio de ligamiento eran
minoría. Los pares que con mayor probabilidad presentaban desequilibrio de ligamiento eran aquellos que estaban íntimamente ligados físicamente, es decir, situados lo suficientemente cerca uno del otro en el mismo cromosoma como para que el entrecruzamiento entre ellos fuera raro. Huttley y sus colegas se fijaron en pares de loci lo
suficientemente cercanos como para que el entrecruzamiento entre ellos ocurriese con
una frecuencia del 4% o menos. De estas parejas, presentaban desequilibrio de ligamiento
exactamente el 4%.
En un estudio similar, Naohiko Miyashita y sus colegas (1999) analizaron el genoma
de la planta Arabidopsis thaliana, un pequeño miembro de la familia de la mostaza. Podría
esperarse que el genoma de Arabidopsis albergara un considerable desequilibrio de ligamiento incluso entre loci que se encuentran alejados o en cromosomas distintos. Esto es
debido a que Arabidopsis se autofecunda, reduciendo drásticamente la oportunidad de
recombinación genética. Miyashita y sus colegas llevaron a cabo unas 70.000 comprobaciones de desequilibrio de ligamiento por parejas entre casi 8000 loci. En estas comprobaciones, cerca del 12% reveló desequilibrio de ligamiento. Los investigadores concluyeron que Arabidopsis debe realizar fecundación cruzada ocasionalmente. Incluso con una
cantidad de recombinación relativamente pequeña se logra una gran reducción del desequilibrio de ligamiento.
Podemos resumir, con un sencillo mensaje, nuestra exploración del análisis para dos
locus de Hardy-Weinberg de la siguiente manera. Los genéticos de poblaciones necesitan estar al tanto de que cualquier locus concreto de interés pueda estar en desequilibrio de ligamiento con otros loci, especialmente con otros loci localizados en las
cercanías. Si el locus de interés está de hecho en desequilibrio de ligamiento con otro,
entonces los modelos de genética de poblaciones para un locus pueden dar lugar a predicciones incorrectas. Sin embargo, en poblaciones con apareamiento al azar, puede
esperarse que muchas de las parejas de loci se encuentren en equilibrio de ligamiento.
En general, podemos esperar que los modelos para un solo locus funcionarán bien la
mayor parte de las veces.
Una razón práctica para medir el desequilibrio de ligamiento
En la introducción de este capítulo, prometimos recompensas a los pacientes lectores que
dominaran las abstracciones de las secciones anteriores. Una de tales recompensas es ésta:
la medida del desequilibrio de ligamiento proporciona claves que son útiles en la reconstrucción de la historia de los genes y de las poblaciones.
Recuerde nuestra discusión sobre el alelo CCR5-∆32 en los Capítulos 4 y 5. Este alelo
es una mutación de pérdida de función del locus CCR5. Protege a los homozigotos contra la transmisión sexual de cepas del VIH-1. Entre las cuestiones no resueltas de la discusión anterior se encuentran éstas: ¿de dónde viene el alelo ∆32? y, ¿por qué es frecuente
sólo en Europa?
J. Claiborne Stephens y sus colegas (1998) abordaron estas preguntas midiendo el desequilibrio de ligamiento entre el locus CCR5 y dos loci localizados cerca en el mismo
Cuando un par de loci se
encuentra en equilibrio de
ligamiento, la selección sobre
un locus no tiene efecto sobre
las frecuencias alélicas del
otro locus, y podemos utilizar
los modelos para un solo
locus con confianza.
Afortunadamente, el sexo es
tan buen reductor del
desequilibrio de ligamiento que
muchos pares de loci se
encuentran en equilibrio de
ligamiento la mayor parte del
tiempo.
210 PARTE II Los mecanismos del cambio evolutivo
cromosoma. Los loci cercanos son lugares con cortas repeticiones en tándem llamadas
GAAT y AFMB. GAAT tiene tres alelos y AFMB cuatro. GAAT y AFMB no codifican
nada y sus alelos parece que no tienen efecto sobre la eficacia. Stephens y sus colegas
determinaron los haplotipos de 192 cromosomas de una muestra de europeos. Como
muestra la Figura 7.9a, GAAT y AFMB están próximos a encontrarse en equilibrio de
ligamiento. Las frecuencias de los distintos alelos del locus AFMB son casi las mismas
en los cromosomas que llevan cualquiera de los alelos del locus GAAT que entre los cromosomas que llevan los otros alelos GAAT. Sin embargo, como muestran las Figuras 7.9b
y 7.9c, el locus CCR5 se encuentra en fuerte desequilibrio de ligamiento tanto con el
locus GAAT como con el locus AFMB. Casi todos los cromosomas que llevan el alelo
∆32 en CCR5 también llevan el alelo 197 en GAAT (Figura 7.9b) y el alelo 215 en
AFMB (Figura 7.9c).
(a)
Locus GAAT STR
191 193
197
213
0,8
215
0,6
0,4
0,2
217
0
Locus AFMB STR
Frecuencia
1,0
219
0 0 0,2 0
0,2 0,4 0,6
Frecuencia
(b)
Locus CCR5
+
∆32 191
193
0,8
0,6
197
0,4
0,2
Locus GAAT STR
Frecuencia
1,0
0
0
0
0,2
Frecuencia
Figura 7.9 ¿De dónde viene el alelo CCR5-⌬32?
(c)
Locus CCR5
+
∆32
Frecuencia
1,0
213
0,8
0,6
215
0,4
0,2
217
219
0
0
0,2 0,4 0,6
0
Frecuencia
0,2
Locus AFMB STR
Todos los gráficos muestran las frecuencias de los
haplotipos en el cromosoma 3 en poblaciones
europeas. El gráfico en barras de (a) muestra que dos
loci neutros cercanos al locus CCR5 están próximos al
equilibrio de ligamiento. Los gráficos en barras de (b) y
de (c) muestran que cada uno de estos loci neutros
están en fuerte desequilibrio de ligamiento con el locus
CCR5. Casi todos los cromosomas que llevan al alelo
CCR5-∆32, también llevan el alelo 197 en el locus
GAAT y el alelo 215 en el locus AFMB. Estos datos
están de acuerdo con el origen del alelo CCR5-∆32 en
un suceso de mutación único, que ocurrió hace entre
275 y 1.875 años. Representación de los datos de
Stephen et al. (1998).
0,2 0,4 0,6
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 211
¿Cómo surgió el desequilibrio de ligamiento entre CCR5 y sus vecinos? Como hemos
demostrado en nuestra discusión anterior sobre lo que origina el desequilibrio de ligamiento, hay tres posibilidades: selección sobre genotipos multilocus, deriva genética y mezcla de poblaciones. La selección sobre genotipos multilocus es un candidato improbable
ya que, como hemos advertido, GAAT y AFMB son loci que no codifican nada y sus alelos parecen ser selectivamente neutros. La mezcla poblacional es también un candidato
improbable ya que requeriría una población en la que la frecuencia del alelo ∆32 fuera
mucho más elevada que en Europa, y tal población no existe. Esto nos lleva a la deriva
genética.
Stephens y sus colegas creen que el desequilibrio de ligamiento entre CCR5 y sus vecinos surgió en un escenario similar al mostrado en la Figura 7.4. En un momento dado en
el pasado, la población europea tenía sólo un alelo en CCR5, el CCR5-+. Luego, en un
cromosoma con el haplotipo CCR5-GAAT-AFMB, +-197-215, se produjo una mutación
que dio lugar al alelo ∆32. Por consiguiente, el antecesor de todos los alelos ∆32 fue un
cromosoma con el haplotipo ∆32-197-215. Finalmente, el nuevo alelo ∆32 fue favorecido por selección natural. Se incrementó hasta frecuencias elevadas, arrastrando consigo a
los alelos vecinos 197 y 215.
La asociación entre el alelo ∆32 de CCR5, el alelo 197 de GAAT y el alelo 215 de
AFMB no es perfecta.Ya que el alelo ∆32 apareció primero, la recombinación o mutaciones adicionales han situado al ∆32 en otros haplotipos, como el ∆32-197-217. En otras
palabras, el desequilibrio de ligamiento entre el locus CCR5 y sus vecinos se está rompiendo. Stephens y sus colegas utilizaron estimas de frecuencias de entrecruzamiento y
mutación para calcular lo rápidamente que se rompería el desequilibrio de ligamiento.
Luego utilizaron estos cálculos para estimar cuánto tiempo hacía que había aparecido por
primera vez el alelo ∆32. Los investigadores concluyeron que el alelo ∆32 apareció hace
entre 275 y 1.875 años, con la mejor estima en unos 700 años (véase el Cuadro 7.4).
La respuesta a nuestra pregunta acerca del origen del alelo ∆32 parece que es ésta: el
alelo se originó por una única mutación que se produjo en Europa en los últimos siglos.
El alelo no se dio fuera de Europa bien porque la mutación que lo originó nunca se ha
dado en una población no europea, o porque cuando la mutación se dio fuera de Europa, no fue favorecida por selección.
Esta respuesta plantea, desde luego, nuevas preguntas. Por ejemplo, la selección que favoreció al alelo ∆32 en Europa debe de haber sido fuerte. Sabemos esto porque sólo la
selección fuerte pudo haber llevado al alelo de una frecuencia prácticamente de cero a una
frecuencia del 10 al 20% en sólo unos 700 años. ¿Cuál fue el agente selectivo responsable? La sospecha más obvia sería una enfermedad epidémica. Una intrigante posibilidad
es la peste bubónica, responsable de la peste negra que asoló a Europa durante el siglo XIV,
matando de la cuarta parte a la mitad de la población. La peste bubónica la provoca la bacteria Yersinia pestis. Quizá el alelo ∆32 protegió también contra la Yersinia pestis. Desde este
trabajo, la hipótesis de la peste bubónica está siendo comprobada por los investigadores en
el laboratorio de Stanley Falkow de la Universidad de Stanford. No se tienen todavía resultados definitivos. Recientemente,Alshad Lalani y sus colegas (1999) comunicaron que el
mixoma, un virus de los conejos de la familia de los poxvirus, puede, al igual que el
VIH-1, utilizar CCR5 para introducirse en las células huésped. Lalani y sus colegas especularon que la enfermedad responsable de la elevada frecuencia del alelo ∆32 en Europa
podría haber sido la viruela.
Si resulta que el agente selectivo que favoreció al alelo ∆32 en Europa fue la peste
bubónica o la viruela, entonces cabría esperar que las mutaciones de pérdida de función
en el gen CCR5 habrían sido favorecidas en otras partes del mundo que también hubieran padecido epidemias de estas enfermedades. De hecho, los investigadores han encon-
Debido a que la lista de
causas que producen
desequilibrio de ligamiento es
corta, la detección de
desequilibrio de ligamiento en
una población proporciona
claves del pasado de la
población.
212 PARTE II Los mecanismos del cambio evolutivo
CUADRO 7.4
Estima de la antigüedad de la mutación CCR5-∆32
E
sbozaremos aquí los cálculos que J. Claiborne Stephens y sus colegas (1998) utilizaron para estimar, de
manera aproximada, la edad de la mutación CCR5-∆32.
Primero, observemos la Figura 7.10. Muestra la ordenación
de los tres loci cruciales en el brazo corto del cromosoma
3: CCR5 está primero, luego GAAT y luego AFMB. Nos
referiremos a los haplotipos del cromosoma 3 indicando
sus genotipos en estos loci, separándolos con guiones. Por
ejemplo, el haplotipo ∆32-197-215 tiene el alelo ∆32 en
el locus CCR5, el alelo 197 en el locus GAAT y el alelo
215 en el locus AMFB.
Advierta que el haplotipo ∆32-197-215 explica el
84,8% de todos los cromosomas que llevan el alelo ∆32 en
el locus CCR5.Además, el haplotipo +-197-215, con una
frecuencia del 36%, es el más frecuente entre los cromosomas que llevan el alelo + en el locus CCR5. Basándose
en estos datos, Stephens et al. concluyeron que la mutación
que dio lugar a la primera copia del alelo ∆32, probablemente ocurrió en un cromosoma +-197-215, convirtiéndolo en un cromosoma ∆32-197-215. Desde que se dio la
mutación, el 84,8% de los cromosomas ∆32-197-215 han
permanecido sin cambio, mientras que el 15,2% se han
convertido en otros haplotipos, bien (1) por entrecruzamiento entre CCR5 y GAAT o entre GAAT y AMFB,
bien (2) por mutación en GAAT o en AFMB.
Stephens y sus colegas desarrollaron una ecuación para
Pg, la probabilidad de que cualquier cromosoma ∆32-197215 haya permanecido sin cambio a lo largo de las g generaciones que han pasado desde que se originó el primer
cromosoma ∆32-197-215. Su razonamiento fue el siguiente: la probabilidad de que un cromosoma ∆32-197215 permanezca sin cambio durante una generación es
igual a
1⫺c⫺
probabilidad de que la mutación del locus GAAT o del
locus AFMB conviertan al cromosoma en un haplotipo
distinto.Así,
Pg ⫽ (1 ⫺ c ⫺ )g
Todo lo que tenemos que hacer para estimar g es desarrollar una estima independiente de Pg, c y , sustituyéndolos en esta ecuación y despejar g.
Ya tenemos una estima de Pg. Es 0,848, la fracción
de cromosomas ∆32 que todavía tienen el haplotipo ∆32197-215.
Stephens y sus colegas estimaron el valor de c asumiendo que los cromosomas ∆32-197-215 prácticamente se
han emparejado siempre con cromosomas CCR5-+, y
que entre los cromosomas CCR5-+ la frecuencia de los
distintos haplotipos ha permanecido constante con el
tiempo. La frecuencia de entrecruzamiento entre CCR5 y
GAAT es de 0,0021. Ya que el 64% de los cromosomas
CCR5-+ tienen un haplotipo distinto del 197-215 en
GAAT y AFMB, el 64% de tales entrecruzamientos romperán el haplotipo ∆32-197-215. La frecuencia de entrecruzamiento entre GAAT y AFMB es de 0,0072.Ya que el
48% de los cromosomas CCR5-+ tienen un genotipo distinto de 215 en AFMB, el 48% de tales entrecruzamientos
romperán el haplotipo ∆32-197-215. Por ello:
c ⫽ (0,64 ⫻ 0,0021) + (0,48 ⫻ 0,0072) ⬇ 0,005
Basándose en las estimas de las tasas de mutación de
otros investigadores en loci similares a GAAT y AFMB,
Stephens et al. estimaron que:
Lo
cu
s
C
C
R
Lo
m cu 5
ar s
ca
do
rG
AA
Lo
T
m cu
ar s
ca
do
rA
FM
B
donde c es la probabilidad de que un entrecruzamiento
convierta al cromosoma en un haplotipo distinto y c es la
(Sobre el brazo
corto del
cromosoma 3)
Frecuencia de
entrecruzamiento en
esta región: 0,0021
Sustituyendo estos valores en la ecuación para Pg da:
0,848 ⫽ (0,994)g
Cromosomas CCR5-∆32:
84,8% ∆32-197-215
15,2% ∆32-otros
Cromosomas CCR5-+:
36% +-197-215
64% +-otros
Frecuencia de
entrecruzamiento en
esta región: 0,0072
⫽ 0,001
52% +-x-215
48% +-x-otros
Figura 7.10 Tres loci del brazo corto del cromosoma 3
y las frecuencias de los haplotipos seleccionados en una
población europea Estas frecuencias haplotípicas
proporcionan la información necesaria para deducir la edad
del alelo CCR5-∆32. Según Stephens et al. (1998).
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 213
CUADRO 7.4 Continuación
Tomando logaritmos de ambos términos tendremos:
log(0,848) ⫽ log[(0,994)g] ⫽ g log (0,994)
Finalmente, despejando g tendremos:
g ⬇ 27,5
Si tomamos en 25 años la duración de una generación
humana, entonces la mutación que dio lugar al alelo ∆32
se produjo hace unos 27,5 ⫻ 25 = 688 años. Basándose en
otros cálculos, Stephens y sus colegas estimaron un intervalo de confianza del 95% alrededor de esta estima que
abarca entre hace 275 años hasta hace 1.875 años.
trado diversas mutaciones en CCR5 (Carrington et al. 1999). Entre éstas hay una mutación de pérdida de función con una frecuencia del 3 al 4% en poblaciones chinas y japonesas (Ansari-Lari et al. 1997). No se ha determinado el origen y significado selectivo de
este alelo.
Hemos demostrado que la comprensión del desequilibrio de ligamiento es una herramienta poderosa para reconstruir la historia del alelo. Otra recompensa que prometimos
a los lectores fue que la comprensión del desequilibrio de ligamiento les ayudaría a comprender el significado adaptativo de la reproducción sexual. El misterio del sexo es el objeto de la siguiente sección.
7.2.
El significado adaptativo del sexo
La reproducción sexual es complicada, costosa y peligrosa. Buscar pareja toma tiempo
y energía, y puede aumentar el riesgo del que busca de ser cazado por un predador. Una
vez encontrada, una pareja potencial puede pedir un esfuerzo o inversión adicional antes
de consentir cooperar. El mismo sexo puede exponer a los participantes a enfermedades transmitidas sexualmente.Y después de todo, el cruce puede ser estéril. ¿Por qué no
evitar todas estas molestias y riesgos, y en su lugar reproducirse simplemente de manera asexual?
Esta pregunta suena estrambótica a los humanos, ya que no tenemos elección: heredamos de nuestros antecesores la incapacidad para reproducirnos de manera distinta de
la sexual. Pero muchos organismos pueden realmente elegir, al menos en un sentido
fisiológico: son capaces de reproducirse tanto sexual como asexualmente y de manera
regular las alternan. Por ejemplo, muchas especies de áfidos tienen poblaciones de primavera y de verano compuestas completamente de hembras asexuales. Estas hembras se
Figura 7.11 Reproducción asexual en
áfidos El áfido grande está dando a luz a
un hijo, producido por partenogénesis, que
es genéticamente idéntico a su madre.
(Peter J. Bryant/University of California at
Irvine/Biological Photo Service)
Muchas especies son capaces
de reproducirse tanto sexual
como asexualmente.
214 PARTE II Los mecanismos del cambio evolutivo
alimentan de secreciones de plantas y, sin la participación de machos, producen descendencia genéticamente idéntica a sus madres (Figura 7.11). Este modo de reproducción, en el que los descendientes se desarrollan a partir de huevos no fecundados, se
denomina partenogénesis. En los áfidos de otoño cambia el modo, produciendo
machos y hembras sexuales. Éstos se cruzan y las hembras ponen huevos que pasarán el
invierno y de los que nacerá, en la primavera siguiente, una nueva generación de hembras partenogenéticas.
Muchos otros organismos pueden reproducirse tanto sexual como asexualmente. Entre
los ejemplos se encuentran Volvox, hidras (Figura 7.12) y muchísimas especies de plantas
que se pueden reproducir por esqueje o desarrollando flores que intercambiarán polen con
otros individuos.
¿Qué tipo de reproducción es mejor, la sexual o la asexual?
La existencia de dos formas diferentes de reproducción en la misma población plantea la
cuestión de si un tipo sustituirá al otro con el tiempo. John Maynard Smith (1978) enfocó esta cuestión desarrollando un modelo nulo. El modelo nulo explora, en los supuestos
más simples posibles, el destino evolutivo de una población en la que algunas hembras se
reproducen sexualmente y otras asexualmente. Maynard Smith se planteó dos supuestos:
1. El tipo de reproducción de la hembra no afecta al número de descendientes que pueden tener.
2. El tipo de reproducción de la hembra no afecta a la probabilidad de supervivencia de
sus descendientes.
Maynard Smith también especificó que todos los descendientes de una hembra partenogenética eran hembras, mientras que los descendientes de una hembra sexual eran mezcla, típicamente con igual número de hijas que de hijos.
(b)
(a)
Figura 7.12 Organismos con dos formas de reproducción (a) Volvox aureus, alga de agua dulce.
Cada esfera grande es un único individuo adulto. Antes de la madurez, cualquier individuo tiene la
potencialidad de desarrollarse como macho sexual, o como hembra sexual o asexual. El individuo de la
parte inferior derecha (completamente visible) es un macho. Los discos orientados al azar son paquetes de
esperma. El gran individuo de arriba hacia la izquierda es una hembra. Cada una de las esferas pilosas
oscuras en su interior son zigotos enquistados. El individuo justo a la izquierda del macho es asexual. Cada
una de las esferas oscuras de su interior es un descendiente, desarrollado por mitosis como un clon del
padre. (Jon C. Herron) (b) Hidra. Este individuo se reproduce tanto sexual como asexualmente. La corona
de tentáculos de la parte superior izquierda rodea la boca de la hidra. A lo largo del cuerpo, debajo de la
boca, hay filas de testículos. Debajo de los testículos hay dos yemas asexuales. (Foto de P.S. Tice de
Buchsbaum y Pearse, Animals Without Backbones, 3ª ed., University of Chicago Press, 1987.)
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 215
En una población de acuerdo con los supuestos de Maynard Smith, las hembras
asexuales producen dos veces más nietos que las hembras sexuales (Figura 7.13). Esto
implica que las hembras asexuales darán lugar a una proporción cada vez mayor de la
población cada generación. Finalmente, las hembras asexuales deberían imponerse totalmente. En principio, todo lo que se necesitaría es una mutación que diese lugar a una sola
hembra asexual en una población exclusivamente sexual. Desde el momento en que se
diera esta mutación, la población estaría destinada a ser invadida por asexuales.
No obstante, esta situación no parece que haya sucedido muy a menudo. La gran mayoría de las especies pluricelulares son sexuales, y hay muchas especies, como los áfidos, Volvox e hidras en las que la reproducción sexual y asexual coexiste de manera estable. El
modelo de Maynard Smith demuestra, tal como él lo intentaba, que estos hechos representan una paradoja para la teoría evolutiva.
Obviamente, el sexo debe conferir beneficios que permitan su permanencia a pesar
de la gran ventaja reproductiva que ofrece la partenogénesis. Pero, ¿cuáles son estos
beneficios? La lógica matemática del modelo de Maynard Smith es correcta, por lo que
los beneficios del sexo se deben encontrar en la falta de cumplimiento de uno o de los
dos supuestos. Éste es el mayor valor del modelo. Haciendo una breve lista de las suposiciones explícitas, Maynard Smith centró la investigación en unos pocos hechos esenciales en biología.
La primera suposición, de que el número de descendientes de una hembra no depende
de si es sexual o asexual, no se cumple en especies en las que los padres proporcionan recursos u otras formas de cuidado paterno esenciales para producir crías. Sin machos que proporcionen ayuda, es probable que las hembras asexuales produzcan menos descendientes.
Ciertamente existen especies en las que el éxito reproductivo de la hembra está limitado por
el cuidado paterno. Los ejemplos incluyen a la especie humana, a muchas aves y peces flauta (véase el Capítulo 9). Sin embargo, las especies con cuidado paterno son minoría. En
muchas especies, en muchos mamíferos e insectos, por ejemplo, los machos contribuyen sólo
con sus genes. Por ello es más probable que una ventaja general del sexo se encuentre en
la violación del segundo supuesto; el que la probabilidad de que los descendientes de una
hembra sobrevivan no depende de si la hembra los produce sexual o asexualmente.
Generación
1
Sexuales
H x M
Proporción de individuos
que son asexuales
1/3
Asexuales
H
2
H x M
H x M
H
H
H
H
1/2
3
H x M
H x M
H
H
H
H
2/3
H x M
H x M
H
H
H
H
H
H
H
H
H
H
H
H
Figura 7.13 La ventaja reproductiva de las hembras asexuales Imagine una población fundada
por tres individuos, una hembra sexual, un macho sexual y una hembra asexual. En cada generación cada
hembra produce cuatro descendientes, después de lo cual los padres mueren. Todos los descendientes
sobreviven para reproducirse. La mitad de los descendientes de las hembras sexuales son hembras, la otra
mitad machos. Todos los descendientes de las hembras asexuales son, desde luego, hembras. De acuerdo
con estas bases elementales, la proporción de individuos de la población que son hembras asexuales
aumentará en cada generación. Según John Maynard Smith (1978).
La persistencia del sexo es
una paradoja, ya que un
modelo simple demuestra que
las hembras asexuales serán
rápidamente las únicas en
cualquier población.
216 PARTE II Los mecanismos del cambio evolutivo
R. L. Dunbrack y sus colegas (1995) comprobaron este segundo supuesto experimentalmente. Demostraron que es erróneo, al menos en las condiciones de sus experimentos.
Dunbrack y sus colegas estudiaron poblaciones de laboratorio del gorgojo de la harina Tribolium castaneum. En cada una de las series de ensayos, los investigadores fundaron poblaciones mixtas con igual número de gorgojos rojos y negros.A los gorgojos de un color se
los denominó como la cepa “sexual” y a los del otro color como la cepa “asexual”. Por ejemplo, en la mitad de los experimentos los gorgojos rojos fueron la cepa sexual y los negros la
cepa asexual. Mantendremos esta asignación en la descripción del protocolo experimental.
Los gorgojos de la harina no son realmente capaces de reproducirse asexualmente, por
lo que los investigadores tuvieron que manipular la población negra de tal manera que
fuera numérica y evolutivamente equivalente a una población en la que los individuos se
reproducen realmente de manera asexual. En cada generación los investigadores contaron
los adultos de la cepa negra y los eliminaron. Luego sustituían a cada uno de los adultos
negros descartados con tres nuevos adultos negros, tomados de una población de reserva
de gorgojos negros de raza pura que no habían estado expuestos a la competencia con los
rojos. Este procedimiento dio efectivamente a la cepa negra una ventaja reproductiva tres
veces superior sobre la cepa roja, pero evitando que se adaptaran al nuevo ambiente.Así,
la cepa negra era análoga a una subpoblación asexual en la que cada generación es genéticamente idéntica a la generación anterior, pero en la que los individuos disfrutan de un
margen reproductivo mayor que la doble ventaja que una cepa asexual real tendría en la
naturaleza. Debido a que en cada generación la población negra era genéticamente idéntica a la generación anterior (excepto en caso de deriva), la cepa negra no podría evolucionar en respuesta a la selección impuesta por la competencia con la roja.
A los adultos rojos se les permitía que se cruzaran entre sí y que permanecieran en el
cultivo experimental. Por ello, constituían una población sexual que podía evolucionar en
respuesta a las interacciones competitivas con la cepa negra (asexual).
Dunbrack y sus colegas añadieron un reto ambiental a sus poblaciones de gorgojos
rociando la harina en la que vivían con el insecticida malation. Esta selección impuesta a
las poblaciones de gorgojos favorecía la evolución de resistencia a insecticidas. Finalmente los investigadores utilizaron un ingenioso procedimiento, cuyos detalles no nos importan aquí, para evitar que los gorgojos rojos y negros se cruzaran entre sí. Los investigadores mantuvieron el experimento durante 30 generaciones, lo que les llevo dos años.
El modelo nulo de Maynard Smith predice que, en cada experiencia, la cepa asexual
debería ocupar una fracción cada vez mayor de la población, hasta que finalmente la cepa
sexual fuera totalmente eliminada. La primera suposición del modelo está incluida en el
experimento; de hecho, los individuos asexuales del experimento producen más descendientes en cada generación que los individuos sexuales. El único modo en que los asexuales no puedan ganar es si el segundo supuesto del modelo no es correcto.
Dunbrack y sus colegas realizaron ocho repeticiones de sus experimentos. Cuatro
fueron como los descritos, con rojos como cepa sexual (evolucionando) y negros como
cepa asexual (no evolucionando). En cada una de estas repeticiones se utilizaron concentraciones diferentes de malation. En las otras cuatro repeticiones la cepa negra era la sexual
(evolucionando) y la cepa roja la asexual (no evolucionando). De nuevo, en cada repetición se utilizaron concentraciones distintas de malation. Los investigadores también
realizaron un control para cada una de las ocho repeticiones. En los controles no se permitió que evolucionaran ni los gorgojos rojos ni los negros, pero un color o el otro tenía
una ventaja reproductiva tres veces superior.
Los resultados se presentan en la Figura 7.14. En los cultivos control (Figura 7.14b y
(d)), el resultado fue siempre consistente con el modelo nulo de Maynard Smith: la cepa
que tenía una ventaja reproductiva tres veces superior eliminaba rápidamente a la otra
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 217
cepa. Sin embargo, en los cultivos experimentales (Figura 7.14a y (c)), el resultado fue
siempre contrario a la predicción del modelo nulo. Inicialmente, la cepa sexual parecía estar
en camino de desaparecer, pero al cabo de unas 20 generaciones, dependiendo de la concentración del malation, la cepa sexual evolucionando se recobraba. Finalmente la cepa
sexual eliminaba completamente a la cepa asexual que no evoluciona, a pesar de la triple
ventaja reproductiva de la cepa asexual.
Podemos concluir que el supuesto 2 del modelo nulo no es correcto. A medida que
pasan una pocas generaciones, los descendientes producidos por reproducción sexual
consiguen una mayor eficacia que los descendientes producidos por reproducción asexual.
Al menos en algunas
condiciones, los
descendientes que se
producen por reproducción
Proporción de rojos
(a) Los rojos sexuales (evolucionan); los negros asexuales (no evolucionan);
los negros tienen una ventaja reproductiva tres veces mayor
sexual logran una mayor
eficacia que los descendientes
que se producen por
1,0
Concentración de malation
1 ppm
3 ppm
5 ppm
10 ppm
0,5
reproducción asexual.
0
Proporción de rojos
(b) Los rojos control: ambos colores son asexuales y no evolucionan; los
negros tienen una ventaja reproductiva tres veces mayor
1,0
Concentración de malation
1 ppm
3 ppm
5 ppm
10 ppm
0,5
0
Proporción de negros
(c) Los negros sexuales (evolucionan); los rojos asexuales (no evolucionan);
los rojos tienen una ventaja reproductiva tres veces mayor
1,0
Concentración de malation
1 ppm
3 ppm
5 ppm
10 ppm
0,5
0
Proporción de negros
(d) Los negros control: ambos colores son asexuales y no evolucionan; los
rojos tienen una ventaja reproductiva tres veces mayor
1,0
Concentración de malation
1 ppm
3 ppm
5 ppm
10 ppm
0,5
0
10
Transferencia
20
30
Figura 7.14 Prueba experimental del supuesto 2 de la
hipótesis nula de Maynard Smith Cada panel muestra la
frecuencia relativa, en una población mezclada, de la cepa del
gorgojo de la harina que ha sido situada en desventaja
reproductiva pero que en (a) y en (c) se reproduce sexualmente y
evoluciona. Las cuatro series temporales de cada panel
representan cultivos tratados con concentraciones diferentes de
malation (ppm = parte por millón). Una transferencia es análoga a
una generación. (a) Los rojos se encuentran en desventaja
reproductiva, pero tienen reproducción sexual y evolucionan. Los
rojos eliminarán finalmente a los negros. (b) Los rojos se
encuentran en desventaja reproductiva y no evolucionan. Los
rojos serán rápidamente eliminados por los negros. (c) Los negros
se encuentran en desventaja reproductiva, pero tienen
reproducción sexual y evolucionan. Los negros eliminarán
rápidamente a los rojos. (b) Los negros se encuentran en
desventaja reproductiva y no evolucionan. Los negros serán
finalmente eliminados por los rojos. Modificado de Dunbrack et
al. (1995). Copyright © 1995,
The Royal Society.
218 PARTE II Los mecanismos del cambio evolutivo
La siguiente pregunta es, ¿por qué? La única diferencia inherente entre los descendientes de una hembra que se reproduce sexualmente de los asexuales es que los descendientes
asexuales son genéticamente idénticos a sus madres y entre sí, mientras que los descendientes sexuales son genéticamente diferentes de sus madres y entre sí. La mayor parte de las teorías sobre los beneficios del sexo se refieren a las razones de por qué las hembras que dan
lugar a descendientes genéticamente diversos verán a muchos más de ellos sobrevivir y reproducirse que lo harán las hembras que producen copias genéticas idénticas de sí mismas.
En este punto advertiremos que hay una enorme diversidad de teorías acerca de las ventajas del sexo. Aquí tenemos espacio sólo para tratar modelos genético-poblacionales y
comprobaciones y sólo un pequeño número de ellos. Para una revisión más amplia del
tema, véase Michod y Levin (1988).
En las poblaciones el sexo significa recombinación genética
En un análisis
genético-poblacional, el sexo
tiene exactamente un efecto:
reducir el desequilibrio de
ligamiento.
Cuando los genéticos de poblaciones hablan acerca del sexo, de lo que normalmente quieren hablar, y de lo que queremos hablar aquí, es de la reproducción implicando (1) meiosis con entrecruzamiento y (2) cruzamientos entre individuos no emparentados, como
ocurre en los apareamientos aleatorios. La consecuencia de estos procesos actuando en
conjunto es la recombinación genética. Si seguimos a un alelo dado a través de varias generaciones en una genealogía, en cada generación el alelo formará parte de un genotipo multilocus diferente. Por ejemplo, un alelo dado para ojos azules puede formar parte de un
genotipo que incluya genes para pelo rubio en una generación y parte de un genotipo que
incluya genes para pelo castaño en la generación siguiente.
En un análisis genético poblacional, la recombinación genética, debido a que mezcla
los genotipos multilocus, reduce el desequilibrio de ligamiento. Ésta fue la conclusión básica de la Sección 7.1.
De hecho, la reducción del desequilibrio de ligamiento es la única consecuencia del sexo
en el contexto de la genética de poblaciones (Felsenstein 1988). En una población que ya
está en equilibrio de ligamiento, el sexo no tiene efecto. Si el sexo no tiene efecto, no
puede conferir beneficios. Por consiguiente, cualquier modelo genético poblacional sobre
los beneficios evolutivos del sexo debe incluir, como mínimo, dos cosas. Primera, el
modelo debe incluir un mecanismo que elimine genotipos multilocus concretos o que dé
lugar a un exceso de otros, dando lugar por consiguiente a desequilibrio de ligamiento.
Segundo, el modelo debe incluir una justificación de por qué se favorece a los genes que
tienden a reducir el desequilibrio de ligamiento, promocionando al sexo.
Basándose en este análisis, Joe Felsenstein divide claramente a casi todos los modelos
genético-poblacionales sobre los beneficios del sexo en dos teorías generales. Estas teorías generales se diferencian por las fuerzas evolutivas que postulan para el origen del desequilibrio de ligamiento.Algunos modelos postulan la deriva genética como el factor que
da lugar al desequilibrio de ligamiento; otros modelos postulan la selección sobre genotipos multilocus.
La deriva genética, en combinación con la mutación,
puede hacer que el sexo sea beneficioso
De acuerdo con la teoría de la deriva del sexo, la mutación y la deriva dan lugar a problemas que el sexo puede resolver. Imagine, por ejemplo, que una hembra asexual sufre
mutaciones genéticas deletéreas en sus células germinales. La hembra pasará la mutación
a todos sus descendientes, que a su vez las pasarán a todos sus descendientes. El linaje de
la hembra estará perjudicado por siempre por la mutación deletérea. La única esperanza
de escapar es si uno de sus descendientes es lo suficientemente afortunado como para
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 219
1
Nota del traductor. Trinquete: (3.ª acepción, RAE) “Garfio que resbala sobre los dientes de una rueda para impedir que
ésta se vuelva hacia atrás”.
Número de
individuos
Al comienzo:
0
1
2 3 4 5
Número de
mutaciones deletéreas
Número de
individuos
Algunas generaciones
después:
0
1
2 3 4 5
Número de
mutaciones deletéreas
Todavía, algunas
generaciones después
Número de
individuos
experimentar bien una mutación retrógrada o una mutación adicional que compense a
la primera. Sin embargo, si la hembra fuera sexual, podría dar lugar inmediatamente a descendientes libres de la mutación, simplemente cruzándose con un macho sin la mutación.
El papel de la deriva en este escenario queda claro cuando subimos en el modelo hasta
el nivel poblacional. El modelo de deriva más famoso es el del trinquete1 de Muller; arguye que las poblaciones asexuales están condenadas a acumular mutaciones deletéreas. H.J.
Muller (1964) imaginó una población asexual finita en la que los individuos sufren, ocasionalmente, mutaciones deletéreas. Debido a que las mutaciones imaginadas por Muller
son deletéreas, la selección actuará contra ellas. La frecuencia de cada alelo mutante de la
población reflejará la tasa de mutación, la fuerza de la selección y la deriva genética
(véanse los Capítulos 5 y 6).
En cualquier momento, la población de Muller puede incluir individuos que no lleven mutaciones, que lleven una mutación, dos mutaciones y así sucesivamente. Debido a
que la población es asexual, podemos pensar en estos grupos como subpoblaciones distintas, y representar el número relativo de individuos de cada subpoblación en un histograma (Figura 7.15). El número de individuos dentro de cada grupo puede ser muy
pequeño, dependiendo del tamaño de la población en conjunto y del equilibrio entre la
mutación y la selección (véase el Capítulo 5). El grupo con cero mutaciones es el único
cuyos miembros, como promedio, gozan de la eficacia más elevada; pero si este grupo es
pequeño, entonces en cualquier generación dada, sucesos aleatorios pueden conspirar para
evitar la reproducción de todos los individuos del grupo. Si esto sucede una sola vez,
entonces se perderá la subpoblación con cero mutaciones y los miembros del grupo con
una mutación serán ahora los individuos con la mayor eficacia. El único modo para que
reaparezca el grupo con cero mutaciones es si un miembro del grupo con una mutación
sufre la mutación retrógrada que le convierta en uno con cero mutaciones.
Con la desaparición del grupo con cero mutaciones, los miembros de la subpoblación con
una mutación gozarán de la máxima eficacia media. Pero este grupo puede ser también muy
pequeño y puede perderse por azar en cualquier generación dada. De nuevo, la pérdida por
deriva del grupo es mucho más fácil que su recreación por mutación retrógrada.A medida
que el trinquete avanza y la población pierde grupo tras grupo con máxima eficacia, la eficacia promedio de la población disminuye con el tiempo. La carga impuesta por las mutaciones que se acumulan, se conoce como carga genética. Finalmente la carga genética
soportada por la población asexual será tan elevada que la población se extinguirá.
El sexo desbarata el trinquete. Si el grupo sin mutaciones se pierde por azar en cualquier generación dada, puede reconstituirse rápidamente por cruzamiento no consanguíneo y recombinación. Si se cruzan dos individuos, y cada uno de ellos lleva una copia de
una mutación deletérea, la cuarta parte de sus descendientes quedarán libres de la mutación. En el sentir de Muller, los genes responsables del sexo se mantienen en las poblaciones debido a que ayudan al origen de genotipos con cero mutaciones. A medida que
estos genotipos con cero mutaciones aumentan en frecuencia, los genes para el sexo
aumentan en frecuencia con ellos, en realidad arrastrados.
En el escenario de Muller, el desequilibrio de ligamiento se origina por deriva. Genotipos multilocus concretos se encuentran en frecuencias menores a las del equilibrio de
ligamiento debido a sucesos aleatorios que los han eliminado. Estos genotipos multilocus
perdidos son los genotipos con cero mutaciones, luego los genotipos con una mutación
y así sucesivamente. El sexo reduce el desequilibrio de ligamiento recreando los genotipos perdidos.
0
1
2 3 4 5
Número de
mutaciones deletéreas
Figura 7.15 El trinquete de
Muller: las poblaciones
asexuales acumulan
mutaciones deletéreas
Cada histograma muestra una
instantánea de una población
asexual finita. En cualquier
generación, la clase con menor
número de mutaciones deletéreas
se puede perder por deriva.
Debido a que la mutación directa
hacia alelos deletéreos es más
probable que la mutación
retrógrada a alelos de tipo
silvestre, la distribución se
desplaza inexorablemente hacia la
derecha. Según Maynard Smith
(1988).
220 PARTE II Los mecanismos del cambio evolutivo
Comienza un
cultivo a partir de
una sola bacteria
Se incuba
durante la noche
Se reinicia el
cultivo a partir
de una sola
bacteria
Se incuba
durante la noche
Se reinicia el
cultivo a partir
de una sola
bacteria
Se incuba
durante la noche
Figura 7.16 Población
bacteriana sujeta a cuellos de
botella periódicos La
población bacteriana se inicia a
partir de un solo individuo (el
cuello de botella), se permite el
crecimiento y la división para
producir una gran colonia, luego
se reinicia de nuevo a partir de un
único individuo. El cuello de
botella proporciona una
oportunidad para que actúe la
deriva genética.
Haigh (1978, revisado en Maynard Smith 1988) desarrolló y exploró un modelo matemático explícito del trinquete de Muller. No es sorprendente que el parámetro más
importante del modelo sea el tamaño poblacional. En poblaciones de 10 individuos o
menos, la deriva es un mecanismo evolutivo potente y el trinquete gira rápidamente. En
poblaciones de más de 1000 individuos, la deriva es un mecanismo evolutivo débil y el
trinquete no gira en absoluto.También son importantes la tasa de mutación y el impacto
de las mutaciones deletéreas. El trinquete gira a la mayor velocidad con mutaciones
medianamente deletéreas. Esto se debe a que las mutaciones deletéreas graves son eliminadas por selección antes de que la deriva pueda fijarlas.
Dan Andersson y Diarmid Hughes (1996) comprobaron experimentalmente el trinquete de Muller en poblaciones de la bacteria Salmonella typhimurium.A partir de una cepa
silvestre tipo,Andersson y Hughes establecieron 444 cultivos experimentales, cada uno a
partir de un solo individuo (Figura 7.16). Después de dejarlos crecer durante toda la noche,
los investigadores propagaron los cultivos de nuevo, a partir de un solo individuo. Después
de otra noche de crecimiento, propagaron los cultivos de nuevo, y así sucesivamente. Las
bacterias se reproducen asexualmente por fisión binaria. Los cuellos de botella periódicos, durante los cuales el tamaño poblacional de los cultivos se redujo a un individuo,
expusieron los cultivos a deriva genética. Los investigadores mantuvieron el experimento durante dos meses, dando a la deriva un total de unas 1.700 generaciones para actuar.
Basándose en el trinquete de Muller,Andersson y Hughes predijeron que los cultivos bacterianos habrían acumulado mutaciones deletéreas.
Andersson y Hughes comprobaron esta predicción comparando la eficacia de cada cultivo experimental respecto de la cepa silvestre que era su antecesor común. Los investigadores midieron la eficacia estimando la tasa de crecimiento poblacional. Entre sus 444
cultivos, Andersson y Hughes encontraron 5, o el 1%, con una eficacia significativamente reducida. El tiempo de generación de estos cinco cultivos iba de 25,0 a 47,5 minutos,
comparado con los 23,2 minutos del antecesor silvestre. Ninguno de los 444 cultivos tenía
una eficacia superior al del tipo silvestre. Estos resultados son consistentes con el trinquete de Muller.
J. David Lambert y Nancy Moran (1998) se aprovecharon de un experimento natural
para comprobar si el trinquete de Muller opera en la naturaleza. Lambert y Moran estudiaron nueve especies de bacterias que viven dentro de células de insectos. Estas bacterias
son endosimbiontes obligados, lo que quiere decir que viven sólo en el interior de las células de los insectos. Las bacterias se transmiten de madres a hijos pasando por el citoplasma del huevo, exactamente como lo hacen las mitocondrias. Advierta que la bacteria
endosimbiótica en el estudio de Lambert y Moran se propagan de una manera muy análoga al protocolo utilizado por Andersson y Hughes en su estudio de laboratorio. La única
diferencia es que en el estudio de Lambert y Moran, las bacterias se han propagado de esta
forma durante muchos millones de años.
Las nueve especies de bacteria que Lambert y Moran estudiaron representan al menos
cuatro inventos distintos del estilo de vida endosimbiótica, y cada grupo de endosimbiontes derivados independientemente tiene parientes próximos que viven de manera libre.
Lambert y Moran comprobaron si los endosimbiontes, comparándolos con sus parientes de
vida libre, habían acumulado mutaciones deletéreas. Los investigadores se centraron en los
genes de RNA de la subunidad pequeña ribosomal (rRNA). A partir de la secuencia de
los genes de rRNA de cada especie, Lambert y Moran calcularon la estabilidad térmica del
rRNA codificado. La estabilidad es beneficiosa para los RNA, y las mutaciones deletéreas
en un gen de rRNA la reducirán. En cada caso, Lambert y Moran encontraron que las bacterias endosimbióticas tenían RNA que era de un 15 a un 25% menos estable que sus
parientes de vida libre. De nuevo, este resultado está de acuerdo con el trinquete de Muller.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 221
Así pues, el trinquete de Muller funciona, tanto en la teoría como en la práctica. Para
contrarrestar el trinquete, el sexo puede ser beneficioso. Sin embargo hay un problema con
modelos que explican el sexo proponiendo a la deriva como causa del desequilibrio de
ligamiento. Los beneficios que confiere el sexo en estos modelos se acumulan sólo durante un tiempo muy largo. Si aparece una hembra asexual en una población sexual, el trinquete de Muller tardaría muchas generaciones para ponerse al día en sus descendientes y
disminuir su eficacia lo suficiente como para llevarlos a la extinción. Mientras tanto, los
descendientes de las hembras asexuales gozarían del beneficio identificado por Maynard
Smith de reproducirse el doble. No obstante, la rareza de las especies asexuales sugiere,
como los experimentos de Dunbrack y sus colegas demuestran, que la ventaja del sexo se
acumula después de pocas generaciones. Este razonamiento ha promovido la investigación
de los beneficios del sexo a corto plazo.
La selección impuesta por un cambio ambiental puede hacer
que el sexo sea beneficioso
Para ver la lógica de las teorías del ambiente cambiante para el sexo, imaginemos primero una hembra asexual y otra sexual viviendo en un ambiente constante. Si estas hembras
sobreviven y se reproducen, y sus descendientes viven en el mismo ambiente, entonces los
descendientes de la hembra asexual probablemente también sobrevivirán para reproducirse. Después de todo, reciben de sus madres exactamente el mismo genotipo ya comprobado. Sin embargo, los descendientes genéticamente diferentes de la hembra sexual,
pueden o no sobrevivir para reproducirse, dependiendo de la naturaleza de las diferencias
genéticas entre ellos mismos y su madre. Por este razonamiento, en un ambiente constante
la reproducción asexual es una apuesta ganadora.
Sin embargo, en un ambiente variable, todas las apuestas son perdedoras. Si el ambiente está cambiando de tal manera que la misma hembra asexual no pueda sobrevivir en las
nuevas condiciones, entonces sus descendientes también tendrán un futuro incierto. Sin
embargo, si el ambiente cambia para una hembra sexual, siempre hay una posibilidad de
que alguno de sus distintos descendientes tengan genotipos que les permitan prosperar en
las nuevas condiciones. Algunas teorías sobre el cambio ambiental se concretan en cambios en el ambiente físico, mientras que otras lo hacen en cambios en el ambiente biológico.Adviértase que todas las teorías sobre el cambio ambiental asumen compromisos, tales
que los genotipos que funcionan relativamente bien en algunos ambientes necesariamente
lo hacen relativamente mal en otros.
A. H. Sturtevant y K. Mather (1938, citado en Felsenstein 1988) fueron los primeros
en considerar un modelo genético poblacional explícito con selección variable. Imaginaron una población en la que la selección favorecía a algunos genotipos multilocus en algunas generaciones (por ejemplo, los genotipos AABB y aabb en un modelo de dos locus)
y a otros genotipos algunas generaciones después (Aabb y aaBB). La población alternaría
entre un régimen de selección que genera desequilibrio de ligamiento con valores positivos de D y un régimen de selección que genera desequilibrio de ligamiento con valores negativos de D (véase el Cuadro 7.1). En estas condiciones, el sexo podría estar favorecido por su capacidad para recrear genotipos que hubieran sido eliminados
recientemente por selección pero que ahora son favorecidos. Como en el trinquete de
Muller, los genes para el sexo aumentan a una gran frecuencia en los genotipos multilocus de eficacia elevada que ayudan a crear.
El patrón variable de selección requerido por las teorías del cambio ambiental puede
imponerse bien por factores físicos ambientales o por interacciones biológicas. Actualmente, la teoría más popular del sexo en ambientes variables, llamada a veces la
“hipótesis de la Reina Roja,” implica una carrera de armamentos evolutivos entre los
El sexo puede ser ventajoso
porque recrea genotipos
multilocus favorables que se
han perdido por deriva.
Entonces, los genes para el
sexo aumentan a gran
frecuencia en los genotipos de
eficacia elevada que ayudan a
crear.
222 PARTE II Los mecanismos del cambio evolutivo
que fueron eliminados
recientemente por selección.
Entonces, los genes para el
sexo aumentan a altas
frecuencias en los genotipos
de eficacia elevada que
ayudaron a crear.
Población de parásitos
Imagine un huésped en el que hay un
compromiso entre una resistencia
individual al genotipo I del parásito
versus al genotipo II. La variación
entre los individuos de la población
podría asemejarse al gráfico de la derecha.
Además, imagine que los parásitos
con genotipo I son más abundantes
que los parásitos con genotipo II.
Figura 7.17 Una carrera de armamentos
entre el parásito y el huésped puede hacer
beneficioso al sexo Los huéspedes resistentes al
genotipo I del parásito son necesariamente
susceptibles al genotipo II del parásito y viceversa. A
medida que la población de parásitos evoluciona en
respuesta a los huéspedes, primero se selecciona en
los huéspedes resistentes al genotipo I del parásito,
luego en los huéspedes resistentes al genotipo II del
parásito. Los genes para el sexo aumentarán a
elevadas frecuencias en los genotipos que ayudan a
crear, que normalmente serán los más adaptados.
I II
Resistencia al genotipo I
del parásito
I II
Estas condiciones seleccionarán a favor
de huéspedes que sean más resistentes
al genotipo II del parásito. El sexo se
favorecerá porque permite una rápida
recreación de los genotipos que favorecen
al huésped.
Ahora, el huésped, como promedio,
es resistente al genotipo II del
parásito y susceptible al genotipo I
del parásito. Esto seleccionará a favor
del genotipo I del parásito
Población de huéspedes
Resistencia al genotipo I
del parásito
Estas condiciones seleccionarán a favor
de huéspedes que sean más resistentes
al genotipo I del parásito.
Ahora, el huésped, como promedio, es
resistente al genotipo I del parásito y
susceptible al genotipo II del parásito.
Esto seleccionará a favor del genotipo
II del parásito.
Resistencia al genotipo II
del parásito
multilocus, ahora favorables,
Resistencia al genotipo II
del parásito
porque recrea genotipos
parásitos y sus huéspedes (para una revisión véase Seger y Hamilton 1988; Lively 1996).
Los parásitos y sus huéspedes están encerrados en una perpetua lucha, evolucionando
el huésped para defenderse a sí mismo y evolucionando el parásito para evadir las
defensas del huésped. Es fácil imaginar que una población de parásitos se seleccionará
a favor de algunos genotipos multilocus del huésped en algunas generaciones y a favor
de otros en otras generaciones. La Figura 7.17 presenta un escenario para tal resultado
de interacción evolutiva.
Curtis Lively (1992) investigó si los parásitos se seleccionan, de hecho, a favor del sexo
en sus huéspedes. Lively estudió el caracol de agua dulce Potamopyrgus antipodarum. Este
caracol, que vive en lagos y ríos en Nueva Zelanda, es el hospedador de una docena de
especies de gusanos tremátodos parásitos. Los tremátodos típicamente castran a sus huéspedes comiéndose sus gónadas. En sentido evolutivo, la castración es equivalente a la muerte: evita la reproducción. Los tremátodos ejercen así sobre las poblaciones de caracoles una
fuerte presión selectiva por la resistencia a la infección. Muchas especies de caracoles tienen dos tipos de hembras: hembras obligadamente sexuales, que producen una mezcla de
descendientes masculinos y femeninos, y hembras obligadamente partenogenéticas, cuyas
hijas son clones de sus madres.(Advierta que ambos tipos de hembras deben de tener un
ovario para reproducirse; la diferencia es que los huevos de las hembras partenogenéticas
no tienen que ser fecundados.) La proporción de sexuales respecto de asexuales varía de
una población a otra.Así lo hace la frecuencia de infección por tremátodos. Si se establece una carrera de armamentos evolutiva entre los caracoles y los tremátodos seleccionando a favor del sexo de los caracoles (véase la Figura 7.17), entonces los caracoles sexuales
deberían ser más frecuentes en las poblaciones con tasas de infección de tremátodos alta.
Resistencia al genotipo II
del parásito
El sexo puede ser ventajoso
Resistencia al genotipo I
del parásito
I II
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 223
Lively tomó muestras de caracoles de 66 lagos, determinó el sexo de cada caracol y si
estaba infectado por parásitos. Lively utilizó la frecuencia de los machos de cada población
como un índice de la frecuencia de hembras sexuales, ya que los machos los producen sólo
las hembras sexuales. Lively encontró que en las poblaciones más fuertemente parasitadas
había una mayor proporción de hembras que eran sexuales (Figura 7.18). Este resultado
está de acuerdo con la teoría de selección variable del sexo.
Lively advirtió que, dado que su estudio era sólo por observación, deberían considerarse explicaciones alternativas para la asociación que él encontró. Por ejemplo, si:
1. Las tasas de infección por tremátodos son mayores en poblaciones de caracoles más
densas debido a que la alta densidad de huéspedes facilita la transmisión del parásito.
2. La frecuencia de hembras partenogenéticas es más elevada en poblaciones de caracoles menos densas porque el beneficio real de la partenogénesis es que permite a las
hembras reproducirse aun cuando los machos son difíciles de encontrar.
Luego la combinación de estos dos efectos daría lugar a una asociación positiva entre
la frecuencia de sexuales y la frecuencia de infección por tremátodos. Lively rechazó esta
explicación alternativa demostrando que aunque hay una correlación positiva entre la tasa
de infección y la densidad de caracoles (el efecto 1 es cierto), hay también una correlación positiva entre la frecuencia de hembras partenogenéticas y la densidad de caracoles
(el efecto 2 es falso). Después de considerar ésta y otras explicaciones alternativas, Lively
concluyó que la explicación más simple para el patrón que encuentra es que los tremátodos realmente han seleccionado a favor de la reproducción sexual a los caracoles.
En resumen, en el contexto de la genética de poblaciones, el efecto del sexo es reducir el desequilibrio de ligamiento. Por consiguiente, un modelo genético poblacional del
valor adaptativo del sexo debe tener dos componentes: un mecanismo que origine el desequilibrio de ligamiento y una razón de por qué la selección favorece caracteres que tienden a reducir el desequilibrio de ligamiento. Hay dos tipos de modelos para el sexo. En
el primer tipo, la deriva genética da lugar al desequilibrio de ligamiento. En ese caso el sexo
se favorece porque ayuda a recrear genotipos con eficacia elevada perdidos por deriva. En
el segundo tipo la selección natural da lugar al desequilibrio de ligamiento. En ese caso el
patrón de selección cambia y el sexo se favorece porque ayuda a recrear los genotipos
ahora favorables recientemente seleccionados en contra. Los distintos escenarios que
favorecen al sexo son compatibles entre sí. Es probable que la selección variable impuesta por cambios tanto en el ambiente biológico como en el físico se combine con el trinquete de Muller para dar lugar a que la ventaja del sexo sea mayor que la ventaja que pueda
conferir cualquier otro factor aislado (Howard y Lively 1998).
(b)
Frecuencia de machos
(a)
Figura 17.8 La frecuencia de individuos
sexuales en poblaciones de un caracol
está positivamente correlacionada con
la frecuencia de sus tremátodos
parásitos (a) El mapa muestra la
0,40
0,30
0,20
0,15
0,10
0,05
0,01
0,00
0,00 0,01 0,05 0,10 0,15 0,20 0,30 0,40 0,50
Infección total
localización de los 66 lagos en los que Lively
hizo un muestreo. En el esquema en círculo
de cada población, la parte blanca representa
la frecuencia de machos. (b) En el eje de
coordenadas se representa la frecuencia de
machos de cada población respecto de la
proporción de caracoles infectados con
tremátodos. En el gráfico se incluye la mejor
regresión lineal. Los machos son más
frecuentes en las poblaciones con más
caracoles infectados. Según Lively (1992).
224 PARTE II Los mecanismos del cambio evolutivo
7.3.
La genética cuantitativa nos
permite analizar la evolución
por selección natural en
caracteres controlados por
muchos loci.
Selección sobre caracteres cuantitativos
Las herramientas conceptuales que desarrollamos en los Capítulos 5 y 6 y las herramientas que hemos desarrollado hasta el momento en el Capítulo 7, nos permiten analizar la
evolución de caracteres controlados por uno o dos loci. Sin embargo, la mayoría de los
caracteres en la mayoría de los organismos están determinados por los efectos combinados de muchos loci diferentes, y también son influenciados por el ambiente. En los ejemplos se incluye la estatura de los humanos, la velocidad de reacción de las lagartijas y el
tamaño de las flores. Tales caracteres muestran variación continua entre individuos y se
denominan caracteres cuantitativos; en contraste con los caracteres cualitativos, como
la fibrosis quística (Capítulos 4 y 5), en los que una persona tiene el fenotipo afectado o
no lo tiene. Necesitamos herramientas que nos permitan analizar y entender la genética
y la evolución de los caracteres cuantitativos, aun cuando no conozcamos la identidad de
muchos de los genes específicos implicados. Estas herramientas son el objeto de la genética cuantitativa y se tratarán en esta última sección del capítulo.
Recuerde los principios básicos de la teoría de la evolución de Darwin por selección
natural: si hay variación heredable en los individuos de una población, y si hay diferencias
en la supervivencia y/o en el éxito reproductivo entre las variantes, entonces la población
evolucionará. La genética cuantitativa abarca herramientas para medir la variación heredable, para medir las diferencias en supervivencia y/o en éxito reproductivo y en la predicción de la respuesta evolutiva a la selección.
Medida de la variación heredable
Imaginemos una población de organismos en la que para algún carácter hay variación continua entre los individuos. Por ejemplo, imaginemos una población humana en la que entre
los individuos hay variación continua para la estatura. Los caracteres de variación continua están distribuidos típicamente de manera normal, por lo que el histograma de un
carácter tiene la familiar forma acampanada. Por ejemplo, en una población humana típica, pocas personas son bajas, muchas tienen más o menos la estatura media y pocas son muy
altas (Figura 7.19). Queremos saber: ¿es heredable la estatura?
Merece la pena pensar cuidadosamente qué significa exactamente esta pregunta. Preguntas acerca de la heredabilidad se expresan a menudo en términos de naturaleza versus
nutrición. Pero tales cuestiones son significativas sólo si se refieren a la comparación entre
individuos. No tiene sentido fijarnos sólo en el estudiante del extremo izquierdo de la
Figura 7.19a y preguntarnos, sin hacer referencia a otros individuos, si este estudiante tiene
4 pies y 10 pulgadas (1,47 m) por sus genes (naturaleza) o por su ambiente (nutrición).
Tiene que tener tanto genes como un ambiente para estar vivo y una estatura dada. Él no
consiguió 3 pies de su estatura por sus genes y 1 pie y 10 pulgadas por su ambiente, por
lo que 3⬘ + 1⬘10 ⬙ = 4⬘10 ⬙. Él consiguió sus 4 pies y 10 pulgadas por la actividad de sus
genes actuando en su ambiente. En dicho estudiante no podemos desligar las influencias
de la naturaleza y de la nutrición.
El único tipo de pregunta que tiene sentido hacerse es la comparativa: el más bajo de los
estudiantes, ¿es más bajo que los estudiantes más altos porque tiene genes distintos, o porque creció en ambientes diferentes, o por ambas causas? Ésta es una pregunta que podemos
responder. Por ejemplo, en principio podríamos tomar un gemelo idéntico del estudiante
de baja estatura y criarlo en el ambiente experimentado por el estudiante más alto. Si este
gemelo crece sólo hasta 4 pies y 10 pulgadas, entonces sabríamos que la diferencia entre los
estudiantes más altos y más bajos se debe completamente a diferencias en sus genes. Si el
gemelo crece hasta 6 pies y 2 pulgadas2 entonces sabríamos que las diferencias entre los estu2
Nota del traductor. Seis pies y 2 pulgadas son 74 pulgadas (estatura del individuo más alto de la distribución de la Figura 7.19b).
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 225
(a)
30
Número de estudiantes
(b)
Figura 7.19 Variación distribuida normalmente de
un carácter (a) Fotografía, publicada en el Journal of
25
20
15
10
5
0
58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
Estatura (en pulgadas)
Heredity en 1914 por Albert Blakeslee, de un grupo de
estudiantes del Connecticut Agricultural College
distribuidos por estatura. La distribución de los
estudiantes forma un histograma vivo. (Compare la foto
de Blakeslee con la de la página 197, tomada en la
misma escuela en 1996.) Reproducido con el permiso de
la Oxford University Press (b) Histograma gráfico que
presenta la distribución de las estaturas entre los
estudiantes mostrados en (a).
diantes más altos y más bajos se debe exclusivamente a diferencias ambientales. De hecho,
el gemelo probablemente crecería hasta una estatura entre 4⬘10 ⬙ y 6⬘2⬙. Esto indicaría que
las diferencias entre los dos estudiantes se deben parcialmente a diferencias en sus genes y
a diferencias en sus ambientes. Considerando la población en conjunto, en lugar de sólo dos
individuos, podemos preguntarnos: ¿qué porcentaje de la variación en estatura entre los
estudiantes se debe a sus genes y qué porcentaje se debe a variaciones en su ambiente?
El porcentaje de la variación total de un carácter que se debe a la variación en los genes
se denomina la heredabilidad del carácter. La variación total de un carácter se denomina variación fenotípica y se simboliza por VP. La variación entre individuos debido a
variación en sus genes se denomina variación genética y se simboliza por VG. La variación entre individuos debido a variación en sus ambientes se denomina variación
ambiental y se simboliza por VE.Así, tenemos:
Vg
VG
heredabilidad ⫽ ᎏᎏ ⫽ ᎏᎏ
VP VG ⫹ VE
De manera más precisa, este porcentaje se conoce como la heredabilidad en sentido
amplio, o grado de determinación genética. Definiremos en breve la heredabilidad en sentido estricto. La heredabilidad es siempre un número entre 0 y 1.
Antes de liarnos más profundamente en abstracciones simbólicas, advirtamos el hecho
cierto de que si la variación entre individuos se debe a la variación en sus genes, entonces los descendientes se parecerán a sus padres. En principio es fácil comprobar si lo son.
Primero representaremos en un eje de coordenadas los valores del carácter de los descendientes en el eje de las y, y el valor del carácter de los padres en el eje de las x (Figura 7.20). Cada descendiente tiene dos padres, por lo que calcularemos el valor medio de
éstos. Si tenemos más de un descendiente en cada familia, utilizaremos también el valor
medio de los hijos. Luego dibujaremos la línea que más se ajusta a los datos. Si los descendientes no se parecen a sus padres, entonces el valor de la pendiente de la línea estará
El primer paso en un análisis
genético cuantitativo es
determinar el grado en el que
el carácter en cuestión es
heredable. Es decir, tenemos
que hacer la partición de la
variación fenotípica total (VP)
en un componente debido a la
variación genética (VG) y otro
componente debido a la
variación ambiental (VE).
226 PARTE II Los mecanismos del cambio evolutivo
(a) Heredabilidad
aproximadamente 0
Alto
Figura 7.20 Representación en un eje de coordenadas de la estatura de los descendientes en
función de la de los padres Cada una de las tres gráficas superiores muestran datos de una población
hipotética, en las que se incluye la mejor regresión lineal a los datos. (a) En esta población los descendientes
no se parecen a sus padres. (b) En esta población los descendientes tienen un cierto parecido con sus padres.
(c) En esta población los descendientes se parecen muchísimo a sus padres. (d) Este gráfico presenta los datos
de una población real de estudiantes de un curso reciente sobre evolución de una Universidad de la costa
Noroeste del Pacífico, U.S.A.
Bajo
Estatura media de los hijos
Bajo
Alto
(b) Heredabilidad
aproximadamente 0,5
Alto
Bajo
Bajo
Alto
(c) Heredabilidad
aproximadamente 1
Alto
Bajo
Estatura media de los hijos (en pulgadas)
Bajo
Alto
Estatura media
de los padres
(d) Estudiantes y
sus padres
76
72
68
Pendiente
= 0,84
64
60
60
64
68
72
76
Estatura media de los padres
(en pulgadas)
La heredabilidad, h2, es una
próxima a 0 (Figura 7.20a); es evidente que la variación de los individuos de la población
se debe a la variación en sus ambientes, no a la variación en sus genes. Si los descendientes se parecen muchísimo a sus padres, el valor de la pendiente será próximo a 1 (Figura
7.20c); esto demuestra que la variación de los individuos de la población se debe a la variación en sus genes, no a la variación en sus ambientes. La mayoría de los caracteres se
encuentran en muchas poblaciones entre ambos valores, con descendientes presentando
un parecido moderado a sus padres (Figura 7.20b); esto prueba que la variación de los individuos se debe parcialmente a la variación en sus ambientes, y parcialmente a la variación
en sus genes. La Figura 7.20d muestra los datos de una población real de estudiantes. (Para
otro ejemplo, vuelva a la Figura 3.4, donde se analiza la heredabilidad de la altura del pico
en los pinzones de Darwin.)
Los ejemplos de la Figura 7.20 ilustran que la pendiente de la línea que más se ajusta en
una representación del valor medio de hijos respecto del valor medio de los padres es un
número entre 0 y 1 que refleja el grado en que la variación de la población se debe a la variación en los genes. En otras palabras, podemos tomar a la pendiente como una estima de la
heredabilidad. Si determinamos la línea que más se ajusta utilizando el método de la regresión lineal de mínimos cuadrados, entonces la pendiente representa una versión de la heredabilidad, simbolizada por h2, que se denomina heredabilidad en sentido estricto. La regresión
lineal por mínimos cuadrados es el método típico que se enseña en textos introductorios de
estadística y que se utiliza en paquetes de programas estadísticos para determinar la línea que
más se ajusta. (Para los lectores familiarizados con la estadística, se puede evitar alguna confusión si advertimos que h2 no es el porcentaje de la variación entre los descendientes que
se explica por la variación en los padres. Dicha cantidad sería r 2. Más bien, h2 es una estima
del porcentaje de la variación entre los padres que se debe a la variación en sus genes.)
Para explicar la diferencia entre la heredabilidad en sentido estricto y la heredabilidad
en sentido amplio, necesitamos distinguir entre dos componentes de la variación genética: la variación genética aditiva y la variación genética de la dominancia. La variación
genética aditiva (VA) es la variación entre los individuos debido a los efectos aditivos de
los genes, mientras que la variación genética de la dominancia (VD) es la variación entre
individuos debida a las interacciones génicas tales como la dominancia3 (véase el Cuadro
7.5). La variación genética total es la suma de la variación genética aditiva y de la dominancia: VG = VA + VD. La heredabilidad en sentido amplio, definida anteriormente, es
VG/VP. La heredabilidad en sentido estricto, h2, se define como,
VA
VA
ᎏ
h2 ⫽ ᎏᎏ ⫽ ᎏ
VP VA ⫹ VD ⫹ VE
Cuando un biólogo evolutivo menciona la heredabilidad sin advertir si está utilizando
el término en sentido amplio o en sentido estricto, casi siempre se refiere a la heredabilidad en sentido estricto. Utilizaremos la heredabilidad en sentido estricto en el resto de esta
medida de la variación
genética (aditiva) de un
carácter.
3
Nota del traductor. Tal como está definida en el texto, la VD engloba tanto a la VD en sentido estricto (variación entre
individuos debida a las relaciones de dominancia entre los alelos de los genes) como a la llamada varianza de la interacción,
VI (variación entre individuos debida a las interacciones entre los distintos genes): es decir, VG = VA + VD + VI.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 227
CUADRO 7.5 Variación genética aditiva respecto de la variación genética de la dominancia
A
quí utilizaremos un ejemplo numérico para distinguir
entre la variación genética aditiva y la variación genética de la dominancia. Para simplificar la discusión, analizaremos la variación genética en un locus con dos alelos
como si estuviéramos analizando un carácter cuantitativo.
Asumiremos que no hay variación ambiental en el carácter
en cuestión: el fenotipo de un individuo está determinado
única y exclusivamente por su genotipo. Los alelos del locus
son A1 y A2; cada uno con una frecuencia de 0,5 y la
población se encuentra en equilibrio de Hardy-Weinberg.
Consideraremos dos situaciones: (1) los alelos son codominantes; (2) el alelo A2 es dominante sobre el alelo A1.
Situación (1): los alelos A1 y A2 son codominantes
Los individuos A1A1 tienen el fenotipo 1. En los individuos A1A2 y A2 A2 cada copia del alelo A2 añade 0,5 al
fenotipo. En la Figura 7.21a, a la izquierda, hay un histograma que muestra la distribución de los fenotipos de la
población. En el centro y a la derecha hay una representación que nos permite analizar la variación genética de la
población. El eje de las x representa al genotipo, con el
número de copias del alelo A2. El eje de las y representa al
fenotipo. La línea gris horizontal indica el fenotipo medio
de la población (=1,5). Las gráficas del centro muestran
que la variación genética total, VG, es función de la desviación de cada punto respecto de la media de la población
(flechas verdes). Podemos cuantificar VG calculando la
suma de las desviaciones al cuadrado. La representación de
la derecha muestra la línea que mejor se ajusta a los puntos (roja). La variación genética aditiva, VA, se define como
aquella fracción de la variación genética total que es explicada por la línea que mejor se ajusta (flechas azules). En
este caso, la línea que mejor se ajusta explica toda la variación genética, por lo que VG = VA. No hay variación
genética de la dominancia.
Situación (2): el alelo A2 es dominante
sobre el alelo A1
Esta vez los individuos A1A1 tienen de nuevo el fenotipo
1. Sin embargo, los efectos al sustituir las copias de A1 por
copias de A2 no son estrictamente aditivos: la primera
copia de A2 (que convierte al genotipo en A1A2) cambia
al fenotipo de 1 a 2. La segunda copia de A2 (que convierte
al genotipo en A2A2) no altera más al fenotipo. A la
izquierda de la Figura 7.21b hay un histograma que muestra la distribución de los fenotipos de la población. En el
centro y a la derecha hay una representación que nos permite analizar la variación genética de la población. La gráfica del centro muestra que la variación genética total, VG,
es función de la desviación de cada punto (flechas verdes)
respecto de la media de la población (línea gris = 1,75). La
representación de la derecha muestra la línea que mejor se
ajusta a los puntos (roja). La variación genética aditiva,
VA, es aquella fracción de la variación genética total que
es explicada por la línea que mejor se ajusta (flechas azules). La variación genética de la dominancia, VD, es aquella fracción de la variación genética total que queda sin
explicar por la línea que mejor se ajusta (flechas amarillas).
En este caso, la línea que mejor se ajusta explica sólo parte
de la variación genética, por lo que VG = VA + VD.
(a) Sin dominancia. Fenotipos: A1A1 = 1; A1A2 = 1,5; A2A2 = 2
Fenotipo
Porcentaje
de población
0,75
0,5
0,25
0
VG
2,5
Histograma
1 1,5 2
Fenotipo
2,5
2
2
1,5
1,5
1
1
0,5
0,5
0
1
2
VG = VA+VD; VD = 0
0
1
2
Genotipo (Número de alelos A2)
(b) Dominancia completa. Fenotipos: A1A1 = 1; A1A2 = 2; A2A2 = 2
Fenotipo
Porcentaje
de población
0,75
0,5
0,25
0
1
1,5
Fenotipo
2
VG
2,5
Histograma
2,5
2
2
1,5
1,5
1
1
0,5
0
1
2
0,5
VG = VA + VD
0
Genotipo (Número de alelos A2)
1
2
Figura 7.21 Variación genética
aditiva respecto de la variación
genética de la dominancia en un
carácter controlado por los dos
alelos de un locus.
228 PARTE II Los mecanismos del cambio evolutivo
y = 0,98x - 0,01
Tamaño medio del pico de los hijos (mm)
6,2
r 2 = 0,496
5,8
5,4
5,4
5,8
6,2
Tamaño medio del pico de los
padres biológicos (mm)
y = - 0,18x + 6,86
6,2
r 2 = 0,011
5,8
5,4
5,4
5,8
6,2
Tamaño medio del pico de los
padres adoptivos (mm)
Figura 7.22 Un experimento
en el campo sobre la
heredabilidad del tamaño del
pico en los gorriones cantores
El gráfico superior muestra las
relaciones entre el tamaño medio
del pico entre los descendientes
(media familiar del tamaño del
pico) y el tamaño del pico de los
padres biológicos (tamaño medio
del pico de los padres biológicos).
El gráfico inferior muestra las
relaciones entre el tamaño medio
del pico entre los descendientes
(media familiar del tamaño del
pico) y el tamaño del pico de los
padres adoptivos (tamaño medio
del pico de los padres adoptivos).
Los pollitos se parecen muchísimo
a sus padres biológicos y nada a
sus padres adoptivos. De Smith y
Dhondt (1980). Copyright ©
1980, Evolution. Reimpreso con el
permiso de Evolution.
discusión. Es la heredabilidad en sentido estricto, h2, la que nos permite predecir cómo responderá una población a la selección.
Cuando se estima la heredabilidad de un carácter en una población, es importante tener
en mente que los descendientes se pueden parecer a sus padres por razones distintas de los
genes que han heredado los descendientes (véase el Cuadro 3.1). El ambiente también va
por familias. Por ejemplo, en la especie humana, algunas familias hacen más ejercicio que
otras y familias distintas toman distintas dietas. Nuestra estima de la heredabilidad será precisa sólo si podemos asegurarnos que no hay correlación entre el ambiente experimentado por los padres y el experimentado por sus hijos. Obviamente esto no lo podemos hacer
en un estudio sobre nuestra especie. Sin embargo, al estudiar animales podemos reunir a
todos los descendientes al nacer y luego adjudicarles padres adoptivos al azar. En un estudio de vegetales, podemos situar las semillas en localizaciones al azar en un campo.
Por ejemplo, James Smith y André Dhondt (1980) estudiaron el gorrión cantor (Melospiza melodia) para determinar la heredabilidad del tamaño del pico. Recogieron crías de
nidos en el campo, a veces huevos y a veces recién eclosionados, y los desplazaron a nidos
de padres adoptivos elegidos al azar. Cuando los pollitos crecieron, Smith y Dhondt calcularon el valor medio de los pollitos descendientes y el valor medio de los padres, tanto
de los biológicos como de los adoptivos. Las gráficas con la relación entre el tamaño de
los picos de los descendientes y el tamaño del pico de los padres aparecen en la Figura
7.22. Los pollitos se parecen muchísimo a sus padres biológicos y en absoluto a sus padres
adoptivos. Estos resultados demuestran que, prácticamente, toda la variación del tamaño
del pico en esta población se debe a la variación en los genes. Smith y Dhondt estimaron
la heredabilidad del tamaño del pico en 0,98.
Hay una serie de métodos diversos para estimar la heredabilidad junto al cálculo de la
pendiente de la línea más ajustada de descendientes respecto de los padres. Por ejemplo,
se pueden utilizar estudios de gemelos. La lógica del estudio de los gemelos es la siguiente. Los gemelos monozigóticos (idénticos) comparten su ambiente y todos sus genes,
mientras que los gemelos dizigóticos (fraternos) comparten su ambiente y la mitad de sus
genes. Si la heredabilidad es alta, y la variación entre individuos se debe básicamente a la
variación en los genes, entonces los gemelos monozigóticos serán más similares entre sí
que los gemelos dizóticos entre sí. Si la heredabilidad es baja, y la variación entre los individuos se debe principalmente a la variación en el ambiente, entonces los gemelos monozigóticos serán tan diferentes entre sí como los gemelos dizigóticos. Para una introducción
detallada sobre métodos para el cálculo de la heredabilidad, véase Falconer (1989). Los
datos sobre la heredabilidad de los caracteres son malinterpretados frecuentemente, especialmente cuando la especie en estudio es la humana.Volveremos a este tema más tarde.
Medida de las diferencias en supervivencia y en éxito reproductor
En los párrafos anteriores hemos desarrollado técnicas para medir la variación heredable en caracteres cuantitativos, el primer principio de la teoría de la evolución de
Darwin por selección natural. El siguiente principio de la teoría de Darwin es que hay
diferencias en la supervivencia y/o en el éxito reproductor entre individuos. Discutiremos ahora las técnicas para medir las diferencias en este éxito, es decir, en la medida de
la fuerza de la selección. Una vez que podamos medir tanto la variación heredable como
la fuerza de la selección, seremos capaces de predecir el cambio evolutivo en respuesta
a la selección.
El tipo de diferencias en el éxito imaginadas en la teoría de Darwin son diferencias sistemáticas. Como promedio, los individuos con algunos valores en un carácter sobreviven
con mayor probabilidad, o producen más descendientes, que individuos con otros valores
del carácter. Para medir la fuerza de la selección, veremos primero quién sobrevive o se
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 229
reproduce y quién no. Luego cuantificaremos la diferencia entre ganadores y perdedores
para el carácter de interés.
En experimentos de selección, la fuerza de la selección es fácil de calcular. Por ejemplo, consideremos un experimento realizado por R. J. Di Masso y sus colegas (1991).
Estos investigadores iniciaron el cruce de ratones con colas más largas. Querían saber
cómo cambiaría el programa de desarrollo que da lugar a la cola de los ratones bajo presión de selección. El embrión del ratón, ¿haría la cola más larga alargando cada una de
sus vértebras o añadiendo vértebras extras? Los investigadores midieron en cada generación las colas de todos los ratones de su población. Luego seleccionaron los ratones
con las colas más largas y dejaron que se cruzaran entre sí para dar lugar a la generación siguiente.
Para ver cómo cuantificar la fuerza de la selección, suponga que los investigadores seleccionaron como padres a un tercio de los ratones con las colas más largas. La medida más
simple de la fuerza de la selección es la diferencia entre la longitud media de la cola de
los padres y la longitud media de la cola de toda la población (Figura 7.23a). Esta medida se denomina diferencial de selección y se simboliza por S.
Hay una segunda medida de la fuerza de la selección que es útil porque es aplicable en
muchos casos. Esta medida se denomina el gradiente de selección (Lande y Arnold 1983).
El gradiente de selección se calcula de la siguiente manera:
1. Asigne la eficacia absoluta a los ratones de la población. Consideraremos a la eficacia
como la supervivencia hasta la edad reproductiva. En nuestra población, 1/3 de los ratones sobrevive lo suficiente como para reproducirse. (Esto no significa necesariamente
que se mate realmente a los ratones de cola corta, ya que son eliminados de la población seleccionada; en cuanto a lo que se refiere a nuestra población seleccionada, los
ratones de cola corta no se cruzan, por lo que no sobreviven lo suficiente como para
(b) El gradiente de selección
6
3
5
Pendiente = Gradiente
2 de selección
Eficacia relativa
Número de individuos
(a) El diferencial de selección
4
3
2
1
1
0
0
1,5
3
t
4,5
t*
Longitud de la cola
6
0
1,5
3
4,5
6
Diferencia entre
medias = diferencial
de selección
Longitud de la cola
Figura 7.23 Medida de la fuerza de la selección (a) El histograma muestra la variación en la
longitud de la cola en una población ficticia de ratones de laboratorio. Las barras rojas representan a los
ratones elegidos como padres de la generación siguiente. El triángulo gris señala la longitud media de la
cola de la población en conjunto; el triángulo rojo señala la longitud media de la cola de los padres
seleccionados. La diferencia entre estas dos medias es el diferencial de selección. (b) En el eje de
coordenadas se presenta para la misma población ficticia de ratones la eficacia relativa (véase el texto) en
función de la longitud de la cola. Los puntos rojos representan a los ratones elegidos como padres de la
generación siguiente. Se incluye el mejor ajuste lineal (en verde). La pendiente de la mejor regresión lineal
es el gradiente de selección.
El segundo paso en un análisis
genético cuantitativo es medir
la fuerza de la selección sobre
el carácter en cuestión. Una
medida es el diferencial de
selección, S, que es igual a la
diferencia entre los individuos
seleccionados y la media del
conjunto de la población.
Una segunda medida
(relacionada) de la fuerza de la
selección es el gradiente de
selección.
230 PARTE II Los mecanismos del cambio evolutivo
reproducirse.) Los 2/3 de ratones de cola corta tienen una eficacia de 0 y 1/3 de los ratones de cola larga tienen una eficacia de 1.
2. Convierta la eficacia absoluta en eficacia relativa. La eficacia media de la población
es 0,33 (por ejemplo, si hay 30 ratones en la población, la media es [{20 ⫻ 0}
+ {10 ⫻ 1}]/30 = 0,33). Calculamos la eficacia relativa de cada ratón dividiendo su
eficacia absoluta (0 ó 1) por la eficacia media (0,33). Los ratones de cola corta tienen
una eficacia relativa de 0; los ratones de cola larga tienen una eficacia relativa de 3.
3. Represente en un eje de coordenadas la eficacia relativa en función de la longitud de
la cola y calcule la pendiente de la línea que mejor se ajusta (Figura 7.23b). La pendiente es el gradiente de selección.
CUADRO 7.6
El gradiente de selección y el diferencial de selección
E
l diferencial de selección es una medida intuitivamente directa de la fuerza de la selección: es la diferencia
entre la media de un carácter entre los supervivientes y la
media del carácter en el conjunto de la población. El
gradiente de selección, aunque más abstracto, tiene varias
ventajas. Entre éstas está el que el gradiente de selección
se puede calcular en una gran variedad de medidas de la
eficacia. El hecho de que el gradiente de selección esté
íntimamente relacionado con el diferencial de selección,
concede al primero algo del atractivo intuitivo del segundo.
Aquí mostraremos que en nuestro ejemplo sobre la longitud de la cola de los ratones (Figura 7.23), el gradiente de
selección t para la longitud de la cola es igual al diferencial
de selección para la longitud de la cola dividido por la
varianza de ésta. Imagine que en nuestra población tenemos 30 ratones. Primero, advierta que el diferencial de
selección es:
S ⫽ t* ⫺ tdonde t* es la longitud media de la cola de los 10 ratones
que hemos seleccionado como padres, y t- es la longitud
media de la cola del conjunto de la población de 30 ratones.
El gradiente de selección es la pendiente de la línea que
mejor se ajusta al relacionar la eficacia relativa w en función
de la longitud de la cola. La pendiente de la línea que
mejor se ajusta en regresión lineal viene dada por la covarianza de y y x dividida por la varianza de x:
cov(y, x)
ᎏ
pendiente ⫽ ᎏ
var(x)
La covarianza de y y x se define como
1 n
cov(y, x) ⫽ ᎏᎏ Σ (yi ⫺ y– )(xi ⫺ x– )
n i ⫽1
y la varianza de x se define como:
1 n
var(x) ⫽ ᎏᎏ Σ (xi ⫺ x– )2
n i ⫽1
donde n es el número de observaciones, –y es el valor
medio de y, y x– es el valor medio de x. El gradiente de
selección para t es, por consiguiente:
cov( w, t)
gradiente de selección ⫽ ᎏᎏ
var(t)
Por ello, lo que necesitamos demostrar es que la cov(w, t) ⫽
⫽t* ⫺ t-.
Debido a que (por definición) la eficacia relativa media
es 1, podemos escribir:
1 30
cov(w,t) ⫽ ᎏᎏ Σ (wi ⫺ 1)(ti ⫺ t )
30 i ⫽1
1 30
1 30
1 30
1 30
⫽ ᎏᎏ Σ (wi ti) ⫺ ᎏᎏ Σ (wi t-) ⫺ ᎏᎏ Σ (ti) ⫹ ᎏᎏ Σ ( t-)
30 i ⫽1
30 i ⫽1
30 i ⫽1
30 i ⫽1
1
⫽ ᎏᎏ
30
1
⫽ ᎏᎏ
30
30
- - ( wi ti) ⫺ t ⫺ t ⫹ t
Σ
i ⫽1
30
( wi ti) ⫺ t ⫽ t * ⫺ t
Σ
i ⫽1
El último paso puede no ser claro. Para ver que
1 30
ᎏᎏ Σ (wi ti) ⫽ t*
30 i ⫽1
advierta que para los primeros 20 ratones wi = 0, y para los
10 últimos wi = 3. Esto significa que:
1
ᎏᎏ
30
30
Σ
1 30
3 30
(
3t
)
⫽
ᎏ
Σ i 3ᎏ0 i ⫽21
Σ (ti)
30 i ⫽21
(wi ti) ⫽ ᎏᎏ
i ⫽1
1 30
Σ (ti) ⫽ t *
10 i ⫽21
⫽ ᎏᎏ
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 231
A primera vista puede parecer que el gradiente de selección y el diferencial de selección
no tengan mucho que ver entre sí. La verdad es que están íntimamente relacionados y cada
uno se puede convertir en el otro. Si estamos analizando la selección sobre un único carácter como la longitud de la cola, entonces el gradiente de selección es igual al diferencial
de selección dividido por la varianza de la longitud de la cola (véase el Cuadro 7.6). Una
ventaja del gradiente de selección es que lo podemos calcular para cualquier valor de la
eficacia, no sólo para la supervivencia. Por ejemplo, podríamos medir la eficacia de una
población natural de ratones por el número de descendientes destetados. Si calculamos primero la eficacia relativa de cada ratón (dividiendo su número de descendientes por el
número medio de descendientes), luego representamos la eficacia relativa en función de
la longitud de la cola y calculamos la pendiente de la línea que mejor se ajusta, entonces
dicha pendiente es el gradiente de selección. (Para una introducción sobre otras ventajas
del gradiente de selección, véase el Cuadro 7.7.)
Di Masso et al. seleccionaron a sus ratones para cola larga durante 18 generaciones
seguidas. Los ratones de la generación 18 tenían una cola más del 10% más larga que los
ratones de la población control. Los ratones de cola larga tenían 28 vértebras en sus colas,
mientras que los controles tenían 26 ó 27. El programa de desarrollo había sido alterado
fabricando más vértebras, no alargando cada una de ellas.
CUADRO 7.7 Selección sobre caracteres múltiples y caracteres correlacionados
E
n el texto analizamos la selección sobre un carácter
cuantitativo cada vez. Sin embargo, en la naturaleza
la selección actúa a menudo sobre varios caracteres a la
vez. Proporcionaremos aquí una breve introducción de
cómo las técnicas de genética cuantitativa pueden extenderse para analizar la selección sobre caracteres múltiples.
Para los detalles matemáticos véase a Lande y Arnold
(1983), Phillips y Arnold (1989) y Brodie, Moore y Janzen (1995).
En el Capítulo 3 discutimos la selección natural sobre el
tamaño del pico en los pinzones de Darwin. Durante la
sequía de 1976-1977 en la isla Daphne Major, los pinzones
terrestres medianos con picos más altos sobrevivieron con
mayor frecuencia. La altura del pico es heredable, por lo que
la población evolucionó. Peter Grant y Rosemary Grant
han reanalizado los datos de este episodio de selección,
buscando la selección sobre varios caracteres simultáneamente. Discutiremos su análisis sobre dos caracteres: altura
y anchura del pico. Sólo presentaremos su aspecto cualitativo; para datos numéricos véase Grant y Grant (1995).
Los pinzones terrestres medianos de Daphne Major
varían tanto en altura como en anchura del pico. Estos dos
caracteres están muy correlacionados. Picos altos tienden a
ser anchos y picos bajos tienden a ser estrechos. Las razones de por qué esto es así van más allá del alcance de esta
discusión. Tomaremos como un hecho el que es difícil o
imposible construir un pinzón con un pico que sea alto y
estrecho o un pico que sea bajo y ancho.
Durante la sequía de 1976-1977, cuando el alimento era
escaso y muchos pinzones pasaron hambre, la selección
actuó tanto sobre la altura del pico como sobre su anchura. Si estuviéramos analizando sólo una de estas características, podríamos medir la fuerza de la selección como la
pendiente de la línea de regresión que relaciona la eficacia
con el tamaño del pico. Éste es el gradiente de selección
introducido en el texto. Para analizar ambas características
a la vez, podemos medir la fuerza de la selección como la
pendiente del plano de regresión múltiple que relacione la
eficacia tanto con la altura del pico como con la anchura.
Esta pendiente es una gradiente de selección de dos
dimensiones.
Observe el gráfico tridimensional de la Figura 7.24a. La
altura del pico está representada por uno de los ejes horizontales; la anchura por el otro. La eficacia está representada por el eje vertical. La superficie dada por la parrilla es el
plano mejor ajustado. La eficacia en cada esquina del plano
mejor ajustado, o superficie de selección, está señalada con
un triángulo azul. La selección favorece a las aves con picos
que sean tanto altos como estrechos. Las aves con mayor probabilidad de supervivencia durante la sequía serían aves con
un pico muy alto y muy estrecho, localizadas en la esquina
derecha posterior de la superficie de selección.
Sin embargo, recuerde que la altura y la anchura del
pico están correlacionados. Es imposible construir un ave
perfecta. La correlación entre la altura y la anchura está
representada por la flecha negra de dos puntas en la base
232 PARTE II Los mecanismos del cambio evolutivo
Continuación
Eficacia
CUADRO 7.7
An
ch
ur
ad
el
p
ico
(a)
Altura del pico
(d)
Eficacia
Anchura
del pico
(c)
Eficacia
(b)
Altura del pico
Anchura del pico
Altura del pico
Figura 7.24 Análisis multidimensional de la selección sobre el tamaño del pico en los pinzones terrestres medianos (a) El
plano muestra las relaciones entre la eficacia y tanto con la altura como con la anchura del pico. Las aves con picos más altos y estrechos tienen
la mayor eficacia; (b), (c) y (d) muestran el mismo escenario en gráficos bidimensionales.
del gráfico tridimensional. Durante la sequía, la selección
presionó más intensamente en la dirección indicada por la
flecha ancha azul oscuro. Esto habría desplazado la media
de la población desde el centro del gráfico, directamente
por el camino más escarpado a lo largo de la superficie de
selección, hacia la forma de pico mejor posible. Pero debido a la correlación entre la altura y la anchura del pico, la
población no pudo desplazarse en la dirección en la que
presionaba la selección. Sólo se pudo desplazar a lo largo
de la flecha negra de dos puntas. La selección favoreció más
intensamente a los picos altos que a los picos estrechos. Por
ello, el promedio de la población se desplazó hacia un pico
que fue más alto y más ancho que antes de la sequía. Este
cambio se representa por la flecha gruesa verde.
Los gráficos tridimensionales pueden ser difíciles de
interpretar, por lo que hemos incluido las Figuras 7.24b, (c)
y (d), que ilustran el mismo análisis en gráficos de dos
dimensiones. La Figura 7.24b presenta el gradiente de
selección de la altura del pico, manteniendo constante la
anchura del pico. La selección favorece a pájaros con picos
más altos. La Figura 7.24c presenta el gradiente de selección de la anchura del pico, manteniendo constante la
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 233
CUADRO 7.7 Continuación
altura del pico. La Figura 7.24d muestra la correlación
entre la anchura y la altura del pico (flecha negra con dos
puntas), representando a la eficacia por la intensidad del
color azul a lo largo del gráfico. La selección presiona a la
media de la población hacia un pájaro con un pico alto y
estrecho (flecha gruesa azul oscuro), pero debido a la
correlación entre la altura y la anchura, la población no
puede ir hacia allí. La selección favorece el aumento de la
altura más intensamente que la disminución de la anchura, por lo que la media de la población se desplaza hacia un
pico más alto y más ancho (flecha gruesa verde).
El análisis de la selección de Grant y Grant sobre los
picos de los pinzones ilustra las ventajas de observar varios
caracteres al mismo tiempo, de utilizar gradientes de selección para medir la fuerza de la selección y de reconocer que
los caracteres pueden estar correlacionados. Imagine que
hubiéramos considerado sólo la anchura del pico y calculado el diferencial de selección. El superviviente promedio
tendría un pico más ancho que el promedio de las aves que
vivían antes de la sequía. El diferencial de selección, la diferencia entre la media de la población antes y después de la
selección, sugeriría que la selección favoreció a los picos
más anchos. Pero el análisis multidimensional revela que
esto no fue así. Se seleccionó en contra de la anchura del
pico, pero fue arrastrada en la carrera como consecuencia
de la fuerte selección a favor de la altura del pico.
Grant y Grant asumieron en su análisis que las relaciones entre la anchura y la altura del pico y la eficacia, era
lineal, como lo demuestra la superficie de selección plana
de la Figura 7.24a. Sin embargo, las relaciones entre un par
de caracteres y la eficacia no siempre es lineal. El trabajo de
Edmund Brodie (1992) nos proporciona un ejemplo. Brodie siguió individualmente la supervivencia de varios
cientos de formas juveniles de serpientes del género Thamnophis marcadas. Estimó el efecto sobre la eficacia de dos
caracteres que ayudan a las serpientes a evadirse de los
predadores: el patrón de color (rayado respecto de no rayado) y el comportamiento de evasión (escape en línea recta
respecto de muchos cambios de dirección). El análisis de
Brodie dio lugar a la superficie de selección que se muestra en la Figura 7.25. Las serpientes con tasas de supervivencia más altas eran las que tenían rayas y se escapaban en
línea recta y aquellas sin rayas y que realizaban muchas
inversiones de dirección. Otras combinaciones de estos
caracteres se seleccionaron en contra.
Dada una superficie de selección, podemos seguir la
evolución de una población rastreando la posición del
individuo promedio. En general, se espera que una población evolucione, por lo que subirá por la pendiente más
empinada desde su actual localización. Sin embargo, como
demostró el estudio de Grant y Grant sobre el pico de los
pinzones, las correlaciones entre los caracteres pueden
impedir que una población siga esta ruta predeterminada.
Superficies de selección como las presentadas en las Figuras 7.24 y 7.25 se denominan a menudo paisajes adaptativos, pero este término tiene una historia compleja y varios
significados distintos (véase el Capítulo 9 en Provine 1986;
Capítulo 11 de Wright 1986;Wright 1988).
5,4
Eficacia
4,3
3,3
2,2
1,1
Figura 7.25 Análisis multidimensional de la
selección sobre las defensas de las serpientes
contra los predadores La superficie de la parrilla
0,1
2,5
Rayado 0,7
–1,1
3,5
1,2
–1,1
Inversión de la marcha
presenta las relaciones entre la eficacia y tanto el patrón
de color como el comportamiento evasivo.
De la Figura 1 de Brodie (1992). Copyright © 1992,
Evolution. Reimpreso con el permiso de Evolution.
234 PARTE II Los mecanismos del cambio evolutivo
Predicción de la respuesta evolutiva a la selección
Una vez que conocemos la heredabilidad y el diferencial de selección, podemos predecir
la respuesta evolutiva a la selección. Ésta es la ecuación para hacerlo:
R = h2S
podemos utilizarlos
para predecir la respuesta
a la selección, R.
Figura 7.26 La respuesta a la selección es igual a la
heredabilidad multiplicada por el diferencial de
selección Los valores medios de padres e hijos están
indicados como puntos en el eje de coordenadas y
como rombos en los ejes x e y. Los símbolos rojos
representan a las 10 familias con los valores medios de
–
los padres más altos. P es el promedio de los valores
medios de los padres para el conjunto de la
población; P* es el promedio de los valores medios de
los padres de las familias con los valores medios de los
–
padres más altos. O es el promedio de los valores
medios de los hijos para el conjunto de la población;
O* es el promedio de los valores medios de los hijos
de las familias con los valores medios de los padres
más altos. Según Falconer (1989).
7
Valor medio de los hijos
Una vez conocido h2 y S,
donde R es la respuesta vaticinada a la selección, h2 es la heredabilidad y S el diferencial
de selección.
La lógica de esta ecuación se muestra gráficamente en la Figura 7.26. En esta figura se
presenta en un eje de coordenadas los valores medios de los descendientes en función del
valor medio de los padres, del mismo modo que en la Figura 7.20. En la Figura 7.26 se
representa la longitud de la cola de una población de 30 familias de ratones. La representación incluye la línea que mejor se ajusta, cuya pendiente es una estima de la heredabilidad h2.
–
Miremos primero al eje de las x. P es el valor promedio de los valores medios de los
padres del conjunto de la población. P* es el promedio de los diez valores medios de
–
los padres más grandes. La diferencia entre P y P* es el diferencial de selección (S) que
hubiéramos aplicado a esta población si hubiéramos elegido como padres sólo a las 10
parejas de padres con los valores medios más altos.
–
Miremos ahora al eje de las y. O es el promedio de los valores medios de los descendientes del conjunto de la población. O* es el promedio de los valores medios de los hijos
–
de las 10 parejas de padres. La diferencia entre O* y O es la respuesta evolutiva (R) que
hubiéramos obtenido como consecuencia de haber seleccionado como padres sólo a las
10 parejas con los valores medios más altos.
La pendiente de una línea se puede calcular como la elevación respecto de su recorrido. Si comparamos los promedios poblacionales con selección y sin selección tenemos una
–
–
elevación de (O* ⫺ O), respecto de un recorrido (P* ⫺ P ), por lo que
–
(O* ⫺ O)
R
h2 ⫽ ᎏᎏ
– ⫽ ᎏᎏ
(P* ⫺ P )
S
2
En otras palabras, R ⫽ h S.
Disponemos ahora de una serie de herramientas para estudiar la evolución de caracteres multilocus sujetos a la selección natural. Podemos estimar cuánta variación de un
carácter se debe a la variación en los genes, cuantificar la fuerza de la selección que resulta de diferencias en supervivencia o reproducción y ponerlos juntos para predecir cuánto cambiará la población de una generación a la siguiente.
6
5
O*
O
4
3
Pendiente = h2 =
2
[P* – P]
R = h2S
1
0
[O* – O]
0
1
2
3
4
5
P
P*
Valor medio de los padres
6
7
=
R
S
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 235
(a)
(b)
Figura 7.27 Una valeriana azul de las
Rocosas (Polemonium viscosum) (a) y un
abejorro (Bombus sp.) (b) [(a) Richard
Parker/Photo Researchers, Inc.;
(b) Stephen Dalton/Photo Researchers, Inc.]
Como ejemplo de los tipos de cuestiones que los biólogos evolutivos se preguntan y contestan con la genética cuantitativa, revisaremos el trabajo de Candace Galen (1996) sobre
el tamaño de la flor de la valeriana azul de las Rocosas (Polemonium viscosum). La valeriana azul es una flor silvestre perenne de las Montañas Rocosas (Figura 7.27a). Galen estudió poblaciones de la montaña Pennsylvania en Colorado, incluyendo poblaciones que
crecían en el límite del bosque y en las zonas más elevadas de la tundra. En el límite del
bosque, las valerianas son polinizadas por una serie de insectos, como moscas, pequeñas
abejas solitarias y algunos abejorros. En la tundra, las valerianas son polinizadas casi exclusivamente por abejorros (Figura 7.27b). Las flores de las valerianas de la tundra tienen,
como promedio, un diámetro un 12% mayor que los del límite del bosque.Anteriormente,
Galen (1989) había observado que las flores más grandes atraen más abejorros visitantes
y que las que atraen más abejorros producen más semillas.
Galen quería saber si la selección sobre el tamaño de la flor, impuesta por los abejorros, era responsable del mayor tamaño de las flores de la tundra. Si fuera así, también quería saber cuánto tiempo tardaría una población de valerianas en aumentar el tamaño
medio de la flor en un 12% por selección de los abejorros: la diferencia entre las flores del
limite del bosque y de la tundra.
Galen trabajó con una población del límite del bosque con flores pequeñas. Su primer paso fue estimar la heredabilidad del tamaño de la flor. Midió los diámetros de 144
flores y recogió sus semillas. Sembró las semillas en su laboratorio y plantó las 617 plántulas resultantes en localizaciones al azar, en el mismo hábitat que habían vivido sus
padres. Siete años después, 58 de las plántulas habían madurado, por lo que Galen pudo
medir sus flores. Esto permitió a Galen representar el diámetro de la flor de los descendientes (corola extendida) en función del diámetro de la flor materna, o de la semilla
paterna (Figura 7.28). La pendiente de la línea que mejor se ajustó fue aproximadamente 0,5. Por razones que van más allá del alcance de esta discusión, la pendiente de la línea
de la mejor regresión de descendientes respecto de un solo padre (en oposición al padre
medio) es una estima de ᎏ12ᎏ h2 (véase Falconer 1989). Por ello, la heredabilidad del tamaño de la flor en la población de valerianas del límite del bosque es, aproximadamente,
2 ⫻ 0,5 = 1. Sin embargo, advierta que el gráfico de la Figura 7.28 presenta bastante dispersión. El análisis estadístico de Galen indicaba que sólo se podría concluir con seguridad que la heredabilidad del tamaño de la flor estaba entre 0,2 y 1. En otras palabras, por
lo menos el 20% de la variación fenotípica en el tamaño de la flor de las valerianas se debe
a variación genética aditiva.
Apertura de la corola (mm)
Valerianas azules y abejorros
19
17
15
13
11
9
7
7
9 11 13 15 17
Apertura de la corola
materna (mm)
Figura 7.28 Estima de la
heredabilidad del tamaño de
la flor (corola extendida) en
valerianas azules Esta
representación muestra la
apertura de la corola de los
descendientes en función de la
apertura de la corola materna en
58 valerianas. La pendiente de la
mejor regresión lineal es 0,5. De
Galen (1996).
236 PARTE II Los mecanismos del cambio evolutivo
Eficacia relativa
5
4
3
2
1
0
8
12
16
20
Apertura de la corola (mm)
Figura 7.29 Estima del
gradiente de selección en
valerianas azules polinizadas
por abejorros Esta
representación muestra la eficacia
relativa (número de descendientes
supervivientes de 6 años dividido
por el número medio de
descendientes supervivientes de 6
años) en función del tamaño de la
flor materna (corola extendida).
La pendiente de la mejor
regresión lineal es 0,13. Preparada
con datos proporcionados por
Candace Galen.
Descendientes de plantas
polinizadas manualmente
8
6
4
4
2
16–18
14–16
12–14
10–12
8–10
Número de
individuos
(a)
Corola extendida (mm)
(b)
Descendientes de plantas
polinizadas por abejorros
7
6
4
16–18
14–16
12–14
10–12
1
8–10
Número de
individuos
16
Corola extendida (mm)
Figura 7.30 Medida de la
respuesta evolutiva a la
selección en valerianas azules
Estos histogramas muestran la
distribución del tamaño de la flor
(corola extendida) en los
descendientes de valerianas
polinizadas manualmente (a)
promedio = 13,1 mm y
polinizadas por abejorros (b)
promedio = 14,4 mm. Modificado
de Galen (1996).
El siguiente paso de Galen fue estimar la fuerza del diferencial de selección impuesto por los abejorros polinizadores. Recuerde que los abejorros prefieren visitar flores
grandes y que más abejorros polinizadores significa más semillas. Galen construyó una
gran jaula rodeada de mamparas en su lugar de estudio, transplantó en su interior 98 valerianas a punto de florecer y añadió abejorros. La jaula mantuvo a los abejorros dentro y
todos los otros polinizadores fuera. Cuando en la jaula florecieron las valerianas, Galen
midió sus flores. Más tarde recogió sus semillas, las sembró en el laboratorio y las plántulas resultantes las plantó en localizaciones al azar fuera del hábitat de sus padres. Seis años
más tarde Galen contó el número de descendientes que sobrevivieron producidos por
cada una de las plantas originales de la jaula. Utilizando el número de descendientes
supervivientes de 6 años de edad como medida de la eficacia, Galen representó la eficacia relativa en función del tamaño de la flor y calculó la pendiente de la recta que mejor
se ajusta (Figura 7.29). La pendiente de esta línea 0,13 es el gradiente de selección que
resulta de la polinización de los abejorros. Multiplicando el gradiente de selección por
la varianza del tamaño de la flor 5,66 se obtiene el diferencial de selección: S = 0,74 mm.
El tamaño promedio de la flor fue de 14,2 mm.Así, el diferencial de selección se puede
0,74
ᎏ ⫽ 0,05, o el 5%.Aproximadamente, esto significa que cuanexpresar también como ᎏ
14,2
do las valerianas intentan reproducirse atrayendo a los abejorros a visitarlas, las plantas
ganadoras tienen flores que son un 5% más grandes que la media de las plantas de la
población.
Galen realizó dos experimentos control para confirmar que los abejorros seleccionaban las flores más grandes. En un control, polinizó valerianas manualmente (sin considerar el tamaño de la flor); en el otro permitió que las valerianas fueran polinizadas por otros
polinizadores naturales con excepción de los abejorros. En ninguno de los controles
hubo ninguna relación entre el tamaño de la flor y la eficacia; solamente los abejorros
seleccionaban flores más grandes.
Los datos permitieron a Galen predecir cómo respondería la población de valerianas de
los límites del bosque a la selección por abejorros. El escenario que imaginó fue que una
población de valerianas de los límites del bosque, que había sido polinizada por una variedad de insectos, se desplazó (por dispersión de las semillas) hacia la tundra, donde las
plantas eran ahora polinizadas exclusivamente por abejorros. Utilizando la estima límite más
baja de h2 = 0,2, y estimando S = 0,05, Galen predijo que la respuesta a la selección sería
R = h2S = 0,2 ⫻ 0,05 = 0,01. Utilizando la estima límite superior de h2 = 1, y estimando S = 0,05, Galen predijo que la respuesta a la selección sería R = h2S = 1 ⫻ 0,05 = 0,05.
En otras palabras, en una sola generación de selección por los abejorros se produciría un
incremento entre el 1 y el 5% en el tamaño medio de la flor de una población de valerianas del límite del bosque trasladada a la tundra.
Por consiguiente, la predicción de Galen fue que el tamaño de la flor evolucionaría
rápidamente, sometida a la selección por los abejorros. ¿Esta predicción es correcta?
Recuerde el experimento descrito anteriormente, en el que Galen crió descendientes
de valerianas del límite del bosque que habían sido polinizadas manualmente y descendientes que habían sido polinizados exclusivamente por abejorros. Galen calculó el
tamaño medio de la flor de cada grupo y encontró que los descendientes polinizados
por abejorros tenían flores que eran, en promedio, un 9% mayores que los polinizados manualmente (Figura 7.30). Su predicción fue correcta: las valerianas presentan una
rápida y fuerte respuesta a la selección. De hecho, la respuesta es incluso mayor que la
pronosticada por Galen.
Galen concluyó que el 12% de la diferencia en el tamaño de la flor entre las valerianas del límite del bosque y de la tundra se puede explicar adecuadamente por el hecho
de que las valerianas del límite del bosque son polinizadas por una diversidad de insectos,
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 237
mientras que las valerianas de la tundra son polinizadas casi exclusivamente por abejorros.
Las valerianas del límite del bosque pueden producir semillas incluso si los abejorros los
evitan, pero las valerianas de la tundra no.Además, siendo polinizadas exclusivamente por
abejorros, las poblaciones de valerianas del límite del bosque tardarían pocas generaciones en evolucionar flores que fueran tan grandes como las de la tundra.
La falacia de la curva en campana y otras falsas
interpretaciones de la heredabilidad
Prometimos en la introducción de este capítulo, que nuestra discusión sobre genética
cuantitativa nos permitiría derribar alegatos erróneos acerca de las diferencias en la puntuación IQ entre grupos étnicos. Estamos listos para cumplir la promesa.
Un punto clave es que la fórmula para la heredabilidad incluye tanto variación genética, VG, como variación ambiental, VE. Por consiguiente, cualquier estima de la heredabilidad es específica para una población concreta que vive en un determinado ambiente.
Por ello, la heredabilidad no nos dice nada acerca de las causas de las diferencias entre
poblaciones que viven en ambientes distintos.
Podemos ilustrar este punto con un experimento imaginario. Los áfidos de los guisantes se reproducen asexualmente durante la primavera y el principio del verano. Imagine
que cogemos un áfido de una docena de campos distintos y los traemos al laboratorio.
Ya que los áfidos provienen de campos distintos, serán genéticamente diferentes entre sí;
nuestra población de laboratorio tendrá variación genética. Pero debido a que cada áfido
de la población se reproduce asexualmente (por mitosis), los descendientes serán genéticamente idénticos a sus madres. En otras palabras, los descendientes de cualquiera de
nuestros doce áfidos originales constituirán un clon.Tomando un miembro de cada uno
de nuestros doce clones, podemos obtener un duplicado de nuestra población de laboratorio original.
Imagine que fundamos dos de tales poblaciones duplicadas. Una población la criamos
en un ambiente cuidadosamente controlado sobre plantas de guisante y los áfidos crecen
hasta tamaños grandes. Debido a que todos los áfidos de esta población comparten el
mismo ambiente, cualquier diferencia entre ellos en el tamaño se deberá totalmente a la
variación genética. Cuando se desarrollen sobre guisantes, la heredabilidad del tamaño en
nuestra población de laboratorio será igual a 1.
Ahora criamos a la otra población duplicada de áfidos sobre tréboles, y los áfidos de
esta población no alcanzan un tamaño tan grande (al fin y al cabo son áfidos del guisante). No obstante, todos los áfidos de esta población comparten el mismo ambiente, por
lo que cualquier diferencia de tamaño entre ellos se deberá a variación genética. Cuando se desarrollen sobre tréboles, la heredabilidad del tamaño en nuestra población será
igual a 1.
En las dos poblaciones tendremos una heredabilidad alta y una diferencia en la media
del tamaño entre las dos poblaciones. ¿Significa esto que la población criada sobre guisantes
es genéticamente superior a la población criada sobre tréboles respecto del tamaño?
Desde luego que no; intencionadamente hemos fundado poblaciones que son idénticas
en su composición genética. El hecho de que la heredabilidad sea alta en las dos poblaciones no
nos dice nada acerca de las causas que producen las diferencias entre las poblaciones, ya que las poblaciones se criaron en ambientes distintos. (Para un experimento real, similar al que hemos descrito, véase Via 1991.)
La noción errónea de que la heredabilidad nos dice algo sobre las causas de las diferencias entre poblaciones ha sido particularmente persistente en estudios sobre la inteligencia humana. En 1994, Charles Murray y Richard J. Herrnstein vendieron miles de
copias de su libro The Bell Curve. Murray y Herrnstein afirmaban que las diferencias en
Los estudios de heredabilidad
se interpretan erróneamente a
menudo al deducir que las
diferencias entre poblaciones
se deben a diferencias en los
genes.
238 PARTE II Los mecanismos del cambio evolutivo
(c)
Figura 7.31 Ilustración de los argumentos erróneos de Murray
y Herrnstein relativos al IQ y las etnias Véase el texto para su
explicación.
Fracción de la población
(b)
Fracción de la población
(a)
Fracción de la población
las puntuaciones IQ promedio entre afroamericanos y americanos europeos se debía a
diferencias genéticas entre estos grupos (nuestro análisis de sus argumentos se basan en un
extracto de su libro publicado en The New Republic [Murray y Herrnstein 1994]).
Murray y Herrnstein tomaron nota del punto que acabamos de desarrollar con los áfidos. Afirman que: “La mayoría de los escolares aceptan que el IQ en la especie humana
es, en conjunto, sustancialmente heredable, más o menos entre el 40% y el 80%, indicando
que gran parte de la variación observada en el IQ es genética. No obstante, esta información no nos dice nada a ciencia cierta acerca del origen de las diferencias entre grupos.”
Sin embargo, habiendo dicho esto, Murray y Herrnstein proceden a desarrollar el siguiente argumento erróneo.
Basándose en varias fuentes, Murray y Herrnstein asumen que el IQ promedio de los
afroamericanos es 85 y que el IQ de los americanos europeos es 100 y que la varianza (una
medida estadística de la variación) de cada grupo es 225. Las curvas en campana que representan estas suposiciones aparecen en la Figura 7.31a. Murray y Herrnstein asumen además que la heredabilidad del IQ en cada grupo es 0,6. Hay razones para discutir cada uno
de los supuestos de Murray y Herrnstein, pero las permitiremos aquí sólo en consideración del argumento. (También hay razones para discutir si los formularios para el IQ miden
algo con significado, pero dejaremos esta discusión a otros.)
0,03
Afroamericanos
Americanos europeos
0,02
0,01
0
50 60 70 80 90 100 110 120 130 140 150
Puntuación IQ
0,05
0,04
Afroamericanos
Americanos europeos
0,03
0,02
0,01
0
0,05
50 60 70 80 90 100 110 120 130 140 150
Puntuación IQ
Afroamericanos
Americanos europeos
0,04
0,03
0,02
0,01
0
50 60 70 80 90 100 110 120 130 140 150
Calidad del ambiente en relación con la inteligencia
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 239
A continuación, Murray y Herrnstein imaginan que las curvas en campana del IQ
serían parecidas si se eliminara toda la variación genética entre los individuos de cada
población. En otras palabras, imaginan que todos los afroamericanos se han hecho genéticamente idénticos al promedio de los afroamericanos y que todos los americanos
europeos se han hecho genéticamente idénticos al promedio de los americanos europeos. En el supuesto que el 60% de la variación dentro de cada grupo se deba a variación
genética, esto deja el 40% de la variación original dentro de cada grupo. Las curvas en
campana que representan este experimento imaginario aparecen en la Figura 7.31b.
Ahora Murray y Herrnstein consideran la propuesta de que las diferencias entre el
IQ promedio de los americanos africanos y el IQ promedio de los americanos europeos
de la Figura 7.31b se deben exclusivamente a las diferencias en el ambiente. De acuerdo con esta propuesta, dicen Murray y Herrnstein, podremos sustituir la etiqueta “puntuación IQ” por la etiqueta “calidad del ambiente en relación con la inteligencia,” como
se muestra en la Figura 7.31c. Murray y Herrnstein no encuentran creible que la diferencia en la calidad del ambiente que han experimentado los afroamericanos respecto
de los americanos europeos sea tan grande como se muestra en la Figura 7.31c. Concluyen que al menos parte de la diferencia entre la media de las puntuaciones IQ de
afroamericanos respecto de americanos europeos tiene que deberse a diferencias genéticas entre los grupos.
Al menos hay dos fallos serios en el argumento de Murray y Herrnstein. Primero, al
sustituir la etiqueta del eje horizontal en la Figura 7.31b por la etiqueta de la Figura 7.31c,
Murray y Herrnstein asumen implícitamente que hay una relación lineal entre el ambiente y el IQ. Esta suposición es casi seguro errónea.
Segundo, el argumento de Murray y Herrnstein de su incredulidad vale como técnica retórica, no como ciencia. Una aproximación científica a la hipótesis de Murray y
Herrnstein sería realizar un experimento como hicimos con los áfidos: criar a americanos europeos y a afroamericanos juntos en un ambiente experimentado típicamente por
los americanos europeos y luego comparar sus puntuaciones de IQ. Este diseño, y el experimento recíproco, en el que cada grupo se criará en un ambiente experimentado típicamente por los afroamericanos, se muestra en la Figura 7.32.
Obviamente, no podemos hacer este experimento con humanos. Pero experimentos
parecidos se han llevado a cabo en animales y en plantas. Por ejemplo, Clausen, Keck y Hiesey (1948) llevaron a cabo una serie de experimentos con la planta Achillea (Figura 7.33).
Criar a cada uno
en un ambiente
típicamente experimentado
por afroamericanos
Porcentaje de
la población
Criar a cada uno en un
ambiente típicamente
experimentado por
americanos europeos
Porcentaje de
la población
Experimento
Resultado si las diferencias
entre grupos se deben a la
diferencia entre genes
50
50
100
150
150
100
Puntuación IQ
Resultado si las diferencias
entre grupos se deben a la
diferencia en los ambientes
50
50
100
150
100
150
Puntuación IQ
Figura 7.32 Experimento que comprobaría la
proposición de Murray y Herrnstein La
columna de la izquierda describe dos tratamientos
experimentales. Las columnas central y de la
derecha muestran los resultados pronosticados de
acuerdo con la hipótesis de que las diferencias entre
grupos se debe a diferencias en los genes respecto
de los resultados pronosticados de acuerdo con la
hipótesis de que las diferencias entre grupos se
deben a diferencias en el ambiente.
240 PARTE II Los mecanismos del cambio evolutivo
Como promedio, las
plantas de las
poblaciones de baja
altitud producen
más tallos que
las plantas de
poblaciones de gran
altitud
(30,90 ± 2,73 versus
28,32 ± 2,54).
Número de
plantas
(a)
10
Número de
plantas
idénticos.
10
Número de
plantas
poblaciones en ambientes
10
Número de
plantas
individuos de cada una de las
10
Número de
plantas
en las poblaciones es criar a
10
Número de
plantas
El único modo de determinar
las causas de las diferencias
Plantas de este género recogidas en poblaciones de poca altitud producen más tallos que
plantas recogidas en poblaciones de gran altitud (Figura 7.33a). ¿Es la diferencia entre plantas de baja altitud y plantas de gran altitud debida a diferencias en sus genes o en sus
ambientes? Cuando las plantas de baja altitud y de gran altitud se cultivan juntas a baja altitud, las plantas de baja altitud producen más tallos (Figura 7.33b). Este resultado está de
acuerdo con la hipótesis de que las plantas que provienen de baja altitud están genéticamente programadas para producir más tallos. Sin embargo, cuando las plantas de baja altitud y de gran altitud se cultivan juntas a gran altitud, las plantas de gran altitud producen
más tallos (Figura 7.33c). Este resultado no estaba en absoluto previsto en el diseño experimental. Revela diferencias genéticas entre las plantas de baja altitud y de gran altitud en
cuanto al modo en que cada una responde al ambiente.También revela que cada población de plantas es superior en su propio ambiente de origen. Este resultado, no previsto,
demuestra que las hipotéticas propuestas acerca de las causas de las diferencias entre poblaciones nunca pueden sustituir a los resultados experimentales.
¿Que sucedería si hiciéramos este tipo de experimento con los afroamericanos y los
americanos europeos? Nadie tiene la más ligera idea. Es engañoso decir que heredabili-
10
Poblaciones de baja altitud
5
0
5
Poblaciones de gran altitud
5
0
5
Achillea
(b)
Cuando Clausen, Keck y
Hiesey (1948) cultivaron
Achillea de ambas poblaciones
a baja altitud, las plantas de
las poblaciones de baja altitud
produjeron más tallos
(30,90 ± 2,73 versus
7,21±1,08).
(c)
Figura 7.33 Datos sobre los experimentos
de Clausen, Keck y Hiesey (1948)
(a) Comparación entre poblaciones de Achillea de
baja altitud (San Gregorio, California) o de gran
altitud (Mather, California). (b) Plantas de baja y
de gran altitud cultivadas juntas a baja altitud
(Stanford, California). (c) Plantas de baja y gran
altitud cultivadas juntas a gran altitud (Mather,
California).
Cuando los investigadores
cultivaron esquejes de las
mismas plantas a gran altitud,
las plantas de gran altitud
produjeron más tallos
(19,89 ± 2,26 versus
28,32 ± 2,54).
15 25 35 45 55 65 75
15 25 35 45 55 65 75
Número de tallos
Poblaciones de baja altitud
5
0
5
15 25 35 45 55 65 75
Poblaciones de gran altitud
5
0
5
15 25 35 45 55 65 75
Número de tallos
Poblaciones de baja altitud
5
0
5
15 25 35 45 55 65 75
Poblaciones de gran altitud
5
0
5
15 25 35 45 55 65 75
Número de tallos
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 241
dades elevadas del IQ dentro de grupos: “No nos dicen nada a ciencia cierta acerca del
origen de las diferencias entre grupos” (Murray y Herrnstein 1994). De hecho, heredabilidades elevadas dentro de grupos no nos dicen nada en absoluto sobre el origen de las diferencias entre grupos.
Finalmente, es importante advertir que la heredabilidad tampoco nos dice nada acerca
del papel de los genes en la determinación de los caracteres que están compartidos por
todos los miembros de una población. No hay variación entre los humanos en cuanto al
número de narices. La heredabilidad del número de narices no está definida, porque
VA/VP = 0/0, Esto, lógicamente, no significa que nuestros genes no sean importantes para
determinar cuántas narices tenemos.
¿Qué tiene de bueno para nosotros medir la heredabilidad de un carácter? Sólo y precisamente esto: nos permite predecir si la selección sobre un carácter dará lugar a que la
población evolucione.
Tipos de selección y mantenimiento de la variación genética
En nuestra discusión sobre la selección de caracteres cuantitativos, hemos supuesto que la
relación entre el fenotipo y la eficacia es simple. En nuestros ratones, la cola corta era mejor
que la cola larga; en las valerianas, las flores más grandes eran mejores que las flores más
pequeñas.Antes de dejar el tema de la selección sobre los caracteres cuantitativos, advertimos que las relaciones entre fenotipo y eficacia pueden ser complejas. Son posibles una
serie de patrones o modos de selección.
La Figura 7.34 muestra tres modos distintos de selección que actúan sobre una población hipotética. Cada columna representa un tipo distinto. Los histogramas de la fila
superior muestran la distribución de los valores fenotípicos de un carácter antes de la selección. Los gráficos de la fila central muestran las relaciones entre el fenotipo y la eficacia,
como probabilidad de supervivencia en función del fenotipo. Los histogramas de la fila
inferior muestran la distribución fenotípica en los supervivientes. Los triángulos y barras
debajo de cada histograma señalan la media y la variación de la población. (La barra representa la variación abarcada por ( 2 desviaciones típicas alrededor de la media, o, aproximadamente, el 95% de los individuos de la población.)
En la selección direccional, la eficacia aumenta (o disminuye) consistentemente
con el valor del carácter (Figura 7.34, primera columna). La selección direccional sobre
un carácter continuo cambia el valor medio del carácter de la población. En la hipotética población que se presenta en la Figura 7.34, el fenotipo medio antes de la selección era
6,9, mientras que el fenotipo medio después de la selección fue 7,4. La selección direccional también reduce la variación de la población, aunque a menudo no drásticamente.
En nuestra población hipotética, la desviación típica antes de la selección era 1,92, mientras que después de la selección fue de 1,89.
En la selección estabilizadora, los individuos con valores intermedios para un carácter tienen la máxima eficacia (Figura 7.34, columna central). La selección estabilizadora
sobre un carácter continuo no altera el valor medio del carácter de la población. Sin
embargo, la selección estabilizadora recorta las colas de la distribución del carácter, reduciendo con ello la variación. En nuestra población hipotética la desviación típica antes de
la selección era 1,92, mientras que después de la selección fue de 1,04.
En la selección disruptiva los individuos con los valores extremos para un carácter
tienen la máxima eficacia (Figura 7.34, última columna). La selección disruptiva sobre un
carácter continuo no altera el valor medio del carácter en la población. Sin embargo, la
selección disruptiva elimina la cima de la distribución del carácter, incrementando por ello
la varianza. En nuestra población hipotética la desviación típica antes de la selección era
1,92, mientras que después de la selección fue de 2,33.
La selección sobre una
población puede actuar de una
serie de formas. La selección
direccional y la estabilizadora
tienden a reducir la cantidad
de variación de la población; la
selección disruptiva tiende a
incrementar la cantidad de
variación.
242 PARTE II Los mecanismos del cambio evolutivo
Selección direccional
Selección estabilizadora
Selección disruptiva
Número de
individuos antes
de la selección
(a)
Probabilidad de
supervivencia
(b)
40
40
40
30
30
30
20
20
20
10
10
10
0
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
1
1
0,8
0,8
0,8
0,6
0,6
0,6
0,4
0,4
0,4
0,2
0,2
0,2
0
0
0 1 2
3 4 5 6
7 8 9 10 11 12 13 14
0 1 2
3 4 5 6
7 8 9 10 11 12 13 14
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 1 2
3 4 5 6
7 8 9 10 11 12 13 14
Número de
individuos después
de la selección
(c)
40
40
40
30
30
30
20
20
20
10
10
10
0
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Fenotipo
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Fenotipo
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Fenotipo
Figura 7.34 Tres tipos de selección Cada columna representa un tipo de selección. Los gráficos de la fila (a) son
histogramas que presentan la distribución fenotípica de un carácter en una población hipotética antes de la selección. Los
gráficos de la fila (b) presentan diferentes patrones de selección; la probabilidad de supervivencia (una medida de la
eficacia) en función del fenotipo. Los gráficos de la fila (c) son histogramas que presentan la distribución fenotípica de un
carácter en los supervivientes. Los triángulos azules debajo de cada histograma señalan la media de la población. Las barras
azules debajo de cada histograma muestran la variación (± 2 desviaciones típicas respecto de la media). Según Cavalli-Sforza
y Bodmer (1971).
Estos tres tipos de selección eliminan los individuos con menor eficacia y preservan a
los individuos con mayor eficacia. Por ello, los tres tipos de selección aumentan la eficacia media de la población.
Ya hemos visto ejemplos de selección direccional. Por ejemplo, en las valerianas azules polinizadas por abejorros las flores más grandes tienen mayor eficacia.Y en pinzones
terrestres medianos, la sequía de 1976-1977 en Daphne Major seleccionó a las aves con
los picos más grandes (véase el Capítulo 3).
La investigación de Arthur Weis y Warren Abrahamson (1986) proporciona un ejemplo
elegante de selección estabilizadora. Weis y Abrahamson estudiaron una mosca llamada
Eurosta solidaginis. La hembra de esta especie inyecta un huevo en una yema de la espigada varilla dorada, Solidago altisima. Después de la eclosión, la larva de la mosca perfora el
tallo e induce a que la planta forme una agalla protectora. A medida que se desarrolla en
el interior de la agalla, la larva puede caer víctima de dos tipos de predadores. Primero,
una hembra de avispa parasitoide le puede inyectar su huevo en la agalla, donde la larva
de la avispa se comerá a la larva de la mosca. Segundo, un ave puede localizar a la agalla,
romperla y comerse la larva de la mosca.Weis y Abrahamson establecieron que la variación genética en las moscas es parcialmente responsable de la variación en el tamaño de
la agalla que inducen. Los investigadores también recogieron varios cientos de agallas y
determinaron, diseccionándolas, el destino de la larva del interior de cada una de ellas.
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 243
Figura 7.35 Selección estabilizadora en un insecto que induce agallas (a) Las avispas parasitoide
matan larvas de la mosca dentro de las agallas pequeñas a un ritmo mayor que las larvas que matan dentro
de las agallas grandes. (b) Las aves matan a las larvas de mosca dentro de las agallas grandes a un ritmo
mayor que las larvas que matan dentro de las agallas pequeñas. (c) La distribución del tamaño de las
agallas antes (naranja claro + la parte azul de las barras) y después (la parte naranja claro de las barras) de
la selección por parasitoides y aves. En conjunto, las larvas del interior de las agallas de tamaño medio
sobreviven con la mayor probabilidad. De la Figura 3 de Weis y Abrahamson (1986). Copyright © 1986,
American Naturalist. Reimpreso con el permiso de The University of Chicago Press.
(a)
1. Muchas poblaciones no se encuentran en equilibrio evolutivo respecto de la selección
direccional y/o estabilizadora. En cualquier población hay un suministro constante, aunque lento, de mutaciones nuevas favorables que dan origen a variación genética en los
caracteres relacionados con la eficacia. Mientras las mutaciones favorables aumenten en
frecuencia, pero todavía no se fijen, la población presentará variación genética para la
eficacia. A esto se le puede llamar “hipótesis del Teorema fundamental de Fisher.”
Ronald Fisher fue el primero en demostrar matemáticamente que la tasa de aumento
90
80
70
60
50
(b)
Predación (%)
50
40
30
20
10
0
12,5
(c)
16,5
20,5
24,5
28,5
Antes de la selección
0,12
Frecuencia relativa
Weis y Abrahamson descubrieron que la avispa parasitoide impone a las moscas que
provocan las agallas una fuerte selección direccional favoreciendo las agallas más grandes
(Figura 7.35a). Casi todas las larvas de las agallas que tenían menos de 16 mm de diámetro
fueron matadas por las avispas, mientras que las larvas de las agallas grandes tenían al menos
una posibilidad de sobrevivir. Sin embargo, los investigadores también encontraron que las
aves imponen a los inductores de las agallas una fuerte selección direccional, favoreciendo a
las agallas más pequeñas (Figura 7.35b). Juntas, la selección por las avispas y la selección por
las aves se suman para dar lugar a la selección estabilizadora del tamaño de la agalla. La Figura 7.35c muestra la distribución de los tamaños de las agallas antes y después de la selección.
La investigación de Thomas Bates Smith (1993) proporciona un ejemplo de selección
disruptiva. Bates Smith estudió un pinzón africano llamado cascanueces de panza negra.
Las aves de esta especie presentan dos tamaños de pico distintos: grande y pequeño. Las
aves de los dos grupos están especializadas en distintos tipos de semillas. Bates Smith siguió
el destino de unos 200 pájaros juveniles. Los gráficos de la Figura 7.36 muestran la distribución de los tamaños del pico entre las formas juveniles y entre los juveniles que sobrevivieron hasta adulto. Los gráficos revelan selección disruptiva: los supervivientes fueron
aves con picos que eran relativamente grandes o relativamente pequeños. Las aves con
picos de tamaño intermedio no sobrevivieron. (Advierta que parece que también está
actuando un aspecto de la selección estabilizadora: excepto en el caso de las aves con picos
extremadamente largos, las aves con los fenotipos más extremos no sobrevivieron.)
Los biólogos evolutivos asumen en general que la selección direccional y la selección
estabilizadora son corrientes, mientras que la selección disruptiva es rara. Sin embargo, si
la preponderancia de la selección direccional y estabilizadora es real, se crea un rompecabezas. Recuerde de la Figura 7.34 que tanto la selección direccional como la estabilizadora reducen la variación fenotípica presente en la población. Si el carácter en cuestión
es heredable, entonces estos tipos de selección reducirán también la variación genética de
la población. Finalmente, la variación genética de cualquier carácter relacionado con la eficacia sería totalmente eliminada y la población alcanzaría una equilibrio en el que el valor
medio del carácter, la variación del carácter, y la eficacia media de la población dejarían
de cambiar. El rompecabezas es que la población presenta típicamente variación genética significativa, incluso en caracteres íntimamente relacionados con la eficacia. ¿Cómo se
mantiene esta variación genética?
Aquí hay tres posibles soluciones para el rompecabezas de cómo se mantiene la variación genética para la eficacia:
Parasitismo (%)
100
Después
de la
selección
0,08
0,04
0,00
12,5
16,5
20,5
24,5
28,5
Diámetro de la agalla (mm)
244 PARTE II Los mecanismos del cambio evolutivo
(a)
60
Número
50
Muere
40
Sobrevive
30
20
10
10
12,8
15,7
18,5
Anchura de la mandíbula
inferior (mm)
(b)
Número
40
30
20
10
6
8,5
11
Longitud de la mandíbula
inferior (mm)
Figura 7.36 Selección
disruptiva sobre el tamaño del
pico del cascanueces de panza
negra.(Pyrenestes o. ostrinus)
Cada gráfico muestra la
distribución de la anchura del pico
inferior (a) o de la longitud (b) en
una población de cascanueces de
panza negra, un pinzón africano.
La parte azul de cada barra
representa a individuos juveniles
que no sobrevivieron hasta adulto;
la parte naranja claro representa a
individuos juveniles que
sobrevivieron hasta adulto. Los
supervivientes fueron aquellos
individuos que tenían picos o bien
relativamente grandes o bien
relativamente pequeños. De Bates
Smith (1993).
de la eficacia media de una población es proporcional a la variación genética aditiva para
la eficacia, un resultado llamado Teorema fundamental de la selección natural.
2. En muchas poblaciones hay un equilibrio entre las mutaciones deletéreas y la selección. En cualquier población hay un suministro constante de nuevas mutaciones deletéreas. En el Capítulo 5 demostramos que, a menos que la tasa de mutación sea alta o
la selección sea débil, la selección mantendrá cualquier alelo deletéreo dado en frecuencia baja. Pero los caracteres cuantitativos están determinados por la influencia combinada de muchos loci de pequeño efecto. La selección sobre alelos de un único locus
que afecte a un carácter cuantitativo puede ser muy débil, permitiendo que persista sustancial variación genética en el equilibrio entre la mutación y la selección.
3. La selección disruptiva, o patrones de selección con efectos similares, puede ser más
corriente de lo que en general se reconoce. Entre otros tipos de selección que pueden
mantener variación genética en poblaciones se encuentra la selección dependiente de
las frecuencias, por la que los fenotipos (o genotipos) raros tienen mayor eficacia que
los fenotipos corrientes, y la selección impuesta por fluctuaciones ambientales.
Todas estas hipótesis son controvertidas y han sido el objeto de considerable investigación
teórica y experimental (véase, por ejemplo, Barton y Turelli 1989). Una discusión detallada va más allá del alcance de este libro. Sin embargo, podemos proporcionar un breve
resumen de un fascinante experimento de Santiago Elena y Richard Lenski.
Elena y Lenski (1997) estudiaron seis poblaciones de la bacteria Escherichia coli. Estas
poblaciones se establecieron a partir de un cultivo antecesor común, por lo que estaban
íntimamente relacionadas entre sí. Cada población se fundó a partir de una sola bacteria,
por lo que en un cultivo dado toda la variación genética había surgido como consecuencia
de mutaciones nuevas. Las seis poblaciones evolucionaron en un ambiente constante de
laboratorio durante 10.000 generaciones. Durante este tiempo, la eficacia media de cada
población, estimada a través de experimentos de competencia, había aumentado un 50%
en relación con su antecesor común. Sin embargo, gran parte del incremento en eficacia
se había producido al principio, en unas pocas miles de generaciones. Después de 10.000
generaciones, parecía que las poblaciones habían llegado a un equilibrio evolutivo. Elena
y Lenski comprobaron la variación genética en eficacia en las distintas cepas presentes en
cada una de las seis poblaciones y encontraron que era significativa. Como promedio, dos
cepas seleccionadas de la misma población diferían en eficacia alrededor de un 4%.
Elena y Lenski comprobaron la hipótesis del Teorema fundamental de Fisher utilizando
la variación genética en la eficacia conseguida en cada población para pronosticar cuánta
mejora adicional en eficacia debería darse en las siguientes 500 generaciones de evolución.
Dependiendo de los supuestos utilizados, los investigadores pronosticaron un incremento adicional en eficacia entre el 4 y el 50%. De hecho, entre las generaciones 10.000 a
10.500 ninguna de las seis poblaciones mostró ningún incremento significativo de la eficacia media. Elena y Lenski concluyeron que la variación genética en eficacia en sus poblaciones de E. coli no es el resultado de un suministro continuo de mutaciones nuevas
favorables en proceso de aumentar hasta la fijación.
Elena y Lenski comprobaron la hipótesis del equilibrio mutación-selección advirtiendo que en dos de las seis poblaciones había evolucionado una tasa de mutación extraordinariamente elevada, del orden de 100 veces superior a la de las otras cuatro poblaciones y a la del antecesor común. Si se mantiene la variación genética en eficacia en cada
población por el equilibrio mutación-selección, entonces las dos poblaciones con tasas de
mutación elevadas deberían presentar, con mucho, la mayor variación genética para la eficacia. Una de las dos poblaciones con mutación elevada realmente exhibían mucha más
variación genética para la eficacia que las cuatro poblaciones con baja mutación. Pero la
otra población con elevada mutación no lo hizo. Elena y Lenski concluyeron que la varia-
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 245
ción genética en eficacia en sus poblaciones de E. coli no se debe probablemente a un equilibrio entre mutaciones deletéreas y selección.
Finalmente Elena y Lenski comprobaron la hipótesis de que la variación genética en eficacia de sus poblaciones se hubiera mantenido por selección dependiente de frecuencias. Los
investigadores utilizaron experimentos de competencia para determinar si las distintas cepas
presentes en cada población gozaban de ventaja en eficacia cuando eran raras. Encontraron
que una cepa típica de E. coli, cuando es rara, realmente tiene un margen de eficacia alrededor del 2% respecto de su población de origen.Además, en las seis poblaciones bacterianas,
la intensidad de la selección dependiente de frecuencias estaba correlacionada significativamente con la cantidad de variación genética para la eficacia presente. Elena y Lenski advirtieron que las tres hipótesis que comprobaron eran mutuamente compatibles. No obstante,
los investigadores concluyeron que la explicación mejor para la variación genética en eficacia en sus poblaciones es la selección dependiente de frecuencias. Si esta conclusión puede
aplicarse a otras poblaciones y organismos es algo que tiene que comprobarse.
Resumen
Los modelos para un solo locus de los Capítulos 5 y 6 son
potentes, pero potencialmente muy simplificados. La
ampliación del análisis de Hardy-Weinberg para dos loci
presenta complicaciones. Cuando los genotipos de un locus
no están asociados al azar con los genotipos de otro locus,
los loci se encuentran en desequilibrio de ligamiento. Incluso bajo las condiciones de Hardy-Weinberg, las frecuencias
cromosómicas cambian a lo largo de las generaciones.Además, la selección sobre un locus puede alterar las frecuencias
alélicas del otro locus, y los modelos para un solo locus
pueden plantear predicciones erróneas. Sin embargo, cuando los genotipos de un locus son independientes de los
genotipos de otro locus, los loci se encuentran en equilibrio
de ligamiento. Las frecuencias cromosómicas no cambian a
lo largo de las generaciones. La selección sobre un locus no
tienen efecto sobre las frecuencias alélicas o genotípicas del
otro locus y podemos usar modelos para un solo locus para
hacer predicciones sobre la evolución.
En una población con apareamiento al azar, la selección
sobre genotipos multilocus, deriva genética y mezcla de
poblaciones puede generar desequilibrio de ligamiento.
Estos tres mecanismos crean un exceso de algunos haplotipos cromosómicos y un déficit de otros. El desequilibrio de
ligamiento se reduce por reproducción sexual. El sexo reúne
cromosomas con haplotipos diferentes y el entrecruzamiento en la meiosis permite que los cromosomas intercambien
genes. Esta recombinación genética tiende a desintegrar a los
haplotipos representados en exceso y crear haplotipos representados en defecto.
El hecho de que la reproducción sexual reduzca el desequilibrio de ligamiento proporciona la clave para comprender por qué la reproducción sexual persiste en las
poblaciones. Argumentos teóricos simples sugieren que la
reproducción asexual llegaría hasta la fijación en cualquier
población en la que apareciese. Sin embargo, observaciones
empíricas y experimentos indican que el sexo confiere beneficios sustanciales. Estos beneficios se pueden encontrar en las
consecuencias genético-poblacionales del sexo. Cuando la
deriva o la selección ha reducido la frecuencia de un genotipo multilocus dado por debajo de los niveles esperados en
el equilibrio de ligamiento, la reproducción sexual se puede
favorecer porque recrea los genotipos perdidos.
La mayoría de los caracteres implican a muchos más de
dos loci y a menudo no conocemos la identidad de estos
loci. La genética cuantitativa nos da las herramientas para
analizar la evolución de tales caracteres. La heredabilidad se
puede estimar examinando las semejanzas entre parientes.
La fuerza de la selección se puede medir analizando las relaciones entre fenotipos y eficacia. Cuando conocemos tanto
la heredabilidad de un carácter como la fuerza de la selección sobre el mismo, podemos predecir cómo evolucionará la población en respuesta a la selección.
La selección sobre caracteres cuantitativos puede seguir
una serie de patrones, como la selección direccional, la selección estabilizadora y la selección disruptiva. La selección
direccional y la selección estabilizadora reducen la variación
genética en las poblaciones. No obstante, la variación genética persiste en muchas poblaciones, incluso en caracteres
íntimamente relacionados con la eficacia. La variación puede
mantenerse porque muchas poblaciones se encuentran en
equilibrio, ya que hay un equilibrio entre la mutación y la
selección o debido a que la selección disuptiva (y patrones
relacionados, como la selección dependiente de frecuencias)
es más común de lo que generalmente se reconoce.
246 PARTE II Los mecanismos del cambio evolutivo
Preguntas
1. En los caballos, el color básico del pelaje está gobernado por
el locus E. Los caballos EE y Ee pueden producir pigmento
negro, mientras que los caballos ee son de color castaño rojizo. Un locus diferentes, el R, puede dar lugar a “ruano”, una
dispersión de pelo blanco en el color básico del pelaje. Sin
embargo, los alelos ruano tienen una seria desventaja: los
embriones RR siempre mueren durante el desarrollo fetal.
Los embriones Rr sobreviven y son ruanos, mientras que los
caballos rr sobreviven pero no son ruanos. El locus E y el
locus R están íntimamente ligados.
Suponga que hace varios siglos, un galeón español con
una carga de caballos de los conquistadores naufragó en una
gran isla llena de hierba. Por azar, los caballos que sobrevivieron al naufragio y nadaron hasta la playa fueron 10 ruanos
de color castaño rojizo (eeRr) y 10 no ruanos homozigóticos
para negro (EErr). En la isla se cruzaron entre sí y establecieron una población silvestre. El ambiente de la isla no ejerció
selección directa sobre el locus E.
a. ¿Cuál fue el coeficiente de desequilibrio de ligamiento, D,
en la población inicial de 20 caballos? ¿Estaba la población
inicial en equilibrio de ligamiento o no? ¿Si no lo estaba,
qué genotipos cromosómicos estaban infrarepresentados?
b. ¿Se espera que la frecuencia del alelo castaño, e, aumente
o disminuya en la primera camada de potrillos? ¿Contestaría de otra manera si la población fundacional hubiera
sido de 10 caballos (5 de cada color)? Explique su razonamiento.
c. Si hoy pudiera viajar a dicha isla, ¿puede predecir cuál sería
el valor de D? ¿Tiene propuestas acerca de si habría más
caballos ruanos que no ruanos, o castaños que negros? Si
no, explique qué información adicional necesitaría.
2. Imagine una población de guisantes que está en equilibrio
de ligamiento para dos loci ligados, el color de la flor
(P = púrpura, p = rojo) y la forma del polen (L = alargada,
l = redonda).
a. ¿Qué tipo de selección daría lugar a desequilibrio de ligamiento? Por ejemplo, ¿la selección sobre un locus (por
ejemplo, todas las plantas con flores rojas mueren) daría
lugar a desequilibrio de ligamiento? ¿Qué ocurriría con la
selección sobre los dos loci (por ejemplo, tanto las plantas
con flores rojas como las plantas con polen alargado mueren)? ¿Qué ocurriría con la selección sobre cierta combinación de genotipos de los dos loci (por ejemplo, sólo
plantas que tienen flores rojas y el polen alargado mueren)?
b. Imagine ahora una población que se encuentra en desequilibrio de ligamiento para estos dos loci. La selección
sobre las flores púrpura, ¿afectará a la evolución del tamaño del polen? ¿Sería su respuesta distinta de la respuesta en
la parte a)? ¿Por qué?
3. La Figura 7.3 muestra cómo la selección sobre genotipos
multilocus puede dar lugar a desequilibrio de ligamiento.
Para la población después de la selección de la Figura 7.3b,
dibuje un gráfico en barras como los de la Figura 7.2. ¿Confirma este gráfico en barras que la población después de la
selección se encuentra en desequilibrio de ligamiento?
4. En el Cuadro 7.1 se demuestra que si gAB = ps, gAb = pt, gaB =
= qs y gab = qt, entonces D = 0. Demuestre que cuando
D = 0, ps = gAB. (Sugerencia: p, la frecuencia del alelo A, es
igual a gAB + gAb. De igual manera, s, la frecuencia del alelo
B, es igual a gAB + gaB. Multiplique estas cantidades y simplifique la expresión. Sabiendo que D = gABgab – gAbgaB = 0,
le permitirá hacer una sustitución clave.)
5. a. En el experimento de la evolución de los gorgojos (Figura 7.14), Dunbrack et al. realmente no utilizaron gorgojos
sexuales y asexuales. En su lugar utilizaron gorgojos sexuales con dos colores, pero forzando a que los gorgojos de
un color se comportan en cuanto al tamaño poblacional
como si fueran asexuales. También hicieron el mismo
experimento con el otro color como “asexual.” ¿Por qué
era importante para los investigadores hacer el experimento de dos maneras? Compare los gráficos de las dos
series de experimentos diferentes (rojo = asexual y negro
= sexual). ¿Se comportarían las dos cepas de gorgojos de
manera diferente?
b. Los gorgojos asexuales reales se reproducirían dos veces
más rápido que los sexuales, pero en el experimento los
autores hicieron que los gorgojos “asexuales” se reprodujeran tres veces más rápido. ¿Por qué cree que hicieron esto?
c. A la población asexual simulada por los investigadores no
se le permitió evolucionar en respuesta a la selección
impuesta por la competencia. ¿Es esto diferente de lo que
hubiera sucedido en una población real de gorgojos asexuales? ¿Cree que el experimento de Dunbrack et al. es
una prueba válida para comparar la reproducción asexual
respecto de la reproducción sexual? Describa brevemente
el experimento que cree que Dunbrack et al. harían para
continuar con este tema.
6. En 1992, Spolsky, Phillips y Uzzell publicaron pruebas genéticas de que los linajes de una salamandra que se reproduce
asexualmente han persistido durante unos 5 millones de
años, un tiempo anormalmente largo. ¿Es esto sorprendente? ¿Por qué sí o por qué no?. Especule acerca de en qué tipo
de ambiente vivirían estas salamandras asexuales y si sus tamaños poblacionales son normalmente pequeños (por ejemplo,
por debajo de 100) o grandes (por ejemplo, por encima de
1.000).
7. Los Volvox (Figura 7.12a) son abundantes y activos en los lagos
durante la primavera y el verano. En el invierno están inactivos,
permaneciendo en estado de reposo como zigotos enquistados
llamados zigosporas. Durante la mayor parte de la primavera
y del verano, Volvox se reproduce asexualmente; pero en
ocasiones cambia y se reproduce sexualmente. ¿Cuándo
Capítulo 7 Evolución en loci múltiples: ligamiento, sexo y genética cuantitativa 247
piensa que Volvox se comportaría sexualmente: en primavera,
a principios del verano o a finales del verano? Explique su razonamiento.
8. Suponga que le está contando a su compañero de habitación
que aprendió en la clase de biología que en cualquier población humana la estatura es muy heredable. Su compañero de
habitación, que estudia nutrición, le dice:“Eso no tiene ningún sentido, ya que hace algunos siglos mucha gente era más
baja de lo que es ahora, y está claro que eso se debe a la dieta.
Si gran parte de la variación en la estatura humana se debe a
los genes, ¿cómo pudo la dieta provocar tan gran diferencia?”
Obviamente, su compañero de habitación tiene razón de que
la dieta pobre puede afectar espectacularmente a la estatura.
¿Cómo le explicaría esta aparente paradoja a su compañero
de habitación?
9. Considere ahora la heredabilidad en un sentido más general.
Suponga que la heredabilidad es muy alta para cierto carácter en una población dada. Hay dos preguntas importantes:
a. Primero, ¿Puede estar el carácter muy afectado por el
ambiente a pesar de su alto valor de heredabilidad? Para
contestar a esta pregunta suponga que todos los individuos
de cierta población han estado expuestos durante toda su
vida al mismo nivel de factores ambientales críticos.
¿Reflejaría el valor de la heredabilidad el hecho de que el
ambiente es muy importante?
b. Segundo, ¿puede el valor de la heredabilidad cambiar si el
ambiente cambia? Para contestar a esta pregunta imagine
que el factor ambiental crítico cambia de tal manera que
individuos distintos están ahora expuestos a niveles distintos de este factor ambiental. ¿Qué le sucede a la variación del carácter en el conjunto de la población? ¿Qué le
sucede al valor de la heredabilidad?
10. En nuestra discusión sobre el trabajo de Weis y Abrahamson
sobre las agallas de la varilla dorada (datos representados en
la Figura 7.35), mencionamos que los investigadores establecieron que hay variación heredable entre las moscas en cuanto al tamaño de las agallas que inducen. ¿Cómo cree que
hicieron esto Weis y Abrahamson? Describa los experimentos necesarios con el mayor detalle posible.
Explorando la bibliografía
11. Si la bacteria endosimbiótica estudiada por Lambert y Moran
(1998) sufre una reducción de eficacia como consecuencia
del trinquete de Muller, entonces las mitocondrías también lo
sufrirían. ¿Lo harían? Véase:
Lynch, M. 1996. Mutation accumulation in transfer RNAs:
Molecular evidence for Muller’s ratchet in mitochondrial
genomes. Molecular Biology and Evolution 13: 209-220.
Lynch, M. 1997. Mutation accumulation in nuclear, organelle, and prokaryotic transfer RNA genes. Molecular Biology
and Evolution 14: 914-925.
12. Muchos patógenos humanos, incluidos bacterias y eucariotas, son capaces tanto de reproducirse asexualmente como de
recombinación genética (es decir, sexo en el sentido genético poblacional). La frecuencia de recombinación en una
población de patógenos puede tener implicaciones médicas.
(Piense, por ejemplo, en lo rápido que evolucionará la resistencia a múltiples antibióticos en una población de bacterias
que tiene recombinación respecto de una población que no
la tiene.) ¿Cómo podemos decir si una población de patógenos dada está comprometida en recombinación genética o es
predominantemente clonal? La recombinación genética es
una fuerza tan poderosa en reducir el desequilibrio de ligamiento que la cantidad de desequilibrio en una población de
patógenos proporciona una pista.Véase:
Maynard Smith, J., N. H. Smith, M. O’Rourke, and B. G.
Spratt. 1993. How clonal are bacteria? Proceedings of the National Academy of Sciences, USA 90: 4384-4388.
Burt,A., D. A. Carter, G. L. Koenig,T. J.White, and J.W.Taylor. 1996. Molecular markers reveal cryptic sex in the human pathogen Coccidioides immitis. Proceedings of the National
Academy of Sciences, USA 93: 770-773.
Go, M. F.,V. Kapur, D. Y. Graham, and J. M. Musser. 1996.
Population genetic analysis of Helicobacter pylori by multilocus enzyme electrophoresis: Extensive allelic diversity and recombinational population structure. Journal of Bacteriology
178: 3934-3938.
Gräser,Y. et al. 1996. Molecular markers reveal that population
structure of the human pathogen Candida albicans exhibits
both clonality and recombination. Proceedings of the National
Academy of Sciences, USA 93: 12473-12477.
Jiménez, M., J. Alvar, and M.Tibayrenc. 1997. Leishmania infantum is clonal in AIDS patients too: Epidemiological implications. AIDS 11: 569-573.
13. ¿En qué grado y a qué velocidad puede la selección direccional desplazar la distribución de un carácter cuantitativo en
una población? Para una respuesta, véase:
Weber, K. E. 1996. Large genetic change at small fitness cost
in large populations of Drosophila melanogaster selected for
wind tunnel flight: Rethinking fitness surfaces. Genetics 144:
205-213.
248 PARTE II Los mecanismos del cambio evolutivo
Bibliografía
Por favor, advierta que gran parte de la genética cuantitativa y de poblaciones de este capítulo está modelizada después de su presentación en los siguientes:
Cavalli-Sforza, L. L., and W. F. Bodmer. 1971. The Genetics of Human Populations.
San Francisco:W. H. Freeman and Company.
Falconer, D. S. 1989. Introduction to Quantitative Genetics. New York: John Wiley &
Sons.
Felsenstein, J. 1997. Theoretical Evolutionary Genetics. Seattle,WA:ASUW Publishing,
University of Washington.
Felsenstein, J. 1988. Sex and the evolution of recombination. In R. E. Michod and
B. R. Levin, eds. The Evolution of Sex. Sunderland, MA: Sinauer, 74-86.
Hartl, D. L. 1981. A Primer of Population Genetics. Sunderland, MA: Sinauer.
Maynard Smith, J. 1998. Evolutionary Genetics, 2nd edition. Oxford: Oxford University Press.
Aquí esta la lista de todas las citas de este capítulo:
Andersson, D. I., and D. Hughes. 1996. Muller’s ratchet decreases fitness of a DNAbased microbe. Proceedings of the National Academy of Sciences, USA 93: 906-907.
Ansari-Lari, M. A., X.-M. Liu, et al. 1997.The extent of genetic variation in the
CCR5 gene. Nature Genetics 16: 221-222.
Barton, N. H., and M.Turelli. 1989. Evolutionary quantitative genetics: How little do we know? Annual Review of Genetics 23: 337-370.
Bates Smith,T. 1993. Disruptive selection and the genetic basis of bill size polymorphism in the African finch Pyrenestes. Nature 363: 618-620.
Blakeslee,A.F. 1914. Corn and men. Journal of Heredity 5:511-518.
Brodie, E. D., III. 1992. Correlational selection for color pattern and antipredator
behavior in the garter snake Thamnophis ordinoides. Evolution 46: 1284-1298.
Brodie, E. D., III, A. J. Moore, and F. J. Janzen. 1995.Visualizing and quantifying
natural selection. Trends in Ecology and Evolution 10: 313-318.
Carrington, M., M. Dean, et al. 1999. Genetics of HIV-1 infection: Chemokine receptor CCR5 polymorphism and its consequences. Human Molecular Genetics
8: 1939-1945.
Cavalli-Sforza, L. L., and W. F. Bodmer. 1971. The Genetics of Human Populations.
San Francisco:W. H. Freeman and Company.
Clausen,J.,D.D.Keck,and W.M.Hiesey.1948.Experimental Studies on the Nature of Species. III. Environmental Responses of Climatic Races of Achillea.Washington, DC: Carnegie Institution of Washington Publication No. 581, 45-86.
Clegg, M.T., J. F. Kidwell, and C. R. Horch. 1980. Dynamics of correlated genetic systems.V. Rates of decay of linkage disequilibria in experimental populations of Drosophila melanogaster. Genetics 94: 217-234.
Di Masso, R. J., G. C. Celoria, and M.T. Font. 1991. Morphometric traits and femoral histomorphometry in mice selected for body conformation. Bone and
Mineral 15: 209-218.
Dunbrack, R. L., C. Coffin, and R. Howe. 1995.The cost of males and the paradox of sex: An experimental investigation of the short-term competitive advantages of evolution in sexual populations. Proceedings of the Royal Society of
London, Series B 262: 45-49.
Elena, S. F., and R. E. Lenski. 1997. Long-term experimental evolution in Escherichia coli.VII. Mechanisms maintaining genetic variability within populations.
Evolution 51: 1058-1067.
Falconer, D. S. 1989. Introduction to Quantitative Genetics. New York: John Wiley &
Sons.
Felsenstein, J. 1988. Sex and the evolution of recombination. In R. E. Michod and
B. R. Levin, eds. The Evolution of Sex. Sunderland, MA: Sinauer, 74-86.
Galen, C. 1989. Measuring pollinator-mediated selection on morphometric floral traits: Bumblebees and the alpine sky pilot, Polemonium viscosum. Evolution
43: 882-890.
Galen, C. 1996. Rates of floral evolution:Adaptation to bumblebee pollination in
an alpine wildflower, Polemonium viscosum. Evolution 50: 120-125.
Grant, P. R., and B. R. Grant. 1995. Predicting microevolutionary responses to directional selection on heritable variation. Evolution 49: 241-251.
Haigh, J. 1978.The accumulation of deleterious mutations in a population: Muller’s ratchet. Theoretical Population Biology 14: 251-267.
Hedrick, P. W. 1983. Genetics of Populations. Boston: Science Books International.
Howard, R. S., and C. M. Lively. 1998.The maintenance of sex by parasitism and
mutation accumulation under epistatic fitness functions. Evolution 52: 604-610.
Huttley, G.A., M.W. Smith, et al. 1999.A scan for linkage disequilibrium across the
human genome. Genetics 152: 1711-1722.
Jennings, H. S. 1917.The numerical results of diverse systems of breeding, with respect to two pairs of characters, linked or independent, with special relation to
the effects of linkage. Genetics 2: 97-154.
Lalani, A. S., J. Masters, et al. 1999. Use of chemokine receptors by poxviruses.
Science 286: 1968-1971.
Lambert, J. D., and N. A. Moran. 1998. Deleterious mutations destabilize ribosomal RNA in endosymbiotic bacteria. Proceedings of the National Academy of
Sciences, USA 95: 4458-4462.
Lande, R., and S. J. Arnold. 1983. The measurement of selection on correlated
characters. Evolution 37: 1210-1226.
Lively, C. M. 1992. Parthenogenesis in a freshwater snail: Reproductive assurance
versus parasitic release. Evolution 46: 907-913.
Lively, C. M. 1996. Host-parasite coevolution and sex. BioScience 46: 107-114.
Maynard Smith, J. 1978. The Evolution of Sex. Cambridge: Cambridge University
Press.
Maynard Smith, J. 1988.The evolution of recombination. In R. E. Michod and B.
R. Levin, eds. The Evolution of Sex. Sunderland, MA: Sinauer, 106-125.
Michod, R. E., and B. R. Levin, eds. 1988. The Evolution of Sex. Sunderland, MA:
Sinauer.
Miyashita, N.T.,A. Kawabe, and H. Innan. 1999. DNA variation in the wild plant
Arabidopsis thaliana revealed by amplified fragment length polymorphism analysis. Genetics 152: 1723-1731.
Muller, H. J. 1964.The relation of recombination to mutational advance. Mutation
Research 1: 2-9.
Murray, C., and R. J. Herrnstein. 1994. Race, genes and I.Q. An apologia. The
New Republic October: 27-37.
Phillips, P. C., and S. J. Arnold. 1989.Visualizing multivariate selection. Evolution
43: 1209-1222.
Provine,W. B. 1986. Sewall Wright and Evolutionary Biology. University of Chicago
Press, Chicago.
Seger, J., and W. D. Hamilton. 1988. Parasites and sex. In R. E. Michod and B. R.
Levin, eds. The Evolution of Sex. Sunderland, MA: Sinauer, 176-193.
Smith, J. M. N., and A. A. Dhondt. 1980. Experimental confirmation of heritable
morphological variation in a natural population of song sparrows. Evolution 34:
1155-1160.
Spolsky, C. M., C. A. Phillips, and T. Uzzell. 1992. Antiquity of clonal salamander
lineages revealed by mitochondrial DNA. Nature 356: 706-710.
Stephens, J. C., D. E. Reich, et al. 1998. Dating the origin of the CCR5-⌬32
AIDS-resistance allele by the coalescence of haplotypes. American Journal of
Human Genetics 62: 1507-1515.
Sturtevant,A. H., and K. Mather. 1938.The interrelations of inversions, heterosis,
and recombination. American Naturalist 72: 447-452.
Via, S. 1991.The genetic structure of host plant adaptation in a spatial patchwork:
Demographic variability among reciprocally transplanted pea aphid clones.
Evolution 45: 827-852.
Weis,A. E., and W. G.Abrahamson. 1986. Evolution of host-plant manipulation by
gall makers: Ecological and genetic factors in the Solidago-Eurosta system. American Naturalist 127: 681-695.
Wright, S. 1986. Evolution: Selected papers. William B. Provine, editor. University of
Chicago Press, Chicago.
Wright, S. 1988. Surfaces of selective value revisited. American Naturalist 131: 115123.
PARTE III
Una jirafa hembra y su cría comiendo hojas. (Walt Anderson/Visuals Unlimited)
ADAPTACIÓN
L
GENÉTICA DE POBLACIONES QUE MOSTRAMOS EN LA
Parte II transmiten un mensaje fundamental: cada una de las cuatro fuerzas evolutivas tiene consecuencias diferentes. La mutación altera aleatoriamente la secuencia del DNA. Como fuente última de
toda variabilidad genética, la mutación proporciona la materia prima que hace posible la evolución. La
migración homogeniza las frecuencias alélicas entre poblaciones. La deriva produce cambios aleatorios
en las frecuencias alélicas, especialmente en poblaciones pequeñas. La selección natural, por el contrario, es el único proceso evolutivo que produce adaptación. Una adaptación es cualquier carácter que permita a un individuo dejar más descendientes que los individuos que no poseen dicho carácter.
Nuestro objetivo en la Parte III es explorar con detenimiento la adaptación. Comenzaremos, en
el Capítulo 8, inspeccionando las técnicas que los biólogos evolutivos usan para estudiar la adaptación.
¿Cómo puede un investigador comprobar, rigurosamente, la hipótesis de que un carácter particular
es adaptativo? Esta discusión se seguirá, en el Capítulo 9, con la exploración de cómo la selección
natural actúa sobre caracteres morfológicos y de comportamiento que permiten a los individuos atraer
parejas. Este tipo de selección se llama selección sexual. Ésta puede producir enormes diferencias en
el comportamiento y apariencia de machos y hembras de una misma especie. El Capítulo 10 explora cómo las interacciones entre individuos que viven en grupos sociales afectan a su eficacia biológica. Explora, también, la base biológica del altruismo e introduce un importante avance conceptual
llamado selección familiar. La Parte III termina planteando cuestiones sobre cuánto tiempo viven los
organismos, con qué frecuencia se reproducen y cuánto invierten en el cuidado de cada uno de sus
descendientes. En conjunto, los capítulos de la Parte III exploran las consecuencias de la selección
natural en todas sus formas.
OS MODELOS Y EXPERIMENTOS DE
CAPÍTULO
8
Estudiando la adaptación: el análisis
evolutivo de la forma y la función
Las flores de Fuchsia excorticata permanecen verdes mientras producen néctar y reciben polen, luego cambian a púrpura oscuro o rojo (Lynda
Delph, Universidad de Indiana).
L
AS JIRAFAS EXIGEN UNA EXPLICACIÓN.
UNA PEQUEÑA CABEZA SOBRE UN
enorme cuello, con todo el conjunto colocado sobre unos zancos; ver sus contorsiones gimnásticas cuando se agachan para tomar un trago es preguntarse si no fueron diseñadas por encargo (Figura 8.1).
Cualquiera sabe, por supuesto, por qué las jirafas tienen un cuello largo. Sus antepasados tuvieron que competir con otras especies ramoneadoras. Las jirafas con cuellos más
largos tenían más comida y, consecuentemente, dejaban más descendientes. Hoy día, sus
descendientes alcanzan alturas de hasta más de cinco metros y son los únicos animales de
pasto en África que pueden alcanzar las copas altas de las acacias.
La explicación del diseño de los organismos se encuentra entre los triunfos de la teoría
de la evolución por selección natural. Los individuos en las generaciones pasadas diferían
en su diseño, y aquellos con el mejor diseño transmitieron sus genes en mayor proporción.
Un carácter, o conjunto integrado de ellos, que aumenta la eficacia de sus portadores se
conoce como una adaptación y se dice que es adaptativo.
Demostrar que los caracteres de los organismos son, de hecho, adaptaciones ha sido una
de las mayores ocupaciones de la biología evolutiva desde los tiempos de Darwin (Mayr
1983). Este esfuerzo investigador es a menudo conocido como el programa adaptacionista.
251
252 PARTE III Adaptación
Figura 8.1 El cuello largo de la jirafa hace
difícil tomar un trago (Joe McDonald/Animals
Animals/Earth Scenes)
Hablando de un modo simplista, para demostrar que un carácter es una adaptación, primero necesitaremos determinar para qué sirve dicho carácter y entonces demostrar que los individuos que lo poseen contribuyen en mayor medida al acervo genético de las generaciones
futuras que aquellos individuos que no lo poseen.
El significado adaptativo de algunos caracteres es obvio: los ojos son estructuras para
detectar objetos en la distancia mediante la captación y análisis de la luz; en muchas especies animales, los individuos con buena visión estarán más capacitados para encontrar
comida y evitar a los depredadores que individuos con visión pobre. Otros caracteres ofrecen ventajas más sutiles, y entender su significado adaptativo requiere de un esfuerzo.
Las explicaciones obvias, en particular, pueden ser peligrosamente seductoras. Como
veremos en la primera sección de este capítulo, nuestra hipótesis adaptativa para el cuello
de las jirafas tiene un serio defecto: no parece que las jirafas se la crean. La moraleja es que
ninguna explicación sobre el valor adaptativo de un carácter debe ser aceptada solamente porque sea plausible y encantadora (Gould y Lewontin 1979).Todas las hipótesis tienen
que comprobarse. Las hipótesis se pueden comprobar usándolas para hacer predicciones
y viendo después si estas predicciones son correctas.
En este capítulo se explora una variedad de métodos que los biólogos evolutivos usan
para comprobar hipótesis sobre adaptaciones, incluyendo experimentos, observaciones y
el método comparativo. En la última sección del capítulo también exploraremos las complejidades de las formas y las funciones biológicas que aún continúan haciendo del programa adaptacionista un área de investigación desafiante y muy activa.
Una hipótesis plausible sobre
el valor adaptativo de un
carácter es el principio de un
estudio cuidadoso, no su fin.
8.1. Todas las hipótesis deben comprobarse:
reconsiderando el cuello de las jirafas
Robert Simmons y Lue Scheepers (1996) cuestionaron la interpretación tradicional de cómo
las jirafas consiguieron su cuello. Simmons y Scheepers observaron comer a las jirafas salvajes y revisaron las observaciones publicadas por otros biólogos. Simmons y Scheepers razo-
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 253
Altura donde se come (metros)
Jirafas macho comiendo
en los bosques
Jirafas hembra comiendo
en los bosques
7
7
6
6
5
5
4
4
3
3
2
2
1
1
20
40
Fracción de lo comido (% de bocados)
Figura 8.2 ¿Se aprovechan las jirafas de su
cuello largo al comer? Estas gráficas muestran
20
40
Fracción de lo comido (% de bocados)
la proporción de tiempo que los machos (izquierda)
y las hembras (derecha) pasan comiendo a distintas
alturas en los bosques de Kenya. Cuanto más ancho
es el gráfico a una altura dada, más tiempo pasan
las jirafas comiendo en ella. Los paneles muestran
las alturas de un macho y de una hembra típicos.
Tomado de las Figuras 5 y 6 de Young y Isbell
(1991). Reimpreso con permiso de Blackwell
Wissenschafts-Verlag, Berlin.
naron que si la hipótesis de la competencia por la comida fuese correcta, entonces, durante la estación seca, cuando la comida es escasa, las jirafas deberían invertir la mayor parte de
su tiempo comiendo por encima del alcance de sus competidores. El hecho es que las jirafas pasan la mayor parte de su tiempo, durante esta estación, buscando arbustos bajos, no
árboles altos. Incluso cuando las jirafas buscan comida por encima del alcance de sus competidores, rara vez lo hacen a una altura cercana a su máximo posible. En Kenya, por ejemplo,Truman Young y Lynne Isbell (1991) encontraron que las jirafas hacían la mayor parte
de su ramoneo en bosques y que preferían comer a la altura de los hombros (Figura 8.2).
Simmons y Scheepers propusieron una explicación alternativa para la evolución del
cuello de las jirafas. Observaron que los machos en ocasiones pelean brutalmente, empleando sus cuellos y cabezas como garrotes y, ocasionalmente, incluso se matan unos a otros
(Figura 8.3). Simmons y Scheepers sugirieron que el cuello de la jirafa evolucionó como
un arma, usada por los machos en los combates pre-apareamiento. De un modo consistente con esta hipótesis, los machos tienen cuellos que son entre 30 y 40 centímetros más
largos y 1,7 veces más pesados que los de las hembras de la misma edad. Además, los
machos tienen cráneos más fuertemente armados y 3,5 veces más pesados.
Figura 8.3 Las jirafas macho emplean sus
cabezas y cuellos como armas cuando pelean
por una oportunidad de apareamiento (Patti
Murria/Animals Animals/Earth Scenes)
254 PARTE III Adaptación
También apoyan la hipótesis del “cuello como arma” los datos sobre el comportamiento
de las jirafas recogidos por David Pratt y Virginia Anderson. Pratt y Anderson (1985) observaron detalladamente las relaciones sociales de las jirafas. La primera vez que Pratt y
Anderson veían a cada uno de los machos pertenecientes a la población que estaban estudiando, lo clasificaban en una de las tres categorías siguientes. Los machos de la clase C eran
adultos jóvenes; los de las clases A y B eran adultos más maduros. Los de la clase A eran,
frecuentemente, más grandes que los de la clase B pero, aún más importante, tenían cuellos más gruesos, cuernos más grandes y cráneos más fuertemente armados. Pratt y Anderson observaron 127 interacciones en las que un macho desplazaba a otro en su grupo
social. Esto tenía lugar cuando,“caminando hacia él con la cabeza en alto o, en ocasiones,
simplemente golpeándole fuertemente, el individuo dominante obligaba al inferior a
retirarse”. Los machos de la clase A dominaban a los de las clases B y C, mientras que los
de la B dominaban a los de la C (Tabla 8.1a).
Pratt y Anderson también observaron interacciones entre machos y hembras. Los
machos controlaban a las hembras para determinar cuándo éstas estaban en celo. Para comprobar la condición reproductiva de una hembra, un macho le acaricia con el hocico en
la grupa. Si ella es receptiva, orinará, y el macho probará la orina. Pratt y Anderson fueron
testigos de numerosos intentos por parte de machos de cada clase de comprobar el estado de las hembras. Éstas fueron mucho más receptivas con machos de tipo A y B que con
machos de tipo C (Tabla 8.1b).Ya que esta clase de conducta, algunas veces, se sigue con el
galanteo y posterior apareamiento, estos datos sugieren que las hembras prefieren aparearse con machos más viejos, más grandes y con cuellos más largos.
Simmons y Scheepers argumentan que entre los ancestros de las actuales jirafas, los
machos de cuellos largos tenían un mayor éxito reproductivo, no porque comiesen más,
sino por que intimidaban a sus rivales y atraían más hembras. ¿Entonces por qué, también
tienen las hembras el cuello largo? Tal vez simplemente porque los machos pasan los genes
que codifican para el cuello largo a sus hijas igual que los pasan a sus hijos.
Tabla 8.1 Tamaño del cuello e interacciones sociales en las jirafas
Los machos de la clase C son adultos jóvenes; los de las clases A y B son más maduros. Los de la
clase A son, habitualmente, más grandes que los de la B, pero más importante, tienen cuellos
más robustos , cuernos más grandes y cráneos más armados.
(a) Tamaño del cuello e interacciones sociales de los machos. Estos números representan observaciones de un macho desplazando a otros en un grupo social.
A desplaza a B,
A desplaza a A,
B desplaza a A,
A desplaza a C, o
B desplaza a B, o
C desplaza a A, o
B desplaza a C
C desplaza a C
C desplaza a B
82
39
6
(b) Tamaño del cuello y elección de la hembra. Estos números representan observaciones de
un macho intentando averiguar si una hembra está en celo mediante una prueba de su orina.
Probar la orina de una hembra por parte de un macho requiere la cooperación de ésta.
Éxito
Fracaso
% de éxito
Machos A
34
22
60,7
Machos B
76
61
55,5
Machos C
45
89
33,6
Fuente: de Pratt y Anderson 1985. Copyright © 1985, Journal of Natural History. Reimpreso con el permiso de
Taylor & Francis Ltd. http://www.tandf.co.uk
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 255
El ejemplo de las jirafas demuestra que no podemos aceptar sin sentido crítico cualquier
hipótesis sobre el significado adaptativo de un carácter simplemente porque sea plausible.
Debemos someter todas las hipótesis a pruebas rigurosas.
Aquí hay otros problemas que hay que tener en mente al estudiar adaptaciones:
• Las diferencias entre poblaciones o especies no siempre son adaptativas. Jirafas de diferentes poblaciones tienen diferentes patrones de manchas en su pelaje. Es posible que
cada patrón de pelaje sea adaptativo en la región donde aparece. Es también posible,
no obstante, que las diferencias regionales en el patrón de pelaje no sean adaptativas
en absoluto. Mutaciones que generen variaciones en los patrones pueden haberse
fijado en diferentes poblaciones de jirafas por deriva genética, tal vez mediante un
efecto fundador (ver Capítulo 6). En el ámbito molecular, mucha de la variación entre
individuos, poblaciones y especies puede ser selectivamente neutra (ver los Capítulos 6 y 18).
• No todos los caracteres de un organismo, o todos los usos que de un carácter haga un
organismo, son una adaptación. Las jirafas, a veces comen en toda su altura, por encima del alcance de sus competidores. Esto no significa necesariamente que los cuellos
largos evolucionasen porque proporcionaban nuevas oportunidades para comer. Los
cuellos largos pueden haber evolucionado por su valor como armas y son, sólo incidentalmente, empleados también por la ventaja que proporcionan para comer.
• No todas las adaptaciones son perfectas. Los cuellos largos pueden ayudar a las jirafas
machos a obtener parejas, pero, como ya hemos visto, hacen difícil el beber.
Todas las hipótesis deben ser
contrastadas.
También hay que considerar
explicaciones alternativas.
En las siguientes tres secciones, revisaremos tres métodos que los biólogos evolutivos
emplean para contrastar hipótesis sobre el significado adaptativo de un carácter. La primera
de estas secciones hace referencia a la experimentación, la segunda a los estudios observacionales y la tercera explora el método comparativo.
8.2.
Experimentos
Los experimentos están entre las herramientas más poderosas en ciencia. Un experimento bien diseñado nos permite aislar y contrastar el efecto que un factor único, bien
definido, tiene sobre el fenómeno en cuestión.Ya hemos repasado una variedad de experimentos en capítulos anteriores. Las Figuras 5.11 y 7.14, por ejemplo, ilustran los
resultados experimentales de poblaciones de insectos mantenidas en el laboratorio.
Aquí prestaremos atención al proceso de planificación e interpretación de experimentos. Hemos elegido nuestros ejemplos porque ilustran varios aspectos de un buen diseño
experimental.
¿Cuál es la función que tienen las marcas en las alas y la conducta
de agitar las alas en la mosca téfrica Zonosemata?
La mosca téfrica Zonosemata vittigera tiene unas bandas oscuras características en sus alas.
Cuando se le molesta, la mosca coloca las alas perpendicularmente a su cuerpo y las agita
de arriba abajo (Figura 8.4). Algunos entomólogos han apreciado que este comportamiento parece imitar al desafío territorial agitando las patas típico de las arañas saltarinas
(especies de la familia Salticidae). Estos entomólogos sugirieron que ya que las arañas saltarinas son rápidas y tienen un desagradable mordisco, una mosca que imitase a una araña
saltarina podría ser evitada por una amplia variedad de otros predadores. Erick Greene y
sus colaboradores (1987) tenían una idea diferente.Ya que las arañas saltarinas son el principal depredador de Zonosemata, Greene et al. propusieron que la mosca usaba las marcas
Los experimentos son el
método más poderoso para
contrastar hipótesis. Un buen
experimento restringe las
diferencias entre grupos de
estudio a una única variable.
256 PARTE III Adaptación
Figura 8.4 ¿Un cordero con
piel de lobo? Esta fotografía
muestra a la mosca téfrica
Zonosemata vittigera (derecha)
enfrentándose a uno de sus
depredadores, la araña saltarina
Phidippus apacheanus (izquierda)
(Erick Greene, University of
Montana).
de sus alas y la conducta de agitar las alas para intimidar a las propias arañas saltarinas. La
mosca, en otras palabras, es una oveja con piel de lobo. Nunca antes se había observado
una presa imitando el comportamiento de su propio depredador.
Ambas explicaciones basadas en la imitación son hipótesis plausibles sobre el comportamiento de la mosca pero, a menos que las contrastemos, no dejan de ser solamente bonitas
historias. ¿Pueden contrastarse estas hipótesis rigurosamente? Greene y sus colaboradores
(1987) fueron capaces de hacerlo experimentalmente.
El primer paso en cualquier análisis evolutivo es plantearse la cuestión lo más concretamente posible. En este caso, ¿las marcas de las alas y agitar las alas imitan el desafío que
usan las arañas saltarinas entre ellas y, por tanto, permite a la mosca no ser depredada? Plantear la pregunta de un modo preciso hace más fácil diseñar un experimento que proporcione una respuesta clara.
El siguiente paso de Green et al. fue enumerar explicaciones alternativas para este comportamiento. Los buenos experimentos deben contrastar cuantas más hipótesis alternativas como sea posible. Nótese que cada una de las siguientes explicaciones alternativas es
viable y biológicamente realista, no espantapájaros propuestos simplemente para dar una
impresión de rigor.
Los buenos diseños
experimentales contrastan las
predicciones hechas por varias
hipótesis alternativas.
H1: Las moscas no imitan a las arañas saltarinas. Ésta es otra posibilidad, ya que otras
especies de moscas también tienen bandas oscuras en las alas y las agitan sin que ello
asuste a los depredadores. En muchas especies, las moscas usan sus marcas y demostraciones durante el cortejo.
H2: Las moscas imitan a las arañas saltarinas, pero se comportan como tales para ahuyentar a otros depredadores, no a las arañas. Otros depredadores de moscas que podrían
asustarse de una araña saltarina, o de algo que se le pareciese, incluye a otras especies
de arañas, bichos asesinos, mantis religiosas e incluso lagartos.
H3: Las moscas imitan a las arañas saltarinas, y este mimetismo funciona específicamente para evitar la depredación por parte de las arañas saltarinas.
Para contrastar estas alternativas, Greene y sus colaboradores necesitaban moscas con
algunas partes, pero no todas, del aspecto de Zonosemata. Los investigadores comprobaron
que podían cortar las alas de Zonosemata y pegárselas después con cola de Elmer.Y que
podían cortar las alas de Zonosemata y reemplazárselas con las alas de una mosca doméstica (Musca domestica), que son claras y sin marcas. Notablemente, las Zonosemata quirúrgicamente alteradas continuaban agitando sus alas de modo normal e incluso podían volar.
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 257
Mediante varias operaciones quirúrgicas, Greene y sus colaboradores crearon un total
de cinco grupos experimentales de moscas (Figura 8.5). Los cinco tratamientos discriminaban entre las tres hipótesis, ya que cada hipótesis plantea un conjunto diferente de
predicciones sobre qué ocurrirá en los encuentros entre depredadores y moscas. Los
tratamientos también permitieron a los investigadores determinar si ambos, las marcas y
la agitación de las alas, eran importantes en el mimetismo. Éste es un diseño experimental potente.
Para hacer los contrastes, Greene et al. necesitaban medir la respuesta de las arañas saltarinas y otros depredadores ante los cinco tipos experimentales de moscas. Cuando fuesen enfrentadas con una mosca de prueba, las arañas ¿se retirarían, acecharían y atacarían
o matarían? Para responder a esta pregunta, los investigadores mantuvieron en ayunas a 20
arañas saltarinas de 11 especies diferentes durante dos días. Luego presentaron una mosca
de cada uno de los cinco tipos experimentales a cada araña, en un orden aleatorio. Los
investigadores hicieron esto en una zona de pruebas y anotaron la respuesta más agresiva
de cada araña saltarina durante un intervalo de cinco minutos. Había una clara diferencia:
las arañas saltarinas tendían a retirarse frente a las moscas que agitaban alas marcadas, pero
atacaban a las moscas que carecían de marcas en las alas, que no las agitaban, o ambas cosas
(Figura 8.6).
Tratamiento
Propósito
A
B
C
D
E
Zonosemata
sin tratar
Zonosemata
con las alas
cortadas y
vueltas a pegar
Zonosemata
con alas de
mosca
Mosca
doméstica con
alas de
Zonosemata
Mosca
doméstica
sin tratar
Comprobar el
efecto de las
marcas en las
alas y de su
movimiento
Control de los
efectos de la
cirugía
Comprobar el
efecto de
mover las alas
pero sin
marcas
Comprobar el
efecto de las
alas marcadas
pero sin
agitación
Comprobar el
efecto de alas
sin marcas y
sin movimiento
Predicciones bajo la hipótesis 1: sin mimetismo
La araña saltarina hará: Atacar
Atacar
Atacar
Atacar
Atacar
Otro depredador hará:
Atacar
Atacar
Atacar
Atacar
Atacar
Predicciones bajo la hipótesis 2: el mimetismo detendrá a otros depredadores
La araña saltarina hará: Atacar
Atacar
Atacar
Atacar
Atacar
Otro depredador hará:
Retirada
Atacar
Atacar
Atacar
Retirada
Predicciones bajo la hipótesis 3: el mimetismo detendrá a las arañas saltarinas
La araña saltarina hará: Retirada
Retirada
Atacar
Atacar
Atacar
Otro depredador hará:
Atacar
Atacar
Atacar
Atacar
Atacar
Figura 8.5 Tratamientos quirúrgicos empleados en los experimentos para comprobar la función de
la agitación de las alas de Zonosemata Esta tabla muestra los resultados predichos cuando diferentes
depredadores se encuentran con las moscas de cada tratamiento. Nótese que cada hipótesis hace un conjunto
único de predicciones. (Las predicciones enumeradas para las hipótesis 2 y 3 asumen que tanto las marcas como el
movimiento de las alas de Zonosemata son necesarios para un mimetismo efectivo.)
258 PARTE III Adaptación
Figura 8.6 Las moscas téfricas imitan a las arañas saltarinas para
evitar la depredación Estos diagramas de barras muestran cómo las arañas
(a)
B
C
D
E
Retirada
20
10
0
Acecho y
ataque
(b)
20
10
0
(c)
20
Matar
Respuesta de la araña saltarina
saltarinas responden a cada uno de los cinco tratamientos y controles
enumerados en la Figura 8.5. El eje vertical representa el número de arañas
saltarinas, de un total de 20, que mostraron cada tipo de respuesta extrema
frente cada tipo de mosca. Así, para las moscas del grupo A (Zonosemata sin
modificar), 15 arañas saltarinas se retiraron de sus moscas prueba [gráfico (a)],
y cinco de las arañas mataron a sus moscas prueba [gráfico (c)]. Para las
moscas del grupo B (Zonosemata con sus alas cortadas y vueltas a pegar), 15
arañas saltarinas se retiraron de sus moscas, dos acecharon y atacaron pero no
mataron a las moscas y tres mataron a sus moscas. De Greene et al. (1987).
Copyright © 1985, Journal of Natural History. Reimpreso con permiso de
Taylor & Francis Ltd. http://www.tandf.co.uk
Nótese que la mayoría de las moscas que movieron sus alas marcadas
(grupos A y B) sobrevivieron ilesas a sus encuentros con arañas, mientras que
la mayoría de las moscas que carecían de marcas, no movían las alas, o
ambas cosas, fueron atacadas y, muchas, matadas. La línea gruesa bajo las
gráficas identifica grupos de tratamiento donde las respuestas de las arañas
no eran estadísticamente distintas. Los grupos A y B eran indistinguibles uno
del otro, pero diferentes de los grupos C, D y E. Dado que a cada araña se le
presentó una mosca de cada tipo, el tamaño de la muestra en cada
tratamiento fue de 20.
A
10
0
Cuando los investigadores probaron moscas de los tratamientos A, C y E frente a otros
depredadores (arañas no saltarinas, bichos asesinos, mantis religiosas y lagartos de cola de
látigo), todas fueron capturadas y comidas. Cuando Greene et al. colocaron moscas frente a estos depredadores, no hubo diferencias entre los tres grupos incluso en el tiempo que
tardaron en ser capturadas.
La comparación de las Figuras 8.5 y 8.6 muestra que estos resultados son consistentes
con la hipótesis H3 pero inconsistentes con las hipótesis H1 y H2. Así pues, los experimentos de Greene et al. dieron un fuerte respaldo a la hipótesis de que las moscas téfricas
imitaban a sus propios depredadores, las arañas saltarinas, para evitar ser comidas por éstas
(véase también Mather y Roitberg 1987).
En términos de diseño experimental, el estudio de Greene et al. ilustra varios puntos
importantes:
Los grupos control
proporcionan un contraste
para los grupos de
tratamiento. Los individuos
control no deben haber sido
tratados en absoluto, o
pueden haber experimentado
un tratamiento que pruebe los
efectos de aquellas
condiciones experimentales de
las que se haya predicho que
no tenían efecto sobre el
resultado final.
• Definir y contrastar grupos de control válidos es crítico. En los estudios de Greene et
al., los grupos A y B (Figuras 8.5 y 8.6) sirvieron de controles. Estos individuos demostraban que la cirugía en las alas, en sí misma, no tenía efecto alguno en el comportamiento de las moscas o de las arañas. Así, cuando las Zonosemata del grupo C fueron
atacadas y comidas por las arañas saltarinas, Greene y sus colegas podían estar seguros
de que esto fue porque las moscas no tenían marcas en sus alas, no simplemente porque sus alas habían sido cortadas y pegadas.
• Todos los tratamientos (control y experimentales) tienen que manipularse exactamente igual. Fue clave que Greene et al. usasen siempre la misma zona de pruebas, los mismos intervalos de tiempo y las mismas definiciones de respuesta del depredador en todas
y cada una de las pruebas. Usar condiciones tipificadas permite a un investigador el evitar sesgos y aumentar la precisión de los datos (Figura 8.7). Piense en los problemas que
podrían haber aparecido si distintas zonas de pruebas se hubiesen empleado para cada
uno de los cinco tratamientos.
• La aleatorización es una técnica importante para homogeneizar otros efectos diversos
entre grupos control y experimentales. En esencia, es otro modo de evitar sesgos. Por ejemplo, Greene y sus colegas presentaban los diferentes tipos de moscas de prueba a las arañas
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 259
Sesgo
Grande
Pequeño
Precision
Alta
Figura 8.7 Sesgo y precisión Cuando se diseña un experimento o conjunto
Baja
de observaciones con el objetivo de estimar algún parámetro, es importante
minimizar el sesgo y maximizar la precisión. En este diagrama el parámetro
estimado en un estudio se representa por la diana y los datos recogidos se
representan por los puntos rojos. Técnicas tales como estandarizar las condiciones
experimentales y aleatorizar otros factores ayudan a minimizar el sesgo y a
aumentar la precisión. Nótese que nuestra habilidad para medir con precisión
depende de disponer de un gran número de datos.
y a los otros depredadores en un orden aleatorio. ¿Qué problemas hubiesen aparecido si
hubiesen presentado los cinco tipos de moscas siempre en la misma secuencia a cada araña?
• Repetir las pruebas con muchos individuos es esencial. Es casi universalmente cierto en
trabajos experimentales (y observacionales) que tamaños muestrales grandes son mejores. Esto es porque el objetivo de todo experimento es estimar un número. En este caso,
ese número fue la probabilidad de que una mosca fuese atacaba por las arañas saltarinas como una función de su habilidad para mover las alas marcadas.
Replicar los experimentos u observaciones tiene dos consecuencias:
• Reduce la cantidad de error de las estimas causado por individuos o circunstancias
inusuales. Por ejemplo, cuatro de las diez Zonosemata con alas marcadas que fueron atacadas, saltaron sobre ellas y las mataron incluso antes de que tuviesen una oportunidad
de mostrarse (grupos A y B en las Figuras 8.5 y 8.6). Como Greene y sus colegas estaban usando condiciones tipificadas, no fue aceptable simplemente eliminar estos datos,
aunque puedan representar mala suerte. Si sucesos como éstos son realmente el resultado de la mala suerte, entonces serán raros y no sesgarán los resultados siempre y cuando el tamaño muestral sea grande.
• Repetir los experimentos permite a los investigadores entender lo precisa que es su estimación, al poder medir la variación entre los datos. Conocer lo precisos que son los
datos permite el uso de pruebas estadísticas. Las pruebas estadísticas, de hecho, nos permiten cuantificar la probabilidad de que el resultado que hemos observado sea debido,
simplemente, al azar (ver el Cuadro 8.1).
En resumen, el diseño experimental de Greene et al. fue exitoso porque permitió contrastar, independientemente, los efectos que el tipo de predador, tipo de ala y movimiento
del ala tenía en la habilidad de Zonosemata para escapar de la predación. Los experimentos
son el método más poderoso de contrastar hipótesis sobre la adaptación. En la siguiente
sección, consideraremos cómo estudios basados en observaciones cuidadosas pueden, a
veces, ser casi tan buenos como la experimentación.
8.3.
Estudios basados en la observación
Algunas hipótesis sobre adaptaciones son difíciles o imposibles de contrastar con experimentos. Es difícil de imaginar, por ejemplo, cómo podemos hacer experimentos con-
Tamaños muestrales grandes
son críticos para el éxito de
los experimentos, pero los
investigadores tienen que
llegar a un compromiso entre
los costes y los beneficios de
reunir conjuntos de datos
infinitamente grandes.
Cuando un experimento es
impracticable, un cuidadoso
estudio basado en la
observación puede ser el mejor
método siguiente para evaluar
hipótesis. Un buen estudio de
observación intentará buscar
circunstancias en la
naturaleza que asemejen un
experimento.
260 PARTE III Adaptación
CUADRO 8.1
E
Una introducción al contraste estadístico
l objetivo fundamental de muchos estudios experimentales y observacionales es estimar un valor
numérico en dos grupos, uno tratado y otro control, y
determinar si existen diferencias para este valor entre
ambos grupos. En los estudios que hemos revisado hasta
ahora, los investigadores han estimado valores tales como
la longitud del pico de los pinzones (Capítulo 3) y la frecuencia con que las moscas son atacadas por las arañas
(este capítulo). Los grupos que queríamos contrastar en
estos ejemplos consistían en pinzones antes y después de la
sequía y moscas con alas marcadas y sin marcar.
Como ejemplo, nos centraremos ahora en la comparación entre moscas de los grupos B y C del experimento de
Greene et al. (Figuras 8.5 y 8.6). Para simplificar la discusión, juntaremos los resultados de “acechada y atacada” con
“matada” en un única categoría, “atacada”. Cuando los
investigadores mostraron una mosca del grupo B ante 20
arañas saltarinas, 15 de las arañas se retiraron y 5 atacaron a
la mosca. Por contra, cuando presentaron a cada una de las
20 arañas una mosca del grupo C, 1 se retiró y 19 atacaron
a la mosca. Ciertamente, parece como si las arañas saltarinas fuesen menos agresivas con las moscas de alas marcadas
(Grupo B) que con moscas con alas sin marcar (Grupo C).
Una vez que hemos hecho una medida en ambos grupos y observado diferencias entre ellos, aparece la cuestión
estadística; ¿es real esta diferencia o simplemente se debe a
variación aleatoria? Es concebible que si probásemos con
una muestra mayor de moscas y arañas, descubriéramos
que, en efecto, las arañas responden del mismo modo ante
moscas con alas sin marcar que con alas marcadas. Bajo este
escenario, la diferencia aparente que observamos era simplemente un resultado aleatorio.
Podemos encontrar una analogía en lanzar una moneda. Imagine que tiene dos monedas. Es concebible que si
lanzase la primera moneda 20 veces saliesen 15 caras y 5
cruces y que al lanzar la segunda moneda saliesen 1 cara y
19 cruces. Parecería que las monedas son diferentes, pero
la verdad es que si lanzase ambas monedas un número
muy grande de veces, descubriría que ambas monedas son
iguales. (Nótese que esta analogía es imperfecta: la probabilidad con la que con una moneda sale cara es 0,5, mientras que la auténtica probabilidad con la que una araña
ataca a una mosca está entre 0 y 1.) Lo que queremos saber
es ¿cuál es la probabilidad de que observemos una diferencia, como la que hemos obtenido, en el comportamiento de las arañas si realmente éstas reaccionasen de
igual modo ante ambos tipos de moscas?
Responder a esta pregunta requiere una prueba estadística. El primer paso de una prueba estadística es especificar una hipótesis nula. Esta hipótesis es que no existen
diferencias entre los grupos. En nuestro ejemplo, la hipótesis nula es que la presencia o ausencia de marcas en las alas
no afecta al modo en que las arañas saltarinas reaccionan
ante las moscas. De acuerdo con esta hipótesis, la probabilidad de ataque es la misma para moscas con alas marcadas
que para moscas con alas sin marcar.
El segundo paso es calcular un valor llamado estadístico de prueba. Un estadístico de prueba es un número que
caracteriza la magnitud de la diferencia entre ambos grupos. Más de un estadístico de prueba sería apropiado para
los datos de Greene et al. Greene y sus colaboradores eligieron un estadístico de prueba que compara las frecuencias de retirada y ataque observadas en el experimento, y
las frecuencias de retirada y ataque esperadas si la hipótesis nula fuese cierta.
El tercer paso es determinar la probabilidad de que,
simplemente por azar, obtuviésemos un estadístico de
prueba como el calculado. En otras palabras, si la hipótesis
nula fuese cierta, e hiciésemos el mismo experimento
muchas veces, ¿con qué frecuencia obtendríamos un valor
del estadístico de prueba mayor que el que hemos calculado? La respuesta proviene de una distribución de referencia. Ésta es una función matemática que especifica la
probabilidad, bajo la hipótesis nula, de todos los posibles
valores del estadístico de prueba. A menudo, es posible
mirar la respuesta en una tabla de valores estadísticos en un
libro, o tener una computadora que la calcule. Para los
datos y el estadístico prueba de Greene et al., la probabilidad de obtener por azar un valor tan grande del estadístico prueba es considerablemente menor que 0,01. En
otras palabras, si la hipótesis nula fuese cierta, y si Greene
et al. hubiesen repetido el experimento muchas veces,
hubiesen obtenido un valor del estadístico prueba mayor
que el observado en menos de 1 en 100 experimentos.
Esto significa que la hipótesis nula es probablemente falsa,
y que existe una diferencia significativa en cómo responden
las arañas saltarinas ante moscas que agitan alas marcadas y
sin marcar.
El cuarto paso, y último, es decidir si consideramos el
resultado del experimento estadísticamente significativo o
no. Por convenio, los científicos consideran generalmente
el valor de un estadístico prueba significativo si su probabilidad bajo la hipótesis nula es menor de 1 en 20, ó 0,05.
Mediante este criterio, los resultados de Greene et al. son
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 261
CUADRO 8.1 Continuación
de sobra significativos. En otras palabras, cuando Greene y
sus colegas afirmaron que habían demostrado que las moscas tenían que tener marcas en sus alas para evitar el ataque de las arañas saltarinas, asumían una probabilidad de
menos de 1 en cada 100 de que alguien que pudiera repetir sus experimentos demostrase posteriormente que estaban equivocados. Esta probabilidad era lo suficientemente
pequeña para ellos como para afirmar que su resultado es
estadísticamente significativo. Si hay un 5% o más de probabilidad que las diferencias observadas se deban al azar se
acepta, por convenio, la hipótesis nula de que no hay diferencias reales entre grupos.
En los artículos científicos, la probabilidad de encontrar
la diferencia observada por azar se representa como un
valor P, donde P significa probabilidad. En el artículo original publicado por Greene et al., por ejemplo, la imagen
que está representada en nuestra Figura 8.6 incluye la frase
“P < 0,01”.
Las pruebas estadísticas se basan en modelos explícitos de
los procesos que generan los datos y del diseño de los experimentos. Muchos tipos diferentes de procesos aleatorios se
modelan estadísticamente. Cuando analicemos datos, es
necesario conocer suficiente estadística como para elegir el
modelo apropiado a los datos recogidos en un estudio.
trolados para contrastar hipótesis alternativas sobre por qué las jirafas tienen el cuello
largo. Para hacer esto, deberíamos ser capaces de crear jirafas que fuesen idénticas en
todos los aspectos excepto en la longitud de sus cuellos. Los experimentos pueden ser
también inapropiados cuando las hipótesis hacen predicciones sobre cómo los organismos se comportarían en la naturaleza. Cuando los experimentos son imposibles o
inapropiados, la observación cuidadosa puede, a veces, generar suficiente información
para evaluar hipótesis.
Comportamiento de termorregulación
La inmensa mayoría de los organismos son poiquilitermos, lo que significa que la
temperatura de su cuerpo está determinada por la temperatura del ambiente. Como la
Figura 8.8 demuestra para las iguanas del desierto (Dipsosaurus dorsalis), la temperatura del
cuerpo tiene un importante efecto en el rendimiento fisiológico de un poiquilitermo. La
iguana del desierto puede sobrevivir a cortas exposiciones a temperaturas corporales tan
bajas como los 0ºC y tan altas como los 47ºC, pero únicamente pueden funcionar entre
los 15ºC y los 45ºC. Dentro de este estrecho margen, las iguanas frías corren y digieren
lentamente, se cansan rápidamente y oyen pobremente.A medida que se van calentando,
corren y digieren más rápidamente, se cansan menos y su oído es más fino. Las capacida-
Resistencia
Velocidad de arranque
Eficiencia digestiva
Eficiencia auditiva
Figura 8.8 Capacidades fisiológicas de la iguana del desierto
(Dipsosaurus dorsalis) en función de la temperatura corporal
20
0,4
15
0,2
TCmáx
0,6
10
0
0 10
20
30
40
Temperatura corporal (ºC)
50
0
Número
0,8
TCmin
Rendimiento relativo
1,0
Los cuadros y círculos coloreados muestran la resistencia locomotora,
velocidad de arranque (aceleración), eficiencia digestiva y capacidad de
audición de las iguanas en función de la temperatura corporal. La
región sombreada es un histograma que muestra la distribución de las
temperaturas corporales de iguanas capturadas en la naturaleza. La
flecha negra indica la temperatura corporal medida en iguanas en el
laboratorio. TCmáx es la temperatura crítica máxima, esto es, la
temperatura letal máxima. TCmin es la temperatura crítica mínima.
Reimpreso de Huey y Kingsolver (1989). Copyright © 1989, Elsevier
Science. Reimpreso con permiso de Elsevier Science.
262 PARTE III Adaptación
des fisiológicas de las iguanas alcanzan su máximo entre los 35ºC y los 40ºC. Por encima
de los 45ºC, están demasiado calientes y se colapsan.
La relación entre el rendimiento fisiológico y la temperatura es conocida como la curva
de rendimiento térmico. La forma de la curva de rendimiento térmico de la iguana del
desierto es la típica de una variedad de procesos fisiológicos en una gran diversidad de
organismos. Dada la sensibilidad de las funciones fisiológicas a la temperatura, podemos
predecir que los poiquilitermos mostrarán un comportamiento de termorregulación.
Esto es, deberán moverse por su entorno de modo que se mantengan a sí mismos cerca
de la temperatura a la que mejor funcionan.
Como la temperatura de su ambiente cambia, las iguanas del desierto por ejemplo, no
aceptan pasivamente las consecuencias. Por el contrario, regulan su temperatura corporal
moviéndose hacia el Sol para calentarse o hacia la sombra para enfriarse. Las iguanas prefieren mantener su temperatura corporal por encima de los 35ºC (Figura 8.8, flecha). Este
es el centro del rango de temperaturas en el que las iguanas funcionan mejor. La temperatura favorita de las iguanas no es sorprendente. Al fin y al cabo, una iguana nunca sabe
cuando querrá perseguir algo para comer, o necesitará huir de un depredador. Por supuesto, en la naturaleza, las iguanas pueden no tener siempre un rango de temperaturas
ambientales suficiente por el que moverse y mantenerse exactamente a su temperatura
favorita. No obstante, como se muestra en el histograma sombreado de temperaturas corporales tomadas en el campo (Figura 8.8), las iguanas lo hacen razonablemente bien.
Nótese que aunque hayamos afirmado que las iguanas del desierto se termorregulan,
el mero hecho de que iguanas capturadas en la naturaleza estén, habitualmente, en o cerca
de su temperatura corporal óptima no prueba, en sí mismo, que ellas mismas mantengan
su temperatura de un modo activo. Podría ser que el ambiente en el que viven estuviese
siempre sobre los 35-40ºC. Para demostrar el comportamiento de termorregulación,
debemos demostrar (1) que el animal en cuestión elige ciertas temperaturas con mayor frecuencia que las que encontraría simplemente moviéndose al azar por su entorno y (2) que
esta elección de temperaturas es adaptativa.
¿Las serpientes de liga hacen elecciones adaptativas cuando buscan
un lugar de descanso nocturno?
Ray Huey y sus colegas (1989b) hicieron un estudio detallado del comportamiento de
termorregulación de la serpiente de liga (Thamnophis elegans) del lago Eagle, California. Las
serpientes de liga están afectadas por la temperatura del mismo modo que las iguanas del desierto, excepto en que para las serpientes la temperatura óptima, preferida, y máxima de supervivencia son todas algunos grados inferiores que las correspondientes de las iguanas. Huey
et al. implantaron quirúrgicamente radio transmisores en miniatura en algunas serpientes.
Cada transmisor implantado emitía una señal de pitidos que permitía a un biólogo con un
receptor de mano y una antena direccional encontrar a la serpiente, incluso cuando ésta estaba escondida bajo una roca o en una madriguera.Además, el transmisor comunicaba la temperatura de la serpiente mediante un cambio en la frecuencia de los pitidos.
Las serpientes de liga, en el laboratorio, prefieren estar a una temperatura entre los 28ºC
y los 32ºC. Huey y sus colegas observaron que en la naturaleza las serpientes hacen un
excelente trabajo termorregulándose en el mismo intervalo. La Figura 8.9 muestra la temperatura corporal de dos de las serpientes implantadas, ambas durante el transcurso de un
período de 24 horas. Ambas serpientes mantuvieron su temperatura dentro o cerca del
rango de preferencia. ¿Cómo hacen las serpientes de liga para termorregularse así de bien?
Las dos serpientes mostradas en la Figura 8.9 pasaron el día bajo o cerca de las rocas. Otras
opciones fueron moverse arriba y abajo en una madriguera o permanecer en la superficie del suelo moviéndose entre el Sol y la sombra constantemente.
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 263
Serpiente 1
29-30 de julio de 1979
(a)
Temperatura (ºC)
60
60
Bajo una roca
Expuesta
50
Serpiente 2
11-12 de julio de 1985
(b)
TCmáx
40
Rango Tp
30
20
Bajo una roca
50
TCmáx
40
Rango Tp
30
20
10 Salida del Sol
Puesta
Sunset
del Sol
TCmin
0
0
3
6
9
12
15
10
TCmin
0
18 21 24
0
3
6
9
12
15
18 21 24
Hora del día
Figura 8.9 Temperatura corporal de las serpientes de liga en la naturaleza (a) La serpiente 1 pasó parte del día debajo de una
roca (puntos y línea rojos) y parte del día al Sol (puntos y línea azul). (b) La serpiente 2 pasó el día entero debajo de una roca. Tp es el
rango de temperaturas preferido, medido en el laboratorio. TCmáx y TCmin se definieron en la Figura 8.8. Ambas serpientes mantuvieron
su temperatura cerca de los 30ºC durante todo el día. De Huey et al. (1989b). Reimpreso con permiso de la American Ecological Society.
Huey y sus colaboradores compararon las ventajas relativas de cada una de estas estrategias termorreguladoras, monitorizando la temperatura ambiental debajo de rocas de
varios tamaños, a varias profundidades en una madriguera y monitorizando la temperatura de un modelo de serpiente dejada en la superficie al Sol o a la sombra (Figura 8.10).
Para una serpiente bajo una roca, el grosor de la roca es crítico. Una serpiente bajo una
roca delgada (Figura 8.10a) podría no solamente quedarse peligrosamente fría durante la
noche, sino que también estaría sobrecalentada durante el día. (Como Huey dice:“La serpiente moriría alrededor de las 11:00, y permanecería muerta hasta casi las 18:00”.) Una
serpiente bajo una roca gruesa (Figura 8.10b) estará a salvo todo el día, pero nunca alcanzará su temperatura favorita. Las rocas de grosor intermedio son perfectas (Figura 8.10c).
Moviéndose bajo una roca de grosor intermedio, una serpiente podría permanecer cerca
de, o dentro de, su rango de temperatura favorito durante todo el día. Una serpiente
moviéndose arriba y abajo en una madriguera se encontrará razonablemente bien (Figura 8.10d), pero podría quedarse más fría por las noches que una serpiente que esté bajo
una roca de grosor intermedio. Finalmente, una serpiente en la superficie puede termorregularse eficientemente durante las horas del día, moviéndose entre el Sol y la sombra,
pero se quedaría peligrosamente fría por la noche (Figura 8.10e). Juntando todas estas
observaciones, parece que las serpientes tienen muchas opciones para termorregularse
durante el día, siempre y cuando eviten rocas demasiado finas o el Sol directo al mediodía. Durante la noche, por el contrario, parece que el mejor lugar para una serpiente es
bajo una roca de grosor intermedio.
La mayoría de las serpientes de liga, de hecho, descansan por las noches bajo rocas. Bajo
la hipótesis del comportamiento de termorregulación, Huey y sus colaboradores predijeron que las serpientes elegirían sus lugares de descanso nocturno adaptativamente. Esto es,
los investigadores predijeron que las serpientes seleccionarían, preferentemente, rocas de
grosor intermedio. Huey et al. contrastaron su predicción comparando la disponibilidad
de rocas de diferentes tamaños en el lago Eagle con el tamaño de las rocas elegidas para
los descansos nocturnos por las serpientes con radiotransmisores (Tabla 8.2). Rocas delgadas, intermedias y gruesas son igualmente abundantes, de modo que si las serpientes eligiesen al azar su lugar de descanso nocturno, deberían encontrarse con igual frecuencia
bajo rocas de todos los tamaños. El hecho es, no obstante, que las serpientes de liga siempre se encuentran bajo rocas intermedias o gruesas. El hecho de que las serpientes eviten
rocas finas es una muy buena evidencia de que las serpientes poseen un activo comportamiento de termorregulación.
Monitorizando las
temperaturas de los sitios
potenciales de descanso, los
investigadores que estudiaban
la termorregulación de las
serpientes de liga mostraron
que el mejor lugar para que
éstas pasasen la noche es
bajo una roca de grosor
intermedio.
264 PARTE III Adaptación
(a) Temperatura bajo una roca delgada
Temperatura (ºC)
60
50
TCmáx
40
30
Rango Tp
20
10
0
(b)
Borde, 4 cm
Centro, 4 cm
0
Temperatura (ºC)
TCmáx
30
Rango Tp
20
10
0
Temperatura (ºC)
3
40
Temperatura (ºC)
TCmin
12 15 18 21 24
30
TCmáx
Rango Tp
20
10
0
3
6
9
TCmin
12 15 18 21 24
Temperatura en una madriguera
2,5 cm
5 cm
15 cm
50 cm
50
TCmáx
40
30
Rango Tp
20
10
0
0
3
6
9
TCmin
12 15 18 21 24
Temperaturas para un modelo en la superficie
60
Temperatura (ºC)
9
Punto D de la roca (30 cm)
Borde Sur
Borde Este
Centro
50
60
donde una serpiente podría ir. (a) Bajo una roca delgada (4 cm), es frío por la noche y
caliente durante el día. (b) Bajo una roca gruesa (43 cm), es frío todo el tiempo. (c) Bajo
una roca de grosor mediano (30 cm), existe siempre un punto dentro del rango de
temperaturas preferido por las serpientes. (d) En una madriguera, se está frío por la
noche y entre fresco y cálido durante el día, con la temperatura exacta dependiendo de
la profundidad en la madriguera. (e) en la superficie, es frío por la noche y entre perfecto
y caliente durante el día, dependiendo de si la serpiente está en la sombra o a la luz
directa del Sol. De Huey et al. (1989b). Reimpreso con el permiso de la American
Ecological Society.
6
Temperatura bajo una roca mediana
0
Figura 8.10 Temperatura ambiental disponible para una serpiente de liga en
el lago Eagle La gráfica muestra el ciclo diario de temperaturas en varios lugares
TCmin
12 15 18 21 24
40
60
(e)
9
Borde, 43 cm
Centro, 43 cm
50
0
(d)
6
Temperatura bajo una roca gruesa
60
(c)
3
Expuesto
Sombreado
50
TCmáx
40
30
Rango Tp
20
10
0
0
3
6
9
TCmin
12 15 18 21 24
Hora del día
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 265
Tabla 8.2 Distribución de las rocas disponibles para las serpientes
y de las elegidas por éstas.
Las rocas finas, intermedias y gruesas son igualmente abundantes en el lago Eagle, pero las
serpientes de liga que descansan bajo una roca por las noches prefieren las rocas de grosor
intermedio (P < 0,05 prueba de chi-cuadrado con las clases delgada y gruesa combinadas
debido a los pequeños tamaños esperados).
Rocas disponibles para las serpientes
Rocas elegidas por las serpientes
Finas
(⬍20 cm)
Intermedias
(20-40 cm)
Gruesas
(⬎40 cm)
32,4%
34,6%
33%
7,7%
61,5%
30,8%
Fuente: de la Tabla 1 de Huey et al. (1989b). Copyright © 1989, Ecological Society of America.
Luego los investigadores
anotaron la disponibilidad de
Lo que hace que el estudio observacional de Huey y sus colegas sea efectivo en contrastar la hipótesis de que las serpientes de liga se termorregulan, es el cuidado con el que
los investigadores monitorizaron el entorno de las serpientes. Determinando las opciones
disponibles para las serpientes, y midiendo la frecuencia de cada opción en el ambiente,
los investigadores pudieron demostrar que las serpientes observadas no elegían el sitio de
descanso al azar, sino que tomaban una decisión adaptativa. En la siguiente sección, consideraremos un tipo de estudios observacionales que buscan adaptaciones en una escala más
amplia. Los biólogos que usan el método comparativo evalúan hipótesis mirando los
patrones de evolución entre distintas especies.
rocas delgadas, intermedias y
gruesas y observaron que las
serpientes elegían rocas
intermedias más
frecuentemente que lo
esperado bajo la hipótesis
nula de que las serpientes
eligen sus lugares de
descanso al azar.
8.4.
El método comparativo
En las Secciones 8.2 y 8.3 hemos considerado cómo pueden usarse experimentos y la
observación de individuos en poblaciones naturales para contrastar hipótesis adaptativas.
Ahora examinaremos cómo la comparación entre especies también puede usarse para el
estudio de la evolución de la forma y la función. Nuestro ejemplo proviene de un grupo
de murciélagos llamados Megachiroptera, el cual incluye a los murciélagos de la fruta y a
las zorros voladores (Figura 8.11a).
¿Por qué algunos murciélagos tienen los testículos
más grandes que otros?
Los machos de algunas de estas especies de murciélagos tienen los testículos más grandes
que otros, en relación al tamaño del cuerpo.Trabajando con una variedad de otros animales, David Hosken (1998) sugirió que los testículos grandes son una adaptación para
la competencia espermática. La competencia espermática ocurre cuando una hembra se
aparea con dos o más machos durante un mismo ciclo menstrual; el esperma de estos
machos participa en una carrera por alcanzar al óvulo. Una manera en la que los machos
pueden aumentar su éxito reproductor desde el punto de vista de la competencia espermática es produciendo eyaculaciones más abundantes. Participando con más esperma en
la carrera, un macho aumenta sus posibilidades de ganarla.Y una manera de producir más
esperma es teniendo testículos mayores.
Para evaluar la hipótesis de la competencia espermática, Hosken necesitaba usarla para
generar una predicción que fuese comprobable. Hosken sabía que los murciélagos de la
fruta y los zorros voladores se posan en grupos y que el tamaño de estos grupos varía enormemente entre especies; desde dos o tres individuos hasta decenas de miles. Hosken razo-
El método comparativo evalúa
hipótesis mediante la
comparación de patrones
entre especies, tales como
correlaciones entre caracteres,
o correlaciones entre los
caracteres y las
características ambientales.
266 PARTE III Adaptación
(a)
volador de cabeza gris (Pteropus
poliocephalus). (Fritz Prenzel/
Animals Animals/Earth Scenes)
(b) Tamaño testicular relativo
(esto es, tamaño de los testículos
corregido por el tamaño del
cuerpo) en función del tamaño
del grupo de nidada para 17
especies de murciélagos de la
fruta y zorros voladores. De
Hosken (1998). Copyright ©
1998, Springer-Verlag GmbH &
Co. KG. Reimpreso con permiso.
Una aplicación correcta del
método comparativo requiere
un conocimiento de las
relaciones evolutivas
existentes entre las especies
estudiadas.
(b)
Valor relativo del logaritmo
de la masa testicular
Figura 8.11 Variación en el
tamaño de los testículos entre
murciélagos de la fruta y
zorros voladores (a) Un zorro
0,4
0,2
0
–0,2
–0,4
–0,6
–0,8
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
Logaritmo del tamaño del grupo social
nó que las hembras que viven en grupos grandes tendrían más oportunidades para apareamientos múltiples y que, por tanto, los machos que vivan en estos grupos experimentarían una mayor competencia espermática. Hosken predijo que si una especie de murciélagos evolucionó en grandes grupos nidificantes, sus machos también habrían
desarrollado testículos desproporcionadamente grandes para su tamaño corporal.
La manera más simple de explorar esta hipótesis es recopilar datos de diferentes especies, y organizarlos en un eje de coordenadas que mostrase el tamaño relativo de los testículos en función del tamaño de la nidada. Cuando Hosken hizo esto, encontró que ambas
variables estaban fuertemente correlacionadas (Figura 8.11b). Las especies de murciélagos
que viven en grandes grupos tienen los testículos grandes en comparación con su tamaño corporal. No obstante, como Hosken sabía, podría haber menos evidencia en esta gráfica de lo que parece a simple vista.
La Figura 8.12 ilustra el porqué. Imagine, por ejemplo, que hubiésemos dibujado esta
gráfica únicamente para seis especies. Llamemos a estas especies A, B, C, D, E y F. La Figura 8.12a muestra una representación del tamaño relativo de los testículos respecto del tamaño del grupo. Al igual que en la gráfica real de la Figura 8.11, ésta también muestra una
correlación positiva entre ambas variables. Ahora imaginemos que la relación evolutiva
existente entre estas seis especies es la que refleja la filogenia de la Figura 8.12b: las especies A, B y C están estrechamente relacionadas entre ellas, como lo están las D, E y F. Podría
ser que las especies A, B y C hubiesen heredado sus pequeños testículos y su afición a anidar en pequeños grupos de su antepasado común (flecha verde). De la misma manera,
podría ser que las especies D, E y F hubiesen heredado sus grandes testículos y su preferencia por anidar en grandes grupos a partir de su antepasado (flecha naranja). La posibilidad de que nuestras seis especies hubiesen heredado estos caracteres a partir de únicamente dos ancestros comunes reduce, considerablemente, el peso de nuestra evidencia.
Cuando preparamos un diagrama de dispersión y lo empleamos como base para nuestras afirmaciones sobre la naturaleza, queremos que todos nuestros datos sean independientes entre sí. Si lo son, entonces cada punto nos dice algo a favor o en contra de nuestras
afirmaciones. Más aún, la independencia de los datos es uno de los requerimientos fundamentales de las pruebas estadísticas. Para asegurarnos de que nuestro diagrama de
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 267
(b)
A
B
C
D
E
F
G
H
I
Tamaño testicular relativo
(a)
D
B
E
Tamaño testicular
relativo
(a)
E
F
D
C
B
A
Tamaño del grupo
(b)
A
B C
D
E
F
(c)
Tamaño testicular
relativo
dispersión refleja fielmente la naturaleza de las evidencias, deberíamos reemplazar los
puntos de las especies A, B y C por solamente uno que representase a su ancestro común,
y lo mismo deberíamos hacer para las especies D, E y F.
La gráfica de la Figura 8.12c muestra este resultado. Podría ser, de hecho, que el tamaño de la nidada y el tamaño de los testículos hayan evolucionado conjuntamente, y podría
ser cierto que la competencia espermática sólo fuese la razón. No obstante, un diagrama
de dispersión con únicamente dos puntos es una evidencia débil con la que sustentar
semejante afirmación.
Joe Felsenstein (1985) desarrolló un método mejor para evaluar correlaciones entre
caracteres entre especies. Lo que vemos con el método de Felsenstein son patrones de
divergencia a medida que especies hermanas evolucionan independientemente a partir de
su ancestro común. La Figura 8.13 muestra una interpretación gráfica de la aproximación
básica del método.
Lo primero que necesitamos es una filogenia de las especies que estamos estudiando.
La Figura 8.13a muestra una filogenia para cinco supuestas especies. Llamaremos a estas
especies A-E. La filogenia también incluye a los ancestros comunes que existieron en todos
los nodos del árbol. Éstas son las especies F-I. Nótese que hay cuatro puntos en esta filogenia donde especies hermanas divergieron a partir de un ancestro común, representado
cada uno por un color diferente. Por ejemplo,A y B son especies hermanas que divergieron a partir de un ancestro G. De igual manera, G y C son especies hermanas que divergieron de un ancestro común H. Lo que queremos saber es: cuando las especies divergen
desde un ancestro común, ¿las especies que han evolucionado testículos más grandes han
evolucionado también una preferencia por nidadas mayores?
Para poder responder a esta pregunta, en primer lugar, dibujaremos en un diagrama de
dispersión todos los pares de especies conectados mediante líneas (Figura 8.13b). A continuación cogeremos cada línea por su extremo más próximo al eje vertical y trasladaremos estos puntos hasta el origen (Figura 8.13c). Finalmente, eliminaremos los puntos del
origen y las líneas de conexión. Nos hemos quedado con un diagrama de dispersión con
únicamente cuatro puntos (Figura 8.13d). Cada punto representa la divergencia, o contraste, que surgió entre un par de especies a medida que evolucionaron a partir de un
Tamaño del grupo
Figura 8.12 Un diagrama de
dispersión simple puede
proporcionar sólo evidencias
débiles de que dos caracteres
evolucionan conjuntamente
Ver el texto para una explicación.
A partir de la Figura A en Lauder
et al. (1995). Reimpreso con
permiso del American Institute of
Biological Sciences y de los
autores.
G
A
H
C
F
Tamaño del grupo
(d)
Contraste para el tamaño
del grupo
Contraste para el tamaño
testicular relativo
(c)
Tamaño del grupo
Tamaño del grupo
Figura 8.13 Interpretación gráfica del procedimiento
básico del método de Felsenstein para evaluar
contrastes independientes filogenéticamente Ver el
texto para una explicación.
268 PARTE III Adaptación
Acerodon mackloti
Pteropus giganteus
Pteropus tonganus
Pteropus poliocephalus
Pteropus alecto
Pteropus scapulatus
Dobsonia peroni
Eidolon helvum
Rousettus aegyptiacus
Rousettus amplexicaudatus
Macroglossus minimus
Macroglossus sobrinus
Eonycteris spelaea
Epomops buettikoferi
Epomophorus anurus
Micropteropus pusillus
Cynopterus sphinx
(b)
Residual del contraste para
la masa testicular
(a)
0,3
0,2
0,1
0
–0,1
–0,2
–0,3
–0,4
–1,5
–1
–0,5
0
0,5
1
1,5
Contraste para el tamaño del grupo
Figura 8.14 Evolución correlacionada del tamaño del grupo y del tamaño testicular en los
murciélagos de la fruta y los zorros voladores (a) Filogenia para 17 especies de murciélagos. (b) Contrastes
independientes para el tamaño testicular relativo versus el tamaño del grupo. Los puntos en la gráfica muestran
que cuando una especie de murciélagos evolucionó un tamaño de grupo mayor (o menor) que sus especies
hermanas, también tendió a evolucionar testículos mayores (o menores) (P = 0,027). De Hosken (1998). Copyright
© 1998, Springer-Verlag GMBH & Co. Reimpreso con permiso.
Cuando formulan y contrastan
hipótesis sobre la adaptación,
los biólogos deben mantener
en mente que los organismos,
y las vidas que éstos viven,
son complejos.
ancestro común. Si los contrastes están correlacionados entre ellos, entonces concluiremos
que cuando una especie evolucionó a un tamaño de nidada mayor que su especie hermana, también tendía a tener testículos mayores. En la práctica, deberemos hacer algunos
reajustes de los datos antes de calcular las pruebas estadísticas que evalúen la consistencia
de los patrones. Estos reajustes se describen en el Cuadro 8.2.
Hosken (1998) repitió su análisis del tamaño de los testículos y de la nidada de los
murciélagos empleando el método de Felsenstein, conocido como el método de los contrastes filogenéticamente independientes. La Figura 8.14a muestra la filogenia de las 17
especies de murciélagos cuyos datos se presentaron en la Figura 8.11b. La Figura 8.14b
muestra una gráfica de los contrastes del tamaño relativo de los testículos frente a los contrastes del tamaño de las nidadas. Existe una correlación positiva significativa entre ambos
contrastes. En otras palabras, los datos indican que cuando una especie de murciélagos
evolucionó una preferencia por anidar en grupos más grandes que su especie hermana,
también evolucionó un tamaño testicular grande. Hosken concluyó que las evidencias
obtenidas a partir de las zorros voladores y de los murciélagos de la fruta eran consistentes
con la hipótesis de que los testículos grandes eran una adaptación para la competencia
espermática.
Hemos considerado hasta ahora tres métodos que los biólogos evolutivos emplean para
evaluar hipótesis alternativas sobre la adaptación. En lo que queda del capítulo, nos centraremos en las complejidades de la forma y la función de los organismos, áreas muy activas de investigación hoy día. En los ejemplos que discutiremos, los investigadores usan
experimentos, estudios observacionales y el método comparativo para investigar hipótesis sobre la plasticidad fenotípica (Sección 8.5), el origen evolutivo de caracteres adaptativos (Sección 8.6), y compromisos y restricciones en la adaptación (Sección 8.7).
8.5.
Plasticidad fenotípica
A lo largo de este libro, hemos tratado los fenotipos como si estuviesen determinados única
y exclusivamente por los genotipos. Sabemos, no obstante, que los fenotipos están también, y muy frecuentemente, influenciados por el ambiente. El Capítulo 7 incluía una sección sobre como estimar cuánta de la variación fenotípica entre individuos era debida a
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 269
CUADRO 8.2 Calculando contrastes filogenéticamente independientes
V
amos a usar un ejemplo de Garland y Adoph (1994)
para ilustrar el cálculo de contrastes independientes a
partir de una filogenia (veáse también: Felsenstein 1985;
Martins y Garland 1991; Garland et al. 1999). La Figura 8.15
muestra la filogenia que utilizaremos. Muestra la relación
entre los osos polares, los osos grizzly y los osos negros y
nos da la masa corporal y el tamaño del territorio de cada
uno de ellos. Calcularemos los contrastes independientes
para cada carácter entre los osos. Los pasos a seguir son:
1. Calcular los contrastes para los pares de especies hermanas en los extremos de la filogenia. En nuestro árbol
de tres especies, hay solamente un par de especies hermanas: los osos polares y los osos grizzly. El contraste
para la masa corporal es:
265 ⫺ 251 ⫽ 14
El contraste oso polar-grizzly para el tamaño del territorio es:
116 ⫺ 83 ⫽ 33
2. Extraer cada par contrastado del árbol y estimar los
valores de los parámetros para su ancestro común
Tamaño
Masa
del
corporal territorio
(Kg)
(Km2)
Longitud de las ramas
(en millones de años)
2
3
Oso polar
265
116
Oso grizzly
251
83
A
tomando para ello la media ponderada de los fenotipos
de los descendientes. Cuando calcule la media ponderada, pondere cada especie por la inversa de la longitud de la rama que le conecta con su ancestro. En
nuestro ejemplo, estamos extrayendo los osos polares y
grizzly del árbol, y estimando la masa corporal y el
tamaño del territorio de su ancestro común A. La longitud de las ramas desde A hasta sus descendientes son
ambas de dos unidades.Así, la media ponderada para la
masa es:
()
()
() ()
1
ᎏᎏ 265 ⫹
2
Masa corporal de la
especie A ⫽
1
ᎏᎏ ⫹
2
1
ᎏᎏ 251
2
⫽ 258
1
ᎏᎏ
2
La media ponderada para el tamaño del territorio es
() ()
() ()
1
ᎏᎏ 116 ⫹
2
Tamaño del territorio de la
especie A ⫽
1
ᎏᎏ ⫹
2
1
ᎏᎏ 83
2
⫽ 99,5
1
ᎏᎏ
2
3. Alargue la longitud de las ramas que conducen al
ancestro común de cada par extraído añadiéndole el
producto de las longitudes de las ramas del ancestro
común a sus descendientes dividido por su suma. En
nuestro ejemplo, alargaremos la rama que lleva hacia la
especie A. La nueva longitud será:
2⫻2
3 ⫹ ᎏᎏ ⫽ 4
2⫹2
B
5
Oso negro
93
Contraste
estandarizado
Contraste
Valor para la
masa corporal
Desviación
estándar
Polar-Grizzly
A-Oso negro
265 – 251 = 14
258 – 93 = 165
2
3
Contraste
Polar-Grizzly
A-Oso negro
Valor para el tamaño
del territorio
116 – 83 = 33
99,5 – 57 = 42,5
Desviación
estándar
2
3
57
7
55
Contraste
estandarizado
16,5
14,17
Figura 8.15 Ejemplo mostrando cómo se ajustan
los datos cuando se calculan contrastes filogenéticamente
independientes De Garland y Adolph (1994). Copyright © 1994,
Physiological Zoology. Reimpreso con permiso de The University of
Chicago Press.
4. Continúe hacia la raíz del árbol calculando los contrastes, estimando los fenotipos de los ancestros comunes y alargando las longitudes de las ramas que
conducen a los ancestros comunes. En nuestro ejemplo,
el único contraste que queda es entre la especie A y el
oso negro. No necesitamos estimar el fenotipo de la
especie B, o la longitud de la rama que conduce a ella
por que la especie B es la raíz del árbol. El contraste
para la especies A-oso negro para la masa corporal es:
258 ⫺ 93 ⫽ 165
El contraste para la especie A-oso negro para el tamaño del territorio es:
99,5 ⫺ 57 ⫽ 42.5
5. Divida cada contraste por su desviación típica para
generar los contrastes tipificados. La desviación típica de
270 PARTE III Adaptación
CUADRO 2.1
Continuación
un contraste es la raíz cuadrada de la suma de las longitudes (ajustadas) de sus ramas. La desviación típica
para el contraste oso polar-grizzly es:
苶苶
⫹苶2 ⫽ 2
兹2
La desviación típica para el contraste entre especie Aoso negro es:
Individuos genéticamente
idénticos criados en
ambientes diferentes pueden
diferir en la forma, fisiología o
comportamiento. Estos
individuos mostrarían
plasticidad fenotípica.
苶苶
⫹苶5 ⫽ 3
兹4
Los contrastes típicos para nuestro ejemplo se dan en la
Figura 8.15.
Una vez se han calculado los contrastes tipificados,
podemos usarlos para preparar un diagrama de dispersión
y calcular las pruebas estadísticas tradicionales.
variación entre genotipos y cuánta debida a variación ambiental. Aquí, nos concentraremos en la interrelación entre genotipo, ambiente y fenotipo.
Otra manera de decir que el fenotipo de un individuo está influenciado por el ambiente es decir que éste es plástico. Cuando los fenotipos son plásticos, individuos con el mismo
genotipo pueden presentar diferentes fenotipos si viven en diferentes ambientes. La plasticidad fenotípica es en sí misma un carácter que puede evolucionar y que puede o no ser
adaptativo.Al igual que con los otros caracteres que hemos estudiado, para demostrar que
un ejemplo de plasticidad fenotípica es adaptativo, primero hemos de determinar para qué
sirve y después demostrar que los individuos que la poseen tienen una eficacia mayor
que aquellos que carecen de ella.
Plasticidad fenotípica en el comportamiento de las pulgas de agua
Figura 8.16 Pulga de agua,
Daphnia sp. Los apéndices
largos ramificados son antenas
que las pulgas usan para nadar
como si se tratase de remos. El
objeto negro cerca de las antenas
es la mancha ocular. También
visibles, a través del caparazón
transparente del individuo, están
los intestinos y otros órganos
internos. Esta fotografía se ha
ampliado 10 veces.
(Omikron/Photo Research, Inc.)
Para ilustrar la plasticidad fenotípica, usaremos a la pulga de agua, Daphnia magna. Daphnia magna es un pequeño crustáceo que vive en lagos de agua dulce (Figura 8.16). Una
gran ventaja para los biólogos evolutivos es que Daphnia se reproduzca asexualmente la
mayor parte del tiempo; esto hace de ella un organismo ideal para estudiar la plasticidad
fenotípica, ya que los investigadores pueden criar individuos genéticamente idénticos en
ambientes diferentes y comparar sus fenotipos.
Luc De Meester (1996) estudió la plasticidad fenotípica de la fototaxis de D. magna. Un
individuo muestra fototaxia positiva si nada hacia la luz y negativa si huye de ella. De
Meester midió el comportamiento fototáctico de genotipos diferentes de D. magna. En
cada experimento, De Meester colocó 10 individuos genéticamente idénticos en una probeta, la iluminó desde arriba, y después de darles cierto tiempo para que se aclimatasen a
su nuevo ambiente, observó hacia dónde nadaban en la columna de agua. De Meester
resumió sus resultados calculando un índice de fototaxis. El índice tomaba valores entre
–1 y +1. Un valor de –1 significa que todas las Daphnia del experimento nadaron hacia
abajo en la columna, huyendo de la luz. Un valor de +1 indica que todas las Daphnia del
experimento nadaron hacia arriba en la columna, hacia la luz. Un valor intermedio indicaba un resultado heterogéneo.
De Meester midió el comportamiento fototáctico de 10 genotipos de Daphnia (también llamados clones) procedentes de tres lagos. Los resultados se indican mediante puntos azules en la Figura 8.17. La población de cada lago contenía considerable variabilidad
genética para el comportamiento fototáctico.
De Meester también midió el comportamiento fototáctico de los mismos 30 genotipos de Daphnia en agua que había sido previamente ocupada por un pez. Los resultados
de este segundo experimento se indican con puntos rojos en la Figura 8.17. El comportamiento fototáctico de Daphnia magna es fenotípicamente plástico. En particular, en el lago
Blankaart, la mayoría de los genotipos de Daphnia mostraban índices considerablemente
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 271
1,0
Blankaart
Driehoekvijver
Citadelpark
Fototaxis (l)
0,6
0,2
Control
Inducido por un pez
-0,2
-0,6
-1,0
Clon-tratamiento
Figura 8.17 Variación en la fototaxis de Daphnia magna Blankaart, Driehoekvijver y Citadelpark son
tres lagunas belgas. Cada punto azul representa la media de entre tres y cinco experimentos de la fototaxis de
genotipos individuales (descritos en el texto principal). Las barras de error representan ⫾2 errores estándares.
Aquellos genotipos (clones) cuyas barras de error no solapan son significativamente distintos. Arriba o debajo
de cada punto azul hay un cuadrado rojo. Este cuadrado rojo representa la media de los resultados de entre
tres y cuatro pruebas de la fototaxis del mismo genotipo. La diferencia entre ambos experimentos es que en
el segundo las Daphnia se probaron en agua que había sido ocupada con anterioridad por un pez. En el lago
Blankaart viven numerosos peces, el lago Driehoekvijver tiene pocos, mientras que en el lago Ditadelpark no
hay. De De Meester (1996). Copyright © 1996, Evolution. Reimpreso con permiso de Evolution.
menores cuando el experimento se hacía en presencia de substancias químicas liberadas
por el pez.
Finalmente, y más importante, los resultados de De Meester demuestran que la plasticidad fenotípica es un carácter que puede evolucionar. Recuerde que un carácter puede
evolucionar en una población únicamente si la población contiene variabilidad genética
para dicho carácter. Cada una de las poblaciones de Daphnia que De Meester estudió contenía variabilidad genética para el carácter plasticidad fenotípica. Esto es, en cada población, algunos genotipos cambiaban su comportamiento más que otros en presencia o en
ausencia del pez (Figura 8.17). La variación genética para la plasticidad fenotípica se llama
interacción genotipo-ambiente.
¿Ha evolucionado la plasticidad fenotípica en las poblaciones de Daphnia que De
Meester estudió? Lo ha hecho. El genotipo promedio en el lago Blankaart muestra considerablemente más plasticidad fenotípica que el genotipo promedio en cualquier otro lago.
El Blankaart es el único de los lagos con una considerable población de peces. Los peces
son predadores visuales, y comen Daphnia. Una interpretación razonable es que la presencia de peces seleccionó Daphnia que evitaba las zonas bien iluminadas en las que los
peces estaban presentes.
8.6. Cada carácter adaptativo evolucionó a partir
de algo distinto
Cuando se estudia la forma y función de los organismos, es conveniente recordar que cada
carácter adaptativo evolucionó a partir de algo distinto. Nuestro ejemplo sobre la investigación del origen de las estructuras adaptativas proviene del oído de los mamíferos.
Cuando existe variabilidad
genética para el grado o el
patrón de plasticidad
fenotípica, la plasticidad
misma puede evolucionar. La
plasticidad es adaptativa
cuando permite a los
individuos ajustar sus
fenotipos de modo que
aumenten su eficacia en el
ambiente particular en el que
se encuentran.
Cada carácter adaptativo
evolucionó a partir de algo
diferente. Ésta es una razón
por la que, en ocasiones,
órganos y organismos parecen
montados a partir de un
¿Cómo evolucionó el oído de los mamíferos?
conjunto de piezas de
Una de las características más fantásticas del oído de los mamíferos es un conjunto de tres
huesos llamados martillo, yunque y estribo. Su función es transmitir la energía de la
vibración de la membrana del tímpano, en el oído externo, hasta la ventana oval de la clo-
repuesto, ninguna de las
cuales encaja perfectamente
en su función.
272 PARTE III Adaptación
Cráneo
Martillo
Yunque
Estribo
Trompa de
Eustaquio
Figura 8.18 El oído medio de los mamíferos Este dibujo del
oído humano muestra la localización de los tres huesecillos: el martillo,
el yunque y el estribo.
Ventana oval
(detrás del estribo)
Membrana
timpánica
quea en el oído interno (Figura 8.18). ¿Por qué tener tres huesos en lugar de uno sólo?
Su acción de palanca amplifica la fuerza transmitida, aumentado así la sensibilidad del oído.
La reducción de treinta veces en la superficie de transmisión, desde la gran membrana timpánica hasta la pequeña ventana oval, también sirve para amplificar la señal. Estos huesecillos son la causa principal por la que los mamíferos oyen tan bien.
Pero, ¿de dónde se originaron estos huesecillos por primera vez? Para saber esto necesitaremos:
1. Establecer la condición ancestral.
2. Entender la secuencia de transformaciones, o cómo y por qué los caracteres cambiaron
a lo largo del tiempo.
Si podemos dar estos pasos, entenderemos los mecanismos primeros y últimos del cambio evolutivo que produjo un órgano manifiestamente adaptativo.
El punto lógico para comenzar nuestro análisis es un animal llamado Acanthostega gunnari (Figura 8.19). Esta criatura es uno de los tetrápodos, o vertebrados con cuatro extremidades, más antiguos conocidos. Acanthostega, un habitante de las ciénagas, que respiraba
aire parcialmente, fue uno de los primeros animales en encontrarse con el problema de
oír sonidos en el aire. Acanthostega vivió hace aproximadamente 360 millones de años.
Figura 8.19 Un tetrápodo primitivo Ésta es una reconstrucción de un Acanthostega gunnari, recuperado
de depósitos del Devónico tardío en el este de Groenlandia. Acanthostega se encuentra entre los tetrápodos más
antiguos encontrados. Los tetrápodos (literalmente, “los de cuatro patas”) son un grupo taxonómico que
incluye a los anfibios, reptiles y mamíferos. Los primeros tetrápodos fueron los primeros vertebrados que
habitaron la tierra firme. El tipo de rocas en el que se encuentran los fósiles de Acanthostega indican que el
animal vivó en ambientes pantanosos. Impresiones en el fósil indican que, probablemente, tuviese tanto
pulmones como branquias internas (ver Coates y Clack 1991).
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 273
Sus antecesores pertenecían a un grupo de peces llamados crosopterigios (Carroll 1998).
Aunque los peces crosopterigios no tenían ninguno de los tres huesecillos del oído, Acanthostega tenía un estribo. El estribo fue el primero de los huesos del oído medio en aparecer en el registro fósil (Clack 1989), y puede que sirviese para detectar sonidos en el
aire.
¿Cuál es la evidencia para esta afirmación? Cráneos fosilizados muestran que uno de
los extremos del estribo de Acanthostega encaja en un hueco en el lado de la cavidad cerebral que conecta con el oído interno, mientras que el otro encaja en una muesca en el
cráneo cerca de una abertura llamada espiráculo (Clack 1994). En fósiles posteriores de
tetrápodos y en algunos anfibios actuales, esta muesca del cráneo sujeta la membrana timpánica (Figura 8.20a).Ya que la forma del estribo es homóloga en Acanthostega y en grupos posteriores, podemos argumentar que su función, transmitir el sonido transportado por
el aire, es homóloga también (Lombard y Bolt 1979; Clack 1983).
(a)
Anfibios
Cerebro
Membrana
timpánica
Oído
interno
Estribo
Trompa de
Eustaquio
Garganta
(b)
Peces
Cerebro
Espiráculo
Oído
interno
Hiomandíbula
Garganta
(c)
Reptiles
Cerebro
Oído
interno
Membrana
timpánica
Estribo
Cuadrado
Garganta
Trompa de
Eustaquio
Articular
Figura 8.20 La localización de los estribos en
varios vertebrados Cada una de las ilustraciones es
una sección transversal de la cabeza, mostrando la
localización y forma de los huesos y otras estructuras
discutidas en el texto. Modificado de Romer, A. S.
1995. The Vertebrate Body. Filadelfia: W.B. Saunders.
274 PARTE III Adaptación
Pero, ¿aparecieron los estribos de la nada? ¿Cómo podemos determinar el estado ancestral de esta novedad evolutiva? Éste es un problema general en el análisis paleontológico.
Recuerde que en el Capítulo 3 revisamos la propuesta de que el “pulgar” del panda gigante evolucionó a partir de un hueso alargado de la muñeca. ¿Cuál es la evidencia para una
afirmación como ésta?
La clave para entender el origen de un carácter derivado es establecer una homología
con un carácter presente en el ancestro. Por ejemplo, en forma y posición, los estribos de
Acanthostega son homólogos con una estructura presente en los crosopterigios y otros peces
llamada hiomandíbula. La hiomandíbula es un hueso que funciona como abrazadera entre
la mandíbula y la caja craneal (Figura 8.20b). Músculos anclados a este hueso inflan las
mejillas. Esta acción de bombeo, de hecho, ventila las branquias y abre y cierra el espiráculo. En los peces pulmonados modernos, la acción de bombeo ventila con aire a los
pulmones. Dado que los fósiles indican que Acanthostega tenía tanto pulmones como
branquias internas, es razonable inducir que los músculos anclados a sus estribos estaban
implicados en la respiración (Clack 1989; Coates and Clack 1991; Clack 1994).
Todos estos hechos hacen de Acanthostega un clásico ejemplo de forma de transición.
Es decir, se trata de un intermedio entre los peces y los tetrápodos (anfibios, reptiles y
mamíferos). Sus estribos eran una modificación de la hiomandíbula que aún funcionaba
en la respiración. Pero era también un hueso que estaba en el lugar adecuado (anatómicamente) y en el momento justo (cuando los vertebrados se aventuraron por primera vez
fuera del agua) para ser utilizado como un transmisor del sonido. La hiomandíbula fue una
preadaptación para oír.
Además de la similitud en la forma y la posición de ambos huesos en Acanthostega y los
peces, hay una segunda línea de evidencias de que el estribo es homólogo a la hiomandíbula. En 1837, mucho antes de que Darwin estableciese una interpretación evolutiva para
las homologías, el anatomista alemán C. B. Reichert examinó embriones de mamíferos y
determinó que, durante el desarrollo, el estribo se originaba a partir del segundo arco branquial (ver Gould 1993, ensayo 6). En los peces, esta misma estructura embrionaria da lugar
a la hiomandíbula. Estas homologías del desarrollo son, exactamente, lo que predeciríamos
si ambas estructuras representasen estados ancestrales y derivados. En combinación con los
datos morfológicos en adultos, tenemos una fuerte evidencia de que ambas estructuras
comparten ancestralidad.
Hasta aquí, hemos sido capaces de establecer el origen embriológico y las condiciones
de ancestralidad de los estribos. Pero, ¿qué pasa con los otros huesecillos del oído, el
martillo y el yunque? Acanthostega no los tiene. Ni tampoco los reptiles ni los anfibios,
incluidas las formas ancestrales extintas de los mamíferos (Allin 1975).Todos estos grupos
transmiten el sonido de la membrana timpánica al oído interno directamente a través de
los estribos (Figuras 8.20a y c).
El martillo y el yunque aparecen por primera vez en los mamíferos fósiles, pero ¿de
dónde? ¿Dónde encontramos el martillo y el yunque en los antecesores de los mamíferos? En posición, son homólogos a dos huesos de la mandíbula (llamados articular y cuadrado) que encontramos en reptiles, anfibios y los primeros mamíferos. De hecho, el martillo, yunque y estribo de los mamíferos actuales aún se desarrollan, como tejidos
embrionarios, exactamente en las mismas posiciones en las que los encontramos en fósiles de adultos del grupo ancestral a los mamíferos.
Durante el desarrollo, el martillo y el yunque también se originan a partir de la estructura de la mandíbula. En los primeros estadios de los embriones de los mamíferos, las células destinadas a convertirse en martillo y yunque derivan del primer arco branquial. En
peces mandibulados, este arco branquial produce las mandíbulas inferior y superior. En
embriones de mamíferos, estas células crean una estructura llamada cartílago de Meckel,
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 275
que forma la mandíbula inferior. El martillo se forma en la parte posterior del cartílago
de Meckel para luego separarse; el yunque se forma a partir de una estructura próxima
(Allin 1975). Una vez más, tenemos fuertes evidencias de homología.
Esto nos lleva al segundo punto de nuestro análisis: examinar cómo el martillo y el yunque cambiaron con el tiempo. ¿Cómo se transformaron unos huesos de la mandíbula en
los huesecillos del oído? Es lógico comenzar donde los dejamos: con los ancestros de los
mamíferos. Éste es un grupo llamado cynodontidos. En los cynodontidos (como en los
modernos anfibios, reptiles y aves), la unión de la mandíbula está constituida por el cuadrado y el articular; el estribo es el único hueso directamente relacionado con la audición.
Los estribos de los cynodontidos, no obstante, sucede que están próximos al articular (Allin
1975). Examinando los fósiles de los cynodontidos a lo largo del tiempo se observan los
siguientes cambios en la mandíbula:
• La parte de la mandíbula inferior próxima a la articulación se hace más larga, y uno de
los músculos principales responsables de cerrar la mandíbula cambió su zona de anclaje desde el hueso angular hasta la mandíbula inferior.
• Un género tardío de cynodontidos, llamado Diarthrognathus, tenía la articulación mandibular ancestral, que implicaba a los huesos cuadrado y articular, y una articulación
derivada entre los huesos superior e inferior de la mandíbula (Figura 8.21a). Diarthrognathus, al igual que Acanthostega, es una forma intermedia. Presenta estados ancestrales
y derivados de un carácter (Colbert y Morales 1991).
• Los mamíferos primitivos sólo tenían la articulación entre las mandíbulas inferior y
superior. Los huesos cuadrado y articular ya no estaban implicados. Éste es un paso clave,
ya que ambos huesos quedan ahora libres para asumir una nueva función, o desaparecer, dependiendo de la dirección de la selección natural.
• En los mamíferos tardíos, los huesos cuadrado y articular se articulan con los estribos. Consecuentemente, se les renombra como yunque y martillo. Se localizan ahora lejos de la
junta de la mandíbula y funcionan solamente en la transmisión de sonidos (Figura 8.21b).
(a)
Diarthrognathus
Escuamoso
Cuadrado
Articular
Dentario
(b)
Mamíferos tardíos
Escuamoso
Figura 8.21 Cambio temporal en las articulaciones de la mandíbula
de los mamíferos La articulación de la mandíbula de un mamífero
Huesecillos
del oído
Articulación
de la mandíbula
Dentario
primitivo, llamado Diarthrognathus, se muestra en (a). El diagrama muestra
cómo la junta implicaba tanto al cuadrado y articular como a los huesos
dentario y escuamoso. En mamíferos posteriores, (b) la articulación de la
mandíbula se hace directamente entre el dentario y el escuamoso . Los
huesecillos del oído se han movido hacia atrás y alejado de la mandíbula.
276 PARTE III Adaptación
A medida que un nuevo
carácter adaptativo
evoluciona, algunos de sus
componentes pueden adquirir
funciones completamente
nuevas.
¿Qué aspectos de la selección natural ayudan a entender este cambio? Aunque la
visión clásica enfatiza la importancia de un aumento en la eficiencia para morder y masticar durante la remodelación de las mandíbulas (véase Manley 1972),Allin argumenta que
una audición mejorada jugó cierto papel favoreciendo a los mutantes que tenían los huesecillos del oído separados de la mandíbula. Su hipótesis se basa en la idea de que la supervivencia de los primitivos mamíferos, pequeños, insectívoros y probablemente nocturnos,
dependía de su capacidad para oír los agudos sonidos de los insectos. Dado que es difícil
oír mientras se mastica, unos huesecillos del oído separados de la mandíbula funcionaban
mejor (Allin 1975).
Resumiendo, muy pronto en la evolución de los mamíferos, tres huesecillos cambiaron su función, redujeron su tamaño, y se desplazaron desde una articulación en la mandíbula. Ahora mismo, la investigación sobre la evolución del oído se centra en entender
los mecanismos genéticos y del desarrollo de estos cambios (véase Rowe 1996; Smith et
al. 1997).
El hecho de que todo evolucione a partir de algo preexistente es una de las razones por
las que los órganos de un organismo, incluso aunque claramente adaptativos, sean en ocasiones imperfectos. Otras razones por las que las adaptaciones pueden ser imperfectas son
el objeto de la siguiente sección.
8.7.
Es imposible construir un
organismo perfecto. El diseño
de los organismos refleja un
compromiso entre
necesidades contrapuestas.
Compromisos y restricciones
Es imposible para cualquier población de organismos el evolucionar al unísono soluciones óptimas para todos los desafíos selectivos.Ya hemos mencionado ejemplos de compromisos de pasada. El cuello largo de la jirafa, por ejemplo, puede ser útil para los machos
que quieren conseguir una pareja, pero parece bastante inconveniente para beber. En esta
sección, exploraremos ejemplos adicionales de investigación sobre los factores que limitan la evolución adaptativa. Estos factores incluyen los compromisos, las restricciones funcionales y la falta de variabilidad genética.
El tamaño de las flores femeninas de Begonia: un compromiso
La planta tropical Begonia involucrata es monoica, esto es, hay flores masculinas y flores
femeninas en una misma planta. Las flores son polinizadas por las abejas. Las abejas viajan entre flores masculinas cargándose de polen, algunas veces, también transfieren
polen entre flores masculinas y flores femeninas. Las flores masculinas ofrecen una
recompensa a las abejas en forma de polen. Las flores femeninas no ofrecen recompensa alguna; en su lugar son polinizadas por engaño (Ågren y Schemske 1991). No es sorprendente pues que las abejas hagan visitas más largas a las flores masculinas que a las
femeninas.
Las flores femeninas se parecen a las masculinas en color, forma y tamaño (Figura
8.22a). Este parecido es presumiblemente adaptativo. Dado que las abejas evitan a las
flores femeninas a favor de las masculinas, la frecuencia con que las flores femeninas
sean visitadas por las abejas dependerá de su grado de parecido con las flores masculinas. La habilidad para atraer polinizadores deberá, de hecho, afectar a la eficacia a través de la función femenina, ya que las semillas dependerán de la disponibilidad de
polen. Doug Schemske y Jon Ågren (1995) estaban interesados en distinguir entre dos
hipótesis sobre el modo de selección que imponían las abejas sobre el tamaño de las
flores femeninas.
Hipótesis 1: cuanto más se parezcan las flores femeninas a las masculinas, más frecuentemente serán visitadas por las abejas. La selección sobre las flores será estabiliza-
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 277
(a)
(b)
Figura 8.22 Begonia involucrata (a) Flores masculinas (izquierda) y femeninas (derecha). Las flores
carecen de pétalos verdaderos; en su lugar, cada una tiene un par de sépalos petalizados. Los sépalos son
blancos o rosados. En el centro de cada flor hay un grupo de anteras o estigmas amarillos. Los estigmas de
las flores femeninas se parecen a las anteras de las masculinas. (b) Una inflorescencia, o tallo con muchas
flores. Cada inflorescencia tiene flores masculinas y femeninas. Típicamente, las flores masculinas se abren
antes, y las femeninas después. La inflorescencia que se muestra es atípica por cuanto tiene flores de ambos
sexos abiertas a la vez. (Doug W. Schemske, University of Washington, Seattle)
Tamaño
promedio
de la flor
masculina
Tamaño de la flor femenina
Pequeño "Mediano" Grande
30
10
0
mm
Tamaño de la flor femenina
(d)
150
70
60
# Número de flores
por inflorescencia
# Número de polinizadores
que se aproximan
20
Tamaño
promedio
de la flor
masculina
(c)
125
100
75
50
50
40
30
20
10
25
0
(b)
Hipótesis de selección direccional
# Número de visitas
de polinizadores
# Número de visitas
de polinizadores
(a) Hipótesis de selección
estabilizadora
Pequeño "Mediano" Grande
Tamaño de la flor artificial
S
M
L
0
50
100
150
200
Área de los sépalos petalizados (mm2)
Figura 8.23 Análisis de la selección sobre el tamaño de las flores femeninas de Begonia involucrata (a) Las dos
hipótesis investigadas por Schemske y Ågren (1995). Véase el texto para detalles. (b) Las tres clases de flores artificiales
de Schemske y Ågren. La clase de tamaño “mediano” es del mismo tamaño que el tamaño promedio de las flores
masculinas naturales. (c) Preferencia de los polinizadores en función del tamaño floral. Las barras azules representan el
número de abejas que se aproximaron a las flores artificiales, las barras naranjas representan el número de
polinizadores que realmente visitaron las flores artificiales. Schemske y Ågren dispusieron un número igual de flores de
cada tamaño en un bosque, pero las flores grandes atrajeron significativamente más aproximaciones y visitas de
abejas. (d) Número de flores femeninas por inflorescencia en función del tamaño floral. Existe un compromiso
estadísticamente significativo entre el tamaño floral y el número de flores. De Schemske y Ågren (1995). Copyright
© 1995, Evolution. Reimpreso con permiso de Evolution.
278 PARTE III Adaptación
dora, siendo idéntico el mejor fenotipo femenino al fenotipo promedio masculino
(Figura 8.23a, izquierda).
Hipótesis 2: cuanto más se parezcan las flores femeninas a la flor masculina que más
premie a las abejas, más frecuentemente serán visitadas por las abejas. Si las flores masculinas grandes ofrecen mayores recompensas, entonces la selección sobre las flores
femeninas será direccional, favoreciendo siempre a las flores más grandes frente a las más
pequeñas (Figura 8.23a, derecha).
parte del cuerpo o a una
función son recursos retraídos
de otra parte o función.
Ovario
(a)
(b)
Zona de abscisión
Figura 8.24 Cambio en el
color de las flores de Fuchsia
excorticata (a) Flor de Fuchsia
excorticata. (b) El eje horizontal
muestra la edad de la flor, en días,
desde su apertura. El eje vertical y
las líneas del gráfico muestran el
porcentaje de flores, de cada
edad, que hay en cada fase. De
Delph y Lively (1989).
Copyright © 1989, Evolution.
Reimpreso con permiso de
Evolution.
Hipantio
(tubo floral)
Pétalo
Sépalo
Estilo
5mm
Estigma
Color del hipantio y los sépalos a lo largo del tiempo
Nectar
100
90
80
Porcentaje de flores
Los recursos dedicados a una
Schemske y Ågren hicieron flores artificiales de tres tamaños diferentes (Figura 8.23b),
distribuyeron un número igual de cada tipo en el bosque y observaron con qué frecuencia se aproximaban las abejas a ellas y las visitaban. Los resultados fueron claros: cuanto más
grande es una flor, más abejas son atraídas a visitarla (Figura 8.23c). La selección que ejercen las abejas sobre el tamaño de las flores femeninas es fuertemente direccional.
Analizados someramente, los resultados de Schemske y Ågren sugieren que el tamaño
de las flores femeninas en Begonia involucrata es poco adaptativo. La selección que ejercen
las abejas favorece flores grandes, aunque las flores femeninas no son mayores que las masculinas. Una solución a esta paradoja es que B. involucrata simplemente carece de la variabilidad genética necesaria para crear flores femeninas más grandes que las masculinas.
Schemske y Ågren no tienen una evidencia directa de esta posibilidad; B. involucrata es una
flor perenne que necesita un tiempo largo para alcanzar la madurez sexual, haciendo muy
difíciles de realizar los experimentos de genética cuantitativa.
Otra solución a esta paradoja es que fijándonos únicamente en las flores femeninas individuales nos da una visión demasiado estrecha de la selección. Schmeske y Ågren extendieron su estudio desde las flores individuales a las influorescencias (Figura 8.22b). Los
investigadores midieron el tamaño y número de las flores femeninas en 74 inflorescencias.
Descubrieron un compromiso: cuanto más grandes son las flores femeninas en una inflorescencia, menos flores tiene dicha inflorescencia (Figura 8.23d). Este compromiso tiene
intuitivamente un sentido. Si una planta tiene un suministro finito de energía y nutrientes para invertir en floración, podría dividir este pastel en pocas piezas grandes o en
muchas piezas pequeñas, pero no en muchas piezas grandes. Inflorescencias con muchas
flores se pueden favorecer por selección por dos razones. En primer lugar, las abejas
podrían ser atraídas por inflorescencias con muchas flores. En segundo lugar, más flores
femeninas significa más potencial para producir semillas. Schemske y Ågren sugirieron la
hipótesis que el tamaño de las flores femeninas en B. involucrata fue determinado, al menos
en parte, por dos fuerzas opuestas: selección direccional para flores grandes, y un compromiso entre el tamaño y el número de flores.
Verde
Rojo
70
60
Eliminado
50
40
30
Intermedio
20
10
0 1
2
3 4 5 6 7 8 9 10 11 12 13 14 15
Días desde la apertura
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 279
El cambio del color en las flores de una Fuchsia: una restricción
Fuchsia excorticata es un árbol polinizado por aves, endémico de Nueva Zelanda (Delph y
Lively 1989). Sus flores cuelgan hacia abajo como campanas (Figura 8.24a y foto de la
página 251). El ovario se encuentra en el fondo de la campana. El cuerpo de la campana
consiste en el hipantio, o tubo floral, y los sépalos. El estilo, que recuerda a un badajo elongado, está rodeado de unos pequeños estambres y de un conjunto de pétalos reducidos.
El hipantio y los sépalos son, con mucho, la parte más visible de la flor; permanecen
verdes unos 5,5 días después de que la flor se abra y a partir de ese momento comienzan
a volverse rojos (Figura 8.24b). La transición desde verde a rojo dura más o menos 1,5 días,
al final de los cuales tanto el hipantio como los sépalos son completamente rojos. Las flores rojas permanecen en el árbol aproximadamente 5 días, pasados los cuales la flor se separa del ovario por la zona de abscisión y cae del árbol.
La polinización tiene lugar durante las fases verde e intermedia y ha de estar completada para cuando la flor es completamente roja. Las flores producen néctar entre los días
1 y 7 (Figura 8.24b). La mayoría de las flores habrán exportado más del 90% de su polen
al final de este período. Los estigmas son receptivos al polen, al menos hasta el segundo
día de la fase roja, pero raramente, si éste llega después del primer día, fertilizará un óvulo.
No es sorprendente pues, que los colibríes y otros pájaros polinizadores prefieran las flores verdes y, virtualmente, ignoren las flores rojas sin néctar (Delph y Lively 1985).
¿Por qué cambian de color las flores de este árbol? Una respuesta general, apoyada por
el estudio de una gran variedad de plantas, es que el cambio de color sirve como señal para
los polinizadores, alertándoles de que las flores no les ofrecen ya ninguna recompensa
(véase Delph y Lively [1989] para una revisión). Prestando atención a esta señal, los polinizadores pueden incrementar su eficiencia alimentaria, no perdiendo el tiempo buscando recompensas inexistentes. Las plantas se benefician porque cuando los polinizadores
buscan comida eficientemente, también transfieren el polen de un modo eficiente; no
depositan polen viable en estigmas no receptivos y no depositan polen no viable en estigmas receptivos.
Sin embargo, esta respuesta sólo es satisfactoria en parte. ¿Por qué F. excorticata no deja
caer sus flores inmediatamente después de completarse la polinización? Desprenderse de
las flores sería una señal inequívoca para los polinizadores de que no se les ofrece ninguna recompensa y, metabolicamente, sería mucho más económico que mantener las flores
rojas durante varios días. Retener las flores más allá del momento de la polinización parece poco adaptativo.
Linda Delph y Curtis Lively (1989) consideraron dos hipótesis de por qué F. excorticata mantiene sus flores (y las cambia a rojo) en lugar de deshacerse de ellas. La primera es
que mostrando las flores rojas aún se podrían atraer polinizadores al árbol, aunque no a las
propias flores rojas. Una vez atraídos, los polinizadores podrían alimentarse en las flores verdes aún presentes.Así pues, retener las flores rojas aumentaría la eficacia global de la polinización del árbol que las retuviese. Si esta hipótesis es correcta, entonces aquellas flores
verdes que estén rodeadas de flores rojas deberían recibir más polen que otras que no lo
estuviesen. Delph y Lively contrastaron esta predicción eliminando las flores rojas de algunos árboles y no de otros, y también eliminando las flores rojas de algunas ramas de ciertos árboles y no de otras. Después, compararon la cantidad de polen depositada en las flores
verdes de los árboles y en las ramas sin flores rojas y en los árboles y ramas con flores rojas.
No encontraron diferencias significativas entre los distintos grupos. La hipótesis de la atracción a los polinizadores no explica por qué F. excorticata mantiene las flores rojas.
La segunda hipótesis que Delph y Lively consideraron es que una restricción fisiológica evita que F. excorticata deje caer sus flores antes de lo que lo hace. Esta restricción fisiológica sería el crecimiento del tubo polínico. Después de que un grano de polen aterriza
280 PARTE III Adaptación
Tabla 8.3 Crecimiento del tubo polínico en Fuchsia excorticata
Días desde la polinización
1
2
3
4
Porcentaje de 10 flores con tubos polínicos
en el ovario
0
20%
100%
100%
Fuente: De Delph y Lively (1989).
Caracteres o
comportamientos que podrían
ser adaptativos pueden ser
fisiológica o mecánicamente
imposibles.
en el estigma, el polen germina. El grano de polen germinado genera un tubo a lo largo
del estilo hasta el ovario. Los dos espermatófitos del grano de polen bajan por este tubo
hasta el ovario, donde uno de ellos fertiliza al óvulo. El crecimiento del tubo polínico
requiere de un tiempo, especialmente en plantas como F. excorticata, que poseen largos estilos. Si la planta dejase caer sus flores antes de que los tubos polínicos tuviesen tiempo de
alcanzar los ovarios, el resultado sería equivalente a si las flores nunca hubiesen sido fecundadas. Delph y Lively polinizaron manualmente 40 flores. Pasadas 24 horas, arrancaron 10
flores, las diseccionaron y observaron al microscopio para ver si los tubos polínicos habían
alcanzado ya el ovario. Pasadas 48 horas, arrancaron y diseccionaron 10 flores más y así
sucesivamente. Los resultados aparecen en la Tabla 8.3. El tubo polínico necesita alrededor de 3 días para alcanzar el ovario.
Este resultado es consistente con la hipótesis de la restricción fisiológica. F. excorticata
no puede comenzar el proceso de eliminación de una flor hasta pasados 3 días desde que
dicha flor recibió el polen. Dejar caer una flor implica la formación de una estructura llamada zona de escisión, que consiste en varias capas de células que forman una división
entre el ovario y la flor. En F. excorticata, el crecimiento de esta zona tarda 1,5 días. La planta está obligada, necesariamente, a retener sus flores alrededor de 5 días. Delph y Lively
sugieren que el cambio de color de las flores es una adaptatión que evolucionó para compensar las restricciones fisiológicas que exigen la retención de las flores. Dado que la planta
ha de retener sus flores, la selección favoreció a aquellos individuos que ofrecían señales
que permitiesen a los polinizadores distinguir entre las flores receptivas y las no receptivas en sus ramas. Los polinizadores depositan el polen únicamente en estigmas receptivos,
y se llevan polen que es viable.
Cambio de hospedador en un escarabajo herbívoro:
¿constreñido por una falta de variabilidad genética?
En varios capítulos previos, hemos destacado que la variación genética es la materia
prima para la evolución por selección natural. Dado que la selección natural es el único
proceso que produce adaptación, la variación genética será también la materia prima a partir de la cual se moldeen las adaptaciones. Por el contrario, habrá poblaciones que no
podrán desarrollar ciertas adaptaciones particulares sencillamente por no tener la necesaria variación genética para hacerlo.
He aquí un ejemplo extremo: los cerdos no han evolucionado la capacidad de volar.
Podemos imaginar que el volar podría ser adaptativo para los cerdos, ya que les permitiría escapar de sus predadores y viajar más lejos en busca de su comida favorita. Sin embargo, los cerdos no vuelan, ya que los patrones de desarrollo de los vertebrados carecen de
la variación genética para generar una mano de cerdo y un ala a partir del mismo hombro. Otros vertebrados han evolucionado una habilidad para volar, por supuesto, pero en
murciélagos y en aves el programa de desarrollo fue modificado para convertir una extremidad completa desde una pata a un ala; en ninguno de estos grupos brotó una nueva
extremidad del cuerpo: demasiado malo para los cerdos.
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 281
El vuelo de los cerdos resulta un ejemplo ilustrativo, pero, en el fondo, es trivial. El deseo
de una adaptación es demasiado poco realista. Douglas Futuyma y sus colegas han intentado determinar si la falta de variación genética ha constreñido la adaptación en un caso
más realista (Funk et al. 1995; Futuyma et al. 1995 y las referencias en ellos citadas).
Futuyma y sus colegas estudiaron las plantas hospedadoras empleadas por escarabajos
comedores de hojas del género Ophraella. Entre estos pequeños escarabajos, cada especie
se alimenta, como larva y adulto, en las hojas de una o muy pocas especies de compuestas íntimamente relacionadas (plantas de la familia de los girasoles, las Asteraceae). Cada
especie de planta hospedadora produce una mezcla única de compuestos químicos tóxicos que le sirve de defensa frente a los herbívoros. Para los escarabajos, la habilidad para
vivir en una especie particular de plantas es una adaptación compleja que incluye la capacidad para reconocer a la planta como un lugar adecuado para comer y poner huevos, así
como la capacidad para destoxificar las defensas químicas de la planta.
En la Figura 8.25 aparece una estimación de la filogenia de 12 especies de escarabajos
de las hojas. La figura también muestra la lista de las especies de plantas hospedadoras para
cada especie de escarabajo. La historia evolutiva del género de escarabajos incluye varios
cambios desde una planta hospedadora a otra. Cuatro de estos cambios fueron entre especies de plantas poco relacionadas, pertenecientes a tribus distintas de las Asteraceae. Estos
cambios se indican en la figura mediante cambios en el color de relleno de la filogenia.
Otros cambios implicaron el movimiento a otra especie nueva de hospedadores del mismo
género que el hospedador ancestral, o de un género relacionado.
Cada combinación de especies de escarabajos y de las plantas hospedadoras empleadas
por otros escarabajos filogenéticamente próximos representa un escenario evolutivo plausible para un cambio de hospedador que pudo haber tenido lugar, pero que no ocurrió.
Por ejemplo, el escarabajo Ophraella arctica podría haber saltado al hospedador Iva axillaris. Futuyma y sus colegas han intentado explicar por qué en unos han ocurrido algunos
cambios de hospedador mientras que en otros no. Hay dos hipótesis:
Hipótesis 1: todos los cambios de hospedador son genéticamente posibles. Esto es, cada
especie de escarabajo contiene suficiente variación genética en sus mecanismos de
Clados de escarabajos
1 = clado pilosa
2 = clado conferta
3 = clado slobodkini
4 = subclado communa
4
3
1
Tribu de hospedadores
Astereae
Anthemideae
Eupatorieae
Heliantheae
2
Especies de
escarabajos
O. arctica
Planta(s)
hospedadora(s)
Solidago multiradiata
O. bilineata
Chrysopsis villosa
O. communa
Ambrosia spp., Iva axillaris
O. artemisiae
Artemisiae spp.
O. nuda
Iva axillaris
O. notulata
Iva frutescens
O. slobodkini
Ambrosia artemisiifolia
O. conferta
Solidago altissima complex
O. sexvittata
Solidago altissima complex
O. cribrata
Solidago juncea, S. altissima
O. notata
Eupatorium spp.
O. pilosa
Aster spp., Solidago bicolor
Figura 8.25 Filogenia de los escarabajos de la hoja, género Ophraella Los números de las ramas definen
las ramas principales (clados) del árbol evolutivo de los escarabajos. El sombreado de las ramas indica la tribu de
las especies hospedadoras. La historia evolutiva de este género de escarabajos incluye cuatro cambios de tribu de
hospedadores. De Futuyma et al. (1995). Copyright © 1995, Evolution. Reimpreso con permiso de Evolution.
282 PARTE III Adaptación
comida y destoxificación para permitir que, al menos, algunos individuos coman y
sobrevivan en cualquier especie potencial de hospedador. Si algunos individuos pueden comer y sobrevivir, pueden ser los fundadores de una nueva población de escarabajos que evolucionará para adaptarse perfectamente a este nuevo hospedador. Dado
que todos los cambios de hospedador son genéticamente posibles, el patrón actual de
cambios se determinó por factores ecológicos y aleatorios. Entre los factores ecológicos se incluirían la abundancia de varias especies de hospedadores dentro del rango geográfico de la especie de escarabajos y los depredadores y competidores asociados con
cada especie de hospedador.
Hipótesis 2: la mayoría de los cambios de hospedador son genéticamente imposibles.
Esto es, la mayoría de las especies de escarabajos carecen de la suficiente variación genética en sus mecanismos para alimentarse y destoxificarse como para permitir a ningún
individuo el comer y sobrevivir en todos los hospedadores potenciales, con la excepción
de unos pocos. El patrón actual de cambios de hospedadores fue determinado, fundamentalmente, por lo que fue genéticamente posible. Se dieron los cambios de hospedador genéticamente posibles; los genéticamente imposibles no.
Hemos presentado estas dos hipótesis como mutuamente excluyentes. De hecho, la verdad es, seguramente, que el patrón actual es el resultado de una mezcla de restricciones
genéticas, factores ecológicos y azar. Lo que Futuyma y sus colaboradores buscaban era
una evidencia concreta de que las restricciones genéticas formaban, al menos, parte del
cuadro.
Futuyma y sus colegas usaron un planteamiento basado en la genética cuantitativa (ver
Capítulo 7) para determinar cuánta variación genética tenían los escarabajos para comer
y sobrevivir en otros hospedadores potenciales. Examinaron varias combinaciones de
cuatro de los escarabajos listados en la Figura 8.25 con seis de las plantas hospedadoras.
Sus pruebas revelaron que había poca variación genética en la mayoría de las especies de
Tabla 8.4 Resumen de las pruebas de variación genética en larvas o
adultos que comen en plantas potencialmente hospedadoras
(a) Pruebas de variación genética en larvas o adultos que comen, por parentesco entre plantas
hospedadoras
¿Variación genética?
Escarabajo probado en una planta que es…
… de la misma tribu que su hospedador actual,
… de una tribu diferente.
Sí
No
7
1
14
17
Conclusión: es más fácil encontrar variación genética para la capacidad de comer cuando un
escarabajo se prueba en un hospedador potencial que está íntimamente relacionado con su
hospedador real.
(b) Pruebas de variación genética en larvas o adultos que comen, por parentesco entre
escarabajos
¿Variación genética?
Escarabajo probado en una planta que es…
Sí
No
... el hospedador de un escarabajo de su clado.
12
4
9
14
… de distinto clado.
Conclusión: es más fácil encontrar variación genética cuando un escarabajo se prueba en un
hospedador potencial que a su vez es hospedador de un escarabajo íntimamente relacionado.
Fuente: de la Tabla 7 de Futuyma et al. (1995). Copyright © 1995, Evolution. Reimpreso con el permiso de Evolution.
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 283
escarabajos para comer y sobrevivir en la mayor parte de los potenciales hospedadores. En
18 de las 39 pruebas en las que se comprobaba si una larva o un adulto reconocían y comían en un hospedador potencial, no encontraron variación genética para la capacidad de
comer. En 14 de las 16 pruebas que se hicieron para ver si una larva era capaz de sobrevivir en un hospedador potencial, no encontraron evidencia de variabilidad genética.
Estos resultados sugieren que la hipótesis 2 es, al menos parcialmente, correcta. Muchos
de los cambios posibles de hospedador parecen ser genéticamente imposibles. Futuyma y sus
colegas realizaron una contrastación adicional de la hipótesis 2 buscando en sus datos algún
patrón de variación genética para la capacidad comedora de larvas y adultos. Si la hipótesis
2 fuese correcta, entonces sería más probable que una especie de escarabajos presentase
variación genética para comer en un hospedador potencial si éste estuviese íntimamente
relacionado con el hospedador real. Los datos de Futuyma et al. confirman esta predicción
(Tabla 8.4a).Así mismo, si la hipótesis 2 fuese correcta, sería más probable que una especie
de escarabajos presentase variación genética para la capacidad de comer en un potencial
nuevo hospedador si éste fuese el hospedador real de una de las especies de escarabajos más
relacionadas. Los datos de Futuyma et al. también confirman esta predicción (Tabla 8.4b).
Futuyma y sus colaboradores concluyeron que la hipótesis 2 es, al menos parcialmente,
correcta. La historia de cambio de hospedadores en los escarabajos del género Ophraella se
ha restringido por la disponibilidad de variación genética para el cambio evolutivo.
8.8.
Las poblaciones a veces
carecen de la variación
genética que proporcionaría la
materia prima para
evolucionar ciertas
adaptaciones.
Estrategias para preguntar cuestiones interesantes
Empezamos este capítulo con una revisión de los planteamientos que los biólogos evolutivos usan para contrastar hipótesis sobre la forma y la función de los organismos. No
obstante, contrastar una hipótesis es sólo la segunda parte de un buen proyecto de investigación. La primera parte es formular una hipótesis. Formular hipótesis interesantes que
contrastar significa hacerse preguntas interesantes para después hacer conjeturas racionales sobre las respuestas.Acabamos este capítulo con una breve lista de estrategias para plantear buenas cuestiones evolutivas:
• Estudiar la historia natural. Los estudios descriptivos pueden orientar hacia el descubrimiento de nuevos patrones que necesitan una explicación.Algunas cosas en la naturaleza simplemente surgen y necesitan una explicación, como el cuello de la jirafa, o la agitación de las alas de Zonosemata.Algunas de las investigaciones más convincentes ocurren
cuando un investigador simplemente elige un organismo y decide aprender a cerca de él.
• Cuestionar las interpretaciones tradicionales. Habitualmente no han sido contrastadas.
Lo que hace tan atractivo el trabajo de Simmons y Scheeper con las jirafas es que desafiaba un escenario adaptativo aceptado durante mucho tiempo.
• Cuestionar las suposiciones en las que se basan hipótesis populares o técnicas de investigación. El desarrollo que Felsenstein hizo de un método mejorado de análisis
comparativo surgió del reconocimiento de que el planteamiento tradicional de la
investigación comparativa violaba sus propios fundamentos.
• Encontrar analogías que transfieran cuestiones de un campo a otro, o de un taxón a otro.
Si los murciélagos de la fruta y los zorros voladores que evolucionaron en grandes grupos también evolucionaron grandes testículos en comparación con su tamaño corporal, ¿no ocurrirá lo mismo en otros tipos de animales?
• Preguntar por qué no. Los estudios que hemos repasado sobre los compromisos y las
restricciones estaban motivados por investigadores que creían que sus organismos de
estudio no hacían algo que pudiera ser adaptativo.
Aprender a plantear buenas
preguntas es tan importante
como aprender a responderlas.
284 PARTE III Adaptación
Resumen
Entre las actividades principales de los biólogos evolutivos
se encuentra el análisis de la forma y la función de los organismos para determinar si, y por qué, un carácter particular
es adaptativo. Para establecer si un carácter es adaptativo, los
investigadores deben formular hipótesis sobre cómo se usa
el carácter y por qué individuos que poseen el carácter son
más eficaces que individuos que carecen de él. Entonces, ya
que no se puede aceptar ninguna hipótesis simplemente
porque sea plausible, los investigadores deben contrastar sus
hipótesis. Las hipótesis se contrastan usándolas para hacer
predicciones. Después se recogen datos que servirán para ver
si las predicciones eran correctas.
Los investigadores usan una variedad de planteamientos
para recoger datos y contrastar sus hipótesis. El método más
eficaz es el experimento controlado. Los experimentos controlados implican a grupos de organismos que son idénticos
excepto en una variable de interés. La variable experimental puede entonces identificarse, fidedignamente, como la
causa de las diferencias en supervivencia y reproducción
entre los grupos. Cuando los experimentos son impracticables, cuidadosos estudios observacionales pueden generar
datos válidos para contrastar hipótesis. Finalmente, la comparación entre especies también puede usarse para confirmar o refutar predicciones, siempre y cuando se tenga en
cuenta la historia evolutiva compartida de las especies estudiadas.
Cuando analicemos adaptaciones, haremos bien en recordar que los organismos son complicados. Los individuos
pueden ser fenotípicamente plásticos, de modo que individuos genéticamente idénticos criados en ambientes diferentes tengan fenotipos diferentes. La función de un carácter en particular puede cambiar a lo largo del tiempo
evolutivo, y puede reflejar el compromiso entre demandas
ambientales o fisiológicas contrapuestas. Finalmente, las
poblaciones pueden, sencillamente, carecer de la variación
genética requerida para adaptarse perfectamente a su entorno. Éstas y otras complicaciones son el objeto de la investigación actual de los biólogos evolutivos.
Preguntas
1. ¿Por qué era importante que Greene y sus colaboradores
comprobasen moscas téfricas cuyas alas habían sido cortadas
y luego pegadas?
2. En los experimentos de Huey et al., las serpientes habitualmente escogían rocas gruesas a pesar del riesgo de estar demasiado frías. Sugiera dos hipótesis de por qué las serpientes,
a veces, eligen rocas gruesas. ¿Son contrastables sus hipótesis?
¿Asumen ambas hipótesis que el carácter de comportamiento “elegir una roca gruesa” es adaptativo?
3. Los geckos son lagartos inusuales, ya que son activos por la
noche en lugar de durante el día. Describa las dificultades con
las que un gecko se enfrentará si trata de usar su comportamiento de termorregulación para mantener su temperatura
durante la noche. ¿Predeciría que los geckos tienen una temperatura óptima para correr que es la misma, mayor o menor
que la de un típico lagarto diurno? Huey et al. (1989a) encontraron que los geckos que estudiaron tenían temperaturas
óptimas que eran iguales a las de los lagartos diurnos (un
hallazgo en oposición a su propia hipótesis). ¿Puede pensar en
una explicación?
4. Imagine que se introdujeran unos peces en el lago Citadelpark, uno de los estudiados por De Meester. ¿Qué predice
que ocurrirá con la plasticidad fenotípica de las Daphnia de
este lago? Describa las observaciones que necesitaría hacer
para comprobar sus predicciones.
5. Al reconstruir la historia del oído de los mamíferos, hemos
empleado evidencias fósiles y embriológicas. En muchos
casos, no tendremos el lujo de disponer de ambos conjuntos
de evidencias. Ejemplos son la evolución de las alas de los
murciélagos, de los que sí tenemos datos embriológicos pero
no fósiles, y la evolución de los adornos del cuello del Triceratops, para los que existen fósiles pero poca embriología. En su
opinión, ¿es necesario disponer de ambos tipos de datos para
determinar la historia evolutiva de un carácter? ¿Hubiesen
sido los datos fósiles (o embriológicos) a solas suficientes para
convencerle de que los huesos del oído medio de los mamíferos evolucionaron de la hiomandíbula, el cuadrado y el articular de los primeros vertebrados? ¿Qué hubiese pensado si
ambos conjuntos de datos hubiesen sido contradictorios?
6. Aparentemente, los primeros tetrápodos no tenían membranas timpánicas, no hay un lugar obvio en sus cráneos donde
una membrana timpánica cupiese.Además, el estribo en estos
animales era un hueso relativamente pesado y, por tanto, poco
probable que transmitiese bien vibraciones de alta frecuencia;
aunque los estribos estaban, claramente, en una buena posición para transmitir vibraciones al oído interno. Se cree que
los primeros tetrápodos tenían una posición corporal tumbada, con sus enormes cabezas habitualmente apoyadas en el
suelo. Con esto en mente, especule sobre qué tipo de habilidades “auditivas” tendría Acanthostega. ¿Son contrastables sus
ideas?
7. Piense sobre los costes y los beneficios de tener un cierto
tamaño corporal. Por ejemplo, un ratón puede sobrevivir fácil-
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 285
mente a una caída de 12 metros. Un humano que cayera 12
metros quedaría, probablemente, herido. Una caída de 12 metros, probablemente, mataría a un elefante. Finalmente, un
estudio reciente sobre la resistencia de los huesos de un Tyranosaurus rex reveló que si un T. rex corriendo rápidamente tropezase, probablemente se mataría (Farlow, Smith y Robinson
1995). Dados estos costes, ¿por qué han evolucionado cuerpos
de gran tamaño? ¿Puede pensar en algún coste para los cuerpos de pequeño tamaño? ¿Cómo contrastaría sus ideas?
8. Imagine que es un explorador que acaba de descubrir dos
grandes islas. Cada isla tiene una población de una especie de
arbusto desconocida en otra parte. En la isla A, el arbusto tiene
en sus hojas una alta concentración de una sustancia química venenosa. En la isla B, el arbusto tiene hojas comestibles,
no venenosas. Las islas difieren en muchas cosas, por ejemplo,
en la isla A llueve menos y hace más frío en invierno que en
la isla B; y existen algunos insectos herbívoros que no viven
en la isla B. La isla A también tiene una gran población de
“muntjacs”, un pequeño ciervo tropical que adora comer
arbustos. Sospecha que los “muntjacs” han sido la fuerza selectiva que ha causado la evolución de las hojas tóxicas. ¿Cómo
comprobaría esta hipótesis? ¿En qué hipótesis alternativas
puede pensar? ¿Qué datos anularían su hipótesis y cuáles las
otras?
9. Un desafío habitual en paleontología es identificar el cambio
selectivo que causó, hace millones de años, que un nuevo
carácter se extendiese en un linaje. Un ejemplo clásico es la
evolución de los dientes con coronas altas en los rumiantes.
Estos dientes proporcionan una protección extra frente a las
partículas abrasivas en la dieta, como las de sílice. Los dientes
con coronas altas han evolucionado independientemente en
docenas de mamíferos terrestres desde el Mioceno, incluyendo antílopes, canguros, caballos y conejos. He aquí dos hipótesis para la evolución de los dientes con coronas altas:
a. Podría estar ligado a la evolución de las hierbas.
b. Podría estar ligado a un aumento de la cantidad de gravilla en la dieta.
¿Son éstas dos hipótesis comprobables? ¿Qué evidencia ayudaría a distinguirse entre ellas? (Para más información sobre
este ejemplo, véase MacFadden 1997, MacFadden et al. 1999.)
10. Considere el color de la piel en los humanos. ¿Muestra este
carácter variación genética? ¿Plasticidad fenotípica? ¿Interacción genotipo-ambiente? Dé ejemplos que ilustren cada
fenómeno. ¿Podría evolucionar la plasticidad fenotípica para
el color de la piel en poblaciones humanas? ¿Cómo?
11. El ejemplo de las Begonias (Sección 8.7) ilustraba que los organismos están, frecuentemente, cogidos entre fuerzas evolutivas opuestas. Cada uno de los siguientes ejemplos también
ilustra una lucha entre diversas fuerzas selectivas. Para cada
ejemplo, especule sobre qué fuerzas selectivas podrían mantener cada uno de los caracteres descritos, y qué fuerzas se
opondrían.
Un macho de alce produce, anualmente, nuevos cuernos
hechos de hueso.
Los abetos de Douglas crecen frecuentemente por encima de los 24 metros de altura.
El intestino de las termitas está lleno de microorganismos
que digieren la celulosa.
Los arces pierden todas sus hojas en otoño.
Una polilla macho tiene antenas enormes, que pueden
detectar las feromonas femeninas.
Un percebe se adhiere permanente a una roca cuando
madura.
12. Schemske y Ågren (1995) usaron flores artificiales, en lugar
de flores naturales, en su experimento (Sección 8.7). ¿Cuáles
son las ventajas de usar flores artificiales? (Hay al menos dos
importantes.) ¿Cuáles son las desventajas?
13. Los medios populares suelen presentar a la evolución como
predecible y con un objetivo final. Por ejemplo, en un episodio de Star Trek:Voyager, el capitán preguntó al computador de
abordo que extrapolase el “curso probable” de la evolución de
un hadrosaurio (un dinosaurio bípedo) si estos animales
hubiesen sido sacados de la Tierra antes de la extinción K-T
y dejados en otro planeta para evolucionar. ¿Qué información
sobre el nuevo ambiente del hadrosaurio hubiese sido útil
para obtener la mejor predicción? Dado lo que conoce sobre
los diversos factores que pueden ejercer una presión de selección sobre un organismo, y lo que sabe sobre la mutación,
migración y deriva genética, ¿cree que es teóricamente posible el predecir, con precisión, el curso de la evolución a largo
plazo?
14. Un ejercicio que se usa en algunos programas de doctorado
es dejar a los estudiantes que enumeren 20 preguntas a las que
les gustaría contestar. Grupos de estudiantes discuten las cuestiones y se ayudan para decidir cuáles son las más interesantes. Hay muchos criterios para decidir si una cuestión es interesante: ¿es nueva? ¿Aborda un gran, o importante, problema?
¿Conducirá a otras cuestiones? ¿Es abordable o será abordable si se desarrolla una nueva técnica? Intente usted mismo
este ejercicio.
Explorando la bibliografía
15. Un aspecto importante al evaluar artículos científicos es considerar otras explicaciones para los datos que se les pueden haber
escapado a los autores. Vea si puede pensar en explicaciones
alternativas para los datos presentados en los siguientes artículos:
Benkman, C.W., and A. K. Lindholm. 1991.The advantages
and evolution of a morphological novelty. Nature 349: 519520.
286 PARTE III Adaptación
Soler, M., and Møller, A. P. 1990. Duration of sympatry and
coevolution between the great spotted cuckoo and its magpie host. Nature 343: 748-750.
Finalmente, vea la siguiente revisión del trabajo de Soler y
Møller como un ejemplo de cómo la crítica científica por
parte de los implicados da lugar a avances científicos.
Lotem, A., and Rothstein, S. I. 1995. Cuckoo-host coevolution: From snapshots of an arms race to the documentation
of microevolution. Trends in Ecology and Evolution 10: 436437.
16. El registro fósil ha sido tradicionalmente la mayor fuente de
datos para preguntarse sobre la historia evolutiva. Desgraciadamente el registro fósil es incompleto y no puede responder a todas las cuestiones. Las modernas técnicas moleculares
y del análisis genético son vistas, habitualmente, como más
útiles. Como resultado, los paleontólogos han tenido que
defender la “utilidad” del registro fósil. Lea los siguientes artículos para explorar esta controversia más profundamente:
Foote, M. 1996. Perspective: Evolutionary patterns in the fossil record. Evolution 50: 1-11.
Benton, M. J., and G.W. Storrs. 1994.Testing the quality of
the fossil record: Paleontological knowledge is improving.
Geology 22: 111-114.
Norell, M. A., and M. J. Novacek. 1992.The fossil record and
evolution: Comparing cladistic and paleontologic evidence
for vertebrate history. Science 255: 1690-1693.
17. En algunas ocasiones, los machos de espinosillo roban huevos de los nidos de otros machos próximos para cuidarlos
ellos mismos. Sievert Rohwer sugirió que el robo de huevos
es una estrategia de cortejo. Los machos, en ocasiones, comen
huevos de sus propios nidos, disminuyendo así el esfuerzo
reproductivo de sus parejas y empleando esta energía en sus
propios esfuerzos reproductivos. Las hembras, en consecuencia, prefieren poner huevos en nidos que ya los contengan de
otra hembra, reduciendo así su propio riesgo. Esta preferencia de las hembras por nidos que ya contengan huevos significa que aquellos machos que no tengan aún huevos en su
nido, ganarán atractivo si los roban de otro macho.Véase:
Rohwer, S. 1978. Parent cannibalism of offspring and egg raiding as a courtship strategy. American Naturalist 112: 429440.
Para un fenómeno parecido en aves, véase:
Gori, D. F., S. Rohwer, and J. Caselle. 1996. Accepting unrelated broods helps replacement male yellow-headed blackbirds attract females. Behavioral Ecology 7: 49-54.
18. Para un ejemplo espectacular de plasticidad fenotípica en el
que un insecto herbívoro usa las defensas químicas de su
hospedador para desarrollar sus propias defensas contra los
depredadores, véase:
Greene, Erick. 1989. A diet-induced developmental polymorphism in a caterpillar. Science 243: 643-646.
19. Entre los desafíos que afrontan los parásitos está el cambiar de
hospedador. Este desafío es un agente selectivo especialmente poderoso para parásitos en los que cada individuo pasa las
diferentes partes de su ciclo vital en hospedadores distintos.
¿Qué adaptaciones esperaría en un parásito que facilitasen su
dispersión de un hospedador a otro? Para un magnífico ejemplo en el que un parásito manipula el comportamiento o apariencia de su hospedador, véase:
Tierney, J. F., F.A. Huntingford, and D.W.T. Crompton. 1993.
The relationship between infectivity of Schistocephalus solidus (Cestoda) and antipredator behavior of its intermediate host, the three-spined stickleback, Gasterosteus aculeatus.
Animal Behavior 46: 603-605.
Lafferty, K. D., and A. K. Morris. 1996.Altered behavior of parasitized killifish increases susceptibility to predation by bird
final hosts. Ecology 77: 1390-1397.
Bakker,T. C. M., D. Mazzi, and S. Zala. 1997. Parasite-induced changes in behavior and color make Gammarus pulex
more prone to fish predation. Ecology 78: 1098-1104.
20. Los cucos de cabeza marrón (Molothrus ater) ponen sus huevos en los nidos de otros pájaros, un comportamiento llamado parasitismo de nido. Cuando esta estrategia funciona, el
pájaro hospedador acepta el huevo como propio y cría al
pollo. Cuando la estrategia falla, el hospedador reconoce el
huevo como impostor y lo tira del nido. ¿Por qué hay especies que aceptan el huevo de los cucos en su nido? Dado el
coste obvio asociado con criar un pollo de otra especie, la
aceptación parece no adaptativa. Los biólogos evolutivos han
propuesto dos hipótesis contrapuestas para explicar por qué
algunas especies de hospedadores aceptan los huevos del
cuco. La hipótesis del retraso evolutivo afirma que las especies que aceptan huevos de cuco lo hacen sencillamente porque aún no han evolucionado un comportamiento de expulsión. O bien la especie hospedadora carece de la variabilidad
genética que le permita evolucionar el comportamiento de
expulsión o, alternativamente, ha estado expuesta poco tiempo al parasitismo de nido para que semejante comportamiento haya tenido tiempo de evolucionar. La hipótesis del
equilibrio evolutivo afirma que las especies de hospedadores
que aceptan huevos de cuco lo hacen porque tienen una restricción mecánica fundamental: sus picos son demasiado
pequeños para permitirles agarrar un huevo de cuco, y si
intentasen perforar el huevo de cuco, destruirían demasiados
de sus propios huevos en el proceso. Dada esta restricción, la
especie hospedadora ha desarrollado una estrategia que minimice el daño. Piense cómo contrastaría estas dos hipótesis.
Después vea:
Rohwer, S., and C. D. Spaw. 1988. Evolutionary lag versus billsize constraints: A comparative study of the acceptance of
cowbird eggs by old hosts. Evolutionary Ecology 1988: 27-36.
Rohwer, S., C. D. Spaw, and E. Røskaft. 1989. Costs to northern orioles of puncture-ejecting parasitic cowbird eggs
from their nests. Auk 106: 734-738.
Capítulo 8 Estudiando la adaptación: el análisis evolutivo de la forma y la función 287
Røskaft, E., S. Rohwer, and C. D. Spaw. 1993. Cost of puncture-ejection compared with costs of rearing cowbird chicks for
northern orioles. Ornis Scandinavica 24: 28-32.
Sealy, S. G. 1996. Evolution of host defenses against brood parasitism: Implications of puncture-ejection by a small passerine. Auk 113: 346-355.
Dado que algunas especies de hospedadores expulsan el
huevo del cuco picándolo primero y luego bajándolo del
nido, ¿qué adaptaciones esperaría en los huevos del cuco?
¿Supondrían algún coste estas adaptacions? Vea:
Spaw, C. D., and S. Rohwer. 1987. A comparative study of
eggshell thickness in cowbirds and other passerines. Condor
89: 307-318.
Picman, J. 1997.Are cowbird eggs unusually strong from the
inside? Auk 114: 66-73.
21. Para ejemplos recientes adicionales en los que los biólogos
evolutivos usan una aproximación comparativa que hace uso
de los contrastes independientes para abordar cuestiones interesantes, vea:
Blumstein, D.T., and K. B.Armitage. 1998. Life history consequences of social complexity: A comparative study of
ground-dwelling sciurids. Behavioral Ecology 9: 8-19.
Iwaniuk,A. N., S. M. Pellis, and I. Q.Whishaw. 1999. Brain size
is not correlated with forelimb dexterity in fissiped carnivores (Carnivora): A comparative test of the principle of
proper mass. Brain, Behavior, and Evolution 54: 167-180.
Bibliografía
Ågren, J., and D.W. Schemske. 1991. Pollination by deceit in a Neotropical monoecious herb, Begonia involucrata. Biotropica 23: 235-241.
Allin, E. F. 1975. Evolution of the mammalian middle ear. Journal of Morphology 147:
403-438.
Carroll, R. L. 1988. Vertebrate Paleontology and Evolution. New York: W.H. Freeman.
Clack, J.A. 1983.The stapes of the Coal Measures embolomere Pholiderpeton scutigerum Huxley (Amphibia: Anthracosauria) and otic evolution in early tetrapods. Zoological Journal of the Linnean Society 79: 121-148.
Clack, J. A. 1989. Discovery of the earliest-known tetrapod stapes. Nature 342:
425-427.
Clack, J.A. 1994. Earliest known tetrapod braincase and the evolution of the stapes and fenestra ovalis. Nature 369: 392-394.
Coates, M. I., and J. A. Clack. 1991. Fish-like gills and breathing in the earliest
known tetrapod. Nature 352: 234-236.
Colbert, E. H., and M. Morales. 1991. Evolution of the Vertebrates. New York:Wiley-Liss.
Delph, L. F., and C. M. Lively. 1985. Pollinator visits to floral colour phases of
Fuchsia excorticata. New Zealand Journal of Zoology 12: 599-603.
Delph, L. F., and C. M. Lively. 1989.The evolution of floral color change: Pollinator attraction versus physiological constraints in Fuchsia excorticata. Evolution 43:
1252-1262.
De Meester, L. 1996. Evolutionary potential and local genetic differentiation in a
phenotypically plastic trait of a cyclical parthenogen, Daphnia magna. Evolution 50: 1293-1298.
Farlow, J. D., M. B. Smith, and J. M. Robinson. 1995. Body mass, bone “strength
indicator,” and cursorial potential of Tyrannosaurus rex. Journal of Vertebrate Paleontology 15: 713-725.
Felsenstein, J. 1985. Phylogenies and the comparative method. The American Naturalist 125: 1-15.
Funk, D. J., D. J. Futuyma, G. Ortí, and A. Meyer. 1995. A history of host associations and evolutionary diversification for Ophraella (Coleoptera: Chrysomelidae): New evidence from mitochondrial DNA. Evolution 49: 1008-1017.
Futuyma, D. J., M. C. Keese, and D. J. Funk. 1995. Genetic constraints on macroevolution:The evolution of host affiliation in the leaf beetle genus Ophraella.
Evolution 49: 797-809.
Garland,T., Jr., and S. C.Adolph. 1994.Why not do two-species comparative studies: Limitations on inferring adaptation. Physiological Zoology 67: 797-828.
Garland,T., Jr., P. E. Midford, and A. R. Ives. 1999. An introduction to phylogenetically based statistical methods, with a new method for confidence intervals on ancestral values. American Zoologist 39: 374-388.
Gilbert, J. J. 1966. Rotifer ecology and embryological induction. Science 151: 12341237.
Gilbert, J. J. 1980. Further observations on developmental polymorphism and its
evolution in the rotifer Brachinonus calyciflorus. Freshwater Biology 10: 281294.
Gould, S. J.1993. Eight Little Piggies. New York:W.W. Norton.
Gould, S. J., and R. C. Lewontin. 1979.The spandrels of San Marco and the Panglossian paradigm:A critique of the adaptationist programme. Proceedings of the
Royal Society of London, Series B 205: 581-598.
Greene, E., L. J. Orsak, and D.W.Whitman. 1987. A tephritid fly mimics the territorial displays of its jumping spider predators. Science 236: 310-312.
Hosken, D. J. 1998.Testes mass in megachiropteran bats varies in accordance with
sperm competition theory. Behavioral Ecology and Sociobiology 44: 169-177.
Huey, R. B., and J. G. Kingsolver. 1989. Evolution of thermal sensitivity of ectotherm performance. Trends in Ecology and Evolution 4: 131-135.
Huey, R. B., P. H. Niewiarowski, J. Kaufmann, and J. C. Herron. 1989a.Thermal
biology of nocturnal ectotherms: Is sprint performance of geckos maximal at
low body temperatures? Physiological Zoology 62: 488-504.
Huey, R. B., C. R. Peterson, S. J. Arnold, and W. P. Porter. 1989b. Hot rocks and
not-so-hot rocks: Retreat-site selection by garter snakes and its thermal consequences. Ecology 70: 931-944.
Johnson,T. P., and A. F. Bennett. 1995.The thermal acclimation of burst escape performance in fish: An integrated study of molecular and cellular physiology
and organismal performance. Journal of Experimental Biology 198: 2165-2175.
Lauder, G.V., R. B. Huey, et al. 1995. Systematics and the study of organismal form
and function. BioScience 45: 696-704.
Lombard, R. E., and J. R. Bolt. 1979. Evolution of the tetrapod ear:An analysis and
reinterpretation. Biological Journal of the Linnean Society 11: 19-76.
Manley, G. A. 1972. A review of some current concepts of the functional evolution of the ear in terrestrial vertebrates. Evolution 26: 608-621.
Martins, E. P., and T. Garland, Jr. 1991. Phylogenetic analyses of the correlated evolution of continuous characters:A simulation study. Evolution 45: 534-557.
Mather, M. H., and B. D. Roitberg. 1987. A sheep in wolf ’s clothing: Tephritid
flies mimic spider predators. Science 236: 308-310.
Mayr, E. 1983. How to carry out the adaptationist program? American Naturalist
121: 324-334.
MacFadden, B. J. 1997. Origin and evolution of the grazing guild in New World
terrestrial mammals. Trends in Ecology and Evolution 12: 182-187.
MacFadden, B. J., N. Solounias, and T. E. Cerling. 1999. Ancient diets, ecology,
and extinction of 5-million-year-old horses from Florida. Science 283: 824827.
Pratt, D. M., and V. H. Anderson. 1985. Giraffe social behavior. Journal of Natural
History 19: 771-781.
Rowe,T. 1996. Coevolution of the mammalian middle ear and neocortex. Science 273: 651-654.
288 PARTE III Adaptación
Schemske, D.W., and J. Ågren. 1995. Deceit pollination and selection on female
flower size in Begonia involucrata: An experimental approach. Evolution 49: 207214.
Simmons, R. E., and L. Scheepers. 1996.Winning by a neck: Sexual selection in
the evolution of the giraffe. American Naturalist 148: 771-786.
Smith, K. K.,A. F. H. van Nievelt, and T. Rowe. 1997. Comparative rates of development in Monodelphis and Didelphis. Science 275: 683-684.
Young,T. P., and L.A. Isbell. 1991. Sex differences in giraffe feeding ecology: Energetic and social constraints. Ethology 87: 79-89.
CAPÍTULO
9
Selección sexual
Iguanas marinas de las Galápagos. La iguana roja es un gran macho adulto. Está rodeado por machos y hembras más pequeños (Martín Wikelski,
University of Illinois at Urbana-Champaign).
L
OS MACHOS Y LAS HEMBRAS SON, FRECUENTEMENTE, MUY DISTINTOS EN SU
tamaño, apariencia y comportamiento. En las iguanas marinas, por ejemplo, los sexos
difieren en el tamaño corporal a razón de dos. Los machos son mayores, y fuertemente territoriales durante la estación de cría. Las hembras son más pequeñas y gregarias durante todo
el año. En los pájaros viuda de cola larga, adultos de sexos distintos tienen plumajes tan diferentes que sería fácil cometer el error de clasificarlos como especies distintas. Los machos
son negro azabache, llevan plumas caudales mucho más largas que su propio cuerpo y tienen
manchas rojas y amarillas en sus hombros. Las hembras son de un críptico color marrón,
con las plumas caudales cortas y sin manchas en los hombros. En las ranas grises arbóreas,
los machos tienen gargantas oscuras y producen llamadas melodiosas. Las hembras, por el
contrario, tienen gargantas blancas y son silenciosas. En las moscas de ojos pedunculados,
ambos sexos tienen los ojos al final de un largo y fino pedúnculo, pero el de los machos es
mucho más largo que el de las hembras. En algunas especies de pez flauta, las hembras tienen bandas azules y la piel plegada en sus vientres, características de las que los machos carecen. Las fotos de machos y hembras en la Figura 9.1 proporcionan ejemplos adicionales.
En humanos, también las hembras y los machos son llamativamente distintos. Las diferencias incluyen no solamente las obvias y esenciales, como nuestra genitalia y órganos
reproductivos, sino también la estructura facial, el tono vocal, la distribución corporal de
grasa y pelo, y el tamaño corporal. La diferencia en el tamaño corporal entre mujeres y
hombres está documentada en la Figura 9.2
289
290 PARTE III Adaptación
(b) Guppies
(a) Ciervo rojo
(c) Sapo dorado
Figura 9.1 Diferencias entre machos y hembras (el dimorfismo sexual) en el ciervo rojo (Cervus elaphus), los guppies
(Poecilia reticulata) y los sapos dorados (Bufo periglenes) En (a), el macho está a la izquierda; en (b) y (c), el macho está arriba.
([a] M. Hamblin/Animals Animals/Earch Scenes; [b] Michael Gunther/PA; [c] M. Fogden/Animals Animals/Earth Scenes)
La diferencia entre los sexos
se conoce como dimorfismo
sexual.
Las diferencias entre los machos y las hembras de una especie se conocen como
dimorfismo sexual. En este capítulo nos preguntaremos por qué el dimorfismo sexual
aparece en tal variedad de organismos. Ésta es una cuestión sobre la que Charles Darwin
(1871) escribió medio libro y que, desde entonces, ha cautivado a los biólogos evolutivos.
En capítulos previos, hemos venido explicando algunas características de los seres vivos
mediante la teoría de la evolución por selección natural. El objetivo ha sido descubrir si
las características en cuestión eran adaptativas, en cuyo caso, comprobar cómo aumenta
la supervivencia o la fecundidad de los individuos que las poseen. Pero las diferencias
Figura 9.2 Los varones y las mujeres difieren en altura Para cada una de más de 200
sociedades, la altura promedio de los varones se representa frente a la altura promedio de las
mujeres. La línea diagonal muestra dónde deberían haber caído los puntos si los varones y mujeres
fuesen de la misma altura. La gente varía mucho en altura entre sociedades: en la sociedad más baja,
el varón promedio es aproximadamente de 143 cm de alto y la mujer promedio sobre los 135 cm;
en la sociedad más alta, el varón promedio es de 180 cm de altura y la mujer promedio de 165 cm.
Pero en todas y cada una de las sociedades el varón promedio es más alto que la mujer promedio,
normalmente alrededor de un 10%. De Rogers y Mukherjee (1992).
Estatura del varón (cm)
180
170
160
150
140
140 150 160 170 180
Estatura de la mujer (cm)
Capítulo 9 Selección sexual 291
entre los sexos son, a menudo, difíciles de explicar con la teoría de la evolución por selección natural.
Por ejemplo, compare la evolución del tamaño del pico en los pinzones de Darwin
(Capítulo 3) con la evolución de una larga cola en los machos del pájaro viuda de cola
larga (Figura 9.3). Surgen dos problemas. Primero, cuando los pinzones sufren una sequía
y las semillas pequeñas y blandas escasean, los picos grandes son tan útiles tanto para los
machos como para las hembras. Pero, si unas plumas caudales largas pueden aumentar la
supervivencia, o la fecundidad, de un pájaro viuda, ¿por qué solo los machos las tienen?
Segundo, los grandes picos ayudan a los pinzones a sobrevivir a las sequías permitiéndoles abrir semillas grandes y duras y tener, así, algo que comer. Pero, ¿cómo pueden esas plumas tan grandes mejorar la supervivencia, o la fecundidad, de los pájaros viuda? Las
plumas grandes caudales, probablemente, hacen a los pájaros viuda más fáciles de ver y de
capturar por los depredadores. Más aún, desarrollar semejantes plumas requiere energía
considerable. Cualquier energía empleada en las plumas es energía que no se empleará en
tener descendientes. Parece, pues, que la teoría de la evolución por selección natural no
puede explicar ni por qué las hembras de los pájaros viuda son diferentes, ni por qué un
carácter tan poco frecuente, como las plumas largas de la cola, no existe.
Como el propio Darwin fue el primero en reconocer, el sexo proporciona una solución al rompecabezas del dimorfismo sexual. Para ver el porqué, consideremos la vida sin
sexo. Para organismos que se reproducen asexualmente (ver el Capitulo 7), pasar sus
genes a la siguiente generación es bastante inmediato. Los dos desafíos únicos son sobrevivir lo suficiente para reproducirse y, llegado el momento, hacerlo. El sexo complica la
vida al añadir un tercer, e importante, desafío: encontrar un miembro del sexo opuesto y
convencerle de cooperar.
Charles Darwin reconoció que los individuos no solamente difieren en su habilidad
para sobrevivir y reproducirse, sino también en su éxito en convencer a los miembros del
sexo opuesto para aparearse. Sobre los pájaros, por ejemplo, Darwin escribió: “En la
medida que el acto del cortejo parece ser, en muchos pájaros, un asunto largo y tedioso,
también ocurre ocasionalmente que ciertos machos y hembras no consiguen, durante la
estación adecuada, excitar al otro al amor y, consecuentemente, no aparean” (1871, página 107). En sus consecuencias evolutivas, no poder aparearse es equivalente a morir joven:
la víctima no contribuye genéticamente a las generaciones venideras. Darwin ya aplicó el
término selección natural a las diferencias entre individuos en supervivencia y reproducción. A las diferencias entre individuos en su capacidad para conseguir parejas lo llamó
selección sexual. Podemos desarrollar una teoría de la evolución por selección sexual que
es lógicamente equivalente a la teoría de la evolución por selección natural. Si hay variación heredable para un carácter que afecte a la capacidad de obtener parejas, entonces las
variantes que conduzcan al éxito irán haciéndose más comunes con el tiempo.
Nuestro objetivo en este capítulo será explorar cómo la teoría de la evolución por selección sexual explica la existencia frecuente de diferencias llamativas entre hembras y
machos, particularmente cuando esas diferencias implican caracteres que parecen desafiar
Figura 9.3 Dimorfismo sexual de los pájaros viuda de
cola larga (Euplectes progne) El macho es negro, con largas
plumas en la cola y manchas rojas y amarillas en los hombros; la
hembra es marrón y críptica.
El dimorfismo sexual es un
rompecabezas, ya que la
selección natural no puede
explicarlo.
292 PARTE III Adaptación
a la supervivencia. Primero revisaremos trabajos clásicos que muestran el mecanismo preciso por el cual la reproducción sexual crea diferentes presiones de selección en hembras
y machos. Luego consideraremos trabajos recientes sobre las consecuencias evolutivas de
estas presiones selectivas diferenciales en distintas especies.
9.1.
La clave para explicar el
dimorfismo sexual es
reconocer que la reproducción
sexual impone diferentes
presiones selectivas a las
hembras y a los machos.
Asimetrías en la reproducción sexual
En esta sección discutiremos que la reproducción sexual crea presiones de selección diferentes para hembras y machos. El desarrollo lógico que seguiremos para apoyar esta
conclusión fue claramente articulado por A. J. Bateman (1948) y perfeccionado por Robert
Trivers (1972). Éste depende de un hecho crucial: los huevos (o la preñez) son más costosos que la eyaculación. En términos más generales las hembras invierten, típicamente, más
en la descendencia que los machos. Por inversión queremos decir la cantidad de energía y
tiempo gastados en producir un descendiente y cuidar de él.Al final, esta inversión paterna se mide en eficacia. El cuidado parental aumenta el éxito reproductivo de los descendientes que lo reciben.Al mismo tiempo, reduce el resto del éxito reproductivo que el padre
inversor podría alcanzar en el futuro al reducir el número de descendientes adicionales.
Consideremos la inversión en cuidado parental hecha por el macho y la hembra de los
orangutanes. Los orangutanes adultos de sexo opuesto se toleran mutuamente con la única
finalidad del apareamiento (Nowak 1991). Tras un pequeño contacto, que incluye una
cópula que dura alrededor de 15 minutos, el macho y la hembra siguen caminos separados. Si se consigue un embarazo, entonces la madre, que pesa cerca de 40 kilogramos, cargará al feto durante 8 meses, dará a luz un bebé de 1 kilogramo, lo cuidará cerca de 3 años
y continuará protegiéndole hasta que alcance una edad de 7 u 8 años. Para el padre, que
pesa aproximadamente 70 kilogramos, el principio y el final de su dedicación parental son
unos gramos de semen, que puede reponer en cuestión de horas o días. En su patrón de
cuidado parental, los orangutanes son mamíferos típicos. En más del 90% de las especies
de mamíferos, las hembras proporcionan sustancial cuidado parental mientras que los
machos nada (Woodroffe y Vincent 1994).
Dado que las hembras de los mamíferos proporcionan semejante cuidado parental, los
mamíferos representan un ejemplo extremo de la disparidad de inversiones. En la mayoría de especies animales, ninguno de los padres se preocupa por los jóvenes: las parejas simplemente producen huevos, los fertilizan y los abandonan. Pero también en estas especies
las hembras hacen una mayor inversión en la descendencia. Los huevos son normalmente grandes y ricos, con una gran reserva de energía y nutrientes. Piense en los huevos de
las tortugas marinas, algunos de los cuales son tan grandes como un huevo de gallina. En
el lado opuesto, la mayoría del espermatozoide no es más que DNA con un propulsor.
Incluso aunque en una única eyaculación se liberan cientos de millones de espermatozoides, el eyaculado rara vez representa algo más que una ínfima fracción de la inversión
contenida en un puñado de huevos.
Reconocer que los huevos son más caros que las eyaculaciones nos permite predecir
que habrá grandes diferencias en los factores que limitan el período reproductivo de hembras y machos. El potencial reproductivo de una hembra es relativamente pequeño, y su
éxito reproductivo eficaz estará, seguramente, más limitado por el número de huevos que
pueda producir (o embarazos que pueda tener) que en el número de machos a los que
pueda convencer para aparearse con ella. Por el contrario, el potencial reproductor de un
macho es relativamente grande, y su potencial reproductivo eficaz estará limitado por el
número de eyaculaciones que pueda hacer. En otras palabras, predecimos la siguiente asimetría fundamental: el acceso a las hembras será el factor limitante para los machos, pero
el acceso a los machos no lo será de las hembras.
Capítulo 9 Selección sexual 293
Límites asimétricos del éxito reproductor en las moscas de la fruta
A. J. Bateman (1948) comprobó esta predicción en poblaciones de laboratorio de la
mosca de la fruta, Drosophila melanogaster. Bateman fundó pequeñas poblaciones de moscas en botellas. Cada población estaba formada por tres hembras vírgenes y por tres
machos vírgenes. Cada mosca era heterozigota para una única mutación genética dominante: una que generaba alas curvadas, por ejemplo, o regiones del cuerpo sin quetas. Bateman permitió que las moscas se apareasen entre ellas y que la descendencia llegara hasta
adultos. Fue capaz de identificar aproximadamente la mitad de los descendientes de cada
padre con solo mirar qué mutaciones heredaban. De este modo, Bateman pudo deducir
qué hembras se habían cruzado y con qué machos, y viceversa.También pudo calcular el
número relativo de descendientes que produjo cada padre. Note que los machos y las
hembras que vivían juntos en una botella todos tuvieron exactamente tres parejas potenciales. Su número real de parejas varió de cero a tres. Si los factores que limitan el éxito
reproductor son diferentes para ambos sexos, entonces los datos para los dos sexos deberán mostrar diferentes relaciones entre el éxito reproductor y el número de parejas reales.
Los resultados combinados de dos docenas de experimentos aparecen en la Figura 9.4.
Estos resultados confirman la predicción de que los dos sexos difieren en los factores que
limitan su éxito reproductor:
• Para los machos, el éxito reproductor aumenta proporcionalmente con el número de
parejas (Figura 9.4a). Los machos también muestran considerable variación en el número de parejas, con muchos machos en las categorías extremas con cero y tres parejas
(Figura 9.4b). Estos dos patrones se combinan para producir considerable variación en
el éxito reproductor entre machos (Figura 9.4c): los machos con tres parejas eran grandes ganadores; los machos con ninguno, grandes perdedores.
Dado que las hembras
invierten normalmente más en
cada descendiente que los
machos, el éxito reproductor
de una hembra está limitado
por el número de huevos que
puede producir. Por el
contrario, el éxito reproductor
de un macho está limitado por
el número de hembras con las
Éxito reproductor
que se puede aparear.
Machos
125
100
Hembras
75
50
25
0
0
1
2
3
Número de parejas
Número de
moscas
(b) Variación en el número de parejas:
Machos
Hembras
30
39
23
28
14
5
0
4
1
1
2
3
0
Número de parejas
1
2
3
Número de parejas
(c) Varianza en el éxito reproductor en los cuatro grupos de experimentos:
Grupo 1
Varianza de los machos
1.604
Varianza de los machos
Varianza de las hembras Varianza de las hembras
985
1,63
Grupo 2
1.700
209
Grupo 3
2.798
993
8,14
2,82
Grupo 4
1.098
277
3,97
Figura 9.4 Resultado combinado de los
experimentos de Bateman En (c) la
variación en el éxito reproductor se caracteriza
por la varianza en el número de descendientes
entre individuos. Para calcular la varianza de
una lista de números, primero calcule la media.
Después tome la diferencia entre cada número
y la media. Estas diferencias se llaman
desviaciones de la media. Ahora calcule el
cuadrado de cada desviación. La media de las
desviaciones al cuadrado es la varianza.
Cuanto mayor es la variación entre los números
de una lista, mayor será la varianza.
De Bateman (1948).
294 PARTE III Adaptación
• Para las hembras, el éxito reproductor no aumentó sustancialmente más allá de una pareja(Figura 9.4a). Más aún, las hembras mostraban menos variación en el número de parejas, teniendo la mayoría una o dos (Figura 9.4b). Estos dos patrones se combinan para
producir poca variación entre hembras para el éxito reproductor (Figura 9.4c): había un
número limitado de grandes ganadores y grandes perdedoras.
En las poblaciones experimentales de Bateman, quedó demostrado que la disponibilidad
de parejas era un factor limitante para los machos, pero no para las hembras. La selección
sexual, o variación en eficacia debida a la variación en la capacidad de conseguir parejas,
era mucho más fuerte en machos que en hembras. Los biólogos evolutivos creen que éste
es un patrón muy general (aunque no universal).Y tiene importantes consecuencias en
cómo los miembros de cada sexo afrontan el apareamiento.
Consecuencias en el comportamiento de los límites asimétricos
de la eficacia
La asimetría en los factores que limitan el éxito reproductor de las hembras y los
machos nos permite predecir diferencias en el comportamiento de apareamiento de
ambos sexos:
La teoría de la selección sexual
predice que los machos
competirán entre ellos por los
apareamientos y que las
hembras serán selectivas.
• Los machos deben ser competitivos. Si la eficacia de un macho está limitada por su acceso a las hembras, entonces podemos predecir que los machos competirán entre ellos por
las oportunidades de aparearse.
• Las hembras deben ser selectivas. Si la eficacia de una hembra no está limitada por las
oportunidades para aparearse, pero como cada apareamiento puede suponer un enorme compromiso de la hembra para con la descendencia, entonces podemos predecir que
las hembras serán selectivas para decidir con quién se aparearán.
La competencia entre machos por conseguir parejas y la selectividad de las hembras pueden actuar en dos direcciones. Primero, en especies en las que los machos pueden monopolizar directamente el acceso a las hembras, los machos normalmente pelearán por tal
monopolio. Las hembras se aparearán con los ganadores. Esta forma de selección sexual
se conoce como selección intrasexual, ya que el suceso clave que determina el éxito
reproductor implica interacciones entre miembros del mismo sexo (la lucha de los
machos). Segundo, en especies en las que los machos no controlan directamente el acceso a las hembras, los machos se exhiben ante las hembras. Las hembras entonces eligen
entre los galanes. Esta forma de selección sexual se llama selección intersexual, ya que
el suceso clave que determina el éxito reproductor implica interacciones entre miembros
de ambos sexos (las hembras eligen a los machos).
Muchos lectores habrán notado que nuestro tratamiento de las asimetrías en la reproducción sexual está lleno de falsas generalizaciones. Queremos enfatizar que las expectativas de luchas entre machos y de elección por las hembras no están basadas en nada
inherente a la condición de ser macho o hembra en sí misma, sino en la observación de
que las hembras invierten, normalmente, mucho más por descendiente que los machos.
Este patrón de inversiones se rompe en un gran número de especies. Cuando los machos
cuidan de los jóvenes, por ejemplo, su inversión en la descendencia puede ser comparable, o incluso mayor, que la de la hembra. Especies con cuidado del padre incluyen a los
humanos, muchos peces, cerca del 5% de las ranas y alrededor del 90% de las aves. Cuando, de hecho, los machos invierten más en la descendencia que las hembras, el acceso a las
parejas será un factor limitante para ellas. Cuando el acceso a las parejas es limitante para
las hembras en lugar de para los machos, predeciremos que las hembras competirán entre
ellas para acceder a los machos, y que los machos serán selectivos. Hacia el final de este capí-
Capítulo 9 Selección sexual 295
tulo, volveremos a las especies con los “papeles sexuales cambiados” para ver si hay excepciones que prueben las reglas de la selección sexual. Por ahora, no obstante, nos centraremos en la selección sexual mediante competencia entre machos y elección femenina.
9.2.
Competencia entre machos: selección intrasexual
La selección sexual por competencia entre machos ocurre cuando éstos monopolizan el
acceso a las hembras. Los machos pueden monopolizar el acceso a las hembras ejerciendo un control directo sobre ellas o mediante el control de algún recurso importante para
ellas. En esta sección, consideraremos ejemplos de tres clases de competencia entre machos:
combate directo, competencia espermática e infanticidio.
Combate
El combate directo es la forma más obvia de competencia entre machos por las parejas.
La selección intrasexual, que implique un combate entre machos por el acceso a las hembras, favorecerá caracteres morfológicos tales como un gran tamaño corporal, armas y
defensas.También seleccionará tácticas eficientes.
Nuestro ejemplo son las iguanas marinas (Amblyrhynchus cristatus) de las Islas Galápagos (Figura 9.5). Entre todos los lagartos, las iguanas marinas tienen un peculiar estilo de
vida. Se alimentan de las algas de la zona intermareal, y entre los momentos de pasto, descansan sobre las rocas al borde del agua. Este descanso calienta a las iguanas, lo que ayuda
a la digestión y las prepara para la siguiente inmersión en las frías aguas. Las iguanas marinas alcanzan diferentes tamaños en diferentes islas, pero, como ya hemos mencionado anteriormente, en cada isla los machos son más grandes que las hembras (Figura 9.6a).
El dimorfismo sexual de las iguanas marinas constituye un ejemplo excelente para el
estudio de la selección sexual, ya que sabemos mucho sobre cómo el tamaño de la iguana marina está afectado por la selección natural (Wikelski et al. 1997;Wikelski y Trillmich
1997). Martín Wikelski y Fritz Trillmich documentaron el efecto de la selección natural
sobre el tamaño corporal mediante la monitorización, durante dos años, de la supervivencia de individuos marcados en dos islas. La selección natural fue mucho más severa en
la isla Genovesa que en la de Santa Fé, pero claramente presente en ambas islas. Más aún,
la selección era estabilizadora; las iguanas con tamaños intermedios sobrevivían con mayor
probabilidad que las pequeñas o grandes (Figura 9.6b).
Hay pocos agentes potenciales para esta selección natural sobre el tamaño corporal. Las
iguanas marinas no compiten con otras especies por la comida y, virtualmente, carecen de
La competencia entre machos
puede tomar la forma de un
combate para ver quién accede
a las hembras.
Figura 9.5 Una iguana marina de las
Galápagos comiendo algas de la zona
intermareal (Martín Wikelski, University of
Illinois at Urbana-Champaign).
296 PARTE III Adaptación
Machos
Santa Fé
(b)
n=
2 51 35 27 27 37 28 15 104 79 6
60 42 32 62 110 103 9
100
80
60
40
20
0
Hembras
40
20
0
Machos
Genovesa
40
20
0
Hembras
Genovesa
Santa Fé
50
Santa Fé
Supervivencia (%)
(a) Histogramas que muestran la distribución de
tamaños de machos y hembras de iguanas
marinas en dos islas diferentes de las Galápagos,
Genovesa y Santa Fé. Los asteriscos marcan el
tamaño máximo que las iguanas eran capaces de
mantener durante dos años diferentes (19911992 y 1992-1993). (b) Tasas de supervivencia
de individuos marcados de distintos tamaños
(longitud de las aperturas del hocico, en mm) de
marzo de 1991 a marzo de 1992 en la Genovesa
y de febrero de 1990 a febrero de 1992 en Santa
Fé. Los tamaños muestrales, o número de
individuos en cada grupo, vienen dados por n.
De Wikelski y Trillmich (1997).
Frecuencia
Figura 9.6 Selección natural para el
tamaño del cuerpo en las iguanas marinas
(a) 60
40
20
0
Hembras
Machos
0
n=
100
50
0
12 19 42 35 44 15
6 22 63 71
Genovesa
Hembras
Machos
110 140 170 200 230 260 290 320 350 380 410 440
-140 -200 -260 -320 -380 >410
Longitud de la apertura del hocico (mm)
Categorías del tamaño (mm)
depredadores.A parte de la competencia por la reproducción, lo único con lo que las iguanas tienen que lidiar es la competencia entre ellas por la comida.
Las iguanas más grandes recogen más algas, y esto les proporciona más energía, pero
también gastan más energía metabólica.Wikelski y sus colaboradores (1997) observaron
que durante dos años diferentes las iguanas pequeñas tenían superávit de energía, pero las
grandes tenían déficit. Consecuentes con la hipótesis de que la disponibilidad de comida
limita el tamaño corporal, las iguanas de Santa Fé y de Genovesa perdieron peso durante
los años 1991-1992, un mal año para las algas, y 1992-1993, un año algo mejor (véase también Wikelski y Thom 2000). El tamaño mayor en el cual las iguanas fueron capaces de
mantener su peso se indica mediante asteriscos en la Figura 9.6a.
Ahora compare la Figura 9.6a con la 9.6b. El tamaño máximo en el cual las iguanas
pueden mantener su peso es muy parecido al tamaño óptimo para su supervivencia. Más
aún, las hembras más grandes de cada población están próximas al tamaño óptimo de
supervivencia, pero los machos más grandes están muy por encima del tamaño óptimo.
Así, el tamaño corporal de los machos de iguana marina constituye un rompecabezas evolutivo: no podemos explicarlo por selección natural ya que, como Wikelski y Trillmich
demostraron, la selección natural actúa en su contra. Es el típico rompecabezas para el cuál
Darwin invocó a la selección sexual.
Como ya discutimos anteriormente, un punto crucial en la selección sexual es la
inversión relativa en el cuidado parental de la descendencia hecho por machos y hembras.
En las iguanas marinas, el cuidado de las hembras es muchísimo mayor. Cada hembra excava un nido en la arena, alejado de las áreas de descanso y comida, entierra a sus huevos,
cuida del nido durante unos pocos días y después lo abandona (Rauch 1988). Los machos
no proporcionan ningún cuidado parental. Así pues, la inversión parental de las hembras
consiste principalmente en poner huevos y la de los machos exclusivamente en eyacular.
Las hembras realizan una única puesta anual de entre uno y seis huevos, en la que invierten aproximadamente el 20% de su masa corporal (Rauch 1985; Rauch 1988;Wikelski y
Trillmich 1997). Comparado con la inversión femenina, el coste de la única eyaculación
necesaria para fecundar todos los huevos de la puesta es irrisoria. Esta diferencia en la
inversión sugiere que el éxito potencial reproductivo máximo de los machos es mucho
mayor que el de las hembras. El número de parejas a lo largo de la vida limitará el éxito
reproductor de los machos, no así el de las hembras.
El comportamiento reproductor de las iguanas marinas es consecuente con estas deducciones. Las hembras solamente copulan una vez en cada estación reproductiva. Martín
Capítulo 9 Selección sexual 297
Figura 9.7 Machos de iguana marina combatiendo (Martín Wikelski,
University of Illinois at Urbana-Champaign).
Wikelski, Silke Bäurle y sus asistentes de campo siguieron a varias docenas de hembras
marcadas en la Genovesa. Los investigadores observaron a las hembras cada día desde el
alba hasta el crepúsculo durante el mes de duración de la estación de apareamiento en
1992-1993 y en 1993-1994 (Wikelski y Bäurle 1996).También observaron a las hembras
marcadas cada día desde el amanecer hasta el anochecer durante la época de anidamiento posterior. Cada hembra marcada que construyó un nido y puso huevos había sido vista
copulando, pero ninguna fue vista copulando más de una vez. Los machos, por contra,
intentaban copular muchas veces con muchas hembras diferentes; pero una oportunidad
para copular es un privilegio por el que un macho de iguana debe luchar (Figura 9.7).
Con anterioridad a la época anual de apareamiento, los machos se reparten territorios sobre las rocas en las que las hembras descansan entre zambullidas. En estos territorios pequeños, abigarrados (Figura 9.8a), los machos intentan reclamar y mantener
terreno desbancando a los intrusos. Los enfrentamientos comienzan con desafiantes
balanceos de la cabeza y aumentan de intensidad hasta choques y empujones con la
Mar
(a)
(b)
6
57
71
62
75
76
78
131
72
69 67 60
59
64
63 N
5
66
65
4
132
(29)
50
3m
10
Número de machos
80
8
6
4
2
0
0 1 2 3 4 5 6 7 8 91 0
Número de cópulas
4 5
Figura 9.8 Éxito reproductor de los machos de iguana marina (a) Un grupo de territorios de
apareamiento de iguanas en el islote Caamaño, Galápagos. Las líneas muestran los límites de los territorios
de apareamiento el 16 de enero de 1978; los números identifican a los propietarios del territorio. Como la
escala del mapa muestra, los territorios de apareamiento son solamente de unos pocos metros cuadrados.
El asterisco azul oscuro indica dónde se sentó Krisztina Trillmich para ver a las iguanas. (El islote de
Caamaño tiene sólo 880 m de costa y alberga una población de cerca de 2000 iguanas.) de Trillmich
(1983). (b) Histograma que muestra la variación en el número de cópulas obtenidas por los machos en los
territorios indicados en (a). Note la interrupción en la escala del eje horizontal; el macho más exitoso, la
iguana 59, consiguió más de cuatro veces el número de cópulas que sus rivales. El histograma incluye sólo
a los machos que reclamaron un territorio, durante al menos un período corto, durante la estación de
apareamiento. De Trillmich (1983).
298 PARTE III Adaptación
Los machos de iguana marina
pelean por los territorios
donde se congregan las
hembras. Las iguanas grandes
vencen en más combates,
consiguen mejores territorios
y, consecuentemente, copulan
con más hembras. Este patrón
de selección sexual conduce a
la evolución de tamaños
corporales grandes en los
machos.
cabeza. Si ningún macho se retira, las peleas pueden acabar con mordiscos que causan
importantes heridas en la cabeza, cuello, ijadas y piernas (Trillmich 1983). Mientras que
un macho posea un territorio, tiene un derecho, más o menos, exclusivo para aparearse con las hembras que usen ese territorio como sitio de descanso (Rauch 1985). Dado
que sólo algunos machos reclaman territorios, y algunos se las ingenian para mantenerlos
más tiempo que otros, existe una gran variación entre machos en el número de cópulas conseguidas (Figura 9.8b).
Como reclamar y mantener un territorio implica combatir con otros machos, los
machos grandes tienden a ganar. En la colonia de iguanas que Krisztina Trillmich (1983)
estudió en la isla Caamaño, el macho que consiguió 45 cópulas (Figura 9.8b), muchas más
que cualquier otro macho, fue la iguana 59 (su territorio se muestra en la Figura 9.8a).
Su vecino, la iguana 65, fue el segundo con más éxito, con 10 cópulas. Sus territorios eran
los sitios favoritos de las hembras para descansar a primera hora de la mañana o a última
de la tarde.Trillmich informó que la iguana 59 era el macho más grande de la colonia,
y que para reclamar su territorio tuvo que expulsar a otros cuatro machos que intentaron
conquistarlo; y que durante su posesión, perdió partes del mismo en beneficio de cuatro
machos vecinos que expandían sus territorios desde los lados.Wikelski y sus colaboradores estudiaron colonias de iguanas en la Genovesa y Santa Fé (Wikelski et al. 1996;
Wikelski y Trillmich 1997). En consecuencia con las observaciones de Krisztina Trillmich, estos investigadores también encontraron que el tamaño medio de los machos que
copularon era significativamente mayor que el de los machos que intentaban copular sin
éxito (Tabla 9.1).
Si asumimos que, en las iguanas marinas, el tamaño corporal es heredable, entonces
tenemos variación, herencia y éxito reproductor diferencial. Éstos son los elementos invocados por la selección sexual: tenemos una explicación de por qué las iguanas marinas son
mucho más grandes que el tamaño óptimo para la supervivencia. Las iguanas marinas
macho se hacen grandes ya que los machos grandes consiguen más parejas y transmiten
más copias de sus genes para “macho grande”.
Combates entre machos, similar a los de las iguanas marinas, ocurren en un gran
número de especies, incluyendo al ciervo rojo mostrado en la Figura 9.1. Cuando las
Tabla 9.1 Diferenciales de selección sexual para el tamaño corporal del
macho en las colonias de iguana marina de Santa Fé y Genovesa
El tamaño corporal se da como longitud de la apertura del hocico (LAH). Los diferenciales de
selección estandarizados (ver Capítulo 7) es la diferencia entre el tamaño corporal promedio de
los machos que copularon al menos una vez y el de todos los machos que intentaron copular,
expresado en desviaciones estándar de la distribución del tamaño corporal de todos los machos
que intentaron copular. (La desviación estándar es la raíz cuadrada de la varianza.) Ambos
diferenciales de selección estandarizados son positivos (P < 0,05), indicando que los machos que
copularon eran mayores en promedio que los machos que intentaron copular. De Wikelski y
Trillmich (1997).
N
Tamaño
Desviación
Diferencial
promedio
estándar
de selección
(LAH)
estandarizado
Santa Fé
Machos que copularon
253
401
13
Todos los machos que lo intentaron
343
390
26
25
243
26
147
227
21
0,42
Genovesa
Machos que copularon
Todos los machos que lo intentaron
0,77
Capítulo 9 Selección sexual 299
oportunidades de apareamiento son un recurso limitante para los machos, y cuando éstos
pueden monopolizar bien a las propias hembras, bien algún recurso vital para ellas que
las atraerá, entonces los machos lucharán entre ellos por el acceso a las hembras o al
recurso.Además de un mayor tamaño corporal, este tipo de selección sexual conlleva la
evolución de otros caracteres útiles en un combate, tales como las armas o los blindajes.
El combate entre machos también puede causar la evolución de estrategias alternativas
(ver el Cuadro 9.1).
Competencia espermática
La competencia entre machos no se detiene necesariamente cuando acaba la cópula. El
determinante real del éxito reproductor de un macho no es el que copule, sino el que