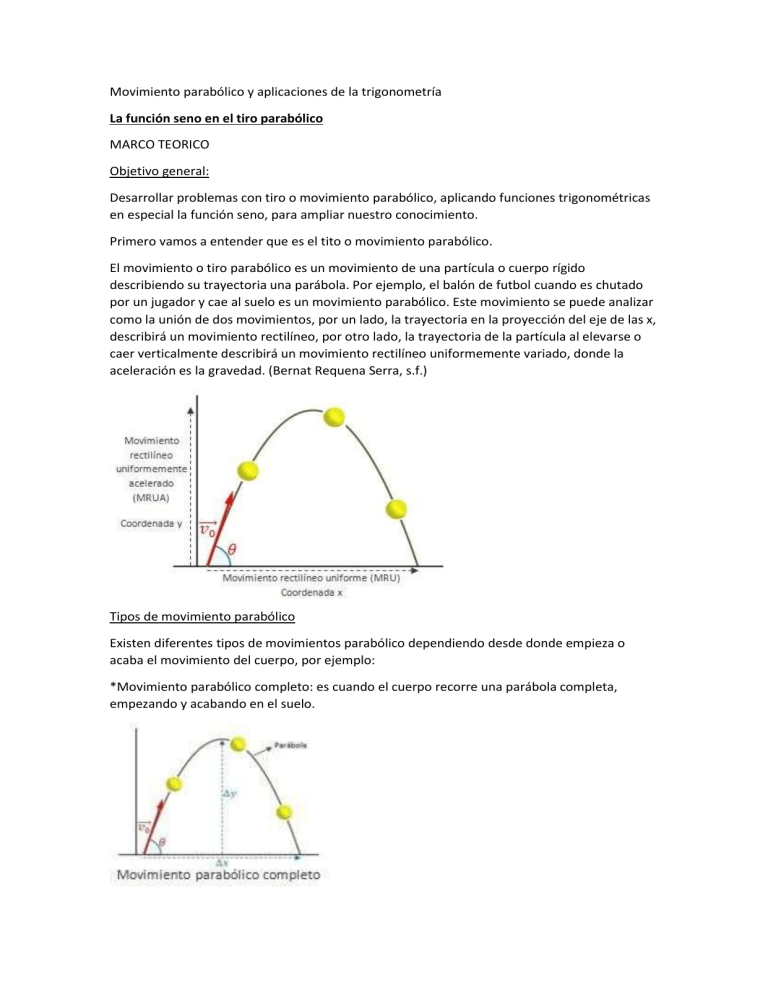
Movimiento parabólico y aplicaciones de la trigonometría La función seno en el tiro parabólico MARCO TEORICO Objetivo general: Desarrollar problemas con tiro o movimiento parabólico, aplicando funciones trigonométricas en especial la función seno, para ampliar nuestro conocimiento. Primero vamos a entender que es el tito o movimiento parabólico. El movimiento o tiro parabólico es un movimiento de una partícula o cuerpo rígido describiendo su trayectoria una parábola. Por ejemplo, el balón de futbol cuando es chutado por un jugador y cae al suelo es un movimiento parabólico. Este movimiento se puede analizar como la unión de dos movimientos, por un lado, la trayectoria en la proyección del eje de las x, describirá un movimiento rectilíneo, por otro lado, la trayectoria de la partícula al elevarse o caer verticalmente describirá un movimiento rectilíneo uniformemente variado, donde la aceleración es la gravedad. (Bernat Requena Serra, s.f.) Tipos de movimiento parabólico Existen diferentes tipos de movimientos parabólico dependiendo desde donde empieza o acaba el movimiento del cuerpo, por ejemplo: *Movimiento parabólico completo: es cuando el cuerpo recorre una parábola completa, empezando y acabando en el suelo. *Movimiento de media parábola: tambien conocido como tiro parabólico completo, el cuerpo empieza el movimiento desde una cierta altura y es lanzado parabólicamente con una fuerza horizontal, en un punto que seria el punto mas lato de una parábola completa ideal Otros movimientos parabólicos: existen muchos casos particularmente del movimiento parabólico, por ejemplo, el lanzamiento de una peloto desde el suelo a la terraza de una casa o el lanzamiento a canasta de un jugador de baloncesto, siempre son tramos de una teoría parábola completa. (Bernat Requena Serra, s.f.) Velocidad Velocidad inicial del cuerpo Vo, tiene dos componentes, la componente en el eje X y la componente en el eje Y. El vector Vo de la velocidad es la suma de los dos vectores componentes: La componente horizontal de la velocidad Vx, es constante en toda la trayectoria ya que es un movimiento rectilíneo uniforme, la componente vertical de la velocidad Vy disminuye inicialmente por la gravedad, hasta hacerse nula en el punto mas alto de la trayectoria. (Bernat Requena Serra, s.f.) Ecuaciones para el movimiento horizontal y vertical MRU X=Xo+Vx.t Vx=Vox=Vx=la velocidad es una constante MRUV y=Yo+1/2(Voy+Vy)t Vx=Voy-gt Y=Yo+Voy.t-1/2gt^2 Vy^2=Voy^2-2g(Y-Yo) (Areaciencias, s.f.) Formulas del movimiento parabólico Aceleración La aceleración solamente esta presente en la componente vertical, el movimiento horizontal es uniforme mientras que sobre la componente e influye la aceleración de la gravedad, que hace que se frene el cuerpo hasta volver a acelerarse al descender y caer al suelo. (Bernat Requena Serra, s.f.) Siendo “g” la gravedad Posición La posición del objeto interviene las fórmulas de la posición del movimiento rectilíneo uniformemente y la posición del movimiento rectilíneo uniformemente variado. El primer sumando se corresponde con la proyección horizontal y se debe al MRU mientras que el segundo sumando es la proyección vertical de la posición, y se debe al MRUV. Siendo (Xo, Yo) las coordenadas de la posición inicial, θ el ángulo de salida, g la aceleración de la gravedad y t el tiempo transcurrido en un tramo de la trayectoria. (Bernat Requena Serra, s.f.) Tiempo de vuelo El tiempo de vuelo es aquel que invierte el cuerpo o el proyectil en realizar un movimiento parabólico completo hasta llegar a la superficie que se desea que llegue, es decir, a la misma altura del punto de donde salió. (Bernat Requena Serra, s.f.) Alcance horizontal máximo La partícula o cuerpo llegara a su alcance horizontal máximo, cuando llegue al suelo, es decir, cuando la altura vuelva a ser cero. Podemos calcular el alcance sin saber el tiempo que ha tardado en recorrer la parábola la partícula o conociéndolo. (Bernat Requena Serra, s.f.) La fórmula del alcance horizontal máximo, siendo el tiempo de trayectoria de la partícula desconocido. Siendo (Xo, Yo) la posición inicial, el ángulo de salida y g la aceleración de la gravedad. Y por las razones trigonométricas del ángulo doble. Altura máxima Un cuerpo tirado con tiro parabólico alcanzara una altura máxima antes de empezar a descender, esta altura depende de la velocidad con la que ha sido lanzada, es obvio que, a mayor velocidad, mayor será la altura alcanzada y a menor velocidad, será menor la altura alcanzada. Para calcular la altura máxima alcanzada, recurrimos a la ecuación del tiro vertical que indica que el cuadrado de la velocidad final es igual a resta del cuadrado de la velocidad inicial vertical menos el doble de la gravedad por la altura alcanzada, desde dicha ecuación podremos despejar a altura alcanzada, ya que se sabe que la velocidad final, es decir, que en el punto más alto será cero. (Curso de física, s.f.) Despeje de ecuaciones Para poder despejar formulas tenemos que seguir ciertos pasos, los cuales son: *Todo numero o toda variable que este sumando pasa al otro lado restando y viceversa todo número que está restando pasa sumando al otro lado 4+x=5 X=5-4 X=1 _x-10=5 X=5+10 X=15 *Todo número que es multiplicando pasa al otro lado dividiendo y viceversa todo numero que este dividiendo pasa al otro lado multiplicando 4x+5=4 4x=4-5 4x=-1 X=-1/4 _3/x+5=7 3/x=7-5 3/x=2 X=2*3 X=6 (autoría propia) Planteamiento del problema Vamos a resolver un problema utilizando teoría, vamos a calcular el ángulo en el que debe ser disparado el proyectil para que alcance una altura máxima de 610 metros, y tambien indicar si el proyectil mencionado podrá llegar hasta 915 metros de altura. Y para resolver esto se va a necesitar el siguiente modelo matemático, para esto vamos a aplicar el análisis de datos, el despejar formulas y tambien implementar los datos bien en el modelo matemático Resultado Conclusiones Bi Bibliografía Areaciencias. (s.f.). Obtenido de Areaciencias: https://www.areaciencias.com/fisica/tiroparabolico-formulas/ Bernat Requena Serra. (s.f.). UNIVERSO FORMULAS: TU WEB DE CIENCIA. Obtenido de UNIVERSO FORMULAS: TU WEB DE CIENCIA: https://www.universoformulas.com/fisica/cinematica/movimiento-parabolico/ Curso de física. (s.f.). Obtenido de Curso de física: https://enfisica.com/cinematicas/movimiento-parabolico/ bliografía





