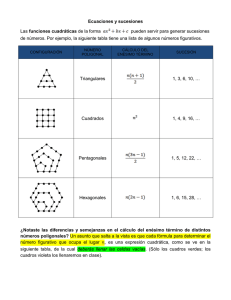
Sucesión cubica: Comprueba que la secuencia sea una secuencia cúbica tomando la diferencia entre cada par consecutivo de números (llamado el "método de las diferencias comunes"). Sigue tomando las diferencias de las diferencias de tres veces en total, momento en el que todas las diferencias deben ser iguales. Ejemplo: Secuencia: 11, 27, 59, 113, 195, 311 Diferencias: 16 32 54 82 116 16 22 28 34 6 6 6 2 Establece un sistema de cuatro ecuaciones con cuatro variables para encontrar los coeficientes a, b, c y d. Utiliza los valores indicados en la secuencia como si fueran puntos en un gráfico en la forma (n, n-ésimo término en secuencia). Es más fácil comenzar con los primeros 4 términos, ya que suelen ser números más pequeños o más sencillos para trabajar. Ejemplo: (1, 11), (2, 27), (3, 59), (4, 113) Ingrésalos a: an ^ 3 + bn ^ 2 + cn + d = enésimo término en la secuencia a + b + c + d = 11 8a + 4b + 2c + d = 27 27a + 9b + 3c + d = 59 64a + 16b + 4c + d = 113 3 Resuelve el sistema de 4 ecuaciones usando tu método favorito. En este ejemplo, los resultados son: a = 1, b = 2, c = 3, d = 5. 4 Escribe la ecuación para el enésimo término de una secuencia utilizando los coeficientes encontrados. ejemplo: enésimo término de la secuencia = n ^ 3 + 2n ^ 2 + 3n + 5 5 Ingresa el valor deseado de n en la ecuación y calcula el enésimo término de la secuencia. ejemplo: n = 10 10 ^ 3 + 2 * 10 ^ 2 + 3 * 10 + 5 = 1235