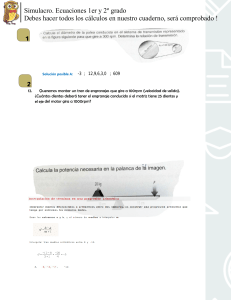
UNIVERSIDAD TECNOLOGICA DEL PERU ELEMENTOS DE MAQUINAS Y FUNDAMENTOS DE DISEÑO Título: Tercer Avance de Trabajo Bomba de Pistones Alumnas: LLANQUE PERALTA JOSE 1420030 VIVANCO SALCEDO DARYL U18209794 ANGEL HUAYNATES HUAMAN U17305810 LUIS FLORES COLLACSO 1111552 Profesor: LOZANO SALAZAR JORGE LUIS Lima, 03 de AGOSTO del 2021 INDICE 1. INTRODUCCION ................................................................................................................ 6 2. MARCO TEORICO ............................................................................................................. 6 2.1 Diagrama cinemático ................................................................................................... 6 2.2 Análisis de posición ..................................................................................................... 7 2.3 Rueda dentada ............................................................................................................ 8 2.4 Engranajes .................................................................................................................. 8 2.5 Relación de transmisión ............................................................................................... 9 3. ESQUEMA CINEMATICO ................................................................................................... 9 4. GRADOS DE LIBERTAD ...................................................................................................10 5. ANALISIS DE POSICION ..................................................................................................11 6. ANALISIS DE VELOCIDAD ...............................................................................................11 7. 8. 6.1 Conversión de RPM ....................................................................................................12 6.2 Velocidad Punto A: .....................................................................................................12 6.3 Velocidad Tramo BA: ..................................................................................................12 6.4 Velocidad Punto B: .....................................................................................................12 CALCULO DE ENGRANAJE .............................................................................................13 7.1 Cálculo de relación de transmisión (i): ........................................................................13 7.2 Numero de dientes......................................................................................................13 7.3 Angulo de inclinación (β) .............................................................................................14 7.4 Angulo de presión (α)..................................................................................................14 7.5 Modulo ........................................................................................................................14 7.6 Cálculos básicos para engranajes ..............................................................................15 SELECCIÓN DEL MATERIAL............................................................................................17 8.1 Flujo de la potencia a través de un par de engranes ...................................................17 Página 1 | 45 8.2 Ecuación de Lewis ......................................................................................................18 8.3 Cálculo de ecuación de Lewis .....................................................................................20 8.4 Factor de geometría....................................................................................................21 8.5 Cálculo de factor de geometría ...................................................................................22 8.6 Numero de esfuerzo flexionante: ................................................................................22 8.7 Factor de sobrecarga (Ko) ..........................................................................................23 8.8 Factor de tamaño (Ks) ................................................................................................23 8.9 Factor de distribución de carga (Km) ..........................................................................23 8.10 Factor de espesor de orilla (Kb) ..................................................................................25 8.11 Factor dinámico (Kv) ...................................................................................................26 8.12 Resultados de esfuerzo Flexionante ...........................................................................27 8.13 Números de esfuerzo flexionante admisibles ajustados: .............................................28 8.14 Factor de ciclos de esfuerzo (YN) ................................................................................29 8.15 Factor de seguridad (SF) ............................................................................................30 8.16 Resultados de esfuerzo Flexionante admisible ...........................................................32 9. CALCULO PARA EL DISEÑO DE EJE ..............................................................................34 9.1 Datos ..........................................................................................................................34 9.2 Cálculo del par de torsión: ..........................................................................................35 9.3 Diagrama de cuerpo libre de pares de torsión y de par de torsión: .............................36 9.4 Cálculo de fuerzas externas........................................................................................37 9.5 Cálculo de reacciones.................................................................................................37 9.6 Cálculo del diámetro en la sección más cargada ........................................................40 10. 10.1 SELECCIÓN DE CHAVETA PARA SISTEMA ................................................................42 ANÁLISIS DE ESFUERZOS PARA DETERMINAR LA LONGITUD DE LAS CHAVETAS 42 11. CONCLUSIONES ...........................................................................................................44 Página 2 | 45 INDICE DE IMAGENES Imagen 1 Diseño de bomba de pistón ........................................................................................ 6 Imagen 2 Diagramas cinemáticos .............................................................................................. 7 Imagen 3 Análisis cinemático ..................................................................................................... 7 Imagen 4 Rueda dentada y Engranajes ..................................................................................... 8 Imagen 5 Relación de transmisión ............................................................................................. 9 Imagen 6 Diseño y análisis cinemático ...................................................................................... 9 Imagen 7 Esquema cinemático .................................................................................................10 Imagen 8 Diagrama de análisis de posición ..............................................................................11 Imagen 9 Diagrama de análisis de velocidades ........................................................................11 Imagen 10 Módulos normalizados.............................................................................................14 Imagen 11 Diagrama de fuerzas en el diente. ...........................................................................17 Imagen 12 Factor de Lewis .......................................................................................................19 Imagen 13 Selección de factor J ...............................................................................................21 Imagen 14 Factores de sobrecarga sugeridos. K0 ....................................................................23 Imagen 15 Factores de tamaño sugeridos Ks ...........................................................................23 Imagen 16 Factor de proporción Cpf .........................................................................................24 Imagen 17 Factor de alineamiento de engranado Cma .............................................................24 Imagen 18 Factor de espesor de orilla ......................................................................................25 Imagen 19 Factor dinámico Kv..................................................................................................26 Imagen 20 Factor admisible Sat ................................................................................................28 Imagen 21 Factor de confiabilidad Kr ........................................................................................28 Imagen 22 Vida de diseño recomendada ..................................................................................29 Imagen 23 Factor de resistencia flexionante por ciclos de esfuerzo Yn ....................................30 Imagen 24 Numero de esfuerzos admisibles para materiales de engranes de acero templado 31 Imagen 25 Calculo de eje .........................................................................................................34 Imagen 26 Diagrama de fuerzas ...............................................................................................35 Imagen 27 Diagrama de cuerpo libre de pares de torsión y de par de torsión ...........................36 Imagen 28 Fuerzas axiales .......................................................................................................37 Página 3 | 45 Imagen 29 Cizalladura y flexión – plano XY ..............................................................................38 Imagen 30 Cizalladura flexión – plano XZ .................................................................................38 Imagen 31 Tabla de esfuerzo por material ................................................................................41 Imagen 32 Dimensiones de chaveteros ....................................................................................42 Imagen 33 Tabla norma DIN 6885 ............................................................................................43 Página 4 | 45 INDICE DE TABLAS Tabla 1 Tabla de cálculos básicos de engranajes .....................................................................15 Tabla 2 Cálculos de piñón .........................................................................................................16 Tabla 3 Cálculos de engranaje conducido.................................................................................16 Tabla 4 Calculo de Lewis ..........................................................................................................20 Tabla 5 Factor de geometría .....................................................................................................22 Tabla 6 Resultados de Flexionante ...........................................................................................27 Tabla 7 Resultados de esfuerzo flexionante admisible ..............................................................32 Página 5 | 45 1. INTRODUCCION El presente trabajo muestra el avance preliminar del diseño de una bomba de pistones accionada por engranajes rectos, para este avance se está considerando medidas preliminares. Imagen 1 Diseño de bomba de pistón 2. MARCO TEORICO 2.1 Diagrama cinemático Al analizar el movimiento de una máquina, generalmente es difícil visualizar el movimiento de componentes individuales y de mecanismos al observar el esquemático del ensamblaje completo. Un diagrama cinemático debe ser dibujado a una escala proporcional al mecanismo real. Por conveniencia, los eslabones son enumerados comenzando con el marco como 1. A las juntas en tanto, para evitar confusión, se les asigna una letra. A continuación se muestra la simbología típicamente empleada en estos diagramas. Página 6 | 45 Imagen 2 Diagramas cinemáticos 2.2 Análisis de posición Un objetivo fundamental del análisis cinemático es determinar las aceleraciones de todas las partes móviles del ensamble. Las fuerzas dinámicas son proporcionales a la aceleración, según la segunda ley de Newton. Es necesario conocer las fuerzas dinámicas para calcular los esfuerzos en los componentes. Imagen 3 Análisis cinemático Página 7 | 45 2.3 Rueda dentada Una rueda dentada es simplemente un elemento mecánico circular en cuya periferia se han tallado dientes iguales y equidistantes, de forma, que en el espacio entre dientes encaje perfectamente un diente de otra rueda dentada. 2.4 Engranajes Cuando, se requiere trasmitir movimiento entre, ejes de una máquina se suelen emplear engranajes, este sistema se constituye, en uno de los mecanismos más empleados y eficientes para trasmitir movimiento entre dos ejes de una máquina, dado que permiten establecer diferentes configuraciones entre los ejes, y no existen problemas de deslizamiento entres los cuerpos que rotan por lo que las velocidades de rotación serán constantes. Un sistema de trasmisión por engranajes está, formado básicamente por dos ruedas dentadas, que engrana entre sí y que a su vez, van montadas en ejes que finalmente trasmiten el movimiento a otro dispositivo o máquina. Técnicamente cuando se hace referencia a una sola rueda, esta se denomina rueda dentada y cuando se hace referencia a dos ruedas solidarias que encajan perfectamente, se denominan engranaje. Es también importante mencionar que a cada rueda del engranaje se le asigna un nombre, rueda o corona, para la rueda dentada más grande y piñón, a la rueda dentada de menor tamaño. Imagen 4 Rueda dentada y Engranajes Las funciones principales de los engranes y de las transmisiones de los engranes, son: reducción de la velocidad, multiplicación del momento de torsión o par motor y permiten variar la posición de los árboles o ejes. Página 8 | 45 2.5 Relación de transmisión Un parámetro fundamental para el diseño de un sistema de engranajes es la relación de transmisión, que para el caso del sistema de trasmisión por engranajes se define como el cociente entre el número de dientes de la rueda conducida y el número de dientes de la rueda conductora. La relación de trasmisión también se puede expresar en términos de la velocidad de rotación de las ruedas. Imagen 5 Relación de transmisión 3. ESQUEMA CINEMATICO Imagen 6 Diseño y análisis cinemático Página 9 | 45 Imagen 7 Esquema cinemático Se considera para la cantidad de “n” número de elementos móviles del mecanismo los siguientes elementos: O-A = Biela 01 B-A = Biela 02 O = Base Elementos de grado Pi = 4 elementos (O, A, B y base) Por lo tanto, se tiene n= 4 4. GRADOS DE LIBERTAD Para el cálculo de los grados de libertad se considerará el número de elementos n, calculados previamente. 𝐺𝑑𝑙 = 3(𝑛 − 1) − 2𝑃𝑖 − 𝑃𝑖𝑖 => 𝐺𝑑𝑙 = 3(4 − 1) − 2(4) => 𝐺𝑑𝑙 = 1 Página 10 | 45 5. ANALISIS DE POSICION Imagen 8 Diagrama de análisis de posición Para el análisis de posición, se consideró a α en 90° y 270° de radio 70mm., formando triángulos rectángulos con una distancia del punto B al pistón de 350mm., de este modo calculamos el ángulo θ: 𝐴𝑟𝑐𝑆𝑒𝑛 ( 70 ) = 11.30° 350 Y una distancia del centro del engranaje al pistón de 343 mm. 6. ANALISIS DE VELOCIDAD Imagen 9 Diagrama de análisis de velocidades Página 11 | 45 6.1 Conversión de RPM Datos: - Velocidad inicial 𝜔= 400 rpm - Velocidad en rad/s 𝜔𝑂𝐴 = 400𝑅𝑃𝑀𝑥 2𝜋 1𝑚𝑖𝑛 𝑥 1 𝑟𝑒𝑣 60 𝜔𝑂𝐴 = 41.89 𝑟𝑎𝑑/𝑠 6.2 Velocidad Punto A: Datos: 𝑟𝑂𝐴 = 70 𝑚𝑚 <> 0.07 𝑚 𝑉𝐴 = 𝜔𝑂𝐴 𝑥 𝑟𝑂𝐴 𝑉𝐴 = 41.89 𝑟𝑎𝑑 𝑥 0.07𝑚 => 𝑉𝐴 = 2.93 𝑚/𝑠 𝑠 6.3 Velocidad Tramo BA: Datos: 𝑟𝐵𝐴 = 350 𝑚𝑚 <> 0.35 𝑚 𝑉𝐵/𝐴 = 𝜔𝑂𝐴 𝑥 𝑟𝐵𝐴 𝑉𝐵/𝐴 = 41.89 𝑟𝑎𝑑 𝑥 𝑠 0.35𝑚 => 𝑉𝐵/𝐴 = 14.66 𝑚/𝑠 6.4 Velocidad Punto B: 2 𝑉𝐵2 = 𝑉𝐴2 + 𝑉𝐵/𝐴 𝑉𝐵 = √2.932 + 14.662 𝑉𝐵 = 14.95 𝑚/𝑠 Página 12 | 45 7. CALCULO DE ENGRANAJE Para el cálculo de los engranajes correspondientes a nuestro diseño, comenzaremos con el cálculo de la relacion de transmisión, para ello ingresaremos con los siguientes datos: n1= 800 RPM y n2 = 400 RPM n1= número de RPM del piñón n2= número de RPM del conducido Estos datos fueron definidos de acuerdo al punto 6, esta son las velocidades que se requieren para el funcionamiento de la máquina. 7.1 Cálculo de relación de transmisión (i): 𝑖= 𝑛1 800 = =2 𝑛2 400 Nos resulta un relacion de transmision i= 2 7.2 Numero de dientes Al tener la relacion de trasnmicion definida procedemos a escoger un numero de dientes preliminar: Datos: Z1= 30 De este modo procedemos con el calculo 𝑖= 2= 𝑧2 30 𝑧2 𝑧1 => 𝑧2 = 2 𝑥 30 => 𝑧2 = 60 𝑑𝑖𝑒𝑛𝑡𝑒𝑠 z1= número de dientes del piñón z2= número de dientes del conducido Página 13 | 45 7.3 Angulo de inclinación (β) El ángulo de inclinación de los dientes para engranajes de dientes rectos β=0 º. 7.4 Angulo de presión (α) El ángulo de presión α del engranaje varía entre los siguientes valores 20°, 22.5°, 25°, para nuestro caso se escogerá el valor de α = 20 º. 7.5 Modulo Para la selección del módulo, nos basaremos ala siguiente tabla. Imagen 10 Módulos normalizados Para nuestra máquina, escogeremos el m= 4 que es comercial. Página 14 | 45 7.6 Cálculos básicos para engranajes Una vez determinados los valores básicos de entrada se procede a calcular los valores de diámetros externos, internos, paso diametral, altura de cabeza, altura de pie, entre otros, que permiten determinar la geométria y dimensiones de los engranajes, dichos valores se obtienen con relaciones básicas. de los engranajes se pueden obtener los demás. De este modo se aplicara la siguiente tabla: ITEM Revoluciones piñón Revoluciones conducido Relacion de transmisión Piñón Conducido Velocidad angular piñón Velocidad angular conducido Modulo Ángulo de presión Paso circunferencial Paso equivalente Paso normalizado Paso diametral Altura de cabeza Altura de cabeza Altura total del diente VARIABLES DATOS UNIDAD FORMULAS n1 800 Rpm n2 400 Rpm I 2 Z1 30 Dientes Z2 60 Dientes ω1 83.78 Rad x seg ω2 41.89 Rad x seg m 4 α 20 Grados 20°, 22.5°, 25° pc 12.57 Mm pc=mπ p 6.35 Mm de acuerdo a tabla normalizado Pn 6.00 Mm de acuerdo a tabla normalizado, dientes x pulgada Pd i=n1/n2 0.25 h1 4 Mm h1 = m h2 5 Mm h1 = 1.25 x m h 9 Mm h = h1 + h2 = 2.25 x m Huelgo radial c 1 Mm c = h2 - h1 = 0.25 x m Distancia entre centros L 180 mm Tabla 1 Tabla de cálculos básicos de engranajes Página 15 | 45 De este modo ya obtenidos los parametros basicos del par de engranajes procedemos a calcular las dimensiones para el piñon y para el engranaje conducido, para ellos revisaremos las siguientes tablas: PIÑON ITEM VARIABLES DATOS UNIDAD FORMULAS Diámetro primitivo piñón Dp1 120.00 mm Dp = mZ Diámetro base piñón Db1 112.76 mm Db= DpCosα Diámetro exterior De 128.00 mm De = D + 2m = m(Z + 2) Diámetro interior Di 110.00 mm Di = D - 2.5m = m(Z - 2.5) Espesor del diente sobre la circunferencia primitiva S 12.57 mm S = pc = mp Velocidad periférica v 301.59 m/min v = πD n Tabla 2 Cálculos de piñón ENGRANAJE CONDUCIDO ITEM VARIABLES DATOS UNIDAD FORMULAS Diámetro primitivo conducido Dp2 240.00 mm Dp = mZ Diámetro base conducido Db2 225.53 mm Db= DpCosα Diámetro exterior De 248.00 mm De = D + 2m = m(Z + 2) Diámetro interior Di 230.00 mm Di = D - 2.5m = m(Z - 2.5) Espesor del diente sobre la circunferencia primitiva S 12.57 mm S = pc = mp Velocidad periférica v 301.59 m/min v = πDp n Tabla 3 Cálculos de engranaje conducido Página 16 | 45 8. SELECCIÓN DEL MATERIAL Para determinar el material que se utilizara de engranaje, haremos uso de los siguientes datos para su selección: Datos: Potencia = 1 Hp n= 800 RPM (Revoluciones del piñón). Con estos datos de entrada procedemos a calcular la ecuación de Lewis. 8.1 Flujo de la potencia a través de un par de engranes El par torsional es el producto de la fuerza que actúa tangente al círculo de paso multiplicado por el radio de paso del piñón. Se usará el símbolo Wt para indicar la fuerza tangencial. la fuerza tangencial sobre los dientes de los engranes produce un par torsional sobre el engrane, igual al producto del radio de paso por Wt. En realidad, la fuerza tangencial Wt es la componente horizontal de la fuerza total existe una componente vertical de la fuerza total, el cual actúa radialmente sobre el diente del engrane, denotado como Wr. Imagen 11 Diagrama de fuerzas en el diente. Página 17 | 45 Wt = Fuerzas en libras (lb) P = Potencias en caballos (hp) (Observe que 1.0 hp equivale a 550 lb·pies) T = Par torsional en lb·pulg n = Velocidad angular en rpm, esto es, rev. min 8.2 Ecuación de Lewis La fuerza tangencial, Wt, produce un momento flexionaste en el diente del engrane parecido al de una viga en voladizo. El esfuerzo flexionaste que resulta es máximo en la base del diente, en el chaflán que une el perfil de involuta con el fondo del espacio entre dientes. Al tomar en cuenta la geometría detallada del diente, Wilfred Lewis dedujo la ecuación del esfuerzo en la base del perfil de involuta; ahora se llama ecuación de Lewis Wt = fuerza tangencial Pd = paso diametral del diente F = ancho de la cara del diente Y = factor de forma de Lewis, que depende de la forma del diente, el ángulo de presión, el paso diametral, el número de dientes en el engrane y el lugar donde actúa Wt. Página 18 | 45 Para la selección del factor de Lewis se usará la siguiente tabla. Imagen 12 Factor de Lewis Página 19 | 45 8.3 Cálculo de ecuación de Lewis Potencia 1.00 Hp 550.00 lb·pies P velocidad angular n 800.00 RPM Fuerza tangencial Wt 1.31 lb Wt (R)=126000x(P)/(nxD) velocidad tangencial vt Pie/min Vt=P/Wt 25142.86 Par torsional T 78.75 lb·pulg Fuerza radial Wr 0.48 lb Fuerza normal Wn 1.40 lb Factor de forma de Lewis Y 0.114 Ecuación de Lewis σt 0.23 ver tabla de factor de Lewis Tabla 4 Calculo de Lewis Página 20 | 45 8.4 Factor de geometría Wt = fuerza tangencial Pd = paso diametral del diente F = ancho de la cara del diente J = factor de geometría J, donde J =Y /Kt Para engranajes rectos estándar (basados en un radio de empalme de diente = 0,35/P) De la hoja de datos 225.01 de AGMA. Imagen 13 Selección de factor J Página 21 | 45 8.5 Cálculo de factor de geometría Factor de geometría J 0.38 Ecuación de Lewis factor de geometría σt 0.07 ver imagen 13 Tabla 5 Factor de geometría 8.6 Numero de esfuerzo flexionante: Haremos uso de la siguiente formula: Donde determinaremos loa valores usados como corresponde a las normas AGMA. Wt = Fuerza tangencial 𝜎𝑡 = 𝑊𝑡𝑥𝑃𝑑 𝐹𝑥𝐽 = Ecuación de Lewis factor de geometría Ko = Factor de sobrecarga para resistencia flexionante Ks = Factor de tamaño para la resistencia flexionante Km = Factor de distribución de carga para la resistencia flexionante KB = Factor de espesor de orilla Kv = Factor dinámico para la resistencia flexionante Página 22 | 45 8.7 Factor de sobrecarga (Ko) Se debe considerar un factor de sobrecarga de 1 para considerar con certeza las variaciones de carga, vibraciones, choques, cambios de velocidades y otros que causen cargas máximas que la fuerza tangencial Wt, aplicada a los dientes del engrane durante el funcionamiento. Imagen 14 Factores de sobrecarga sugeridos. K0 8.8 Factor de tamaño (Ks) Las indicaciones del factor de tamaño recomiendan considerar el valor igual a 1, excepto para engranajes con dientes grandes o anchos de cara, pero como se recomienda para engranajes con modulo menor a 5 y paso diametral mayor a 5, consideramos el valor de 1. Imagen 15 Factores de tamaño sugeridos Ks 8.9 Factor de distribución de carga (Km) La intensidad de carga del piñón será variable por los cambios de velocidad o vibraciones realizadas, entonces consideramos la siguiente formula: Página 23 | 45 Para los valores de Cpf entraremos con el ancho de cara del engranaje y la relacion F/Dp, los cuales son F= ½” y F/Dp= 0.1 con ello usaremos las siguientes tablas para su respectivo valor. Imagen 16 Factor de proporción Cpf Para los valores Cma, usaremos las siguientes tablas para sus respectivos valores. Imagen 17 Factor de alineamiento de engranado Cma Donde obtendremos lo siguiente de ambas tablas: 𝐶𝑝𝑓 = 0.20 , 𝐶𝑚𝑎 = 0.31 Reemplazando los valores para hallar Km, 𝐾𝑚 = 1 + 0.2 + 0.31 𝐾𝑚 = 1.51 Página 24 | 45 8.10 Factor de espesor de orilla (Kb) Para determinar el factor de espesor de orilla, debemos obtener la relación de respaldo entre el espesor de la orilla y la profundidad total del diente 𝑚𝐵 = 𝑡𝑅 ℎ𝑡 mB= relación de espesor de orilla tr = espesor de orilla ht = profundidad total de diente Datos: tr= 50.8 mm <> 2” ht = 9 mm 𝑚𝐵 = 50.8 9 𝑚𝐵 = 5.64 Imagen 18 Factor de espesor de orilla Por lo tanto para valores de mb>1.2, se considera el factor Kb = 1. Página 25 | 45 8.11 Factor dinámico (Kv) Para obtener el valor del factor dinámico, tendremos como entrada a la velocidad tangencial de 25142.86 pie/min y consideraremos al número de calibración de la exactitud de la transmisión igual a 8, con estos datos señalados se obtiene el factor dinámico, en la siguiente tabla: Imagen 19 Factor dinámico Kv Como el valor de la velocidad de la línea de paso excede a las mediciones del cuadro, prolongando las líneas, obtenemos que el valor de Kv= 1.8. Página 26 | 45 8.12 Resultados de esfuerzo Flexionante Factor de sobrecarga para resistencia flexionante K0 1.00 Ver imagen 14 maquina uniforme y fuente uniforme factor 1 Factor de tamaño para la resistencia flexionante Ks 1.00 Ver imagen 15 entrar con paso diametral y modulo en nuestro caso es ks 1 0.10 F/Dp (f= ancho de engranaje y Dp= diámetro primitivo del Piñón) Cpf 0.20 Para valores menores a relacion de 0.5 ver imagen 16 Factor por alineamiento de Cma engranado 0.31 Relacion F/Dp Factor de proporción del piñón Factor de distribución de carga para resistencia flexionante ver imagen 17 Km 1.51 tr 50.8 Profundidad total diente mb 5.64 Factor de espesor de orilla Kb 1.00 Ver imagen 18 Número de calificación de la exactitud de la transmisión Qv 8 entrar con la Vt a la tabla, se escogerá un Qv de 8 Factor dinámico para la resistencia flexionante Kv 1.80 ver imagen 19 Numero de esfuerzo flexionante St 0.19 Espesor de orilla considerar 2" se recalcula con el diámetro del eje Tabla 6 Resultados de Flexionante Página 27 | 45 8.13 Números de esfuerzo flexionante admisibles ajustados: Para hallar los números de esfuerzo flexionante admisibles ajustados, hicimos uso de su fórmula correspondiente, haciendo uso del factor de seguridad, factor por ciclos de esfuerzo, factor de confiabilidad y, como en este factor se considera la incertidumbre en el análisis de diseño, usaremos el ya calculado número de esfuerzo flexionante admisibles. Imagen 20 Factor admisible Sat Imagen 21 Factor de confiabilidad Kr Página 28 | 45 8.14 Factor de ciclos de esfuerzo (YN) La tabla de norma AGMA, señala que para entrar a la tabla se hace necesario de tener el número de ciclos de carga (NC), para ello hacemos los correspondientes cálculos. Con respecto a la vida de diseño, en horas, el mecanismo al cual se va a incluir los engranajes es una bomba de presión, entonces consideramos el siguiente intervalo. Imagen 22 Vida de diseño recomendada El número de aplicaciones de carga por revolución, se estima que el mecanismo tendrá una carga por revolución. Con el resultado correspondiente de 2640000000 <> 2.64 𝑥 109 ciclos de carga esperado, ubicaremos el valor del factor de ciclos por esfuerzo. Página 29 | 45 Imagen 23 Factor de resistencia flexionante por ciclos de esfuerzo Yn 8.15 Factor de seguridad (SF) Debido a que este es un factor calculable por la capacidad máxima del sistema y el valor del requerimiento esperado real al que el mecanismo estará sometido, la norma AGMA recomienda tomar un valor modesto entre 1.00 y 1.50, por lo que consideramos un valor medio entre ambos. SF = 1.25 Página 30 | 45 Imagen 24 Numero de esfuerzos admisibles para materiales de engranes de acero templado Página 31 | 45 8.16 Resultados de esfuerzo Flexionante admisible factor de confiabilidad KR 1.00 Vida de diseño en horas L 55000 numero de aplicaciones de carga por revolución q 1.00 numero de ciclos de carga esperado Nc Factor por ciclos de esfuerzo YN 0.84 Dureza Brinell HB 160.00 Numero de esfuerzo flexionante admisible horas Imagen 23 valor asumido 2640000000 ciclos Se selecciono 160HB 165.00 Mpa 23.93 Ksi Sat Factor de seguridad SF 1.25 Números de esfuerzo flexionante admisibles ajustados S´at 110.25 Selección de material Imagen 22 se ingresó con la dureza Brinell de 160 hb y el grado 1 Factor de seguridad entre 1 a 1.5 Mpa TEMPLADO POR LLAMA O POR INDUCCION - 50 HRC VER IMAGEN 25 Tabla 7 Resultados de esfuerzo flexionante admisible Página 32 | 45 Página 33 | 45 9. CALCULO PARA EL DISEÑO DE EJE 9.1 Datos Para el diseño del eje de nuestro sistema de bomba, nos enfocaremos en el eje del engranaje conducido, el cual tiene las siguientes medidas: Imagen 25 Calculo de eje Datos del engranaje conducido: Dp = 240 mm Página 34 | 45 Para el desarrollo de los cálculos procedemos a realizar un diagrama de fuerzas. Imagen 26 Diagrama de fuerzas 9.2 Cálculo del par de torsión: Para el calculo del par de torsión se utilizará la siguiente formula: T= 60P 2π𝑛 T= Par de torsión. P= Potencia – 1hp <> 746 Watts n= revoluciones por minuto. – 400 RPM T= 60 (746) 2π (400) T = 17.8 Nm Página 35 | 45 9.3 Diagrama de cuerpo libre de pares de torsión y de par de torsión: De acuerdo al Torque calculado representaremos el diagrama de par de torsión. Imagen 27 Diagrama de cuerpo libre de pares de torsión y de par de torsión Página 36 | 45 9.4 Cálculo de fuerzas externas En la rueda dentada, la única componente que produce torsión en el eje es la fuerza tangencial, Ft. El par de torsión producido por esta fuerza está dado por: Ft = 2T 2(17.8) = = 0.62 𝑁 Db 0.240 De las expresiones dadas en el enunciado tenemos que: Fa = 0.20Ft = 0.20 x 0.6 = 0.12 N Fr = 0.27Ft = 0.27 x 0.6 = 0.17 N Para el cálculo de la fuerza Ft1 y Ft2, como las dos tiene el mismo radio de giro de 70 mm y asu vez Ft1 = Ft2 realizaremos lo siguiente: Ft1 = Ft2 = Radio - R = 70 mm <>0.07m Ft1 = Ft2 = T 17.8 Nm = = 254.42 𝑁 R 0.07 m La fuerza Ft1 y Ft2 son las fuerzas que se producen en el empuje de las manivelas a los cilindros del pistón, la cual seria de 254.42 N de empuje al pistón. 9.5 Cálculo de reacciones A- Fuerzas axiales Imagen 28 Fuerzas axiales Página 37 | 45 B- Cizalladura y flexión – plano XY Imagen 29 Cizalladura y flexión – plano XY C- Cizalladura flexión – plano XZ Imagen 30 Cizalladura flexión – plano XZ Página 38 | 45 Planteando las ecuaciones de equilibrio, es decir, la suma de fuerzas en las direcciones x, y y z, y la suma de momentos en los planos xy y xz, se tiene: ∑ 𝐹𝑥 = 0; 𝐹𝑎 − 𝑅𝑐𝑥 = 0 ∑ 𝐹𝑦 = 0; 𝑅𝑏𝑦 + 𝑅𝑑𝑦 − 𝐹𝑟 = 0 ∑ 𝑀𝑎𝑥𝑦 = 0; 0.038(𝑅𝑏𝑦) + 0.083(𝑅𝑑𝑦) − 0.0605(𝐹𝑟) + 𝑀𝐹𝑎 = 0 ∑ 𝐹𝑧 = 0; 𝐹𝑡1 + 𝐹𝑡2 + 𝑅𝑏𝑧 + 𝑅𝑑𝑧 − 𝐹𝑡 = 0 ∑ 𝑀𝑎𝑥𝑧 = 0; 0.038(𝑅𝑏𝑧) + 0.083(𝑅𝑑𝑧) + 0.121(𝐹𝑡2) − 0.0605(𝐹𝑡) = 0 De donde: Reacciones en X 𝐹𝑥 => 𝐹𝑎 = 𝑅𝑐𝑥 => 𝑅𝑐𝑥 = 0.12 𝑁 Reacciones en Y 𝐹𝑦 => 𝑅𝑏𝑦 + 𝑅𝑑𝑦 = 0.17𝑁 → 𝑅𝑏𝑦 = 0.17 − 𝑅𝑑𝑦 ∑ 𝑀𝑎𝑥𝑦 → 0.038(𝑅𝑏𝑦) + 0.083(𝑅𝑑𝑦) − 0.0605(0.17) + (0.12x0.12) = 0 0.038𝑅𝑏𝑦 + 0.083𝑅𝑑𝑦 = −0.00411𝑁𝑚 Por lo tanto reemplazamos Rby 0.038(0.17 − 𝑅𝑑𝑦) + 0.083𝑅𝑑𝑦 = −0.00411𝑁𝑚 𝑅𝑑𝑦 = −0.04772 𝑁 Con el valor de Rdy vamos a hallar Rby 𝑅𝑏𝑦 = 0.17 − 𝑅𝑑𝑦 𝑅𝑏𝑦 = 0.17 − (−0.04772) 𝑅𝑏𝑦 = 1.234 𝑁 Página 39 | 45 Reacciones en Z 𝐹𝑧 => 254.42 + 254.42 + 𝑅𝑏𝑧 + 𝑅𝑑𝑧 − 0.62𝑁 = 0 => 𝑅𝑏𝑧 + 𝑅𝑑𝑧 = −508.22 𝑁 𝑅𝑏𝑧 = −508.22 − 𝑅𝑑𝑧 ∑ 𝑀𝑎𝑥𝑧 → 0.038(𝑅𝑏𝑧) + 0.083(𝑅𝑑𝑧) + 0.121(𝐹𝑡2) − 0.0605(𝐹𝑡) = 0 0.038(𝑅𝑏𝑧) + 0.083(𝑅𝑑𝑧) = −30.74 Por lo tanto reemplazamos Rbz 0.038(−508.22 − 𝑅𝑑𝑧) + 0.083(𝑅𝑑𝑧) = −30.74 𝑅𝑑𝑧 = −253.93𝑁 Con el valor de Rdz vamos a hallar Rbz 𝑅𝑏𝑧 = −508.22 − 𝑅𝑑𝑧 𝑅𝑏𝑧 = −508.22 − (−253.93) 𝑅𝑏𝑧 = −254.29 𝑁 De donde 𝑅𝑐𝑥 = 0.12 𝑁 , 𝑅𝑑𝑦 = −0.04772 𝑁 , 𝑅𝑏𝑦 = 1.234 𝑁, 𝑅𝑑𝑧 = −253.93𝑁, 𝑅𝑏𝑧 = −254.29 𝑁 9.6 Cálculo del diámetro en la sección más cargada La sección con más carga será el tramo BD en el punto C, por lo cual se consideran los siguientes datos: N= 1.5 𝑀 = (0.12x0.12) = 0.0144 Nm 𝑇 = 17.8 𝑁𝑚 𝐹 = 0.12𝑁 Sy = 179 MPa – Laminado en Caliente (De acuerdo con el material escogido). Página 40 | 45 Imagen 31 Tabla de esfuerzo por material De acuerdo al cálculo, obtendremos un diámetro de eje de D=5 mm <> 0.05m por lo que en el diseño del eje se ha utilizado un eje de diámetro 30 mm lo que nos asegura que nuestro eje soportara las cargas de nuestro sistema. Página 41 | 45 10. SELECCIÓN DE CHAVETA PARA SISTEMA Para la selección de la chaveta nos apoyaremos de la norma DIN 6885/1, y de tablas de fabricantes de chavetas, así como también de cálculos. 10.1 ANÁLISIS DE ESFUERZOS PARA DETERMINAR LA LONGITUD DE LAS CHAVETAS Sy = 179 MPa – Laminado en Caliente (De acuerdo con el material escogido) N = 1.5 Por lo tanto el cálculo de 𝜏 = 59.66 𝑀𝑝𝑎 Para la longitud de acuerdo al calculo de Tau, se obtiene 𝐿 = 20 𝑚𝑚 Una vez calculada la longitud ubicaremos en la tabla de dimensiones de chavetas de acuerdo ala norma DIN6885 ubicaremos el modelo de chaveta a usar que será chaveta rectangular. Imagen 32 Dimensiones de chaveteros Página 42 | 45 Imagen 33 Tabla norma DIN 6885 Para ingresar a la tabla de chavetas, será con el diámetro de eje que es de 30 mm y el largo calculado de 20 mm. De acuerdo a la tabla seleccionaremos una chaveta de 8 x 7 por una longitud de 20 mm. Página 43 | 45 11. CONCLUSIONES 1. Los engranajes se emplean para transmitir movimiento giratorio, al usar los apropiados se logra transformar un desplazamiento alternativo en giratorio viceversa. En una gran cantidad de herramientas y máquinas existe la trasmisión de movimiento de rotación de un eje a otro. Los engranes o ruedas dentadas, constituyen uno de los mejores medios para realizar este fin. 2. Los engranajes son sistemas mecánicos que transmiten el movimiento de rotación desde un eje hasta otro mediante el contacto sucesivo de pequeñas levas denominadas dientes. Los dientes de una rueda dentada pueden ser cilíndricos o helicoidales. 3. Para verificar la veracidad de las aproximaciones utilizadas en las fórmulas y las gráficas incluidas en el programa se ha utilizado uno de los ejercicios que se utilizan en el estudio de la asignatura y, tal y como se ha podido observar, todas las aproximaciones utilizadas son válidas 4. La determinación de la configuración geométrica de una rueda dentada generalmente se realiza a partir de procedimientos de cálculos previamente establecidos, también juega un papel fundamental la experiencia del diseñador que ayudará en la determinación de decisiones a la hora de elegir factores, coeficientes, etc., pero siempre deben realizarse cálculos que tengan en cuenta la resistencia a los esfuerzos de contacto o a los esfuerzos de flexión, según sea el caso, para lo cual existen diversos criterios. 5. Después de revisar la teoría sobre engranes, queda claro que han sido fundamentales para el desarrollo de la industria. El gran desarrollo que este tipo de mecanismos ha tenido demuestra que sus aplicaciones son muy variadas. 6. El material de acero laminado en frio o caliente comúnmente es seleccionado por potenciar las propiedades mecánicas como la resistencia a la tracción o el límite elástico, debido a su bajo espesor; el acero laminado en caliente es el más económico de fabricar y mas exacto de producir en comparación del laminado en frio que no suelen tener formas tan precisas ni tolerancias bajas, pero si suelen tener mas dureza en el acero y menor valor de ductilidad (capacidad de deformarse plásticamente). 7. Los valores de fuerza calculados con anterioridad tienen valores por debajo a los requeridos en la tabla de selección de material, por lo que se ha seleccionado el material a utilizar por su bajo costo y por ser el material más recurrente para utilizar en este tipo de bombas de presión. Página 44 | 45
 0
0
Anuncio
Documentos relacionados
Descargar
Anuncio
Añadir este documento a la recogida (s)
Puede agregar este documento a su colección de estudio (s)
Iniciar sesión Disponible sólo para usuarios autorizadosAñadir a este documento guardado
Puede agregar este documento a su lista guardada
Iniciar sesión Disponible sólo para usuarios autorizados