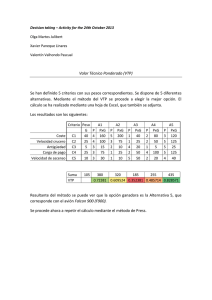
lOMoARcPSD|13722145 Tablas momentos de inercia de superficies Estática (Pontificia Universidad Católica del Perú) StuDocu is not sponsored or endorsed by any college or university Downloaded by Diego Vega ([email protected]) lOMoARcPSD|13722145 ESTÁTICA Pág. 1 Momentos de inercia de áreas planas Superficie y Área yG h xG G bh h/2 Momentos y productos de inercia centroidales b h3 3 I xG = bh 3 12 3 Iy = b h 3 I yG = b3h 12 Ix = b/2 Rectángulo Momentos y productos de inercia x b 2 2 Px y = b h 4 PxG yG = 0 b h3 Ix = 12 I xG = b h3 36 I xG = b h3 36 yG Triángulo h G h/3 xG x bh 2 b/2 b/2 y yG 3 I x = bh 12 b/3 Triángulo rectángulo h xG G bh 2 3 Iy = b h 12 2 2 Px y = b h 24 h/3 x 3 I yG = b h 36 PxG yG = − b yG y b/3 Triángulo rectángulo h G xG h/3 x b Pontificia Universidad Católica del Perú bh 2 b2 h2 72 Ix = b h3 12 I xG = bh 3 36 Iy = b3h 12 I yG = b3h 36 Px y = − b2h2 24 PxG yG = b2h2 72 Sección de Ingeniería Mecánica – Área de Diseño Downloaded by Diego Vega ([email protected]) lOMoARcPSD|13722145 ESTÁTICA Pág. 2 Momentos Área y productos de inercia Superficie Momentos y productos de inercia centroidales yG I xG = R Círculo xG G π R2 Ix = 5π R 4 4 I yG = π R4 4 π R4 PxG yG R 4 =0 x yG y Ix = 4R 3π Semicírculo R x G y 2 Iy = I xG = 8 5π R 4 I yG = 8 2R 4 Px y = 3 π R4 8 4 − 8 R = 0,1098 R 4 9π π R4 8 PxG yG = 0 yG Ix = 4R 3π Cuarto de círculo π R2 π R4 πR xG G 2 4 x 4R 3π π R4 I xG = 16 π R4 Iy = 16 4 Px y = R 8 π R4 16 − 4R 4 = 0,0549 R 4 9π I yG = 0,0549 R 4 PxG yG = − 0,01647 R 4 R yG y Ix = Cuarto de círculo π R2 4R 3π xG G 4R 3π Iy = 4 x Px y π R4 I xG = 16 π R4 π R4 I yG = 0,0549 R 4 16 4 =− R 8 PxG yG = − R y yG I x = I xG = Sector Circular θ θ G 2 R senθ 3θ x θ R2 Iy = 4 − 4 R = 0,0549 R 4 16 9π (9π − 32) R 4 = 0,01647 R 4 72 π R4 1 θ − sen 2θ 4 2 R4 1 θ + sen 2θ 4 2 Px y = 0 R Pontificia Universidad Católica del Perú Sección de Ingeniería Mecánica – Área de Diseño Downloaded by Diego Vega ([email protected])