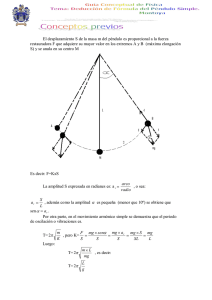
UNIVERSIDAD DEL QUINDIO FACULTAD DE INGENIERÍA INGENIERÍA CIVIL UNIDAD I: LOS MOVIMIENTOS PERIÓDICOS Y EL MOVIMIENTO ARMÓNICO SIMPLE. TEMA: El movimiento pendular. Facilitador: Alcione de J. López Quintero. GUIA DE LABORATORIO No 1 Estudiante: _______________________________________Semestre: ________Fecha: ____________ I. INTRODUCCION. El movimiento pendular es un movimiento oscilatorio realizado por una masa suspendida de un hilo a lado y lado de su posición de equilibrio en virtud de la aceleración de la gravedad y la inercia. La presente guía nos permitirá comprobar las leyes del movimiento pendular y algunos de los elementos físicos de los movimientos periódicos. II. OBJETIVOS. Al término de la presente guía de laboratorio, el estudiante estará en capacidad de: a. b. c. d. e. Construir un péndulo simple, identificando sus elementos principales. Enunciar cada una de las leyes del movimiento pendular desde el contexto de la experiencia. Medir experimentalmente la aceleración de la gravedad en su sitio de trabajo. Enumerar algunas de las aplicaciones más importantes del movimiento pendular. Trabajar en equipo y presentar informes de laboratorio ordenados y de acuerdo con las normas que rigen este tipo de informes. II. RECURSOS. Guía de laboratorio No 1, metro, regla, masas de diferentes materiales, piola o hilo, cronómetro, cinta pegante transparente. IV. INSTRUCIONES GENERALES. a. Lea la guía de laboratorio completamente, antes de hacer cualquier cosa. b. Mantenga el orden y la disciplina dentro de su grupo de trabajo. c. Escriba lo que observa en cada práctica, responda cada una de las preguntas, argumentándolas, cuando sea necesario y llene los cuadros que aparecen en la guía con los resultados que va obteniendo en cada una de las prácticas, cuando estos existan. d. Presente el informe de laboratorio con su grupo de trabajo de acuerdo con las normas que señale el profesor. e. Cada persona integrante del grupo debe realizar las mediciones (Mínimo dos mediciones) f. Tiempo previsto: 3 períodos. V. PROCEDIMIENTO. A. El período de un péndulo y la naturaleza de la masa pendular. Arme un péndulo simple como se indica en la figura. La longitud del hilo es de 30 cm y la amplitud debe ser para cada caso de 150 . Este ángulo se puede medir, indirectamente aplicando la relación sen, veamos: Sen150 = 𝑋 𝑙 → x = lsen150 = 30 cm x 0.2588190451= 7.76 cm 𝜃 Ahora, seleccione 5 objetos de masas aproximadamente iguales, por ejemplo, una canica, una bola fabricada con papel aluminio, etc. Haga oscilar el péndulo construido y cuente 20 oscilaciones completas y mida el tiempo que tarda en realizarlas, cambie la naturaleza de la masa y repita la misma experiencia y así sucesivamente y llene la siguiente tabla. Material Aluminio Papel Vidrio Plástico Plastilina n 20 20 20 20 20 Tiempo (s) L x Frecuencia Período 1. ¿Cómo son los períodos calculados para cada caso? 2. ¿Qué conclusión puede elaborar? B. El período de un péndulo y su longitud. Arme sendos péndulos con una canica, con las longitudes que se indican en la tabla y con amplitud de 200. Haga la medida de la amplitud de manera semejante a la forma empleada en la práctica anterior. Cronometre el tiempo que tarda el péndulo en realizar 10 oscilaciones completas. Coloque los datos en la siguiente tabla: Longitud (cm) 20 40 60 80 100 n 10 10 10 10 10 Tiempo (s) 3. ¿Cómo son los períodos calculados para cada caso? 4. ¿Qué conclusión puede elaborar? -2- Frecuencia Período C. El período de un péndulo y las pequeñas oscilaciones. Arme un péndulo simple, con una canica, con una longitud de 30 cm, con las amplitudes que se muestran en la tabla. Haga las medidas de la amplitud de manera semejante a la forma empleada en las prácticas anteriores. Cronometre el tiempo que tarda el péndulo en realizar 15 oscilaciones completas. Coloque los datos en la siguiente tabla: Amplitud (𝜃 0 ) 2 4 6 8 10 n 10 10 10 10 10 Tiempo (s) Frecuencia Período 5. ¿Cómo son los períodos calculados para cada caso? 6. ¿Qué conclusión puede elaborar? D. El período de un péndulo y la aceleración de la gravedad. Arme un péndulo simple, con una canica, con una longitud de 25 cm y una amplitud de 200 , póngalo oscilar y cronometre el tiempo que tarda el péndulo en realizar 12 oscilaciones completas, con el tiempo cronometrado y las 12 oscilaciones, calcule el período de oscilación del péndulo. 𝐿 Con la ecuación para el período de oscilación de un péndulo simple T = √ . Calcule la aceleración de la 𝑔 gravedad en su sitio de trabajo. Sus compañeros de equipo de trabajo han calculado la aceleración de la gravedad en sus sitios de trabajo. Con esos datos llene la siguiente tabla: Estudiante Estudiante 1 Estudiante 2 Estudiante3 n 12 12 12 Tiempo (s) Frecuencia (Hertz) Período (s) g(m/s2) Al comparar la aceleración de la gravedad, calculada en tres sitios diferentes y el período de oscilación del péndulo 7. ¿Cómo son los períodos calculados para cada caso? 8. ¿Qué conclusión puede elaborar? E. Resonancia. Amarre los extremos de una piola de dos soportes, separados entre sí, por lo menos 1 m, como se muestra en la figura a. Fig a. Fig b. Ahora arme dos péndulos de 50 cm de longitud, utilizando dos canicas de igual masa. Separados entre sí 20 cm, como se indica en la figura b. -3– Ahora, haga oscilar uno de los péndulos con ángulo de 200, no toque el segundo péndulo, y no permita que el péndulo excitado choque con el segundo péndulo. Observe detenidamente el comportamiento de los dos péndulos. 9. ¿Por qué razón o razones el segundo péndulo comienza a oscilar, sin haber sido excitado? Argumente su respuesta. 10. ¿Cómo es la frecuencia de oscilación del segundo péndulo con respecto a la del primero, después de cierto tiempo? 11. ¿Por qué razón o razones después de transcurrido el tiempo, los péndulos se detienen? 12. ¿De acuerdo con la teoría, ¿cómo se puede mantener el movimiento de los dos péndulos? Arme dos nuevos péndulos de 30 cm de longitud con canicas de igual masa a la que conforman los péndulos de 50 cm que ya tiene armados y colóquelos en la cuerda, como se ilustra en la figura c. Haga oscilar uno de los péndulos de 50 cm de longitud, con una amplitud de 200, observe detenidamente los cuatro péndulos. Fig c. 13. ¿Cuál o cuáles péndulos empiezan a oscilar? 14. ¿Por qué? Deje que los péndulos queden en reposo. Haga oscilar uno de los péndulos de 30 cm de longitud, con una amplitud de 200, observe detenidamente los cuatro péndulos. 15. ¿Cuál o cuáles péndulos empiezan a oscilar? 16. ¿Por qué? 17. Elabore una conclusión general sobre las características que deben cumplir los péndulos de esta práctica para que presenten el fenómeno de resonancia. Consulta Bibliográfica y webgráfica. 1. ¿Qué es un péndulo compuesto y para que se utiliza? 2. ¿Qué es un péndulo compensado y porque se fabrica? 3. ¿Qué son las figuras de Lissajous y como se pueden graficar empleando un péndulo? 4. Qué es la frecuencia natural en un movimiento Armónico Simple? 5. ¿Cuáles son las características del péndulo de Foucault y cuáles son sus aplicaciones? 6. ¿Existe en nuestra universidad un péndulo de Foucault y si existe dónde se encuentra? 7. Busque en internet el video “Colapso del puente de Tacoma” Obsérvelo con cuidado y responda las siguientes preguntas. 8. ¿Por qué comenzó a oscilar el péndulo? 9. Por qué se cayó? 10. En Dónde fallaron sus constructores? -4-