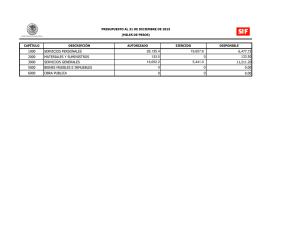
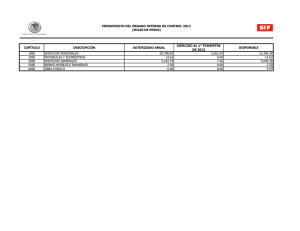
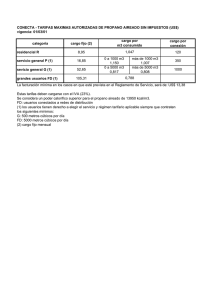
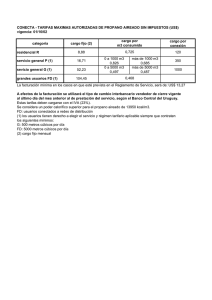
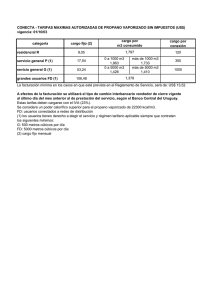
Problemas de aplicación LIMITES PROBLEMA N° 1: Parte 1 Una población crece según la siguiente función: f t = número de años transcurridos. a) Calcular la población actual. b) ¿Crecerá indefinidamente la población? 5000𝑡+1000 , 2𝑡+1 donde t es el 1° COMPRENDER: Debemos estudiar la función en t = 0 y en el infinito. 2° PLANIFICAR: a) La población actual será para t = 0: f(0)= b) 5000𝑥+1000 2𝑥+1 𝑥→∞+ lim = ∞ ∞ 5000 .0 +1000 2 .0 +1 = 1.000 habitantes. PROBLEMA N° 1: Parte 2 El resultado es una indeterminación. Como el numerador y el denominador son polinomios del mismo grado, la solución es el cociente entre los términos que acompañan al termino de mayor grado: 5000𝑥 + 1000 lim = lim 𝑥→∞+ 𝑥→∞+ 2𝑥 + 1 5000𝑥 1000 𝑥 + 𝑥 = 5000 = 2500 2𝑥 1 2 + 𝑥 𝑥 La población no pasara de los 2500 habitantes. PROBLEMA N° 2: Parte 1 PROBLEMA N° 2: Parte 2 PROBLEMA N° 2: Parte 3 PROBLEMA N° 3: PROBLEMA N° 4: