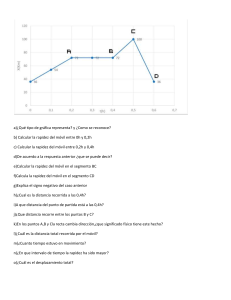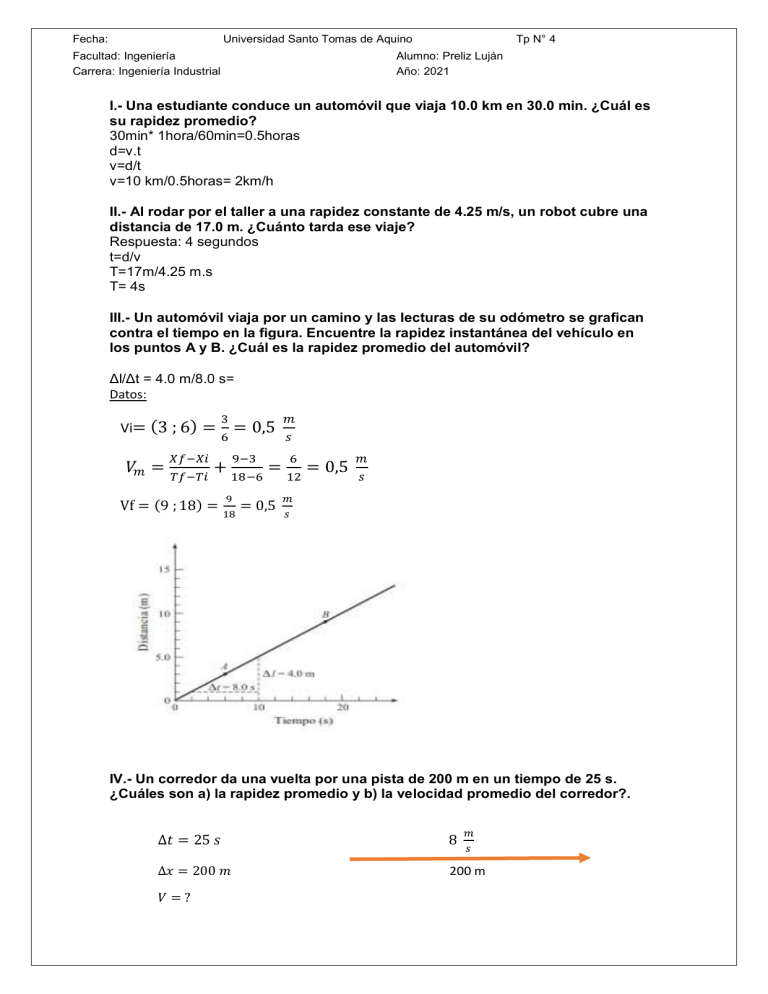
Fecha: Universidad Santo Tomas de Aquino Facultad: Ingeniería Carrera: Ingeniería Industrial Tp N° 4 Alumno: Preliz Luján Año: 2021 I.- Una estudiante conduce un automóvil que viaja 10.0 km en 30.0 min. ¿Cuál es su rapidez promedio? 30min* 1hora/60min=0.5horas d=v.t v=d/t v=10 km/0.5horas= 2km/h II.- Al rodar por el taller a una rapidez constante de 4.25 m/s, un robot cubre una distancia de 17.0 m. ¿Cuánto tarda ese viaje? Respuesta: 4 segundos t=d/v T=17m/4.25 m.s T= 4s III.- Un automóvil viaja por un camino y las lecturas de su odómetro se grafican contra el tiempo en la figura. Encuentre la rapidez instantánea del vehículo en los puntos A y B. ¿Cuál es la rapidez promedio del automóvil? Δl/Δt = 4.0 m/8.0 s= Datos: Vi= (3 ; 6) = 𝑉𝑚 = 𝑋𝑓−𝑋𝑖 𝑇𝑓−𝑇𝑖 3 = 0,5 6 𝑚 𝑠 9−3 6 + 18−6 = 12 = 0,5 9 Vf = (9 ; 18) = 18 = 0,5 𝑚 𝑠 𝑚 𝑠 IV.- Un corredor da una vuelta por una pista de 200 m en un tiempo de 25 s. ¿Cuáles son a) la rapidez promedio y b) la velocidad promedio del corredor?. 𝑚 ∆𝑡 = 25 𝑠 8 ∆𝑥 = 200 𝑚 200 m 𝑉 =? 𝑠 V= ∆𝑥 ∆𝑡 𝑉𝑚 = = 𝑉𝑜 200 𝑚 25 𝑠 = ∆𝑡 0 =8 =0 25 𝑚 𝑠 𝑚 𝑠 V.- Convierte la rapidez 0.200 cm/s a unidades de kilómetros por año. 0:200 cm/s= (0:200 cm/s) (105 km/cm) (3600 s/ h) (24 h/ d) (365 d/a) = 63.1 km/a VI.- Si A = -12^i + 25 j^ + 13k^ y B = - 3^i +7 j^, encuentre la resultante cuando A se resta de B. B - A = (-3 j^ + 7k^) - (-12^i + 25 j^ + 13k^) = -3^ j + 7k^ + 12^i - 25^ j - 13k^ = 12^i - 28^ j - 6k^ VII- Un avión viaja hacia el este con una rapidez de 500 km/h. Pero un viento de 90 km/h sopla hacia el sur. ¿Cuáles son la dirección y la rapidez respecto al suelo? Datos: 𝑘𝑚 𝑉𝑎 = 500 𝑉𝑣 = 90 𝑉𝑎 = 500 N ℎ 𝑘𝑚 O ℎ ℎ E S 90° 𝑉𝑣 = 90 o tan−1 𝑉𝑎/𝑣 = √𝑉𝑎2 + 𝑉𝑣 2 𝑘𝑚 ℎ 𝑉𝑣 𝑉𝑎 90 = √5002 + 902 𝑜 tan−1 = √250.000 + 8.100 𝑜 = 0,18° 𝑉𝑎/𝑣 = 508 𝑘𝑚 500 𝑘𝑚 ℎ VIII.- La lectura del odómetro de un automóvil es de 22 687 km al comienzo de un viaje y de 22 791 km al final. El viaje tardó 4.0 horas. ¿Cuál fue la rapidez promedio del automóvil en km/h y en m/s? Datos: 𝑥1 = 22.687 km 4.0 h 𝑥2 = 22.791 km 𝑉𝑝𝑟𝑜𝑚 = 𝑋1−𝑋2 ∆𝑡 = 22.687 22.791−22.687 4 = 104 4 22.791 = 26 𝑘𝑚 ℎ 𝑉𝑝𝑟𝑜𝑚 = 𝑋1−𝑋2 ∆𝑡 = 26 𝑘𝑚 ℎ . 1.000𝑚 1𝑘𝑚 1ℎ . 3.600𝑠 = 260 36 = 7,2 𝑚 𝑠 IX.- Un automóvil viaja a razón de 25 km/h durante 4.0 minutos, después a 50 km/h durante 8.0 minutos, y por último a 20 km/h durante 2.0 minutos. Encuentre a) la distancia total cubierta en km, y b) la rapidez promedio para el viaje completo en m/s. La distancia total cubierta en km es de 9 km y la velocidad promedio es de 10,7 m/seg Explicación: Datos: V₁ = 25 km/h t₁ = 4min(1h/60min) = 0,067 h V₂ =50km/h t₂ = 8 (1h/60min) =0,1333 h V₃ = 20km/h t₃ = 2min (1h/60min) = 0,0333 h a) la distancia total cubierta en km d = V*t DT = d₁+d₂+d₃ DT = (25 km/h*0,067h) +(50km/h*0,1333h) + ( 20 km/h*0,0333h) DT = 1,675 km+6,665 km+0,666 km DT = 9,006 km b) la rapidez promedio para el viaje completo en m/s. Distancia en metros: DT = 9 km(1000m/1km) =9000 metros Tiempo en segundos: tT= 240 seg + 480 seg + 120 seg = 840 seg Vpromedio = 9000m/840seg Vpromedio = 10,7 m/seg X.- Desde el centro de una ciudad, un vehículo viaja hacia el este durante 80.0 km y luego da vuelta al sur durante otros 192 km, hasta que se le acaba la gasolina. Determinar el desplazamiento del automóvil detenido desde el centro de la ciudad. Datos: N 𝑉𝑥1 = 80 𝑘𝑚 E O 𝑉𝑥2 = 192 𝑘𝑚 S α ⃗⃗⃗⃗ 𝑑1 = 80𝑘𝑚 ⃗⃗⃗⃗ 𝑑2 = 192 𝑘𝑚 ⃗⃗⃗ 𝑑𝑡 d= √(80 km2) + (192km2) d= 208 km θ= cos-1(80km/200km) θ= -67. 38°SE XI.- Calcule algebraicamente la resultante de los siguientes desplazamientos coplanares: 20.0 m a 30.0°, 40.0 m a 120.0°, 25 m a 180.0°, 42.0 m a 270.0° y 12.0 m a 315.0°. Confirme la respuesta con una solución gráfica. respuesta: 20.1m a 197° XII.- Datos: ⃗ + 𝐶 = (7 𝑖̂ + 6𝑗̂) + (−3𝑖̂ + 12𝑗̂) + (4𝑖̂ − 4𝑗̂) = (8𝑖̂ + 2𝑗̂) a)- 𝐴 + 𝐵 ⃗ = (7𝑖̂ + 6𝑗̂) − (−3𝑖̂ + 12𝑗̂) = (10𝑖̂ + 18𝑗̂) b)- 𝐴 − 𝐵 ⃗ = (7𝑖̂ + 6𝑗̂) − (4𝑖̂ − 4𝑗̂) = (3𝑖̂ − 2𝑗̂) c)- 𝐴 − 𝐵 XIII- Datos: 7 𝑅⃗ = √7.02 + (−12)2 tan 𝛼 = 12 𝑅⃗ = √49 + 144 tan 𝛼 = 0,583 𝑅⃗ = √193 𝛼 = tan−1 30° 𝑅⃗ = 13,9 XIV- Determine el vector desplazamiento que debe sumarse al desplazamiento (25i-16j) m para obtener un desplazamiento de 7.0 m que apunta en la dirección +x. (x , y) (20, - 16) + (x, y) = (7, 0) (x , y) = (7, 0) - (20, - 16) = (- 13, 16) V= (- 13 i + 16 j) XV.- Durante una carrera en una pista ovalada, un automóvil viaja a una rapidez promedio de 200 km/h. a) ¿Qué distancia viajó en 45.0 min? b) Determine su velocidad promedio al final de su tercera vuelta. Velocidad= 200 km/h tiempo= 45 min Distancia= v.t distancia= 200 km/h x 0,75 h distancia= 150 km XVII-Un camión avanza hacia el norte con una rapidez de 70 km/h. El tubo de escape encima de la cabina del camión deja un rastro de humo que hace un ángulo de 20° sureste detrás del camión. Si el viento sopla directamente hacia el este, ¿cuál es la rapidez del viento en ese lugar? N 20° E O S tan 20° = 𝑉𝑐 𝑉ℎ 𝑉ℎ = 𝑉𝑐 . tan 20° = 70 𝑘𝑚 ℎ . tan 20° = 25,5 𝑘𝑚 ℎ XVIII- Una embarcación viaja justo hacia el este a 10 km/h. ¿Cuál debe ser la rapidez de una segunda embarcación que se dirige con un rumbo (respecto al norte) de 30° al noreste si siempre está directamente al norte de la primera embarcación? 𝑉2 =? 𝛼 𝑉1 = 10 ⃗⃗⃗ 𝑉2 = ⃗⃗⃗ 𝑉1 + ⃗⃗⃗⃗⃗⃗⃗⃗ 𝑉2−1 ‖𝑉2 ‖ = ‖𝑉1 ‖ sin 𝛼 sin 𝛼 = 𝑉1 𝑉2 = 30° 10 sin 30° ∴ 𝑉2 = 𝑘𝑚 ℎ = 20 𝑉1 sin 𝛼 𝑘𝑚 ℎ 30° IXX-Un bote, impulsado para viajar con una rapidez de 0.50 m/s en aguas tranquilas, atraviesa un río de 60 m de ancho. El flujo del río tiene una rapidez de 0.30 m_s. a) ¿A cuál ángulo, respecto a la dirección directamente transversal, debe apuntar el bote? b) ¿Cuánto tarda el bote en atravesar el río? B = 60 N O 𝑉𝑐 E 𝑉𝑒 S Datos: 𝑉𝑒 = 0,5 𝑉𝑐 = 0,3 𝑚 𝑉ℎ = √0,52 + 0,32 = 𝑉ℎ 𝑠 𝑚 𝑉ℎ = 𝑠 𝑏 𝑡 𝑏 ∴𝑡=𝑉 = ℎ 60𝑚 𝑉ℎ 𝑏 = 60 𝑚 𝑚 𝑉 (‖𝑣 ‖ = 0,5 𝑠 ) 𝑉𝑐 ⃗⃗⃗⃗ ‖ ‖𝑉 ⃗⃗⃗⃗ ‖ ‖𝑉 𝑒 𝑐 cos 𝛼 = ‖𝑉⃗⃗⃗⃗𝑐 ‖ ∴ 𝛼 = cos −1 (‖𝑉⃗⃗⃗⃗𝑒‖) 0,3 𝛼 = cos −1 (0,5) = 53,13° XX.- Un automóvil viaja a 20.0 m/s cuando el conductor pisa los frenos y se detiene en una línea recta en 4.2 s. ¿Cuál es la magnitud de su aceleración media? Los datos del enunciado son: Vo = 20 m/s Vf = 0 t = 4,2 s a=? De la Cinemática del MRUA conocemos: Vf = Vo + at despejando a = (Vf - Vo)/t a = (0-20)/4,2 a = -4,76 m/s² aceleración retardatriz XXI.- Un objeto parte del reposo con una aceleración constante de 8.00 m/s2 a lo largo de una línea recta. Encuentre: a)la rapidez después de 5.00 s, b) la rapidez media para el intervalo de 5.00 s y c) la distancia total recorrida en los 5.00 s. Datos: 𝑎 = 𝑐𝑡𝑒 = 8 𝑚 ∆𝑡 = 𝑆𝑠 𝑠𝑖 𝑡𝑜 = 0 𝑠2 ∆𝑡 = 𝑡 − 𝑡 = 𝑆𝑠 Movimiento rectilíneo 𝑉𝑜 = 0 𝑚 𝑠 𝑥𝑠𝑆𝑠 = 100𝑚 0 𝑥𝑠 a)- 𝑉𝑓 = 𝑉𝑖 + 𝑎. 𝑡 = 0 + 8.5 = 40 b)- 𝑉𝑚𝑒𝑑 = c)- 𝑉𝑓 +𝑉𝑖 2 = 40+0 2 = 40 1 𝑚 𝑠 𝑚 𝑠 1 𝑥 = 𝑉1 . 𝑡 + 2 . 𝑎. 𝑡 2 = 0. 𝑡 + 2 . 8𝑚 𝑠2 . 𝑠 2 = 100 𝑚 XXII.- La rapidez de un camión se incrementa uniformemente desde 15 km/h hasta 60 km/h en 20 s. Determine: a) la rapidez promedio, b) la aceleración y c) la distancia recorrida, todo en unidades de metros y segundos. Los datos: vi = 15 km/h vf = 60 km/h t = 20 s rm = ? a=? d=? vi = (15 km/h) (1000 m) / (1 km) (1 h) / (3600 s) = 4,17 m/s vf = (60 km/h) (1000 m) / (1 km) (1 h) / (3600 s) = 16,67 m/s Calculamos la rapidez media. rm = (vf + vi)/2 rm = (16,67 m/s + 4,17 m/s)/2 rm = 20,84 m/s / 2 rm = 10,42 m/s Calculamos la aceleración. a = (vf - vi)/t a = (16,67 m/s - 4,17 m/s)/20s a = (12,5 m/s)/20s a = 0,625 m/s² Calculamos distancia. d = (vf + vi)/2 * t d = (16,67 m/s + 4,17 m/s)/2 * 20s d = (20,84 m/s)/2 * 20s d = 10,42 m/s * 20s d = 208,4 m XXIII.- El movimiento de un objeto a lo largo del eje x está graficado en la figura 2-1. Describa su movimiento. 0 – 2: no se mueve 2 – 4: se mueve // MRU V= 𝛥𝑥 𝛥𝑡 = Xf – 𝑥𝑖 𝑡𝑓 – ti = 3–0 4–2 3 = = 1,5 cm/s 2 4 – 6: no se mueve: V = 0 6 – 10 : se mueve // MRU V = Δx / Δt = xf – xi / tf – ti = -2 -3 / 10 -6 = -5 / 4 = -1,25 cm/s XXIV.- Un automóvil acelera uniformemente mientras pasa por dos puntos marcados que están separados 30 m. El tiempo que tarda en recorrer la distancia entre los dos puntos es de 4.0 s y la rapidez del automóvil en el primer punto marcado es de 5.0 m/s. Encuentre la aceleración del automóvil y su rapidez al llegar al segundo punto marcado. Datos *Δx=30m *t= 4s *Va= 5m/s Δ=( Δx Δt 2 . 2. Va+Vb 2 = Va + ). Δt Vb 2 Δx/ = Va Δt Δx Δt Vb = + Vb - Va = Vb 2 .30 4 −5 m/s Vb = 15 – 5 Vb = 10 [m/s] A=Vb - Va 10 – 5 = Δt 4 = 5 = 1,25 4 [m/s²] Verificación Vb² = Va² + 2 . a .Δx Vb² - Va² = 2 . a .Δx Vb² − Va² 2 Δx A= =a 10² − 5² 2 .30 = 100 – 25 60 = 75 60 = 1,25 [m/s²] XXV.- Una canica, que rueda con una rapidez de 20 cm/s, cae por el borde de una mesa que tiene una altura de 80 cm. a) ¿Cuánto tiempo necesita para chocar con el piso? b) ¿A qué distancia horizontal del borde de la mesa chocará la canica contra el piso? Datos: VoX= 20 cm/s H= 80 cm g = 9,8m/s² y= 80cm = 80 100 = 0,8 m Y= VoY . t + ½ . g . t² Y= ½ . g . t² 2𝑦 𝑔 t=√ t=√ 2 .0,8𝑚 9,8𝑚/𝑠² = 0,4s x = Vx . t = Vox . t = 20 cm/s . 0,4s = 8 cm XXIV.- Un automóvil acelera uniformemente mientras pasa por dos puntos marcados que están separados 30 m. el tiempo que tarda en recorrer la distancia entre los dos puntos es de 4.0 s y la rapidez del automóvil en el primer punto marcado es de 5.0 m/s. Encuentre la aceleración del automóvil y su rapidez al llegar al segundo punto marcado. d = Vo·t + (1/2)·a·t² 30 m = (5 m/s)·(4 s) + (1/2)·a·(4s)² 10 m = (1/2)·a·(4s)² a = 1.25 m/s² Vf = Vo + a·t Vf = 5 m/s + (1.25 m/s²)·(4 s) Vf = 10 m/s Por tanto, el automóvil lleva una aceleración de 1.25 m/s y llega al segundo punto con una velocidad de 10 m/s. 1.- Se lanza un proyectil desde una plataforma de 50 metros, a una velocidad de 450 km h1 y con un ángulo de 25°. Considerando que no hay rozamiento con el aire, y que la aceleración de la gravedad es constante y vale 9,8 m s-2 . Calcular: a) Tiempo total de vuelo. b) Alcance y altura máxima desde el suelo. c) Calcular la velocidad y la posición cuando transcurrieron 2 y 6 segundos desde el lanzamiento. Realizar gráficas de Y (t), X (t), Vy (t), Vx (t), Y (X) Comprobar gráficamente los valores de velocidad obtenidos en el apartado c). Tv= t1 + t2 𝒎 𝒉 Vo = 450 . 𝟏𝟎𝟎𝟎𝐦 𝟏𝐤𝐦 . 𝟏𝐡 𝟑𝟔𝟎𝟎𝐬 Vo = 125 m/s VoX = 125 . Cos 25° = 113,3m/s VoY= 125 . sen 25°= 52,8m/s Tv = 5,38 +39,23 = 44,61 s T1 = T1 = 𝐕𝐨 .𝐬𝐞𝐧𝜶 𝐠 𝟓𝟐,𝟖𝒎/𝒔 𝟗,𝟖𝒎/𝒔² H max = = 𝑽𝒐𝒀 𝒈 𝜶= 52,8s (𝑽𝒐𝟐 . 𝒔𝒆𝒏𝟐 )² 𝑽𝒐² . 𝒔𝒆𝒏² 𝜶= 𝟐.𝒈 𝟐.𝒈 = 𝑽𝒐𝒀² 𝟐.𝒈 = 𝟓𝟐,𝟖² 𝟐 .𝟗,𝟖 = 142,23m Yt= Vy . t + ½ g . t² 𝟐 .𝒚𝒕 𝒈 T2 = √ =√ 𝟐 .𝟏𝟗𝟐,𝟐𝟑 𝟗,𝟖 X1 = Vo . T1 X1 = 113,3 . 5,38 X1 = 609,5m = 𝟑𝟗, 𝟐𝟑𝒔 X2 = VoX + t2 X2= 133,3 . 39,23 X2= 4444,7m R = x1 + x2 = 5054,2 =5km PARA 2 SEG Y= Vo . t – ½ . t² = 52,8 . 2 – ½ . 9,8 . 2² = 86 m/s² X = Vox . t = 113,3 . 2 = 226,6 m/s Vy= Voy- g . t = 52,8 . 2 = 33,2m/s Vy= Vox= 113,3 √√𝒙 ² + √√𝟑𝟑, 𝟐 ² √𝒚² + √𝟏𝟏𝟑, 𝟑² √𝟑𝟑, 𝟐 + 𝟏𝟏𝟑, 𝟑 √𝟏𝟒𝟔, 𝟓 V= 12,1 m/s 2.- Se lanzan desde el suelo dos proyectiles con iguales velocidades, pero con ángulos de 30° y 60°. Considerando nula la fricción con el aire, y una aceleración constante de 9,8 m s-2 , calcular analíticamente: a) ¿Cuánto vale el alcance para ambos casos? b) ¿En qué difieren ambos movimientos? c) ¿Qué sucedería si los ángulos fueran de 20° y 70°? d) ¿Con qué ángulo se logra el máximo alcance DATOS a = cte =9,8 m/s² 𝛼1= 30° 𝛼2=60° R1 = R1= R2 = 𝐕𝐨² 𝐠 . sen 2𝜶 = 𝐕𝐨² . 𝟗,𝟖 𝐕𝐨² 𝐠 𝐕𝐨² 𝟗,𝟖 𝐦/𝐬² . sen 2 . 30° sen 60° = Vo² . 0,088 . sen 2. 𝛼2 = 𝐕𝐨² 𝟗,𝟖 . sen 60° = 𝐕𝐨² 𝟗,𝟖 . sen 120° = 0,088 B) La diferencia es la altura el de 60° alcanza una mayor altura que el de 30° c) 𝛼= 20º 𝐕𝐨² 𝐠 . sen 2 . 20 = 𝐯𝐨² 𝟗,𝟖 . sen 40° = 0,0655 𝛼70² R= 𝐕𝐨² . 𝐬𝐞𝐧 𝟐 𝐠 𝐯𝐨² 𝐠 . 𝟕𝟎 = 𝐕𝐨² 𝟗,𝟖 . 𝐬𝐞𝐧 𝟏𝟒𝟎°= 0,0655 . sen 2.𝛼 Rmax --> sen 2𝛼 <-- max sen 2𝛼 =1 𝛼= 90 / 2 =45° Rmax = 1 𝐕𝐨² 𝐠 90° sen ( 2𝛼 ) sen 90° *Se lograra el mayor alcance con el angulo 1 3.- Dos móviles se mueven en forma perpendicular siguiendo los ejes cartesianos. El móvil 1 se mueve siguiendo la dirección positiva del eje Y, con una velocidad constante de 30 m s -1 . El móvil 2 se mueve en dirección del eje X positivo con una velocidad inicial de 40 m s-1 y con una aceleración de – 4 m s-2 . Calcular: a) Distancia que separa a ambos móviles cuando el tiempo vale 4 y 10 segundos. b) Velocidad relativa del móvil 1 respecto del móvil 2, cuando el tiempo es de 3 y 15 segundos. Datos, móvil 1: Datos, Movil 2: V1:cte= 30m/s V2: cte= 40m/S A= -4m/s Móvil 1: Y= v1 . 30 m/s . 4 = 120 Móvil 2: X = vi . t + ½ . a . t² X = 40 . 4 + ½ . 4 . 4 X = 160 – 32 X = 128 Movil 1: Y= V1Y . t . = 30m/s . 10s = 300m √𝟏𝟐𝟎² + 𝟏𝟐𝟖² = Movil 2: 175,5m √𝟑𝟎𝟎² + 𝟑𝟔𝟖² = 474,7m X = V2X . t + ½ . a . t² X = 40m/s . 10s - ½ . 4m/s . 4² s X = 400m – 32m X = 368 m Movil 1: Cuando t= 38 V1= 30 m/s Movil 2: Cuando t= 38 Movil2: cuando t= 155 Vex o + o . t V2 = V v2= 40 – 4 .15 V2 = 40 – 4 . 3 v2= -20 m/s V2 = 40 – 12 V2 = 28 m/s 𝟏 √ = √𝑽𝟏² + 𝑽𝟐² 𝟑 V ½ = √𝟏𝟓² + (−𝟐𝟎)² = 36,05 m/s 𝟏 𝟐 √ = √𝟑𝟎² + 𝟐𝟖² = 42,04 m 4.- Una piedra se lanza hacia arriba con una rapidez de 20 m_s. En su camino hacia abajo es atrapada en un punto situado a 5.0 m por encima del lugar desde donde se lanzó. a) ¿Qué rapidez tenía cuando fue atrapada? b) ¿Cuánto tiempo tomó el recorrido? Solucion: Vo= 20m/s ymax = 𝐕𝐨² 𝟐 .g= 𝟐𝟎² . 𝟐 9,8 =20,4m y1 = y max - 5 =20,4 -5 = 15,4m vf = √𝟐. 𝐠. 𝐲𝟏 √= 𝟐. 𝟗, 𝟖 . 𝟏𝟓, 𝟒 = 𝟏𝟕, 𝟒 𝐦/𝐬 t1= 𝐕𝐨 = 𝐠 𝟐𝟎 𝟗,𝟖 =2,04 s t2= 𝐕𝐟 𝐠 𝟏𝟕,𝟒 𝟗,𝟖 =1,77s = tv= t1 +t2 = 3,81 s 5.- Una piedra se lanza verticalmente hacia arriba y se eleva a una altura de 20 m. ¿Con qué rapidez se lanzó? Vf²= Vo2 – 2 g . Δy Vf² + 2 g . Δy = Vo ² √𝒗𝒇² + 𝟐𝐠 . 𝚫𝐲 =Vo Vo = √𝟎² + 𝟐 . 𝟗, 𝟖 . 𝟐𝟎 Vo = 19,8 m/s 6.- Se lanza una pelota de béisbol verticalmente hacia arriba en la superficie lunar con una rapidez inicial de 35 m/s. Calcule: a) la máxima altura que alcanza la pelota, b) el tiempo que tarda en alcanzar esa altura, c) su velocidad 30 s después de lanzarse y d) cuándo la pelota está a 100 m de altura. En la Luna, g=1,60 m/s2 Datos: g= 1,6m/s² v1= 35m/s Solucion: tmax= tmax= 𝐕𝟐 − 𝐕𝐫 −𝐠 𝟎 − 𝟑𝟓 𝟏,𝟔 = 22 s hmax = V1 . tmax - ½ . g . tmax² hmax = 35 . 22 – ½ . 1,6 . 22² hmax= 383 m cuando 3 = 3s Vf = V1- g . t Vf= 35 -1,6 . 3 Vf= 30,2 m/s Cuando y= 100m Vf²= Vo² - 2g .y Vf = √𝟑𝟓² − 𝟐 . 𝟏, 𝟔. 𝟏𝟎𝟎 Vf = 30 m/s 7.- Se lanza una pelota hacia arriba formando un ángulo de 30° con la horizontal y cae en la parte más alta de un edificio que está a 20 m de distancia. El borde superior se encuentra a 5.0 m por encima del punto de lanzamiento. ¿Con qué rapidez se lanzó la pelota? Solucion: Y max = V1 . t + ½ . g . t² S= 0 + ½ . 9,8 . t² 𝟐𝟓 𝟒,𝟖 T=√ 𝟏𝟎 = √ = 1,01 s 𝟗,𝟖 Vx= VoX= Vo . cos 30° = Vo= 𝒙 𝒕.𝐜𝐨𝐬 𝟑𝟎° 𝟐𝟎 𝟏,𝟎𝟏 .𝐜𝐨𝐬 𝟑𝟎° = 𝒙 𝒕 = 22,86 m/s