representacion de ondas electromagneticas (correccion 1 reduc)

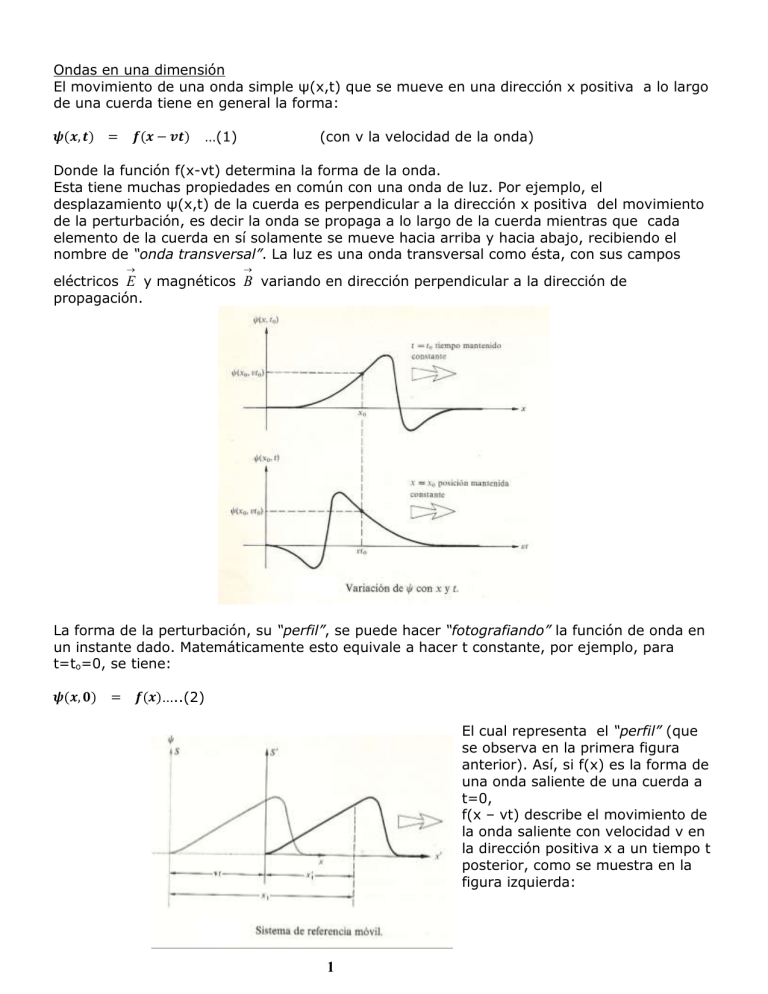
Ondas en una dimensión
El movimiento de una onda simple ψ(x,t) que se mueve en una dirección x positiva a lo largo
de una cuerda tiene en general la forma:
𝝍(𝒙, 𝒕) =
𝒇(𝒙 − 𝒗𝒕)
…(1)
(con v la velocidad de la onda)
Donde la función f(x-vt) determina la forma de la onda.
Esta tiene muchas propiedades en común con una onda de luz. Por ejemplo, el
desplazamiento ψ(x,t) de la cuerda es perpendicular a la dirección x positiva del movimiento
de la perturbación, es decir la onda se propaga a lo largo de la cuerda mientras que cada
elemento de la cuerda en sí solamente se mueve hacia arriba y hacia abajo, recibiendo el
nombre de “onda transversal”. La luz es una onda transversal como ésta, con sus campos


eléctricos E y magnéticos B variando en dirección perpendicular a la dirección de
propagación.
La forma de la perturbación, su “perfil”, se puede hacer “fotografiando” la función de onda en
un instante dado. Matemáticamente esto equivale a hacer t constante, por ejemplo, para
t=to=0, se tiene:
𝝍(𝒙, 𝟎) = 𝒇(𝒙)…..(2)
El cual representa el “perfil” (que
se observa en la primera figura
anterior). Así, si f(x) es la forma de
una onda saliente de una cuerda a
t=0,
f(x – vt) describe el movimiento de
la onda saliente con velocidad v en
la dirección positiva x a un tiempo t
posterior, como se muestra en la
figura izquierda:
1
En dicha figura se tienen 2 sistemas de coordenadas S y S’. El sistema S’ se mueve a una
velocidad v en la misma dirección de la onda, cuya coordenada x’ es igual a:
x’ = x –vt ……(3)
Luego en el sistema S’ el perfil de la onda permanece invariable (es decir, para dicho sistema
la onda no se mueve), tal que la función de onda esta dada por:
𝝍(𝒙, 𝒕) =
𝒇(𝒙′) …..(4)
En la misma forma, g(x+vt) representa una onda que se propaga en la dirección de las x
negativas
Ondas sinusoidales
Una onda que tiene como perfil una sinusoide (como en la figura siguiente) se dice
“armónica”. Estas ondas son de interés particular porque los perfiles más complicados se
pueden sintetizar matemáticamente como sumas de funciones sinusoidales por los métodos
de Fourier. Luego si  ( x,0)  A sen(kx) entonces la onda viajera tiene la forma:
 ( x, t )  A sen k ( x  vt)
….(5)
que es una onda armónica.
El argumento de la función sinusoidal tiene que ser adimensional para tal fin se ha
introducido la constante positiva k, llamada “número de onda” o “número de propagación”. El
máximo valor de la magnitud ψ(x,t) es A, la amplitud. Ahora bien, la función de onda se repite
a si misma después de un período espacial o longitud de onda λ, tal que, ψ(x,t) = ψ(x+λ,t).
Para que este sea el caso el número de onda debe ser igual a k=2π/λ. Análogamente, sí la
onda se repite a si misma después de un período temporal τ, esto es, ψ(x,t)= ψ(x,t+τ), se
sigue que τ=λ/v. considerando que la relación entre el período τ y la frecuencia f es f=1/τ, se
tiene que:
v = fλ …(6)
En forma análoga a la mecánica se introduce aquí la frecuencia angular ω=2πf=2π/τ (que
nosotros conocimos como velocidad angular) cuyas unidades son radianes/segundo. En
consecuencia la forma de la función de onda puede replantearse como:
 ( x, t )  A sen (k x  t )
…(7)
2
En donde se ha considerado que v=ω/k.
La anterior onda armónica va desde - ∞ a +∞, tanto en el espacio como en el tiempo, y es,
por lo tanto, una abstracción matemática. La onda (7) se llama monocromática. Ninguna
perturbación física real tiene esta forma aunque existen aproximaciones en grados diferentes
que se llaman cuasi-monocromáticas.
Fase y velocidad de fase
Uno de los conceptos útiles al tratar con ondas armónicas es el de fase φ, que se define
simplemente como el argumento de la función sinusoidal:
φ = kx – ωt …(8)
La función de onda que se escribe como (7) es realmente un caso especial, puesto que para
t=0 y x=0, ψ(0,0)=0. No hay razón para que la magnitud de la onda ψ no pueda tener
cualquier valor diferente de cero para t=0 y x=0. Esto se consigue trasladando la función
sinusoidal, mediante la introducción de una fase inicial ε tal que:
φ = kx – ωt + ε … (9)
si se imagina una onda armónica que pasa, su velocidad se determina observando el
movimiento de un punto en el que la magnitud de la perturbación permanezca constante. Para
tal punto, la fase debe ser igualmente constante. Así la velocidad de la onda es la velocidad a
la cual viaja la condición de fase constante, esto es:
 x 
v   
 t 
 / t x
 / x t



k
….(10)
La cantidad positiva v, que es la velocidad de propagación de la onda armónica también se
llama la velocidad de fase.
Ondas tridimensionales
Es posible generalizar el concepto de onda en una dimensión a tres dimensiones escribiendo la
parte espacial de la ecuación (7) como:



 ( r )  A sen ( k  r ) … (11)

Sí consideramos que la fase k

 r = constante define una familia de planos en el espacio


todos perpendiculares al vector k (llamado vector de propagación) entonces  ( r ) define una
onda plana cuya perturbación varía sinusoidalmente. Y como antes, para convertir ésta en una
onda plana viajera, simplemente escribimos la ecuación (11) como:



 ( r, t )  A sen ( k  r  t ) …(12)
3
Donde el signo menos corresponde al movimiento

en la dirección positiva de k y el signo más al

movimiento en la dirección negativa de k .
La figura siguiente muestra las variaciones de una
onda sinusoidal plana
de la misma manera se obtiene la forma de una
onda esférica armónica cuya expresión es:
 ( r, t ) 
B
r
sen k ( r  vt) …(13)
Donde la constante B se llama intensidad de la
fuente. Observe que la amplitud B/r es
inversamente proporcional a la distancia desde la
fuente de la onda. Esta es una condición para la
conservación de la energía. La figura siguiente
muestra las variaciones de una onda sinusoidal esférica.
4
Ejercicios:
1. Dada la función de onda (en unidades de SI) para una onda de luz
𝝍(𝒙, 𝒕) = 𝟏𝟎𝟎 𝒔𝒆𝒏 𝟐𝝅( 𝟑 ∙ 𝟏𝟎𝟔 𝒙 − 𝟗 ∙ 𝟏𝟎𝟏𝟒 𝒕)
Determine (a) la amplitud, (b) la velocidad, (c) la longitud de onda, (d) la
frecuencia, (e) el período
2. Dada la función de onda (en unidades de SI) para una onda de luz
𝝍(𝒙, 𝒕) = 𝟏𝟎 𝒔𝒆𝒏 𝟐𝝅( 𝟎. 𝟓 ∙ 𝟏𝟎𝟕 𝒙 − 𝟏. 𝟓 ∙ 𝟏𝟎𝟏𝟓 𝒕)
Determine (a) la amplitud, (b) la velocidad, (c) la longitud de onda, (d) la
frecuencia, (e) el período
Fórmulas
𝒗=
𝝎
𝒌
𝒌=
𝟐𝝅
𝝀
5
𝝎 = 𝟐𝝅𝒇
𝝉=
𝟏
𝒇
Nota:
Toda luz lineal, circular o elípticamente polarizada esta formada por una combinación de

dos ondas linealmente polarizadas con sus campos eléctricos E ortogonales o normales
(perpendiculares) satisfaciendo el principio de superposición de las ondas:
Principio de Superposición
Dos o más ondas pueden atravesar el mismo espacio independientemente una de las otras
Luego:
Cuando dos o más ondas interfieren en un punto del medio, la perturbación en el punto será
igual a la suma vectorial de las perturbaciones (desplazamientos, campos eléctricos,
presiones, cualquier perturbación que produzca una onda) que cada onda produzca en el
punto (esta adición vectorial es llamada superposición)
La siguiente figura ilustra este principio.
INTERFERENCIA CONSTRUCTIVA
DE DOS CRESTAS
A
INTERFERENCIA DESTRUCTIVA
DE UNA CRESTA Y UN VALLE
A
-A (FIJATE EN EL
SIGNO MENOS)
A-A=0 (SUMA
VECTORIAL CERO)
2A
Caso 1. Luz linealmente polarizada
⃗⃗ 𝒙 (𝒛, 𝒕) = 𝒊̂𝑬
⃗⃗ 𝒐𝒙 𝒄𝒐𝒔 (𝒌𝒛 − 𝝎𝒕)
𝑬
con iˆ un vector unitario a lo largo del eje x positivo
⃗⃗ 𝒚 (𝒛, 𝒕) = 𝒋̂𝑬
⃗⃗ 𝒐𝒚 𝒄𝒐𝒔 (𝒌𝒛 − 𝝎𝒕 + 𝝐)
𝑬
con ĵ un vector unitario a lo largo del eje y positivo
Las ondas se mueven en la dirección positiva de z y tienen una fase relativa de ε. El plano de

vibración de E x ( z, t )

Corresponde al plano xz, mientras que E y ( z, t ) permanece en el plano yz, La perturbación

resultante E ( z, t ) de sumar ambas ondas varia con ε:



E ( z , t ) = E x ( z, t ) + E y ( z , t )
6
En el ejemplo específico cuando ε = 0 o un múltiplo entero de ±2π los campos componentes
están en fase (su cresta coincide con su cresta, su valle coincide con su valle) y :

E ( z, t ) = ( iˆ E0x + ĵ E0y) cos (kz – wt)
La amplitud iˆ E0x + ĵ E0y , es constante y así la onda resultante está polarizada en un plano
o polarizada linealmente, como se muestra en la siguiente figura A. Análogamente, cuando ε
es un múltiplo entero impar de ±π los campos componentes están fuera de fase y

E ( z, t ) = ( iˆ E0x - ĵ E0y) cos (kz – wt)
Nuevamente la resultante tiene una amplitud constante y la onda está linealmente polarizada
como lo muestra la siguiente figura B.
Figura A
Figura B
Principio de Huygens
Se puede trazar el avance de un frente de onda a través de un medio aplicando el principio de
Huygens, que establece:
“En una sustancia isotrópica homogénea cada punto del frente puede considerarse como una
fuente de ondas secundarias cuya envolvente en algún instante posterior corresponde a la
onda primaria en ese instante. Las ondas secundarias son esféricas, desplazándose en todas
las direcciones con la misma velocidad y frecuencia que la onda primaria”
En un medio se puede imaginar que la onda primaria estimula los átomos para emitir las
ondas secundarias, las cuáles a su vez, avanzan a la siguiente capa de átomos. La siguiente
figura explica este principio.
7
Propagación de un frente de onda por medio del principio de Huygens
Irradiancia
Una onda luminosa que recorre el espacio a 3x108 m/s conduce energía electromagnética y
por esto puede interactuar con un detector, sea éste una película, la retina o una célula
fotoeléctrica. La energía fluye en la dirección en que avanza la onda, esto es en la dirección


perpendicular al plano que el campo eléctrico E y el campo magnético B forman. En
consecuencia, la energía por unidad de área y por unidad de tiempo que fluyen
perpendicularmente dentro de una superficie en el espacio libre está dada por el vector de

Poynting S , donde:

S

c 2 o
2


E  B ….(14)

Energía sobre tiempo es potencia, así que las unidades en Si de S son Watt/m2 . A las



frecuencias que ocurren en óptica E , B y S todas oscilan a una velocidad extremadamente

rápida y no es práctico medir valores instantáneos de S directamente. En su lugar se
determina su valor promedio

S
sobre un intervalo de tiempo conveniente. Este valor se
conoce como la densidad de flujo radiante. Cuando la energía emerge de una superficie, la
densidad de flujo se llama excitancia; cuando la energía es incidente la densidad de flujo se

llama irradiancia y se simboliza por I= S .
Para una onda armónica plana, polarizada linealmente, viajando a través del espacio libre en

la dirección de k tal que:






E ( r, t )  E o
B( r, t )  B o




sen ( k  r  t )
sen ( k  r  t )
La irradiancia es igual a:
I

c o
2
E 02
La irradiancia es por consiguiente proporcional al cuadrado de la amplitud del campo eléctrico.
Dos formas alternas adicionales de decir la misma cosa son:
8
I
I

c
2
o
B
 c o
E
2
Dentro de un dieléctrico isotrópico, homogéneo y lineal, la expresión para la irradiancia
queda:
I
2
 v
E
Con v la velocidad de la luz en el cristal, ε la permitividad eléctrica del cristal,  la
permeabilidad magnética del cristal, εo la permitividad eléctrica del vacío y o la permeabilidad
magnética del vacío (εo≈8.85x 10-12 s2C2/m3 kg y o≈4πx10-7m kg/C2), tal que:
v 
1

Fotones (energía y cantidad de movimiento)
El modelo fotónico describe la emisión y absorción de la energía radiante luminosa Ɛ en la
forma de paquetes de energía o quantums (fotones) que tienen un valor de:
Ɛ= hf
Es decir, que un fotón tiene una energía Ɛ proporcional a su frecuencia f. La constante de
proporcionalidad
h=6.6256 x 10-34 J ∙ s se llama constante de Planck. Se puede demostrar clásicamente, que la
energía electromagnética y la cantidad de movimiento p están relacionadas por:
𝒑 =
Ɛ
𝒄
𝒑 =
𝒉
𝝀
Luego ya que Ɛ= hf se tiene entonces que:
O en forma vectorial
⃗
⃗ = ℏ𝒌
𝒑
𝒉
donde ℏ = 𝟐𝝅
9
Ejercicios:
3. La longitud de onda de la luz varía aproximadamente desde el violeta en los 390 nm al rojo en los 780 nm. Su
velocidad en el vacío es alrededor de 3x108 m/s, como en el caso de todas las ondas electromagnéticas.
Determinar el correspondiente intervalo de variación de la frecuencia.
4. ¿Cuántas ondas de luz amarillas (λ= 580 nm) caben en una distancia en el espacio igual al grosor de una hoja
de papel (0.003 pulgadas de grueso tiene una hoja de papel) ¿Qué tan lejos se extenderá el mismo número de
microondas (f=1010Hz, es decir 10 GHz y v=3x108m/s)
5. Considere una onda luminosa que tiene una velocidad de fase de 3x108m/s y una frecuencia de 6x1014Hz.
¿Cuál es la distancia más corta a lo largo de la onda entre 2 puntos que tienen una diferencia de fase de 30o?
¿Qué cambio de fase ocurre en un punto dado en 10-6 s? y ¿Cuántas ondas han pasado en ese tiempo?
6. La hipótesis de De Broglie afirma que cada partícula tiene asociada a ella una longitud de onda dad por la
constante de Planck (h= 6.6 x 10-34J s) dividida por el momento lineal de la partícula. Compare la longitud de
onda de una piedra de 6.0 kg moviéndose a una velocidad de 1.0 m/s con la de la luz.
7. (a) ¿Cuál es la longitud de una onda electromagnética que tiene una frecuencia de 100 Hertz?(1 Hertz = 1 /1s)
(b) ¿Cuál es la frecuencia de una onda con una longitud de onda de 1 m?
(c) Una onda de luz anaranjada de frecuencia 50 THz existe en una región del espacio ¿cuánto varía la fase en un
tiempo de 1x10-9s respecto a un punto fijo en la onda? ¿Cuánta distancia recorre en este tiempo?
8. Una onda infrarroja armónica plana que se desplaza en un medio transparente está dada por:
𝑬𝒙 (𝒙, 𝒕) = 𝑬𝒐𝒙 𝒔𝒆𝒏 𝟐𝝅(𝟎. 𝟐 ∙ 𝟏𝟎𝟕 𝒚 − 𝟑 ∙ 𝟏𝟎𝟏𝟒 𝒕)
en unidades de SI. Determine el índice de refracción del medio a esa frecuencia y la longitud de onda de la
perturbación en el vacío (considere que la frecuencia f de la onda no cambia al pasar del medio al vacío).
9. Un láser emite un haz de luz altamente colimado formando una mancha circular de 2 mm de diámetro
a un nivel de potencia, o flujo radiante, de 100 mW. Despreciando cualquier divergencia del haz,
calcule su irradiancia.

10. Una onda electromagnética plana que se mueve a través del espacio libre tiene un campo E (también
llamado campo óptico) dado por Ex=0, Ey=0 y
𝑬𝒛 (𝒙, 𝒕) =
𝟏𝟎𝟎 𝒔𝒆𝒏[𝟖𝝅 ⋅ 𝟏𝟎𝟏𝟒
(𝒕
−
𝟎. 𝟑𝟑 ∙ 𝟏𝟎−𝟖 𝒙)]
Calcule la densidad de flujo correspondiente
10. Imaginase una onda electromagnética plana que se propaga en el espacio a lo largo de la dirección del eje

y. Sí el campo E esta linealmente polarizado en el plano yz y si λo= 500 nm, hallar la expresión del campo

B correspondiente cuando la irradiancia es 53.2 W/m2.
10