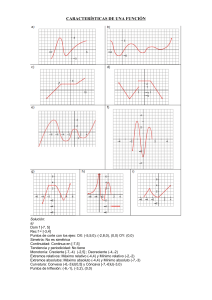
ASIGNATURA CÁLCULO I UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS 2021-2 SEMESTRE ACADÉMICO 2021-2 1 UNIDAD IV SEMANA 13 SESIÓN 1 TEMA: VALORES EXTREMOS DE UNA FUNCIÓN CRITERIO/CAPACIDAD Al finalizar la sesión, El estudiante calcula intervalos de crecimientos y decrecimientos de una función, puntos críticos y puntos de inflexión aplicando los criterios de la primera y segunda derivada. COMPETENCIA Resuelve problemas de contexto real con la utilización de estrategias y procedimientos matemáticos para las aplicaciones de la derivada de una función. Contenido 01 Valores extremos de una función Definición 02 Teoremas Criterio de la primera derivada Criterio de la segunda derivada 03 Optimización VALORES EXTREMOS DE UNA FUNCIÓN Definición 1: Sea 𝑐 un número en el dominio 𝐷 de una función 𝑓. Entonces: ▪ 𝑓(𝑐) es el valor máximo absoluto de 𝑓 sobre 𝐷 si 𝑓(𝑐) ≥ 𝑓 (𝑥) para toda 𝑥 en 𝐷. ▪ 𝑓(𝑐) es el valor mínimo absoluto de 𝑓 sobre 𝐷 si 𝑓(𝑐) ≤ 𝑓 (𝑥) para toda 𝑥 en 𝐷. Los valores máximo y mínimo de 𝑓 se llaman valores extremos de 𝑓. • Mínimo absoluto 𝑓(𝑎), • Máximo absoluto 𝑓(𝑑), • Mínimos locales 𝑓(𝑐), 𝑓(𝑒), • Máximos locales 𝑓(𝑏), 𝑓(𝑑) Definición 2: El número 𝑓(𝑐) es un ▪ valor máximo local de 𝑓 si 𝑓(𝑐) ≥ 𝑓 (𝑥) cuando 𝑥 está cerca de 𝑐. ▪ valor mínimo local de 𝑓 si 𝑓(𝑐) ≤ 𝑓 (𝑥) cuando 𝑥 está cerca de 𝑐. 𝑓(4) = 5 es un mínimo local 𝑓(12) = 3 es un mínimo local y el mínimo absoluto 𝑓(8) = 7 es un máximo local 𝑓(1) = 8 es un máximo absoluto En la gráfica de la función 𝑓(𝑥) = 𝑥 3 , que se muestra en la siguiente figura, se ve que no tiene valor máximo absoluto ni valor mínimo absoluto. De hecho, tampoco posee valores extremos locales. No hay mínimo ni máximo Ejemplo 3 La gráfica de la función 𝑓 𝑥 = 3𝑥 4 − 16𝑥 3 + 18𝑥 2 , −1 ≤ 𝑥 ≤ 4 se muestra en la siguiente figura. Observación: o 𝑓(1) = 5 es un máximo local o 𝑓(−1) = 37 es un máximo absoluto (pero no es un máximo local porque se presenta en un punto extremo) o 𝑓(0) = 0 es un mínimo local o 𝑓 3 = −27 es un mínimo tanto local como absoluto o En 𝑥 = 4, 𝑓 no tiene valor local ni máximo absoluto. Teorema del valor extremo Si 𝑓 es continua sobre un intervalo cerrado 𝑎, 𝑏 , entonces 𝑓 alcanza un valor máximo absoluto 𝑓(𝑐) y un valor mínimo absoluto 𝑓(𝑑) en algunos números 𝑐 y 𝑑 en 𝑎, 𝑏 . En la figura siguiente se ilustra el teorema del valor extremo Método del intervalo cerrado Para hallar los valores máximo y mínimo absolutos de una función continua f sobre un intervalo cerrado 𝑎, 𝑏 : 1. Encuentre los valores de f en los puntos críticos de f en 𝑎, 𝑏 . 2. Halle los valores de f en los puntos extremos del intervalo. 3. El más grande de los valores de los pasos 1 y 2 es el valor máximo absoluto; el más pequeño, el valor mínimo absoluto. Ejemplo Encuentre los valores absolutos máximo y mínimo de la función 1 3 2 𝑓 𝑥 = 𝑥 − 3𝑥 + 1, − ≤𝑥≤4 2 Solución Por el teorema del intervalo cerrado se tiene que: 1. 𝑓 ′ 𝑥 = 3𝑥 2 − 6𝑥 = 3𝑥 𝑥 − 2 Puntos críticos (PC): 𝑥 = 0 y 𝑥 = 2. Los valores de 𝑓 en estos PC son: 𝑓(0) = 1 y 𝑓 2 = −3 2. Los valores de 𝑓 en los puntos extremos del intervalo son 1 2 1 8 𝑓(− ) = y 𝑓 4 = 17 3. Comparando estos cuatro números, vemos que: El valor máximo absoluto es 𝑓 4 = 17 y El valor mínimo absoluto es 𝑓 2 = −3. TEOREMAS I. Criterio de la primera derivada para extremos relativos Sea 𝑐 un punto crítico de una función 𝑓 definida en una vecindad ℧𝛿 𝑐 = 𝑐 − 𝛿; 𝑐 + 𝛿 tal que: 𝑓 es continua en ℧𝛿 𝑐 y 𝑓 es derivable en ℧𝛿 𝑐 , excepto tal vez en 𝑐. Entonces 𝑓(𝑐) puede clasificarse así: ▪ Si 𝑓 ′ 𝑥 > 0, ∀ 𝑥 ∈ 𝑐 − 𝛿; 𝑐 y 𝑓 ′ 𝑥 < 0, ∀ 𝑥 ∈ 𝑐; 𝑐 + 𝛿 , entonces 𝒇(𝒄) es un valor máximo local de 𝒇. ▪ Si 𝑓 ′ 𝑥 < 0, ∀ 𝑥 ∈ 𝑐 − 𝛿; 𝑐 y 𝑓 ′ 𝑥 > 0, ∀ 𝑥 ∈ 𝑐; 𝑐 + 𝛿 , entonces 𝒇(𝒄) es un valor mínimo local de 𝒇. ▪ Si 𝑓 ′ 𝑥 > 0, ∀ 𝑥 ∈ 𝑐 − 𝛿; 𝑐 y 𝑓 ′ 𝑥 > 0, ∀ 𝑥 ∈ 𝑐; 𝑐 + 𝛿 o si 𝑓 ′ 𝑥 < 0, ∀ 𝑥 ∈ 𝑐 − 𝛿; 𝑐 y 𝑓 ′ 𝑥 < 0, ∀ 𝑥 ∈ 𝑐; 𝑐 + 𝛿 , entonces 𝒇(𝒄) no es un valor máximo o un mínimo local de 𝒇. Interpretación geométrica de la primera derivada Ejemplo: Halle los extremos relativos de la función 𝑓 𝑥 = 𝑥 4 − 4𝑥 3 + 10. Solución: Paso 1: 𝐷𝑜𝑚(𝑓) = ℝ Paso 2: derivando la función 𝑓′ 𝑥 = 4𝑥 3 − 12𝑥 2 = 4𝑥 2 𝑥 − 3 Paso 3: hallando los puntos críticos (PC) 𝑓′ 𝑥 = 0 4𝑥 2 𝑥 − 3 = 0 ⟹ 𝑥 = 0, 𝑥 = 3 Entonces, los PC son: 𝑥 = 0, 𝑥 = 3. Paso 5: aplicando el criterio de la primera derivada. Paso 6: Graficando II. Criterio de la segunda derivada para extremos relativos Sea 𝑓 una función para la cual existe la segunda derivada de 𝑓 sobre un intervalo 𝑎, 𝑏 que contiene al punto crítico 𝑥 = 𝑐 (es decir 𝑓 ′ 𝑐 = 0): ▪ Si 𝑓′′(𝑐) > 0, entonces 𝑓(𝑐) es un mínimo relativo. ▪ Si 𝑓′′ 𝑐 < 0, entonces 𝑓(𝑐) es un máximo relativo. ▪ Si 𝑓′′ 𝑐 = 0, entonces la prueba falla y 𝑓(𝑐) puede ser o no un extremo relativo. En este caso se usa la prueba de la primera derivada. Ejemplo 1: Encontrar los extremos relativos correspondientes a 𝑓 𝑥 = 𝑥 4 + 1 usando el criterio de la segunda derivada. Solución: Para este ejemplo, el criterio de la segunda derivada falla, y si usamos el primer criterio se verifica que 𝑓 0 = 1 es mínimo. Ejemplo: Encontrar los extremos relativos correspondientes a la función 𝑓 𝑥 = −3𝑥 5 + 5𝑥 3 Solución: Paso 1: hallando los puntos críticos de 𝑓: 𝑓´ 𝑥 = 15𝑥 2 1 − 𝑥 2 = 0 ⇒ 𝑥 = −1,0,1 Paso 2: 𝑓´´ 𝑥 = 30 −2𝑥 3 + 𝑥 = 30𝑥 −2𝑥 2 + 1 y aplicando el criterio de la segunda derivada, tenemos Como el criterio de la segunda derivada no decide en (0, 0), debemos utilizar el criterio de la primera derivada. Paso 4: Graficando APLICACIONES DE LA DERIVADA (OPTIMIZACIÓN) En ciencia e ingeniería a menudo tenemos interés en los valores máximo y mínimo de una función; por ejemplo, una empresa tiene interés natural en maximizar sus ganancias a la vez que minimiza los costos. Cuando vaya al 1 mercado, observe que todas las latas que contienen, por ejemplo, litro de 2 gaseosa tienen el mismo aspecto físico, es decir, son de la misma forma (mismos radio y altura) pero esto no es coincidencia, puesto que hay dimensiones específicas que minimizan la cantidad de metal usado y, entonces, reducen los costos de construcción de la lata a una empresa. Hemos oído hablar de utilidad (beneficio) máxima(o), mínimo costo, tiempo mínimo, voltaje máximo, forma óptima, tamaño mínimo, máxima resistencia y máxima distancia. Veamos un ejemplo: Ejemplo: Se va un fabricar una lata metálica cilíndrica que ha de contener 1 Litro de aceite. Encuentre las dimensiones que debe tener la lata de manera que minimicen el costo del metal para fabricarla. Solución: Paso 1: graficar para esto usamos el volumen de la lata de aceite de 1 L, que tomamos como 1000𝑐𝑚3 , entonces 𝑣 = 1000 = 𝜋𝑟 2 ℎ … (2) De (1) y (2) tenemos la función en una variable que queremos minimizar 2000 2 𝐴 𝑟 = 2𝜋𝑟 + donde 𝑟 > 0 𝑟 Paso 5: Para encontrar los PC hacemos 𝐴´ 𝑟 = 0 dando 𝑟= Paso 2: las formas que puede tener el envase de 1L son muy diversas, donde se observa que están variando el radio 𝒓 de la base y la altura 𝒉 del cilindro. Paso 3: La lata de aceite comprende la superficie total del cilindro cuya área es: 𝐴 𝑟, ℎ = 2𝜋𝑟 2 + 2𝜋𝑟ℎ … (1) que es una función en 2 variables: r y h. Paso 4: Para minimizar el costo de la lata debemos minimizar el área total de la lata, donde la función área debe ser en una variable, 3 500 𝜋 y para este valor, haciendo un análisis, se verifica que se presenta un mínimo y reemplazando en h 1000 tenemos ℎ = 𝜋𝑟 2 =2r Es decir, para minimizar el costo de la lata el radio de la base debe ser 𝑟 = 3 500 𝜋 y la altura debe ser ℎ = 2𝑟. Gracias! Equipo de los Docentes de Cálculo 1