estruct crist

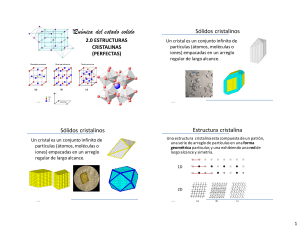
Química del estado solido
2.0 ESTRUCTURAS
CRISTALINAS
(PERFECTAS)
A.S.P.
Sólidos cristalinos
Un cristal es un conjunto infinito de
partículas (átomos, moléculas o
iones) empacadas en un arreglo
regular de largo alcance.
A.S.P.
Estructura cristalina
Sólidos cristalinos
Un cristal es un conjunto infinito de
partículas (átomos, moléculas o
iones) empacadas en un arreglo
regular de largo alcance.
Una estructura cristalina esta compuesta de un patrón,
una serie de arreglo de partículas en una forma
geométrica particular, y una exhibiendo una red de
largo alcance y simetría.
1D



























2D
A.S.P.
A.S.P.
1
Redes cristalinas
Red (lattice) 2D; ordenamiento regular en forma
geométrica de partículas en una estructura.
Redes cristalinas
Red (lattice) 2D; ordenamiento regular en forma
geométrica de partículas en una estructura.
Punto de red
(Puntos que
conforman la red)
En el plano solo existen 5
posibles tipos de redes,
que reciben el nombre de
redes planas:
A.S.P.
A.S.P.
Redes cristalinas
Red (lattice) cristalina; ordenamiento regular de
partículas (átomos, moléculas o iones de una sustancia)
en una estructura cristalina.
Celda unitaria
Puntos de red (Puntos que conforman la red
cristalina. Lo que rodea a cada punto de red es
idéntico en cualquier otra parte del material)
A.S.P.
Tipos de redes tridimesionales
Si consideramos en una celda (objeto tridimensional) la
ubicación de las partículas se tiene 4 tipos de redes
tridimensionales;
C, centradas, si solo contiene puntos de
red centradas en dos caras opuestas
entre si.
I ó B, centrada en el cuerpo, si
contiene un punto de red en el
centro del paralelepípedo.
A.S.P.
2
Tipos de redes tridimesionales
Si consideramos en una celda (objeto tridimensional) la
ubicación de las partículas se tiene 4 tipos de redes
tridimensionales;
C, centradas
S o P, simple
o primitiva
F, facial
I ó B, centrada
en el cuerpo
A.S.P.
Estructura cristalina
Las partículas siguen un patrón que
es repetido a los largo del espacio
(translación) sin rotación ni
espacios vacios o traslapes para
generar todo el cristal.
La unidad mínima de este patrón que posee la mayor simetría se
llama celda unitaria.
Celda primitiva; paralelogramos (2D) o paralelepípedos (3D) que
constituyen la menor subdivisión de una red cristalina que
conserva las características generales de toda la retícula, de
modo que por simple traslación de la misma, puede reconstruirse
la red al completo en cualquier punto
A.S.P.
Celda unitaria
Celda unitaria
La forma de una celda unitaria es
descrita por seis parámetros:
•Tres longitudes (vectoriales unitarios)
axiales, ejes cristalográficos designados a,
b y c expresadas en términos de Å
(Angstroms), y
•Tres ángulos interaxiales, a , b y g dados
en términos de ° (grados).
El ángulo a es el ángulo formado entre los ejes b y c;
b es el ángulo formado entre los ejes a y c;
g es el ángulo formado entre los ejes a y b.
A.S.P.
A.S.P.
3
Sistemas cristalinos (Tipos de celda)
Sistema cristalino; es el forma geométrica tridimensional
(paralelepípedo elemental) que adopta la celda unitaria
A.S.P.
No. Sistema
cristalino
1 Cubico
Longitudes Ángulos de
de celda
celda
a=b=c
a= b = g = 90°
2
Tetragonal
a=bc
a= b = g = 90°
3
Ortorrómbico a  b  c
a= b = g = 90°
4
Trigonal /
a=b=c
Romboédrica
a= b = g  90°
A.S.P.
Sistemas cristalinos (Tipos de celda)
No. Sistema
cristalino
5 Triclínico
Sistemas cristalinos (Tipos de celda)
Longitudes Ángulos de
de celda
celda
abc
a b  g  90°
6
Monoclínico
abc
a  90°
b = g = 90°
7
Hexagonal
a=bc
a=b = 90°
g = 120°
Red 3D + sistema cristalino
Combinando los 7 sistemas
cristalinos con los 4 tipos de
red, se obtendrían 28
posibles combinaciones. En
realidad, como demostró
Auguste Bravais en 1848,
sólo existen 14
configuraciones básicas,
pudiéndose obtener el resto
a partir de ellas.
Las 14 redes de Bravais
A.S.P.
4
Tipos de redes tridimesionales
Ocupación de las celdas cristalinas
Una partícula no contribuye por completo en la
ocupación de una celda, solo lo hace en cierta medida.
Esto depende del sitio donde se ubique.
¿De qué tipo de red son las siguientes celdas?
C (diamante), Si, Ge
Contribución de las partículas
en la ocupación de la celda
Posición
Ocupación
Cuerpo
1
Aristas
1/8
Cara
1/2
Blenda de Zinc (ZnS), Arseniuro de Galio,
fosfuro de Indio, Carburo de silicio
(cubico) y nitruro de Galio (cubico)
A.S.P.
A.S.P.
Ocupación de las celdas cristalinas
Una partícula no contribuye por completo en la
ocupación de una celda, solo lo hace en cierta medida.
Esto depende del sitio donde se ubique.
Numero de partículas en los cuatro tipos de celdas
Tipo
Primitiva
# de
partículas en
celda unitaria
Pregunta:
Y en arreglo compacto hexagonal,
característico de muchos metales,
¿con cuanto contribuye cada partícula
a la ocupación de la celda?
Contribución de las partículas
en la ocupación de la celda HCP
Posición Ocupación Total
P
1
Centrada en el
cuerpo
I, B
2
Cuerpo
1 (3)
3
Centrada en la
cara
A, C
2
Aristas
1/6 (12)
2
4
Cara
1/2 (2)
1
Total
6
Centrada en
todas las caras
A.S.P.
Símbolo
Ejercicio 3;
F
A.S.P.
5
Ocupación de las celdas cristalinas
La densidad de la celda cristalina depende tanto de su tamaño como
del numero de partículas que los constituyan.
No.
Sistema cristalino
1
Triclínico
abc (1 - cos 2a-cos 2b-cos2g + 2 cos a cos b cos g )1/2
2
Monoclínico
abc sin b
3
Ortorrómbico
abc
4
Hexagonal
(3/2) a2 c = 0.866 a2 c
5
Tetragonal
a2 c
6
Cubico
a3
 m
V
P.M  Z
 
V  N av
Volumen
Planos cristalinos
Planos cristalinos son planos geométricos determinado con tres
puntos que no sean colineales. El plano puede especificarse
dando las coordenadas de los puntos en función de las longitudes
reticulares a, b y c.
West, p.380
P.M ( g / mol )  Z

3   1.66
 cm 
V ( A3 )
  g
A.S.P.
A.S.P.
Planos cristalinos
Índices de Miller
Es un conjunto de 3 números enteros denotados
como (h k l) que permiten describir:
¿Cómo se describen los planos cristalinos?
A.S.P.
•
•
•
•
•
•
Puntos en la celda
Direcciones en el cristal
Planos en la celda
Distancias interplanares
Volumen de la celda
Densidad
A.S.P.
6
Índices de Miller
Índices de Miller y direcciones en una celda unitaria
Como un cristal es un arreglo periódico, existen familias de direcciones y
planos equivalentes. Hay una notación que permite distinguir un plano o una
dirección en especifico.
Usar la notación;
[ ] para identificar una dirección especifica,
p. e. [1 0 -1].
< > para identificar una familia de direcciones
equivalentes, p. e. <110>.
( ) para identificar un plano en especifico (p. e
(113).
{ } para identificar una familia de planos
equivalentes, p. e {311}.
una barra sobre un numero índice es equivalente a
un signo menos.
Índices de Miller (planos)
Índices de Miller (planos)
El procedimiento para determinar los índices de Miller para un
plano de un cristal cúbico es el siguiente:
• Escoger un plano que no pase por el origen en (0,0,0)
• Determinar los puntos en los cuales el plano cristalino
intercepta los ejes cristalográficos de la celda. Estas
intersecciones pueden ser fraccionarias.
• Construir los recíprocos de las intersecciones.
• Despejar fracciones y determinar el conjunto más pequeño de
números enteros que estén en la misma razón de las
intersecciones. Estos números enteros son los índices de
Miller de un plano cristalográfico y se encierran entre
paréntesis sin usar comas.
La notación (hkl) se emplea para indicar los índices de Miller en
sentido general, donde h, k, y l son los índices de Miller para
un plano de un cristal cúbico de ejes x, y, y z respectivamente.
A.S.P.
A.S.P.
7
Distancia interplanar
Distancia interplanar
La distancia interplanar entre planos adyacentes en la serie (h k l) puede
ser calculada usando;
No.
Sistema
cristalino
Espacio interplanar
La distancia interplanar entre planos adyacentes en la serie (h k l) puede
ser calculada usando;
No.
1
Cubico
1 h k l

d2
a2
2
Tetragonal
1 h 2  k 2 l2

 2
d2
a2
c
5
3
Ortorrómbico
1 h 2 k 2 l2

 
d 2 a 2 b2 c2
6
2
2
2
4
Sistema
cristalino
Espacio interplanar
1 4  h 2  hk  k 2  l 2
  2
 
d 2 3 
a2
 c
2
2
2
2


Monoclínico 1  1  h  k sin b  l  2hl cos b 
2
2
2
2

d
sin b  a
b
c2
a  c 
1
1
Triclínico


d2 V2
Hexagonal
Véase West, p.380
West, p.380
A.S.P.
A.S.P.
Celdas hexagonales
Celdas hexagonales
Índices de Miller - Bravais
Índices de Miller - Bravais
Usa 4 índices en lugar de 3, se
denominan índices Miller-Bravais, son
representados por las letras h, k, i, l y
encerrados entre paréntesis (h k i l).
Estos índices hexagonales están basados
en un sistema coordenado de cuatro
ejes, tres ejes básicos a1,a2,a3 que
forman 120° entre sí, el cuarto eje o eje
c es el eje vertical y está localizado en el
centro de la celda unidad
A.S.P.
c
a3
a2
a1
A.S.P.
8
Celdas hexagonales
Algunos Planos
Descripción de la estructura del cristal
La estructura de un cristal puede ser descrita en diversas formas. La
manera mas común es referida al tamaño y forma de la celda
unidad y la posición de los átomos (o iones) dentro de la celda. Sin
embargo, esta información en muchos casos es insuficiente para
permitir comprender la estructura correcta en tres dimensiones.
El método mas aplicable para describir
las estructuras solidas de tanto los
elementos químicos como de los
metales así como la mayoría de los
compuestos empleados ya sea como
semiconductores o aislantes es la
aproximación de empaquetamiento
compacto o cerrado.
A.S.P.
A.S.P.
Descripción de la estructura del cristal
Empaquetamiento y energía
Distribución aleatoria
(No denso)
Energía de
enlace
Distribución ordenada
(denso)
A.S.P.
Descripción de la estructura del cristal
Estructuras cristalinas metálicas
Razones para el empaquetamiento denso:
- Generalmente solo está presente un
elemento, por lo que todos los radios
atómicos son iguales.
- El enlace metálico no es direccional.
- Las distancias a los primeros vecinos
tienden a ser cortas para reducir la energía
del enlace.
- La nube electrónica cubre a los núcleos
• los metales tienen las estructuras
cristalinas más simples.
A.S.P.
9
Descripción de la estructura del cristal
Descripción de la estructura del cristal
El modelo de empaquetamiento compacto o cerrado asume:
a) Los átomos se consideran como esferas duras de igual tamaño,
b) El empaquetamiento es hecho de tal forma que los átomos
ocupan el máximo espacio disponible.
C. F. Gauss demostró que la
mayor densidad media que
puede obtenerse con una
disposición periódica es 0.74048
Muchas estructuras cristalinas
están basadas en
empaquetamientos compactos de
átomos, iones, o grandes iones
con otros más pequeños
rellenando el espacio entre ellos.
A.S.P.
A.S.P.
Empaquetamiento compacto
Empaquetamiento compacto
1. Se asume que los átomos son esferas duras de igual tamaño.
1. Se asume que los átomos son esferas duras de igual tamaño.
2. El empaquetamiento es hecho de tal forma que los átomos ocupan el
máximo espacio disponible.
2. El empaquetamiento es hecho de tal forma que los átomos ocupan el
máximo espacio disponible.
¿Cómo acomodar los átomos para minimizar el espacio vacío?
hcp
ccp
Este tipo de empaquetamiento se conoce como empaquetamiento
compacto o cerrado
A.S.P.
1 capa
Una segunda capa, ¿Dónde?
A.S.P.
10
Empaquetamiento compacto
Empaquetamiento compacto
Una segunda capa, ¿Dónde?
A.S.P.
Y una tercer capa, ahora ¿Dónde?
A.S.P.
Empaquetamiento compacto
Empaquetamiento compacto
hcp
En el primer caso, izquierda, no hay esferas/ átomos en la misma posición en
las 3 primeras capas, pero en el segundo caso se puede observar que la capa
3 este en la misma posición que la capa 1.
Así, se tienen varios posibles acomodos:
1..2..3..1..2..3..1..2..3……. Tres diferentes capas, se denomina empacamiento
cerrado cubico (ccp).
1..2..1..2..1..2..1..2..1……. Dos diferente capas, se denomina empacamiento
cerrado hexagonal (hcp).
A.S.P.
ccp (o fcc)
A.S.P.
11
Empaquetamiento compacto
Empaquetamiento compacto
Numero de coordinación es numero de átomos o
partículas, primeros vecinos, que rodean a un
partícula o átomo en una estructura.
hcp y ccp son las estructuras de empaquetamiento más simples y
comunes. Cada átomo esta rodeado por otros 12 átomos dando
en ambas estructuras un numero de coordinación de 12.
A.S.P.
A.S.P.
Empaquetamiento compacto
Empaquetamiento compacto
Numero de coordinación en estructuras ccp y hcp
Arreglo cúbico centrado en el cuerpo (bcc) puede
no ser un arreglo compacto.
A
NC = 8
Densidad de empacamiento = 68%
B
A
c.c.p
A.S.P.
A.S.P.
12
Factor de empaquetamiento atómico
Vacancias Octaédricas y tetraédricas
Hay sitios tetraédricos vacios
(vacancias) rodeados por cuatro
(4) átomos arreglados en la
esquina de un tetraedro.
Similarmente, hay sitios vacios
octaédricos que están rodeados
por seis (6) átomos ubicados en
los vértices de un octaedro.
A.S.P.
Factor de empaquetamiento atómico
Ocupación del espacio en la celda cristalina
Representa la fracción de espacio ocupado por las partículas (esferas
rígidas) que conforman la celda.
Estructura
ao (r)
N.C. F. E. A.
Metales
Cs
2r
6 0.52
Ninguno
bcc
4r/31/2
8 0.68
Fe, Ti, W, Nb, Mo, Ta, K, Na,
V, Cr, Zr
fcc
4r/21/2
12 0.74
Fe, Cu, Al, Au, Ag, Pb, Ni, Pt
hc
ao =2r
12 0.74
Ti, Mg, Zn, Be, Co, Zr, Cd
co =1.633ao
FEA 
A.S.P.
Representación poliedral
Cristalinidad
Se refiere al grado de orden estructural en un sólido. Generalmente,
se expresa como el porcentaje del volumen de un solido que es
cristalino
Cristalinidad tiene influencia en
•Dureza
•Densidad
•Transparencia
•Difusión
Presente en;
•Metales y aleaciones
•Polímeros
•Materiales cerámicos
•“Vidrios”
A.S.P.
Z v
Vc
Pero también, en un material completamente
cristalino puede haber;
a) Regiones cristalinas independientes
(gramos o cristalitos), varias orientaciones
separadas por fronteras de gramos.
b) Defectos o dislocaciones
Es usual representar la estructura de un cristal en
forma de poliedros. Aquí, los aniones son
representados por los puntos en las vértices del
poliedro de coordinación.
Esta aproximación es basada en el principio que
los aniones, los cuales tienen mayor radio iónico
que los cationes, ocultan al catión y están
preferentemente arreglados en acordancia con un
patrón estándar de densidad electrónica.
La posición de los cationes y el numero de
coordinación, el cual determina las características
de la estructura cristalina, están claramente
presentes en esta aproximación.
A.S.P.
13
Representación poliedral
Estructuras cristalinas importantes
Estructura tipo CsCl.
Red cúbica primitiva de Clcon Cs + en el centro (bcc)
Una fórmula por celda
unidad.
Número de coordinación 8.
Es compartida por CsBr, Csl,
TlX y NH4X.
Compuestos que presentan esta estructura cristalina se dice tienen
estructura, o estructura tipo, de CsCl.
A.S.P.
Estructuras cristalinas importantes
Estructura tipo NaCl, o sal
de roca.
Los cationes forman una red fcc,
así también los aniones.
Cuatro fórmulas por celda
unidad.
Número de coordinación 6. Cada
catión esta rodeado por seis
aniones, y viceversa. Así, el
poliedro de coordinación es
un octaedro.
Sustancias que cristalizan con esta estructura se incluyen a casi todos los
haluros alcalinos (LiF, LiCl,. . ., NaF, NaCl,. . ., RbF, RbCl,. . .), los óxidos de
alcalinotérreos (como son MgO y CaO), y un sulfuro importante, el PbS.
Estructuras cristalinas importantes
Estructura tipo NaCl, o sal
de roca.
NaCl, o sal de roca;
Red; fcc
NC; 6.
Poliedro; octaedro.
Sustancias que cristalizan con esta estructura se incluyen a casi todos los
haluros alcalinos (LiF, LiCl,. . ., NaF, NaCl,. . ., RbF, RbCl,. . .), los óxidos de
alcalinotérreos (como son MgO y CaO), y un sulfuro importante, el PbS.
14
Estructuras cristalinas importantes
Estructura tipo Blenda de Zinc
(ZnS)
Los átomos de zinc y los átomos de
azufre cada uno forman una red de
fcc.
Empaquetamientos ABCABC... (blenda)
o ABABAB... (wurtzita) de S, con Zn
en la mitad ordenada de huecos
tetraédricos. Son dos polimorfos.
Esta estructura es característica de
compuestos con esencialmente
enlace covalente.
La coordinación es cuatro.
Estructuras cristalinas importantes
Estructura tipo Arseniuro de
Níquel, NiAs.
Equivalente a NaCl, pero con
empaquetamiento ABAB... de
As. Cada Ni esta rodeado
octaédricamente de As, y cada
As ocupa el centro de un prisma
trigonal de átomos de Ni.
Estructuras cristalinas importantes
Estructura tipo Blenda de Zinc
(ZnS)
Los átomos de zinc y los átomos de
azufre cada uno forman una red de
fcc.
Esta estructura es característica de compuestos con esencialmente
enlace covalente. Algunos compuestos con esta estructura son: CuCl, Cul,
HgS, y un numero de importantes compuestos semiconductores tales
como CdS y GaAs.
Estructuras cristalinas importantes
Estructura tipo Cinnabar
(HgS).
También conocido como cinabrio o
bermellón (por su color rojo
bermellón) forman un sistema
trigonal
15
Estructuras cristalinas importantes
ESTRUCTURAS COVALENTES EXTENSAS
Diamante
Estructura cúbica centrada en
las caras con ocupación del 50%
de los huecos tetraédricos. Los
átomos ocupan las posiciones de
Zn y S en la blenda.
Todos los átomos son iguales,
con coordinación tetraédrica,
y distancia C-C =1.54 Å. El
número de coordinación 4.
ESTRUCTURAS COVALENTES EXTENSAS
Grafito
Polimorfo del carbono. Capas de
átomos de carbono formando
una red hexagonal, con enlaces
C-C de 1.42 Å, menor que en el
diamante, (enlace múltiple).
La distancia entre láminas es de
3.35 Å y están unidas entre sí
por fuerzas de Van der Waals.
Estructuras cristalinas importantes
Estructuras covalentes extensas
Fullereno
En estado sólido las esferas
Es un polimorfo del C descubierto en
1985. Existe en forma molecular y
consiste en una red esférica de 60
átomos de C (C60). Las caras de la red
esférica son hexagonales (20) y
pentagonales (12), como un balón de
fútbol, de modo que no hay dos
pentágonos compartiendo arista.
Estructuras cristalinas importantes
forman una estructura
cristalina con
empaquetamiento ABC.
Estructuras cristalinas importantes
Estructuras covalentes extensas
Cuarzo
Una forma de sílice. La forma beta
consta de tetraedros [SiO 4] unidos
entre sí, cada O esta compartido por
dos tetraedros. Los tetraedros forman
hélices a lo largo del cristal, es un
material anisotrópico y desvía el
plano de la luz polarizada, según la
dirección de la hélice (enantiomorfos)
16
Estructuras cristalinas importantes
Estructuras de óxidos mixtos: Espinela,
Espinela, MgAl2O4.
Estructuras cristalinas importantes
Estructuras de óxidos mixtos: Espinela,
Espinelas, MgAl2O4(A2+B3+2O2–4)
La estructura general tipo espinela (AB2X4)
pueden adoptarla compuestos con iones
con las siguientes cargas formales:
A
B
X
(VI)
(IV)
(II)
(I)
(II)
(III)
(-II)
(-II)
(-II)
La estructura es un empaquetamiento cubico compacto de iones
óxido, con iones A ²+ en huecos tetraédricos y B³+ en octaédricos. En
la estructura de la espinela inversa, B(AB)O 4 los A están en huecos
octaédricos y los B se reparten al 50% entre octaédricos y
tetraédricos.
Estructuras cristalinas importantes
Los cationes (usualmente metales) ocupan 1/8 de los sitios
tetraédricos y 1/2 de los sitios octaédricos y hay 32 iones O-2 en
la celda unitaria.
Estructuras cristalinas importantes
Estructuras de óxidos mixtos: Perovskita,
Perovskita (CaTiO3 = ABX3).
Estructuras de óxidos mixtos: Perovskita,
Perovskita (CaTiO3 = ABX3).
Varia posibles descripciones:
-El átomo A ocupa el centro de un cubo
cuyos vértices ocupan los iones B con
iones óxido (X) en los puntos medio de
todas las aristas.
Varia posibles descripciones:
-El átomo A ocupa el centro de un cubo cuyos vértices ocupan
los iones B con iones óxido (X) en los puntos medio de todas las
aristas.
Perovskita,
CaTiO3 (XII A2+VII B4+X2–3)
Ca;(0,0,0)
Ti;(½, ½, ½)
O; (½, ½, ,0).
17
Estructuras cristalinas importantes
Estructuras de óxidos mixtos: Perovskita,
Ilmenita Fe II Ti IV O3.
Óxidos de formula ABO3 (A y B con
tamaños similares y carga total +6).
Empaquetamiento hexagonal
compacto de oxígenos con cationes
ocupando 2/3 de los huecos
octaédricos. Fe y Ti ocupan capas
alternadas.
La Ilmenita es muy similar en
estructura a la hematita, pero con
aproximadamente la mitad del
hierro sustituido con titanio.
Estructuras iónicas de formula general MX2
• Estructuras tipo fluorita y antifluorita. La
fluorita, CaF2, es una red cúbica centrada
en las caras de Ca ² +, con iones F- ocupando
todos los huecos tetraédricos. Los Ca ² +
tienen coordinación 8 y los F - tienen
coordinación 4. La estructura tipo
antifluorita resulta del intercambio de
posiciones de los aniones y los cationes.
• Estructuras tipo Cloruro y Ioduro de
Cadmio. El anión adopta una estructura
ABCABC...(Cl-) o ABABAB...(I-) y el catión
ocupa la mitad de los huecos octaédricos.
El anión está tricoordinado y el catión
octaédricamente coordinado. Los huecos
ocupados están todos en una interlámina
de aniones, cada dos.
Estructuras iónicas de formula general MX2
Estructuras iónicas de formula general MX2
• Estructura tipo rutilo, TiO2. La celda unidad es tetragonal, con
coordinación 6:3 para catión y anión, respectivamente
(octaedro y triángulo). Ambos sufren una ligera distorsión.
• Estructura tipo beta-cristobalita, SiO2 Los átomos de silicio
ocupan las posiciones de Zn y S en blenda y cada par de iones
Si tiene un ion óxido intermedio. La coordinación es 4 (Si) y 2
(oxígeno).
18
Otras estructuras
• Corindón, alpha-Al2O3. Hexagonal
compacta de iones óxido con 2/3 de
huecos octaédricos ocupados por
átomos de aluminio. La coordinación es
3 (Al) y 3 (oxígeno)
Representación poliedral
O2-
Al3+
• Trióxido de Renio, ReO3 También se
llama estructura tipo fluoruro de
aluminio. Octaedros [MO 6] unidos a
través de todos los vértices, dando lugar
a una estructura tridimensional.
La estructura tipo es uno de los criterios para la similitud o diferencia de
estructuras cristalinas. Una estructura tipo es usualmente nombrada
después que una sustancia cristaliza con la estructura en cuestión.
Representación polihedral de diversos tipos de estructura: (a) Rutilo,
(b) Brucita, (c) Fluorita, (d) Corundum, (e) Perovskita .
Relación de radios iónicos
Cuando hay combinación de dos especies iónicas,
¿Qué estructura cristalina adoptaran?
Radios iónicos
Relación de radios limitante para los diferentes números de
coordinación.
Numero de
coordinación
Geometría
3
Trigonal
4
Tetraédrica
Relación de
radios
Posible estructura
0.155
0.225
Wurtzita, blenda de zinc
0.414
6
Octaédrica
Sal de roca, rutilo
0.732
8
Cubica
CsCl, fluorita
1.0
19
Radios iónicos
Oxido
Relación de radios
calculada
CO2
0.1
CN = 2
Molecular
CN = 2
SiO2
0.32
CN = 4
Sílica
CN = 4
GeO2
0.43
CN = 4
Sílica
CN = 4
0.54
CN = 6
Rutilo
CN = 6
TiO2
0.59
CN = 6
Rutilo
CN = 6
HfO2
0.68
CN = 6
Fluorita
CN = 8
0.77
CN = 8
0.75
CN = 6
Fluorita
CN = 8
0.88
CN = 8
CeO2
Tipo de estructura
encontrada
La relación de radios depende
mucho de cual tabla de radios
iónicos es consultada y estas
aparecen ser no una clara
ventaja en usar una u otra
mas tradicional
• La relación de radios tiene una cantidad limitada de aciertos
por lo que es mejor considerarla como una guía.
Polimorfismo
Acorde a la definición de McCrone*, “el polimorfismo de cualquier
elemento o compuesto es su capacidad para cristalizar en mas
de una distinta especie cristalina”
En general, se denominan polimorfos a los diferentes arreglos
cristalinos de la misma composición química
Cristalinos
Polimorfos Amorfos
Solvatos e hidratos (efecto del disolvente)
Aprox. 1/3 parte de los compuestos orgánicos y cerca del 80 %
de los fármacos disponibles en el mercado exhiben
polimorfismo bajo condiciones accesibles experimentalmente.
*McCrone, W.C. (1965), Phys. Chem. Org. Solid State, 2, 725-767
 S. Lohani & D. J. W. Grant in “Polymorphism: in the Pharmaceutical Industry”, R.
Hilfiker(editor), Wiley-VCH, 2006
Polimorfismo
Polimorfismo
Aprox. 1/3 parte de los compuestos
orgánicos y cerca del 80 % de los
fármacos disponibles en el mercado
exhiben polimorfismo bajo condiciones
accesibles experimentalmente.*
Se denominan polimorfos a los diferentes arreglos cristalinos de
la misma composición química
Los polimorfos presentan diferencias en:
• Interacciones intra- e intermoleculares (Van der Waals, P.
Hidrogeno, etc.)
• Energías libres (DG y DS)
Diferentes polimorfos presentan diferencias en sus propiedades
físicas como:
✓Solubilidad,
✓Estabilidad química,
✓Punto de fusión,
✓Densidad, etc.
Estructuras cristalinas polimórficas del
fármaco paracetamol: a) monoclínico, b)
ortorrómbico (Wood 1997).
Herná ndez-Abad, V.; Sá nchez G., E.; Yépez M., L.; Jung C., H.; (2007). Rel evancia del polimorfismo en el
á rea fa rmacéutica. Revista Mexicana de Ciencias Farmacéuticas, 38(2) 57
Á. Ma rtín Is l án, E. Mol i na Montes (2006), Ámbi to Fa rmacéutico, 25 (8) 94
Ma rc-Antoi ne Perrin, et al (2009), Chem. Commun., 3181 (forma III)
20
Polimorfismo
Polimorfismo
Los polimorfos de importancia practica son los solvatos, también
llamados pseudo-polimorfos donde las moléculas de solvente
están incorporadas en las red cristalina en forma
estequimétrica o no estequimétrica .
Se denominan mesofases a los sólidos que presentan un
ordenamiento parcial entre lo que es un arreglo cristalino y
un estado amorfo.
Bajo condiciones experimentales bien definidas:
Solo un polimorfo tiene la menor energía libre. Este
polimorfo es termodinámicamente estable.
Todos los demás son denominadas formas metaestables.
Una forma metaestable es termodinámicamente inestable
pero tiene una existencia finita como resultado de su
relativamente baja velocidad de transformación.
Polimorfos;
•Cristalinos: Conteniendo
moléculas no volátiles (cocristales)
•Amorfos
•Solvatos (molec. metaestable a
Temp. y P. amb.) e hidratos (agua)
* Rolf Hilfiker(editor), “Polymorphism: in the Pharmaceutical Industry”, Wiley-VCH, 2006
Polimorfismo
Polimorfismo
La estabilidad relativa de los polimorfos depende de sus energías
libres.
La estabilidad relativa de los polimorfos depende de sus energías
libres.
* S. Lohani & D. J. W. Grant in “Polymorphism: in the Pharmaceutical Industry”, R.
Hilfiker(editor), Wiley-VCH, 2006
* S. Lohani & D. J. W. Grant in “Polymorphism: in the Pharmaceutical Industry”, R.
Hilfiker(editor), Wiley-VCH, 2006
21
Polimorfismo y diagrama de fases P vs T
Polimorfismo
Una fase de un material, es una parte homogénea del
mismo que difiere de las demás en su composición,
estado o estructura. Al conjunto de las representaciones
de los estados posibles en función de variables de
estado se denomina diagramas de fases.
Diagrama de fases del agua
Para una fase que está en equilibrio con otra fase, la ley
de fases de Gibbs se mantiene;
F +P = C + 2
Donde F es el numero de grados de libertad
(variables de estado como P y T)
P es el numero de fases
C es el numero de componentes
Un diagrama de fases P vs T muestra la existencia de intervalos para las diferentes fases
de un sistema comprendiendo solo un componente.
✓Dentro de cada campo marcado solo la correspondiente fase es estable
✓Las diferentes modificaciones son designadas por números romanos.
W. Dobi nski (2006), Earth-Sci. Rev., 79 (3-4),229-240.
M. Cha pl in, Wa ter Structure a nd Behavi or (2006) http://www.Is bu.ac.uk./water/
Polimorfismo
Polimorfismo y diagrama de fases T vs [x]
Estructura cristalina hexagonal del agua congelada (hielo)
Los diagramas de fases para un sistema de dos componentes la representación es de la
composición vs una de las variables de estado. La mas común es [x] vs T (a P normal)
Ih ;
Densidad, 0.917 g/cm³ (a -180 °C es
0.9340 g/cm³).
Calor latente de fusión; 5987 J/mol,
Calor latente de sublimación;
50911 J/mol.
Índice de refracción; 1.31.
M. Chaplin, Water Structure and Behavior (2006) http://www.Isbu.ac.uk./water/
Ley de Raoult;
Ptot = Pi
Pi =   P 0
22
Polimorfismo
Diagrama de fase en
sistema binario
Fe – Fe3C
Polimorfismo y diagrama de fases T vs [x]
Los diagramas de fases para un sistema de dos componentes la representación es de la
composición vs una de las variables de estado. La mas común es [x] vs T (a P normal)
Mezcla eutéctica, es una mezcla de 2 o más sólidos (como una aleación metálica), en la
cual el punto de fusión es menor a la de los componentes puros (punto eutéctico) y todos
sus constituyentes se cristalizan simultáneamente a partir del líquido.
Véa s e; W. D. Ca l l ister, D. G. Rethwisch, Fundamentals of Materials Science and Engineering: An
Integrated Approach, 4th. Edi t, Wi l ey, 2012, Ch. 10, p. 399
Műl l er, U., Inorganic Structural Chemistry (Inorganic chemistry; A textbook s eri es), Wiley, 1993, Ch. 3
Polimorfismo - diagramas de fase
Polimorfismo del carbono
Polimorfismo de los elementos puros es conocido como alotropía.
Un ejemplo de alotropía es como el carbono forma el diamante, el
grafito, los nanotubos, los fulerenos, etc.
La línea horizontal que pasa a través del punto eutéctico se le conoce como línea eutéctica.
Hay curvas que tienen una “torcedura” o deviación de su trayectoria que “cubre” un
máximo esperado, ese punto forma parte de la conocida como línea peritéctica.
Műl l er, U., Inorganic Structural Chemistry (Inorganic chemistry; A textbook s eri es), Wiley, 1993, Ch. 3
23
Polimorfismo (alotropía) en el hierro
Algunos metales presentan diferentes estructuras a diferentes temperaturas y
presiones.
Hierro (Fe) es un metal y a presión atmosférica, un simple cambio en la temperatura
cambiará su estructura:
Por encima de 1809K – Liquido – (No presenta estructura cristalina)
1809K – 1665K – Delta-Fe (ferrita) – bcc
1665K – 1184K – γ-Fe (austerita)– fcc, no magnético
abajo de 1184K – α-Fe – bcc, magnético
Polimorfismo (alotropía) en óxidos binarios
Algunos óxidos metálicos presentan diferentes estructuras a diferentes
temperaturas y presiones.
Meta l oxi des Pha s e
α-pha s e
CrO2
β-pha s e
Cr2O3
Fe 2O3
Bi 2O3
In 2O3
Condi ti ons of P a nd T
Ambi ent conditions
RT a nd 14 GPa
RT a nd 12±3 GPa
Corundum pha se
Ambi ent conditions
Hi gh pressure phase RT a nd 35 GPa
α-pha s e
Ambi ent conditions
β-pha s e
Bel ow 773 K
γ-pha s e
Up to 933 K
ε-pha s e
-α-pha s e
Ambi ent conditions
β-pha s e
603-923 K a nd 1 a tm
γ-pha s e
773-912 K or RT a nd 1 a tm
δ-pha s e
912-1097 K a nd 1 a tm
Bi xbyi te-type phase Ambi ent conditions
Corundum-type
15-25 GPa a t 1273 K
Rh 2O3(II)-type
100 GPa a nd 1000 K
Structure/Spa ce Group
Ruti l e-type Tetragonal (P42/mnm)
Ca Cl 2-type Orthorhombi c
Corundum-type Rhombohedral (R3c)
Rh 2O3-II type,
Corundum-type Rhombohedral (R3c)
Body centered cubic (Ia3)
Cubi c, s pi nel s tructure (Fd3m)
Rhombi c (Pna 21)
Monocl l inic (P21/c)
Tetra gonal
Body centered cubic
FCC (Fm-3m)
Cubi c (Ia 3)
Corundum-type Hexa gonal (R3c)
Orthorhombi c
S. Sood, P. Gouma (2013), "Pol ymorphi sm i n nanocrystalline binary meta l oxides“ i n Na nomaterials
a nd Energy, 2(2), 82-89. E-ISSN 2045-984X
Polimorfismo (alotropía) en óxidos binarios
Meta l oxi des
Al 2O3
SnO2
Ti O2
ZrO2
MoO3
WO3
Pha s e
α-pha s e
γ-pha s e
α-pha s e
Ca Cl 2-type pha se
α-PbO2-type
Ruti l e
Ana ta se
Brooki te
Monocl i nic phase
Tetra gonal phase
Fl uori te-type phase
α-pha s e
β-pha s e
h-pha se
MoO3-II
ε-pha s e
δ-pha s e
γ-pha s e
β-pha s e
α-pha s e
Condi ti ons of P a nd T
Ambi ent conditions
773 K a nd 1 a tm
Ambi ent conditions
15 KBa r a t 1073 K
Above 18 KBa r
Ambi ent conditions
Above 1073 K
Hi gh pressure phase
Ambi ent conditions
Above 1443 K
Above 2643 K
553-673 K & 1 a tm
553-673 K & 1 a tm
Hi gh pressure a nd high
tempera ture phase
60 kba r a nd 973 K
Up to 220 K
220-300 K
300-623 K
623-900 K
Above 900 K
Structure/Spa ce Group
Corundum-type Tri gonal, (R3c)
Cubi c (Fd-3m)
Ruti l e-type Tetragonal (P42/mnm)
Orthorhombi c, Ca Cl 2-type (Pnnm)
α-PbO2-type (Pbcn)
Ruti l e-type Tetragonal
Tetra gonal (I41/amd)
Orthorhombi c (Pca b)
Monocl i nic (P21/c)
Tetra gonal (P42/nmc)
Fl uori te-type (Fm3m) cubi c structure
Orthorhombi c (Pbnm)
Monocl i nic
Hexa gonal (P6a /m or P6a )
Monocl i nic
Monocl i nic (Pc)
Tri cl i nic (P1)
Monocl i nic (P21/n)
Orthorhombi c (Pnma )
Tetra gonal (P4/ncc)
24