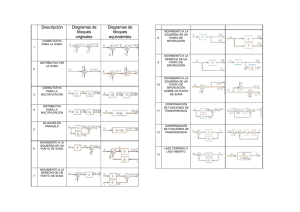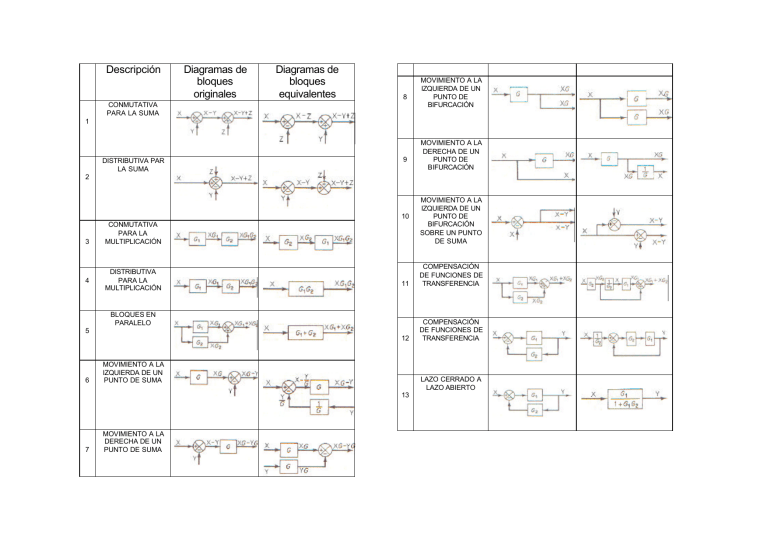
Descripción Diagramas de bloques originales Diagramas de bloques equivalentes 8 CONMUTATIVA PARA LA SUMA MOVIMIENTO A LA IZQUIERDA DE UN PUNTO DE BIFURCACIÓN 1 DISTRIBUTIVA PAR LA SUMA 9 MOVIMIENTO A LA DERECHA DE UN PUNTO DE BIFURCACIÓN 2 10 3 4 CONMUTATIVA PARA LA MULTIPLICACIÓN DISTRIBUTIVA PARA LA MULTIPLICACIÓN 11 COMPENSACIÓN DE FUNCIONES DE TRANSFERENCIA 12 COMPENSACIÓN DE FUNCIONES DE TRANSFERENCIA BLOQUES EN PARALELO 5 6 MOVIMIENTO A LA IZQUIERDA DE UN PUNTO DE SUMA LAZO CERRADO A LAZO ABIERTO 13 7 MOVIMIENTO A LA DERECHA DE UN PUNTO DE SUMA MOVIMIENTO A LA IZQUIERDA DE UN PUNTO DE BIFURCACIÓN SOBRE UN PUNTO DE SUMA Procedimiento para trazar diagrama de bloques. 5. Regresar al paso 4 hasta que la entrada sea considerada y todas las variables del sistema sean consideradas. Un diagrama a bloques es una representación matemática gráfica del modelo matemático de un sistema. En muchos casos, estos diagramas nos permiten entender el comportamiento y conexión del sistema y a su vez, esta descripción puede ser programada en simuladores que tienen un ambiente gráfico como lo es el simulink de Matlab. 6. Después de obtener las ecuaciones se generan los diagramas a bloques de cada una. Debido al procedimiento utilizado los bloques quedan prácticamente para ser conectados a partir del bloque de salida. Con el objeto de trazar un diagrama de bloques de un sistema se sugiere seguir los siguientes pasos: Teniendo el diagrama a bloques en algunos casos es necesario simplificarlo hasta una sola función de transferencia. Para esto existen varios procedimientos, uno de ellos es utilizando las propiedades del álgebra de bloques y otro, utilizando gráficos de flujo de señal que se verá mas adelante. 1. Es necesario conocer las ecuaciones diferenciales que describen el comportamiento dinámico del sistema a analizar y la salida y entrada consideradas. 2. Se obtiene la transformada de Laplace de estas ecuaciones, en este caso como el diagrama a bloques son representaciones de funciones de transferencia, las condiciones iniciales se consideran cero. 3. De las ecuaciones transformadas se despeja aquella donde esté involucrada la salida del sistema. 4. De la ecuación obtenida se ubican las variables que están como entrada y que deben de ser salidas de otros bloques. Se despejan esas variables de otras ecuaciones. Recuerda nunca utilizar una ecuación que ya se utilizó previamente. Simplificación de un diagrama a Bloques Una regla general para simplificar un diagrama de bloques consiste en mover los puntos de bifurcación y los puntos suma, intercambiar los puntos suma y después reducir las mallas internas de realimentación. Es importante que no se altere las señales involucradas en el movimiento compensando con las funciones necesarias. Ejemplo: Para el siguiente sistema hidráulico obtenga la función de transferencia utilizando diagrama a bloques (considere qin entrada y q 3 salida). Suponga que: C1 , C2 , C3 , R1 , R2 , R3 =2 Ecuación Para el tanque 1. dh C1 1 = qin − q1 dt Para el tanque 2. dh C 2 2 = q1 − q2 dt Para el tanque 3. dh C3 3 = q2 − q3 dt h1 − h2 q1 ; R1 = ; h − h3 R2 = 2 q2 ; R3 = Transformando para 1. 1 H 1 ( s) = (Qin ( s) − Q1 (s) ) C1 (s) Transformando para 2. 1 H 2 ( s) = (Q1 (s ) − Q2 (s) ) C 2 (s ) Transformando para 3. 1 H 3 ( s) = (Q2 (s ) − Q3 (s )) C 3 ( s) h3 q3 ; q1 = ⇒ h − h3 q2 = 2 R2 Q1 (s) = 1 H 1 ( s) = (Qin ( s) − Q1 ( s)) C1 (s ) 1 Q1 (s) = 1 ( H 1 ( s) − H 2 ( s) ) R1 2 H 2 ( s) = 1 (Q1 (s ) − Q2 (s) ) C 2 ( s) 2 Q2 (s) = 1 ( H 2 (s ) − H 3 ( s)) R2 3 H 3 (s) = 1 (Q2 (s) − Q3 (s) ) C3 ( s ) h1 − h2 R1 ⇒ ⇒ q3 = Diagrama de bloques. 1 h3 R3 1 ( H 1 ( s) − H 2 ( s) ) R1 ; 1 Q2 (s) = ( H 2 ( s) − H 3 ( s) ) R2 ; Q3 ( s) = 1 ( H 3 ( s) ) R3 3 Q3 (s) = 1 (H 3 (s)) R3 Arreglo Arreglo Por lo tanto la función de transferencia es: 1 2 2 16 s + 8 s + 1 + 8s 2 + 4 s [8s + 4] [ ] [ ] GRAFICOS DE FLUJO DE SEÑAL. S.J. MASON. Es un diagrama que representa un conjunto de ecuaciones algebraicas lineales simultaneas, donde cada: • • • Nodo ; Variables del sistema. Rama ; multiplicador ecuación transformada y transmitancia. Dirección ; Sentido del flujo. de donde: PK : ganancia o transmitancia de trayectoria de la k-ésima trayectoria directa. ∆ : determinante del grafico: 1 − ∑ La + ∑ LbLc − ∑ LdLeLf + ..... a b, c Ejemplo1. Solución : Gráfico de flujo de señal: Fórmula de ganancia de Mason: 1 P = ∑ PK ∆ K ∆ K d ,e , f , ∆ K : Cofactor del determinante de la k-ésima trayectoria directa del grafico, con los lazos que tocan la trayectoria directa k-ésima eliminados. Ejemplo Hidráulico. Entrada: q in Salida: q 2 Grafico de Señal: Trayectorias directas: P1 = G1G 2G3 L1 = G1G 2 H 1 Lazos: L2 = −G 2 G3 H 2 L = −G G G 3 1 2 3 ∆ = 1 − ( L1 +L2 + L3 ) ∆1 = 1 Solución: P∆ P= 1 ∆ G1G 2G 3 P= 1 − G1G 2 H 1 + G 2 G3 H 2 + G1G 2 G3 P1 = Lazos : L1 = 1 C1 (s) R1C 2 (s) R2 Trayectori a Directa . −1 −1 −1 ; L2 = ; L3 = . R1C1 (s) R1C 2 (s ) R2 C 2 (s) L1 y L3 Adjuntos. ∆1 = 1 ; ∆ = 1 − (L1 + L2 + L3 ) + L1 L3 1 P∆ R1 R2 C1C 2 (s 2 ) P= 1 1 = 1 1 1 1 ∆ 1+ + + + R1C1 ( s) R1C 2 ( s) R2 C 2 ( s) R1 R2 C1C 2 (s 2 ) P= 1 R1 R2 C1C 2 ( s ) + (R 2C 2 + R2 C1 + R1C1 )(s) + 1 2 Ejemplo 3. P1 = G1G 2G3 G4 G5 P2 = G1G6 G4 G5 P3 = G1G2 G7 L1 = −G 4 H 1 L2 = G 2 G 7 H 2 L3 = −G6 G 4G5 H 2 . ∆ = 1 − ( L1 + L2 + L3 ) + L1 L2 ∆ 1 = 1; ∆ 2 = 1; ∆ 3 = 1 − L1 Grafico de flujo de señal. P= G1G 2G 3G4 G5 + G1G6 G4 G5 + G1G 2 G7 (1 + G4 H 1 ) . 1 + G 4 H 1 + G 2 G7 H 2 + G6 G 4G5 H 2 + G2 G 4G 7 H 1 H 2 ;