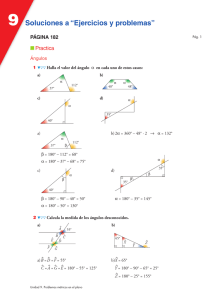
A. Verdadero. Ya que los rectángulos tienen sus ángulos iguales a 90 grados. B. Verdadero. Los ángulos de todos los triángulos equiláteros miden 60 grados. C. Verdadero. Si son semejantes ya que, si dos polígonos son congruentes, entonces sus longitudes y las medidas de los ángulos también son congruentes. D. Falso. Para que dos triángulos sean semejantes los tres ángulos deben ser iguales. EJEMPLO: Si al tener un triángulo rectángulo con ángulos 100,45,35 y otro con ángulos 60,60,60. E. Falso. Porque solo son semejantes los que tienen la misma cantidad de lados. EJEMPLO: Los ángulos de un polígono regular de 4 lados miden 90. mientras que los de un polígono regular de 3 lados miden 60, por tanto, no son semejantes. A. 4 5 12 ∗ 5 60 = = = = 15 12 𝑥 4 4 𝑥 = 15 𝑥) = Y) 37º, ya que los ángulos son los mismos Z) 90º + 37º − 180º = 53º 𝑍 = 53° B. 2 0,8 4 ∗ 0,8 3,2 = = = = 1,6 4 𝑥 2 2 𝑥 = 1,6 𝑋= Y) 70° 2 3 4 ∗ 3 12 𝑍) = = = =6 4 𝑧 2 2 𝑧=6 1 25 430 ∗ 1 430 = = = = 17.2 𝑥 430 25 25 𝑥 = 17,2 de ancho 1 25 680 ∗ 1 680 = = = = 27.2 𝑥 680 25 25 𝑥 = 27,2 𝑑𝑒 𝑙𝑎𝑟𝑔𝑜 A) 9 1 9 = = 9 20 180 13 1 9 = = 9 20 260 B) 9 1 9 = = 9 9 81 13 1 9 = = 9 9 117 PRIMERA POSIBLE MEDIDA y=15 x=12 5 15 4 = 12 Es semejante Segunda posible medida X= 25 y=20 5 25 4 = 20 Es semejante SI son semejantes 4 𝑥 4 ∗ 5 20 = = = = 2.5 8 5 8 8 𝑥 = 2.5 A. 𝑟2 = 𝑠2 + 𝑟2 = 𝑟2 = 𝑠2 + 𝑟2 Verdadero cumple con el teorema B 𝑓 2 = √𝑑2 − 𝑒 2 = 𝑓 = √𝑒 2 + 𝑑2 Es falsa, no cumple con el teorema C 𝑐 = √𝑎2 − 𝑏 2 = 𝑐 = √𝑎2 − 𝑏 2 Verdadero cumple con el teorema D 𝑥2 + 𝑦2 = 𝑧2 = 𝑥2 + 𝑦2 = 𝑧2 Verdadero cumple con el teorema 𝑐 2 = 102 − 82 𝑐 2 = 100 − 64 𝑐 2 = 36 𝑐 = √36 𝑐=6 Un chico esta esta de bajo de la sombra del primer arbol y y ve que hay un globo diagonalmente a 80 m de distancia, a ese globlo se le cae algo a 30 metros donde esta el, el quiere saber cuantos metros decendio hasta caer 𝑐 2 = 802 − 30 𝑐 2 = 6400 − 900 𝑐 2 = 5500 𝑐 = √5500 𝑐 = 74.16 decendio 74.16 m