EJEMPLOS DE PROBLEMAS RESUELTOS CIRCUITOS RLC

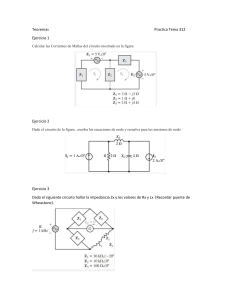
Ing. José Antonio Martínez Hernández
Academia de Electrotecnia, IE, ESIME Zacatenco, IPN
EJEMPLOS DE PROBLEMAS RESUELTOS CIRCUITOS RL, RC Y RLC SERIE
Ejemplo número 2.1
Un inductor de 350Ω de reactancia se conecta en serie con una resistencia de 470Ω. ¿Cuál
es la magnitud de la impedancia de la combinación?
XL= 350Ω
R= 470Ω
Ejemplo número 2.1
Solución:
Z  R2  X L 
Z  586, 00 
2
4702  3502
Ejemplo número 2.2
Un inductor de 0,2H se conecta en serie con una resistencia de 150Ω. ¿Cuál es la magnitud
de la impedancia de la combinación?, si f=60Hz.
L= 0,2H
R= 150Ω
Solución:
X L  wL  2 fL  (2 )(60)(0, 2) 
Ejemplo número 2.2
X L  75,39 
Z  R2  X L2 
Z  167,88 
150    75,39 
2
2

Ejemplo número 2.3
En la carga de un circuito se toman las siguientes lecturas: tensión 350V de C.A, corriente
0,9 A, potencia activa 250W. ¿Cuál es el factor de potencia (F.P)?
S=
5
31
VA
Triángulo de potencia,
Q
ejemplo número 2.4
θ
P= 250W
En un circuito eléctrico se presentan tres tipos de potencia la consumida P, la entregada por
la compañía suministradora denominada potencia aparente S y la producida por el efecto
reactivo de las cargas Q. La potencia aparente (S): es el producto de tensión eficaz por la
corriente eficaz entregada en un circuito de CA.
Solución:
S  VI   350V  0,9A   315VA
F .P.  cos 
cateto adyacente 250W

 0, 79
hipotenusa
315VA
Ejemplo número 2.4
Un inductor tiene una inductancia de 0,1mH, se conecta en serie con una resistencia de 1kΩ
y se energiza con una fuente que tiene una frecuencia de 1,59kHz. ¿Cuál es la magnitud de
la impedancia de la combinación serie?
L= 0,1H
|Z
|
XL
θ
R= 1kΩ
R
Circuito y triángulo de impedancias, ejemplo número 2.4
Solución:
X L   L  2 fL  (2 )(1,59kHz)  0,1mH 
X L  1
Z  R2  X L2 
1k   1 
2
2
Z 1k 
Para fines prácticos, cuando uno de los valores de los términos al cuadrado de una impedancia
R y X es 20 veces o más grande que el otro, se considera Z ≈ al más grande.
Ejemplo número 2.5
Del ejemplo 2.4 determine: a) el desfasamiento entre la tensión y la corriente (θ); b) el factor
de potencia, c) diga si el FP está en adelanto o retraso y por qué.
Solución:
XL
1

 0º
R 1000
b) FP  cos  Cos  0,05 1
a)   tan 1
c) Se encuentra ligeramente adelantada la tensión con respecto a la corriente, ya que hay un
pequeño predominio del efecto inductivo; sin embargo, prácticamente están en fase.
Ejemplo número 2.6
Un circuito RL serie tiene una reactancia inductiva de 370Ω, si la impedancia total es de
740Ω, encontrar: a) el valor de R, b) la I total si se le aplica una tensión de 120V, c) la tensión
en cada elemento, d) la impedancia por el método de volt-ampere, e) la potencia aparente, f)
la potencia reactiva, g) la potencia activa, h) el desfasamiento, i) el factor de potencia, j)
construir el triángulo de tensiones, k) construir el triángulo de impedancias, l) construir el
triángulo de potencias, m) exprese su punto de vista para corregir el factor de potencia.
Solución:
a) Z 2  R2  X L 2 ; de donde: R  Z 2  X L 2 
V 120V

 0,16 A
Z 740
c) VR  RI   640,86  0,16A   103,92 V
b) I t 
VL  X L I   370  0,16A   60V
 740    370 
2
2
 640,85 
VR 2  VXL 2
V

d) Z  
I
I
103,92V    60V 
2
0,16A
2
 740 
e) S  VI  120V  0,16A   19, 46 VA
f) Q  I 2 X L   0,16A  370   9,73 VAR
2
g) P  I 2 R   0,16A   640,86   16,85 W
2
catetoopuesto
9, 73VAR
 tan 1
 30º
catetoadyacente
16,85W
i) F .P.  cos  cos  30   0,86
j).-Triángulo de tensiones
h)   tan 1
VT
VL
θ
VR
k).-Triángulo de impedancias
|Z
|
XL
θ
R
l).- Triángulo de potencias
S
Q
θ
P
m) Dado que la reactancia inductiva es mayor que el valor de la resistencia R y que esta
diferencia hace que el ángulo sea igual a 30°, dando un FP de 0,86, se requiere disminuir la
carga inductiva para incrementar el FP hasta los límites establecidos por norma.
Ejemplo número 2.7
Un inductor se conecta en serie con un resistor de 680Ω, si la tensión en el inductor es de
75V y a través del circuito fluye una corriente de 0.15A. ¿Cuál es el valor de la tensión
aplicada?
I=0,15A
RL
L
680
+ 75V -
VT
Solución:
Circuito, ejemplo número 2.7
VR  RI  6800.15A  102V
102V 2  752
VT  VR  VXL 
2
2
 126.6056871V
Ejemplo número 2.8
De manera literal y considerando valores eficaces diga que expresión utilizaría para evaluar
los siguientes parámetros de un circuito serie RL.
a)
b)
c)
d)
e)
f)
g)
Impedancia por el método de volt-ampere.
Impedancia si se conoce R y XL.
Impedancia si se conoce R, f y L.
Tensión en R, VR.
Tensión en L, VL.
Tensión aplicada si se conoce VR y VL.
Si se conoce R y Z como encontrar el F.P.
Solución:
VR  VXL
V

a) Z 
IT
IT
2
b) Z  R 2  X L
2
c) Z  R 2  2fL
2
d) VR  RI
e) VL  X L I
f) VT  VR  VL
R
g) FP 
Z
2
2
2
Ejemplo número 2.9
Determinar Zx en el circuito de la figura.
6,5  20 A
10
j 6
17445V
ZX
Solución:
Circuito, ejemplo número 2.9
Encontrando Z
V
17945
Z 
 27,5465
I 6,5  20
Entonces, como las impedancias están en serie se suman
Z  10  j 6  Z X  27,5465
Z X  27,5465  (10  j 6)  19, 0385, 06
Ejemplo número 2.10
Determinar Z eq e I del circuito de la figura y compruebe la LKV.
I
12018Vrms
V1
Z1  2020
V2
Z 2  830
V3
Z3  2010
Circuito, ejemplo número 2.10
Solución:
Como el circuito está en serie
Z eq  Z1  Z 2  Z 3  2020  830  2010
Z eq  47, 6217, 49
I
VT
12018
 2,520,51 A
Z eq 47, 6217, 49
V1  IZ1  (2,520,51)(2020)  50, 4020,51V
V2  IZ 2  (2,520,51)(830)  20,1630,51V
V3  IZ 3  (2,520,51)(2010)  50, 4010,51V
De acuerdo a la LKV:
VT  V1  V2  V3
VT  12018V
Ejemplo número 2.11
Determinar R1, X y Z del circuito de la figura y diga que efecto predomina.
1010 A
12030V
Z
Circuito, ejemplo 2.11
Solución:
Por ley de Ohm Z 
V 12030

 1220
1010
I
Por lo tanto:
Z  12(cos 20  jsen 20)  11, 28  j 4,10
La parte real de Z corresponde a R y la parte imaginaria a X, por lo tanto:
R  11, 28
y
X  4,10
Dado que la parte imaginaria es positiva, predomina el efecto inductivo.
Ejemplo número 2.12
Un circuito serie tiene una tensión v=180sen(376,8t +30°) y una corriente i=18,3sen(376,8t
-8°), ¿cuántos elementos tiene y cuáles son sus valores?
Solución:
En forma fasorial
V  18030V
I  18,3  8 A
Por ley de Ohm:
Z
V 18030

 9,8438
I 18,3  8
De la misma manera que en el problema 2.12
Z  9,8438  7, 75  j 6, 06
Por lo tanto el circuito tiene dos elementos y sus valores son:
R  7, 75;
X L  L L 
XL


6, 06
 20 mH
376,8
Ejemplo número 2.13
A un circuito serie RLC, con R=220Ω, L=1,2H, y C=10μF se le aplica una tensión senoidal
v que tiene una frecuencia angular de 376,8 rad/s, determinar el ángulo de fase y diga si la
corriente está adelantada o retrasada.
Solución:
Las reactancias son:
X L   L  (376,8)(1, 2)  452,16
1
106

 256,39
C (376,8)(10)
La impedancia compleja es
XC 
Z  R  j( X L  X C )
Z  220  j (452,16  265,39)
Z  220  j186, 77
El triángulo de impedancias es:
X L  186, 77
θ
R  220
Por lo tanto;   tan 1
186, 77
 40,33 y como predomina el efecto inductivo, la corriente
220
está retrasada.
Ejemplo número 2.14
Del circuito, usando la Regla del Divisor de Tensión encuentre VR , VL y VC
VR
VL
VC
220
1, 2H
10 F
18010V
Solución:
Z R  2200
Z X L  452,1690
Z X C  265,39  90
ZT  220  j186, 77  288,5940,33
Aplicando la RDV para cada elemento pasivo se tiene:
Circuito, ejemplo número 2.14
VX 
ZX
Z
2200
VT VR  R VT 
(18018)V  137, 22  22,33V
ZT
ZT
288,5940,33
VX L 
Z XL
VX C 
Z XC
ZT
ZT
VT 
456, 2290
(18018)V  282, 0267, 67V
288,5940,33
VT 
265,39  90
(18018)V  165,53  112,33V
288,5940,33