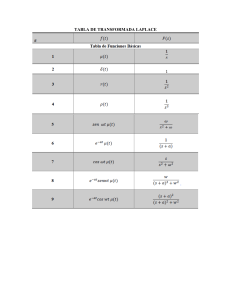
Guı́a 1: Ejercicios sobre transformada z
Alumno: Guillermo M. Tabeni Couvert
Profesor: Ing. Carlos A. Espinoza
J.T.P.: Ing. Daniel R. Graff
Cátedra de Ingenierı́a Industrial
Universidad Tecnológica Nacional, F.R.A.
2 de julio de 2007
Objetivo: Realizar distintos ejercicios numéricos de mano y con el uso de Matlab.
Ejercicio 1
Para la función Y (z), determinar los polos y ceros y ubicarlos dentro del plano z. Los teoremas del valor
inicial y final son aplicables en dicha función. ¿Por qué? Hallar sus valores.
Y (z) =
0, 792z 2
(z − 1)(z 2 − 0, 416z + 0, 208)
Para hallar los polos y ceros de Y (z), introducimos los comandos:
z=tf(’z’);
Yz=.792*z^2/((z-1)*(z^2-0.416*z+.208))
[ceros,polos,K]=zpkdata(Yz,’v’)
Vemos que hay un cero doble en el origen, un polo real en 1 y un par de polos complejos conjugados:
ceros =
0
0
polos =
1.0000
0.2080 + 0.4059i
0.2080 - 0.4059i
K =
0.7920
Ahora, graficamos el plano z con los ceros y polos obtenidos:
[num,den]=tfdata(Yz,’v’);
zplane(num,den)
zgrid
Por el teorema del valor inicial:
0, 792z 2
z→∞ z 3 − 1, 416z 2 + 0, 624z − 0, 208
0, 792/z
= lı́m
=0
z→∞ 1 − 1, 416/z + 0, 624/z 2 − 0, 208/z 3
y(t = 0) = lı́m Y (z) = lı́m
z→∞
Por el teorema del valor final:
z−1
0, 792z 2
2
z→1
z (z − 1)(z − 0, 416z + 0, 208)
0, 792z
= lı́m 2
=1
z→1 z − 0, 416z + 0, 208
y(t → ∞) = lı́m [1 − z −1 Y (z)] = lı́m
z→1
Estos teoremas son aplicables porque, por definición, existen los lı́mites calculados.
Alumno: Guillermo Tabeni, UTN, FRA, 2007
1/11
Ejercicio 2
Obtenga la transformada z de la siguiente función donde a es una constante. Grafique y compare en
Matlab la función en tiempo continuo y la función en tiempo discreto.
x(t) =
1
(1 − e−at )
a
Distribuyendo, tenemos
1 e−at
−
a
a
Luego, por la transformada del escalón y la propiedad lineal de la transformada z,
x(t) =
1
1
−
−1
a(1 − z ) a(1 − e−ak z −1 )
1 − e−ak z −1 − 1 + z −1
=
a(1 − z −1 )(1 − e−ak z −1 )
1
z −1 (1 − e−ak )
=
a 1 − z −1 (1 + e−ak ) + z −2 e−ak
X(z) =
(1)
En el Matlab comparamos la respuesta del sistema continuo (en rojo) con la del sistema discreto (azul):
num=[0 1-exp(-1) 0];
den=[1 -1-exp(-1) exp(-1)];
t=0:0.2:10;
xt=(1-exp(-t));
plot(t,xt,’r’)
hold;
impz(num,den)
Alumno: Guillermo Tabeni, UTN, FRA, 2007
2/11
Ejercicio 3
Para la función G(z) = Y (z)/X(z), hallar la transformada inversa z mediante el método Matlab (comando
filter) hasta k = 10. Graficar la secuencia (comando stem).
Y (z) = 0, 01409z 3 + 0, 028z 2 + 0, 01409z
X(z) = z 3 − 2, 7624z 2 + 2, 5811z − 0, 8187
Con el siguiente programa graficamos los 10 primeros elementos de la secuencia de Y (z)/X(z).
num=[0.01409 0.028 0.01409 0];
den=[1 -2.7624 2.5811 -0.8187];
Xz=[1 zeros(1,10)];
Yz=filter(num,den,Xz);
n=0:1:10;
stem(n,Yz);
xlabel(’k’);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
3/11
Ejercicio 4
Para la ecuación en diferencias encontrar la serie en forma recursiva realizando un programa en Matlab.
Luego, hallar la transformada Z mediante cálculo de mano y luego, mediante el método de Matlab (comando
filter), encontrar la transformada inversa Z hasta k = 30. Verificar ambos gráficos y hallar conclusiones.
x(k + 2) = x(k + 1) + x(k),
donde x(0) = 0 y x(1) = 1
Las transformadas z de x(k + 2), x(k + 1) y x(k) están dadas, respectivamente, por
Z[x(k + 2)] = z 2 X(z) − z 2 x(0) − zx(1)
Z[x(k + 1)] = zX(z) − zx(0)
Z[x(k)] = X(z)
Al tomar las transformadas z de ambos miembros de la ecuación en diferencias dada, se obtiene
z 2 X(z) − z = zX(z) + X(z)
donde se han reemplazado las condiciones iniciales dadas.
Finalmente, despejando y simplificando,
X(z) =
z
z2 − z − 1
(2)
que es la transformada z buscada.
Ahora utilizo el siguiente programa para comparar el método manual con el método de Matlab.
%Metodo manual
x(1)=0;
x(2)=1;
N=30;
for k=1:N-1
x(k+2)=x(k+1)+x(k)
end
n=0:N;
subplot(2,1,2);
stem(n,x,’r’);
title(’Metodo manual’);
%Metodo Matlab
num=[0 1 0];
den=[1 -1 -1];
n=0:1:N;
x=[1 zeros(1,N)];
y=filter(num,den,x);
subplot(2,1,1);
stem(n,y,’b’);
title(’Metodo Matlab’);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
4/11
Ejercicio 5
Encontrar la expresión en forma cerrada de y[n] usando el método de la transformada Z. Donde u[n]
representa la función escalón.
y[n] − (5/6)y[n − 1] + (1/6)y[n − 2] = (1/5)n u[n],
donde y[−1] = 6 e y[−2] = 25
Las transformadas z de secuencias desplazadas son:
Z[y(n − 1)] = Y (z)z −1 + y(−1)
Z[y(n − 2)] = Y (z)z −2 + y(−1)z −1 + y(−2)
Además, la transformada z de an u[n] es,
Z[an u(n)] =
1
1 − (z/a)−1
Al tomar las transformadas z de ambos miembros de la ecuación en diferencias dada, se obtiene
Y (z) −
1
5
Y (z)z −1 + 6 +
Y (z)z −2 + 6z −1 + 25 =
6
6
1
z −1
1−
5
3
5
1
25
z
Y (z) z 2 − z +
− 5z 2 + z + z 2 =
6
6
6
1
z−
5
31
1
1
11
7
1
Y (z) z 3 − z 2 + z −
=
z3 − z2 + z
30
3
30
6
6
5
Despejando Y (z)/z, para luego aplicar el método de inversión por fracciones parciales:
Y (z)
=
z
1
11 2 7
z − z+
6
6
5
1
1
31
z3 − z2 + z −
30
3
30
Factorizando el denominador, la función expandida tendrá la forma:
Y (z)
=
z
Alumno: Guillermo Tabeni, UTN, FRA, 2007
a1
1
z−
2
+
a2
1
z−
3
+
a3
z−
1
5
5/11
donde los coeficientes son:
1 Y (z)
3
a1 = (z − ) ·
=
2
z z= 1
2
2
1 Y (z)
2
a2 = (z − ) ·
=−
3
z z= 1
3
3
1 Y (z)
a3 = (z − ) ·
=1
5
z z= 1
5
La descomposición en fracciones parciales podrı́a haberse realizado con Matlab, de la siguiente manera:
num=[0 11/6 -7/6 1/5];
den=[1 -31/30 1/3 -1/30];
[R,P,K]=residue(num,den)
R =
1.5000
-0.6667
1.0000
P =
0.5000
0.3333
0.2000
K =
[]
Reemplazando y multiplicando ambos miembros por z:
Y (z) =
3/2
2/3
1
−
+
1 − 12 z −1
1 − 13 z −1
1 − 15 z −1
La transformada inversa, resulta:
y(n) =
3
2n+1
−
2
3n+1
+
1
5n
(3)
que es la forma cerrada pedida.
Con el siguiente programa podemos comparar las secuencias obtenidas con la ecuación de diferencias
dada al comienzo del problema y la forma cerrada obtenida:
%Metodo itarativo - Ecuacion de diferencias
y(1)=25;
y(2)=6;
N=30;
u=[0 0 ones(1,N+1)];
for n=1:N+1
y(n+2)=(1/5)^(n-1)*u(n+2)+(5/6)*y(n+1)-(1/6)*y(n)
end
n=-2:N;
subplot(2,1,1);
stem(n,y);
title(’Metodo itarativo - Ecuacion de diferencias’);
%Metodo iterativo - Expresion en forma cerrada
for n=1:N+1
y(n)=3/(2^(n-2))-2/(3^(n-2))+1/(5^(n-3))
end
n=-2:N;
subplot(2,1,2);
stem(n,y,’r’);
title(’Metodo iterativo - Expresion en forma cerrada’);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
6/11
Ejercicio 6
Resuelva la siguiente ecuación en diferencias tanto de manera analı́tica como por computadora con
Matlab. La función de entrada u[k] = 1 para k = 0, 1, 2, . . ..
x(k + 2) − x(k + 1) + 0, 25x(k) = u(k + 2),
donde x(0) = 1 y x(1) = 2
Las transformadas z de x(k), x(k + 1) y x(k + 2) están dadas, respectivamente, por
Z[x(k)] = X(z)
Z[x(k + 1)] = zX(z) − zx(0)
Z[x(k + 2)] = z 2 X(z) − z 2 x(0) − zx(1)
Además, la transformada z de u[k + 2] es
Z[u(k + 2)] = z 2 U (z) − z 2 u(0) − zu(1) =
z2
− z2 − z
1 − z −1
ya que u(0) = u(1) = 1.
Al tomar las transformadas z de ambos miembros de la ecuación en diferencias dada, se obtiene
z 2 X(z) − z 2 − 2z − zX(z) + z + 0, 25X(z) =
z2
− z2 − z
1 − z −1
Despejando X(z)/z, para luego aplicar el método de inversión por fracciones parciales:
X(z)
z2
z2
= 3
=
2
z
z − 2z + 1, 25z − 0, 25
(z − 1)(z − 12 )2
La función expandida tendrá la forma:
a3
X(z)
a2
a1
+
+
=
z−1
z
z − 12
(z − 12 )2
donde los coeficientes son:
1
1 2 X(z)
=−
a1 = (z − 2 ) ·
z
2
z= 12
d
X(z)
= −3
a2 =
(z − 12 )2 ·
dz
z
z= 12
X(z)
a3 = (z − 1) ·
=4
z
z=1
Alumno: Guillermo Tabeni, UTN, FRA, 2007
7/11
Reemplazando y multiplicando ambos miembros por z:
X(z) = −
(1
1 −1
2z
− 12 z −1 )2
−
3
4
+
1 − z −1
1 − 12 z −1
La transformada inversa, resulta:
k
3
− k +4
(4)
2k
2
Con el siguiente programa podemos comparar las secuencias obtenidas con la ecuación de diferencias
dada al comienzo del problema y la forma cerrada obtenida:
x(k) = −
%Metodo itarativo - Ecuacion de diferencias
x(1)=1;
x(2)=2;
N=30;
u=[ones(1,N+3)];
for k=1:N-1
x(k+2)=u(k+2)+x(k+1)-0.25*x(k);
end
k=0:N;
subplot(2,1,1);
stem(k,x);
title(’Metodo itarativo - Ecuacion de diferencias’);
%Metodo iterativo - Expresion en forma cerrada
for k=1:N+1
x(k)=-(k-1)/(2^(k-1))-3/(2^(k-1))+4
end k=0:N;
subplot(2,1,2);
stem(k,x,’r’);
title(’Metodo iterativo - Expresion en forma cerrada’);
Ejercicio 7
Usar el método de la división directa para obtener la transformada z inversa. Decidir si el sistema es
estable o no. ¿Por qué? Mostrar el diagrama de polos y ceros en el plano z. Si el sistema es inestable,
implementar la modificación necesaria para que deje de serlo.
Alumno: Guillermo Tabeni, UTN, FRA, 2007
8/11
X(z) =
z −1 (1 − z −2 )
(1 + z −2 )2
Primero, expreso X(z) en polinomios de z −1 :
X(z) =
z −1 − z −3
1 + 2x−2 + z −4
Luego, efectuando la división:
+z −1
−z −1
−z −3
−2z −3
−3z −3
+3z −3
−z −5
−z −5
+6z −5
+5z −5
−5z −5
/1 + 2z −2 + z −4
z −1 − 3z −3 + 5z −5 − 7z −7 + 9z −9 − · · ·
+3z −7
+3z −7
−10z −7 −5z −9
−7z −7
−5z −9
...
...
P∞
Comparando directamente X(z) = 0 x(k)z −k , tenemos
x(0) = 0
x(1) = 1
x(2) = 0
x(3) = −3
x(4) = 0
x(5) = 5
x(6) = 0
x(7) = −7
x(8) = 0
x(9) = 9
..
.
Como vemos, la secuencia x(n) es alternadamente creciente; por lo tanto, el sistema es inestable.
Graficamos los polos y ceros de X(z) mediante la siguiente secuencia de comandos:
num=[0 1 0 -1 0];
den=[1 0 2 0 1];
zplane(num,den);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
9/11
Confirmamos con el diagrama de polos y ceros que el sistema es inestable, ya que posee polos múltiples
sobre el cı́rculo unitario (es condición suficiente, pág. 183 del libro de Ogata).
Ejercicio 8
Encuentre la transformada inversa Z utilizando el método de expansión en fracciones parciales y con el
Matlab (comando residuez).
X(z) =
z −1 (0, 5 − z −1 )
(1 − 0, 5z −1 )(1 − 0, 8z −1 )
Multiplicamos numerador y denominador por z 2 y luego, divido ambos miembros por z para expresar
X(z)/z en potencias de z:
0, 5(z − 2)
X(z)
=
z
z(z − 0, 5)(z − 0, 8)
La función expandida tendrá la forma:
X(z) =
a1
a2
a3
+
+
z − 0, 5 z − 0, 8
z
donde los coeficientes son:
Y (z)
a1 = (z − 0, 5) ·
=5
z z=0,5
Y (z)
a2 = (z − 0, 8) ·
= −2, 5
z z=0,8
Y (z)
a3 = (z) ·
= −2, 5
z z=0
Reemplazando y multiplicando ambos miembros por z:
X(z) =
2, 5
5
−
− 2, 5
1 − 0, 5z −1
1 − 0, 8z −1
La descomposición en fracciones parciales podrı́a haberse realizado con Matlab, de la siguiente manera:
num=[0 .5 -1];
% En potencias asc. de z^{-1} o desc de z
den=[1 -1.3 .4];
[R,P,K]=residuez(num,den)
R =
-2.5000
5.000
P =
0.8000
0.5000
K =
-2.5
Por simple inspección de la tabla, la transformada inversa resulta:
x(k) = 5 · (0, 5)k − 2,5 · (0, 8)k − 2, 5 · δ(k)
(5)
que es el resultado de la ecuación en diferencias en forma cerrada.
Para verificar el resultado, puedo compararlo con el método de Matlab.
N=30;
delta=[1 zeros(1,N)]
%Metodo iterativo - Expresion en forma cerrada
for k=1:N+1
x(k)=5*(0.5)^(k-1)-2.5*(0.8)^(k-1)-2.5*delta(k);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
10/11
end
k=0:N;
subplot(2,1,1);
stem(k,x);
title(’Metodo iterativo - Expresion en forma cerrada’);
%Metodo Matlab
num=[0 .5 -1];
den=[1 -1.3 .4];
n=0:1:N;
x=[1 zeros(1,N)];
y=filter(num,den,x);
subplot(2,1,2);
stem(n,y,’r’);
title(’Metodo Matlab’);
Alumno: Guillermo Tabeni, UTN, FRA, 2007
11/11