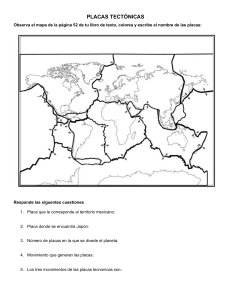
286362347-Una-Gran-Placa-Movil-Esta-Colocada-Entre-Dos-Grandes-Placas-Fijas

Estudiante: Isaac Álvarez Gutiérrez.
Ing. Rafael Ramírez
Mecánica de Fluidos.
Septiembre 8 del 2015
Grupo 2B
Ingeniería Mecánica VI semestre UA
Ejercicio 1.64 Fundamentos de la Mecánica de fluidos Munson Young
Una gran placa móvil está colocada entre dos grandes placas fijas, como se
muestra en la figura 1.64. Dos fluidos newtonianos con las viscosidades
indicadas están contenidos entre placas.
Figura 1.64
Determinar la magnitud y dirección de los esfuerzos cortantes que actúan sobre
las paredes fijas cuando la placa móvil posee una velocidad de 4 m/s, como se
muestra. Suponer que la distribución de velocidades es lineal.
SOLUCION
En primer lugar es necesario graficar el problema.
Placa
τ
h1 = 6mm
τ
μ=0.02 N· s/m2
Placa
h2 = 3mm
τ
μ=0.01 N· s/m2
Velocida
d 4 m/s
τ
Placa
Las placas fijas se encuentran graficadas de color negro, mientras que la placa
móvil está representada por el color azul, al ser una distribución lineal de
velocidades se puede establecer que en las placas fijas el movimiento será cero e
irá incrementando esta velocidad hacia la placa móvil de forma lineal como se
muestra en la figura (flechas rojas), el esfuerzo cortante
τ , en la placa móvil
tendrá sentido contrario al movimiento de la placa, pero tendrá sentido un sentido
contrario a este en las placas fijas, por tanto el esfuerzo cortante en las placas
fijas irá de izquierda a derecha (dirección del desplazamiento).
El esfuerzo cortante está determinado por la siguiente fórmula:
τ =μ
du
dy
Donde la constante de proporcionalidad se designa por la letra griega
μ
y
corresponde a los valores de viscosidad indicados en el problema.
du
dy
Corresponde a un gradiente de velocidad que para el presente caso es
constante ya que la velocidad con la cual se desplaza la placa móvil y la altura de
la película del fluido es la misma por tanto:
τ =μ
du U
=
dy h
Para la placa 1 o placa superior se tiene:
τ 1=μ
U
s
4 m/s
=0.02 N· 2 ·
−3
h1
m 6∗10 m
τ 1=13.33 N /m2
Para la placa 2 o placa inferior se tiene:
τ 2=μ
U
s
4 m/ s
=0.0 1 N· 2 ·
h1
m 3∗10−3 m
τ 2=13.33 N /m2
Análisis dimensional:
F
¿
T
[¿ ]
¿
¿
Respuesta: Para las paredes de ambas placas el esfuerzo cortante es el
mismo 13.33 Pa y los esfuerzos actúan sobre las paredes fijas en dirección
de la placa de movimiento.