INFORME DE LABORATORIO DE FISICA ELECTRONICA (GRUPO 03)

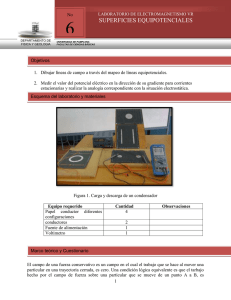
UNIVERSIDAD NACIONAL DE TRUJILLO
FACULTAD DE INGENIERÍA
ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA DE SISTEMAS
INFORME:
LABORATORIO DE CURVAS EQUIPOTENCIALES
AUTORES:
CURSO:
FÍSICA ELECTRÓNICA
DOCENTE:
Lic. HURTADO BUTRÓN FERNANDO JAVIER
SEDE VALLE JEQUETEPEQUE
GUADALUPE – PERÚ
2021
1.
TÍTULO:
CURVAS EQUIPOTENCIALES
2.
OBJETIVOS:
2.1. Graficar las curvas equipotenciales de varias configuraciones de carga
eléctrica, dentro del simulador.
2.2. Obtener las curvas equipotenciales formadas por los electrodos
alimentados de una fuente en C.C. (Corriente Continua).
3.
PROBLEMA:
¿Cómo se puede obtener las curvas equipotenciales que se forman en electrodos
alimentados eléctricamente?
4.
HIPÓTESIS:
Las curvas equipotenciales se pueden obtener en este caso mediante una
simulación virtual, en el cual pondremos el valor de nuestras cargas y así obtener los
datos requeridos.
5.
RESUMEN:
En el presente informe detallaremos por medio del uso de una simulación virtual, la
obtención de resultados que aproximan el entendimiento. En esta simulación
demostramos el desarrollo detallado y las conclusiones a las cuales hemos llegado
al realizar un proyecto de experimentación en donde buscamos entender y explicar
la naturaleza y el comportamiento de las curvas equipotenciales dentro de un Campo
eléctrico, con distintas herramientas virtuales tal como lo es el simulador oPhysics,
el cual nos sirvió para poder estudiar las curvas equipotenciales y tomar los datos
correspondientes a nuestro estudio.
Y, en conclusión, el análisis mostró que las curvas equipotenciales obtenidas no se
obtuvieron de cargas con la misma magnitud, sino que mantuvieron el
comportamiento perteneciente a cargas de diferentes órdenes de magnitud, para lo
cual se obtuvo una relación aproximada de cargas, la cual fue de 4 a 1 con respecto
a la punta de carga negativa con mayor magnitud.
Palabras claves.
Curvas Equipotenciales, Campo eléctrico.
6.
FUNDAMENTO TEÓRICO:
Al hablar de curvas equipotenciales tenemos que mencionar muchos conceptos
tales como:
a) Campo Eléctrico
Existen muchos ejemplos de campos, por ejemplo, el flujo de agua de un río es un
campo de vectores, llamado campo de flujo. Cada punto en el agua lleva asociado
consigo una cantidad vectorial, la velocidad con la cual pasa el agua por el punto. A
los puntos cercanos a la superficie terrestre se le puede asociar también un vector
de intensidad gravitacional.
El espacio que rodea a una varilla cargada parece estar afectado por la varilla, y a
este espacio lo denominamos campo eléctrico.
Esto es, si colocamos una carga q1, ésta produce un campo eléctrico en el espacio
que lo rodea. Ahora si colocamos, esta vez, una carga de prueba q2, ésta
experimentaría una fuerza. Se deduce que el campo juega un papel intermedio en
las fuerzas que obran entre las cargas. Entonces podemos decir que el campo
eléctrico está íntimamente ligado a la distribución de cargas que lo denominaremos
Con todo esto, se define al Campo Eléctrico utilizando el método operacional, como
un vector que sólo requiere conocer la distribución de cargas
.
Se define de esta forma, ya que, si q fuera comparable con Q, entonces afectaría al
campo creado por este último.
Para una distribución de carga
, tomamos un elemento de contribución, y luego
integramos en todo su volumen:
b) Potencial Eléctrico
Una distribución de carga produce un campo eléctrico
, esta información es hasta
cierto punto un poco incompleta y complicada de manejar, esto nos lleva a tratar de
encontrar una magnitud que nos exprese en forma sencilla cómo una distribución de
carga puede modificar su espacio de entorno.
Analicemos si el campo electrostático
es un campo conservativo. Es decir, para
una fuerza existe una función escalar U tal que cumple con la siguiente condición:
Entonces:
c) Líneas de Fuerza
Son líneas imaginarias que representan la trayectoria de una partícula cargada si es
que fuese colocada en algún campo eléctrico.
Las líneas de fuerza presentan las siguientes características:
● Las líneas de fuerza comienzan en las cargas positivas y terminan en las
negativas.
● La densidad de líneas es proporcional al valor del campo.
● No existe intersección entre las líneas de fuerza resultantes.
● La tangente a la línea en cualquier punto es paralela a la dirección del campo
eléctrico en ese punto.
La forma de las líneas de fuerza depende exclusivamente de la distribución de carga.
d) Curvas Equipotenciales
Los conceptos mencionados anteriormente son muy importantes para reconocer las
superficies equipotenciales. La distribución del potencial eléctrico en una cierta
región donde existe un campo eléctrico
puede representarse de manera gráfica
mediante superficies equipotenciales.
Una curva o superficie equipotencial es el lugar geométrico de los puntos de igual
potencial, donde se cumple que el potencial eléctrico generado por alguna
distribución de carga o carga puntual es constante.
Si el potencial eléctrico es constante, la diferencia de potencial se define de la
siguiente manera.
Si 𝛥𝑉 = 𝑉𝐵 − 𝑉𝐴 pero 𝑉𝐵 = 𝑉𝐴, entonces 𝑉𝐵 − 𝑉𝐴 = 𝑉𝐵 − 𝑉𝐵 = 0
Como q no es cero, el producto escalar de los vectores 𝐹 y 𝑑𝑟 es cero:
𝐹 × 𝑑𝑟 = 0 en otras palabras, se puede afirmar lo siguiente:
Como 𝑑𝑟 pertenece a la superficie equipotencial, por álgebra vectorial se concluye 𝐹
es ortogonal a 𝑑𝑟, de aquí se puede determinar que las líneas de fuerza siempre son
perpendiculares a las superficies equipotenciales y como el campo eléctrico 𝐸 es
paralelo a la fuerza eléctrica, se puede concluir también que el campo eléctrico
también es perpendicular a una superficie equipotencial, también se puede concluir
que el trabajo requerido para llevar a una carga de un sitio 𝐴 a un sitio 𝐵 (siendo 𝐴 y
𝐵 pertenecientes a la equipotencial) es cero.
Por otra parte se puede afirmar que la superficie equipotencial que pasa por
cualquier punto es perpendicular a la dirección del campo eléctrico
en ese punto.
Finalmente las líneas de fuerzas y las superficies equipotenciales forman una red de
líneas y superficies perpendiculares entre sí. En general las líneas de fuerzas de un
campo son curvas y las equipotenciales son superficies curvas. Podemos afirmar,
asimismo, que todas las cargas que están en reposo en un conductor, entonces la
superficie del conductor siempre será una superficie equipotencial.
En el dibujo, como se puede apreciar, las líneas de fuerza, las de color azul son
perpendiculares a las curvas equipotenciales denotadas de color verde, en este caso
generadas por una carga positiva.
PARTIENDO DE LA ECUACIÓN:
, esta expresión estaría definida para relacionar el campo
eléctrico en una sola dimensión definida.
Relacionando el 𝑡𝑟𝑎𝑏𝑎𝑗𝑜 − 𝑒𝑛𝑒𝑟𝑔í𝑎 potencial eléctrico, con el potencial, tendríamos:
, lo cual define:
La relación de:
se conoce como la magnitud del gradiente de potencial y
es igual al componente del campo eléctrico en la dirección de estudio, pero con el
signo contrario.
En una curva equipotencial,
la diferencia de potencial es nula indicando
que los potenciales están definidos a la misma distancia de separación.
7.
METODOLOGÍA:
8.1 EXPERIMENTACIÓN: Obtención de curvas equipotenciales
8.1.1 Diseño del montaje experimental
Para la experimentación hemos utilizado la siguiente aplicación y la tabla N°1
Tabla para trazar las curvas equipotenciales:
●
Laboratorio
Virtual
de
(https://ophysics.com/em9.html)
Curvas
Equipotenciales
Figura.01: Laboratorio Virtual de Curvas Equipotenciales
(oPhysics: Simulaciones interactivas de física)
Tabla Nª 01. Tabla para trazar las curvas equipotenciales
8.1.2 Procedimiento experimental
Con ayuda del laboratorio virtual de física sobre la “Curvas Equipotenciales”
hemos realizado lo siguiente:
✔ Primero hemos cambiado los valores tanto para la Carga Positiva como
para la Carga Negativa; dándole los valores de 4 ,4.5; y -4, -4.5.
Figura 02: Ingreso de valores en el programa
✔ Luego posicionamos los valores de X y Y proporcionados en la Tabla
N°01 Tabla para trazar las curvas equipotenciales, y pasamos a
anotar las medidas del Voltaje en cada posición:
Figura 03: Medida del voltaje.
✔ Después de anotar todos los Voltaje de las posiciones dadas en la tabla,
continuamos completando la Tabla°01 en la columna V (Voltaje, voltios),
formando así una nueva Tabla°02:
Tabla Nª 02. Tabla para trazar las curvas equipotenciales completa medida en Voltios.
(Con los datos obtenidos en programa virtual)
8.1.3 Datos experimentales
Con los datos obtenidos anteriormente, pasamos a crear en Excel nuestra
Tabla° 03, la cual nos servirá para poder graficar las superficies potenciales:
Tabla Nª 03. Tabla para trazar las curvas equipotenciales medida en Voltios.
8.
ANÁLISIS DE DATOS Y RESULTADOS:
9.1 EXPERIMENTACIÓN:
De acuerdo a los datos obtenidos de la Tabla N°03. Tabla para trazar las curvas
equipotenciales medida en Voltios, calculamos la gráfica:
✔ Con los datos de la Tabla Nº03 graficamos:
-Gráfico desde un ángulo
80
60
40
1
3
20
5
-1
0
-5
-20
-4
-3
-2
-1
-3
0
5
4
3
2
1
-5
-40
-60
-80
Curvas Equipotenciales
-80--60
-60--40
-40--20
-20-0
0-20
20-40
40-60
60-80
-Gráfico desde un ángulo
80
60
40
20
0
-20
-40
-60
-80
Curvas Equipotenciales
-80--60
-60--40
-40--20
-20-0
0-20
20-40
40-60
60-80
-Gráfico desde un ángulo
-Gráfico desde un ángulo
-
Gráfico desde un ángulo
✔
INTERPRETACIÓN
-
El potencial eléctrico aumenta a medida que se acerca al electrodo
cargado positivamente y va disminuyendo en dirección al electrodo con
carga negativa.
-
Las líneas de campo eléctrico comienzan en las cargas positivas y
terminan en las cargas negativas.
-
Las líneas de campo nunca se cruzan. Debido a que no existe un punto
en el campo eléctrico que pueda tener dos voltajes al mismo tiempo.
9.2 RESULTADOS:
✔
Las curvas equipotenciales no se cruzan.
✔
Las curvas equipotenciales no necesariamente son simétricas respecto al
eje de las primeras componentes.
✔
Se puede ver que las curvas equipotenciales no son exactamente
circunferencias.
10. CONCLUSIONES:
-
Durante el desarrollo de este laboratorio comprendimos con mayor claridad el
concepto de líneas equipotenciales, siendo estas la representación gráfica de
las superficies equipotenciales, las cuales son superficies tridimensionales con
un mismo valor de potencial eléctrico.
-
Mientras que en las curvas equipotenciales podemos llegar a la conclusión
que existe una simetría con respecto al eje horizontal, sin embargo, no
podemos afirmar lo mismo para la parte vertical, porque parece estar siempre
más cerca al electrodo cargado negativamente.
11. REFERENCIAS BIBLIOGRÁFICAS
Malpartida, O. D. (25 de mayo de 2015). slideshare. Obtenido de slideshare:
https://es.slideshare.net/emiliocoaquirachambi/myslidees-curvas-equipotenciales
Física General III, ASMAT AZAHUANCHE, Humberto, pp. 134,135, SAGSA S.A.,
1995, Perú, Lima.
Floriano, D. S. (6 de Julio de 2012). academia.edu. Obtenido de academia.edu:
https://www.academia.edu/34979755/PR%C3%81CTICA_N_5_MULTIMETRO_DIGITA
L
Sears F. W., Zemansky M., Young H., Freedman R.: Física Universitaria, Vol. II
Undécima edición, Editorial Pearson Education; pag: 997-1001.
Serway R.; Jewet J.: Física, Vol. II 3ra edición, Editorial Thomson, 2005; pag : 5357.
Facultad de Ciencias de la Universidad Nacional de Ingeniería: Manual de
Laboratorio de Física General, 2007; pag: 104-107.
Miztegui Alberto P. – Sabato Jorge A.: Física, Vol. I, Editorial Kapelusz, 1972; pag:
187-223.
Tipler Paul A.: Fisica para la Ciencia y Tecnología, Vol. I, Editorial Reverte, 2001;
pag: 798-799.