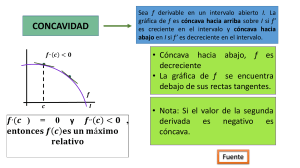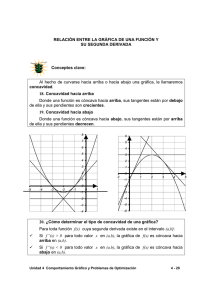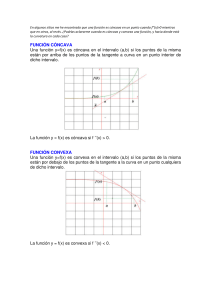
Sesión 4 MATEMÁTICA II SESIÓN 4: Aplicación al trazado de gráficas de funciones Optimización INGENIERÍA INDUSTRIAL UCV Sesión 4 UCV 4.1 Concavidad y puntos de inflexión Fig. 1 Una curva cóncava hacia arriba y otra curva cóncava hacia abajo Definición 1 Sea 𝑓: 𝐼 ℝ → ℝ una función derivable en el intervalo abierto 𝐼 de ℝ. a) Se dice que la gráfica de 𝑓(𝑥) es cóncava hacia arriba si 𝑓 ′ (𝑥) es creciente en 𝐼. b) Se dice que la gráfica de 𝑓(𝑥) es cóncava hacia abajo si 𝑓 ′ (𝑥) es decreciente en 𝐼. Teorema 1 𝑓: 𝐼 ℝ → ℝ, función dos veces derivable en el intervalo abierto 𝐼 de ℝ. a) Se dice que la gráfica de 𝑓(𝑥) es cóncava hacia arriba si 𝑓 ′′ (𝑥) > 0 en 𝐼. b) Se dice que la gráfica de 𝑓(𝑥) es cóncava hacia abajo si 𝑓 ′′ (𝑥) < 0 en 𝐼. Ejemplo 1. A continuación se muestra, la gráfica, de la segunda derivada 𝑓 ′′ de una función 𝑓. En qué intervalo la función 𝑓 es cóncava hacia arriba y en que intervalo es cóncava hacia abajo. Fig. 2 Solución Según el teorema 1, 𝑓(𝑥) es cóncava hacia arriba en ⟨0,1⟩ ∪ ⟨3, 4⟩ y cóncava hacia abajo en ⟨1,2⟩ ∪ ⟨2, 3⟩. Definición 2 ( Punto de Inflexión ) El punto (𝑐, 𝑓(𝑐)) es un punto de inflexión de la gráfica de la función 𝑓 si la gráfica tiene una recta tangente en ese punto, y si existe un intervalo abierto 𝐼 que contiene a 𝑐 tal que si 𝑥 está en 𝐼, entonces: i) 𝑓 ′′ (𝑥) < 0 si 𝑥 < 𝑐 y 𝑓 ′′ (𝑥) > 0 si 𝑥 > 𝑐; o ′′ (𝑥) ii)𝑓 > 0 si 𝑥 < 𝑐 y 𝑓 ′′ (𝑥) < 0 si 𝑥 > 𝑐. Sesión 4 UCV Fig. 3 El punto (1,2) es punto de inflexión Ejemplo 2 Determine el sentido de concavidad de la gráfica de la función 𝑓(𝑥) = 𝑥 6 + 𝑥 4 + 5𝑥 2 + 7. Solución Derivando sucesivamente: 𝑓 ′ (𝑥) = 6𝑥 5 + 4𝑥 3 + 10𝑥 𝑓 ′′ (𝑥) = 30𝑥 4 + 12𝑥 2 + 10 Vemos que 𝑓 > 0 en todo ℝ, entonces diremos que la gráfica de 𝑓(𝑥) es cóncava hacia arriba en todo ℝ. Ver Fig. 16. ′′ (𝑥) Fig. 4 La gráfica de f(x) es cóncava hacia arriba en todo ℝ. Ejemplo 3 Suponga que 𝑡 horas después de iniciar un trabajo a las 7 am. un obrero, en una línea de ensamble, ha realizado una tarea particular de 𝑓(𝑡) unidades donde 𝑓(𝑡) = 21𝑡 + 9𝑡 2 − 𝑡 3, 0 ≤ 𝑡 ≤ 5. Determine los intervalos de concavidad y su punto de inflexión. Solución Derivando sucesivamente: 𝑓 ′ (𝑡) = −3𝑡 2 + 18𝑡 + 21 𝑓 ′′ (𝑡) = −6𝑡 + 18 De −6𝑡 + 18 > 0, obtenemos que 𝑓 es cóncava hacia arriba en <0,3>. De −6𝑡 + 18 < 0, obtenemos que 𝑓 es cóncava hacia abajo en <3,5>. Resolviendo la ecuación −6𝑡 + 18 = 0, 𝑡 = 3 y su punto de inflexión es (3,117). Fig. 5 Sesión 4 UCV 4.2 Optimización En esta sección resolveremos problemas como los de maximizar áreas, volúmenes y utilidad, y minimizar tiempos, costos, etc. Antes de presentar los problemas de optimización, daremos algunos pasos a tener en cuenta para resolverlos. Pasos para la resolución de problemas de optimización 1. 2. 3. 4. 5. Comprenda el problema: ¿Cuál es la incógnita? ¿Cuáles son las cantidades dadas? ¿Cuáles son las condiciones dadas? Dibuje un diagrama: identificando las cantidades dadas y requeridas. Introduzca notación: Simbolice todas las variables. Expresar una ecuación que involucre la variable a optimizar y las demás variables dependientes. Aplicar los métodos dados anteriormente: Criterio de la primera derivada o el criterio de la segunda derivada, para hallar los valores máximos o mínimos. Ejemplo 4. Un granjero tiene 3600 metros de cerca y desea cercar un campo rectangular que limita con un río recto. No necesita cercar a lo largo del río. ¿Cuáles son las dimensiones del campo que tiene el área más grande? Solución 400 Algunas posibilidades particulares, vistas gráficamente: 2400 1600 3000 1600 600 600 300 300 Area=300×3000=900000 Area=600×2400=1440000 Area=1500×600=640000 En la siguiente figura, se ilustra el caso general, y A x x Obtenemos las ecuaciones: 𝐴 = 𝑥𝑦 2𝑥 + 𝑦 = 3600 Entonces 𝐴 = 𝑥(3600 − 2𝑥) 𝐴′ = −4𝑥 + 3600 𝑥 = 900 (punto crítico) Para aplicar el 2do criterio, hallamos la segunda derivada: 𝐴,, = 4 Por lo tanto en 𝑥 = 900,𝑦 = 1800, hay un área máxima. Area= xy Ejemplo 5. Se va a fabricar una lata de forma cilíndrica de capacidad de 2 litros de aceite. ¿Cuáles son las dimensiones de la lata que minimizan los costos del metal? Solución Dibujando la lata cilíndrica, tenemos: h r Donde 𝑟 es el radio y ℎ la altura (ambos en cm). Para minimizar el costo del metal, se debe minimizar el área de la superficie total del tarro. 𝐴 = 2𝜋𝑟 2 + 2𝜋𝑟ℎ (1) Como la capacidad del tarro es 2000cm3, tenemos: 𝑉 = 𝜋𝑟 2 ℎ = 2000 (2) Sesión 4 UCV De (2) en (1), 𝑉 = 2𝜋𝑟 2 + r 𝑉´ = 4𝜋𝑟 − 2000 𝑟2 = 0, 𝑟 = 4000 𝑟 10 3 √𝜋 (punto crítico) Para aplicar el 2do criterio, hallamos la segunda derivada: 𝑉´´ = 4𝜋 + Por lo tanto en 𝑟 = 2 Area=2(𝜋𝑟 ) Area=(2𝜋𝑟)ℎ 10 3 √𝜋 4000 >0 𝑟3 , hay un mínimo. Ejemplo 6. Encuentre el punto sobre la parábola 𝑦 2 = 4𝑥 más cercano al punto (1,3) Solución La distancia entre el punto (1,3) y el punto (𝑥, 𝑦) es (1,3) (x,y) 𝑦 2 = 4𝑥 𝑑 = √(𝑥 − 1)2 + (𝑦 − 3)2 (1) Como (𝑥, 𝑦) está en la parábola, entonces 𝑦 2 = 4𝑥 (2) Reemplazando (2) en (1), obtenemos: 2 𝑦2 𝑑 = √( − 1) + (𝑦 − 3)2 4 Minimizar 𝑑 2 = 𝑓(𝑦) = ( 𝑦2 4 2 − 1) + (𝑦 − 3)2 𝑓´(𝑦) = 𝑦3 4 + 𝑦 − 6 = 0, 𝑦 = 2.42 3 Para aplicar el 2do criterio, hallamos la segunda derivada: 𝑓´´(𝑦) = 4 𝑦 2 + 1 > 0 Entonces en 𝑦 = 2.42 hay un mínimo, y el punto buscado es (1.472, 2.42). Ejemplo 7. Una tienda ha vendido 40 TV Plasma a la semana, a S/1100 cada una. Un analista indica que por cada S/10 de descuento que se ofrezca a los compradores, el número de aparatos vendidos se incrementa en 6 por semana. Encuentre las funciones de demanda y de ingreso. ¿Qué tan grande debe ser la rebaja para maximizar el ingreso? Solución Formamos la función de manda: 𝑝(𝑥) = 1100 − 10 3500 5 (𝑥 − 40) = − 𝑥 6 3 3 La función de ingreso es 𝑅(𝑥) = 𝑥𝑝(𝑥) = 𝑅´(𝑥) = 3500 3 − 10 3 3500𝑥 5 2 − 𝑥 3 3 𝑥 = 0, entonces 𝑥 = 350. Para aplicar el segundo criterio, hallamos 𝑅´´ = ingreso. Y el precio correspondiente es 𝑝(350) = −10 3 < 0. Por lo tanto cuando 𝑥 = 350, se tiene un máximo 3500 5 − (350) = 583.3 3 3 y el descuento es 1100-583.3=516.5. Por lo tanto para maximizar el ingreso se debe hacer un descuento de S/516.5. Sesión 4 UCV Ejemplo 8. La cantidad (en mg de carbón/m3/h) en que se lleva a cabo la fotosíntesis de una especie de fitoplancton se diseña mediante la función 𝑃= 100𝐼 𝐼2 + 𝐼 + 4 Donde 𝐼 es la intensidad de luz (que se mide en millares de bujía-pie). ¿Para qué intensidad de luz P es máxima? Solución Derivando P respecto a I, obtenemos: 𝑑𝑃 400 − 100𝐼2 = = 0, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 𝐼 = 2 𝑑𝐼 (𝐼2 + 𝐼 + 4)2 Aplicando el primer criterio, como 𝑑𝑃 𝑑𝐼 > 0, para I<2 y 𝑑𝑃 𝑑𝐼 < 0 para I>2, entonces en I=2 hay una máxima cantidad de fotosíntesis. Ejemplo 9. El área de un poster tiene que ser de 180 m2, y los márgenes laterales e inferiores deben medir 1 m y el margen superior debe ser de 2 m. ¿Qué dimensiones darán el área impresa máxima? Solución Usando el siguiente diagrama, se obtiene: (1) 𝑥𝑦 = 180 2 Área de impresión 𝐴 = (𝑥 − 2)(𝑦 − 3) 1 1 x Reemplazando (1) en (2), 𝐴´ = −3 + 𝐴´´ = − 1 y (2) 720 𝑥3 360 𝑥2 180 𝐴 = (𝑥 − 2)( − 3) 𝑥 = 0, 𝑥 = 2√30. < 0, entonces la dimensiones del poster deben ser: 𝑥 = 2√30, 𝑦 = 3√30. Ejemplo 10. Se inscribe un cilindro circular recto en una esfera de radio 4m. Encuentre el volumen más grande de ese cilindro. Solución Con la ayuda del siguiente gráfico, 4 √16 − 𝑥 2 x obtenemos el volumen del cilindro: Sesión 4 UCV 𝑉 = 2𝜋𝑥 2 √16 − 𝑥 2 𝑉´ = 4𝜋𝑥√16 − 𝑥 2 − 2𝜋𝑥 3 √16 − 𝑥 2 =0 4𝜋𝑥(16 − 𝑥 2 ) − 2𝜋𝑥 3 = 0 𝑥2 = 32 , 3 32 𝑥=√ 3 Para aplicar el segundo criterio, hallamos la segunda derivada: 32 𝑉´´ (√ ) < 0 3 Por lo tanto el volumen máximo del cilindro inscrito es 𝑉 = 256√3 9 𝜋.