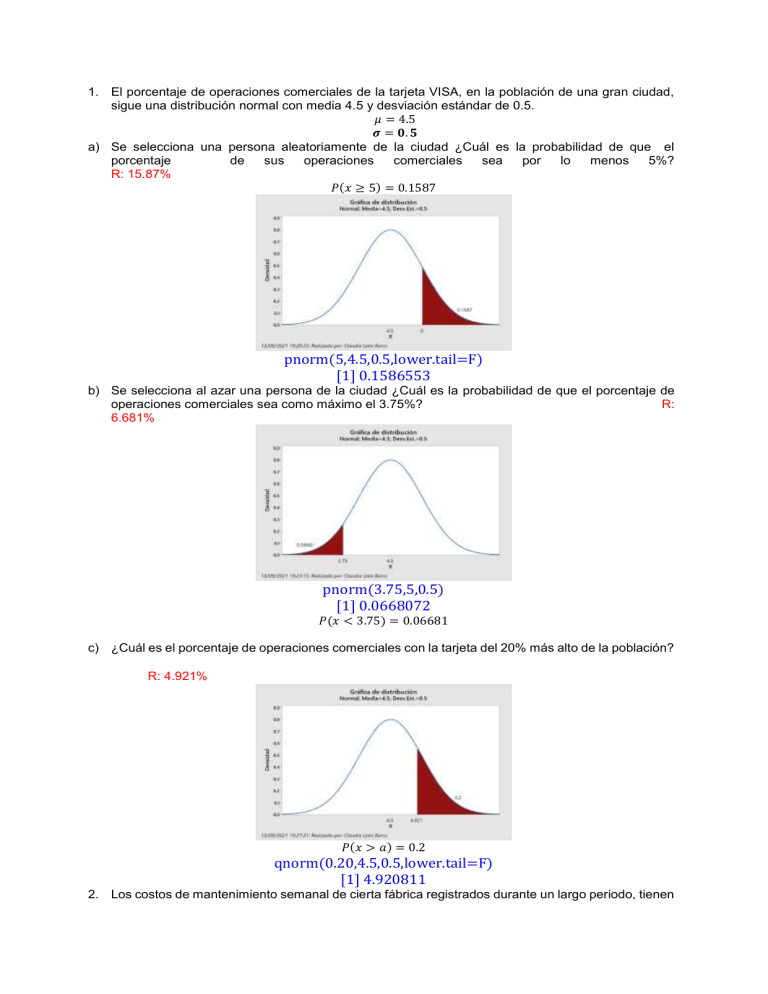
1. El porcentaje de operaciones comerciales de la tarjeta VISA, en la población de una gran ciudad, sigue una distribución normal con media 4.5 y desviación estándar de 0.5. 𝜇 = 4.5 𝝈 = 𝟎. 𝟓 a) Se selecciona una persona aleatoriamente de la ciudad ¿Cuál es la probabilidad de que el porcentaje de sus operaciones comerciales sea por lo menos 5%? R: 15.87% 𝑃(𝑥 ≥ 5) = 0.1587 pnorm(5,4.5,0.5,lower.tail=F) [1] 0.1586553 b) Se selecciona al azar una persona de la ciudad ¿Cuál es la probabilidad de que el porcentaje de operaciones comerciales sea como máximo el 3.75%? R: 6.681% pnorm(3.75,5,0.5) [1] 0.0668072 𝑃(𝑥 < 3.75) = 0.06681 c) ¿Cuál es el porcentaje de operaciones comerciales con la tarjeta del 20% más alto de la población? R: 4.921% 𝑃(𝑥 > 𝑎) = 0.2 qnorm(0.20,4.5,0.5,lower.tail=F) [1] 4.920811 2. Los costos de mantenimiento semanal de cierta fábrica registrados durante un largo periodo, tienen una distribución Normal con una media igual a 1,680 soles; además se sabe que 0.70 es la probabilidad de que el costo de una semana sea como máximo 1,627.56 soles. 𝜇 = 1680 𝑥 − 1680 1627.56 − 1680 𝑃( ≤ ) = 0.7 𝜎 𝜎 1627.56 − 1680 𝑃 (𝑍 ≤ ) = 0.7 𝜎 qnorm(0.7) [1] 0.5244005 𝑍= 1627.56 − 1680 1627.56 − 1680 = 0.5244005 → σ = = −100 𝜎 0.5244005 𝝈 = 𝟏𝟎𝟎 a) Hallar el valor de la desviación estándar de la distribución Normal. R: 100 b) Hallar la probabilidad de que el costo de una semana se diferencie del promedio en no más de 150 soles. R: 0.8663858 𝑃(1680 − 150 < 𝑥 < 1680 + 150) = 𝑃(1530 < 𝑥 < 1830) pnorm(1830,1680,100)-pnorm(1530,1680,100) [1] 0.8663856 c) ¿Cuál será el costo semanal máximo que se observará en una semana con probabilidad 0.75? R: 1747.45 qnorm(0.75,1680,100) [1] 1747.449 3. Se supone que el peso del contenido de un paquete de café Sabor es una variable con distribución Normal con desviación estándar de = 0.04 kilogramos. Se sabe que sólo 2% de los paquetes tienen un peso menor a 4 kilogramos. 𝝈 = 𝟎. 𝟎𝟒 𝒙−𝝁 𝟒−𝝁 𝑷(𝒙 < 𝟒) = 𝟎. 𝟎𝟐 → 𝑷(𝒙 − 𝝁 < 𝟒 − 𝝁) = 𝟎. 𝟎𝟐 → 𝑷 ( < ) = 𝟎. 𝟎𝟐 𝝈 𝝈 qnorm(0.02) [1] -2.053749 𝑷(𝒁 < −𝟐. 𝟎𝟓𝟑𝟕𝟒𝟗) = 𝟎. 𝟎𝟐 𝟒−𝝁 −𝟐. 𝟎𝟓𝟑𝟕𝟒𝟗 = → 𝝁 = 𝟒 + 𝟐. 𝟎𝟓𝟑𝟕𝟒𝟗 ∗ 𝟎. 𝟎𝟒 → 𝝁 = 𝟒. 𝟎𝟖𝟐𝟏𝟓 𝟎. 𝟎𝟒 a) Halle el peso promedio y luego calcule el porcentaje de paquetes de café Sabor con un peso superior a 4.13 kilogramos. R: Media=4.08216, Porcentaje=11.58 % pnorm(4.13,4.08215,0.04,lower.tail=F) [1] 0.1157995 b) De acuerdo con su peso, los paquetes de café Sabor se clasifican en 3 categorías, como sigue: Categoría A (los más livianos) son el 10%, Categoría B (los de peso intermedio) son el 85% y el 5% restante (los más pesados) están en la categoría C. Calcule los valores límite del peso en cada categoría (en kilogramos). R: K1= 4.031, K2=4.148 qnorm(0.10,4.08215,0.04) [1] 4.030888 qnorm(0.10+0.85,4.08215,0.04) [1] 4.147944