zapatascontinuas-180912113530

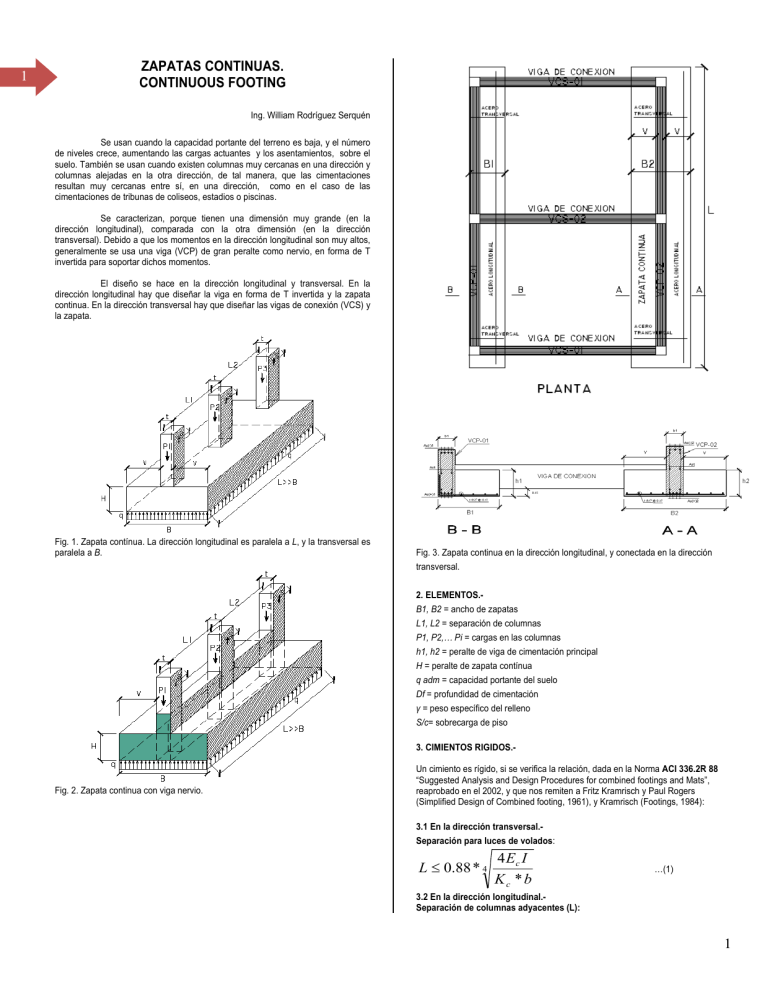
1
ZAPATAS CONTINUAS.
CONTINUOUS FOOTING
Ing. William Rodríguez Serquén
Se usan cuando la capacidad portante del terreno es baja, y el número
de niveles crece, aumentando las cargas actuantes y los asentamientos, sobre el
suelo. También se usan cuando existen columnas muy cercanas en una dirección y
columnas alejadas en la otra dirección, de tal manera, que las cimentaciones
resultan muy cercanas entre sí, en una dirección, como en el caso de las
cimentaciones de tribunas de coliseos, estadios o piscinas.
Se caracterizan, porque tienen una dimensión muy grande (en la
dirección longitudinal), comparada con la otra dimensión (en la dirección
transversal). Debido a que los momentos en la dirección longitudinal son muy altos,
generalmente se usa una viga (VCP) de gran peralte como nervio, en forma de T
invertida para soportar dichos momentos.
El diseño se hace en la dirección longitudinal y transversal. En la
dirección longitudinal hay que diseñar la viga en forma de T invertida y la zapata
continua. En la dirección transversal hay que diseñar las vigas de conexión (VCS) y
la zapata.
Fig. 1. Zapata contínua. La dirección longitudinal es paralela a L, y la transversal es
paralela a B.
Fig. 3. Zapata continua en la dirección longitudinal, y conectada en la dirección
transversal.
2. ELEMENTOS.B1, B2 = ancho de zapatas
L1, L2 = separación de columnas
P1, P2,… Pi = cargas en las columnas
h1, h2 = peralte de viga de cimentación principal
H = peralte de zapata contínua
q adm = capacidad portante del suelo
Df = profundidad de cimentación
γ = peso específico del relleno
S/c= sobrecarga de piso
3. CIMIENTOS RIGIDOS.-
Fig. 2. Zapata continua con viga nervio.
Un cimiento es rígido, si se verifica la relación, dada en la Norma ACI 336.2R 88
“Suggested Analysis and Design Procedures for combined footings and Mats”,
reaprobado en el 2002, y que nos remiten a Fritz Kramrisch y Paul Rogers
(Simplified Design of Combined footing, 1961), y Kramrisch (Footings, 1984):
3.1 En la dirección transversal.Separación para luces de volados:
L ≤ 0.88 * 4
4 Ec I
Kc * b
…(1)
3.2 En la dirección longitudinal.Separación de columnas adyacentes (L):
1
2
L ≤ 1.75 * 4
4 Ec I
Kc *b
.k = k 0,3 * (1/2 - 0.15 / B)2
…(2)
Con un valor de B grande
Donnde:
t = espesor
e
de la zapatta.
v= loongitud del volado
b = ancho del cimientoo
__
Ec = 15000 √fc
.k arenas aproxximadamente = 0,25* k 0,30
…(66)
MÓDULO DE BALASTO,
B
K, EN ARCILLAS
S.-
Ec = 2.17 x 10 6 ton/m22, para fc = 210 kgg/cm2.
En suelos arcillossos, el coeficiente dde balasto afectadoo por el factor de foorma,
para placa circular es:
K = q / d = Módulo de balasto =
= Módulo de Winkler
= Módulo de reaccióón de subrasante.
4. EL
E MÓDULO DE
D BALASTO (O
( DE SULZBE
ERGER), K30.l relación esfuerzzo vs asentamiento, que se obtienee de la gráfica resuultante
Es la
del Ensayo de Placa de carga, en el insstante que el asentamiento del suelo es de
0.055 de pulgada (0,05”” = 1/20”). El coeficciente así obtenido es el correspondiente a
una placa de 30 cm dee diámetro, K30.
…(77)
nes rectangulares en suelos arcillossos, de dimension
nes BxL:
Para cimentacion
…(88)
K(BxB), corresponde a placa cuadradda, la cual se puedee obtener con la reelación (7),
y reemplazándola en (8) resulta:
B

1 + 0.5 
30 
L
k c = k 30 * *
B  1.5 




…(9)
L = longitud de la zapata
z
corrida.
Si L>>B resulta, quue en arcillas:
p
de carga y definición
d
de Móduulo de
Fig. 4. Resultados dee la prueba de la placa
balaasto. K30 = s1 / 0,127cm
k aproximadameente = 20 *
k 300
B
…(10)
c
de balaasto K30, del ensayoo de placa de cargga, tiene que correggirse y
El coeficiente
adecuarse al tamaño de la zapata, ya que
q se realiza con una placa de 30 cm de
metro.
diám
Paraa convertir el k300 de placa al Kc de campo, se tieenen que relacionnar los
asenntamientos y anchhos de placa (Sp, Bp); con los asenntamientos y anchhos de
cam
mpo (Sc, Bc), a travvés de un factor de incidencia CB que considere el anchoo de la
cimeentación prevista, obtenido
o
con la expperimentación:
Kc = CB*K30
…(3)
CB = Factor de incidenncia del ancho de laa cimentación
MÓ
ÓDULO DE BAL
LASTO, K, EN
N ARENAS.En suelos
s
arenosos, hay que afectar el Módulo de Balastoo por un factor de forma,
f
paraa considerar, el ancho del cimiento B, el ancho de la plaaca (0,30m) y la
proffundidad de cimentación D:
Fig. 5. Vista del equipo para el ensayyo de placa de cargga.
….(4)
Donnde n varía entre 2 y 3.
Paraa n = 2 y B >>D ressulta:
De aquí
a se obtiene:
…(5)
2
3
Fig. 6. Arreglo de la prueba
p
de placa (oo plato) de carga. Una
U placa usual es de B=
c
a la profunddidad Df<2m.
0 300 m, y la placa, se coloca
Fig. 9. Valores del K30 dada por Braja Das.
n proporciona unna gráfica donde relaciona K30 conn el valor
Crespo Villalaz, nos
relativo de soporte CBR:
Fig. 7. Comparación dee los resultados dee pruebas de campoo según D’Appolonnia.
Fuente. Braja Das.
d CBR vs. El K30,, según Crespo Villlaláz.
Fig. 10. Relación del
d
de esfuuerzos en el suelo, entre la placa de carga
c
Fig.8. Diferencias de distribución
y el cimiento.
os se cumple:
Paraa suelos arcilloso
SF * BF = SP * B P
…(11)
Paraa suelos arenososs:
SF = SP * [ 2 BF / (BF + BP) ]2
SF = asentamiento de la cimentación
BF = ancho de la cimenntación
SP = asentamiento de la
l placa
BP = ancho de la placaa
…(12)
d placa de cargaa. Ensayo
Fig. 11. Otra forma de presentacción del ensayo de
ejecutado en Talarra, Piura. Perú.
ores de k30, según Braja Das:
Valo
3
4
EL MODULO DE BALASTO Y EL ENSAYO SPT.-
Suelos granulares.-
Scout en 1981, dio una relación para hallar k30, en función del valor de N del
ensayo de penetración estándar corregido:
…(19)
-z = profundidad donde se calcula kh
Para suelos arenosos:
K 30 (MN/m3) = 18 N corregido
-B = ancho del cimiento
…(13)
-nh = coeficiente, que se obtiene de la siguiente gráfica.
Terzaghi-Peck 1948, 1968:
K30 (kg/cm3) = (N/7.35) – 0.31
…(14)
Meyerhof, 1964:
K30 (kg/cm3) = N/5.08 para B ‹ = 1,20 m
=
N/7.62,
…(15.1)
para B mayor que 1,20 m
…(15.2)
MODULO DE BALASTO VERTICAL kv1.El Ing. Augusto José Leoni, de la U. La Plata, Argentina, ha propuesto las
siguientes ecuaciones:
… para arenas secas o húmedas
…(16)
Fig. 13. Valores de nh vs N del ensayo de SPT.
… para arenas saturadas y
sumergidas.
…(17)
Cuyas gráficas se muestran a continuación:
5. RELACION VOLADO/CANTO, POR RAZONES DE
DISTRIBUCION DE PRESIONES UNIFORME, SOBRE EL
SUELO.EN LA DIRECCIÓN TRANSVERSAL.-
Fig. 13 Elementos de la sección transversal de zapata continua.
Para voladizos, usando la ecuación (1):
L ≤ 0.88 * 4
E * h4
3 * Kc * h
L = v = longitud del volado
Tomando la mitad del módulo de elasticidad:
Fig. 12. Relación entre el Módulo de balasto y el ensayo de penetración.
Em = Ec/2 = 108 685 kg/cm2
MODULO DE BALASTO HORIZONTAL kh.-
L ≤ 0.88 * 4
108685 * h 4
3 * Kc * h
v ≤ 0.88 * 4
36228 * h 4
Kc * h
Suelos cohesivos.- Terzaghi propuso:
…(18)
B = ancho del cimiento,
kv1 = Módulo de balasto vertical
v
12.14
≤
h 4 kc * h
…(20)
Con h = 1.1 d
4
5
B

1 + 0.5 
30 
L
k c = k 30 * *
B  1.5 




La expresión general de volado/canto, resulta:
v
13.04
≤
d 4 kc * d
…(21)
5.1 CIMENTACIONES EN ARENAS:
…(27)
L = longitud de la zapata corrida.
Para valores prácticos se reduce a:
k c = 20 *
k 30
B
…(28)
Esto en la relación de vuelo canto, Ec. (21), se convierte en:
…(22)
Relación Volado vs. Canto vs. k30 en arcillas:
…(23)
-k es aproximadamente = 0.25 *k30
La relación Volado vs. Canto vs. k30 en arenas es:
v
18.44
≤
d 4 k 30 * d
…(24)
v
≤
d
7.34
4
d
k 30 *
B
…(29)
Haciendo B aproximadamente = 2 * v
La Ec.(24) se representa en el siguiente gráfico:
v3/ 4
≤
d
4
7.34
k 30 * d
…(30)
La Ec. (30) se representa en el siguiente gráfico:
Fig. 14. Relación de volado y peralte de zapata vs. K
30
de balasto en suelo
granular, en zapatas continuas.
5.2 CIMENTACIONES EN ARCILLAS.-
Fig. 15. Relación de volado y peralte de zapata vs. K
30
de balasto en suelo
cohesivo, en zapatas continuas.
…(25)
Para cimentaciones rectangulares de dimensiones BxL:
6. RELACION SEPARACION DE COLUMNAS/PERALTE,
POR RAZONES DE DISTRIBUCION DE PRESIONES.EN LA DIRECCIÓN LONGITUDINAL.Usando la Ec.(1) se obtiene la ecuación general:
…(26)
Kc y K300, están relacionados mediante:
25.93
L
≤
d 4 k 30 * d
…(31)
EN ARENAS:
5
6
L
36.67
≤
d 4 k 30 * d
…(32)
qneto = qadm – γDf – s/c piso
EN ARCILLAS:
L
27.14
≤
d 4 k 30 * d
-Hallamos el esfuerzo neto
-Hallamos la resultante
…(33)
Las Ecs. (32) y (33), se representan gráficamente, y se muestran a continuación.
R = ∑Pi
-Dimensionamos el área de la zapata 2:
BxL ≥ R / qneto
-Ubicamos la resultante:
xo* R = = ∑Pi*xi
Fig. 16. Relación de separación de columnas, peralte de zapata y K 30 de balasto
en suelo granular, en zapatas continuas.
Fig. 18. Diagrama de cargas en zapata contínua.
-La excentricidad vale:
e = xo – L/2
-Los esfuerzos valen:
q1 = (R / BxL) ( 1 – 6 e / L)
q2 = (R / BxL) ( 1 + 6 e / L)
Chequeamos que:
q1, q2 ≤ q neto, luego aceptamos las dimensiones BxL.
7.2 DIMENSIONADO EN ELEVACION
7.2.1 DIMENSIONADO EN LA DIRECCION TRANSVERSAL.-Obtenido el ancho B de zapata, y con el coeficiente de balasto K30, usando las
gráficas anteriores, se obtiene un peralte mínimo d, para que la distribución de
esfuerzos sea uniforme en la dirección transversal.
Fig. 17. Relación de separación de columnas, peralte de zapata y K 30 de balasto
en suelo cohesivo, en zapatas continuas.
7.2.2 DIMENSIONADO EN LA DIRECCION LONGITUDINAL.-Con la separación de columnas L, y con el coeficiente de balasto K30, usando las
gráficas anteriores se obtiene otro peralte mínimo d, por razones de distribución de
7. DIMENSIONAMIENTO DE ZAPATAS CONTINUAS.-
presiones.
8. DISEÑO DE VIGA VCP.-
7.1 DIMENSIONADO EN PLANTA.-
6
7
Se hallan los esfuerzos últimos del suelo, luego se resuelve la estructura, y se
-Con el peralte de la viga bw x d se calcula el acero de viga.
obtiene el diagrama de momentos:
q i ( x ' , y ' )u =
Mxu * y ' Myu * x '
Ru
±
±
Area
Ix
Iy
q1u = (Ru / BxL) ( 1 – 6 e / B)
q2u = (Ru / BxL) ( 1 + 6 e / B)
Fig. 20. Diagrama de aceros en zapata continua.
Con el momento máximo negativo se halla el acero negativo. Con el momento
positivo se halla el acero positivo.
Fig. 19. Diagrama de momentos en zapatas continuas.
-Con el diagrama de momentos se halla el acero requerido. Estos momentos son
resistidos por la viga de cimentación VCP-02.
El peralte de la viga se pre-dimensiona con:
d=
Mu (+ )
φ * fy * ρ * b(1 − 0.59 * ρ *
fy
fc
Fig. 21. Sección transversal de viga de zapata continua, para momento positivo.
Usar la cuantía ρ= 0.004 (R. Morales)
7
As (-)
8
As temperatura
AsL 2
z
As(+)
Mut
Ast 2
qut2
mayor que Ld
Fig. 22. Sección transversal de viga de zapata continua, para momento negativo.
-Para el momento positivo el acero se calcula con:
MOMENTO EN LA DIRECCION TRANSVERSAL
Fig. 23. Aceros en la sección transversal de zapata continua.
As = Mu(+) / φfy(d – a/2)
a = As*fy/(0.85 fc bw)
Mut = qut* z2/2
-Para el momento negativo, se diseña como viga T. Se calcula el tamaño del
El acero mínimo en la losa de la zapata es As mín = (0.7√f’c / fy) * 100 * peralte
rectángulo a:
efectivo de la zapata, para cada metro de losa.
As = Mu(-)/φfy(d – a/2)
-La viga VCP-01 se diseña de manera similar.
a = Asfy/(0.85 fc b)
-Las vigas VCS-01 y VCS-02 se diseñan con el modelo de las
zapatas
conectadas, donde se producen momentos negativos altos debido a la zapata
-Si hf es mayor o igual que a (Eje neutro 1 y 2), usar:
excéntrica.
As = Mu(-)/φfy(d – a/2)
a = Asfy/(0.85 fc b)
-Si hf es menor que a (Eje meutro 3), se calcula el acero superponiendo por
separado la contribución de las alas y del nervio:
As1 = 0.85 fc*hf*(b-bw) / fy
(contribución de las alas)
Mu1 = φ As1 * fy* (d – hf / 2) (momento resistente por las alas)
Dado que
Mu(-) = φ (Mu1 + Mu2),
φ=0.90
Mu2 = [ Mu(-) / φ ] - Mu1 = momento resistente por el nervio
Se calcula el área de acero debido al nervio resolviendo estas dos ecuaciones:
a2 = As2*fy / (0.85 fc * bw)
As2 = Mu2 / fy (d – a2 /2)
Por tanto el acero negativo vale:
As(-) = As1 + As2
Hacer corte de varillas.
m y n valen:
m = máx (d, 12 db)
n = 36 db, es la longitud de traslape.
-Se calcula el momento en la dirección transversal, considerando la zapata como
viga en voladizo:
8
9
ANEXO
9
10
10