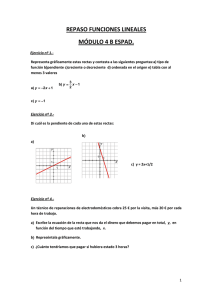
Ejercicio nº 1.Halla la expresión analítica de la función cuya gráfica es la siguiente:
Solución:
− Buscamos la ecuación de cada uno de los tramos de rectas que forman la función:
⎯ Para x < 3, la recta es y = −2.
⎯ Para 3 ≤ x ≤ 5, la recta pasa por (3, −2) y (5, 1):
m=
3
2
→
y −1=
3
( x − 5)
2
→
y=
3
15
x−
+1 →
2
2
y=
3
13
x−
2
2
⎯ Para x > 5, la recta es y = 1.
− Así pues, la expresión analítica de esa función es:
⎧−2
⎪3
13
⎪
y =⎨ x−
2
⎪2
⎪⎩1
si x < 3
si 3 ≤ x ≤ 5
si x > 5
Ejercicio nº 2.Un comercial tiene un sueldo fijo mensual de 800 €; además, recibe el 20% de las ventas
que haga. Busca la expresión analítica de esta función y represéntala tomando una
escala adecuada en cada eje.
Solución:
Llamamos x al dinero que se obtiene mensualmente por las ventas.
El comercial recibe el 20% de x = 0,2x.
Llamamos y al dinero que recibe mensualmente el comercial:
y = SUELDO FIJO + 0,2x → y = 800 + 0,2x
Hacemos una tabla de valores para representar la función:
x
500
1 000
1 500
2 000
y
900
1 000
1 100
1 200
Ejercicio nº 3.-
Representa gráficamente la función y =
1 2
x − 2 x + 4.
4
Solución:
Por ser una función cuadrática, su representación es una parábola.
− Hallamos su vértice:
x=
2
1
2⋅
4
=4
→
y=
1
⋅ 16 − 8 + 4 = 0
4
→ V ( 4, 0 )
− Puntos de corte con los ejes:
⎯ Con el eje X
→
x=
⎯ Con eje Y
→
y =0
→
1 2
x − 2x + 4 = 0
4
8 ± 64 − 64 8
= =4
2
2
→
x=0
→
y=4
( 4, 0 ) ,
→
→
→
x 2 − 8 x + 16 = 0
→
que coincide, lógicamente, con el vértice.
(0, 4)
− Puntos próximos al vértice:
x
1
2
3
6
8
y
9
4
1
1
4
1
4
Ejercicio nº 4.Relaciona cada una de las siguientes expresiones con su gráfica correspondiente:
a) y = −x2 − 3x
b) y = (x − 3)2
c) y = −2 − 3x2
d) y =
1 2
x − x −1
3
Solución:
a) → I
b) → IV
c) → II
d) → III
Ejercicio nº 5.Completa las expresiones de estas dos parábolas:
a) y = x 2 +
b) y =
x+
x 2 + 4x
Solución:
a) Punto de corte con el eje Y: (0, 6) → c = 6
V ( −3, − 3 )
→
−b
⎫
= −3 ⎪
2a
⎬ →
a = 1⎪⎭
b=6
La ecuación de la parábola es: y = x2+ 6x + 6.
b) V ( 2, 4 )
→
−b
⎫
= 2⎪
2a
⎬
b = 4 ⎪⎭
→
− 4 = 4a
→
a = −1
La ecuación de la parábola es: y = −x2 + 4x.
Ejercicio nº 6.Representa la siguiente función:
si x < −2
⎧− 4
⎪1
⎪
y = ⎨ ( 4 x − 4 ) si −2 ≤ x < 1
⎪32
⎪⎩ x − 4
si x ≥ 1
Solución:
− El primer trozo es la recta constante y = −4 definida para x < − 2.
− Representamos la recta y =
x
−2
y
−4
1
(4x − 4)
3
si
− 2 ≤ x < 1:
0
−
4
3
− El último tramo es un trozo de la parábola y = x2 − 4 definida para x ≥ 1:
x
1
2
3
y
−3
0
5
Ejercicio nº 7.Asocia a cada gráfica una de las siguientes expresiones:
a) y = log7 x
b) y =
c) y =
x +1
2
1− x
⎛2⎞
d) y = ⎜ ⎟
⎝3⎠
x
Solución:
a) → III
b) → I
c) → IV
d) → II
Ejercicio nº 8.Representa gráficamente las siguientes funciones:
a) y = 2x + 3 − 1
b ) y = −1 +
2
x −5
Solución:
⎡ 3
⎞
a) Dominio de definición: ⎢ − , + ∞ ⎟
2
⎣
⎠
Tabla de valores:
3
2
−1
1
2
3
13
2
11
33
2
2x + 3
0
1
4
9
16
25
36
2x + 3
0
1
2
3
4
5
6
2x + 3 − 1
−1
0
1
2
3
4
5
x
−
b) Dominio de definición: \ − {5}
Calculamos algunos puntos próximos a x = 5:
x
4
4,5
4,9
5,1
5,5
6
y
−3
−5
−21
19
3
1
Otros puntos interesantes:
−95
x
−45
−5
−1,02 −1,04 −1,2
y
15
55
105
−0,8 −0,96 −0,98
Se observa que los valores de y son muy próximos a −1 cuando x crece o decrece
mucho. Las asíntotas son las rectas x = 5, y = −1.
Ejercicio nº 9.a) Pon en forma exponencial 40,5x y representa la función y = 40,5x.
b) Comprueba si pertenecen a la gráfica de y = log5 x los puntos (−1, 2), (5, 1),
⎛1
⎞
⎜ , − 1⎟ , ( 3, −2 ) y ( 25, 2 ) .
⎝5
⎠
Solución:
x
x
⎛ 1⎞
= ⎜ 4 2 ⎟ = 4 = 2x
⎝ ⎠
Representar la función y = 40,5x equivale a representar la función y = 2x.
(
a) 40,5 x = 40,5
)
x
( )
Hacemos una tabla de valores:
x
−4
−2
−1
0
1
2
3
4
y
1
16
1
4
1
2
1
2
4
8
16
b) El dominio de definición de y = log5 x es (0, +∞), luego el punto (−1, 2) no pertenece al
dominio por ser x = −1 < 0. El resto de puntos tienen abscisa positiva, luego pueden
pertenecer a la gráfica de la función:
( 5, 1)
51 = 5 ⎫
⎪
1
1 ⎬ Pertenecen a la gráfica.
⎛1
⎞
−1
−
→
−
=
→
=
,
1
1
log
5
5
⎜5
⎟
5
5 ⎪⎭
⎝
⎠
( 3,
→
1 = log 5 5
→
− 2 ) → −2 = log 5 3 → 5 −2 =
( 25, 2 )
1
1
=
≠3
5 2 25
No pertenece a la gráfica.
→ 2 = log 5 25 → 52 = 25 → Pertenece a la gráfica.
⎛1
⎞
Los puntos que pertenecen a la gráfica son: ( 5, 1) , ⎜ , − 1⎟ y
5
⎝
⎠
( 25, 2 ) .
Ejercicio nº 10.Expresa el lado de un cuadrado en función de su área. ¿Qué tipo de función obtienes?
¿Cuál es su dominio? Represéntala gráficamente.
Solución:
A → área del cuadrado ⎫
2
⎬A=l
l → lado del cuadrado ⎭
→
l= A
La función obtenida es una función radical.
Dominio de definición = (0, +∞)
Para representarla gráficamente, hacemos una tabla de valores:
A
1
4
9
25
I
1
2
3
5