264842

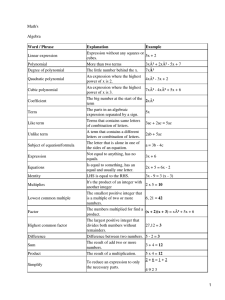
Hindawi Publishing Corporation
Journal of Applied Mathematics
Volume 2012, Article ID 264842, 18 pages
doi:10.1155/2012/264842
Research Article
Some Properties of the p, q-Fibonacci and
p, q-Lucas Polynomials
GwangYeon Lee1 and Mustafa Asci2
1
2
Department of Mathematics, Hanseo University, Seosan, Chungnam 356-706, Republic of Korea
Department of Mathematics, Science and Arts Faculty, Pamukkale University, Denizli, Turkey
Correspondence should be addressed to GwangYeon Lee, [email protected]
Received 23 May 2012; Revised 10 July 2012; Accepted 11 July 2012
Academic Editor: Shan Zhao
Copyright q 2012 G. Lee and M. Asci. This is an open access article distributed under the Creative
Commons Attribution License, which permits unrestricted use, distribution, and reproduction in
any medium, provided the original work is properly cited.
Riordan arrays are useful for solving the combinatorial sums by the help of generating functions.
Many theorems can be easily proved by Riordan arrays. In this paper we consider the Pascal matrix
and define a new generalization of Fibonacci polynomials called p, q-Fibonacci polynomials. We
obtain combinatorial identities and by using Riordan method we get factorizations of Pascal matrix
involving p, q-Fibonacci polynomials.
1. Introduction
Large classes of polynomials can be defined by Fibonacci-like recurrence relation and yield
Fibonacci numbers 1. Such polynomials, called the Fibonacci polynomials, were studied in
1883 by the Belgian Mathematician Eugene Charles Catalan and the German Mathematician
E. Jacobsthal. The polynomials fn x studied by Catalan are defined by the recurrence relation
fn x xfn−1 x fn−2 x,
1.1
where f1 x 1, f2 x x, and n ≥ 3. Notice that fn 1 Fn , the nth Fibonacci number. The
Fibonacci polynomials studied by Jacobsthal were defined by
Jn x Jn−1 x xJn−2 x,
1.2
where J1 x 1 J2 x and n ≥ 3. The Pell polynomials pn x are defined by
pn x 2xpn−1 x pn−2 x,
1.3
2
Journal of Applied Mathematics
where p0 x 0, p1 x 1 and n ≥ 2. The Lucas polynomials Ln x, originally studied in
1970 by Bicknell, are defined by
Ln x xLn−1 x Ln−2 x,
1.4
where L0 x 2, L1 x x, and n ≥ 2.
Horadam 2 introduced the polynomial sequence {wn x} defined recursively by
wn x pxwn−1 x qxwn−2 x,
n ≥ 2,
1.5
where
w0 x c0 ,
w1 x c1 xd ,
pxc2 xd ,
qx c3 xd
1.6
in which c0 , c1 , c2 , c3 are constants and d 0 or 1. Special cases of the wx with given initial
conditions are given in Table 1.
For a fixed n, Brawer and Pirovino 3 defined the n × n lower triangular Pascal as
matrix Pn pi,j i,j1,2,...,n
Pi,j
⎧
⎪
⎪
⎨ i−1
j −1
⎪
⎪
⎩0
if i ≥ j,
1.7
otherwise.
The Pascal matrices have many applications in probability, numerical analysis, surface
reconstruction, and combinatorics. In 4 the relationships between the Pascal matrix and
the Vandermonde, Frobenius, Stirling matrices are studied. Also in 4 other applications
in stability properties of numerical methods for solving ordinary differential equations are
shown. In 5–8 the binomial coefficients, fibonomial coefficients, Pascal matrix, and its
generalizations are studied. The authors in 9 factorized the Pascal matrix involving the
Fibonacci matrix.
Lee et al. 10 defined the n × n Fibonacci matrix as follows:
Fn fij Fi−j1
if i − j 1 ≥ 0,
0
if i − j 1 < 0.
1.8
Also in 10 factorizations and eigenvalues of Fibonacci and symmetric Fibonacci matrices
are studied. The inverse of this matrix is given as follows;
⎡
Fn−1
1
⎢−1
⎢
⎢−1
⎢
⎢
⎢
⎢0
⎢
⎢ ..
⎣ .
0
0 ···
0 ···
0 ···
.
−1 −1 1 . .
.. .. .. ..
. . . .
· · · 0 −1 −1
0 0
1 0
−1 1
⎤
0
0⎥
⎥
0⎥
⎥
.. ⎥
⎥.
.⎥
⎥
⎥
0⎦
1
1.9
Journal of Applied Mathematics
3
Table 1: Special cases of the wx with given initial conditions are given.
px
x
2x
1
3x
2x
qx
1
1
2x
−2
−1
w0 x 0, w1 x 1
Fibonacci Polynomial
Pell Polynomial
Jacobsthal Poly
Fermat Polynomial
Cheby. Poly. 2nd kind
w0 x 2, w1 x x
Lucas Polynomial
Pell-Lucas Polynomial
Jacobsthal-Lucas Poly.
Fermat-Lucas Polynomial
Cheby. Poly. first kind
The Riordan group was introduced by Shapiro et al. in 6 as follows.
n
Let R rij i,j≥0 be an infinite matrix with complex entries. Let ci t ∞
n≥0 rn,i t be the
generating function of the ith column of R. We call R a Riordan matrix if ci t gtfti ,
where
gt 1 g1 t g2 t2 g3 t3 · · · ,
ft t f2 t2 f3 t3 · · · .
1.10
In this case we write R gt, ft and we denote by R the set of Riordan matrices. Then
the set R is a group under matrix multiplication ∗, with the following properties:
R1 gt, ft ∗ ht, lt gthft, lft,
R2 I 1, t is the identity element,
R3 the inverse of R is given by R−1 1/gft, ft, where ft is the compositional
inverse of ft, that is, fft fft t,
R4 if a0 , a1 , a2 , . . .T is a column vector with the generating function At, then
multiplying R gt, ft on the right by this column vector yields a column
vector with the generating function Bt gtAft.
This group has many applications. Three of them are given in 6 such as Euler’s
problem of the King walk, binomial and inverse identities, and Bessel-Neumann expansion.
Riordan arrays are also useful for solving the combinatorial sums by the help of
generating functions. For example, in 11, Cheon, Kim, and Shapiro have many results
including a generalized Lucas polynomial sequences from Riordan array and combinatorial
interpretations for a pair of generalized Lucas polynomial sequences.
2. The p, q-Fibonacci and p, q-Lucas Polynomials with
Some Properties
In 12, the authors introduced the hx-Fibonacci polynomials, where hx is a polynomial
with real coefficients. The hx-Fibonacci polynomials {Fh,n x}∞
n0 are defined by the recurrence relation
Fh,n1 x hxFh,n x Fh,n−1 x,
n ≥ 1,
with initial conditions Fh,0 x 0, Fh,1 x 1.
In this paper, we introduce a generalization of the hx-Fibonacci polynomials.
2.1
4
Journal of Applied Mathematics
Definition 2.1. Let px and qx be polynomials with real coefficients. The p, q-Fibonacci
are defined by the recurrence relation
polynomials {Fp,q,n x}∞
n0
Fp,q,n1 x pxFp,q,n x qxFp,q,n−1 x,
n≥1
2.2
with the initial conditions Fp,q,0 x 0 and Fp,q,1 x 1.
For later use Fp,q,2 x px, Fp,q,3 x p2 x qx, Fp,q,4 x p3 x 2pxqx,
Fp,q,5 x p4 x 3p2 xqx q2 x · · · .
as the following definition.
Now, we introduce p, q-Lucas polynomials {Lp,q,n x}∞
n0
Definition 2.2. The p, q-Lucas polynomials {Lp,q,n x}∞
are defined by the recurrence
n0
relation
Lp,q,n x Fp,q,n1 x qxFp,q,n−1 x.
2.3
Also for later use Lp,q,0 x 2, Lp,q,1 x px, Lp,q,2 x p2 x 2qx, Lp,q,3 x p x 3pxqx, Lp,q,4 x p4 x 4p2 xqx 2q2 x · · · .
In 12, the authors defined hx-Lucas polynomials as follows:
3
Lh,n1 x hxLh,n x Lh,n−1 x,
n ≥ 1,
2.4
with initial conditions Lh,0 x 2, Lh,1 x hx. However, we defined p, q-Lucas
polynomials in the Definition 2.2 which is different from hx-Lucas polynomials. From the
Definition 2.2, for px 1 and qx 1, we obtain the usual Lucas numbers. And, for
px hx and qx 1, we obtain the hx-Lucas polynomials.
For the special cases of px and qx, we can get the polynomials given in Table 1.
The generating function gF t of the sequence {Fp,q,n x} is defined by
gF t ∞
Fp,q,n xtn .
2.5
n0
We know that the generating function gF t is a convergence formal series.
Theorem 2.3. Let gF t be the generating function of the p, q-Fibonacci polynomial sequence
Fp,q,n x. Then
gF t t
.
1 − pxt − qxt2
2.6
Journal of Applied Mathematics
5
Proof. Let gF t be the generating function of the p, q-Fibonacci polynomial sequence
Fp,q,n x, then
gF t ∞
Fp,q,n xtn
n0
Fp,q,1 xt Fp,q,2 xt2 ∞
Fp,q,n xtn
n3
t t2 px ∞
pxFp,q,n−1 x qxFp,q,n−2 x tn
n3
t t2 px ∞
pxFp,q,n−1 xtn n3
t t2 px t
∞
qxFp,q,n−2 xtn
n3
∞
pxFp,q,n−1 xtn−1 t2
n3
t t2 px tpx
∞
2.7
qxFp,q,n−2 xtn−2
n3
∞
∞
Fp,q,n xtn t2 qx Fp,q,n xtn
n2
t t2 px tpx
n1
∞
∞
Fp,q,n xtn − t t2 qx Fp,q,n xtn
n1
n1
t t2 px tpx gF t − t t2 qxgF t.
By taking gF t parenthesis we get
gF t t
.
1 − pxt − qxt2
2.8
The proof is completed.
Corollary 2.4. Let gL t be the generating function of the p, q-Lucas polynomial sequence Lp,q,n x.
Then
gL t 2 − pxt
.
1 − pxt − qxt2
2.9
The Binet formula is also very important in Fibonacci numbers theory. Now we can
get the Binet formula of p, q-Fibonacci polynomials. Let αx and βx be the roots of the
characteristic equation
t2 − pxt − qx 0
2.10
6
Journal of Applied Mathematics
of the recurrence relation 2.2. Then
αx px p2 x 4qx
2
βx ,
px −
p2 x 4qx
2
.
2.11
Note that αxβx px and αxβx −qx. Now we can give the Binet formula
for the p, q-Fibonacci and p, q-Lucas polynomials.
Theorem 2.5. For n ≥ 0
Fp,q,n x αn x − βn x
,
αx − βx
2.12
Lp,q,n x α x β x.
n
n
Proof. The theorem can be proved by mathematical induction on n.
Lemma 2.6. For n ≥ 1,
tn Fp,q,n xt qxFp,q,n−1 x.
2.13
Proof. From the characteristic equation of the p, q-Fibonacci polynomials we have
t2 pxt qx
Fp,q,2 xt qxFp,q,1 x.
2.14
By induction on n we get
tn1 tn t
Fp,q,n xt qxFp,q,n−1 x t
Fp,q,n xt2 qxtFp,q,n−1 x
Fp,q,n x pxt qx qxtFp,q,n−1 x
Fp,q,n xpx qxFp,q,n−1 x t qxFp,q,n x
2.15
Fp,q,n1 xt qxFp,q,n x.
Thus we have
tn Fp,q,n xt qxFp,q,n−1 x.
2.16
Journal of Applied Mathematics
7
Theorem 2.7. Let Lp,q,n x Fp,q,n1 x qxFp,q,n−1 x. Then for n ≥ 3,
Lp,q,n x pxLp,q,n−1 x qxLp,q,n−2 x.
2.17
Proof. If n 3 then
Lp,q,3 p3 x 3pxqx
pxLp,q,2 x qxLp,q,1 x.
2.18
By induction on n we have
pxLp,q,n x qxLp,q,n−1 x px Fp,q,n1 x qxFp,q,n−1 x
qx Fp,q,n x qxFp,q,n−2 x
pxFp,q,n1 x pxqxFp,q,n−1 x
qxFp,q,n x q2 xFp,q,n−2 x
pxFp,q,n1 x qxFp,q,n x
qx pxFp,q,n−1 x qxFp,q,n−2 x
2.19
Fp,q,n2 x qxFp,q,n x
Lp,q,n1 x.
In 12, the author introduced the matrix Qh x that plays the role of the Q-matrix. The
Q-matrix is associated with the Fibonacci numbers and is defined as
1 1
Q
.
1 0
2.20
Actually, in 12, Nalli and Pentti defined the matrix Qh x as follows
Qh x hx 1
.
1 0
2.21
We now introduce the matrix Qp,q x which is a generalization of the Qh x.
Definition 2.8. Let Qp,q x denote the 2 × 2 matrix defined as
Qp,q x px qx
.
1
0
2.22
8
Journal of Applied Mathematics
Theorem 2.9. Let n ≥ 1. Then
n
Qp,q
x Fp,q,n1 x qxFp,q,n x
.
Fp,q,n x qxFp,q,n−1 x
2.23
Proof. We can prove the theorem by induction on n. The result holds for n 1. Suppose that
it holds for n m m ≥ 1. Then
m1
m
Qp,q
x Qp,q
x · Qp,q x
Fp,q,m1 x
Fp,q,m x
F
x
p,q,m2
Fp,q,m1 x
qxFp,q,m x
qxFp,q,m−1 x
qxFp,q,m1 x
qxFp,q,m x
px qx
1
0
2.24
which completes the proof.
Corollary 2.10. Let m, n ≥ 0. Then
Fp,q,mn1 x Fp,q,m1 xFp,q,n1 x qxFp,q,m xFp,q,n x.
2.25
If an integer a /
0 divides an integer b, we denote a | b.
Corollary 2.11. For k ≥ 1,
Fp,q,n x | Fp,q,kn x.
2.26
n
Corollary 2.12. The roots of characteristic equation of Qp,q
x are αn x and βn x.
Corollary 2.13. For n ≥ 1
Fp,q,n x n−1/2
n0
n − i n−2i
p xqi x.
i
2.27
The following identities of which originated from Koshy 1998 1 are a generalization
of Koshy’s results.
Theorem 2.14. For k ≥ 1, one has
⎧
j
k
⎪
⎪
⎪ Fp,q,nkj xp x Fp,q,j x − Fp,q,nkkj x Fp,q,k−j x −qx ,
⎪
n
⎨
pk x − Lp,q,k x 1
Fp,q,kij x k
k
⎪
Fp,q,nkj xp xFp,q,j x−Fp,q,nkkj xFp,q,j−k x −qx
⎪
i0
⎪
⎪
,
⎩
pk x − Lp,q,k x 1
j < k,
otherwise.
2.28
Journal of Applied Mathematics
9
Proof. We know that
αx − βx p2 x 4qx,
2.29
Lp,q,n x αn x βn x.
Since Fp,q,n x αn x − βn x/ p2 x 4qx, from Theorem 2.5, we have
n
Fp,q,kij x i0
n
αkij x − βkij x
i0
p2 x 4qx
1
n
n
α x αki x − βj x βki x
j
p2 x 4qx
i0
i0
1
βnkk x − 1
αnkk x − 1
αj x k
− βj x k
α x − 1
β x − 1
p2 x 4qx
1
p2 x 4qx
2.30
αnkkj x − αj x βnkkj x − βj x
−
αk x − 1
βk x − 1
.
Set 1/ p2 x 4qx Ax and
Cx Then we have
n
Fp,q,kij x k
j
Fp,q,k−j x −qx
k
Fp,q,j−k x −qx
if j < k,
2.31
otherwise.
Ax
− αk x βk x 1
αxβx
× αnkkj xβk x − αj xβk x − αnkkj x αj x − βnkkj xαk x
i0
αk xβj x βn x
Ax
pk x − Lp,q,k x 1
1
1
1
Fp,q,j x
− Fp,q,nkkj x
× Fp,q,nkj pk x
Ax
Ax
Ax
αk xβj x − αj xβk x
Fp,q,nkj xpk x Fp,q,j x − Fp,q,nkkj x Cx
pk x − Lp,q,k x 1
.
2.32
Thus the proof is completed.
10
Journal of Applied Mathematics
Theorem 2.15. For n ≥ 0 one has
n n
k0
k
pk xqn−k xFp,q,k x Fp,q,2n x.
2.33
Proof. By Theorem 2.5 we have
n n αk x − βk x
n k
n k
p xqn−k xFp,q,k x p xqn−k x
k
k
αx − βx
k0
k0
1
αx − βx
1
αx − βx
n n k
n−k
k
k
p xq x α x − β x
k
k0
n n k0
−
k
n n k0
k
pxαx qn−k x
k
k
pxβx q
n−k
x
n n 1
pxαx qx pxβx qx .
αx − βx
2.34
Since αx and βx are the solutions of the equation t2 − pxt − qx 0,
α2 x pxαx qx,
β2 x pxβx qx.
2.35
Thus we have
2 n 2 n
n α x − β x
n k
n−k
p xq xFp,q,k x k
αx − βx
k0
2.36
Fp,q,2n x.
The proof is completed.
Theorem 2.16. For n ≥ 0, one has
n n k
n−k
n k n p x −qx
−2qx Fp,q,2n−k x.
Fp,q,k x k
k
k0
k0
2.37
Journal of Applied Mathematics
11
Proof. By Theorem 2.5 we have
n n
k0
n n−k
n−k αk x − βk x
n k Fp,q,k x p x −qx
p x −qx
k
k
αx − βx
k0
k
1
αx − βx
1
αx − βx
n n
k0
k
n n k0
−
k n−k
pxαx −qx
k
n n k0
n−k k
α x − βk x
p x −qx
k
k
n−k
k pxβx −qx
n n 1
pxαx − qx pxβx − qx .
αx − βx
2.38
Since αx and βx are the solutions of the equation t2 − pxt − qx 0,
pxαx − qx α2 x − 2qx,
pxβx − qx β2 x − 2qx.
2.39
Thus we have
n n
2
α x − 2qx − β2 x − 2qx
n−k
Fp,q,k x pk x −qx
k
αx − βx
n n
k0
n n k0
k
k
−2qx Fp,q,2n−k x.
2.40
The proof is completed.
Corollary 2.17. For n ≥ 0 one has
n n n−k
p x−1k Lp,q,k x Lp,q,n x.
k
k0
Proof. Since px − αx −qx/αx and px − βx −qx/βx, we have
n n
k0
k
p
n−k
n n n−k
p x−1k αk x βk x
x−1 Lp,q,k x k
k0
k
n n n−k
p x−1k −αxk
k
k0
2.41
12
Journal of Applied Mathematics
n k
n n−k
p x−1k −βx
k
k0
n n
px − αx px − βx
qx n
qx n
−
−
αx
βx
n αn x βn x
−qx n
αxβx
Lp,q,n x.
2.42
Corollary 2.18. For n ≥ 0,
Fp,q,2n x Fp,q,n xLp,q,n x.
2.43
m
Fp,q,nm x − −qx Fp,q,n−m x Fp,q,m xLp,q,n x.
2.44
Corollary 2.19. For n ≥ m,
Proof. From the Binet formula of the p, q-Fibonacci and Lucas polynomials we have
m
Fp,q,nm x − −qx Fp,q,n−m x
m αn−m x − βn−m x
αnm x − βnm x − −qx
αx − βx
αx − βx
m
αnm x − βnm x − −qx
αn−m x − βn−m x
.
αx − βx
Since αxβx −qx then
m
Fp,q,nm x − −qx Fp,q,n−m x
m n−m
αnm x − βnm x − αxβx
α x − βn−m x
αx − βx
αnm x − βnm x − αn xβm x − αm xβn x
αx − βx
2.45
Journal of Applied Mathematics
m
α x − βm x − αn x βn x
αx − βx
13
αm x − βm x n
α x βn x
αx − βx
Fp,q,m xLp,q,n x.
2.46
Corollary 2.20. For n ≥ 0 one has
n n
k0
k
pk xqn−k xLp,q,k x Lp,q,2n x.
2.47
Theorem 2.21. For n ≥ 1, one has
2
Fp,q,n−1 xFp,q,n1 x − Fp,q,n
x −1n qn−1 x.
2.48
Proof. We will prove the theorem by mathematical induction on n. Since
2
Fp,q,0 xFp,q,1 x − Fp,q,1
x 0px − 12 0 − 1
−11 q0 x ,
2.49
the given statement is true when n 1.
Now, we assume that it is true for an arbitrary positive integer k, that is,
2
Fp,q,k−1 xFp,q,k1 x − Fp,q,k
x −1k qk−1 x.
2.50
Then
2
Fp,q,k xFp,q,k2 x − Fp,q,k1
x 1 Fp,q,k1 x − qxFp,q,k−1 x
px
2
× pxFp,q,k1 x qxFp,q,k x − Fp,q,k1
x
1 2
qxFp,q,k1 xFp,q,k x pxFp,q,k1
x
px
−q2 xFp,q,k xFp,q,k−1 x − pxqxFp,q,k−1 xFp,q,k1 x
2
− Fp,q,k1
x
14
Journal of Applied Mathematics
qx
q2 x
2
Fp,q,k1 xFp,q,k xFp,q,k1
Fp,q,k xFp,q,k−1 x
x−
px
px
2
− qxFp,q,k−1 xFp,q,k1 x − Fp,q,k1
x
qx
q2 x
Fp,q,k1 xFp,q,k x −
Fp,q,k xFp,q,k−1 x
px
px
− qxFp,q,k−1 xFp,q,k1 x.
2.51
By assumption we have
2
Fp,q,k xFp,q,k2 x − Fp,q,k1
x qx
Fp,q,k1 xFp,q,k x
px
−
q2 x
2
Fp,q,k xFp,q,k−1 x − qx −1k qk x Fp,q,k
x
px
qx
q2 x
Fp,q,k1 xFp,q,k x −
Fp,q,k xFp,q,k−1 x
px
px
2
− qxFp,q,k
x − −1k qk x
qx
Fp,q,k1 xFp,q,k x − qxFp,q,k x
px
qx
Fp,q,k−1 x Fp,q,k x −1k1 qk x
×
px
qx
Fp,q,k1 xFp,q,k x
px
− qxFp,q,k x
1
Fp,q,k1 x −1k1 qk x
px
−1k1 qk x.
2.52
Thus the formula works for n k 1. So by mathematical induction, the statement is true for
every integer n ≥ 1.
3. The Infinite p, q-Fibonacci and p, q-Lucas Polynomial Matrix
In this section we define a new matrix which we call p, q-Fibonacci polynomials matrix. The
infinite p, q-Fibonacci polynomials matrix
Fx Fp,q,i,j x
3.1
Journal of Applied Mathematics
15
is defined as follows:
⎡
1
0
0
0
⎤
⎢
. ⎥
⎢
px
1
0 0 .. ⎥
⎢
⎥
⎢
.. ⎥
Fx ⎢
⎥
2
⎢ p x qx
px
1 0 . ⎥
⎢ 3
⎥
⎣p x 2pxqx p2 x qx px 1
⎦
···
···
gFx t, fFx t .
3.2
The matrix Fx is an element of the set of Riordan matrices. Since the first column of Fx is
1, px, p2 x qx, p3 x 2pxqx, p4 x 3p2 xqx q2 x, . . .
T
,
3.3
n
2
then it is obvious that gFx t ∞
n0 Fp,q,n xt 1/1 − pxt − qxt . In the matrix Fx
each entry has a rule with the upper two rows, that is,
Fp,q,n1,j x pxFp,q,n,j x qxFp,q,n−1,j x.
3.4
Fx gFx t, fFx t
1
,
t
;
1 − pxt − qxt2
3.5
Then fF t t, that is,
hence Fx is in R.
Similarly we can define the p, q-Lucas polynomials matrix. The infinite p, q-Lucas
polynomials matrix
Lx Lp,q,i,j x
3.6
Lx gLx t, fLx t
2 − pxt
,
t
.
1 − pxt − qxt2
3.7
can be written as
In this section we give two factorizations of Pascal Matrix involving the p, qFibonacci polynomial matrix. For these factorizations we need to define two matrices. Firstly
we define an infinite matrix Mx mij x as follows:
mij x i−1
i−2
i−3
− px
− qx
.
j −1
j −1
j −1
3.8
16
Journal of Applied Mathematics
We have the infinite matrix Mx as follows:
⎡
⎤
0
⎢
0 ⎥
⎢
⎥
⎢
⎥
.
⎢
⎥
Mx ⎢1 − px − qx
2 − px
1
0 ..⎥.
⎢
⎥
⎣1 − px − qx 3 − 2px − qx 3 − px 1 ⎦
···
1
1 − px
0
1
0
0
3.9
Now we can give the first factorization of the infinite Pascal matrix via the infinite
p, q-Fibonacci polynomial matrix and the infinite matrix Mx defined in 3.8 by the
following theorem.
Theorem 3.1. Let Mx be the infinite matrix as in 3.8 and Fx be the infinite p, q-Fibonacci
polynomial matrix; then,
P x Fx ∗ Mx,
3.10
where P is the usual Pascal matrix.
Proof. From the definitions of the infinite Pascal matrix and the infinite p, q-Fibonacci
polynomial matrix we have the following Riordan representations:
P
t
1
,
,
1−t 1−t
Fx 1
,
t
.
1 − pxt − qxt2
3.11
Now we can find the Riordan representation of the infinite matrix
Mx gMx t, fMx t
3.12
as follows:
⎡
⎤
0
⎢
0 ⎥
⎢
⎥
⎢
..⎥
⎥
Mx ⎢
⎢1 − px − qx
2 − px
1
0 .⎥.
⎢
⎥
⎣1 − px − qx 3 − 2px − qx 3 − px 1 ⎦
···
1
1 − px
0
1
0
0
3.13
From the first column of the matrix Mx we obtain
gMx t 1 − pxt − qxt2
.
1−t
3.14
Journal of Applied Mathematics
17
From the rule of the matrix Mx, fMx t t/1 − t. Thus
Mx 1 − pxt − qxt2 t
,
1−t
1−t
3.15
.
Finally by the Riordan representations of the matrices Fx and Mx we complete the proof.
Now we define the n × n matrix Rx rij x as follows:
rij x i−1
i−1
i−1
− px
− qx
.
j −1
j
j 1
3.16
We have the infinite matrix Rx as follows.
⎤
0
⎢
0 ⎥
⎥
⎢
⎢
..⎥
⎥
Rx ⎢
⎢ 1 − 2px − qx
2 − px
1
0 .⎥.
⎥
⎢
⎣1 − 3px − 3qx 3 − 3px − qx 3 − px 1 ⎦
···
⎡
1
1 − px
0
1
0
0
3.17
Now we can give second factorization of Pascal matrix via the infinite p, q-Fibonacci
polynomial matrix by the following corollary.
Corollary 3.2. Let Rx be the matrix as in 3.16. Then
P Rx ∗ Fx.
3.18
We can find the inverses of the matrices by using the Riordan representations of the
matrices easily.
Corollary 3.3. One has
F−1 x 1 − pxt − qxt2 , t
−1
M x t
1t
,
1 2 − px t − 1 − px − qx t2 1 t
1 − pxt − qxt2
−1
,t .
L 2 − pxt
3.19
Acknowledgment
The authors would like to thank the referees for helpful comments and pointing out some
typographical errors.
18
Journal of Applied Mathematics
References
1 T. Koshy, Fibonacci and Lucas Numbers with Applications, Toronto, New York, NY, USA, 2001.
2 A. F. Horadam, “Extension of a synthesis for a class of polynomial sequences,” Fibonacci Quarterly,
vol. 34, no. 1, pp. 68–74, 1996.
3 R. Brawer and M. Pirovino, “The linear algebra of the pascal matrix,” Linear Algebra and Its
Applications, vol. 174, pp. 13–23, 1992.
4 M. Bayat and H. Teimoori, “The linear algebra of the generalized Pascal functional matrix,” Linear
Algebra and Its Applications, vol. 295, no. 1–3, pp. 81–89, 1999.
5 G. S. Call and D. J. Velleman, “Pascal’s matrices,” American Mathematical Monthly, vol. 100, pp. 372–
376, 1993.
6 L. W. Shapiro, S. Getu, W. J. Woan, and L. C. Woodson, “The Riordan group,” Discrete Applied
Mathematics, vol. 34, no. 1–3, pp. 229–239, 1991.
7 J. Seibert and P. Trojovsky, “On certain identities for the Fibonomial coeffcients,” Tatra Mountains
Mathematical Publications, vol. 32, pp. 119–127, 2005.
8 Z. Zhizheng, “The linear algebra of the generalized Pascal matrix,” Linear Algebra and Its Applications,
vol. 250, pp. 51–60, 1997.
9 Z. Zhang and X. Wang, “A factorization of the symmetric Pascal matrix involving the Fibonacci
matrix,” Discrete Applied Mathematics, vol. 155, no. 17, pp. 2371–2376, 2007.
10 G. Y. Lee, J. S. Kim, and S. G. Lee, “Factorizations and eigenvalues of Fibonacci and symmetric
Fibonacci matrices,” Fibonacci Quarterly, vol. 40, no. 3, pp. 203–211, 2002.
11 G. S. Cheon, H. Kim, and L. W. Shapiro, “A generalization of Lucas polynomial sequence,” Discrete
Applied Mathematics, vol. 157, no. 5, pp. 920–927, 2009.
12 A. Nalli and P. Haukkanen, “On generalized Fibonacci and Lucas polynomials,” Chaos, Solitons and
Fractals, vol. 42, no. 5, pp. 3179–3186, 2009.
Advances in
Operations Research
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Advances in
Decision Sciences
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Mathematical Problems
in Engineering
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Journal of
Algebra
Hindawi Publishing Corporation
http://www.hindawi.com
Probability and Statistics
Volume 2014
The Scientific
World Journal
Hindawi Publishing Corporation
http://www.hindawi.com
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
International Journal of
Differential Equations
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Volume 2014
Submit your manuscripts at
http://www.hindawi.com
International Journal of
Advances in
Combinatorics
Hindawi Publishing Corporation
http://www.hindawi.com
Mathematical Physics
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Journal of
Complex Analysis
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
International
Journal of
Mathematics and
Mathematical
Sciences
Journal of
Hindawi Publishing Corporation
http://www.hindawi.com
Stochastic Analysis
Abstract and
Applied Analysis
Hindawi Publishing Corporation
http://www.hindawi.com
Hindawi Publishing Corporation
http://www.hindawi.com
International Journal of
Mathematics
Volume 2014
Volume 2014
Discrete Dynamics in
Nature and Society
Volume 2014
Volume 2014
Journal of
Journal of
Discrete Mathematics
Journal of
Volume 2014
Hindawi Publishing Corporation
http://www.hindawi.com
Applied Mathematics
Journal of
Function Spaces
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Optimization
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014
Hindawi Publishing Corporation
http://www.hindawi.com
Volume 2014