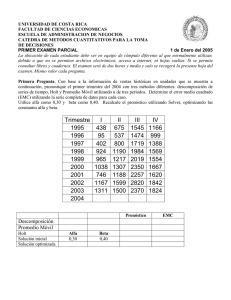
FACULTAD DE CIENCIAS DE LA INGENIERÍA Y APLICADAS CARRERA DE INGENIERÍA EN ELECTRICIDAD TEMA: TRABAJO EN CLASE EJERCICIOS DE OPTIMIZACIÓN CON PROGRAMACIÓN NO LINEAL GRUPO 1 Integrantes: Francis Andrés Acosta Melo Alex Dario Lata Gualancañay Cesar Agustin Tasinchana Casa Curso: Sexto Paralelo: “B” Asignatura: Sistemas de Ingeniería Año: 2021 – 2021 2 Tema: Optimización con programación no lineal. Objetivo General Formular un modelo de programación no lineal mediante la identificación de problemas reales que puedan resolverse con este tipo de modelo. Objetivos específicos ● Entender el modelo de programación no lineal entero y establecer el problema de optimización (variables, función objetivo y restricciones) ● Resolver el modelo en el lenguaje de programación Matlab y analizar sus resultados. ● Establecer un formato informe de presentación de los resultados, el cual incluya, tema, objetivos, procedimiento, resultados, análisis de resultados y conclusiones. 2. Actividades: Teniendo en cuenta la importancia de formular un modelo de programación no lineal mediante la identificación de problemas reales que puedan resolverse con este tipo de modelo, el siguiente ejercicio deberá resolverlo siguiendo las siguientes fases: Problema: Una compañía petrolífera debe determinar cuántos barriles de petróleo hay que extraer en los próximos dos años. Si la compañía extrae x1 millones de barriles durante un año, se podrá vender cada barril a 30 − x1 euros. Si extrae x2 millones de barriles durante el segundo año, se podrá vender cada barril a 35 − x2 euros. El costo para extraer x1 millones de barriles en el primer año es de x12 millones de euros y el costo para extraer x2 millones de barriles durante el segundo año es de 2x22 millones de euros. Se puede obtener como máximo un total de 20 millones de barriles de petróleo, y se puede gastar como máximo 250 millones de euros en la extracción. Formular el problema de optimización no lineal para ayudar a la empresa a maximizar sus ganancias para los próximos dos años. Desarrollo: Resolución ● Las variables de decisión del problema son: x1 : millones de barriles extraídos durante el primer año x2 : millones de barriles extraídos durante el segundo año ● Función objetivo: El objetivo es maximizar los ingresos 3 Restricciones del problema: - Gastar como maximo 250 euros en la extracción, - Obtener como máximo 20 millones de barriles de petróleo ● Restricciones: Por lo tanto: Resolución En Matlab 4 Función 5 Restricciones Resultados 6 Explicación: Para maximizar tenemos que x1 : millones de barriles extraídos durante el primer año debe ser 7.5 millones de barriles para el primer año y x2 : millones de barriles extraídos durante el segundo año debe ser 5.83 millones de barriles para el segundo año con un máximo de 214.5833 millones de euros. Análisis: En el respectivo ejercicio se pretende determinar cuántos barriles de petróleo hay que extraer y a su vez maximizar las ganancias para los próximos dos años, a través de una función objetivo que presenta un comportamiento no lineal y de igual forma su primera restricción es de forma no lineal. Conclusiones: ● Este problema es un problema no lineal con restricciones de desigualdad y a través de eso establecimos nuestras variables, función objetivo y respectivas restricciones para poner obtener la resolución en el programa. ● A través del software Matlab se llega a determinar que se necesita de 7.5 millones de barriles de petróleo durante el primer año y 5.83 millones de barriles de petróleo durante el segundo año para maximizar las ganancias, con una función objetiva que toma un valor de 214.5833. ● Los resultados se presentan en un informe acorde a lo solicitado, también se utiliza adecuadamente el programa Matlab para la resolución del problema de programación no lineal en donde se logró obtener sus respectivos pasos y resultado.