Teorema de Muestreo de Nyquist

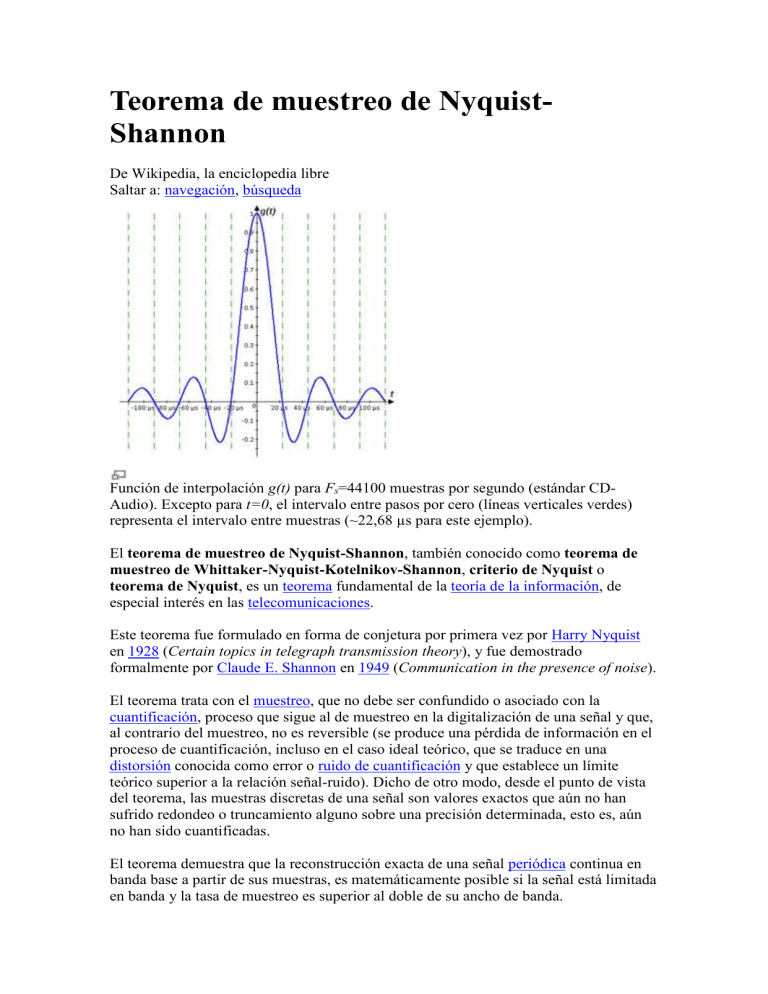
Teorema de muestreo de NyquistShannon
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
Función de interpolación g(t) para Fs=44100 muestras por segundo (estándar CDAudio). Excepto para t=0, el intervalo entre pasos por cero (líneas verticales verdes)
representa el intervalo entre muestras (~22,68 µs para este ejemplo).
El teorema de muestreo de Nyquist-Shannon, también conocido como teorema de
muestreo de Whittaker-Nyquist-Kotelnikov-Shannon, criterio de Nyquist o
teorema de Nyquist, es un teorema fundamental de la teoría de la información, de
especial interés en las telecomunicaciones.
Este teorema fue formulado en forma de conjetura por primera vez por Harry Nyquist
en 1928 (Certain topics in telegraph transmission theory), y fue demostrado
formalmente por Claude E. Shannon en 1949 (Communication in the presence of noise).
El teorema trata con el muestreo, que no debe ser confundido o asociado con la
cuantificación, proceso que sigue al de muestreo en la digitalización de una señal y que,
al contrario del muestreo, no es reversible (se produce una pérdida de información en el
proceso de cuantificación, incluso en el caso ideal teórico, que se traduce en una
distorsión conocida como error o ruido de cuantificación y que establece un límite
teórico superior a la relación señal-ruido). Dicho de otro modo, desde el punto de vista
del teorema, las muestras discretas de una señal son valores exactos que aún no han
sufrido redondeo o truncamiento alguno sobre una precisión determinada, esto es, aún
no han sido cuantificadas.
El teorema demuestra que la reconstrucción exacta de una señal periódica continua en
banda base a partir de sus muestras, es matemáticamente posible si la señal está limitada
en banda y la tasa de muestreo es superior al doble de su ancho de banda.
Dicho de otro modo, la información completa de la señal analógica original que cumple
el criterio anterior está descrita por la serie total de muestras que resultaron del proceso
de muestreo. No hay nada, por tanto, de la evolución de la señal entre muestras que no
esté perfectamente definido por la serie total de muestras.
Si la frecuencia más alta contenida en una señal analógica
es
y la
señal se muestrea a una tasa
, entonces
se puede recuperar
totalmente a partir de sus muestras mediante la siguiente función de interpolación:
Ejemplo de reconstrucción de una señal de 14,7 kHz (línea gris discontinua) con sólo
cinco muestras. Cada ciclo se compone de sólo 3 muestras a 44100 muestras por
segundo. La reconstrucción teórica resulta de la suma ponderada de la función de
interpolación g(t) y sus versiones correspondientes desplazadas en el tiempo g(t-nT) con
, donde los coeficientes de ponderación son las muestras x(n). En esta
imagen cada función de interpolación está representada con un color (en total, cinco) y
están ponderadas al valor de su correspondiente muestra (el máximo de cada función
pasa por un punto azul que representa la muestra).
Así,
donde
se puede expresar como:
son las muestras de
.
Hay que notar que el concepto de ancho de banda no necesariamente es sinónimo del
valor de la frecuencia más alta en la señal de interés. A las señales para las cuales esto sí
es cierto se les llama señales de banda base, y no todas las señales comparten tal
característica (por ejemplo, las ondas de radio en frecuencia modulada).
Si el criterio no es satisfecho, existirán frecuencias cuyo muestreo coincide con otras (el
llamado aliasing).
Contenido
[ocultar]





1 Errores de interpretación frecuentes en relación con el teorema y el proceso de
muestreo
o 1.1 Nuevos formatos y su relación con las interpretaciones erróneas
sobre el teorema y su utilidad práctica
2 Bibliografía
3 Referencias
4 Véase también
5 Enlaces externos
Errores de interpretación frecuentes en relación con el
teorema y el proceso de muestreo
Es un error frecuente y extendido creer que, una vez satisfechos los criterios del teorema
(criterios de Nyquist), la calidad de la reconstrucción de una señal en toda su banda (lo
que excluye el uso de técnicas de Noise Shaping para alterar selectivamente la
distorsión consecuencia del proceso de cuantificación en señales completamente
digitalizadas, esto es, muestreadas y cuantificadas) es función de la tasa de muestreo
empleada en el proceso de muestreo. Esto es totalmente falso desde la perspectiva
matemática del teorema y un error, una vez consideradas las limitaciones prácticas, en
el ámbito práctico de la física o la ingeniería.[1] El proceso de muestreo (que no debe ser
confundido con el de cuantificación) es, desde el punto de vista matemático
perfectamente reversible, esto es, su reconstrucción es exacta, no aproximada. Dicho de
otro modo, desde el punto de vista matemático al que se refiere el teorema de muestreo
de Nyquist-Shannon, la reconstrucción de una señal periódica con componentes de hasta
10 kHz es idéntica tanto si se obtiene de una tasa de muestreo de 25000 muestras por
segundo como de una de 50000 muestras por segundo. Matemáticamente, no aporta
nada incrementar la tasa de muestreo una vez que esta cumple el criterio de Nyquist: la
información necesaria para su reconstrucción total existe desde que la tasa cumple el
criterio. También son errores frecuentes y extendidos, relacionados directamente con lo
expuesto en este párrafo, creer que los puntos que resultan del proceso de muestreo se
unen en la reconstrucción mediante rectas (interpolación lineal) formando dientes de
sierra en las frecuencias representadas por pocas muestras o que existe un proceso de
cálculo que realiza la interpolación de manera predictiva. En resumen, el teorema de
muestreo demuestra que toda la información de una señal contenida en el intervalo
temporal entre dos muestras cualesquiera está descrita por la serie total de muestras
siempre que la señal registrada sea de naturaleza periódica (como lo es el sonido) y no
tenga componentes de frecuencia igual o superior a la mitad de la tasa de muestreo; no
es necesario inventar o predecir la evolución de la señal entre muestras.
En la práctica y dado que no existen los filtros analógicos pasa-bajo ideales, se debe
dejar un margen entre la frecuencia máxima que se desea registrar y la frecuencia de
Nyquist (frecuencia crítica) que resulta de la tasa de muestreo elegida (por ejemplo, para
CD-Audio la frecuencia máxima de los componentes a registrar y reproducir es de 20
kHz y la frecuencia crítica de la tasa de 44100 muestras por segundo empleada es de
22,05 kHz; un margen del 10% aproximadamente para esta aplicación). Pero este
margen es una necesidad que resulta de las limitaciones físicas de un filtro de
reconstrucción (o filtro antialiasing) real, y no una consideración que contemple (o deba
contemplar) el teorema, que pretende establecer el marco teórico (matemático) en el que
se deben fundamentar los profesionales que tratan con el procesamiento digital de
señales. En ocasiones se emplean técnicas de sobremuestreo para la reconstrucción de
una señal con objeto de aumentar artificialmente este margen y permitir el uso de filtros
de fase lineal (retardo de grupo constante) en la banda pasante y, en general, más
sencillos y económicos con pendientes de atenuación más suaves. En todo caso, tanto el
margen como el uso de técnicas de sobremuestreo son recursos de ingeniería para tratar
restricciones prácticas que en nada invalidan la demostración y el contenido del
teorema. El teorema es, de hecho, el marco analítico sobre el que las restricciones reales
(no ideales) deben ser estudiadas.
Nuevos formatos y su relación con las interpretaciones erróneas sobre el
teorema y su utilidad práctica
La aparición reciente de nuevos formatos de audio (denominados frecuentemente
formatos de alta resolución) para usuario final que contienen señales muestreadas con
tasas más elevadas a la empleada en CD-Audio han contribuido a extender la idea
errónea de que la calidad en la reconstrucción de una señal en toda su banda (hasta la
frecuencia crítica) es función directa de la tasa de muestreo empleada. En todo caso,
parece evidente que el potencial para registrar y reproducir ultrasonidos no forma parte
de los mensajes de mercadotecnia que pretenden promocionar estos en el mercado. Un
argumento que suele tener la forma general de "si los nuevos formatos de alta
resolución registran señales con tasas de muestreo más elevadas para la
reconstrucción de señales con el mismo ancho de banda es porque el teorema de
muestreo no aplica/no es válido/es erróneo y esta mayor tasa contribuye a una mejora
en la calidad".
Los nuevos formatos de audio que recientemente han aparecido (aunque con escaso
éxito comercial) que emplean Modulación por impulsos codificados (PCM) sin pérdida
por compresión con tasas de muestreo más altas a las empleadas en el CD-Audio,
(DVD-Audio, por ejemplo) para registrar y reproducir señales de idéntico ancho de
banda se justifican porque permiten el empleo de filtros de reconstrucción más
benignos, sencillos y económicos sacrificando un recurso cada vez más económico y de
menor trascendencia (la capacidad de almacenamiento, un recurso crítico en el pasado)
y porque, además, satisfacen simultáneamente las expectativas de un mercado como el
audiófilo, caracterizado por dogmas[2] entre los que se encuentra muy extendida la falsa
creencia de que esto representa una mejora en la calidad de la señal reconstruida (en
particular, de sus componentes de alta frecuencia). Este error es sólo una consecuencia
de una clara incomprensión del alcance y significado del teorema de muestreo y de
establecer comparaciones falaces como, por ejemplo, con la digitalización de imágenes
(donde no se realiza la reconstrucción de una señal periódica), etc.
La elevada tasa de muestreo de otro formato de audio de reciente aparición, el SACD o
Super Audio CD, es una consecuencia del uso de una tecnología denominada
comercialmente Direct Stream Digital™ (DSD) basada en un tipo de codificación
digital denominado Modulación por densidad de impulsos (PDM). Si bien la tasa de
muestreo es 64 veces la del CD-Audio, es necesario tener presente que se trata de una
cuantificación de 1 bit (en lugar de los 16 empleados en el CD-Audio) y basado en
técnicas de Noise Shaping (modelado de ruido). No es posible, por tanto, establecer
comparaciones superficiales con el PCM de CD-Audio ó DVD-Audio (ambos PCM), ya
que en este caso la relación señal-ruido no es constante respecto de la frecuencia[3] (en
CD-Audio el ruido de cuantificación es independiente de la frecuencia y sólo depende
de los intervalos de amplitud empleados en el proceso de cuantificación, es decir, es de
unos 98,09 dB[4] constantes para los 16 bits de este estándar CD-Audio en todo el
espectro útil). Un SACD puede registrar y reproducir señales con componentes de hasta
33 kHz con una relación señal-ruido equivalente al de un CD-Audio (aunque 33 kHz
está casi una octava por encima del máximo audible y, por tanto, una ventaja sobre el
CD-Audio de dudosa utilidad práctica) y mantener una relación señal-ruido de
aproximadamente 122 dB para el espectro audible (un potencial, el equivalente
aproximado a 20 bits, también de dudosa utilidad práctica como formato final de
usuario considerando los medios y entornos de reproducción de este formato).
Entre las ventajas objetivas de estos formatos (DVD-Audio y SACD) se encuentra el
potencial multicanal (registro de más de dos canales) y la capacidad para el empleo de
técnicas de protección de copia (algo de extraordinario interés para las compañías
discográficas y, probablemente, la auténtica justificación industrial y comercial de estos
productos junto con el evidente beneficio resultante de la sustitución de todos los
equipos reproductores y grabadores del mundo).
Se han publicado trabajos experimentales rigurosos[5] que concluyen que no existen
diferencias audibles entre los formatos denominados de alta resolución y el tradicional
soporte de audio digital CD-Audio (PCM 16 bits;44100 muestras/s).
Asimismo, también se han probado indistinguibles entre sí los formatos de alta
resolución SACD y DVD-Audio.[6] [7
Frecuencia de muestreo
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
Escuche este artículo
(info)
Esta narración de audio fue creada a partir de una versión específica de este artículo y no refleja las posibles ediciones subsecuentes.
Más artículos grabados
¿Problemas al reproducir este archivo?
Vea Ayuda:Multimedia.
Señal original y muestreo de la misma.
La tasa o frecuencia de muestreo es el número de muestras por unidad de tiempo que
se toman de una señal continua para producir una señal discreta, durante el proceso
necesario para convertirla de analógica en digital. Como todas las frecuencias,
generalmente se expresa en hercios (Hz, ciclos por segundo) o múltiplos suyos, como el
kilohercio (kHz), aunque pueden utilizarse otras magnitudes.
Contenido
[ocultar]










1 Teorema de Nyquist
2 Frecuencias de muestreo para audio y vídeo
o 2.1 Vídeo
3 Efecto aliasing
4 Filtro antialiasing
5 Sobremuestreo
6 Modificación de la frecuencia de muestreo
7 Bibliografía
8 Véase también
9 Referencias
10 Enlaces externos
Teorema de Nyquist
Artículo principal: Teorema de muestreo de Nyquist-Shannon
Según el teorema de muestreo de Nyquist-Shannon, para poder replicar con exactitud
(es decir, siendo matemáticamente reversible en su totalidad) la forma de una onda es
necesario que la frecuencia de muestreo sea superior al doble de la máxima frecuencia a
muestrear.
Es un error frecuente y extendido creer que una misma señal muestreada con una tasa
elevada se reconstruye mejor que una muestreada con una tasa inferior.[1] Esto es falso
(siempre que la tasas empleadas cumplan el criterio de Nyquist, naturalmente). El
proceso de muestreo (que no debe ser confundido con el de cuantificación) es, desde el
punto de vista matemático perfectamente reversible, esto es, su reconstrucción es
exacta, no aproximada. Dicho de otro modo, desde el punto de vista matemático al que
se refiere el teorema de muestreo de Nyquist-Shannon, la reconstrucción de una señal de
10 kHz es idéntica tanto si se obtiene de una tasa de muestreo de 25000 muestras por
segundo como de una de 50000 muestras por segundo. No aporta nada incrementar la
tasa de muestreo una vez que ésta cumple el criterio de Nyquist. También son errores
frecuentes y extendidos, relacionados con lo expuesto en este párrafo, creer que los
puntos que resultan del proceso de muestreo se unen en la reconstrucción mediante
rectas formando dientes de sierra o que existe un proceso de cálculo que realiza la
interpolación de manera simulada. En resumen, el teorema de muestreo demuestra que
toda la información de una señal contenida en el intervalo temporal entre dos muestras
cualesquiera está descrita por la serie total de muestras siempre que la señal registrada
sea de naturaleza periódica (como lo es el sonido) y no tenga componentes de
frecuencia igual o superior a la mitad de la tasa de muestreo; no es necesario inventar la
evolución de la señal entre muestras.
En la práctica y dado que no existen los filtros analógicos pasa-bajo ideales, se debe
dejar un margen entre la frecuencia máxima que se desea registrar y la frecuencia de
Nyquist (frecuencia crítica) que resulta de la tasa de muestreo elegida (por ejemplo, para
CD-Audio la frecuencia máxima de los componentes a registrar y reproducir es de 20
kHz y la frecuencia crítica de la tasa de 44100 muestras por segundo empleada es de
22,05 kHz; un margen del 10% aproximadamente para esta aplicación). Pero este
margen es una necesidad que resulta de las limitaciones físicas de un filtro de
reconstrucción (o filtro antialiasing) real, y no una consideración que contemple (o deba
contemplar) el teorema. Con frecuencia en los conversores modernos de CD-Audio,
para la reconstrucción de una señal se emplean técnicas de sobremuestreo con objeto de
aumentar este margen y permitir el uso de filtros de fase lineal (retardo de grupo nulo)
en la banda pasante y, en general, más sencillos y económicos con pendientes de
atenuación más suaves.
Los nuevos formatos de audio que recientemente han aparecido (aunque con escaso
éxito comercial) que emplean PCM sin pérdida por compresión con tasas de muestreo
más altas a las empleadas en el CD-Audio, (DVD-Audio, por ejemplo) para registrar y
reproducir señales de idéntico ancho de banda se justifican porque permiten el empleo
de filtros de reconstrucción más benignos, sencillos y económicos sacrificando un
recurso cada vez más económico y de menor trascendencia (la capacidad de
almacenamiento, un recurso crítico en el pasado) y porque, además, satisfacen
simultáneamente las espectativas de un mercado como el audiófilo, caracterizado por
dogmas[2] entre los que se encuentra muy extendida la falsa creencia de que esto
representa una mejora en la calidad de la señal reconstruida (en particular, de sus
componentes de alta frecuencia). Este error es sólo una consecuencia de una clara
incomprensión de las consecuencias del teorema de muestreo y de establecer
comparaciones falaces como, por ejemplo, con la digitalización de imágenes (donde no
se realiza una reconstrucción de una señal periódica), etc.
La alta tasa de muestreo de otro formato de audio de reciente aparición, el SACD o
Super Audio CD, es una consecuencia del uso de una tecnología denominada
modulación Sigma-Delta (Direct Stream Digital). Si bien la tasa de muestreo es 64
veces la del CD-Audio, es necesario tener presente que se trata de una cuantificación de
1 bit (en lugar de los 16 empleados en el CD-Audio) y basado en técnicas de Noise
Shaping (modelado de ruido). No es posible, por tanto, establecer comparaciones
superficiales con el PCM de CD-Audio, ya que en este caso la relación señal-ruido no
es constante respecto de la frecuencia (en CD-Audio el ruido de cuantificación es
independiente de la frecuencia y sólo depende de los intervalos de amplitud empleados
en el proceso de cuantificación, es decir, de unos 98,09 dB constantes para los 16 bits de
este estándar CD-Audio en todo el espectro útil). Un SACD puede registrar y reproducir
señales con componentes de hasta 33 kHz con una relación señal-ruido equivalente al de
un CD-Audio (aunque 33 kHz está casi una octava por encima del máximo audible y,
por tanto, una ventaja sobre el CD-Audio de dudosa utilidad) y mantener una relación
señal-ruido de aproximadamente 122 dB para el espectro audible (un potencial, el
equivalente aproximado a 20 bits,[3] también de dudosa utilidad práctica como formato
final de usuario). Entre las ventajas objetivas de estos formatos recientes (DVD-Audio y
SACD) se encuentra el potencial multicanal (registro de más de dos canales) y la
capacidad para el empleo de técnicas de protección de copia (algo de extraordinario
interés para las compañías discográficas). Ninguna prueba doble-ciego realizada en
condiciones controladas ha probado que existan diferencias audibles entre estos
formatos denominados de "alta resolución".[4] [5]
Frecuencias de muestreo para audio y vídeo
En audio, la máxima audiofrecuencia perceptible para el oído humano joven y sano está
en torno a los 20 kHz, por lo que teóricamente una frecuencia de muestreo de 40000
sería suficiente para su muestreo; no obstante, el estándar introducido por el CD, se
estableció en 44100 muestras por segundo. La frecuencia de muestreo ligeramente
superior permite compensar los filtros utilizados durante la conversión analógicadigital.
Hay que tener en cuenta que no todas las fuentes sonoras se aproximan a los 20 kHz que
corresponden a esta frecuencia máxima; la mayoría de los sonidos está muy por debajo
de ésta. Por ejemplo, si se va a grabar la voz de una soprano, la máxima frecuencia que
la cantante será capaz de producir no tendrá armónicos de nivel significativo en la
última octava (de 10 a 20 kHz), con lo que utilizar una frecuencia de muestreo de 44100
muestras por segundo sería innecesario (se estaría empleando una capacidad de
almacenamiento extra que se podría economizar).
Frecuencias de muestreo típicas
8000 muestras/s
22050 muestras/s
32000 muestras/s
44100 muestras/s
47250 muestras/s
48000 muestras/s
50000 muestras/s
96000 ó 192400
muestras/s
2 822 400
muestras/s
Para audio
Teléfonos, adecuado para la voz humana pero no para la reproducción musical.
En la práctica permite reproducir señales con componentes de hasta 3,5 kHz.
Radio En la práctica permite reproducir señales con componentes de hasta 10
kHz.
Vídeo digital en formato miniDV.
CD, En la práctica permite reproducir señales con componentes de hasta 20
kHz. También común en audio en formatos MPEG-1 (VCD, SVCD, MP3).
Formato PCM de Nippon Columbia (Denon). En la práctica permite reproducir
señales con componentes de hasta 22 kHz.
Sonido digital utilizado en la televisión digital, DVD, formato de películas,
audio profesional y sistemas DAT.
Primeros sistemas de grabación de audio digital de finales de los 70 de las
empresas 3M y Soundstream.
HD DVD, audio de alta definición para DVD y BD-ROM (Blu-ray Disc).
SACD, Direct Stream Digital, desarrollado por Sony y Philips.
Para vídeo
Vídeo PAL.
50 Hz
Vídeo NTSC.
60 Hz
El estándar del CD-Audio está fijado en 44100 muestras por segundo, pero esto no
significa que esa sea la frecuencia que utilizan todos los equipos. Los sistemas
domésticos de baja calidad pueden utilizar tasas de 22050 muestras por segundo o de
11025 muestras por segundo (limitando así la frecuencia de los componentes que
pueden formar la señal). Además, las tarjetas de sonido de los equipos informáticos
utilizan frecuencias por encima o por debajo de este estándar, muchas veces
seleccionándolas en función de las necesidades concretas (sobre todo, en aplicaciones
de audio profesional).
Algunas frecuencias de muestreo típicas en sistemas de audio y vídeo aparecen
resumidas en tablas, más arriba.
Vídeo
En vídeo digital, la frecuencia entre fotogramas es utilizada para definir la frecuencia de
muestreo de la imagen en lugar del ritmo de cambios de los píxeles individuales. La
frecuencia de muestreo de la imagen es el ritmo de repetición del período de integración
del CCD. Dado que el periodo de integración puede ser significativamente más corto
que el tiempo entre repeticiones, la frecuencia de muestreo puede diferir de la inversa
del tiempo de muestreo.
Efecto aliasing
Si se utiliza una frecuencia menor a la establecida por el teorema de Nyquist, se produce
una distorsión conocida como aliasing; algunos autores traducen este término como
solapamiento. El aliasing impide recuperar correctamente la señal cuando las muestras
de ésta se obtienen a intervalos de tiempo demasiado largos. La forma de la onda
recuperada presenta pendientes muy abruptas.
Filtro antialiasing
Para eliminar el aliasing, los sistemas de digitalización incluyen filtros paso bajo, que
eliminan todas las frecuencias que sobrepasan la frecuencia crítica (la que corresponde a
la mitad de la frecuencia de muestreo elegida) en la señal de entrada. Es decir, todas las
frecuencias que queden por encima de la frecuencia máxima a muestrear seleccionada,
son eliminadas. El filtro paso bajo para este uso concreto recibe el nombre de filtro
antialiasing. Sin embargo, abusar de los filtros antialiasing, puede producir el mismo
efecto que se quiere evitar. Cuando se conectan varios filtros en cascada (en el
muestreo, en la conversión digital-analógica, etc.), un filtrado excesivo de una onda que
ya cumplía con el requisito para su correcta transformación A/D puede degenerar y
provocar que la onda final presente una pendiente marcada. Por esta desventaja del filtro
antialiasing se ha generalizado la técnica conocida como sobremuestreo de la señal.
Sobremuestreo
Para evitar las caídas abruptas se utiliza la técnica conocida como sobremuestreo
(oversampling), que permite reconstruir, tras la conversión D/A, una señal de pendiente
suave.
Un sobremuestreo consiste en aplicar un filtro digital que actúa sobre el tiempo
(dominio de frecuencia), cambiando de lugar las muestras, de forma que al
superponerlas, se creen muestreos simultáneos virtuales. Estos muestreos simultáneos
no son reales, son simulaciones generadas por el propio filtro. Estos muestreos
simultáneos se obtienen utilizando el llamado coeficiente de sobremuestreo (n), que
viene indicado por la expresión
(
,
,
, ...).
Las muestras obtenidas se superponen con los datos originales y los conversores A/D
los promedian, obteniendo una única muestra ponderada (por ejemplo, si se hacen tres
muestreos, finalmente, la muestra tomada no es ninguna de las tres, sino su valor
medio). Para evitar el aliasing, también se introduce a la entrada un filtro paso bajo
digital, que elimine aquellas frecuencias por encima de la mitad de la frecuencia de
muestreo. No obstante, a la salida, la frecuencia de muestreo utilizada para reproducir la
señal ya no es la misma que se utilizó para tomar las muestras a la entrada, sino que es
tantas veces mayor como números de muestreo se hayan hecho.
Consideremos un ejemplo característico de la digitalización de música en formato CD.
Imaginemos que para digitalizar el CD se hacen 3 muestreos a 44,1 kHz que se
interpolan. Se introduce un filtro paso bajo, llamado decimator, que elimina las
frecuencias por encima de los 20 kHz, pero la frecuencia de muestreo utilizada para
reconstruir la señal será tres veces mayor: 132,3 kHz. De este modo se reconstruye la
señal suavizando la pendiente. A este proceso de filtrado durante la conversión D/A se
lo conoce como diezmado.
Sin embargo, es evidente que incorporar la técnica del sobremuestreo encarece
considerablemente el equipo.
Modificación de la frecuencia de muestreo
Dada una señal analógica x(t), la muestreamos a una Fm determinada y obtenemos la
señal discreta x(n), para adaptar esta señal discreta un reproductor de distinta frecuencia
de muestreo, usaremos la interpolación ( para aumentar la frecuencia ) y el diezmo (para
disminuir la frecuencia ).
Una vez tengamos la señal discreta x(n), donde 'n' es un entero, aplicamos la TFSD
(Transformada de Fourier de Señales Discretas).
x(n) ———TFSD——— X(e^jΩ)
Interpolación factor L de X(e^jΩ):
Xi(e^jΩ)= L·X(e^LΩ)·Σ[Π(Ω-2·pi·k)/(2·pi/L)] Π:filtro paso bajas k:(-infinito,
+infinito)
Bibliografía





FRIES, Bruce y FRIES, Marty. Audio digital práctico. Ed. Anaya Multimedia.
2005. ISBN 84-415-1892-0
RUMSEY, Francis y McCORMICK, Tim. Sonido y grabación. Introducción a
las técnicas sonoras. 2004.
RUSS, Martin. Síntesis y muestreo de sonido. (Guía práctica sobre los
sintetizadores). 1999. ISBN 84-88788-35-5
WATKINSON, J. El arte del audio digital. IORTV, Madrid, 1993
WATKINSON, John. Introducción al audio digital. 2003. ISBN 84-932844-9-1.
Aliasing
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
En estadística, procesamiento de señales, computación gráfica y disciplinas
relacionadas, el aliasing es el efecto que causa que señales continuas distintas se tornen
indistinguibles cuando se muestrean digitalmente. Cuando esto sucede, la señal original
no puede ser reconstruida de forma unívoca a partir de la señal digital. Una imagen
limitada en banda y muestreada por debajo de su frecuencia de Nyquist en las
direcciones "x" e "y", resulta en una superposición de las replicaciones periódicas del
espectro G(fx, fy). Este fenómeno de superposición periódica sucesiva es lo que se
conoce como aliasing o Efecto Nyquist.
El aliasing es un motivo de preocupación mayor en lo que concierne a la conversión
analógica-digital de señales de audio y vídeo: el muestreo incorrecto de señales
analógicas puede provocar que señales de alta frecuencia presenten dicho aliasing con
respecto a señales de baja frecuencia. El aliasing es también una preocupación en el área
de la computación gráfica e infografía, donde puede dar origen a patrones de moiré (en
las imágenes con muchos detalles finos) y también a bordes dentados. El aliasing nos
puede traer problemas sobre todo en el campo de visión por computadores, ya que al
procesar imágenes, si no es correcta la imagen obtenida con la realidad, podemos tener
problemas con el hardware.
Contenido
[ocultar]


1 Generalidades
o 1.1 Aliasing en fenómenos periódicos
o 1.2 Muestreo de una señal sinusoidal
o 1.3 Aliasing espacial
o 1.4 Criterio de Nyquist
o 1.5 En la computación gráfica
2 Véase también
Generalidades
Aliasing en fenómenos periódicos
El Sol tiene un movimiento aparente de este a oeste en la bóveda celeste, con 24 horas
entre cada amanecer. Si tomásemos una fotografía del cielo cada 23 horas, el sol
parecería moverse de oeste a este, con 24·23=552 horas entre cada amanecer. El mismo
fenómeno causa que las aspas de un ventilador parezcan a veces girar en el sentido
inverso del que en realidad lo hacen, cuando se les filma o cuando son iluminadas por
una fuente de luz parpadeante, tal como una lámpara estroboscópica, un tubo de rayos
catódicos o una lámpara fluorescente, o simplemente, cuando el ventilador es iluminado
por la parpadeante luz de la televisión.
Muestreo de una señal sinusoidal
Cuando se obtienen muestras periódicas de una señal sinusoidal, puede ocurrir que se
obtengan las mismas muestras que se obtendrían de una señal sinusoidal igualmente
pero con frecuencia más baja. Específicamente, si una sinusoide de frecuencia f Hz es
muestreada s veces por segundo, y s ≤ 2·f, entonces las muestras resultantes también
serán compatibles con una sinusoide de frecuencia fm - f, donde fm es la frecuencia de
muestreo. En la jerga inglesa de procesamiento de señales, cada una de las sinusoides se
convierte en un "alias" para la otra.
Por tanto, si se muestrea a la frecuencia s una señal analógica que contiene las dos
frecuencias, la señal no podrá ser reconstruida con exactitud.
•Velocidad de muestreo recomendada: –2xfrecuencia mayor (medida de frecuencia) –
10xfrecuencia mayor (detalle de la forma de onda)
Aliasing espacial
Imagen correctamente muestreada de una muralla de ladrillos.
Aliasing espacial en la forma de un patrón de muaré.
Así como se define una frecuencia temporal, sobre imágenes se puede definir también
una frecuencia espacial y, por lo tanto, el muestreo mínimo (en píxeles/cm) con que
necesita ser escaneada una imagen para evitar el efecto.
Criterio de Nyquist
Está demostrado rigurosamente que para evitar el aliasing es necesario asegurarse de
que en la señal analógica a muestrear con una frecuencia s, no existen componentes
sinusoidales de frecuencia mayor a s/2. Esta condición es llamada el criterio de Nyquist,
y es equivalente a decir que la frecuencia de muestreo s debe ser al menos dos veces
mayor que el ancho de banda de la señal.
El Teorema de Nyquist indica que la frecuencia de muestreo mínima que tenemos que
utilizar debe ser mayor que 2·fmax, donde fmax es la frecuencia máxima de la señal
compleja. Si utilizamos esa frecuencia de muestreo, podremos reproducir
posteriormente la señal a partir de las muestras tomadas. En la práctica, debido a las
limitaciones de los circuitos, la utilización de una frecuencia más alta que la que nos
dice Nyquist permite obtener una representación más exacta de la señal de entrada.
En la computación gráfica
En informática y particularmente en computación gráfica, el aliasing es el artefacto
gráfico característico que hace que en una pantalla ciertas curvas y líneas inclinadas
presenten un efecto visual tipo "sierra" o "escalón". El aliasing ocurre cuando se intenta
representar una imagen con curvas y líneas inclinadas en una pantalla, framebuffer o
imagen, pero que debido a la resolución finita del sustrato resulta que éste sea incapaz
de representar la curva como tal, y por tanto dichas curvas se muestran en pantalla
dentadas al estar compuestas por pequeños cuadrados (los píxeles).
Véase también

Antialiasing
Muestreo digital
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda
El muestreo digital es una de las partes del proceso de digitalización de las señales.
Consiste en tomar muestras de una señal analógica a una frecuencia o tasa de muestreo
constante, para cuantificarlas posteriormente.
Contenido
[ocultar]

1 Descripción del proceso






2 Muestreo teórico
3 Teorema de Muestras
4 Muestreo práctico
o 4.1 Clases de muestreo práctico
5 Influencia de los filtros
6 El teorema de muestras práctico
7 Véase también
[editar] Descripción del proceso
El muestreo está basado en el teorema de muestreo, que es la base de la representación
discreta de una señal continua en banda limitada. Es útil en la digitalización de señales
(y por consiguiente en las telecomunicaciones) y en la codificación del sonido en
formato digital.
Independientemente del uso final, el error total de las muestras será igual al error total
del sistema de adquisición y conversión más los errores añadidos por el ordenador o
cualquier sistema digital.
Para dispositivos incrementales, tales como motores paso a paso y conmutadores, el
error medio de los datos muestreados no es tan importante como para los dispositivos
que requieren señales de control continuas.
[editar] Muestreo teórico
Sea la señal de banda limitada y paso-bajo
(dominio de la frecuencia) es nulo para:
El producto
de
(dominio del tiempo) cuyo espectro
. Sea también la onda:
es una onda formada por deltas de peso igual a las muestras
:
,
que dará lugar a otro tren de deltas:
Función escala fs.
La transformada de
es la de
repetida y centrada en cada armónico de la
frecuencia de muestreo, exceptuando el término constante o la función escala
.
No se producirá solapamiento entre los espectros parciales de
De la observación del espectro
simplemente pasando
la condición:
si se verifica que:
se deduce la posibilidad de recuperar
por un filtro paso-bajo cuya frecuencia de corte
cumpla
[editar] Teorema de Muestras
Espectro X(f) de la señal paso-bajo.
Se considera la señal paso-bajo
espectro
, que cumple:
se representa en la figura.
para
, cuyo
Es posible establecer un desarrollo en Serie de Fourier de
del modo siguiente:
, limitado a
,
en dónde los coeficientes
Ahora bien, si
del desarrollo vienen dados por:
es la transformada inversa de
:
,
de dónde se infiere una relación inmediata entre los
concretamente:
Así pues, puede escribirse el espectro
muestras
ecuación anterior:
de
y valores particulares de
en términos de las propias
sin más que sustituir los valores de
de
Para hallar los términos de
así:
,
dados en la
bastará con calcular la transformada inversa, resultando
Obsérvese que éste resultado es consecuencia de la limitación de banda
y que la
operación de muestreo aparece en el curso de la especificación de
. De esta
manera, se demuestra el denominado Teorema de Muestras, el cual afirma que toda
señal de banda limitada puede expresarse de modo único en función de sus muestras o
valores puntuales tomados a intervalos regulares
. El valor de
será tal que:
, siendo
la máxima frecuencia espectral de la señal.
Este teorema es igualmente válido, adaptando ciertas condiciones para muestreo no
uniforme y por supuesto para señales paso banda, dependiendo en éste caso de la
frecuencia de muestreo de la anchura de banda de paso y de la frecuencia central de la
señal.
Como corolario del teorema, se puede afirmar que dada la colección discreta de valores
existe una función
y sólo una de banda limitada a
los puntos dados y se construye mediante la última ecuación.
que pasa por todos
[editar] Muestreo práctico
Muestreo práctico instantáneo.
Muestreo práctico natural.
El Teorema de muestreo no impone ninguna exigencia en cuanto al modo de obtener las
muestras, por lo que la señal se podrá reconstruir a partir de algún método más
susceptible de implementación práctica.
El muestreo práctico difiere del teórico en tres aspectos principales:



La onda muestreadora está constituida por trenes de impulsos de duración no
nula.
Los filtros prácticos de reconstrucción no son ideales.
Los mensajes a los que se aplica el teorema no están estrictamente limitados en
banda, ni pueden, ya que se trata de señales limitadas en el tiempo.
[editar] Clases de muestreo práctico
Sea un impulso arbitrario cualquiera
, tal que:
evita que se solapen los impulsos básicos) y sea la onda:
para
(lo que
Una posible forma de transmitir las muestras
es utilizar las muestras como
amplitud del impulso m-ésimo, centrado en el instante del muestreo, es decir, formar la
señal:
,
que es un tren de impulsos, cada uno de los cuales viene afectado por un factor de escala
(peso o amplitud) igual al valor instantáneo
. La señal anterior constituye un
ejemplo básico de muestreo práctico instantáneo.
En el caso del muestreo práctico natural, en vez de afectar a cada impulso con un
valor instantáneo de
se le multiplica punto a punto por cada uno de los valores de
en el intervalo de existencia, en otras palabras, se forma el producto genérico
. Sumando tales productos se obtiene este tipo de muestreo, que se puede representar
mediante la ecuación:
[editar] Influencia de los filtros
La influencia de los filtros de reconstrucción no ideales se observa fácilmente en el
dominio de la frecuencia. En la siguiente figura se representa parte del espectro de una
señal muestreada, supuesto sin distorsión y una posible característica de transferencia de
un filtro paso-bajo real.
Fragmento del espectro de una señal muestreada.
Si tal característica es razonablemente plana en la banda pasante de la señal
,
la salida del filtro consistirá en
más unas componentes en frecuencias próximas a
fuera de dicha banda. Sin embargo estas componentes están fuertemente
atenuadas en relación con las del espectro básico de
.
Para señales vocales esas componentes como zumbidos de alta frecuencia sólo están
presentes cuando lo está la señal
que por su mayor nivel, tiende a enmascararlas, y
por tanto su presencia es fácilmente tolerable. Éstas componentes pueden suprimirse
mediante un diseño adecuado del filtro y para un filtro dado, aumentando la frecuencia
de muestreo (y por consiguiente
) e introduce bandas de guarda en el espectro.
[editar] El teorema de muestras práctico
Se puede resumir el enunciado del Teorema contemplando señales y métodos de
muestreo reales, del modo siguiente: Si una señal
ha sido filtrada en paso-bajo de
modo que tiene componentes espectrales por encima de
, puede describirse
adecuadamente para muchas aplicaciones mediante muestras instantáneas o de duración
no nula, separadas uniformemente en el tiempo por un intervalo
.
Si se ha muestreado la señal al régimen de Nyquist o mayor y las muestras se
representan mediante impulsos periódicos cuya amplitud sea proporcional a sus valores,
puede reconstruirse aproximadamente la señal a partir de sus muestras mediante un
filtraje paso-bajo.
[editar] Véase también
Menu Principal
Principal
Quién es Eveliux?
Curso de Redes y Telecomunicaciones
Artículos
Artículos por Temáticas
Ligas de Interes
-------
Contactos
Registrate
Foro de Discusión
Otras Secciones
Estadísticas - Eveliux
SiteMap
Intercambio de Links
Tienda de Libros
Translate
35 languages
English
en
UTF-8
auto
http://vivociti.com
Agreganos
Book - Convergence
Libro Digitalización y Convergencia Global
Google Friend Connect
twitter
Teoria del muestreo de
Nyquist
Valoración de los usuarios:
Pobre
124
El mejor
/ 44
Valoración
vote
com_content
http://w w w .eveli
Escrito por Evelio Martinez
Martes 10 de Julio de 2007 02:57
Desarrollado por H. Nyquist, quien afirmaba que una señal analógica puede ser
reconstruída, sin error, de muestras tomadas en iguales intervalos de tiempo. La razón
de muestreo debe ser igual, o mayor, al doble de su ancho de banda de la señal
analógica".
La teoría del muestreo define que para una señal de ancho de banda limitado, la
frecuencia de muestreo, fm, debe ser mayor que dos veces su ancho de banda [B] medida
en Hertz [Hz].
fm > 2·B
Supongamos que la señal a ser digitalizada es la voz...el ancho de banda de la voz es de
4,000 Hz aproximandamente. Entonces, su razón de muestreo sera 2*B= 2*(4,000 Hz),
es igual a 8000 Hz, equivalente a 8,000 muestras por segundo (1/8000). Entonces la
razón de muestreo de la voz debe ser de al menos 8000 Hz, para que puede regenerarse
sin error.
La frecuencia 2*B es llamada la razón de muestreo de Nyquist. La mitad de su valor, es
llamada algunas veces la frecuencia de Nyquist.
El teorema de muestreo fue desarrollado en 1928 por Nyquist y probado
matematicamente por Claude Shannon en 1949.
Ejemplos prácticos:
El en área de la MÚSICA, a veces es necesario convertir material analógico [en acetato,
cassetes, cintas magneticas, etc] a formato digital [en CD, DVD]. Los ingenieros de
sonido pueden definir el rango de frecuencia de interés.
Como resultado, los filtros analógicos son algunas veces usados para remover los
componentes de frecuencias fuera del rango de interes antes de que la señal sea
muestreada.
Por ejemplo, el oído humano puede detectar sonidos en el rango de frecuencias de 20
Hz a 20 KHz. De acuerdo al teorema de muestreo, uno puede muestrear la señal al
menos a 40 KHz para reconstruir la señal de sonido aceptable al oísdo humano. Los
componentes más arriba de 40 KHz no podrán ser detectados y podrían contaminar la
señal. Estos componentes arriba de los 40 KHz son removidos a través de filtros pasa
banda o filtros pasa bajas.
Algunos de las razones de muestreos utilizadas para grabar musica digital son las
siguientes:
Razón de muestreo/ Frecuencia de Nyquist
22,050 kHz = 11,025 kHz (Nyquist)
24,000 kHz = 12,000 kHz
30,000 kHz = 15,000 kHz
44,100 kHz = 22,050 kHz
48,000 kHz = 24,000 kHz
Es muy importante tomar en consideración que la frecuencia más alta del material de
audio será grabada. Si la frecuencia de 14,080 Hz es grabada, una razón de muestreo de
44.1 kHz deberá ser la opción elegida. 14,080 Hz cae dentro del rango de Nyquist de
44.1 kHz el cual es 22.05 kHz.
La razón de muestreo elegida determina el ancho de banda del audio de la grabadora
usada. Considerando que el rango del oido es de 20 Hz a 20 kHz, una razón de
muestreo de 44.1 kHz teoricamente deberá satisfacer las necesidade