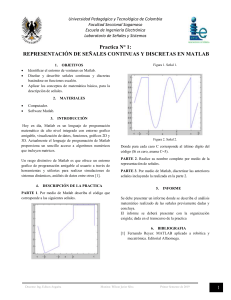
EIE Escuela de Ingeniería Eléctrica IE0409 – Análisis de Sistemas I - 2017 Práctica guiada de MATLAB Objetivo: Introducir al estudiante en las cuestiones básicas del uso de MATLAB y Simulink. Instrucciones 1. Inicie MATLAB. La interfaz que le debe aparecer debe ser parecidad a la de la figura 1. Figura 1: Interfaz de MATLAB La subventana con el título “Command Window” corresponde a un tipo de consola en donde se puede introducir comandos y mostrar los resultados. A la izquierda, la ventana con el título “Current Folder” muestra los archivos de la carpeta de trabajo actual. En la subventana de la derecha con el título “Workspace”, se presentan todas las variables que están accesibles en el scope1 actual. 2. El primer y más importante comando que se debe conocer cuando se utiliza MATLAB es el comando help. a) Si se escribe nada más help, MATLAB presenta todos los toolboxes que están instalados, con los enlaces a la lista de las funciones de cada uno. b) Si se escribe help <nombre de una función> MATLAB presenta la ayuda asociada a esa función. c) El help del MATLAB es muy bueno, incluso, se puede hacer help help y MATLAB devuelve la ayuda de la función help. 1 El scope se define como el conjunto de variables que son accesibles desde la función que se está ejecutando. 1 de 3 IE0409 – Análisis de Sistemas I - 2017 Práctica guiada de MATLAB d) Como ejemplo, escriba en el Command Window help roots y estudie qué hace esa función. 3. Al contrario de otros lenguajes, NO es necesario definir las variables antes de utilizarlas. MATLAB las define automáticamente cuando se les asigna un valor la primera vez. Un error muy común entre los estudiantes de Ingeniería Eléctrica es querer definir una variable utilizando el comando sym. Este comando sólo es válido cuando se utiliza el toolbox de cálculo simbólico, por lo que a menos que se utilice ese toolbox, las variables se crearán automáticamente la primera vez que se les asigne un valor. Un aspecto importante es que las variables básicas de trabajo son las matrices. Todas las funciones de MATLAB están escritas de manera que la entrada debe ser una matriz (entiéndase que puede ser también un vector y por consiguiente un escalar también). a) Una matriz se introduce en MATLAB con paréntesis cuadrados. En el command window, cree las siguientes matrices y vectores: A = [1, 2, 3; 4, 5, 6; 7, 8, 9] B = [10, 11, 12] C = [13; 14; 15] b) Realice las siguientes operaciones en el command window: A^2 A.^2 (¿para qué sirve el punto antes del ^?) B*A B*C C*B A+C*B A*C*B A.*(C*B) (note el punto antes del *) D = [A,A*C*B] A*B c) Normalmente los cálculos no se hacen en el command window directamente, sino que se escribe un archivo de texto que luego es ejecutado en MATLAB en el mismo orden en el que se escribe el documento. A este archivo se le llama script y generalmente tiene extensión .m. MATLAB cuenta con un editor especializado para este tipo de archivos. Para crear un archivo .m, simplemente presione el botón “nuevo” en la interfaz de MATLAB. d) en un script, 1) cree una matriz de nombre X de tamaño 10x10 con números aleatorios distribuidos uniformemente. El rango de cada uno de los elementos de la matriz es 0 ≤ Xi,j ≤ 10. (Sugerencia: revisar las funciones rand y randn) 2) Si Xi,j representa el elemento de la matriz X que se encuentra en la fila i y columna j, cree una variable llamada x tal que x = X(6, 7)∗A(8, 2)∗A(4, 3). (Note que la variable x es distinta a la variable X) 3) Extraiga la fila 5 de A y guárdela en una variable llamada z. (Sugerencia utilice el operador “:” [dos puntos]) 4) Utilizando la función roots, encuentre las raíces del siguiente polinomio: x4 + 4x3 − 25x2 + 5x − 10 = 0 e) En otro script: 1) Siempre es mejor realizar todas las operaciones haciendo uso de matrices, porque MATLAB está optimizado para ello y no para ejecutar for’s y while’s. escriba el siguiente script: 2 de 3 IE0409 – Análisis de Sistemas I - 2017 Práctica guiada de MATLAB x f = 10000; x = 0:0.001: xf ; n = length ( x ) ; tic y1 = 0 ; for i = 1:n y1 = y1+x ( i ) ^2 ∗ sin ( x ( i ) ) ; end t l o o p = toc ; % tic x2 = x . ^ 2 ; xseno = sin ( x ) ; y2 = x2 ∗ xseno . ’ ; t p l a i n = toc ; disp ( [ ’ Resultados : Loop : ’ , num2str ( y1 ) , ’ V e c t o r i a l : ’ , num2str ( y2 ) ] ) ; disp ( [ ’ Tiempo de l o o p : ’ , num2str ( t l o o p ) ] ) ; disp ( [ ’ Tiempo de operaciones v e c t o r i a l e s : ’ , num2str ( t p l a i n ) ] ) ; disp ( [ ’ R e l a c i o n l o o p / v e c t o r i a l : ’ , num2str ( t l o o p / t p l a i n ) ] ) ; Pruebe con diferentes valores de xf y compare los resultados. f ) Todo lo que haga en MATLAB tiene que estar vectorizado. Incluso hacer figuras en MATLAB representa crear al menos un par de vectores que representen la “x” y las “y” para dibujarlas en un plano, utilizando la función plot. Realice los siguientes ejercicios en un script de MATLAB: 1) Cree un vector t de valores desde 0 hasta 10 con un espaciamiento de 0,01. (Puede utilizar el operador “:” [dos puntos]) 2) Calcule los “x” y “y” de la siguiente manera: x = 16sin3 (t) y = 13cos(t) − 5cos(2t) − 2cos(3t) − cos(4t) 3) Cree una gráfica de “y” contra “x”. (Revise las funciones plot, xlabel, ylabel, title, grid) Gráfica tridimensional 4) Cree dos vectores x y y desde -5 hasta 5 con un espaciado de 0,1. 5) Use la función meshgrid para mapear x y y en dos matrices X y Y. (¿cuál es el resultado de meshgrid) 6) Utilizando X y Y, calcule la matriz: p Z = sin( X2 + Y2 ) nota: esta operación debe realizarse elemento a elemento, utilice las operaciones con punto. 7) Utilice el comando surf para dibujar Z contra X y Y. No olvide escribir bien los títulos de los ejes. 4. Abra el archivo Matlab_Introduccion_Ejemplos.m y revise los comandos utilizados, comente y descomente líneas a placer para ver los resultados. Utilice la función help para entender bien los comandos. 3 de 3