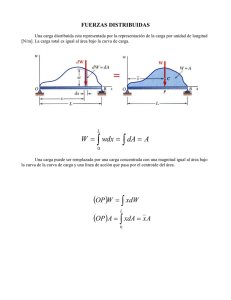
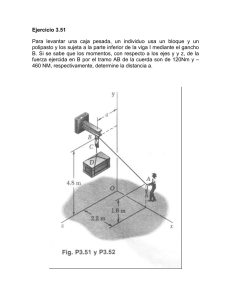
CALCULO APLICADO A LA FÍSICA 1 Segunda Condición de Equilibrio Prof. Mg. Juan Carlos Grande Ccalla S06.s2 LOGRO DE APRENDIZAJE Al finalizar la sesión, el estudiante describe los sistemas que se encuentran en equilibrio estático calculando magnitudes físicas. La Clase anterior • Producto Vectorial Temas • Momento de una fuerza, formulación escalar. • Producto cruz. • Momento de una fuerza, Formulación vectorial. • Centro de gravedad. • Condiciones para el equilibrio de un cuerpo rígido. 1. Momento de una fuerza, formulación escalar • Cuando una fuerza se aplica a un cuerpo, ésta producirá una tendencia a que el cuerpo gire alrededor de un punto que no está en la línea de acción de la fuerza. • Esta tendencia a girar se conoce en ocasiones como par de torsión, pero con mayor frecuencia se denomina el momento de una fuerza o simplemente el momento. Momento de una fuerza • Magnitud. La magnitud de 𝑀𝑂 es donde 𝑑 es el brazo de momento o distancia perpendicular desde el eje en el punto O hasta la línea de acción de la fuerza. • Dirección. La dirección de 𝑀𝑂 está definida por su eje de momento, el cual es perpendicular al plano que contiene la fuerza F, y por su brazo de momento d. Momento resultante Como convención consideraremos de manera general los momentos positivos como en sentido contrario al de las manecillas del reloj por estar dirigidos a lo largo del eje positivo 𝑧 (fuera de la página). Los momentos en el sentido de las manecillas del reloj serán negativos. Para cada caso ilustrado en la figura, determine el momento de la fuerza con respecto al punto O. Problema 1 Determine el momento de la fuerza con respecto al punto O Problema 2 Determine el momento de la fuerza con respecto al punto O. No tome en cuenta el grosor del elemento Problema 3 Determine el momento de la fuerza F con respecto al punto O. Exprese el resultado como un vector cartesiano. 2. Centro de gravedad Centro de gravedad El centro de gravedad (cg) y el centro de masa (cm) de un cuerpo extendido. Si 𝒈 tiene el mismo valor en todos los puntos de un cuerpo, su centro de gravedad es idéntico a su centro de masa Localización y uso del centro de gravedad 3. Condiciones para el equilibrio de un cuerpo rígido • El equilibrio de un cuerpo se expresa como: • La primera de estas ecuaciones establece que la suma de las fuerzas que actúan sobre el cuerpo es igual a cero. • La segunda ecuación establece que la suma de los momentos de todas las fuerzas en el sistema con respecto al punto O, añadida a todos los momentos de par es igual a cero. Diagramas de cuerpo libre • Si un soporte evita la traslación de un cuerpo en una dirección dada, entonces se desarrolla una fuerza sobre el cuerpo en esa dirección. • Si se evita una rotación, se ejerce un momento de par sobre el cuerpo. Problema 4 El transformador eléctrico de 300 lb con centro de gravedad en G se sostiene mediante un pasador en A y una plataforma lisa en B. Determine las componentes horizontal y vertical de la reacción en el pasador A y la reacción de la plataforma B sobre el transformador. Problema 5 a) Dibuje el diagrama de cuerpo libre de la viga de la figura. b) Determine la tensión en la cuerda y las reacciones en B. Problema 6 Una viga uniforme tiene 5,0 𝑚 de largo y tiene una masa de 53 𝑘𝑔. En la figura, la viga está apoyada en posición horizontal por una bisagra y un cable, con un ángulo 𝜃 = 60°. En notación de vector unitario, ¿cuál es la fuerza sobre el rayo desde la bisagra? Problema 7 En la figura, una barra uniforme de masa 𝑚 está articulada a un edificio en su extremo inferior, mientras que su extremo superior se mantiene en su lugar mediante una cuerda unida a la pared. Si el ángulo 𝜃1 = 60°, ¿qué valor debe tener el ángulo 𝜃2 para que la tensión en la cuerda sea igual a 𝑚𝑔/2? Problema 8 El sistema de la figura está en equilibrio. Un bloque de hormigón de masa de 225 𝑘𝑔 cuelga del extremo del puntal uniforme de masa de 45,0 𝑘𝑔. Un cable corre desde el suelo, sobre la parte superior del puntal, y baja al bloque, manteniendo el bloque en su lugar. Para ángulos 𝜙 = 30,0° y 𝜃 = 45,0°, encuentre (a) la tensión 𝑇 en el cable y (b) los componentes horizontal y (c) vertical de la fuerza sobre el puntal desde la bisagra Problema 9 En la figura, un extremo de una viga uniforme de peso 222 𝑁 está articulado a una pared; El otro extremo está soportado por un cable que forma ángulos 𝜃 = 30,0° con la pared y la viga. Encuentre (a) la tensión en el alambre y (b) los componentes horizontal y (c) vertical de la fuerza de la bisagra sobre la viga. La Clase siguiente • Laboratorio 2 BIBLIOGRAFÍA Serway, R. y Jewett, J.W. (2015) Física para ciencias e ingeniería. Volumen I. México. Ed. Thomson. Sears F., Zemansky M.W., Young H. D., Freedman R.A. (2013) Física Universitaria Volumen I Undécima Edición. México. Pearson Educación.