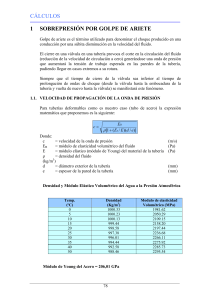
FENÓMENO TRANSITORIO DEL GOLPE DE ARIETE EXPLICACIÓN, CÁLCULOS, CAUSAS Y PREVENCIÓN Robert Rubio i Vicent. Brigades Rurals d’Emergència. Formador del Institut Valencià de Seguretat Pública (IVASP) - [email protected] HISTORIA DE SU ESTUDIO EL GOLPE DE ARIETE FACTORES QUE INFLUYEN EN EL GOLPE DE ARIETE Se denomina golpe de ariete al fenómeno transitorio consistente en la variación de la presión como consecuencia de los cambios en la velocidad del agua, provocados por las operaciones de regulación y control en instalaciones hidráulicas a presión. Gustave Michaud Suiza 1860-1924. Nikolay E. Zhukovskii. Rusia 1847-1921. Lorenzo Allievi Italia, 1856-1941 Propuso la primera fórmula para valorar el golpe de ariete (1878). En esta ecuación no valoró ni la compresibilidad del agua ni la elasticidad de la tubería. Joukowsky. Estableció la ley que permite calcular presión máxima provocada por el cierre instantáneo de la válvula instalada en un conducto a presión. (1898) Amplió los estudios de Joukowsky. Corrigió los cálculos de Michaud y estableció las ecuaciones necesarias para los cálculos (1903). Es una onda cíclica de presión que se desplaza a lo largo de los tendidos y puede causar daños, incluso la destrucción de las tuberías y los equipos de bombeo, debido a las sobrepresiones generadas. Es una fuerza destructiva de gran magnitud que existe en todos los sistemas de bombeo. Las maniobras de detenimiento total del caudal implican necesariamente los golpes de ariete de máxima intensidad, puesto que se pone de manifiesto la transformación total de la energía de movimiento en energía de presión. Velocidad de cierre Longitud del tendido Características elásticas de la conducción Diámetro de la conducción Velocidad del fluido Características del fluido Presión de la instalación RIETE A E D E RE GOLP R SOB L A E U T R C S EVITA MOS A E D ANZA O L PARA P S A E MENT E DE L R R E I ÚNICA C PO DE M E I EL T CASOS EN LOS QUE SE PUEDE PRODUCIR En general, el fenómeno transitorio aparecerá cuando en una instalación hidráulica se produzcan variaciones de velocidad y, por consiguiente, de presión, motivadas por abrir o cerrar una válvula y poner en marcha o parar una máquina hidráulica. Se produce en maniobras necesarias para el adecuado manejo y operación del recurso, por lo que su frecuencia es importante y no un fenómeno eventual. ¿COMO EVITAR EL GOLPE DE ARIETE? El golpe de ariete es función del tiempo de cierre de las válvulas por lo que la única prevención posible es la manipulación progresiva de las lanzas. PROCESO DEL GOLPE DE ARIETE PROPAGACIÓN DE LAS ONDAS DE PRESIÓN DEBIDO AL CIERRE INSTANTÁNEO DE LA VÁLVULA L D VALOR MÁXIMO DEL GOLPE DE ARIETE FÓRMULA DE MICHAUD FÓRMULA DE ALLIEVI a V H g 2 L V H g T V No hay perturbación. Régimen permanente. El líquido en la tubería se desplaza con velocidad V desde la bomba hacia la válvula. Diámetro de la tubería normal D. ∆H = Valor de la sobrepresión [mca] a = Celeridad [m/s] V = Velocidad del fluido (antes del cierre de la válvula) [m/s] L = Longitud real [m] g = Aceleración de la gravedad [m/s2] T = Tiempo de parada [s] L D a CÁLCULO DEL GOLPE DE ARIETE Al estudiar este tipo de transitorios no es posible seguir manteniendo las hipótesis de un fluido incompresible y conducciones indeformables. Por el contrario, las capacidades del fluido de modificar su densidad por los efectos de la presión y de las conducciones de deformarse son fundamentales en la descripción del fenómeno. TIEMPO CRÍTICO TIEMPO DE PARADA Las máximas sobrepresiones posibles se logran para los casos en que la maniobra de cierre sea menor que el tiempo que tarda la onda en su viaje de ida y vuelta al obturador. Este tiempo se conoce como tiempo crítico Tc, El tiempo que tarda la onda en recorrer la distancia entre la válvula y el depósito es: Es el intervalo entre la iniciación y la terminación de la maniobra de cierre de válvulas. El valor del tiempo de parada influye en el golpe de ariete de modo que a menor tiempo, mayor golpe. El valor del tiempo de parada viene expresado por una fórmula empírica, que expresa el tiempo en segundos, según Mendiluce L Longitud Tc c celeridad Tc = 0 Es un caso teórico Cierre rápido 0<Tc<2L/c La sobrepresión es la misma que en el cierre instantáneo. La onda de presión no tiene tiempo de ir al origen de la presión, reflejarse y volver a la válvula, antes de que termine medio ciclo Cierre lento Tc > 2 L/c La presión máxima es menor que en el caso anterior y no provoca daños en las instalaciones Cierre instantáneo V D T = Tiempo de parada en segundos. C= Coeficiente según la pendiente de la conducción. Empírico K= Valor que depende de la conducción. Empírico L = Longitud real de la conducción en m V= Velocidad del agua en la conducción en m/s g = Constante de la gravedad (9,8 m/seg2) Hm= Altura manométrica en metros. Pendiente 1 0’5 0 Valor K m m m m 1,75 1,50 1,25 1 CELERIDAD O ACELERACIÓN Velocidad de propagación de las ondas de presión. Es función de las características elásticas del sistema fluido-tubería. La longitud del tramo de tubería regido por la ecuación de Michaud se conoce como longitud crítica (Lc), y su valor se obtiene igualando las fórmulas de Michaud y Allievi. K a T Lc a 2 Lc<L Cuando la longitud crítica es menor que la longitud real, se denomina conducción larga y se resuelve con la fórmula de Allievi. Valor C 0-20 % 30 % >40 % LONGITUD CRÍTICA Lc>L Cuando la longitud crítica es mayor que la longitud real, se denomina conducción corta y se resolverá con la fórmula de Michaud. A medida que la onda se desplaza la velocidad del líquido se anula en toda la tubería, el tubo se dilata ∆D y la densidad del agua aumenta. El resto del fluido continúa moviéndose hacia la válvula a una velocidad V. Con el paso del tiempo más zonas del fluido son frenadas y comprimidas. L < 500 1000 >1500 2000 Lc=L En este caso se podrá solucionar con cualquiera de las fórmulas Allievi o Michaud. La sobrepresión es una onda de presión o pulso de compresión que se crea en la válvula y se propaga aguas arriba a una velocidad finita a llamada celeridad. K L V T C g Hm Longitud Representando gráficamente las ecuaciones de Allievi y de Michaud se observa que, si la conducción es lo suficientemente larga, las dos rectas se cortan en un punto, denominado punto crítico. La válvula se cierra instantáneamente. En ese momento el fluido adyacente a la válvula se frena y es comprimido por el resto del fluido aumentando su presión. La compresibilidad del fluido y la elasticidad de la tubería permiten que la densidad del fluido aumente y que el tramo de tubería que le rodea se dilate. Para el caso del agua: a K D 1 E 9.900 D 48'3 G e a es la celeridad de la onda elástica del fluido en la tubería, [m/s] K es el módulo de elasticidad del fluido (módulo de Bulk), [N/m2] ρ es la densidad del líquido, [kg/m3] D es el diámetro de la tubería, [m] E es el módulo de elasticidad de la tubería, [N/m2] δ es el espesor de la tubería, [m] COMPARACIÓN GRÁFICA ENTRE EL CÁLCULO DE ALLIEVI Y MICHAUD a V D+∆D La onda de presión se ha propagado hacia la bomba con celeridad a, y el frente de onda ha llegado a la mitad de la tubería. Mitad derecha de la tubería dilatada por la sobrepresión. Mitad izquierda, diámetro normal. En esa mitad izquierda el agua sigue circulando con velocidad V hacia la válvula. En la mitad derecha V=0. El fluido está comprimido. L V a D+∆D V=0 La onda de presión ha llegado a la bomba. En toda la tubería el líquido está en reposo, V=0, pero no en equilibrio, pues se encuentra comprimido. Toda la tubería está dilatada. La onda energética ha llegado al origen de la presión y golpea contra los álabes de la bomba. Puesto que esta energía se descarga siempre contra el mismo punto de la bomba provoca fatiga de los materiales. L V D1 D+∆D a Como un resorte que se recupera tras la compresión, el agua de la tubería comienza a moverse con velocidad V, pero dirigida en sentido contrario, hacia la bomba, y así lo hará mientras la suma de la energía de presión acumulada más la cinética sea superior al impulso de la bomba. El líquido comienza a ponerse en movimiento justo en la zona inmediatamente después de la unión bomba-tubería. La bomba continúa impulsando. La mitad izquierda de la tubería se ha contraído a su diámetro normal por la descarga de líquido. La onda sigue propagándose hacia la válvula con velocidad a. En la mitad izquierda de la tubería el fluido circula a velocidad V . L V COMPORTAMIENTO DE LA PRESIÓN EN UNA TUBERÍA DURANTE EL GOLPE DE ARIETE D1 a Diámetro de toda la tubería D1. Todo el fluido de la tubería en movimiento desde la válvula hacia la bomba con velocidad v. No hay sobrepresión en ninguna parte de la tubería pero por la inercia la onda energética continúa hasta golpear en la llave cerrada, la presión en el interior continúa disminuyendo hasta igualar la presión de impulsión de la bomba. La onda elástica se sigue propagando. L D1 V a Comienzo de un nuevo ciclo. En este punto estamos como al inicio, se vuelve a repetir el proceso cada 4L/a segundos. El sistema se estabiliza debido a las pérdidas de carga provocadas por el rozamiento. BIBLIOGARFÍA Abreu, J.M. Cabrera, E. Iglesias, P.L. (1995). El golpe de ariete en tuberías de impulsión. Comentarios a las expresiones de Mendiluce. Ingeniería del Agua vol. 2, núm. 2. Cabrera, E., Espert, V., García-Serra, J. (1996). Ingeniería Hidráulica aplicada a los sistemas de distribución de agua. Volúmenes I y II. Universidad Politécnica de Valencia. Unidad Docente de Mecánica de Fluidos. Mancebo del Castillo, U. (1992). Teoría del golpe de ariete y sus aplicaciones en ingeniería hidráulica. Editorial Limusa. Mendiluce, E. (1987). El golpe de ariete en impulsiones. Bellisco Librería Editorial. Pérez Farrás, L.E. y Guitelman, A. (2005). Estudio de Transitorios: El Golpe de Ariete. Universidad de Buenos Aires. Facultad de Ingeniería. Departamento de Hidráulica. Cátedra de Construcciones Hidráulicas. Rivas, Alejandro y Sánchez, Gorka (2004). Transitorios en Instalaciones. Golpe de Ariete. Campus Tecnológico de la Universidad de Navarra, Escuela Superior de Ingenieros. Laboratorio de Mecánica de Fluidos. Rubio i Vicent, R. (2009). Curso de Especialización. Mantenimiento, conducción segura y 4x4 de autobombas forestales. IVASP. Silvestre, P. (1987). Fundamentos de Hidráulica General. Editorial Limusa. Suay Belenguer, J.M. (2002) Apuntes de Hidráulica.