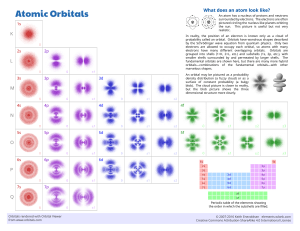
Organic Chemistry I Bonding: Atomic Orbitals & Molecular Orbitals Reference: Vollhardt & Schore, Organic Chemistry, W.H.Freeman The electron is described by wave equations. (A) A wave. The signs of the amplitude are assigned arbitrarily. At points of zero amplitude, called nodes, the wave changes sign. (B) Waves with amplitudes of like sing (in phase) reinforce each other to make a larger wave. (C) Waves out of phase subtract from each other to make a smaller wave. Bonds are made by in-phase overlap of atomic orbitals. In-phase (bonding) and out-of-phase (antibonding) combinations of 1s atomic orbitals. The + and - signs denote the sign of the wave function, not charges. Electrons in bonding molecular orbitals have a high probability of occupying the space between the atomic nuclei, as required for good bonding. The antibonding molecular orbital has a nodal plane where the probability of finding electrons is zero. Electrons in antibonding molecular orbitals are most likely to be found outside the space between the nuclei and therefore do not contribute to bonding. !2 Schematic representation of the interaction of (A) two singly occupied atomic orbitals (as in H2) and (B) two doubly occupied atomic orbitals (as in He2) to give two molecular orbitals (MO). (These diagrams are not drawn to scale.) Formation of an H-H bond is favorable because it stabilizes two electrons. Formation of an He-He bond stabilizes two electrons (in the bonding MO) but destabilizes two others (in the antibonding MO). Bonding between He and He thus results in no net stabilization. Therefore, He is monoatomic. The overlap of atomic orbitals gives rise to sigma and pi bonds. Bonding between atomic orbitals. (A) 1s and 1s (e.g., H2), (B) 1s and 2p (e.g., HF), (C) 2p and 2p (e.g., F2), (D) 2p and 3p (e.g., FCl) aligned along internuclear axes, σ bonds; (E) 2p and 2p perpendicular to internuclear axis (e.g., H2C=CH2), a π bond. Note the arbitrary use of + and - signs to indicate in-phase interactions of the wave functions.