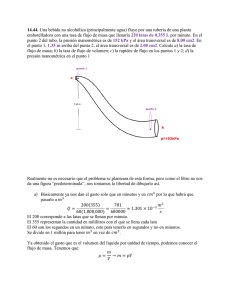
Ejemplos misceláneos para fluidos Preguntas de concepto 10.1. Usted está dentro de una balsa que flota en una pequeña alberca cuyo nivel ha sido medido cuidadosamente. En cierto momento, usted tira algunos bloques de madera que traía consigo y mira como flotan en el agua fuera de la balsa. ¿Qué sucede con el nivel del agua medido previamente? ¿El nivel del agua se comportaría de manera diferente si los bloques fueran de concreto y se hundieran hasta el fondo de la alberca? Respuestas: 1.1 El nivel permanece igual, pues la fuerza boyante es la misma, es decir, cuando los bloques permanecen dentro de la balsa, la fuerza boyante soporta todo el peso de los bloques más la persona; al arrojarlos al agua lo único que hace es soportar el peso de los bloques y la balsa por separado, pero la fuerza resultante sería la misma. 1.2 No, pues la fuerza boyante permanecería igual y el nivel no cambiaría. Es decir, se trata de un caso similar al anterior, aunque los bloques no floten, experimentarán la misma fuerza boyante debida a su masa, esta no cambia si están dentro o fuera de la balsa. M. en C. Abraham Vilchis Uribe Ejercicios Numéricos 14.31. Un bloque cúbico de madera de 10.0 cm por lado flota en la interfaz entre aceite y agua con su superficie inferior 1.50 cm bajo la interfaz (figura 14.35). La densidad del aceite es de 790 kg/m3. a) ¿Qué presión manométrica hay en la superficie superior del bloque? b) ¿Y en la cara inferior? c) ¿Qué masa y densidad tiene el bloque? I. El cubo está sometido a varias fuerzas y presiones, pues está dentro de dos fluidos distintos; se parece mucho a cuando consideramos e o no la presión atmosférica. D. E. L = 10.0 cm = 0.1 m; H1 = 1.50 cm = 0.015 m; a) Pa = ?; b) Pb = ?; c) mcubo = ?, rcubo = ? D. I. Pman = rgh; F = PA; A = L3 E. Calcular las presiones pedidas y hacer un balance de fuerzas para obtener la masa. A. a) Pa = racgH1 = (790)(9.8)(0.015) = 116.25 Pa b) Pb = raguagH1 + racgHac = (1000)(9.8)(0.015) + (790)(9.8)(0.10) = 921.35 Pa Notar que aquí se debe agregar lapresión ejercida por el aceitte de acuerdo con el Principio de Pascal. c) Haciendo un balance de fuerzas: Pb A – Pa A – mcubo g = 0 ó Pb A– Pa A = mcubo g mcubo = (Pb – Pa)A/g Pa A mcubo = (921.35 – 116.25)(.01)/9.8 = 0.8217 kg rcubo = (0.8217)/(.001) = 821.65 kg/m3 wcubo S. a) Sí, pues solamente soporta un poc de aceite en su cara superior. M. en C. Abraham Vilchis Uribe Pb A b) Sí, pues hay que añadir la presión que ejerce el peso del aceite al agua. c) Sí, pues es una masa razonable para un cubo de madera y, buscando en tablas, parece ser un cubo de Cedro o Alerce. 14.39. Un tanque sellado que contiene agua de mar hasta una altura de 11.0 m contiene también aire sobre el agua a una presión manométrica de 3.00 atm. Sale agua del tanque a través de un agujero pequeño en el fondo. Calcule la rapidez de salida del agua. 3.0 atm I. Se trata de una ecuación de dinámica de fluidos, así pues, es Punto 1 necesario realizar el balance de energía y de masa. Ver esquema. 11.0 m Punto 2, U = 0 D. E. H = 11.0 m; Pa = 3.00 atm; v = ? D. I. Ecuación de Bernoulli; P1 + rgh1 + ½ rv12 = P2 + rgh2 + ½ rv22 r = 1000kg/m3 1 atm = 1.01325 x105 Pa E. Escribir las ecuaciones de balance de energía y masa para los puntos indicados. No olvidar señalar el cero de energía potencial. 3.0 atm A. Punto 1 Del esquema se puede observar que: v1 = 0; h2 = 0; 11.0 m h1 = 11.0 m; P1 – P2 = 3.0 atm Punto 2, U = 0 P1 + rgh1 = P2 + ½ rv22 𝑣" = $ ó 𝑣" = $ "([1.3](5351"6)*(5333)(7.8)(55.3)) 5333 "(&' (&) * ,-.' ) , = 28.70 m/s S. Sí, es una velocidad razonable dado el tamaño del contenedor. M. en C. Abraham Vilchis Uribe 14.30. Una esfera hueca de plástico se mantiene por debajo de la superficie de un lago de agua dulce mediante una cuerda anclada al fondo del lago. La esfera tiene un volumen de 0.650 m3 y la tensión en la cuerda es de 900 N. (ra = 1000kg/m3, g = 9.8 m/s2) a) Calcule la fuerza de flotación que ejerce el agua sobre la esfera. b) ¿Cuál es la masa de la esfera? c) La cuerda se rompe y la esfera se eleva a la superficie. wE Cuando la esfera llega al reposo, ¿qué fracción de su B T volumen estará sumergida? I. Del esquema se pueden ver las fuerzas que actúan en la esfera. Para el caso en el que se corta la cuerda, basta con hacer la tensión igual a cero. D. E. VE = 0.650 m3; T = 900 N; a) B = ? b) mE = ? c) Vd = ? D. I. B = ragVd; (ra = 1000kg/m3, g = 9.8 m/s2); ∑F = 0; E. a) Calcular directamente B; b) De la sumatoria de fuerzas despejat para la masa; c) Calcular el volumen desalojado directamente de B. A. a) B = ragVd = (1000)(9.8)(0.650) = 6370.00 N b) T + B + w = 0 ó m = (–T + B)/g = (–900 + 6370)/9.8 = 558.16 kg c) B = ragVd = mg ó Vd = m/ra = 558.16/1000 = 0.55816 m3 ≈ 85.87% V S. Sí, en general se obtienen resultados razonables dados los datos de entrada. 14.42. En un punto de una tubería, la rapidez del agua es de 3.00 m/s y la presión manométrica es de 5.00 x104 Pa. Calcule la presión manométrica en otro punto de la tubería, 11.0 más abajo, si el diámetro del tubo ahí es el doble que en el primer punto. M. en C. Abraham Vilchis Uribe I. Se trata de un ejercicio de hidrodinámica, así pues, se deben resolver simultáneamente la ecuación de continuidad y la de Bernoulli. P1 A1 v1 Ver esquema. H D. E. v1 = 3.00 m/s; H = 11.0 m; D. I. P2 A2 v2 P1 = 5.00 x104 Pa; D2 = 2D1; U=0 P2 = ? A1v1 = A2v2; A = ¼ πD2; P1 + rgh1 + ½ rv12 = P2 + rgh2 + ½ rv22; r = 1000 kg/m3. E. Plantear las ecuaciones de Continuidad y de Bernoulli, resolver simultáneamente y despejar para P2. A. De la ecuación de continuidad: v1 = A2v2/ A1 ó A1v1 = A2v2; A1 = ¼ πD12; A2 = ¼ πD22 = πD12; v1 = (πD12)v2/ (¼ πD12) v1 = 4v2 De la ecuación de Bernoulli, con h1 = 11.0 m y h2 = 0: P1 + rgH + 2rv22 = P2 + ½ rv22; ó P2 = P1 + rgH + (3/2)rv22 P2 = (5.00 x104) + (1000)(9.8)(11) + (3/2)(1000)(3/4)2 = 1.59 x105 Pa. S. Sí, pues la presión debe ser mayor, pues la velocidad es menor. 14.45. En cierto punto de una tubería horizontal, la rapidez del agua es de 2.50 m/s, y la presión manométrica es de 1.80 x 104 Pa. Calcule la presión manométrica en un segundo punto donde el área transversal es el doble que en el primero. I. Se trata de realizar un balance de masa y energía en dos secciones de una tubería horizontal, así pues, se deben resolver simultáneamente la ecuación de continuidad y la de Bernoulli. Ver esquema. M. en C. Abraham Vilchis Uribe P1 A1 v1 P2 A2 v2 D. E. v1 = 2.50 m/s; P1 = 1.80 x 104 Pa; A2 = 2A1; P2 = ? D. I. A1v1 = A2v2; P1 + rgh1 + ½ rv12 = P2 + rgh2 + ½ rv22; h1 = h2 r = 1000 kg/m3 E. Plantear las ecuaciones de continuidad y Bernoulli para los dos puntos y resolver para la presión. A. A1v1 = 2A1v2; ó v1 = 2v2; P1 + ½ rv12 = P2 + ½ rv22; ó P1 + ½ r(2v2)2 = P2 + ½ rv22; P2 = P1 + ½ r(2v2)2 – ½ rv22 = P1 + (3/2)(r)(v2)2 P2 = (1.80 x 104) + (3/2)(1000)(2.50/2)2 = 20343.75 Pa S. Sí, es una presión razonable, alrededor del doble de la presión atmosférica. M. en C. Abraham Vilchis Uribe