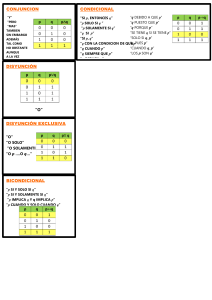
Tipos de enunciados: Guía de trabajo ENUNCIADOS SIMPLES Y COMPLEJOS Tras la lectura de "El reconocimiento de argumentos", sabemos que un argumento es un conjunto de enunciados en donde podemos reconocer premisas y conclusión. Sabemos también qué son los enunciados. Ahora bien, hay distintos tipos de enunciados y en lo que sigue presentaremos algunas clasificaciones. Nos detenemos en este punto porque entender estas clasificaciones nos permitirá eventualmente distinguir diferentes tipos de argumentos y evaluarlos. Es hora entonces de comenzar a leer el material de lectura “Tipos de enunciados”. Una vez que hayas concluido con la primera sección "Enunciados simples y complejos" realizá los siguientes ejercicios. Ejercicio 1 Teniendo en cuenta la distinción entre enunciados simples y complejos, elija qué características son propias de uno y otro tipo de enunciados. a. b. c. d. e. Contiene expresiones lógicas. Se puede descomponer en otros enunciados. No contiene expresiones lógicas. No se puede descomponer en otros enunciados. Para determinar si el enunciado es verdadero o falso hay que conocer el valor de verdad de los enunciados que se combinan y el funcionamiento semántico de la expresión lógica que se utiliza para combinarlos. Ejercicio 2 Determine si la siguiente oración es simple o compleja: De acuerdo con el censo realizado en 2010, la población argentina asciende a 40.117.096 de habitantes. Ejercicio 3 Determine si la siguiente oración es simple o compleja: Leibniz y Newton desarrollaron concepciones propias sobre la naturaleza de la gravedad. Ejercicio 4 Determine si la siguiente oración es simple o compleja: Si las lluvias persisten, entonces habrá que evacuar a los vecinos de la zona. CONJUNCIONES Es hora de distinguir distintos tipos de enunciados complejos atendiendo a las conectivas que se usan para formarlos. Teniendo en cuenta esto, diferenciaremos conjunciones, disyunciones (inclusivas y exclusivas), negaciones, condicionales y bicondicionales. Comencemos con las conjunciones, tras la lectura del apartado "Conjunciones" podrás aplicar lo aprendido en los siguientes ejercicios. Ejercicio 5 Determine si el siguiente enunciado es verdadero o falso. Deténgase a reflexionar sobre las razones que motivaron su respuesta. Los gatos y los perros son mamíferos. Ejercicio 6 Determine si el siguiente enunciado es verdadero o falso. Deténgase a reflexionar sobre las razones que motivaron su respuesta. 2+2=4 pero 2+1 también. Ejercicio 7 Determine si el siguiente enunciado es verdadero o falso. Deténgase a reflexionar sobre las razones que motivaron su respuesta. Todos los enunciados son oraciones pero no todas las oraciones son enunciados.* Ejercicio 8 Dadas dos oraciones cualesquiera (llamémoslas "A" y "B") y puestas en conjunción formando la oración "A y B", determine cuál sería el valor veritativo de esa oración compleja si "A" y "B" tuvieran los valores que se señalan a continuación (seleccione la opción correcta en cada caso). a. b. c. d. Si tanto A como B son verdaderas… Si tanto A como B son falsas… Si A es verdadera pero B falsa… Si B es verdadera pero A falsa... DISYUNCIONES Las oraciones disyuntivas o disyunciones combinan dos o más enunciados pero, a diferencia de lo que ocurre con las conjunciones, no se afirma que las proposiciones involucradas sean el caso, sino solo que al menos una de ellas lo es. Luego de leer la sección "disyunciones" deberías poder identificar este tipo de enunciados y distinguir las disyunciones inclusivas de las exclusivas. Más ejercicios para practicar... Ejercicio 9 Dado el siguiente enunciado, determine si se trata o no de una disyunción. Y, en caso de serlo, si se trata de una disyunción inclusiva o exclusiva. Para responder tenga en cuenta en qué condiciones estaría dispuesta a aceptar el enunciado como verdadero. Damián fue a la cancha este domingo o el anterior. Ejercicio 10 Dado el siguiente enunciado, determine si se trata o no de una disyunción. Y, en caso de serlo, si se trata de una disyunción inclusiva o exclusiva. Para responder tenga en cuenta en qué condiciones estaría dispuesta a aceptar el enunciado como verdadero. O bien Gladys tiene de mascota un gato, o bien tiene un perro. Ejercicio 11 Dado el siguiente enunciado, determine si se trata o no de una disyunción. Y, en caso de serlo, si se trata de una disyunción inclusiva o exclusiva. Para responder tenga en cuenta en qué condiciones estaría dispuesta a aceptar el enunciado como verdadero. Racing o Independiente ganará el partido en el que se enfrentan este domingo. Ejercicio 12 Dado el siguiente enunciado, determine si se trata o no de una disyunción. Y, en caso de serlo, si se trata de una disyunción inclusiva o exclusiva. Para responder tenga en cuenta en qué condiciones estaría dispuesta a aceptar el enunciado como verdadero. Maximiliano es amante de los deportes y de la música. Ejercicio 13 Teniendo en cuenta que los siguientes enunciados son verdaderos: - Júpiter es un planeta del Sistema Solar - El Sistema Solar es parte de la Vía Láctea. Determine si el siguiente enunciado es verdadero o falso: O bien Júpiter es un planeta del Sistema Solar o bien el Sistema Solar es parte de la Vía Láctea. Ejercicio 14 Teniendo en cuenta que los siguientes enunciados son verdaderos: - Júpiter es un planeta del Sistema Solar - El Sistema Solar es parte de la Vía Láctea. Determine si el siguiente enunciado es verdadero o falso: Júpiter es un planeta del Sistema Solar o el Sistema Solar es parte de la Vía Láctea. Ejercicio 15 Teniendo en cuenta que los siguientes enunciados son verdaderos: - Júpiter es un planeta del Sistema Solar - El Sistema Solar es parte de la Vía Láctea. Determine si el siguiente enunciado es verdadero o falso: Júpiter no es un planeta del Sistema Solar o el Sistema Solar no es parte de la Vía Láctea.* Ejercicio 16 Dados dos enunciados cualesquiera (llamémoslos "A" y "B") y puestos en disyunción (inclusiva) formando el enunciado "A o B", determine cuál sería el valor veritativo de ese enunciado complejo si "A" y "B" tuvieran los valores que se señalan a continuación (seleccione la opción correcta en cada caso). a. Si tanto A como B son verdaderos… b. Si tanto A como B son falsos… c. Si A es verdadero pero B falso… d. Si B es verdadero pero A falso... Ejercicio 17 Dados dos enunciados cualesquiera (llamémoslos "A" y "B") y puestos en disyunción (exclusiva) formando el enunciado "o bien A o bien B", determine cuál sería el valor veritativo de ese enunciado complejo si "A" y "B" tuvieran los valores que se señalan a continuación (seleccione la opción correcta en cada caso). a. Si tanto A como B son verdaderos… b. Si tanto A como B son falsos… c. Si A es verdadero pero B falso… d. Si B es verdadero pero A falso… CONDICIONALES Los condicionales son otro tipo de enunciados complejos. Luego de leer la sección que corresponde a este tipo de enunciados te sugerimos que tomes nota de los distintos modos de formular enunciados condicionales. ¿Qué diferencia existe entre condiciones necesarias y suficientes? ¿cómo identificar los enunciados que expresan uno y otro tipo de condición? ¿cuáles son las condiciones de verdad de los enunciados que expresan condiciones necesarias y cuáles las de aquellos que expresan condiciones suficientes? Una vez que tengas en claro la respuesta a estos interrogantes podrás resolver los ejercicios que consignamos abajo. Ejercicio 18 Dados los siguientes enunciados, determine si se trata o no de un enunciado condicional. De ser un enunciado condicional, determine si expresa una condición necesaria, una suficiente o si es un bicondicional. a. b. c. d. e. f. g. Si un metal es sometido al calor, se dilata. Los quarks, los leptones y los bosones son considerados partículas elementales. Solo si Beatriz madruga, Dios la ayudará. Lavinia aprobará solo si estudia. Es necesario ser mayor de 18 años para consumir bebidas alcohólicas. Ramiro tiene un ocho de promedio y aprobará la materia. Ramiro promocionará siempre y cuando su promedio sea mayor a siete. Ejercicio 19 Para cada enunciado listado, elija cuál de las siguientes opciones (1 , 2 o 3) resulta equivalente a dicho enunciado. (Le recomendamos que atienda a las expresiones involucradas.) Opciones: 1. Si llueve, el partido se suspende. 2. Sólo si llueve, el partido se suspende. 3. Llueve y el partido se suspende. Enunciados: a. El partido se suspende, si llueve. b. Es suficiente que llueva para que el partido se suspenda. c. El partido se suspende sólo si llueve. d. Es necesario que llueva para que el partido se suspenda. e. El partido se suspende y llueve. Ejercicio 20 Determine en qué situación resultaría falsa la siguiente oración. Si un metal es sometido al calor, se dilata. (Recuerde que si se trata de una oración condicional habrá una única situación en que la oración resultará ser falsa; en cambio, si la oración es bicondicional, serán dos las situaciones.) Seleccione una: a. El metal no es sometido al calor y no se dilata. b. El metal es sometido al calor y se dilata. c. El metal es sometido al calor y no se dilata. d. El metal no es sometido al calor y se dilata. Ejercicio 21 Determine en qué situación resultaría falsa la siguiente oración. Lavinia aprobará sólo si estudia. (Recuerde que si se trata de una oración condicional habrá una única situación en que la oración resultará ser falsa; en cambio, si la oración es bicondicional, serán dos las situaciones.) Seleccione una: a. Lavinia no aprueba y no estudia. b. Lavinia aprueba y no estudia. c. Lavinia no aprueba y estudia. d. Lavinia aprueba y estudia. Ejercicio 22 Determine en qué situación resultaría falsa la siguiente oración. Ana María irá siempre y cuando Magdalena vaya. (Recuerde que si se trata de una oración condicional habrá una única situación en que la oración resultará ser falsa; en cambio, si la oración es bicondicional, serán dos las situaciones.) Seleccione una o más de una: a. Ana María irá y Magdalena también. b. Ana María no irá pero Magdalena sí. c. Ana María irá pero Magdalena no. d. Ana María no irá y Magdalena tampoco. Ejercicio 23 Teniendo en cuenta que los siguientes enunciados son verdaderos: - Júpiter es un planeta del Sistema Solar - El Sistema Solar es parte de la Vía Láctea. Determine la verdad o falsedad de los siguientes enunciados condicionales. a. Si Júpiter es un planeta del Sistema Solar, el Sistema Solar es parte de la Vía Láctea. b. Solo si Júpiter es un planeta del Sistema Solar, el Sistema Solar es parte de la Vía Láctea. c. Si el Sistema Solar es parte de la Vía Láctea, Júpiter es un planeta del Sistema Solar. d. Solo si el Sistema Solar es parte de la Vía Láctea, Júpiter es un planeta del Sistema Solar. e. El Sistema Solar es parte de la Vía Láctea siempre y cuando Júpiter sea un planeta del Sistema Solar. f. Si el Sistema Solar es parte de la Vía Láctea, Júpiter no es un planeta del Sistema Solar. g. Solo si el Sistema Solar no es parte de la Vía Láctea, Júpiter es un planeta del Sistema Solar. h. Júpiter es un planeta del Sistema Solar solo si el Sistema Solar no es parte de la Vía Láctea. i. El Sistema Solar es parte de la Vía Láctea siempre y cuando Júpiter no sea un planeta del Sistema Solar. Ejercicio 24 Dadas dos oraciones, llamémoslas "p" y "q" y construyendo con ellas la oración "Si p entonces q", determine cuál sería el valor veritativo de esa oración compleja si “p” y “q” tuvieran los valores que se señalan a continuación. Seleccione la opción correcta en cada caso. Le recomendamos que primero identifique qué parte funciona como antecedente y como consecuente en dicha oración. a. Si "p" es verdadera y "q" falsa, la oración condicional 'Si p entonces q' es… b. Si tanto "p" como "q" son verdaderas, la oración condicional 'Si p entonces q' es… c. Si tanto p como q son falsas, la oración condicional 'Si p entonces q' es… d. Si "p" es falsa pero "q" verdadera, la oración condicional 'Si p entonces q' es... Ejercicio 25 Dadas dos oraciones, llamémoslas "p" y "q" y construyendo con ellas la oración "Solo si p entonces q", determine cuál sería el valor veritativo de esa oración compleja si “p” y “q” tuvieran los valores que se señalan a continuación. Seleccione la opción correcta en cada caso. Le recomendamos que primero identifique qué parte funciona como antecedente y como consecuente en dicha oración. a. Si "p" es verdadera y "q" falsa, la oración condicional 'Solo si p entonces q' es… b. Si tanto "p" como "q" son verdaderas, la oración condicional 'Solo si p entonces q' es… c. Si tanto p como q son falsas, la oración condicional 'Solo si p entonces q' es… d. Si "p" es falsa pero "q" verdadera, la oración condicional 'Solo si p entonces q' es… Ejercicio 26 Dadas dos oraciones, llamémoslas "p" y "q" y construyendo con ellas la oración "p siempre y cuando q", determine cuál sería el valor veritativo de esa oración compleja si “p” y “q” tuvieran los valores que se señalan a continuación. Seleccione la opción correcta en cada caso. a. b. c. d. Si "p" es verdadera y "q" falsa, la oración 'p siempre y cuando q' es… Si tanto "p" como "q" son verdaderas, la oración 'p siempre y cuando q' es… Si tanto p como q son falsas, la oración 'p siempre y cuando q' es… Si "p" es falsa pero "q" verdadera, la oración 'p siempre y cuando q' es... NEGACIONES Las negaciones no comportan mayores dificultades. Luego de leer la sección "negaciones" podrás resolver los siguientes ejercicios. Ejercicio 27 Teniendo en cuenta que el siguiente enunciado es verdadero: - Júpiter tiene más de una luna. Determine la verdad o falsedad de los siguientes enunciados: a. b. c. d. Júpiter no tiene más de una luna. No es cierto que Júpiter tenga más de una luna. Es cierto que Júpiter tiene más de una luna. No es verdad que Júpiter tenga más de una luna. Ejercicio 28 Teniendo en cuenta que los siguientes enunciados son verdaderos: - Júpiter tiene más de una luna. - La Tierra tiene una sola luna. Determine la verdad o falsedad de los siguientes enunciados complejos. a. b. c. d. e. f. g. h. i. Júpiter tiene más de una Luna o la Tierra tiene una sola. O bien Júpiter tiene más de una Luna o bien la Tierra tiene una sola. Ni Júpiter tiene más de una Luna ni la Tierra tiene una sola. Solo si la Tierra tiene una sola luna, Júpiter tiene más de una. La Tierra tiene una sola luna, si Júpiter tiene más de una. Solo si la Tierra no tiene una sola luna, Júpiter tiene más de una. La Tierra no tiene una sola luna, si Júpiter tiene más de una. La Tierra no tiene una sola luna siempre y cuando Júpiter no tenga más de una. No es cierto que Júpiter tenga más de una luna pero la Tierra tiene una sola. Enunciados singulares, universales, existenciales y probabilísticos Hasta aquí hemos clasificado los enunciados atendiendo a la presencia –o ausencia– de conectivas lógicas. Pero existen otros tipos de expresiones lógicas que no tienen la función de conectar oraciones, esto da lugar a una nueva clasificación entre diferentes tipos de enunciados: singulares, universales, existenciales y probabilísticos o estadísticos. Lee la sección del material de lectura que corresponde a estos tipos de enunciados y reflexioná en torno a las diferencias entre ellos. Podría ser una buena idea realizar un cuadro comparativo. Luego estarás en condiciones de resolver los ejercicios que te proponemos aquí. ¡Y vamos que ya falta poquito! Ejercicio 29 Clasifique los siguientes enunciados. Determine si se trata de enunciados singulares, universales, existenciales o estadísticos. a. b. c. d. e. Algunos animales son mamíferos. Todos los planetas generan fuerza de gravedad. Albert Einstein predijo la existencia de gravitación cuántica. Los delfines son mamíferos. Las chances de que salga un número par en un dado de seis caras es 50%. Ejercicio 30 Determine la verdad o falsedad de las siguientes oraciones. a. Para refutar una oración de la forma “Algunos S son P”, alcanza con encontrar algunos S que no sean P. b. Para refutar una oración de la forma “Todos los S son P” alcanza con encontrar un caso de S que no sea P. c. Para establecer la verdad de “Todos los S son P” alcanza con encontrar suficientes casos de S que sean P. d. No resulta sencillo probar la verdad o falsedad de los enunciados estadísticos o probabilísticos. e. Para establecer la verdad o falsedad de los enunciados singulares basta considerar el caso o individuo al que se refiere el enunciado. Contingencias, tautologías o contradicciones ¡Llegamos a la última sección del material de lectura! Hemos realizado una distinción entre distintos tipos de oraciones atendiendo a su forma y a sus condiciones de verdad. Hemos identificado oraciones simples y complejas y, dentro de las complejas: conjunciones, disyunciones, condicionales, bicondicionales y negaciones. Presentamos, también, otro nivel de análisis atendiendo al alcance de las oraciones: ya no se trata de combinar enunciados, sino de determinar a qué o a quiénes se refiere cada oración. Eso nos permitió identificar oraciones singulares, universales, existenciales y probabilísticas. En el apartado "Contingencias, tautologías y contradicciones" se ofrece una clasificación entre tipos de enunciados que responde a un criterio diferente. ¿Cuál es ese criterio? ¿en qué se diferencian estos tres tipos de oraciones? Podrás discutir estas preguntas en los foros temáticos, cuando tengas una respuesta, abordá las actividades que aquí te proponemos. Ejercicio 31 ¿Qué es una tautología? Complete la siguiente oración: Una tautología es un enunciado que es... Ejercicio 32 ¿Qué es una contradicción? Complete la siguiente oración: Una contradicción es un enunciado que es... Ejercicio 33 ¿Qué es una contingencia? Complete la siguiente oración: Una contingencia es un enunciado que... Ejercicio 34 Para cada uno de los siguientes enunciados, determine si son contingencias, tautologías o contradicciones. a. b. c. d. e. f. g. Si Hernán es presidente, Hernán es presidente. O hay vida en otro planeta o no la hay. Hay vida en otro planeta y no la hay. Buenos Aires es la capital de la República Argentina. Viedma es la capital de la República Argentina. Te quiero y no te quiero. No es cierto que te quiera y no te quiera. Ejercicio 35 Complete el siguiente enunciado. Seleccione una de las opciones que se ofrecen a continuación. Si una oración es contingente, su negación será una … (Para resolver este ejercicio, debe tener en cuenta no solo las definiciones de las nociones en cuestión, sino también las condiciones veritativas de los diferentes tipos de oraciones estudiadas). Seleccione una: a. Contradicción b. Tautología c. Contingencia Ejercicio 36 Complete el siguiente enunciado. Seleccione una de las opciones que se ofrecen a continuación. Si una oración es una contradicción, su negación será una … (Para resolver este ejercicio, debe tener en cuenta no solo las definiciones de las nociones en cuestión, sino también las condiciones veritativas de los diferentes tipos de oraciones estudiadas). Seleccione una: a. Contradicción b. Tautología c. Contingencia Ejercicio 37 Complete el siguiente enunciado. Seleccione una de las opciones que se ofrecen a continuación. Si una oración es una tautología y se la pone en conjunción con otra tautología, la oración resultante será una … (Para resolver este ejercicio, debe tener en cuenta no solo las definiciones de las nociones en cuestión, sino también las condiciones veritativas de los diferentes tipos de oraciones estudiadas). Seleccione una: a. Contradicción b. Tautología c. Contingencia Ejercicio 38 Complete el siguiente enunciado. Seleccione una de las opciones que se ofrecen a continuación. Si una oración es una tautología y se la pone en conjunción con una contingencia, la oración resultante será una… * (Para resolver este ejercicio, debe tener en cuenta no solo las definiciones de las nociones en cuestión, sino también las condiciones veritativas de los diferentes tipos de oraciones estudiadas). Seleccione una: a. contradicción b. Tautología c. contingencia Tipos de enunciados: Guía de trabajo - Respuestas Ejercicio 1 a. Complejo b. Complejo c. Simple d. Simple e. Complejo Ejercicio 2 El enunciado es simple. Este es un enunciado simple pues no contiene expresiones lógicas (las cuales no han sido caracterizadas exhaustivamente aún). De modo que para la determinación de su verdad, sólo deberemos recurrir a los registros del INDEC. Ejercicio 3 La oración es compleja. Se trata de una oración compleja, la cual surge a partir de la combinación de dos oraciones simples mediante la expresión "y". Esas oraciones simples son: "Leibniz desarrolló una concepción propia sobre la naturaleza de la gravedad" y "Newton desarrolló una concepción propia sobre la naturaleza de la gravedad". De modo que para que la oración compleja "Leibniz y Newton desarrollaron concepciones propias sobre la naturaleza de la gravedad" sea verdadera, ambas oraciones simples deberían serlo. Bastaría que una de ellas fuera falsa para que la oración compleja también lo fuera. Ejercicio 4 La oración es compleja. Se trata de una oración compleja, la cual surge a partir de la combinación de dos oraciones simples mediante la expresión "Si… entonces...". Esas oraciones son: "las lluvias persisten " y "habrá que evacuar a los vecinos de la zona”. Tal como indicaremos más adelante, esta oración no afirma que las lluvias persisten ni que habrá que evacuar a los vecinos de la zona; simplemente establece una conexión entre ambos eventos. Por esa razón, la oración será falsa cuando se dé que las lluvias persistan y no se dé que haya que evacuar a los vecinos. Otro punto importante a advertir es que las expresiones lógicas combinan cualquier tipo de oraciones –no necesariamente simples–; este es el caso, por ejemplo, de la oración: “Si las lluvias persisten o la crecida del río continúa, entonces habrá que evacuar a los vecinos de la zona”. Ejercicio 5 El enunciado es verdadero. Ahora bien, la pregunta que nos interesa formular es ¿por qué? Y la respuesta que debe tener en mente es: "porque los perros son mamíferos y los gatos también lo son". Eso está muy bien, pero lo que queremos poner de relieve es que su veredicto fue que la conjunción era verdadera, precisamente porque cada uno de los conyuntos involucrados lo era. Siendo ambos conyuntos: "Los gatos son mamíferos" y "Los perros son mamíferos". Ejercicio 6 La oración es falsa ¿Por qué la oración recibe ese valor de verdad? La oración es falsa porque se trata de una conjunción (como vimos "pero" sirve para formar conjunciones) y, si bien es verdad que 2+2=4, no lo es que 2+1=4. La oración que resulta de la conjunción de ambas es falsa, pues, insistimos, para que una conjunción sea verdadera, todos los conyuntos deben serlo. Ejercicio 7 El enunciado es verdadero. Se trata de la conjunción de dos enunciados: - Todos los enunciados son oraciones. - No todas las oraciones son enunciados. En donde ambos conyuntos comportan algún tipo de complejidad. En el primer enunciado dado por el "todo", en el segundo se suma además el empleo de la expresión "no". Sin entrar en detalles, pues estudiaremos esto más adelante, tras lo aprendido en el material de trabajo (y dado que somos hablantes competentes del castellano y usamos estas expresiones a diario), podemos afirmar que ambos conyuntos son verdaderos. Por lo tanto, la conjunción de ambos también lo es. Ejercicio 8 a. … la conjunción es verdadera. b…. la conjunción es falsa. c…. la conjunción es falsa. d…. la conjunción es falsa. Ejercicio 9 Es una disyunción inclusiva. Esta oración es efectivamente una disyunción, podemos advertirlo por el empleo de la expresión "o". Por ser una disyunción, deberíamos catalogarla de falsa si no fuera cierto que Damián hubiera ido a la cancha este domingo y tampoco fuera cierto que fue el anterior. Ahora bien, si al menos alguno de los disyuntos fuera verdadero, la disyunción de ambos también lo sería. ¿Pero qué ocurriría si resultara ser que fue ambos domingos? ¿Sería falsa la oración? No. La oración sólo se comprometía con la asistencia de Damián uno de los dos días, pero no excluía la posibilidad de que fuera ambos. Por esa razón, podemos considerar que la disyunción aquí involucrada tiene carácter inclusivo. Ejercicio 10 Es una disyunción exclusiva. Para su identificación resulta crucial atender a las expresiones "o bien.. o bien..." que suelen utilizarse para indicar que uno de los disyuntos es verdadero pero que no lo son ambos. Ejercicio 11 Es una disyunción exclusiva. Para su identificación resulta crucial atender al sentido de la oración, pues en este caso no se utiliza la expresión "o bien.. o bien…", sin embargo la disyunción tiene carácter excluyente. La razón radica en que dado que no pueden ganar ambos equipos, lo que la oración afirma es que uno de ellos (pero no los dos) ganará el partido en el que se enfrentan. Ejercicio 12 No es una disyunción. Esta oración no es una disyunción; sino una conjunción. La expresión lógica que da lugar a este enunciado complejo es la "y" y lo que este enunciado afirma es que ocurren conjuntamente dos cosas y no solo una de ellas. Esto es, para que este enunciado resulte ser verdadero tiene que darse tanto que Maximiliano ame los deportes como la música, no basta con que uno de los disyuntos resulte verdadero. Ejercicio 13 El enunciado es falso. La razón radica en que se trata de una disyunción exclusiva (las expresiones "o bien... o bien" lo sugerían), lo cual equivale a afirmar que uno de los dos disyuntos es verdadero pero no ambos. Sin embargo, en este caso ambos disyuntos son verdaderos. De modo que la oración compleja resulta ser falsa. Ejercicio 14 El enunciado es verdadero. La razón radica en que, a diferencia del ejercicio anterior, esta es una disyunción inclusiva (repará en la expresión). Ahora bien, afirmar una disyunción inclusiva equivale a afirmar que uno de los dos disyuntos es verdadero, o que ambos los son. Esto último ocurre en este ejercicio, ambos disyuntos son verdaderos. De modo que la oración compleja resulta ser verdadera. Ejercicio 15 El enunciado es falso. La razón radica en que, tal como en el ejercicio anterior, estamos frente a una disyunción inclusiva, pero a diferencia de aquel, ahora ambos disyuntos son falsos. Este ejercicio tiene un asterisco porque supone algo que no hemos estudiado aún, pero que podés saber por hablar castellano. Si una oración es verdadera, su negación será falsa. Y lo que ocurre aquí es que ambos disyuntos son la negación de una oración verdadera, de modo que ambos disyuntos son falsos. Ahora bien, una disyunción inclusiva será verdadera en caso de que uno o ambos disyuntos sean verdaderos, aquí ambos son falsos, por lo tanto, la oración a analizar resulta falsa. Ejercicio 16 a. ...la disyunción (inclusiva) es verdadera. b. ...la disyunción (inclusiva) es falsa. c. ...la disyunción (inclusiva) es verdadera. d. ...la disyunción (inclusiva) es verdadera. Ejercicio 17 a. … la disyunción (exclusiva) es falsa. b. … la disyunción (exclusiva) es falsa. c. … la disyunción (exclusiva) es verdadera. d. … la disyunción (exclusiva) es verdadera. Ejercicio 18 a. Enunciado condicional (condición suficiente) b. No es un enunciado condicional. c. Enunciado condicional (condición necesaria) d. Enunciado condicional (condición necesaria) e. Enunciado condicional (condición necesaria) f. No es un enunciado condicional. g. Enunciado bicondicional. Ejercicio 19 a-1 b-1 c-2 d-2 e-3 Ejercicio 20 La respuesta correcta es la “c”. Para determinar las condiciones de verdad de una oración condicional es necesario determinar qué tipo de condición está involucrada, si necesaria o suficiente, e identificar qué parte de la oración expresa dicha condición. Esta oración afirma que es condición suficiente que se someta al calor un metal para que se dilate. Lo primero es entonces el antecedente y lo segundo el consecuente. Sabemos que una oración condicional solo es falsa cuando su antecedente es verdadero y su consecuente falso, y ese es precisamente el caso representado por esta opción. Ejercicio 21 La respuesta correcta es la “b”. En esta situación el enunciado condicional resultaría falso. Para determinar las condiciones de verdad de una oración condicional es necesario determinar qué tipo de condición está involucrada, si necesaria o suficiente, e identificar qué parte de la oración expresa dicha condición. Esta oración afirma que es condición necesaria que Laviña estudie para que apruebe. Recordemos que la expresión "solo sí" indica que la condición es necesaria e introduce el consecuente del condicional. De modo que el antecedente será "Laviña aprueba". (¡Si esto te resulta extraño te recomendamos que revises el material de lectura!). Como cualquier enunciado condicional, solo es falso cuando su antecedente es verdadero y su consecuente falso. Ejercicio 22 La respuesta es “c” y “b”. La oración es una oración bicondicional, por ello hemos reconocido dos respuestas que responden a dos situaciones. Si ambas partes de la oración tienen el mismo valor de verdad, la oración será verdadera; por el contrario, si ambas partes reciben valor de verdad diferente -tal como ocurre en estos dos casos-, la oración condicional será falsa. Ejercicio 23 a. b. c. d. e. f. g. h. i. Verdadero Verdadero Verdadero Verdadero Verdadero Falso Falso Falso Falso Ejercicio 24 a. Falsa b. Verdadera c. Verdadera d. Verdadera Ejercicio 25 a. Verdadera b. Verdadera c. Verdadera d. Falsa Ejercicio 26 a. Falsa b. Verdadera c. Verdadera d. Falsa Ejercicio 27 a. Falsa b. Falsa c. Verdadera d. Falsa Ejercicio 28 a. Verdadera b. Falsa c. Falsa d. Verdadera e. Verdadera f. Falsa g. Falsa h. Verdadera i. Falsa Ejercicio 29 a. Existencial b. Universal c. Singular d. Universal e. Estadístico Ejercicio 30 a. Falsa b. Verdadera c. Falsa d. Verdadera e. Verdadera Ejercicio 31 Respuesta posible es "Una tautología es un enunciado que es siempre verdadero". Las tautologías son aquellos enunciados que son verdaderos en toda situación, que no hay modo de que sean falsos. Hay ciertas formas de enunciados que resultan tautológicas ¿te acordás de algunas de ellas? Ejercicio 32 Una respuesta posible es "Una contradicción es un enunciado que es siempre falso". Las contradicciones son aquellos enunciados que son falsos en toda situación, que no hay modo de que sean verdaderos. Hay ciertas formas de enunciados que resultan contradictorias ¿te acordás de algunas de ellas? Ejercicio 33 Una respuesta posible es "Una contingencia es un enunciado que puede ser verdadero o falso dependiendo del caso". Las contingencias son aquellas oraciones que pueden resultar ser verdaderas o falsas según sea el caso, según se dé o no el estado de cosas afirmado en ellas. A diferencia de lo que ocurre con las tautologías y las contradicciones -en donde la verdad de dichas oraciones está determinada por la forma de las oraciones-, las contingencias son tales que su verdad o falsedad depende de su contenido. Si la realidad fuera otra, otro podría ser su valor de verdad. Incluso con oraciones como "La Tierra está en movimiento", la cual nos parece obviamente verdadera, son contingencias. Pues si bien se trata de una oración verdadera (o al menos eso creemos hoy en día), su verdad no depende de la estructura de la oración sino de qué ocurra con la Tierra. Y, obviamente, podría resultar ser falsa (tal vez nuestros antepasados estaban en lo cierto después de todo). Ejercicio 34 a. Tautología b. Tautología c. Contradicción d. Contingencia e. Contingencia f. Contradicción g. Tautología Ejercicio 35 La respuesta es “c”. Si una oración es una contingencia, entonces sabemos que hay ciertas situaciones en las que es verdadera y otras en las que es falsa. Ahora bien, la negación de una oración precisamente invierte los valores veritativos. Si la oración que se niega era verdadera, su negación será falsa; y si era falsa, su negación será verdadera. Eso nos asegura que habrá situaciones en las que la oración negada resulte ser falsa y otras en las que resulte ser verdadera. Por lo tanto, también será contingente. Ejercicio 36 La respuesta es “b”. Una oración es una contradicción, entonces sabemos que es falsa en todos los casos, es necesariamente falsa. Ahora bien, la negación de una oración precisamente invierte los valores veritativos. Si la oración que se niega era verdadera, su negación será falsa; y si era falsa, su negación será verdadera. Eso nos asegura que en todas las situaciones la oración negada será verdadera. Por lo tanto, será tautológica. Ejercicio 37 La respuesta es “b” Efectivamente, si una oración es una tautología, entonces sabemos que es verdadera en todos los casos, es necesariamente verdadera. Ahora bien, la conjunción entre dos oraciones es verdadera únicamente cuando ambas son verdaderas. Dado que ambas oraciones son verdaderas en todos los casos, su conjunción también lo será. Por lo tanto, será tautológica. Ejercicio 38 La respuesta correcta es “c”. Si una oración es una tautología, entonces sabemos que es verdadera en todos los casos, es necesariamente verdadera. Por su parte, una contingencia es verdadera en algunos casos y falsa en otros. Ahora bien, la conjunción entre dos oraciones es verdadera únicamente cuando ambas son verdaderas, en el resto de los casos es falsa. Dado que uno de los conyuntos será verdadero en algunos casos y falso en otros, su conjunción con una oración siempre verdadera será verdadera en los casos en que la contingencia sea verdadera y falsa cuando sea falsa. Por lo tanto, será una contingencia.