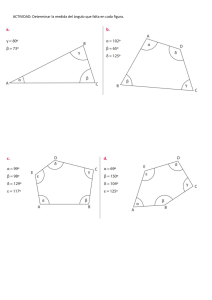
III BIM – GEOMETRÍA Símbolos Año Autor 1228 Fibonacci 1464 Regiomontano 1489 Widmann 2+3=5 1557 Recorde 30º 1571 Reinhold decimales 1585 Stevin 2,17 1617 Naiper Log 27 1624 Naiper 1629 Girard 1631 Harriot 1637 Descartes 1675 Leibniz F(x) 1734 Euler 1736 Euler e 1739 Euler Sen, cos 1753 Euler 1755 Euler i 1777 Euler Ángulos 1816 Crelle 3·4 3+4 4–3 3<4 4 >3 25 III BIM – GEOMETRÍA NIVEL: SECUNDARIA GEOMETRÍA IEP LISCAY EL ÁNGULO DEFINICION Es la figura geométrica formada por la unión de dos rayos mediante un origen común llamado VÉRTICE DEL ÁNGULO, los rayos son los lados del ángulo. A O ELEMENTOS º A Lados : ....................................... Vértice : ....................................... Notación ....................................... m∢AOB ....................................... MEDICIÓN ANGULAR Para poder diferenciar a los ángulos de acuerdo a su abertura se crearon diferentes sistemas de medición angular, tales como: El Sistema Sexagesimal o Sistema Inglés. El sistema centesimal o Sistema Francés y el sistema radial o circular o sistema internacional. El sistema que estudiaremos es el SISTEMA SEXAGESIMAL o SISTEMA INGLÉS. Sus creadores tomaron como base a una circunferencia dividiéndola a ésta en 360 partes iguales y cada parte la llamaron un grado sexagesimal, además a cada grado también lo dividieron pero en 60 partes siendo cada parte un minuto sexagesimal, a este minuto lo dividieron en 60 partes, siendo cada parte un segundo sexagesimal. En este capítulo haremos uso del transportador como instrumento de medición, para ello observa con bastante atención, pues la figura muestra el uso de un transportador para medir ángulos. C B 90º D 60º m∢AOB = 55º ; m AOC = 90º ; m∠AOD = 150º 50º 150º m AOE = 180º 0º 180º E A O ÁNGULOS CONGRUENTES Se dice que dos ángulos son congruentes si tienen igual medida. A Si el ángulo ABC es congruente con el ángulo E EOF, entonces escribiremos: ABC ≅ EOF B C O También: F m ABC m EOF III BIM – GEOMETRÍA a) 45º EJERCICIOS DE APLICACIÓN B b) 60º c) 30º d) 15º 1. De acuerdo a la figura, relacione correctamente los datos de ambas columnas. O A 6. En la figura, AOB y COD son congruentes, halle el valor de “x” B O º + 30º e) 20º B D A a) OA ( ) notación del ángulo b) O ( ) Medida del ángulo c) Lado del ángulo d) AOB ( ) Vértice del ángulo 2. Indique si es verdadero (V) o falso (F) lo que a continuación se menciona. La notación de un ángulo se hace con letras minúsculas. ( ) Los rayos que forman al ángulo son sus lados. ( ) La medida de un ángulo geométrico es un número negativo. ( ) El ángulo es formado por la unión de dos semirrectas. ( ) O 30º O A a) 10º b) 20º d) 40º e) 50º 2x - 10º C c) 30º 7. Haciendo uso del transportador, dibuje un ángulo de 30º 180º O 0º 8. Haciendo uso del transportador obtenga un ángulo de 90º 3. Si dos ángulos tienen la misma medida, se dicen que son: a) Agudos b) Suplementarios c) Complementarios d) Congruentes 180º e) N.A. 4. Si el ángulo mostrado tiene como medida 60º. Halle el valor de “x”. O 0º 9. Con ayuda del transportador, dibuja un ángulo de 120º B a) 30 b) 20 180º c) 60 d) 12 e) 5 3xº O A 5. El ángulo mostrado mide 45º, halle el valor de “”. O 0º III BIM – GEOMETRÍA 10. Haciendo uso del transportador mide los ángulos: AOB y COD Indique su conclusión a) C B b) c) d) 2 e) N.A. O D A 11. La figura muestra una circunferencia, obtenga con el transportador la medida de una semicircunferencia (O : centro) a) 120º b) 130º c) 180º O d) 90º e) 45º 12. Del problema anterior, indique la medida angular de la cuarta parte de la circunferencia. a) 45º d) 120º b) 90º e) 360º c) 180º 13. De la figura y con ayuda del transportador, encuentre la relación entre “” y “”. a) b) c) d) e) 2 14. Con la ayuda del transportador, encuentre aproximadamente el valor de : . a) 90º b) 180º c) 270º d) 360º e) 45º 15. Haciendo uso del transportador obtenga una relación entre “” “” a) b) c) d) e)