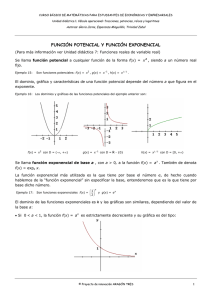
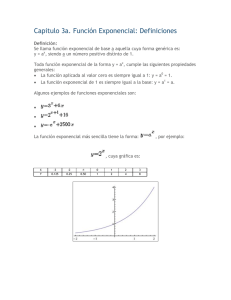
GUÍA DE TRABAJO AUTÓNOMO El trabajo autónomo es la capacidad de realizar tareas por nosotros mismos, sin necesidad de que nuestros/as docentes estén presentes. Centro Educativo: Liceo de Guardia Educadora: Sheila Rodríguez López Nivel: Undécimo año Asignatura: Matemática Conocimientos: Ecuaciones exponenciales Función logarítmica INTRUCCIONES GENERALES PARA RESOLVER ESTA GUÍA: Lea muy bien las indicaciones de cada parte de esta guía. Debe resolver esta guía, según la semana del mes que corresponda. Puede ser resuelta con lápiz, para realizar fácilmente posibles correcciones. Imprima esta guía de trabajo autónomo y resuelva todos los ejercicios propuestos. Si no tiene acceso a imprimir, copie y resuelva en su cuaderno los ejercicios propuestos, Revise las respuestas correctas que se le brindan de los ejercicios propuestos como práctica, haga una auto reflexión e identifique sus posibles errores, corríjalos hasta obtener buenos resultados. No salga de su casa a imprimir esta guía. ¡Quédate en casa! 1. Me preparo para hacer la guía Pautas que debo verificar antes de iniciar mi trabajo. Materiales o recursos que voy a necesitar Condiciones que debe tener el lugar donde voy a trabajar Tiempo en que se espera que realice la guía Papel, lápiz, puede usar calculadora únicamente para verificar resultados. Buena iluminación, mesa con silla o un lugar donde pueda apoyar el cuaderno cómodamente, buena ventilación. El que sea necesario para terminarla (no excederse más de una semana en cada guía). 2. Voy a recordar lo aprendido y aprendo. Indicaciones Se recomienda repasar y aprenderse las características de la función exponencial, para alcanzar un mayor entendimiento y un aprendizaje significativo de la materia. En cada ejercicio, escriba todos los pasos que utilizó para obtener cada resultado. En esta sección repasaremos algunos de los componentes del Programa de Estudio de Matemática para undécimo año, según los indicadores del aprendizaje esperado en este nivel: Plantear y resolver problemas en contextos reales utilizando ecuaciones exponenciales. Actividad Se espera que, con la realización de esta guía, Usted desarrolle habilidades relacionadas al tema de propiedades de las potencias y ecuaciones exponenciales. Usted debe realizar paso a paso las actividades que se le proponen, lea con detenimiento los textos, responda y escriba las respuestas a las preguntas que se le van presentando. Las preguntas que se presentan a continuación, pretenden ayudarle a recordar lo visto del tema anteriormente. Preguntas 1. Para la función 𝑓 dada por 𝑓(𝑥 ) = 3−𝑥 , en el criterio de dicha función, para el valor de la base corresponde a: reflexionar y 1 ( )−𝑥 ( )−3 ( )3 ( ) responder 3 2. El dominio de la función 𝑓 dada por 𝑓 (𝑥 ) 3 ( ) [ , +∞[ 2 3. La gráfica dada por ( )( 4 , 0) 5 3 ( ) ]−∞, ] 2 3 𝑥 = (2) es: ( )ℝ + ( )ℝ 4 𝑥 𝑓 ( 𝑥 ) = (5) , interseca al eje 𝑦 en: 4 ( ) (0 , ) 5 ( ) ( 0 ,1 ) ( ) ( 1 ,0 ) Pero antes de realizar esta guía le sugiero tener su cuaderno de Matemática a la mano para que pueda consultar o hacer anotaciones de datos e información importante que le pueda ayudar a comprender la materia. Si es posible y tiene conexión a internet, puede ver el video que se encuentra en el siguiente enlace: https://www.youtube.com/watch?v=nR3INhQWHGc 3. Lo que debo saber y pongo en práctica lo aprendido. Para iniciar el trabajo de esta semana, una vez vistos y entendidos los videos anteriores, vamos a empezar a leer cada texto, observar los ejemplos resueltos y contestar lo que se nos solicita. Ecuaciones Exponenciales Son aquellas ecuaciones que presentan a la incógnita en el exponente. Para resolver una ecuación exponencial debemos tener presente los siguientes casos: Ley de bases iguales: Si en una igualdad de dos potencias las bases son iguales, entonces sus exponentes también serán iguales. Si 𝑥 𝑎 = 𝑥 𝑏 ⇒ 𝑎=𝑏 Ejemplos 𝟐𝒙 = 𝟐𝟕 bases iguales ⇒𝒙 = 𝟕 𝟑𝟑𝒙 = 𝟑𝟗 𝟑𝒙 = 𝟗 𝒙 = 𝟗 𝟑 𝒙 = 𝟑 𝟓𝟐𝒙 = 𝟓𝟔 𝟐𝒙 = 𝟔 𝒙 = 𝟔 𝟐 𝟕𝒙+𝟐 = 𝟕𝟑 𝒙 = 𝟑 𝒙 + 𝟐 = 𝟑 𝒙 = 𝟑 − 𝟐 𝒙 = 𝟏 Otros ejemplos Halle el valor de x: Halle el valor de x: 2𝑥 = 16 Como las bases deben ser iguales en ambos lados de la igualdad y 323𝑥 = 167 (25 )3𝑥 = 16 = Entonces 2𝑥 = 24 𝑥 = 4 5𝑥−1 = 1 25 5𝑥−1 = 1 52 (24 )7 215𝑥 = 228 24 Halle el valor de x: 15𝑥 = 28 5𝑥−1 = 5−2 28 𝑥 = 15 𝑥 − 1 = −2 𝑥 = −2 + 1 𝑥 = −1 Determine el valor de x: 165𝑥−1 ÷ 25 = 8 (24 )5𝑥−1 ÷ 25 = 23 220𝑥−4 ÷ 25 = 23 220𝑥−4−5 = 23 20𝑥 − 9 = 3 20𝑥 = 3 + 9 20𝑥 = 12 12 3 𝑥 = = 20 5 3 √72𝑥−5 = 49 2𝑥−5 7 3 Observemos estos otros ejemplos = 7 2 73𝑥−12 − 5 = −4 73𝑥−12 = −4 + 5 73𝑥−12 = 1 2𝑥 − 5 = 2 3 73𝑥−12 = 70 2𝑥 − 5 = 2 ∙ 3 3𝑥 − 12 = 0 2𝑥 − 5 = 6 3𝑥 = 0 + 12 2𝑥 = 6 + 5 3𝑥 = 12 2𝑥 = 11 𝑥 = 11 2 𝑥 = 12 3 𝑥 = 4 Se simplificó por 4 Aplicación en un contexto real Ejemplo: En un laboratorio se realiza un cultivo bacteriano, el peso se duplica cada día y el peso inicial es de 5 𝑔𝑟𝑎𝑚𝑜𝑠; determine el criterio de la función que cumple con estas condiciones, realice la tabulación con algunos valores, elabore la gráfica correspondiente y determine cuántos días pasaron si el crecimiento corresponde a 5 120 gramos. Paso 1: Interpretación Paso 2: Gráfica de 𝒇( 𝒙 ) = 𝟓 ∙ 𝟐𝒙 Peso inicial: 5 gramos Crecimiento por día: el doble Días 0 1 2 3 4 5 … Crecimiento 5∙1 = 5 5 ∙ 2 = 10 5 ∙ 2 ∙ 2 = 20 5 ∙ 2 ∙ 2 ∙ 2 = 40 5 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 80 5 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 160 ………… Paso 3: Función 𝑓( 𝑥 ) = 5 ∙ 2𝑥 5 120 = 5 ∙ 2𝑥 5 120 = 2𝑥 5 1024 = 2𝑥 210 = 2𝑥 10 = 𝑥 Relación 5 ∙ 20 5 ∙ 21 5 ∙ 22 5 ∙ 23 5 ∙ 24 5 ∙ 25 5 ∙ 2𝑛 Paso 4: Respuesta Cuando el crecimiento es igual a 5 120 gramos han pasado 10 días. Ejercicios propuestos INSTRUCCIONES: Copie los ejercicios o imprima esta página y péguela en su cuaderno. Resuelva las siguientes ecuaciones exponenciales. 3𝑥 = 27 2𝑥+2 = 16 4𝑥 ∙ 16𝑥 = 4 42𝑥−5 = 64 22(𝑥+1) = 26 3𝑥+1 = 243 Resuelva el siguiente problema: En el año 2015 en una ciudad, se realiza un censo y se obtiene que está conformada por 131 000 habitantes, si la tasa relativa de crecimiento es de un 1 , 47 % ; determine la cantidad aproximada de habitantes que aumentará en el año 2023. ESTUDIANTE: Con este instrumento usted puede realizar un proceso de autorregulación y evaluación del trabajo realizado: Con el trabajo autónomo voy a aprender a aprender Reviso las acciones realizadas durante la construcción del trabajo. Marco una X encima de cada símbolo al responder las siguientes preguntas ¿Leí las indicaciones con detenimiento? ¿Me devolví a leer las indicaciones cuando no comprendí qué hacer? Con el trabajo autónomo voy a aprender a aprender Valoro lo realizado al terminar por completo el trabajo. Marca una X encima de cada símbolo al responder las siguientes preguntas ¿Leí mi trabajo para saber si es comprensible lo escrito o realizado? ¿Revisé mi trabajo para asegurarme si todo lo solicitado fue realizado? ¿Me siento satisfecho con el trabajo que realicé? Explico ¿Cuál fue la parte favorita del trabajo? ¿Qué puedo mejorar, la próxima vez que realice la guía de trabajo autónomo? Autoevalúo mi nivel de desempeño Al finalizar mi trabajo por completo, autoevalúo el nivel de desempeño que alcancé. Marco con una X la casilla correspondiente. Indicadores del aprendizaje esperado Interpreto datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial. Nivel de desempeño Inicial Intermedio Avanzado Menciono datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Inicial Brindo particularidades acerca de los datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Indico de manera específica los datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Intermedio Avanzado Anoto las condiciones que cumple una situación determinada, que le hacen corresponder a una función exponencial. Destaco aspectos relevantes acerca del modelo de función exponencial que puede utilizar para dar solución a un problema. Asigno los pasos necesarios para solucionar un problema utilizando el modelo de función exponencial. Indicadores del aprendizaje esperado Establezco los pasos necesarios para hallar la solución de un problema utilizando la función exponencial. 1. Me preparo para hacer la guía Pautas que debo verificar antes de iniciar mi trabajo. Materiales o recursos que voy a necesitar Condiciones que debe tener el lugar donde voy a trabajar Tiempo en que se espera que realice la guía Papel, lápiz, puede usar calculadora únicamente para verificar resultados. Buena iluminación, mesa con silla o un lugar donde pueda apoyar el cuaderno cómodamente, buena ventilación. El que sea necesario para terminarla (no excederse más de una semana en cada guía). 2. Voy a recordar lo aprendido y aprendo. Indicaciones Se recomienda repasar y aprenderse las características de la función exponencial, para alcanzar un mayor entendimiento y un aprendizaje significativo de la materia. En cada ejercicio, escriba todos los pasos que utilizó para obtener cada resultado. En esta sección repasaremos algunos de los componentes del Programa de Estudio de Matemática para undécimo año, según los indicadores del aprendizaje esperado en este nivel: Identificar la función logarítmica como la inversa de la función exponencial. Analizar gráfica y algebraicamente las funciones logarítmicas. Actividad Preguntas para reflexionar y responder Se espera que, con la realización de esta guía, Usted desarrolle habilidades relacionadas al tema de propiedades de las potencias y ecuaciones exponenciales. Usted debe realizar paso a paso las actividades que se le proponen, lea con detenimiento los textos, responda y escriba las respuestas a las preguntas que se le van presentando. Las preguntas que se presentan a continuación, pretenden ayudarle a recordar lo visto del tema anteriormente. 1. En condiciones ideales se sabe que cierta población de bacterias se duplica cada 3 horas, suponga que primero hay 100 bacterias. a) ¿ Cuál es el tamaño de la población después de 15 horas ? b) ¿ Cuál es el tamaño después de 𝑡 horas ? c) Estime el tamaño de la población después de 20 horas. 2. En una ciudad de 9000 habitantes se esparce un rumor de modo que cada hora se duplica la cantidad de personas que se enteran del mismo. ¿ Cuántas personas conocerán el rumor al cabo de 12 horas ? Pero antes de realizar esta guía le sugiero tener su cuaderno de Matemática a la mano para que pueda consultar o hacer anotaciones de datos e información importante que le pueda ayudar a comprender la materia. Si es posible y tiene conexión a internet, puede ver el video que se encuentra en el siguiente enlace: https://www.youtube.com/watch?v=Dl-8PKOHgbQ La función inversa de la exponencial La función exponencial 𝑓 ( 𝑥 ) = 𝑎 𝑥 , 𝑓: ℝ → ℝ+ en donde 𝑎 > 0 ; 𝑎 ≠ 0 𝑦 𝑎 ≠ 1 ; es una función inyectiva y su codominio es igual al ámbito, por lo tanto posee su correspondiente función inversa, a continuación se detalla un ejemplo en donde se analiza el criterio de la función exponencial, la tabulación y la gráfica. A partir de la función 𝑓 se obtendrá la tabulación y la gráfica de 𝑓 −1 . Ejemplo Criterio 𝒇 ( 𝒙 ) = 𝟑𝒙 Tabulación de 𝑓 𝑥 𝑦 −3 0,03 −2 0,11 −1 0,33 0 1 1 3 2 9 3 27 (2 , 9) (3 , 27) 9 2 27 3 Pares ordenados de 𝒇 (−3 ; 0,03 ) (−2 , 0,11 ) (−1 ; 0,33) (0 , 1) (1 , 3) Tabulación de 𝒇−𝟏 𝑥 𝑦 0,03 −3 0,11 −2 Gráfica de 𝒇 𝒚 𝒇−𝟏 0,33 −1 1 0 3 1 Función Logarítmica Es la función inversa de la función exponencial. Está presente en una gran cantidad de fenómenos observables. La función exponencial 𝑓 con base 𝑎 y variable 𝑥 , se denota mediante la expresión: 𝑓 ( 𝑥 ) = 𝑎 𝑥 , 𝑓 ∶ ℝ → ℝ+ en donde 𝑎 > 0 , 𝑎 ≠ 0 𝑦 𝑎 ≠ 1 ; así mismo se define su función inversa logarítmica 𝑓 con base 𝑎 y argumento 𝑥 , en donde se denota mediante la expresión: 𝑓 ( 𝑥 ) = 𝑙𝑜𝑔𝑎 𝑥 , 𝑓 ∶ ℝ+ → ℝ en donde 𝑎 > 0 , 𝑎 ≠ 0 𝑦 𝑎 ≠ 1. Características de la Función Logarítmica No interseca al eje 𝑦 Es asintótica al eje 𝑦 negativo Interseca al eje 𝑥 en 1 ,0 Ámbito: ℝ Dominio: ℝ+ Es inyectiva I Caso: Estrictamente creciente Si la base es mayor que uno: 𝑎 > 1. Considera estas tablas de valores usando la base 2. Tabla 1 Entrada x, un exponente Salida y x −3 y = 2x Tabla 2 Entrada x, un número que es una potencia de 2 x = 2y Salida y, el exponente de 2 y −3 −2 −2 −1 −1 0 1 1 0 1 2 2 1 2 4 4 2 3 8 8 3 Observa que las dos tablas son iguales excepto que las columnas están invertidas; el punto (1, 2) tomado de la primera tabla será el punto (2, 1) en la segunda tabla. Las gráficas de estas dos relaciones deben tener en general la misma forma. Como se muestra en la gráfica, las dos curvas son simétricas en la línea y = x. Otra manera de decirlo, si rotas la curva roja sobre la línea y = x, va a coincidir con la curva azul. (Esto tiene sentido, porque 𝑦 en la primera tabla se vuelve 𝑥 en la segunda tabla y viceversa.) La ecuación x = 2y normalmente se escribe como una función logarítmica (también llamada función log). La función logarítmica de x = 2y se escribe como y = log2 x o f(x) = log2 x. El número 2 se sigue llamando base. En general y = logb x se lee como, “y igual al logaritmo base b de x.” Al igual que con las funciones exponenciales, b > 0 y b ≠ 1. Puedes ver en la gráfica que el rango (valores de y) de la función exponencial (en rojo) es todos los números reales positivos. Como la entrada y la salida se han cambiado, el dominio (valores de x) de la función logarítmica (en azul) es todos los números reales positivos. De manera similar, el dominio de la función exponencial (en rojo) es todos los números reales. El rango de la función logarítmica (en azul) es todos los números reales. Otros ejemplos de funciones logarítmicas con base mayor que uno. Gráfica y = log3 x Gráfica y = log4x Gráfica y = log2 x II Caso: Estrictamente decreciente Si la base es mayor que uno: 0 < 𝑎 < 1. Ejemplo: Graficar 𝑓 ( 𝑥 ) = 𝑙𝑜𝑔1 𝑥 4 𝑦 = 𝑙𝑜𝑔1 𝑥 4 x 16 4 1 1 4 1 16 1 𝑦 ( ) =𝑥 4 y -2 -1 0 1 2 Otros ejemplos de funciones logarítmicas estrictamente decrecientes 𝒇 ( 𝒙 ) = 𝒍𝒐𝒈𝟓 𝒙 𝒇 ( 𝒙 ) = −𝒍𝒐𝒈𝟖 𝒙 = 𝒍𝒐𝒈𝟏 𝒙 𝟖 𝟔 La base corresponde a: 5 La base corresponde a: ̅ = 0 , 83 6 Por lo tanto 5 Por lo tanto 6 < 1 1 8 1 8 = 0 , 125 < 1 Las funciones logarítmicas la conforman una base constante y un argumento variable. Criterio Base 3 Argumento 𝑥 2 5 𝑥 4,6 𝑥 𝑓 ( 𝑥 ) = 𝑙𝑜𝑔3 𝑥 𝑔 ( 𝑥 ) = 𝑙𝑜𝑔2 𝑥 5 ℎ ( 𝑥 ) = 𝑙𝑜𝑔4 ,6 𝑥 Criterios de funciones que no corresponden a Funciones logarítmicas La base NO puede ser negativa ni cero. 𝑣 ( 𝑥 ) = 𝑙𝑜𝑔(−4)𝑥 Base: −4 𝑎 ( 𝑥 ) = 𝑙𝑜𝑔5 7 𝑥 La base no puede ser una variable. 𝑧 ( 𝑥 ) = 𝑙𝑜𝑔𝑥 𝑥 7 7 Argumento: El argumento NO puede ser una constante. Base: 5 Argumento: 7 Base: 𝑥 Argumento: 𝑥 3. Lo que debo saber y pongo en práctica lo aprendido. Ejercicios propuestos INSTRUCCIONES: Copie los ejercicios o imprima esta página y péguela en su cuaderno. 1. Determine cuáles de los siguientes criterios se clasifican como funciones logarítmicas. Anote sobre la línea si o no según corresponda. 𝑓 (𝑥 ) = 𝑙𝑜𝑔4 𝑥 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔1 (5𝑥 )_____ 𝑓 (𝑥 ) = −𝑙𝑜𝑔1 𝑥 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔8 𝑥 _____ 4 4 𝑓(𝑥) = 𝑙𝑜𝑔10 6 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔−6 𝑥 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔5 𝑥 _____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔0 𝑥 _____ 2. Clasifique las siguientes funciones logarítmicas como crecientes o decrecientes. Anote sobre la línea creciente ( c ) o decreciente ( d ) según corresponda. 𝑓 (𝑥 ) = 𝑙𝑜𝑔3 𝑥 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔2 ( 3𝑥 ) ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔8 𝑥 ____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔4 ( 5𝑥 )____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔0 ,15𝑥 _____ 𝑓 (𝑥 ) = 𝑙𝑜𝑔6 𝑥 _____ 7 7 3. Para las siguientes funciones logarítmicas, elabore la gráfica y determine las características que se le solicitan en cada caso. Criterio de la función 𝑓 (𝑥 ) = 𝑙𝑜𝑔3 𝑥 , 𝑓: ℝ+ → ℝ Dominio Ámbito Imagen solicitada Régimen de Variación Esbozo de gráfica 𝑓 ( 81 ) Sugerencia: Se recomienda elaborar el esbozo de la gráfica en un espacio cómodo. ESTUDIANTE: Con este instrumento usted puede realizar un proceso de autorregulación y evaluación del trabajo realizado: Con el trabajo autónomo voy a aprender a aprender Reviso las acciones realizadas durante la construcción del trabajo. Marco una X encima de cada símbolo al responder las siguientes preguntas ¿Leí las indicaciones con detenimiento? ¿Me devolví a leer las indicaciones cuando no comprendí qué hacer? Con el trabajo autónomo voy a aprender a aprender Valoro lo realizado al terminar por completo el trabajo. Marca una X encima de cada símbolo al responder las siguientes preguntas ¿Leí mi trabajo para saber si es comprensible lo escrito o realizado? ¿Revisé mi trabajo para asegurarme si todo lo solicitado fue realizado? ¿Me siento satisfecho con el trabajo que realicé? Explico ¿Cuál fue la parte favorita del trabajo? ¿Qué puedo mejorar, la próxima vez que realice la guía de trabajo autónomo? Autoevalúo mi nivel de desempeño Al finalizar mi trabajo por completo, autoevalúo el nivel de desempeño que alcancé. Marco con una X la casilla correspondiente. Indicadores del aprendizaje esperado Interpreto datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial. Nivel de desempeño Inicial Intermedio Avanzado Menciono datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Brindo particularidades acerca de los datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Indico de manera específica los datos o hechos relacionados con un problema que se resuelve utilizando la función exponencial, a través del planteamiento de ecuaciones exponenciales. Inicial Intermedio Avanzado Anoto las condiciones que cumple una situación determinada, que le hacen corresponder a una función exponencial. Inicial Destaco aspectos relevantes acerca del modelo de función exponencial que puede utilizar para dar solución a un problema. Asigno los pasos necesarios para solucionar un problema utilizando el modelo de función exponencial. Intermedio Avanzado Relato generalidades de una situación determinada, que le permite reconocerla como función logarítmica a partir de observarla como inversa de una función exponencial. Inicial Emito criterios específicos acerca las características que presenta una situación determinada, a partir de distinguirla como inversa de una función exponencial. Detallo características relevantes que presenta una situación determinada, a partir de distinguirla como un situación que corresponde como la inversa de una función exponencial. Avanzado Anoto las características de una función logarítmica representada de manera gráfica, tabular, verbal o algebraica, a partir de reconocerla como inversa de la función exponencial. Inicial Aludo las características de una función logarítmica representada de manera gráfica, tabular, verbal o algebraica, a partir de reconocerla como inversa de la función exponencial. Intermedio Fundament las características de una función logarítmica representada de manera gráfica, tabular, verbal o algebraica, a partir de reconocerla como inversa de la función exponencial. Avanzado Relato generalidades de las ideas principales del análisis de la gráfica de la función logarítmica, para dar respuesta a un problema. Emito criterios específicos del análisis de la gráfica de la función logarítmica, para dar respuesta a un problema. Detallo aspectos relevantes del análisis de la gráfica de la función logarítmica, para dar respuesta a un problema. Indicadores del aprendizaje esperado Establezco los pasos necesarios para hallar la solución de un problema utilizando la función exponencial. Indicadores del aprendizaje esperado Examino los factores que presenta una situación determinada, que la caracterizan como un modelo de función logarítmica. Intermedio Indicadores del aprendizaje esperado Justifico las características de una función logarítmica representada de manera gráfica, tabular, verbal o algebraica. Indicadores del aprendizaje esperado Examino las ideas principales de una situación que se me presenta para dar respuesta a un problema que involucra un modelo de función logarítmica.