•12~
...~
- ~
"
19..
'~{r•1.~-:~ ~~: (~-~~ ..•.,tt\f":':',"1
i
1,ANGULO CENTRJ\l (LA)
2
.
j
ÁNGULOS EN LA
CIRCUNFERENCIA
w
'f_ANGULO
_ _....:..._..=_
EX~-- 1..NSCRII O
.l
)
1!
~ ~
·.•
:,
'J~'"'d ,
t
"., ..
5
l''i..!'
1I
J
'•J
'--:--,.,-_..,.
, ",.:.,e--:-_-:
_,.,.
, .,.
...,.
, ,'"'·."'
~..,.
,.,,,.,..._-,., -,,.,,e~,.,~.;--,;-,,.J.,, ~
~°'ÁNGULO EXHRIOII
~
fil
C. SECANTES
o
OB
AU
PQ
1.
LP =90° l 2,
T
.r.
3.
A(!j!} Z;¿Lo
l ~U>._.;,}:-..'~
l./.
r A =l'O
r.,
L,
L,
%
rJ
1--- - -- - -.~
l-+~
ro
6-0
,r•
~·.J :;'-~;
A
mi 5.0 [3
p
e®
~
~
C. TANGENTES EXTERIORES
M
Si Al3.h.OM
⇒ AN = NO; y
mAM=mMB
'
.,
o
R - r < 00
, , <R +r
ET
4
A
,_
POSICIONES
RELATIVAS
DE DOS
CIRCUNíERENCIAS
PROPIEDADES
I'~
,~. oc~
:-;,~
r
ltL.~ft-.,.\ .SM"<l'-;,,~1,t.C;.\ ~
_..
A
c
O•
•:,..;,. -;'' '\
~
j
i
-- ~:m::
C. TANGENTES INHRIORES
o
Si AU // CD
⇒ mAC.=mOO
⇒ mAU = m CD
~
0 ,0 ,= R+ r
i
C
V
D
Si AB = CD
' _.. ~ ~..
7. ~ í l
D
•
o
.,
1,1
t~
~
~
0 0 = R- r
1-
Si ON = OM
⇒ All = CD
filaii&irtaU, :i:.(~;,.. ,:..... L k ~ ~I.A;.: _,.,,; , , ... , .~);)
1
'
..-,r .,.,, ...,,'1:i,.n':-;d
ÁNGULO INTERIOR
[>
~
,1
CENTRO:
RADIO:
DIÁMHRO.
CUERDA:
SECANTE:
TANGENTE:
NO RMAL:
FLECHA:
ARCO :
~
- . ~f - ,~. - -,. ~
, .••
- CB--(D
'U
ELEMi NTQs , :: • / .. .,.,,,,.,,/ I
A
BJ }
-,.-.- - -,-<·-·-,.-,,.',-,
~
C. EXTERIORES
·'.}••!~
R + r < 0 ,0 ,
11
'1
,~. .wnnrmr:J
f
LI
~
~
'E
~~-...J;¡;;¡¡:¿[i ___ _ _
r}
3ANGULO SEMI-INSCIUTO
.,,
"!"~
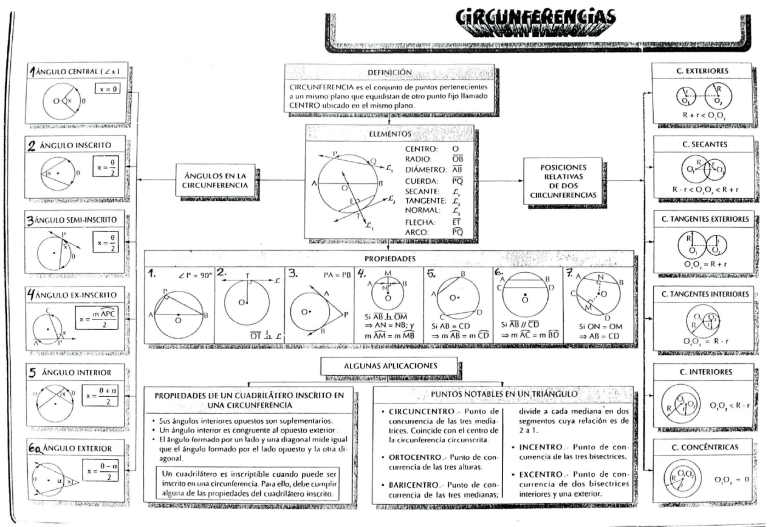
CI RCUNí[RENCIA es el conjunlo de punlos pcrlenecientes
J un mi smo plano que e4u1d1s1an de otro punto fijo llamado
CENTRO ubrc;icJo en el mismo plano .
i'
€:) BJ
~
DHl ~ ICIÓ N
0 º~Jll
ÁNGULO INSCR ITO
-
X =
1~
o- u
2-
;;.¡, _.,.,~ - ; , a,.1-:;J.0.,1,1
,.
1
ALGUNAS APLICACIONES
~~ :t r:..•J
---------'~
PROPIEDADES UE .UN CUAD~ IL,\TÉRO INSCímo EN
UNA CIRCÜNHRENé lA
• Sus ángulos interiores opueslos son suplementarios.
• Un áneulo interior es congruente al opuesto exterior .
• El ángulo formado por un lado y una diagonal mide igual
que el ángulo formado por el lado opuesto y l,1 otr,1 di-
agonal.
~
Un cuaJrilátero es inscriptible cuanclo puede ser
inscrilo e n una circunferencia. Para ello, deLe cumpl ir
_ ;ilguna ele las prop iedades d el cu;icJril~tero inscrilo.
J(-
·4
·\
..9..:
.lll. .
:;r.r,n.:.~
.' l!i :.; ~- ·
11
PUNTOS NOTABLES EN ~N,TRIÁNGUL0
'
.~
• ORTOCENTRO .- Punto de concurrencia de las tres alturas .
~
• IJARICENTRO .- Punto de concurrencia ele las tres media nas;
.41
•
1
•
·l
.l
~.
1
1-~
'- .. ,. 'i1
•
clrvide a cada medi;ina 'en dos
segmentos cuya relación es de
2 a 1.
I
• INCENTRO .- Punto de con -
,j'
1~
1
c.urrencia de las tres bisectrices.
\. L.
• EXCENTRO .- Punto de con -
lt- - 1'_ t
· ,
• .\
w
'®
1
C. INTERIORES
• CIRCU NCENTRO .- Punto de
toncurrencia de las tres mecliatriccs. Coincide con el centro de
la circ unferencia cir cunscrita .
.
·I
~
••!Ul#I
M
J
c 111renc ia ele dos bisec tri ce s
inleriores y una exterior.
·~
~2
1
º·º· <R -•
"''
j
c. CONCÉNTRICAS
@)
1.:dinMiL-li:r___.-. n.:-. ¡
~I:
I!
,.
" t~
00 = 0
•
-:-:íii:r.t..,,1!«',+iJii..:~t,~
( 1 1)
(1 O)
( 12)
B
A
@
X
B
mL
OC= 2(0A)
C
A= 21 e
,
(15).
'. 13)
m AB = m AC
D
m L C = 26º
~
(
,-...
B
,-...
m AE = 62º , m EC = x
8
{ l 7J
g
··-........_
e
A
A
rn 0C=44º ;
m L C = 36º
,-...
,-...
m AD= 152º ; AB = 3C = CD
m AB = Sx ; m BD = 2x
nCCl= i 1° , mAD=90º
(24)
(23)
¡(2i.} .,..
D
e
1
º º
1
1
. X
BC // AD
(25)
.
e
¡(
1
e
e
(26)
(27)
0-----c,
1
(28)
----;7 º
,e
A,
....-..
m BC = 28º
t-.8 = 8D , m AE = 86º
1(29)
1
(30)
1
(32)
(31)
e
a.
X:
or
'D ; rn. ooC = E') 0
~ ~ ¡·1 "·
c. = 65°
AD= DC = A'a, m L BDC = 36ª
1
(33)
(35)
r2d10 :: 2 cm ; m BC = x
(36)
1
e
,-...
m 80 = X
r
= 12
----
m cF - 86°
:n ,-...
/..':3 = ,?:•'
(2)
(4)
(3)
A
AT = 6 cm : BE = x
(8)
(7)
(6)
EF=18cm ; mLC=37º
'
X
18
ll
(10)
(11)
T
---=---- -L
A B
A. - - - - . P
X
223º
(14)
T // AP ; m Al= 71 º
BC // AD
EF // PO
(16)
(15)
X
H
A
E
HF 1- AB ; mAB = 22 cm
(18)
---
-SH 1- -EJ ; m JHE = 116º
(19)
X
EH 1- AB ; m AE = 37º
(20)
e
JB~= 4--/3 ; m LA= 30º
(22)
m L HBO = 37º
(23)
B
(24)
o
m L ABO= 37º
T JI AB ; m AB = 16 cm
AE = 5 ; BQ = 3
m LOCB=31 º
BC =3"'3 ; 80 =x