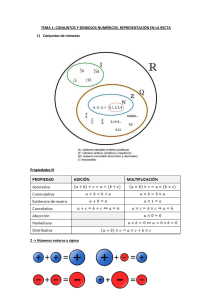
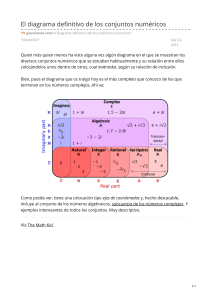
CONJUNTOS NUMÉRICOS Y TRANSFORMACIONES Objetivo: Definir los Conjuntos Numéricos, Clasificar los números según su Conjunto Numérico y Transformar de decimales finitos, infinitos periódicos y semiperiódicos y mixtos a fracción; en el desarrollo de la siguiente Guía. RECUERDA En cada clase, debes anotar en tu cuaderno la FECHA y el OBJETIVO, salvo que se considere el objetivo de la Guía o Ensayo SIMCE. Las Guías o Ensayos, debe estar PEGADOS en el cuaderno. I. CONJUNTOS NUMÉRICOS. Un número es una idea que expresa una cantidad, por medio de una representación gráfica (imagen) o un símbolo (número). El sistema universalmente aceptado actualmente es el Sistema de Numeración Decimal. Es un sistema de numeración en el que las cantidades se representan utilizando como base diez cifras, que van desde el cero 0 hasta el nueve 9. Ejemplo: Completa la siguiente tabla de cifras con su correspondiente Numeración Romana y Decimal, para luego escribir la cifra en letras. Objeto Numeración Romana Numeración Decimal En Palabras III 3 tres AAAAAAAAAAAAAA AAAAAAAAAAAAAA AAAAAAAAAAA 39 XXVII AHORA TÚ: Construye una tabla en tu cuaderno, con 3 series objetos que expresen cantidad (recuerda que éstos deben ser iguales) y complétala con sus correspondientes numeraciones Romana y Decimal, para luego escribir la cifra en palabras. I. CONJUNTOS NUMÉRICOS. Los números se agrupan en conjuntos o estructuras diversas; cada una contiene a la anterior y es más completa y con mayores posibilidades en sus operaciones. Estos son: I. CONJUNTOS NUMÉRICOS. Número 2Q –5,5 N 3 Z 7 0N ZN Sí No AHORA TÚ: Responde si los siguientes pertenecen o no, a los conjuntos numéricos dados, indicando el porqué. Justificación: porque… 3. DIAGRAMA DE VENN. Son ilustraciones usadas en la Matemática para representar a los Conjuntos, es decir, estos diagramas se usan para mostrar gráficamente la agrupación de cosas o elementos, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos. En el caso de los Conjuntos Numéricos, su correspondiente Diagrama de Venn, considerando a los Números Naturales, Enteros y Racionales es el siguiente: Diagrama de Venn: Conjuntos Numéricos “QUEBRADOS” CERO AHORA TÚ: A. Clasifica los siguientes números según el conjunto numérico al que pertenecen, pinta según su color: Naturales = amarillo, Enteros = rojo, Racionales (decimales) = verde, Racionales (Fracciones) = azul; si observas que un número pareciera “pertenecer” a más de un conjunto, decídete por el más grande. I. CONJUNTOS NUMÉRICOS. CONJUNTO NUMÉRICO DE LOS NÚMEROS REALES “QUEBRADOS” CERO II. TRANSFORMACIÓN DE DECIMALES FINITOS, INFINITOS PERIÓDICOS Y SEMIPERIÓDICOS A ENTEROS. 1. EXPRESIÓN DECIMAL FINITA: Se pone por numerador la cantidad que se encuentra después de la coma y por denominador la unidad seguida de tantos ceros como cifras se encuentran después de la coma; si se puede al finalizar, se simplifica. II. TRANSFORMACIÓN DE DECIMALES FINITOS, INFINITOS PERIÓDICOS Y SEMIPERIÓDICOS A ENTEROS. 2. EXPRESIÓN DECIMAL PERIÓDICA: En el numerador se anota la cifra completa y se le resta el valor que no es periodo, en el denominador se anotan tanto nueves sean las cifras del período; si se puede al finalizar, se simplifica. II. TRANSFORMACIÓN DE DECIMALES FINITOS, INFINITOS PERIÓDICOS Y SEMIPERIÓDICOS A ENTEROS. 3. EXPRESIÓN DECIMAL SEMI – PERIÓDICA: En el numerador se anota la cifra completa y se le resta el valor que no es periodo, en el denominador se colocan tanto 9 sean los números del período y tanto 0 como sea el ante período; si se puede al finalizar, se simplifica. II. TRANSFORMACIÓN DE DECIMALES FINITOS, INFINITOS PERIÓDICOS Y SEMIPERIÓDICOS A ENTEROS. 4. TRANSFORMACIÓN DE NÚMEROS MIXTOS A FRACCIÓN: El denominador ser multiplica por el entero y se le suma el numerador, se coloca en la parte de arriba de la nueva fracción; se mantiene el denominador.