El Espiropentagrama Propuesta de represe

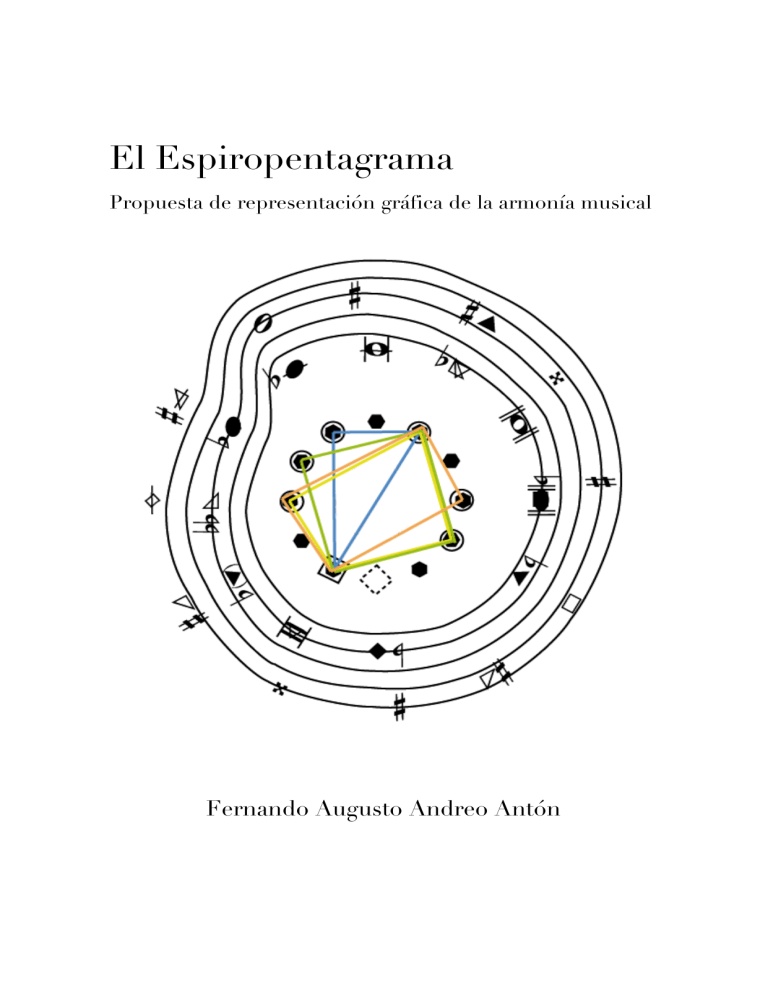
El Espiropentagrama
Propuesta de representación gráfica de la armonía musical
Fernando Augusto Andreo Antón
1
Índice
Introducción . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1. Evolución de la enseñanza de la Armonía
1.1. Antecedentes . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. La metodología tradicional . . . . . . . . . . . . . . . . . . .
1.3. Nuevos enfoques del s. XX . . . . . . . . . . . . . . . . . . .
1.3.1. A. Schoenberg, un pequeño paso adelante . . . . . . .
1.4. Dos teorías cognitivas recientes de la Armónia . . . . . . . .
1.4.1. Longuet-Higgins y su espacio armónico bidimensional
1.4.2. Balzano con su red . . . . . . . . . . . . . . . . . . .
1.5. La enseñanza de la Armonía en la actualidad . . . . . . . . .
1.5.1. La Armonía en el mundo . . . . . . . . . . . . . . . .
1.5.2. La Armonía entre nuestros muros . . . . . . . . . . .
2. Fundamentos de esta didáctica
2.1. Música y formas . . . . . . . .
2.2. Música y color . . . . . . . . .
2.3. Música y movimiento . . . . .
2.4. Música y texturas . . . . . . .
2.5. Otras posibles vinculaciones .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3. Los árboles armónicos
3.0.1. Como interpretar y usar los árboles . . . . . . . . . .
3.0.2. Grafías de los árboles armónicos . . . . . . . . . . . .
3.0.3. Estados de crecimiento de un árbol . . . . . . . . . .
3.1. El árbol de Dominante . . . . . . . . . . . . . . . . . . . . .
3.1.1. El árbol de Dominante de un modo Mayor . . . . . .
3.1.2. El árbol de Dominante de un modo menor . . . . . .
3.2. El árbol de Subdominante-Tónica . . . . . . . . . . . . . . .
3.2.1. El árbol de Subdominante-Tónica en un modo Mayor
3.2.2. El árbol de subdominante-tónica en un modo menor .
3.3. El árbol Tonal . . . . . . . . . . . . . . . . . . . . . . . . . .
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
.
.
.
.
.
.
.
.
.
.
10
11
13
15
15
17
18
22
24
24
24
.
.
.
.
.
26
26
27
28
29
30
.
.
.
.
.
.
.
.
.
.
31
32
32
33
34
35
35
36
36
37
37
3
ÍNDICE
3.3.1. El árbol Tonal en un modo Mayor . . . . . .
3.3.2. El árbol Tonal en un modo menor . . . . . .
3.4. Otro tipo de árboles . . . . . . . . . . . . . . . . .
3.4.1. Un árbol para la realización contrapuntística
.
.
.
.
4. El Espiropentagrama
4.1. Las marcas de presencia . . . . . . . . . . . . . . . .
4.1.1. De orden melódico . . . . . . . . . . . . . . .
4.1.2. De orden armónico . . . . . . . . . . . . . . .
4.2. Manejo del Espiropentagrama . . . . . . . . . . . . .
4.2.1. Un caso práctico . . . . . . . . . . . . . . . .
4.3. Otras propuestas próximas . . . . . . . . . . . . . . .
4.3.1. Simple clock calculator de Larry J. Solomon .
4.3.1.1. Diferencias con el Espiropentagrama
4.3.2. La Rueda Armónica de Luis Nuño . . . . . . .
4.3.2.1. Diferencias con el Espiropentagrama
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
37
38
38
39
.
.
.
.
.
.
.
.
.
.
41
47
47
48
49
49
49
50
50
51
53
5. Representaciones poligonales de las sonoridades
5.1. Consideraciones preliminares de las figuras . . . . . . . . . . . . . . . . . . . . .
5.1.1. El diámetro: el tritono . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.2. Un cuadrante: la tercera menor . . . . . . . . . . . . . . . . . . . . . . .
5.1.3. Los ejes de simetría: propiedades, inversión y transposición limitada . . .
5.1.3.1. Propiedades derivadas de la simetría . . . . . . . . . . . . . . .
5.1.3.2. La inversión . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.3.3. La transposición limitada . . . . . . . . . . . . . . . . . . . . .
5.1.4. El área, un índice orientativo del grado de disonancia . . . . . . . . . . .
5.1.5. Aplicación a nuestro sistema tonal . . . . . . . . . . . . . . . . . . . . . .
5.1.5.1. Consideraciones preliminares sobre intervalos consonantes y disonantes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1.5.2. El parámetro inmensurable: la subjetividad de la tradición . . .
5.1.5.3. En grupos con un mismo número de sonidos . . . . . . . . . . .
5.1.5.4. En grupos con diferente número de sonidos . . . . . . . . . . .
5.1.5.5. El coeficiente de consonancia . . . . . . . . . . . . . . . . . . .
5.1.5.6. Excepciones notorias . . . . . . . . . . . . . . . . . . . . . . . .
5.1.5.7. La propuesta de Hindemith . . . . . . . . . . . . . . . . . . . .
5.2. Las divisiones simétricas regulares de la circunferencia . . . . . . . . . . . . . . .
5.2.1. Modos de transposiciones limitadas de Messiaen . . . . . . . . . . . . . .
5.2.1.1. Modo 1 de transposición limitada de Messiaen . . . . . . . . . .
5.2.1.2. Modo 2 de transposición limitada de Messiaen . . . . . . . . . .
5.2.1.3. Modo 3 de transposición limitada de Messiaen . . . . . . . . . .
55
55
56
57
58
58
60
61
62
63
63
64
65
67
67
68
69
70
72
73
73
73
ÍNDICE
4
5.2.1.4. Modo 4 de transposición limitada de Messiaen . . . . . . . . . . 74
5.2.1.5. Modo 5 de transposición limitada de Messiaen . . . . . . . . . . 75
5.2.1.6. Modo 6 de transposición limitada de Messiaen . . . . . . . . . . 76
5.2.1.7. Modo 7 de transposición limitada de Messiaen . . . . . . . . . . 77
5.2.2. Otros casos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
5.2.2.1. El acorde de quinta aumentada . . . . . . . . . . . . . . . . . . 78
5.2.2.2. El acorde de séptima disminuida . . . . . . . . . . . . . . . . . 78
5.2.2.3. La sexta aumentada francesa. . . . . . . . . . . . . . . . . . . . 78
5.3. Las divisiones simétricas irregulares de la circunferencia . . . . . . . . . . . . . . 79
5.3.1. El heptágono diatónico . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
5.3.2. Escalas sintéticas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5.4. Divisiones tradicionales de la circunferencia en conjuntos de tres y cuatro sonidos 81
5.4.1. Acordes tríadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5.4.1.1. El acorde perfecto mayor . . . . . . . . . . . . . . . . . . . . . 82
5.4.1.2. El acorde perfecto menor . . . . . . . . . . . . . . . . . . . . . 83
5.4.1.3. El acorde de 5ª aumentada . . . . . . . . . . . . . . . . . . . . 84
5.4.1.4. El acorde de 5ª disminuida . . . . . . . . . . . . . . . . . . . . 85
5.4.2. Acordes cuatríadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
5.4.2.1. Acordes con 7ª de 1ª especie (P. M. con 7ª menor): 7ª natural . 87
5.4.2.2. Acordes con 7ª de 2ª especie (P. m. con 7ª menor): 7ª menor . 88
5.4.2.3. Acordes con 7ª de 3ª especie (disminuido con 7ª menor): 7ª
Submenor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
5.4.2.4. Acordes con 7ª de 4ª especie (P. M. con 7ª Mayor): 7ª Mayor . 90
5.4.2.5. Acordes con 7ª de 5ª especie (P. m. con 7ª Mayor): 7ª sobre
menor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
5.4.2.6. Acordes con 7ª de 6ª especie (aumentado con 7ª Mayor): 7ª
sobre aumentado . . . . . . . . . . . . . . . . . . . . . . . . . . 92
5.4.2.7. Acordes con 7ª de 7ª especie: 7ª disminuida . . . . . . . . . . . 93
5.4.3. Los acordes de sexta aumentada . . . . . . . . . . . . . . . . . . . . . . . 94
5.4.3.1. La sexta aumentada italiana . . . . . . . . . . . . . . . . . . . . 95
5.4.3.2. La sexta aumentada francesa . . . . . . . . . . . . . . . . . . . 96
5.4.3.3. La sexta aumentada alemana . . . . . . . . . . . . . . . . . . . 97
5.4.3.4. La sexta aumentada suiza (acorde de 4ª doble aumentada) . . . 99
5.5. El color como marca funcional . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
6. Aplicaciones del Espiropentagrama
103
6.1. Sistemas de afinación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
6.2. Procesos contrapuntísticos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
6.2.1. La transposición . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
ÍNDICE
5
6.2.2. La inversión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
6.2.3. La retrogradación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
6.2.4. La combinación de estos procesos . . . . . . . . . . . . . . . . . . . . . . 112
6.3. La modulación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
6.3.0.1. Organización de las posibilidades . . . . . . . . . . . . . . . . . 116
6.3.1. Normas elementales para la comparación de árboles . . . . . . . . . . . . 122
6.3.2. La modulación por nota común . . . . . . . . . . . . . . . . . . . . . . . 122
6.3.3. La modulación diatónica o por acorde común . . . . . . . . . . . . . . . 122
6.3.3.1. Comparación de los árboles de Dominante entre sí (Caso 1:
D1 =D2 ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
6.3.3.2. Comparación del árbol de Subdominante-Tónica de la tonalidad
de partida con el de Dominante de la de llegada (Caso 2: st1 =D2 )124
6.3.3.3. Comparación del árbol de Dominante de la tonalidad de partida
con el de Subdominante-Tónica de la de llegada (Caso 3: D1 =ST2 )126
6.3.3.4. Comparación de los árboles de Subdominante-Tónica entre sí
(Caso 4: st1 =ST2 ) . . . . . . . . . . . . . . . . . . . . . . . . . 128
6.3.4. La modulación enarmónica . . . . . . . . . . . . . . . . . . . . . . . . . . 130
6.3.4.1. Comparación de los árboles de Dominante entre sí (Caso 1:
D1 ≡D2 ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
6.3.4.2. Comparación del árbol de Subdominante-Tónica de la tonalidad
de partida con el de Dominante de la de llegada (Caso 2: st1 ≡D2 )133
6.3.4.3. Comparación del árbol de Dominante de la tonalidad de partida con el de Subdominante-Tónica de la de llegada (Caso 3:
D1 ≡ST2 ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136
6.3.4.4. Comparación de los árboles de Subdominante-Tónica entre sí
(Caso 4: st1 ≡ST2 ) . . . . . . . . . . . . . . . . . . . . . . . . . 138
6.3.5. La modulación cromática . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
6.3.5.1. Comparación de los árboles de Dominante entre sí (Caso 1:
D1 ~D2 ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141
6.3.5.2. Comparación del árbol de subdominante-tónica de la tonalidad
de partida con el de Dominante de la de llegada (Caso 2: st1 ~D2 )143
6.3.5.3. Comparación del árbol de Dominante de la tonalidad de partida
con el de Subdominante-Tónica de la de llegada (Caso 3: D1 ~ST2 )145
6.3.5.4. Comparación de los árboles de Subdominante-Tónica entre sí
(Caso 4: st1 ~ST2 ) . . . . . . . . . . . . . . . . . . . . . . . . . . 147
6.3.6. Utilización de los resultados y proceso de asimilación . . . . . . . . . . . 149
6.4. La set-theory (teoría de conjuntos) . . . . . . . . . . . . . . . . . . . . . . . . . 152
6.4.1. La inversión de conjuntos de sonidos . . . . . . . . . . . . . . . . . . . . 153
6.4.2. La Forma Normal (Normal From) . . . . . . . . . . . . . . . . . . . . . . 153
6
ÍNDICE
6.4.3. La Forma Orignal (Prime Form) . . . . . .
6.4.3.1. ¿De qué sirve la Forma Original?
6.5. Los mapas armónicos . . . . . . . . . . . . . . . .
6.5.1. Comparación de mapas armónicos . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7. Propuesta de aplicación de esta didáctica
7.1. En la enseñanza general . . . . . . . . . . . . . . . . . . .
7.1.1. En el ámbito de Preescolar . . . . . . . . . . . . . .
7.1.2. En el ámbito de Primaria . . . . . . . . . . . . . .
7.1.2.1. Primer ciclo . . . . . . . . . . . . . . . . .
7.1.2.2. Segundo ciclo . . . . . . . . . . . . . . . .
7.1.2.3. Tercer ciclo . . . . . . . . . . . . . . . . .
7.1.3. En el ámbito de Secundaria . . . . . . . . . . . . .
7.1.3.1. Primer ciclo . . . . . . . . . . . . . . . . .
7.1.3.2. Segundo ciclo . . . . . . . . . . . . . . . .
7.2. Dentro de las enseñanzas artísticas . . . . . . . . . . . . .
7.2.1. En las Enseñanzas Elementales . . . . . . . . . . .
7.2.1.1. Primer curso de Lenguaje Musical . . . .
7.2.1.2. Segundo curso de Lenguaje Musical . . . .
7.2.1.3. Tercer curso de Lenguaje Musical . . . . .
7.2.1.4. Cuarto curso de Lenguaje Musical . . . .
7.2.2. En las Enseñanzas Profesionales . . . . . . . . . . .
7.2.2.1. Lenguaje musical . . . . . . . . . . . . . .
7.2.2.2. Armonía . . . . . . . . . . . . . . . . . . .
7.2.2.3. Análisis . . . . . . . . . . . . . . . . . . .
7.2.2.4. Fundamentos de Composición . . . . . . .
7.2.3. En las Enseñanzas Superiores . . . . . . . . . . . .
7.2.3.1. Análisis . . . . . . . . . . . . . . . . . . .
7.2.3.2. Armonía . . . . . . . . . . . . . . . . . . .
7.2.3.3. Contrapunto . . . . . . . . . . . . . . . .
7.2.3.4. Otras asignaturas que podrían beneficiarse
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
155
158
159
162
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
166
. 166
. 167
. 169
. 169
. 169
. 170
. 170
. 170
. 171
. 173
. 173
. 173
. 174
. 174
. 176
. 177
. 177
. 180
. 180
. 181
. 181
. 181
. 182
. 182
. 182
Conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184
Bibliografía
186
0.1.
Introducción
Este trabajo pretende ofrecer una didáctica para acercar los estudios de Armonía a etapas
anteriores a las que prevé nuestro currículo actual, básicamente desde la iniciación del niño a
la música. Para ello conecta las sonoridades, esencialmente, con figuras geométricas y colores
-dejando abierta una también válida y posible relación con figuras tridimensionales y texturas-,
en función a diversos parámetros que justifican esta vinculación.
Evidentemente, el acercamiento al niño a entes musicales más complejos como puede ser
cualquier acorde, expresado de manera tan primaria como formas y colores y no como elementos
de categorías teóricas complejas, posibilita que esta propuesta no sólo sea coherente sino muy
prometedora.
Además de esto, de lo importante que puede ser el ir acercando al alumno más joven a esta
dimensión musical que apenas se trata en los planteamientos didácticos de la actualidad, este
método tiene una proyección mucho más amplia ya que las figuras y colores que el niño ha
manejado como un juego, cuando no tenía por qué saber qué eran las funciones tonales o los
acordes cuatríadas, seguirán teniendo vigencia y utilidad incluso en los estadíos más avanzados
del estudio de esta disciplina. Esta propuesta didáctica pretende que esas figuras policromas
que han quedado conectadas con sonoridades en la mente infantil, le faciliten la comprensión
de las características no sólo del funcionamiento del sistema tonal, de acordes y estructuras,
sino también del ámbito atonal, modal o incluso de cualquier sistema musical diferente.
Los principios que este método emplea se fundamentan en investigaciones de la psicología de
la percepción, en los principios básicos de la geometría de polígonos y en conceptos de estudios
de la musicología moderna, por ello, su campo de aplicación no se restringe a una introducción
lúdica en las clases de Lenguaje musical o de la enseñanza primaria, sino que sirve de analogía
explicativa del sistema de afinación temperado, alcanza a colaborar determinantemente en el
estudio de la modulación tonal o descubre nuevos atalayas para la práctica y la observación de
la composición contemporánea.
El estudio de la Armonía se inicia normalmente en las Enseñanzas Profesionales de las
Enseñanzas Profesionales de música, si bien, cierta introducción a los acordes y las funciones
ya se comienza en los últimos cursos de Lenguaje Musical de las Enseñanzas Elementales.
No obstante, estas enseñanzas van a ser principalmente teóricas y apenas van a poder tener
una verdadera realidad en la práctica hasta las Enseñanzas Profesionales, que en la asignatura
de Fundamentos de Composición, encontrarán su realización en ejercicios escritos y en cierto
acercamiento a dictados y el aprendizaje de secuencias armónicas. Esto va en perjuicio del
alumnado que nunca termina de tener un verdadero dominio de la materia sonora con que
trata la Armonía, y, por lo general, reduce esta asignatura a un conjunto de reglas de aplicación
teórica y casi exclusivamente, a los ejercicios propuestos en clase.
En cuanto a la metodología aplicada para la elaboración de este trabajo podría resumirse
así:
7
INTRODUCCIÓN
8
en una primera fase, tras haberse producido la idea germinal: un método pedagógico con
que enseñar Armonía, se inicia una investigación a través de publicaciones de muy diversa
índole y variedad, en relación a los diferentes temas que resultan afines (temas como la
Didáctica de la música, la Psicología evolutiva, la Geometría, obviamente la Armonía, etc).
Este estudio se llevó a cabo para establecer una base sobre la que desarrollar el método
aquí propuesto, así como compararlo con otras experiencias que pudieran serle afines, para
contextualizarlo y situarlo en relación a otras propuestas y otros métodos consagrados. Así
pues, aún tratándose únicamente de un supuesto educativo, se ha intentado fundamentar
todo cuanto se proyecta con estudios y trabajos previos, que puedan servir de aval y
ofrecer cierta garantía respecto de la validez de las ideas que en las próximas páginas se
exponen.
en segundo término, se comenzó la elaboración escrita de estas páginas, si bien nunca
dejó de aparecer nueva información que parecía relevante considerar y que ayudaron a ir
perfilando, modificando y corrigiendo. Para el proceso de escritura, especialmente, en lo
tocante a las ilustraciones que aquí aparecen y que son verdaderamente imprescindibles,
hubo que aprender a trabajar con un software informático que posibilitara trasladar al
papel los ejemplos que era pertinente incluir, a colación de lo que se explica, máxime,
siendo una propuesta didáctica basada en la observación de la solidaridad existente entre
sonoridades y figuras poligonales. Asimismo, se ha trabajado en la creación de aplicaciones interactivas que permitan manipular lo que aquí se describe en un mundo físico
(con papeles y láminas transparentes), en un mundo virtual informático, más llamativo e
interesante, sobre todo para un alumnado que ha nacido en este mundo tecnológico.
por último, aunque para ser fieles a la verdad habría que confesar que, parcialmente, algo
se fue poniendo a prueba mientras se estaba creando, queda la comprobación real y total
de las ventajas que este método puede o no tener. No obstante, mientras se hacía acopio
y se elaboraba todo el material que aquí se ofrece, hubo varias entrevistas con educadores
y teóricos que ofrecieron no cortas esperanzas sobre la validez y la consistencia de esta
metodología; así como también resultaron positivos y prometedores, ciertos pequeños
experimentos que inevitablemente para ellos, tuvieron que sufrir algunos de mis alumnos.
Así pues, la intención de este trabajo es iniciar mucho antes en el mundo armónico al alumnado;
no sólo al de las instituciones de enseñanza musical especializada, sino incluso en el ámbito de
la enseñanza general. El mayor problema que puede representar, a juicio nuestro, el tratar de
acercar a niños de una edad más temprana a la teoría armónica es la complejidad de los términos
y los conceptos que su comprensión teórica requiere. Sin embargo, al asimilar las sonoridades a
elementos visuales más sencillos, como pueden ser polígonos y colores, el niño ya no trabajará
con una nomenclatura complicada e inaprehensible (como acorde de séptima disminuida sobre
el cuarto elevado), sino con figuras y colores que lleva manejando desde que era un bebé (como
un cuadrado amarillo, que sería el equivalente al acorde nombrado en el paréntesis anterior).
INTRODUCCIÓN
9
No obstante, esta propuesta no es que pretenda únicamente adelantar el inicio de los alumnos
en el mundo de la Armonía, la idea es que estas figuras geométricas policrómicas con que se
pretende facilitar su acceso, se vayan incorporando y asimilando dentro de su mente porque su
utilidad no se restringirá a estos primeros años o a la educación general, sino que estas mismas
figuras y colores, les serán de una enorme utilidad para entender y aprehender con mayor
facilidad y profundidad, conceptos mucho más complejos e intrincados, como la enarmonización
de acordes o los modos de transposición limitada de Oliver Messiaen, por citar algunos de los
ejemplos ilustrativos que se recogen a lo largo de estas páginas. Creo que resultará convincente
pensar que, si para una persona que no ha sido formada con las referencias que este proyecto
educativo propone, ya puede hacerse patente la practicidad, sistematicidad y exhaustividad
con que aborda la dificultosa realidad de los conjuntos sonoros -especialmente aquí tratadas
las entidades armónicas tonales más tradicionales-, para alguien que, ya con cierta madurez
teórica musical, haya imbrincado casi en su subconsciente por haberlo trabajado así desde
temprana edad, ciertas imágenes con ciertas sonoridades (tanto a nivel mental teórico como a
nivel acústico), este método le reportará una enorme ventaja sobre cualquiera de los alumnos
que se enfrentan hoy día, armados únicamente de sus mayores o menores conocimientos, al
mundo de la teoría compositiva en cualquiera de sus facetas: armonía, contrapunto, análisis...;
sin que podamos olvidar, en ningún caso, su patente repercusión en otras disciplinas como la
educación auditiva o la improvisación.
Tampoco podemos dejar de aclarar que esta metodología educativa, aunque nacida y aquí
esbozada dentro del ámbito de la música occidental, no tiene en modo alguno por qué verse
restringida a ésta y que, de hecho, puede resultar de extrema validez para comparar sistemas
de afinación de diversas culturas musicales o de diversos períodos históricos; si bien, lamentablemente, esto escapa de los introductorios objetivos con que ve la luz el modesto elenco de
posibilidades que aquí sucintamente se presentan.
En definitiva, la monografía que están a punto de leer, sin darse por acabada ni por inmutable, sino como un guión más o menos desarrollado de otro modo de acercar al alumnado de
música, tanto en los círculos más especializados como en los menos, a la compleja dimensión de
la realidad organizativa de esta disciplina; tanto en el plano de sistema musical derivado de un
sistema de afinación, como en su dimensión sintáctica de sonoridades dispuestas en un discurso
de tensiones y distensiones, apenas inteligible para la mayoría de legos en la materia más allá
de su intuición, y que desde luego podía serlo no ya mucho más comprensible, sino más cercana,
para aquellos que han sido, están siendo y serán instruidos en el maravilloso e inigualable arte
de la música.
Capítulo 1
Evolución de la enseñanza de la
Armonía
En primer lugar, por concretar un poco de qué estamos hablando, definiremos el objeto
de estudio, la Armonía. Según nos dice el “New Grove Dictionary of Music and Musicians”,
el término procede del griego harmonia, y significa “la combinación de notas simultáneas,
para producir acordes y, sucesivamente, para producir progresiones acórdicas. El término se
usa descriptivamente para denotar notas y acordes en combinación, y prescriptivamente para
denotar un sistema de principios estructurales que gobiernan su combinación.” Debemos darnos
cuenta cómo esta explicación contempla la disciplina desde dos planos; a un lado en su dimensión
apenas descriptiva y, en el otro -producto del anterior, en realidad-, como conjunto de normas
y reglas con que organizar su puesta en práctica.
Otra definición interesante la tenemos en el Harvard Dictionary of Music Apel (1969), que
nos dice que se trata de “la estructura acórdica (o vertical) de una composición musical, al
contrario que Contrapunto, que trata de la estructura melódica (u horizontal).” Como podemos
observar, esta definición de mayor brevedad, vuelve a centrarse en el carácter estructural del
término y en la dimensión vertical de simultaneidad de sonidos.
Por enriquecer un poco la visión, veamos también lo que nos dice A. Schoenberg al comienzo
del segundo capítulo de su Harmonielehre 1 (Schoenberg, 1979): “Armonía: el estudio de sonidos simultáneos (acordes) y de cómo pueden enlazarse teniendo en cuenta sus características
arquitectónicas, melódicas y rítmicas, y su significación, o sea, el peso relativo de unos respecto
a otros.” Tal vez, lo más llamativo de las palabras de Schoenberg, sea cómo pone su atención
en el hecho del contexto, como medio para atribuir significación a los conjuntos de sonidos
simultáneos; sin duda, es un factor esencial para entender los estudios armónicos, la asunción
del carácter relativo que poseen las sonoridades según su marco, tanto a nivel general dentro
de un sistema o lenguaje musical, como a nivel concreto de las sonoridades adyacentes en que
se encuadra cada una.
1
Cuya primera edición en alemán es de 1911.
10
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
11
Llegados a este punto, parece conveniente desligar el concepto de Armonía del de acorde,
al menos, de su noción ortodoxa que lo reduce a una yuxtaposición de terceras, y concebir
la armonía como un estudio de los elementos sonoros simultáneos, que llegados al s. XXI,
tendrán muchas muestras de simultaneidades sonoras que se apartarían notoriamente de las
clasificaciones clásicas o incluso, de las progresistas, pero obviamente siempre tonales y he ahí
la mayor diferencia de concepción, decimonónicas. El método didáctico que en estas páginas se
propone, tiene por objetivo poder abarcar todo el corpus armónico, sea de la procedencia que
sea e indistintamente al sistema musical al que se adscriba.
Ahora bien, aclaremos que cuando aquí hablamos de la enseñanza de la Armonía -ya en
el título de esta parte y en el del propio capítulo-, nos estamos refiriendo, como explicaba la
primera definición que veíamos, a la enseñanza de los principios estructurales que gobiernan
su combinación, es decir, la construcción y enlace de acordes siguiendo unas directrices de
coherencia determinadas, que, normalmente, no son otras que las deducidas del análisis y el
estudio de un estilo y/o un período histórico; por lo general, los del período de la práctica común
o período tonal, que abarcaría de manera aproximada desde 1600 hasta 1900. De esta forma,
los estudios de Armonía, como asignatura dentro del currículum de los estudios superiores de
música de nuestro país -según está recogido en la legislación vigente2 -, tendría un carácter
histórico y práctico muy pronunciado, y será de especial utilidad para el mejor entendimiento
de otras asignaturas como Historia de la Música o Análisis, así como para la práctica de la
improvisación.
1.1.
Antecedentes
La enseñanza de la Armonía, tal y como la entendemos nosotros partiendo de la última parte
de la definición anterior, esto es, no entendida como especulación teórica sino como disciplina
práctica, se remonta a la escuela del bajo cifrado, que se extendió a principios del s. XVIII y
que se convirtió en una teoría de composición libre, que se oponía al contrapunto, la teoría de
la composición estricta. En realidad, podríamos afirmar que su origen coincide grosso modo,
con el establecimiento de la tonalidad, reforzado durante los ss. XIX y XX por un robusto
marco institucional de conservatorios, universidades y academias que continuaron situando
esta disciplina, la Armonía, en el núcleo de sus enseñanzas básicas a intérpretes, compositores
e incluso, aficionados.
Aún así, la frontera que divide la teoría de la práctica es difícil de situar, sobre todo en
Así, hasta este curso 2009/2010 que tenía vigencia el Decreto 617/1995, de 21 de abril, nos dice que
en Armonía se estudiaría: “Elementos y procedimientos armónicos relativos al sistema tonal, y evolución de
la armonía en la música posterior al mismo. Realización escrita de trabajos estilísticos y libres, vocales e
instrumentales. Práctica instrumental de los elementos y procedimientos estudiados.”
No está de más el aclarar que este próximo curso 2010-2011, dará comienzo el nuevo plan educativo a nivel
europeo implantado según los acuerdos de Bolonia, en el primer curso de las enseñanzas de música de las
Enseñanzas Superiores; si bien, la legislación que atañirá a este nuevo plan aún no está definida cuando se
escriben estas palabras y, por lo tanto, no podemos referirnos a ella.
2
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
12
los comienzos, de forma que podemos encontrar ya una instrucción compositiva respecto de la
escritura a varias voces en tomos explícitamente especulativos como la “Synopsis” de Lippius,
de 1612. De igual forma, los primeros manuales de clase desarrollaron también conceptos que
acabaron finalmente asumidos en la corriente de los estudios especulativos, como sería el caso de
los acordes de paso en los tratados de Richter (1853) y Mayerberger (1878), que serían cruciales
para el desarrollo de las teorías schenkerianas del Schichten y la Ursatz. Asimismo, la oposición
que antes le concedíamos respecto del Contrapunto, al hablar de teoría de la composición
estricta y de la composición libre, debe tomarse también con cautela, ya que, precisamente
los primeros orígenes de la enseñanza práctica de la armonía pueden establecerse en algunas
páginas de tratados de Contrapunto de principios del s. XVI que enumeran las combinaciones
aceptables en la composición a cuatro voces; éste sería el caso del tratado de Baryphonus de
1615. Desde sus comienzos, la armonía práctica ha servido como ejercicio preparatorio para
tres actividades: improvisación, composición y análisis, que aunque distintas en su finalidad,
sus contenidos se entrecruzan con mucha frecuencia. La mayoría de los trabajos de armonía
del s. XVII tenían como objetivo la instrucción de intérpretes de bajo continuo en el arte
improvisatorio mediante la realización del bajo. Durante el s. XVIII, en Alemania, la realización
del bajo continuo se empezó a cultivar no sólo por intérpretes del mismo, sino también como
parte de la educación de los compositores, así C. P. E. Bach nos explica que los alumnos
de composición de su padre “debían empezar sus estudios por la realización de puro bajo
cifrado a cuatro partes. Después pasaba a los corales; primero le añadía los bajos hechos por
él, y ellos debían inventar el alto y el tenor, más tarde les enseñaba a construir los bajos
por sí mismos.” La tarea más avanzada de éstas requería comprender no sólo la escritura a
voces, sino también la sintaxis armónica, un tema que había sido tratado en los manuales
de bajo continuo de finales del s. XVII en referencia a la realización de bajos no figurados
(ej. Penna, 1672). Cuando a finales del s. XVIII, el papel del bajo continuo quedó relegado,
la improvisación dejó de ser el objetivo principal del entrenamiento armónico y ya no habrá
continuación en la tradición de los textos sobre improvisación hasta la década de 1950, cuando
los músicos de jazz empezaron a codificar sus métodos. Ahora bien, hablando con propiedad, la
fundación de la escuela armónica práctica debe atribuirse de manera universal, a la teoría del
bajo fundamental de Rameau, que aunque estuvo diseminada en diferentes partes de sus escritos,
después de su muerte, en 1764, se convirtió en la base de la práctica pedagógica común, que fue
configurándose en una forma muy similar a la manera actual, durante esa segunda mitad del s.
XVIII. Aportaciones determinantes fueron las de Marpurg que desarrolló una taxonomía para
las notas no reales, y John Trydell que empezó a indicar las fundamentales como grados de la
escala en relación a una tónica3 , pero quizás las más importantes serían las de Kirnberger (177179) y H. C. Koch (1782-93) en sus tratados de composición, cuando empezaron a considerar
el papel de la armonía como un mecanismo de articulación de las frases y los movimientos.
Si bien, Trydell representaba los grados mediante números arábigos, no con números romanos que es la
forma habitual hoy día, y que proviene de los escritos de Vogler.
3
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
13
Estas contribuciones tuvieron como finalidad un claro matiz analítico y compositivo, durante el
siguiente siglo. El análisis armónico usando números romanos fue sustituido al final del s. XIX
por Riemann, que proponía la teoría del dualismo, junto con la teoría de las funciones tonales,
en una serie de escritos pedagógicos. Después de la muerte de Riemann, la teoría funcional
se separó del dualismo, que había encontrado pocos defensores entre los tratadistas modernos,
y dominó la pedagogía en Alemania, Escandinavia y Europa del Este, pero incluso en estos
lugares no ha sustituido completamente el método de los números romanos. Podríamos decir
que la influencia de Riemann en el Sur de Europa y en el mundo anglosajón ha sido mínima, de
forma que si aún a día de hoy podemos hablar de dos escuelas de análisis armónico principales,
existe una clara primacía del modelo que hace uso de los números romanos, a nivel mundial y
también, en nuestro contexto académico español.
Podríamos sintetizar pues y decir que desde finales del s. XVIII, nuestros métodos de enseñanza de la armonía han continuado básicamente igual, sirviéndose de ejemplos normalmente
tomados del canon del repertorio clásico y romántico, se inferían unas reglas que servían para la
realización de ejercicios armónicos que, como abstracciones especulativas teóricas, perseguían
más la adquisición de técnicas que la verdadera imitación de estilos. Otra de las posibles críticas
que se pueden lanzar contra esta didáctica, mayoritariamente extendida, es que parece conceder
más importancia al aprendizaje de unos mecanismos gráficos y no tanto a la experiencia auditiva de los mismos; si bien, esto no tendría por qué ser así siempre, sí parece deducirse desde
la propia orientación del sistema, en el que el aspecto sonoro parece hacer aparición más como
complemento necesario, que como elemento central. Algunos autores como R. O. Morris (1968)
iniciaron movimientos pedagógicos que trataron de tomar el teclado como punto de referencia,
en las primeras décadas de la segunda mitad del s. XX, pero sus métodos aunque han tenido
repercusión en otros países, sobre todo en Estados Unidos, aquí en España apenas ha tenido
un eco exiguo en algunos imitadores.
1.2.
La metodología tradicional
Los métodos tradicionales de enseñanza de la armonía se centran en la armonización a
cuatro partes de melodías (de tiple o de bajo) dadas; ejemplos de este tipo de metodología
serían las propuestas de Rockstro (1881), Piston (1991)4 y Gauldin (2004)5 . El estudiante debe
construir voces independientes horizontalmente que vayan bien con una línea melódica previa.
Los ejemplos melódicos tratan de ilustrar la llamada práctica común de los compositores de
los ss. XVIII y XIX. El cuadro 1.1 (que incluye cinco figuras) sirve para ilustrar el proceso
de armonización homofónica usando los acordes mayores I, IV y V, como una simplificación
e ilustra los principales pasos, descritos más abajo, que se les aconseja seguir a los aprendices
para la armonización de melodías.
4
5
Primera edición en inglés de 1978.
Primera edición de 1997.
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
(a) Listado de posibles acordes
(b) Depuración de las opciones
(c) Segunda depuración de las opciones
(d) Escritura de una melodía para el bajo
14
(e) Escritura de las demás voces
Cuadro 1.1: Pasos de la armonización según la metodología tradicional
1. Listar todos los acordes posibles. Todos los acordes que pueden ser asociados con cada nota
deben explicitarse en números romanos. La figura 1.1a muestra las 32 posibles progresiones
armónicas que admite la melodía.
2. Depurar las opciones. Las piezas de música tonal casi siempre empiezan y acaban en el
mismo acorde de tónica (acorde de I). Si se eliminan las posibilidades que comenzaban y
terminaban por un acorde diferente, todavía quedan 8 progresiones posibles, como muestra
la figura 1.1b.
3. Depurar aún más las opciones. El bagaje musical es lo que requiere ahora el alumno, para
elegir una progresión acórdica que sea musicalmente significativa de entre las alternativas
que se le ofrecen. La figura 1.1c muestra la progresión de acordes como sería escogida
por un compositor experimentado ya que contiene el giro más ampliamente repetido (de
longitud 3).
4. Escribir una melodía para el bajo. Ha de cumplir un número considerable de condiciones:
progresión acórdica, ámbito, movimiento preferentemente contrario al soprano y dejar
espacio para el movimiento de las voces internas y entre ellas. La figura 1.1d muestra una
solución que cumple estas condiciones.
5. Escribir las demás voces. Otra vez deben satisfacerse una serie de prerrogativas: progresión
armónica, ámbito, evitar el cruzamiento de voces y evitar octavas y quintas paralelas y
directas. La figura 1.1e muestra una posible disposición para las voces internas.
Las limitaciones pedagógicas de la manera tradicional de enseñar armonía, responde, obviamente, a ciertas dificultades observadas en los principiantes:
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
15
Conocimiento teórico musical previo elevado; los ejercicios requieren que el alumno posea
un considerable bagaje teórico musical de otros elementos como el ritmo, el contrapunto
y la forma, lo que supone una complejidad añadida para el proceso de aprendizaje.
Análisis armónico de las melodías (elección de grados); el análisis armónico es el proceso de
asignar unos grados a las partes de una partitura. Si la partitura posee sólo una melodía,
puede aceptar diversas alternativas de progresiones armónicas –como sucedía en la figura
1.1a- y la elección de la mejor alternativa que encaje perfectamente es el objetivo último
de este proceso analítico -figura 1.1c-. Sin embargo, los principiantes suelen carecer de
la experiencia necesaria para esta tarea, y no entienden qué significa “la mejor” en este
contexto. Así que existe la tendencia, por parte del profesor, de imponer en los alumnos
las “progresiones armónicas aceptables” que, de esta forma, se incorporan al vocabulario
armónico del estudiante.
Armonizar una melodía (escribiendo notas en las voces); una vez elegidos los grados que
irán con las notas de la melodía, las notas deben colocarse en las voces restantes de
acuerdo con el análisis armónico (véase los pasos 4 y 5 ilustrados con las figuras 1.1d
y 1.1e respectivamente). Sin embargo, dependiendo del grado de adecuación del análisis
armónico, puede ser difícil, o incluso imposible, colocar las notas en las voces sin quebrar
alguna/s de las reglas musicales impuestas.
Didáctica centrada en el profesor; en los métodos tradicionales el profesor normalmente
da clases (Peters, 1982) a un grupo de alumnos, analizando armónicamente fragmentos de
piezas musicales, proponiendo ejercicios y corrigiendo algunas de las soluciones aportadas
por los alumnos.
Ingente corpus de piezas tonales; los métodos tradicionales requieren de un gran y heterogéneo corpus de fragmentos de piezas musicales como sonatas, conciertos e incluso
canciones populares, para ilustrar las prácticas armónicas académicas.
1.3.
Nuevos enfoques del s. XX
Con el siglo XX tuvieron lugar importantes cambios dentro del plano musical, no es de
extrañar que no sólo los compositores, sino también teóricos e intérpretes, buscaran otras formas
de entender la música y otras formas de explicarla.
1.3.1.
A. Schoenberg, un pequeño paso adelante
Algo antes de la primera guerra mundial, aunque algún eco mayor obtuvo después de la
misma, en 1911, Arnold Schoenberg publicaba su Harmonielehre -que tardaría en aparecer en
España más de medio siglo (Schoenberg, 1979)-. En él, Schoenberg, escapando de la presión de
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
16
la imitación de cánones estilísticos, consigue superar ciertas trabas que la enseñanza tradicional
tenía, como serían los siguientes:
Requiere de un menor conocimiento teórico previo del alumno y trata de aislar otros
elementos de la música (ritmo, contrapunto y forma) de la enseñanza de la armonía;
Guía al estudiante a la hora de escoger los grados en los ejercicios y no requiere análisis
armónico;
Evita la armonización de una melodía, con la finalidad de darle al estudiante más alternativas en la distribución de notas por voces;
Se centra más en el alumno a la hora de enseñarle, con el objetivo de maximizar su
creatividad;
Evita el inmenso corpus de piezas tonales.
Podríamos recordar otros métodos que siguen algunos de los principios recogidos arriba, por
ejemplo, hay métodos que enfatizan el enlace correcto sin prestar mucha atención a otros
elementos de la música, así sería el caso de Riemann, por ejemplo, que enfatizaba las funciones
tonales, pero que obviamente obliga a determinados movimientos y se desliga de promover
la creatividad del alumno. Los escritos de Schoenberg también están centrados en el enlace
correcto de los acordes, sin embargo, no es lo principal, le preocupa más evitar la imposición
de “progresiones aceptables” en los estudiantes y en darles una mayor libertad de elección.
Schoenberg creía que los estudiantes, a través de la experimentación no sólo de “progresiones
armónicas aceptables” y valorando sus preferencias por sí mismos, eran capaces de desarrollar
su propio sentido armónico sin el fuerte condicionamiento del vocabulario armónico impuesto
por los métodos tradicionales. El método de Schoenberg se distingue por un programa que
no incluye la armonización de melodías y que incorpora una calculada estrategia evolutiva de
presentación y práctica de nuevos conceptos. El cuadro 1.2 ilustra los principales pasos, descritos
más abajo, seguidos por los estudiantes en los ejercicios propuestos.
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
(a) Paso 1
(b) Paso 2
(c) Paso 3
(d) Paso 4
(e) Paso 4
(f) Paso 4
17
Cuadro 1.2: Método de Schoenberg
Pasos para la solución de un ejercicio:
1. Definición de la secuencia de acordes. El estudiante, siguiendo unas instrucciones, escoge
los grados con que va a trabajar (así se ve en la figura 1.2a).
2. Colocación de notas para el primer acorde. El estudiante decide la posición del acorde
inicial y le asigna las notas a las voces observando las condiciones constructivas del acorde
(como queda ilustrado en la figura 1.2b).
3. Colocación de notas para el siguiente acorde. El estudiante coloca las notas en el acorde
que sigue a la derecha del anterior, vigilando las normas de construcción propias del acorde
en concreto, así como las de enlace respecto del anterior (según se aprecia en la figura
1.2c).
4. Repetimos el paso tres con el resto de acordes. Los estudiantes repiten el paso tres hasta
que se han asignado todas las notas de todos los acordes de la progresión (tal y como
queda reflejado en las figuras 1.2d, 1.2e y 1.2f).
1.4.
Dos teorías cognitivas recientes de la Armónia
Estas dos teorías aportan dos puntos de vista diferentes de la Armonía, que permiten acercar
la disciplina a personas que, careciendo de los conocimientos teóricos o la habilidad instrumental necesaria, se verían totalmente desprovistos de una posibilidad en el entorno de aprendizaje
acostumbrado. Se trata de los estudios de Longuet-Higgins (1962) y de Balzano (1980); que
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
18
aunque parten cada uno de puntos diferentes, ofrecen dos visiones bastante similares del funcionamiento de la Armonía. Y así lo explica muy bien Simon Holland en su artículo New Cognitive
Theories of Harmony applied to direct manipulation tools for novices (1987).
1.4.1.
Longuet-Higgins y su espacio armónico bidimensional
En mi opinión, los primeros pasos de importancia, hacia una verdaderamente nueva manera
de explicar Armonía deberíamos atribuírselos a Longuet-Higgins que desarrolló una nueva teoría
cognitiva de la armonía (1962). El sistema se basa en la configuración de una red de notas
dispuestas en columnas y filas, de forma que los miembros de cada columna son notas separadas
una 5ª, mientras las filas están construidas separando las notas una tercera mayor . La teoría
de Longuet-Higgins se fundamenta en que el conjunto de intervalos posible en la música tonal
occidental es aquel que sucede entre notas cuyas frecuencias están en una proporción expresable
como el producto de tres números: 2, 3 y 5 y ningún otro6 . Teniendo en cuenta esta premisa, se
desprende el hecho de que el conjunto de tres intervalos formado por la octava, la quinta justa
y la tercera mayor es el único espacio coordinado no redundante para todos los intervalos que
usamos. Podemos representar este espacio gráficamente colocando las notas en capas en una
red tridimensional en la que las notas van ascendiendo en octavas, terceras mayores y quintas
justas, a lo largo de los tres ejes. Sin embargo, en la mayoría de representaciones se omite el eje
de la dimensión de la octava dado que da lugar a planos paralelos y a la conveniencia práctica
que supone centrarse en las otras dos dimensiones (fig. 1.4.1).
Longuet-Higgins fue desarrollado por Steedman, en su tesis doctoral: “The formal description of musical
perception”, University of Edinburgh, 1972.
6
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
19
Figura 1.4.1: Espacio armónico (sin enarmonías) de Longuet-Higgins
Como podemos ver en la figura de arriba, hemos enmarcado todas las notas de la escala diatónica con una línea en una pequeña región de dos columnas y siete casillas (dado que la escala
posee siete grados). Si imaginamos que este marco, manteniendo su forma, pudiera deslizarse
alrededor de la tabla de notas libremente y delimitar diferentes conjuntos de notas, descubriríamos que si lo movemos hacia arriba una fila estaríamos en la tonalidad de la Dominante, y que
si lo bajamos una fila estaríamos en la de la Subdominante. Se pueden encontrar otras tonalidades trasladando el marco en otras direcciones, aunque convenga recordar que las notas no
siempre mantendrán el mismo nombre en las diferentes tonalidades, sino que podrán estar enarmonizadas (sonidos homófonos). Sin embargo, en virtud de la finalidad didáctica, reducimos el
espacio Longuet-Higgins a una nomenclatura de doce sonidos de un sistema tonal temperado,
resultando lo que llamaremos “espacio armónico Longuet-Higgins de 12 notas bidimensional”
o, simplemente, espacio armónico bidimensional, para abreviar. Consecuentemente perdemos
los doble sostenidos y doble bemoles de la figura 1 y el espacio ahora se repite exactamente en
todas las direcciones (véase fig. 1.4.2). Las notas con el mismo nombre son realmente la misma
nota en este espacio. De hecho, bastará una pequeña reflexión para darnos cuenta de que este
espacio es en realidad un toro7 que hemos desplegado y repetido como si fuera un motivo para
empapelar algo. Uno de los resultados que produce esta figura es que en lugar de un único
marco de tonalidad, tenemos el marco repetido.
Un toro es una superficie o una figura geométrica tridimensional formada por la rotación de una curva
cerrada, especialmente un círculo, alrededor de una línea que se haya en el mismo plano pero que no intersecciona
con ella (ej. un anillo con forma de donut).
7
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
20
Figura 1.4.2: Espacio armónico Longuet-Higgins de 12 notas bidimensional
Fijémonos ahora en la representación de los tríadas y los centros tonales. En el espacio armónico bidimensional, los acordes mayores tienen forma de L (cf. fig. 1.4.3). Vemos también como
los acordes de Dominante y Subdominante, tríadas mayores, están extremadamente próximos
a la tríada de tónica. Al mismo tiempo, podemos observar que los tres tríadas fundamentales
contienen todas las notas de la escala diatónica y cómo también este diagrama sirve de metáfora
del lugar central que ocupa la tónica (y así sucedería en cualquier tonalidad). Igualmente podemos distinguir cómo los tríadas menores corresponden con una L invertida, y cómo también
forman la escala menor y disponen su tónica (la tríada menor de La) en una posición central.
Para completar la escala, quedaría marcar el tríada disminuido, que se configura marcando una
línea oblicua. Algunos estilos armónicos perfectamente asumidos en el repertorio de estudio,
hacen uso de los acordes cuatríadas y quintíadas, que también tienen formas fácilmente reconocibles dentro del espacio armónico bidimensional (véase fig. 1.4.4 para la representación de
las séptimas diatónicas propias de la escala natural).
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
21
Figura 1.4.3: Acordes tríadas en el espacio armónico bidimensional Longuet-Higgins
Figura 1.4.4: Acordes cuatríadas en el espacio armónico bidimensional Longuet-Higgins
Hagamos ahora, tras la descripción del sistema, un ejercicio de abstracción para imaginar
una manipulación virtual directa de este entorno, utilizando un programa informático. Supongamos que podemos utilizar el ratón para elegir un modelo geométrico que represente un tipo
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
22
de sonoridad y, hecho esto, pudiéramos hacer sonar las notas que elige, cada vez que su botón
esté pulsado (como si estuviésemos seleccionando cosas, en cualquier entorno de Windows); ésta
sería la propuesta del Dr. Simon Holland para, aplicando las explicaciones de Longuet-Higgins,
acercar a un alumnado novel al manejo de las sonoridades, de la Armonía en definitiva, de
forma intuitiva.
1.4.2.
Balzano con su red
Balzano en su artículo The Group-theoretic description of 12-fold and microtonal pitch
systems (1980) describía dos posibles modos de trasladar, todo considerado desde el punto
de vista matemático8 , a un espacio bidimensional circular nuestro sistema musical de doce
sonidos, en realidad nada nuevo aunque fundamentado mediante expresiones matemáticas: el
círculo de quintas y el círculo cromático9 (adjuntamos la figura 1.4.5 a modo de ilustración).
Resultan llamativas las observaciones de cómo, sobre el círculo de quintas, los sonidos diatónicos
quedan representados ocupando justamente la mitad del círculo y cómo, según qué vamos
moviendo esta mitad, rotándolo dentro del cículo vamos obteniendo los sonidos propios de las
escalas o los modos, con alteraciones en menos o con alteraciones en más, según el sentido sea,
respectivamente, el contrario o el mismo de las agujas del reloj.
Figura 1.4.5: Modelos del sistema musical dodecafónico en un espacio bidimensional
Sin embargo, no fue ninguna de estas dos proyecciones la que S. Holland (1987) adoptó
como base para su elaboración didáctica, sino la que Balzano consideraba más válida para la
observación de los aspectos armónicos, una tercera traslación a un espacio bidimensional que
tendría la forma de una red (que podemos observar abajo, en la fig. 1.4.6). Fuera de las evi8
Para ello, los doce sonidos son tomados como los doce primeros números enteros (y así puede observarse en
las ilustraciones que de sus propuestas se adjuntan en este apartado); esto es: do = 1, do# = 2, re = 3, mib =
4, mi = 5, fa = 6, fa# = 7, sol = 8, lab = 9, la = 10, sib = 11 y si = 12.
9
Esta proyección bidimensional, estudiada como ya decimos por este autor (Balzano, 1980), servirá de base
para su adaptación a un sistema de lectura ya no lingüístico-textual, sino puramente musical, y así nacerá
el Espiropentagrama -núcleo del corpus gráfico de la propuesta de estas páginas y que está explicado con
detenimiento en el capítulo 4 en la página 41.
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
23
dentes aportaciones visuales (con formaciones geométricas diversas) que esta red aportaba a la
observación de los diferentes conjuntos de sonidos; Balzano en este trabajo también demostraba
la adaptabilidad y la permanencia de diversas propiedades de los conjuntos sonoros, cuando se
trabaja con sistemas diferentes de dividir la octava a la nuestra (que lo hace en doce partes),
incluyendo como ejemplo en este artículo, una red que reflejase la división de la octava en veinte
partes, o sea, utilizando intervalos microtonales.
Figura 1.4.6: La red de Balzano señalando los sonidos de la escala diatónica dentro del cuadrante
de los doce
Pues bien, esta red, como decíamos, es la otra base que va a servir para los propósitos
pedagógicos que el Dr. Holland desarrollaba en 1987 y que tanto nos han servido de inspiración
para el desarrollo de este trabajo. La aplicación en esta red tendría un desarrollo análogo al que
describíamos al final del punto anterior; esto es, su incorporación en un software informático
que permitiera a gente no iniciada dentro de los complejos conocimientos musicales que requiere
la Armonía, acercarse e incluso ejercitarse dentro del mundo de la pluralidad sonora armónica.
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
1.5.
24
La enseñanza de la Armonía en la actualidad
En la actualidad, hay una notable diferencia en cuanto a la enseñanza de la Armonía según
en qué ámbito geográfico nos situemos e incluso, precisando más, en qué institución de qué
lugar. Por ello, en este apartado vamos a hablar, por un lado, de forma generalizada de cómo
tenemos noticia que se desarrolla esta enseñanza en el conjunto de nuestro mundo occidental,
y de otro, de cómo se desarrolla en nuestro país, tomando como especial foco de observación
nuestra región y las instituciones que en ella existen destinadas a la formación musical.
1.5.1.
La Armonía en el mundo
Parece incuestionable que nuestro mundo occidental tiene una nación que ejerce el claro
papel de cabeza del conjunto, me refiero claro está, a Estados Unidos. Como en cualquier período
de la historia, los estudios más avanzados de las artes y las humanidades, como cualquier otra
disciplina, encuentran pronto su lugar, partiendo de su tradición y evolucionando a partir de
ésta, en las paredes de la casa más poderosa. De este modo, no es de extrañar que parta de
esta nación la mayor parte de las directrices de cambio, respecto de la metodología tradicional
(que desarrollábamos en este mismo capítulo, en la sección 1.2 en la página 13).
Así pues, conjuntamente con una encomiable asimilación de las aportaciones que la evolución de la música popular de cierta entidad, ha aportado a la música académica; los métodos
norteamericanos desde hace varias décadas tienden a una mayor practicidad de sus enseñanzas,
a una mayor ejercitación sonora de las mismas -por lo general sobre el teclado- y a una reflexión
teórica considerablemente menor.
1.5.2.
La Armonía entre nuestros muros
Nuestro país, con sus ventajas y sus inconvenientes, no ha ido mal que le pese, nunca a la
cabeza en general, de la investigación, y en particular, en lo tocante a la investigación musical,
menos aún si cabe. Para hacernos una idea, haré un somero repaso de las publicaciones que aún
a día de hoy fundamentan la bibliografía básica de nuestros centros educativos, cuánto hace
que llegaron y cuando lo hicieron, con cuánto retraso llegaban desde que habían visto la luz en
otros idiomas. Quizá el libro que ocupaba hasta la fecha las principales referencias en las aulas
de Armonía de nuestra región, fuera el de Armonía de W. Piston, este libro fue publicado por
primera vez por la Norton, en 1941, sin embargo, la primera edición en España, por la editorial
Labor, no llegó hasta medio siglo después, y éste, un libro que cuenta a día de hoy con casi
70 años de antigüedad, es el libro probablemente más utilizado en nuestro país. Otros libros
que también tienen y han tenido una enorme repercusión no han corrido, por desgracia, mejor
suerte; éste sería el caso, por ejemplo del tratado de Armonía y de Funciones estructurales de
la Armonía de A. Schoenberg que nacieron respectivamente, en 1922 y 1954 y sin embargo
no se pudieron ver en nuestras librerías hasta 1974 y 1990. Y hablamos, obviamente de libros
CAPÍTULO 1. EVOLUCIÓN DE LA ENSEÑANZA DE LA ARMONÍA
25
capitales dentro de lo que se considera la disciplina Armónica a día de hoy, no hablaremos de
los que ni siquiera han llegado a ser traducidos o, depués de haberlo sido, no han encontrado
manera de publicarse.
Bien es cierto, en cualquier caso, que también ha habido teóricos en nuestro territorio
que han sido de notable prestigio (dentro del mismo) y que han contribuido enormemente a la
difusión de principios de otros grandes autores del resto de Europa o América, pero incluso éstos,
que otrora fueran verdaderos adalides de una información innovadora e ilustrativa, después de
pasar más de tres, cuatro o cinco décadas, creo que podemos afirmar que se hayan quedado
algo anticuados. Hablamos, por ejemplo, de Zamacois que publicara en 1945 su primera edición
de su revelador Tratado de Armonía.
De esta forma, podemos resumir que la situación es algo desalentadora, que aunque no faltan
diversos focos individuales (como los casos de Martínez-Oña (1991) y de Sánchez Navarro (n.d.),
que se recogen en nuestra bibliografía en la página ??) que tratan de renovar y modernizar la
didáctica armónica en nuestras aulas, tienen un eco ínfimo y un marco de actuación que, con
frecuencia, apenas alcanza más allá de sus propias clases. Existe muy poco interés por parte
de instituciones que podrían patrocinar su actualización, probablemente por su orientación
hacia un público tan minoritario. Un público que además, acostumbrado a esta situación, la
ha tratado de solventar con su propia iniciativa y sus propios recursos, aunque siempre haya
quedado en esfuerzos y resultados de poca mayor extensión que aislados casos individuales.
Capítulo 2
Fundamentos de esta didáctica
Esta didáctica tiene por finalidad, la incorporación a la teorética armónica de un corpus
de analogías -especialmente de carácter visual- que sirva para construir un método didáctico
que responda mejor a las directrices de la pedagogía y de la psicología evolutiva. Para ello,
fundamenta sus principios en los elementos visuales más elementales (como figuras geométricas
sencillas y colores), al tiempo que se apoya en otras conexiones como el movimiento, algo que
en conjunto, contribuirá a favorecer el acercamiento, el manejo y la comprensión de realidades
musicales armónicas, y de esta forma ayudará a incorporarlas a la vida del niño desde una edad
temprana.
De este modo, se persigue el que esta propuesta de significantes quede aceptada y asimilada
en la mente infantil, para partiendo de este punto, poder ir creciendo con él a lo largo de su
educación musical, abriéndole un camino mucho más amplio y prometedor que el que la actual
propuesta educativa le ofrece.
2.1.
Música y formas
Es interesante el trabajo llevado a cabo en la Universidad de Illinois (Urbana Champaign)
por tres profesores de la misma, Bergstrom (2007); en este artículo, utilizando una red Tonnetz1 ,
se propone una visualización de la estructura de la música, de su armonía. Este trabajo no es
más que uno entre los muchos que podríamos encontrar que muestran las conexiones que pueden
señalarse entre la música y entidades visuales derivadas, más que de ningún otro campo, de las
Matemáticas.
Existen, como ya apuntábamos, numerosos estudios que buscan analizar desde el punto de
vista matemático, la realidad musical y que aportan incluso, posibles construcciones bidimensionales (Longuet-Higgins, 1962, Balzano, 1980, Holland, 1987, Clough, 1998, Rappaport, 2007)
y tridimensionales (Bancroft, 1993, Gollin, 1998, Bergstrom, 2007) que sirvieran para explicar
mejor la manera de existir y funcionar de la música. Sin embargo, y he aquí quizá, la verdadera
Un Tonnetz es un modelo geométrico espacial, bien en dos o bien en tres dimensiones, que representa las
propiedades de un conjunto de sonidos.
1
26
CAPÍTULO 2. FUNDAMENTOS DE ESTA DIDÁCTICA
27
innovación de estas páginas, ninguna de ellas buscaba más que expresar estas similitudes de
forma descriptivo; observar su funcionamiento y hacerlo aún más patente mediante la muestra
de un conjunto de representaciones acordes. Este trabajo se propone ir más allá, se propone utilizar y desarrollar algunas de estas investigaciones para proponer un método que sea agradable
y ofrezca un avance progresivo a los estudiantes de música, permitiéndoles acceder a realidades
teóricas de elevada complejidad mediante esta especie de adaptaciones visuales geométricas,
nada deleznables.
2.2.
Música y color
La primera referencia importante que podemos señalar en relación a la conexión entre música
y color, que se hace en el ámbito de nuestra cultura, corresponde a Isaac Newton2 que en su
tratado Opticks 3 (Newton, 1704) señaló la posible correlación entre estas dos realidades del
mundo físico, en base a sus propiedades científicas. De este modo, conectó, en función de su
frecuencia, los sonidos de la escala Mayor, con los colores que aparecían en la naturaleza de
forma natural, los colores del Arcoiris, en función de las longitudes de onda de sus espectros
(así podemos observarlo en la figura 2.2.1 anexa que, aunque no en color, aparecía de tal cual
en la publicación de Newton).
Figura 2.2.1: Disco de la música y color de I. Newton
La fundamentación de Newton, de índole puramente física, es incontestable aunque no por
ello deja de ser algo arbitraria. No obstante, la que vamos a tomar aquí, como base para
elaborar las correlaciones entre combinaciones de sonidos y colores, no se va a fundamentar en
los principios de Newton, sino en principios del campo de la psicología de la percepción. De
Los diversos estudios de I. Newton quedan explicados con notable claridad, en inglés, en la url:
http://home.vicnet.net.au/~colmusic/opticks1.htm
3
Este tratado puede ser consultado en internet e incluso descargado en formato pdf en la sección de books
de Google.
2
CAPÍTULO 2. FUNDAMENTOS DE ESTA DIDÁCTICA
28
esta forma, y no siendo los primeros que utilizamos el color como elemento para coadyuvar
a la comprensión de la música (destaca el memorable caso del compositor A. Scriabin -cuya
propuesta está sintetizada en el círculo recogido en la figura 2.2.2 de abajo- o el más reciente
O. Messiaen) e incluso su uso con fines educativos sobre todo los estudios de Galeyev (1975) y
Vanechkina (1994) que hemos citado en la Bibliografía.
Figura 2.2.2: Círculo de quintas en colores de A. Scriabin
Nuestro trabajo, siguiendo en parte la estela de estos ilustres predecesores, busca conectar
las emociones suscitadas por los colores (siguiendo los trabajos de Warner Schaie (1961) y
D’Andrade (1974)) con las propiedades que, en nuestro caso, dentro del sistema tonal, se le
atribuyen a diversos grados y funciones. De este modo, se busca la confección de una didáctica
más asequible y coherente a la mente humana infantil.
2.3.
Música y movimiento
Desde Schopenhauer hasta infinidad de autores de la teorética musical -quizá deberíamos
destacar a Dalcroze (1965)- han subrayado la sobresaliente cualidad motora de la música; muchos llegan a afirmar que “la música es movimiento”. De este modo está más que refutado que
el uso de esta vinculación puede ser más que fructífera para la enseñanza de la música y no
va a ser aquí donde repasemos todas las enormes aportaciones que esta unión posibilita; entre
otros motivos, porque la conexión que en esta propuesta didáctica se va a exponer va a tomar
apenas los más elementales parámetros y sólo con la finalidad de colaborar con los elementos
que sí se desarrollan, de índole visual.
Así pues, en el último capítulo, en el que se realiza una propuesta de aplicación de este
método didáctico, sí se aportan algunos ejemplos de cómo podría trabajarse y fomentarse el
empleo de coreografías y de determinados movimientos expresivos, sobre todo con un alumnado
de corta edad, para estimular su atención y favorecer la asimilación de las analogías que en el
transcurso de estas páginas van a proponerse.
CAPÍTULO 2. FUNDAMENTOS DE ESTA DIDÁCTICA
2.4.
29
Música y texturas
Analizamos ahora la conexión de la música con las texturas, más que por su influencia en el
método didáctico que vamos a exponer en este trabajo, por redondear el círculo sinestésico de
elementos con que hemos relacionado la música y también, por abrir una puerta a la posibilidad
de realizar maquetas y utilizar texturas en conjunción a los colores para representar lo mismo
que aquellos y así insistir a través de otro elemento más (aunque hoy día mucho menos fácil de
aplicar y extender), en las propiedades que queramos observar en determinadas sonoridades.
Además, no podemos dejar pasar el importante papel que podría desarrollar esta relación, para
apoyar el aprendizaje de la disciplina armónica en personas con algún tipo de discapacidad
visual.
Investigando en este tema, ha sido sorprendente cómo apenas existen publicaciones que
hayan desarrollado esta relación. Como precedentes señalables, de relativa fecha reciente, podríamos mencionar la conexión con la arquitectura que repasaba un artículo de la revista
“Leonardo” en 1993 (Bancroft, 1993) y la general revisión respecto a la música en Braile que
podemos ver en el “Musical Educators Journal” en 1998 (Smaligo, 1998). De esta manera, parece que la propuesta que en este apartado apenas vamos a esbozar, podría ser de una importante
trascendencia dentro de este campo de la pedagogía, como consecuencia de la escasa aportación
de recursos que existe.
La idea sería tomar las representaciones tridimensionales que se han creado tomando las 12
alturas de nuestro sistema temperado, o sea un Tonnetz tridimensional, como el que proponía
Gollin en su artículo Some Aspects of three-dimensional Tonnetze (1998), dedicado a explicar
espacialmente, sobre todo, las propiedades de los cuatríadas.
CAPÍTULO 2. FUNDAMENTOS DE ESTA DIDÁCTICA
30
Figura 2.4.1: Tonnetz tridimensional propuesto por E. Gollin
2.5.
Otras posibles vinculaciones
Siguiendo la línea que plantea este capítulo, esta línea de construcción de relaciones sinestésicas entre elementos sonoros y elementos de percepción que pertenezcan a otros sentidos
diferentes a la audición, no podemos dejar de al menos enunciar la posibilidad de conectar
también las realidades sonoras a sabores y a olores, siguiendo exactamente los mismos procedimientos de coherencia y justificación para la elaboración de vínculos que hemos seguido en
estas páginas. De hecho, aunque extremadamente atrevido y con escasa o ninguna referencia
que pueda ofrecer una base de comparación para la sugerencia que se aporta en este apartado,
es indudable que cualquier colaboración de contenidos abstractos con símiles va a facilitar su
captación, máxime, si estos símiles no son también de tipo abstracto y lingüístico, sino que son
entes perceptibles sensorialmente.
Además, al igual que sucedía con el apartado anterior, esta vía que aquí apenas se esboza,
sería con seguridad, de una enorme relevancia en enseñanzas de carácter especial, con un alumnado que tuviera algún tipo de deficiencias sensoriales o motrices, y no pudiera ver o palpar las
analogías de caracter visual o espacial.
Capítulo 3
Los árboles armónicos
Un árbol1 armónico va a servir como un esquema para sintetizar las cualidades de cada
sonido dentro de un conjunto cualquiera, creado en función de sean cual sean los parámetros
a que se quiera atender para su configuración. Del mismo modo, este tipo de abstracción será
también muy práctica cuando se quiera comparar varios conjuntos de sonidos (y las cualidades
de los mismos). Evidentemente, es fácil deducir que dentro del ámbito de la tonalidad tiene una
aplicación aún más obvia, si tenemos en cuenta por ejemplo, las consideraciones funcionales
de la práctica común. De hecho, las explicaciones más extensas y en el campo que más hemos
trabajado con estos “árboles”, ha sido en el de la tonalidad; ahora bien, cabe la posibilidad que
el lector encuentre algunos puntos en los que quizá, difiera con mayor o menor determinación,
sobre algunas consideraciones que aquí se hacen, no creo que huelgue decir que en este trabajo
no se trata de argumentar la funcionalidad de un grado concreto (que según su contexto es
probable que varíe, obviamente), sino de un modo de esquematizarlo y representarlo como
todo o parte de un conjunto; esta es nuestra intención y ante las leves disensiones que puedan
existir, apelamos al oportuno criterio del lector para adaptar los símbolos y los conjuntos aquí
propuestos, hasta adecuarlos más a su planteamiento teórico y, entonces, si los cree útiles, hacer
uso de esta propuesta de botánica armónica.
Las cualidades se van a representar dentro de los árboles armónicos, haciendo uso de diferentes tipos de grafemas para escribir la cabeza del sonido. Así, por ejemplo, se puede indicar si
una nota tiene tendencia descendente con una grafía que colaborara en este sentido (verbigracia
).
De esta forma, concebida la tonalidad como dos ejes, un eje tendencial (asimilable a la
función de Dominante) y uno no tendencial (vinculado con las tradicionalmente llamadas funciones de subdominante y tónica), podríamos decir que el eje tendencial comprendería todos
los sonidos que pueden participar dentro de sonoridades tendenciales en el ámbito de una úni-
3
La razón para adoptar este nombre para este tipo de representaciones gráficas esquemáticas no es casual,
ya que además de que la forma de algunos de estos esquemas recuerdan por su modo de ramificarse a ciertas
manifestaciones vegetales, también la matemática asume este término para nombrar -en la corriente de la Graph
Theory- cierto tipo de gráfico. Un gráfico acíclico se denomina un “árbol” y cuando éste aparece conectado con
otro u otros, se le llama “bosque” (véase la página 13 y siguientes del libro Graph Theory (Diestel, 2005)).
1
31
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
32
ca tonalidad, es decir, todas las posibles variantes de la función de dominante que pudieran
contemplarse; mientras el eje no tendencial contaría con el resto de sonoridades, o lo que es lo
mismo, las posibles variantes de las tradicionalmente expresadas como funciones de subdominante y de tónica. Por consiguiente, los respectivos esquemas de cada eje se denominan árbol
de Dominante y árbol de Subdominante-Tónica, y en conjunto, representan todas las posibilidades sonoras de una tonalidad concreta, bien circunscritas a unas condiciones (por ejemplo,
estilísticas o cronológicas) o bien de forma genérica. A la yuxtaposición de los dos árboles, la
denominaremos árbol tonal, y será la síntesis de la tonalidad, en cuanto a sus posibilidades, su
discurso y sus características.
3.0.1.
Como interpretar y usar los árboles
Los árboles, al contemplar todas las posibilidades de manifestación de una sonoridad, manejan algunas que se niegan entre sí. Por ejemplo, no podremos usar, al mismo tiempo, una nota
alterada y esta misma nota en su estado normal, esto queda reflejado en los árboles mediante
la bifurcación de sus ramas. De esta forma, cuando desde una nota más grave procedemos de
forma ascendente hacia las siguientes posibilidades, sólo podremos optar a las notas que estén
aledañas a la que partimos; o sea, yendo hacia arriba y o bien, simplemente encima o bien
en la línea vertical contigua a la derecha o a la izquierda (ej. tener que elegir entre la novena
mayor o la novena menor en un acorde de Dominante de un tono mayor -véase la fig. 3.1.1 en la
página 35 que representa un árbol de Dominante-). No podremos “saltar”, por decirlo de algún
modo, a una nota que se halle más allá de las verticales contiguas a la que está la nota desde
la que estamos.
De un modo similar, en un nivel horizontal, se podrán tomar varias notas si no están
adyacentes y tienen separándolas, al menos una, que no se podrá elegir; siempre que se proviniera
desde el centro del árbol, que permite optar a ambos lados de una trifurcación (ej. tomar la
quinta en más y en menos, pero no la quinta natural -Cf. esquema del árbol de Dominante
representado en la fig. 3.1.1 en la página 35-).
3.0.2.
Grafías de los árboles armónicos
Según se aprecia en la figura 3.0.1, en los símbolos habría dos clases principales: los rellenados
o negros y los huecos o blancos. Los blancos son aquellos que son propios del modo Mayor (que
tomamos como base) o son notas alteradas. Los negros son sonidos tomados de escalas diferentes
al modo Mayor, casi siempre provendrán del modo menor, pero también encontraremos entre
ellas la sensible de la dominante, por ejemplo. Un caso especial, de este segundo tipo es el
segundo grado rebajado (que será la fundamental del acorde de sexta napolitana) que por su
tradicional disposición en primera inversión, se indicará en los árboles mostrando la nota (con
una cabeza triangular rellena que marque su tendencia descendente) entre paréntesis.
33
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
Otra peculiaridad de la simbología escogida es que usa cabezas con líneas (una o dos)
verticales a los lados, para destacar los sonidos que constituyen los grados tonales: I, IV y V.
Tónica
Dominante
Subdominante
Sensible
Supertónica
Superdominante
Sensible de la
dominante
Subtónica (nota del
área de la
subdominante)
Superdominante del
modo menor
Mediante
Mediante del modo
menor
Nota alterada con
tendencia ascendente
Nota con tendencia
descendente
Nota con tendencia
descendente de otro
modo
Nota alterada con
tendencia descendente
Figura 3.0.1: Grafías de los árboles armónicos
3.0.3.
Estados de crecimiento de un árbol
Podemos reconocer esencialmente, tres fases o niveles de expresión de estos esquemas que
llamamos árboles, que corresponderían hasta cierto punto con la evolución cronológica histórica
de la tonalidad, pero más bien, con la organización y distribución progresiva de contenidos que
se utiliza en la enseñanza y práctica académica de la disciplina armónica. Por lo tanto, en un
comienzo los árboles, como esquema de posibilidades conocidas, son apenas un testimonio de
lo más elemental y van creciendo conforme va aumentando el conocimiento en la materia, del
alumnado.
De este modo, el primer nivel contendría la base o tronco de los dos tipos de árboles que
aquí vamos a estudiar; es fácil de deducir, se contaría básicamente con las notas propias de las
escalas de cada modo; la escala mayor natural, en el modo Mayor, y las escalas menor melódica
y armónica, en el modo menor, que participan de cada una de los dos tipos de sonoridades:
tendencial o de Dominante, y no tendencial o de Subdominante. Así pues, en el cuadro 3.1
vemos la versión de los primeros árboles con que los alumnos nóveles habrían de enfrentarse.
Tipo de árbol
Árboles de
SubdominanteTónica
Modo Mayor
Árboles de
Dominante
Cuadro 3.1: El tronco de los árboles armónicos
Modo menor
34
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
En un segundo estadío, se añadiría las notas tomadas de otros modos, así como la posibilidad
de la novena (mayor y menor) para el acorde de dominante y, consecuentemente, también para
la formación del séptima disminuida y del séptima de sensible; el segundo grado rebajado para
construir el acorde napolitano y la sensible de la Dominante con que elaborar los acordes de
Dominante de la Dominante. Éste podríamos decir que sería el estado de madurez de los árboles,
cuyo resultado queda reflejado en el cuadro 3.2 de abajo.
Tipos de
árboles
Árboles de
SubdominanteTónica
Modo Mayor
Modo menor
Árboles de
Dominante
Cuadro 3.2: Árboles armónicos en estado de madurez
Por último, contaríamos con la adicción de la subtónica -que se interpretaría más como
una referencia al área de la subdominante, que como una nota verdaderamente propia de esta
tonalidad- y de las notas alteradas en más y en menos. Con esto tendríamos los árboles armónicos completos que será con los que vamos a trabajar en las próximas páginas, describiendo
específicamente sus características y su configuración en los apartados 3.1 y 3.2.
3.1.
El árbol de Dominante
El árbol de dominante recoge todas las posibilidades sonoras armónicas que pueden existir
dentro de un tono, que tendrían función de Dominante; es decir, sonoridades que colaboran a
reafirmar el papel de tónica del primer grado. Como podemos observar en la figuras 3.1.1 y
3.1.2 de más abajo, en un árbol de Dominante de una tonalidad mayor o menor, casi todas las
notas que aparecen en la sonoridad de dominante son tendenciales, por este motivo tienen la
grafía triangular que apunta, según es conveniente, ascendente o descendentemente. De hecho,
sólo unas pocas de las notas que aparecen en este tipo de árboles no tienen obligatoriedad a la
hora de resolver.
Por otra parte, el sonido que está representado por un rombo relleno, que correspondería
con el VII rebajado (el grado natural en el menor), implicaría un área de subdominante, ya que
la negación de la sensible es, innegablemente, un indicativo de flexión armónica. Sin embargo,
dado que tanto la Dominante como esta supuesta área de subdominante (aunque de muy
diferente forma, eso está claro) tienen tendencia hacia el eje Subdominante-Tónica, por eso
ha sido incluida esta nota, en este árbol. No obstante, conviene recordar que estos árboles
son ejemplificaciones de cómo se podría trabajar y que lo importante es la manera nueva de
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
35
esquematizar, más que uno u otro autor puedan o no coincidir con el resultado que aquí se
ofrece; puesto que en definitiva, bastaría adaptar el esquema a las condiciones que se crea más
satisfactorias.
Si nos fijamos, podremos deducir que hay dos sonidos que específicamente, nunca podrían
estar dentro de este árbol, se trata, a un lado, de la nota tónica a la que estas sonoridades
van a apuntar, y a otro lado, la sensible de la dominante, que apunta hacia la fundamental del
acorde y por tanto, tampoco podría jamás tener sitio aquí. Es llamativo que estas dos notas
estén, precisamente, a distancia de tritono2
3.1.1.
El árbol de Dominante de un modo Mayor
Cuenta con once notas, si bien, como se puede apreciar en el ejemplo ilustrativo en la
tonalidad de Do Mayor, en realidad sólo son diez sonidos3 dado que dos son enarmónicas
(en este caso el sib y la# ); se trata de el III’ del menor y la 5ª alterada ascendentemente.
Fuera de este detalle, vemos que el tronco estaría constituido por el acorde de séptima de
Dominante y que tendría ramificaciones a la derecha y a la izquierda; hacia la derecha estarían
las posibilidades propias del mayor y sus notas alteradas ascendentes, y hacia la izquierda las
tomadas, normalmente, del menor, así como las notas alteradas descendentes.
Figura 3.1.1: El árbol de Dominante de Do Mayor
3.1.2.
El árbol de Dominante de un modo menor
Los árboles del modo menor surgen partiendo del modelo del modo Mayor, por eso, mantiene
con grafemas rellenos las notas propias del modo menor (como la novena menor o el III de este
modo). Básicamente, como se muestra en la figura 3.1.2, los árboles de Dominante de una
Este detalle, el que estén a distancia de tritono los dos sonidos imposibles para una sonoridad de dominante,
será un elemento de apoyo a la hora de visualizar este tipo de esquemas en el Espiropentagrama, ya que,
como veremos más adelante, estos dos sonidos están representados en puntos diametralmente opuestos de la
circunferencia, con lo que formarán una especie de diámetro hueco que dividirá como en dos mitades, los puntos
de representación de los sonidos participantes: cinco y cinco en la representación del árbol de Dominante del
modo Mayor (exactamente la misma forma que el modo 7 de transposiciones limitadas de Messiaen, como
podemos ver en el apartado 5.2.1.7 en la página 77) y cuatro y cuatro en el del modo menor (véase la fig. 6.3.2
en la página 117, para una mayor comprensión de estas palabras).
3
Las únicas dos notas que no quedan asumidas en este corpus son: la sensible de la dominante y la propia
tónica de la tonalidad en la que esta sonoridad tendrá una función tendencial.
2
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
36
tonalidad Mayor y menor cuentan con un mismo tronco (el acorde de Dominante con séptima)
y las ramificaciones de la parte izquierda, careciendo el menor de las de la derecha (que incluyen
las notas alteradas ascendentes o las notas propias como la novena mayor o el III propio del
modo Mayor).
Figura 3.1.2: El árbol de Dominante de La menor
3.2.
El árbol de Subdominante-Tónica
Este árbol va a servir para esquematizar las posibilidades de combinaciones de sonidos
que va a tener una tonalidad, formando sonoridades que van a desempeñar los papeles de
Subdominante y de Tónica dentro del discurso armónico; o sea, no van a tener tendencia a
ninguna tónica, ni van a colaborar a su confirmación, como sucedía con las sonoridades con
función de Dominante. Sólo hay un sonido imposible para este árbol, que es la sensible, la nota
propia de la sonoridad de Dominante. Asimismo, este árbol contaría con dos sonidos exclusivos
(aunque no imprescindibles, como sucediera con la sensible, el sonido exclusivo de la sonoridad
de Dominante): la tónica y la sensible de la Dominante.
3.2.1.
El árbol de Subdominante-Tónica en un modo Mayor
Este árbol en el tono Mayor, como podemos ver en la figura 3.2.1 -en la representación más
completa de su árbol-, posee once de los doce sonidos (recordemos que además de los propios
de su escala, toma sonidos de la escala homónima menor) e incluso tres de ellos los posee en
varias de sus lecturas o enarmonías; en el caso de Do Mayor que vemos en la figura de abajo,
son do# o reb , re# o mib y fa# o solb .
Figura 3.2.1: El árbol de Subdominante-Tónica de Do Mayor
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
3.2.2.
37
El árbol de subdominante-tónica en un modo menor
Tiene dos diferencias principales, sin tener en cuenta los sonidos alterados, con el árbol de
Subdominante-Tónica del modo Mayor, que carece del III propio del modo Mayor y que su VI<
posee una tendencia ascendente, propia de las escalas dórica y melódica en las que se justifica,
que no se manifestaba en aquella versión. No obstante, vemos que también tiene once sonidos
-en esta representación completa que cuenta con sonidos alterados- y que carece únicamente
de la sensible entre sus posibilidades. Tal y como pasaba en el árbol propio del modo Mayor,
también aparecen tres enarmonías en este árbol; en la menor, que el árbol que se muestra en
la figura que ilustra este apartado, serían do# o reb , re# o mib y la# o sib .
Figura 3.2.2: El árbol de subdominante-tónica de La menor
3.3.
El árbol Tonal
Como síntesis de los dos, tenemos esta construcción que muestra en dos pentagramas ambos
árboles: el de Subdominante-Tónica encima, y el de Dominante debajo. Pretende ser un esquema
visual de las posibilidades que ofrece en conjunto, una tonalidad, mostrando con qué sonidos
cuenta (que son todos) y cómo se comportan.
3.3.1.
El árbol Tonal en un modo Mayor
Ésta sería la síntesis de posibilidades armónicas de un modo Mayor, tanto en sus variantes
con función de Dominante, como en las de Subdominante o en las de Tónica. En la figura
siguiente se muestra el árbol Tonal de Do Mayor.
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
38
Figura 3.3.1: El árbol Tonal de Do Mayor
3.3.2.
El árbol Tonal en un modo menor
Con este tipo de árbol representamos las posibilidades de combinación sonora que tienen
todos los sonidos que son posibles en un modo menor, en cualquiera de las tres funciones:
Dominante, subdominante o tónica. Para ilustrarlo, en la figura de abajo se presenta el árbol
Tonal de la menor.
Figura 3.3.2: El árbol Tonal de La menor
3.4.
Otro tipo de árboles
Los árboles son simplemente una manera de organizar, una concreción simbólica de una
taxonomía. De esta forma, el que aquí se haya expuesto y se vaya a trabajar con ellos (especialmente en el apartado dedicado a la modulación en la página 115), no quiere decir que no exista
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
39
la posibilidad de aplicar la noción de atribuir unas cabezas de notas y distribuir espacialmente
en el pentagrama un complejo de sonidos con el fin de indicar su idiosincrasia. Así pues, a modo
de ejemplo, vamos a mostrar otro esquema de trabajo.
3.4.1.
Un árbol para la realización contrapuntística
Figura 3.4.1: Un árbol para la realización contrapuntística
El árbol que vamos a ofrecer a continuación, analiza todas las posibilidades que pueden
ofrecerse, siguiendo los principios del contrapunto renacentista del s. XVI, para construir dos
contra-melodías, o sea, dos líneas de contrapunto, para una nota dada cualesquiera (la nota
dada -que pertenecería a un Cantus Firmus completo-, en la ilustración 3.4.1 de arriba, sería
). De hecho, teniendo en cuenta que los acordes que se
la representada en el centro como
pueden utilizar en esta etapa histórica son únicamente los tríadas, podríamos decir que resume
las posibilidades del contrapunto de este período.
Para ello utiliza dos tipos de cabezas: las rectangulares y las elipses y dos tipos de relleno:
blanco y negro. La base de inteligibilidad de este árbol descansaría en la oposición de estos dos
rangos diferenciales, y su aplicación respondería a las siguientes normas:
1. Sólo se puede escoger una figura negra: el rectángulo o la elipse; pero sí dos figuras blancas.
2. Sólo se puede escoger una figura geométrica: una elipse y un rectángulo.
3. Las figuras negras producen faltas, vigilaremos su llegada desde y salida a una figura de
otra especie (puesto que no pueden repetirse estas figuras negras para dos notas consecutivas dadas).
4. El rectángulo negro entre paréntesis no se puede utilizar como bajo.
5. La elipse negra entre paréntesis no se puede utilizar si la nota dada está en el bajo.
6. La elipse blanca con el cierre del paréntesis no puede ser bajo en simultáneidad con el
rectángulo blanco.
7. El cuadrado negro con la apertura de paréntesis no puede utilizarse de estar a una 5ª
disminuida de la nota dada cuando dicha nota actúe como bajo.
CAPÍTULO 3. LOS ÁRBOLES ARMÓNICOS
40
8. Se puede utilizar la nota dada una 8ª por encima o por debajo, pero es preferible evitar
hacer esto y se tratará tal y como una nota negra.
9. Para empezar y terminar se utilizará únicamente la nota dada en unísono o a la 8ª superior
o inferior.
Capítulo 4
El Espiropentagrama
Figura 4.0.1: Espiropentagrama mudo
Basándose en la ordenación del conjunto de sonidos musicales en una disposición circular,
que nos daba un círculo cromático de sonidos, se elabora este dispositivo que permite leer
sobre un pentagrama construido describiendo una espiral irregular, los sonidos de la escala
41
CAPÍTULO 4. EL ESPIROPENTAGRAMA
42
cromática. Es obvio que sería una versión musicalizada de los diagramas de reloj con que
entre otros ya han trabajado, como Solomon (1997) y Rappaport (2007). En la figura 4.0.1
en la página anterior podemos ver una versión muda del mismo, en el que no aparecen las
alteraciones que podrían servir de guía, para permitir su utilización con cualquier clave musical.
Se añaden dos circunferencias marcadas en líneas discontinuas, que pueden ayudar a observar
el funcionamiento de la herramienta en su futura disposición sobre una base circular1 .
Figura 4.0.2: Espiropentagrama en clave de sol
Como podemos ver en la figura 4.0.2, la apariencia del Espiropentagrama cuando se le
añaden las alteraciones -lo que obligaría a una lectura en clave de sol en 2ª línea, en este casopara servir de guía en su manejo. La idea central de este instrumento es servir a la transposición
de sonidos, ya que a cada giro de 30o , una nota cualesquiera dispuesta sobre él, comporta una
El tamaño del Espiropentagrama viene a ser de las medidas de un disco CD o DVD estándar (aproximadamente 12 cm de diámetro), de esta forma, para hacer más operativo el instrumento, asentaríamos el
Espiropentagrama como fondo inferior en una caja vacía de cedés (de las llamadas tarrinas), como base sobre
la que iríamos añadiendo las transparencias que servirían para operar en él, aprovechando tanto el eje central,
como, en general, la forma del contenedor de plástico para maniobrar y almacenar mejor las construcciones que
elaboremos.
1
CAPÍTULO 4. EL ESPIROPENTAGRAMA
43
relectura de la misma con un cambio de un semitono. Si el giro se realiza en sentido de las agujas
del reloj, se producirá en sentido ascendente y si es al contrario, en sentido descendente. Al
mismo tiempo, vemos que las alteraciones describen dos posibilidades de lectura, a una distancia
de séptima aumentada; esto servirá para poder atender a las posibilidades de enarmonía más
frecuentes, de un mismo sonido.
Figura 4.0.3: Plantilla de un sonido
De esta forma, teniendo una plantilla de un sonido cualesquiera -y su enarmonía- (véase la
figura 4.0.3 de arriba), al colocarlo sobre el Espiropentagrama daría lugar a las figuras 4.0.4
y 4.0.5 que muestran cómo funcionaría el Espiropentagrama, sometiendo a una nota y a su
enarmonía a todos los giros posibles, comenzando desde do / si# .
CAPÍTULO 4. EL ESPIROPENTAGRAMA
Figura 4.0.4: Las notas en el Espiropentagrama (a)
44
CAPÍTULO 4. EL ESPIROPENTAGRAMA
Figura 4.0.5: Las notas en el Espiropentagrama (b)
45
CAPÍTULO 4. EL ESPIROPENTAGRAMA
46
Según podemos observar en las ilustraciones, cada sonido (así como su enarmonía) está
distribuido en una de las dos circunferencias concéntricas, que no son visibles, que van cruzando
la espiral irregular en la que se inscribe el pentagrama, de forma que da lugar a los diferentes
sonidos según se van produciendo los giros. Para servir de guía, sobre todo cuando se comparan
conjuntos de varios sonidos, se añade una tercera circunferencia concéntrica más pequeña,
también invisible, en la que se marca la presencia de un sonido en el esquema. Esto permitirá
una mejor observación de las coincidencias entre sonidos –indistintamente a que sean un sonido
enarmónico o el mismo-, cuando se comparen varios conjuntos, superponiendo plantillas. En la
figura 4.0.6 que vemos a continuación, se muestran estas tres circunferencias, que normalmente
no veríamos, en el Espiropentagrama con un acorde y estas marcas de apoyo.
Figura 4.0.6: Las tres circunferencias del Espiropentagrama
Esta última línea también será de gran ayuda para poder observar las figuras geométricas
(véase apartado 5 en la página 55) a que dan lugar los acordes al representarse sobre el círculo cromático. En las páginas siguientes, cuando tratemos cada uno de los acordes tríadas y
cuatríadas, veremos cómo en el ejemplo se marca, con líneas discontinuas, el polígono inscrito
CAPÍTULO 4. EL ESPIROPENTAGRAMA
47
determinado, en dicha circunferencia interior sobreentendida, por las marcas de presencia.
4.1.
Las marcas de presencia
Las marcas de presencia son unos elementos de apoyo que aparecen en la circunferencia
invisible interior del Espiropentagrama (véase la figura 4.0.6 en la página anterior).
4.1.1.
De orden melódico
Cuando la finalidad de un gráfico es trabajar con un motivo melódico, entonces lo ideal
sería utilizar números que marquen su secuencia de aparición. Pongamos por caso un motivo
melódico como el siguiente:
Este motivo tendría la siguiente conversión al Espiropentagrama:
Figura 4.1.1: Marcas de orden melódico
48
CAPÍTULO 4. EL ESPIROPENTAGRAMA
Como podemos imaginar, este modo de trabajo será muy útil para desarrollar imitaciones y
otras manipulaciones de orden melódico; siendo de especial utilidad en métodos compositivos
que sean eminentemente horizontales como el dodecafonismo. Así podemos verlo en el capítulo 7, Aplicaciones del Espiropentagrama, en el apartado de Procesos contrapuntísticos en la
página 105.
4.1.2.
De orden armónico
Para trabajar dentro del campo armónico, nuestra propuesta trabaja con los llamados árboles armónicos y es, especialmente dentro de este ámbito donde la aplicación de las marcas
de presencia cobra mayor importancia. En este sentido, son símbolos geométricos de seis tipos
diferentes según el tipo de árbol en el que aparecen y el papel que desempeñan en él. Atendiendo
a la figura 4.1.2 veríamos que son ocho categorías:
a) notas del árbol Subdominante-Tónica de la tonalidad de partida,
b) notas del árbol de Subdominante-Tónica de la tonalidad de llegada,
c) notas del árbol de Dominante de la tonalidad de partida,
d) notas del árbol de dominante de la tonalidad de llegada,
e) sensible de la tonalidad de partida,
f) sensible de la tonalidad de llegada,
g) subtónica de la tonalidad de partida y
h) subtónica de la tonalidad de llegada.
a)
b)
c)
d)
e)
f)
g)
h)
Figura 4.1.2: Marcas de presencia en los árboles armónicos
Las diferentes formas de cada una de ellas tienen como finalidad el hacer más sencilla
la comparación; aparecen huecas las figuras que remiten a los árboles de partida y rellenas
aquellas que pertenecen a los árboles de llegada. Los hexágonos pertenecen a los árboles de
Subdominante-Tónica y los círculos y cuadrados a los árboles de Dominante.
Estas marcas van a tener dos funciones:
servir de vértices para los polígonos, representaciones de los acordes posibles en cualquier
caso, que los conjuntos de sonidos podrán contener.
marcar los sonidos (del grupo de doce posibles) que aparecen en el conjunto y ayudar a
su comparación con otros conjuntos.
CAPÍTULO 4. EL ESPIROPENTAGRAMA
4.2.
49
Manejo del Espiropentagrama
Para manejar el Espiropentagrama, lo que habría de hacerse sería construir, a partir de
láminas transparentes, plantillas circulares que sirvan para el propósito concreto de estudio.
Dado que de manera intencionada el Espiropentagrama tiene las mismas dimensiones que un
disco compacto, se puede utilizar uno cualquiera para utilizarlo como modelo -o incluso, directamente y sin tener que preparar nada, usar alguno de los separadores de plástico transparente
que algunas cajas llevan-. Sobre esta lámina escribiríamos con rotuladores indelebles o permanentes aquello que queramos utilizar en varias ocasiones y, con rotuladores no permanentes,
observaciones sobre casos particulares que podremos borrar tan pronto hayamos acabado de
estudiar dicho caso.
4.2.1.
Un caso práctico
Más adelante, en el capítulo 6 (página 103) dedicado a las aplicaciones del Espiropentagrama, se explica con una especial atención su beneficio para el estudio de la modulación
(apartado 6.3 en la página 115). Así pues, se utilizan los árboles armónicos (de los que hablábamos en el capítulo 3 en la página 31) proyectados sobre el Espiropentagrama; para hacerlo,
situaremos una lámina transparente circular de las mismas dimensiones que el Espiropentagrama sobre el mismo, e iremos escribiendo con un utensilio de escritura resistente al roce los
sonidos que aparecen (empleando las cabezas de nota que se proponía para los árboles armónicos, evidentemente). Así, lograremos tener las plantillas de los diferentes árboles armónicos
de las tonalidades de partida y de llegada. Una vez hecho esto, cuando estemos utilizándolos
y comparándolos, es posible que queramos señalar algunos sonidos en concreto que queramos
que participen o que hayamos escogido, o las figuras que representen los acordes que pueden
participar en el proceso. En ese momento utilizaremos rotuladores normales, que no se queden
fijados sobre la lámina transparente para que, de esta forma, podamos no perder las reflexiones
que hemos realizado para este ejercicio y además, cuando hayamos acabado, poder borrar todas
estas marcas accesorias y variables según el caso particular, utilizando simple y comodamente,
un pañuelo de papel.
4.3.
Otras propuestas próximas
En esta sección, comentaremos dos utensilios de aspecto similar al Espiropentagrama y que
también ofrecen interesantes aportaciones dentro de la teorética y la práctica musical armónica,
analítica e incluso interpretativa.
CAPÍTULO 4. EL ESPIROPENTAGRAMA
4.3.1.
50
Simple clock calculator de Larry J. Solomon
Figura 4.3.1: Simple Clock Calculator para el análisis teórico de Conjuntos de sonidos
El Clock Calcutator2 se trata de una circunferencia dividida en doce partes que, como en el
Espiropentagrama, representarán los doce sonidos del sistema temperado y ordenados también
de la misma forma, cromáticamente (así queda reflejado en la figura 4.3.1 que veíamos arriba).
Este utensilio, verdaderamente próximo al que en estas páginas se ha explicado, se ha pensado
con una finalidad expresa, facilitar el análisis de música serial, sirviendo como ayuda para
obtener la Prime Form de Forte y su set name, determinar los subconjuntos de un conjunto de
sonidos, analizar series, calcular vectores interválicos y una forma de catalogar los sonidos de
una sonoridad que el autor denomina la Solomon prime.
4.3.1.1.
Diferencias con el Espiropentagrama
Existen dos diferencias principales entre el Clock Calculator y el Espiropentagrana: la manera de anotar las alturas de los sonidos y su finalidad.
Mientras el dispositivo ideado por Solomon expresa las alturas mediante los nombres de
las notas (concretamente siguiendo la nomenclatura inglesa), como bien hemos comprobado, el
Espiropentagrama lo hace utilizando un pentagrama en Espiral que permite su lectura como
sonidos en una partitura.
Por otra parte, la finalidad, el Espiropentagrama está pensado como una herramienta abierta
en la que se pueden estudiar y comparar las propiedades de cualquier conjunto de sonidos,
Los datos aquí explicados sobre el Clock Calculator se han extraído de la páginas web Solomon’s Music
Resourcesrealizada por el autor, que tiene por URL http://solomonsmusic.net.
2
CAPÍTULO 4. EL ESPIROPENTAGRAMA
51
elegido en base a cualquier criterio. El Clock Calculator, por su parte, tiene como objetivo la
música serial (aunque pueda servir, ciertamente, para otras cuestiones), algo que también es
posible observar en el Espiropentagrama; de hecho, siguiendo el modelo propuesto por Solomon,
ha sido explicada esta aplicación de la herramienta propuesta en estas páginas, en el apartado 6.4
en la página 152.
Aparte de estas dos diferencias capitales, también hemos de tener en cuenta que el Espiropentagrama, más que servir como guía indicativa de un conjunto de sonidos, atiende a
las figuras poligonales que surgen al situarse los sonidos sobre él, de forma que es en función
de estos polígonos de donde se extrae toda una concepción didáctica que pretende formar al
alumno e integrarlo en este lenguaje simbólico, con la finalidad de facilitarle su comprensión,
desde su fase de iniciación en los estudios musicales hasta las más evolucionadas. Además, el
Espiropentagrama tiene en sí mismo una forma dinámica -no estática o predeterminada- que
le va a permitir evolucionar con el alumno en función de sus conocimientos y sus necesidades,
y no aportar, únicamente, ayuda a un asunto concreto e invariable, propio exclusivamente de
un estadío avanzado de instrucción musical.
4.3.2.
La Rueda Armónica de Luis Nuño
Se trata de un dispositivo principalmente orientado a su aplicación en el campo de la improvisación3 especialmente en la música de Jazz; no obstante, tal y como afirma su autor, puede
utilizarse en música occidental de diversos estilos, con bastante provecho. Se basa en el uso de
unas plantillas preestablecidas que al girar, aportan al usuario posibilidades de escalas, acordes,
arpegios que aplicar según le pueda interesar, bien sobre un determinado acorde o tonalidad, o
bien para enlazar entre dos diferentes.
La construcción de esta “Rueda Armónica” se fundamenta en cinco círculos de quintas
concéntricos, expresados en un mismo plano, sobre el que se dispone una lámina transparente
que, utilizando algunas líneas, colores y números, indican los acordes, escalas, etc.
Aunque la Rueda Armónica ya muestra sus posibilidades orientadas a la improvisación, es más bien otro
aparato de similares caracterísiticas, llamado Improchart, también ideado por este autor, el que va a estar más
destinado a estos menesteres.
3
CAPÍTULO 4. EL ESPIROPENTAGRAMA
52
Figura 4.3.2: La rueda armónica
Las aplicaciones de la Rueda Armónica, según nos explica en las instrucciones que acompañan a la misma, su autor, serían las siguientes:
1. Identificación de notas enarmónicas;
2. Notas consonantes con respecto a una nota concreta y acordes Mayores y menores, aumentados y de séptima disminuida que la contienen;
3. Notas constituyentes de acordes tríadas Mayores, menores, aumentados y de séptima
disminuida;
4. Tonalidad mayor y menor que se corresponden a una armadura con un número determinado de alteraciones;
5. Notas propias de una escala Mayor o menor;
6. Acordes propios tríadas y cuatríadas de los grados de una escala Mayor o menor;
7. Acordes propios de una escala que contienen una nota;
CAPÍTULO 4. EL ESPIROPENTAGRAMA
53
8. Acordes cercanos (con más notas dentro de la escala) y lejanos (con ninguna nota dentro
de la escala) respecto de una tonalidad;
9. Transporte de secuencias de acordes a otra tonalidad del mismo modo, o adaptación a su
modo opuesto.
4.3.2.1.
Diferencias con el Espiropentagrama
Como primera cuestión que podemos resaltar tras comparar estos dos dispositivos, tendríamos el hecho de que la Rueda Armónica, según se anuncia en sus propias instrucciones adjuntas,
no requiere de conocimientos musicales ya que todo queda escrito con los nombres de las notas.
Sin embargo, el Espiropentagrama da los nombres de los sonidos representándolos tal y como
se hace en las partituras, esto es, utilizando cabezas de notas que coloca sobre un pentagrama.
Otra diferencia que también se percibe a primera vista al echarle un vistazo a estas dos
herramientas, es que mientras la Rueda Armónica se basa en el círculo de quintas, el Espiropentagrama lo hace en el círculo cromático. Asimismo, el Espiropentagrama sólo dispone los
sonidos en una única línea circular, mientras la Rueda Armónica hace uso de cinco circunferencias concéntricas que disponen las notas sobre doce radios (esto sí sucede igual en ambos
casos), estando las notas del mismo radio distantes una tercera menor descendente conforme
la circunferencia es más externa. Esto lo hace así para aprovechar la relación de las notas que
estarían de forma diagonal en la circunferencia adyacente externa, en el siguiente radio a la
derecha (notas a un intervalo de tercera mayor ascendente conforme nos separamos del centro
de las cinco circunferencias), y así construir los acordes mayores, por ejemplo.
Por otra parte, una vez señaladas las divergencias más notables en la forma de construirse,
sería el momento de señalar las diferencias en cuanto a finalidades. Mientras la Rueda Armónica
pretende ser una herramienta que aporta unos resultados en el momento y no tiene finalidades
pedagógicas, ni colabora a la mayor comprensión de las sonoridades ilustrando sus propiedades o
sus relaciones. El Espiropentagrama busca conectar figuras geométricas y colores con el aspecto
sonoro de determinados conjuntos de sonidos, sin embargo, la Rueda Armónica no tiene en
cuenta ningún tipo de elemento geométrico ni las posibilidades de la policromía, dentro de sus
resultados o sus acciones.
Otra importante cuestión a señalar es cómo mientras la invención de Luis Nuño aporta todos
sus resultados desde la misma plantilla única, sin atender a una posible evolución del usuario
respecto del dispositivo, o adaptarse a la necesidad que tenga el usuario en cada momento.
Este hecho de usar una única plantilla es más cómodo pero al mismo tiempo resulta en una
mayor complejidad y perjudica un tanto su manejo. El Espiropentagrama, por el contrario,
está contemplado como una base sobre la que cada uno pueda confeccionar las plantillas que
necesite en función de sus conocimientos y de sus intereses. Incluso, en definitiva, podríamos
decir que el Espiropentagrama tiene como objetivo abandonar el plano físico y quedar asimilado
en el nivel intelectual del sujeto, para que así pueda ser utilizado subliminalmente, sin requerir
CAPÍTULO 4. EL ESPIROPENTAGRAMA
tener el objeto en sí.
54
Capítulo 5
Representaciones poligonales de las
sonoridades
El uso de las representaciones poligonales de conjuntos de sonidos, como los acordes, nos
va a aportar un acercamiento y comprensión mucho más profundos de sus propiedades y características, dado que los polígonos a que vamos a adscribir cada acorde no sólo comparten
la mayoría de ellas, sino que van a hacerlas aún más patentes con su morfología. Asimismo,
será más sencillo entender aspectos complejos de los conjuntos sonoros con que habitualmente
trabaja la música occidental, al asimilarlos a la problemática de la geometría más básica con
la que todos, desde niños, estamos más familiarizados.
El aspecto básico elemental que fundamenta esta representación geométrica de los acordes,
es la proporcionalidad que existe entre las distancias que se dan a nivel acústico y las que se
pueden observar al proyectarlas como cuerdas1 -que serán los futuros lados de los polígonosde una circunferencia en un espacio bidimensional. Para ejemplificar este hecho, analicemos el
ejemplo del acorde perfecto menor sobre el Espiropentagrama (podemos ver claramente como
el segmento que correspondería con el intervalo
No sería injusto atribuir gran mérito de la popularidad que este tipo de representaciones
tienen en la actualidad a los trabajos de David Rappaport (Rappaport, July 31 - August 3
2005)
5.1.
Consideraciones preliminares de las figuras
En este apartado queremos reflexionar hacia ciertos elementos que van a ayudar a entender
mejor qué hace que las figuras sirvan como medio icónico para una observación más rápida de
las posibilidades de un conjunto de sonidos (escala, acorde, etc.) cualesquiera.
Entiéndase la acepción propia del campo de la Geometría que recoge el Diccionario de la RAE de esta
manera: Segmento de recta entre dos puntos de un arco.
1
55
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.1.1.
56
El diámetro: el tritono
Figura 5.1.1: El tritono representado como un diámetro
Cuando un conjunto de sonidos presenta dos o más pares de notas en el lado opuesto
de la circunferencia2 , o lo que es lo mismo, uno o más pares de puntos que permiten trazar
diámetros, podremos deducir que un conjunto cualesquiera de sonidos, representados en
el Espiropentagrama, tiene tantos tritonos como diámetros posibles pueden trazarse en
la circunferencia imaginaria en la que están representados.
De esto también se puede deducir, aplicando conocimientos básicos de geometría, que a
cada vez que observemos la aparición de uno o varios ángulos cuya suma o valor, sea de 180º,
estaremos ante la existencia de un tritono. En tanto en cuanto, el tritono es una de las marcas
principales que definen la tonalidad, desempeñando un papel especial dentro de los acordes con
Para hallar un diámetro podría usarse cualquiera de las tres descritas en el apartado 4 en la página 41, pero
se observará mejor en la interior, que tiene las marcas de referencia y representa en la misma circunferencia
los sonidos, sin atender a las diferencias enarmónicas, que sí contemplan las otras dos y que podrían llevar a
confusión.
2
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
57
función de dominante, cuando aparece un tritono podríamos deducir, algo osadamente quizá,
pero cierto, que cualquier acorde que cuente con un tritono puede tener función de dominante
y por tanto, servir para determinar una tonalidad. Si además atendemos a las posibilidades
enarmónicas, entonces podríamos añadir que, dado que cualquiera de los sonidos que se haya
a la derecha (en sentido de las agujas del reloj) de los extremos del diámetro, puede ser la
tónica de una nueva tonalidad, con lo que al mismo tiempo hablaríamos de dos y hasta cuatro
tonalidades posibles, cada vez que aparece un tritono o, lo que es lo mismo, su representación
como diámetro en el Espiropentagrama.
5.1.2.
Un cuadrante: la tercera menor
Figura 5.1.2: La tercera menor como un lado del cuadrado
Este intervalo puede reconocerse también muy fácilmente en el Espiropentagrama porque
tiene la forma de una cuerda, geométricamente hablando, que se corta en dos puntos de la
circunferencia con una separación de un ángulo de 90º, o sea, tal y como si fuera un lado
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
58
de un cuadrado que quedara inscrito dentro de una circunferencia. De esta manera, es fácil
entender que un acorde disminuido contará con dos lados del cuadrado y un acorde de séptima
disminuida no será otra cosa que un cuadrado exacto (véase fig. 5.4.13 en la página 93).
5.1.3.
Los ejes de simetría: propiedades, inversión y transposición
limitada
En primer lugar hemos de distinguir que, según su situación respecto de un polígono cualquiera, hay tres tipos posibles de ejes de simetría:
a) el que no pasa por ninguno de los vértices de la figura;
b) el que pasa por uno de los vértices de la figura; y
c) el que pasa por dos de los vértices de la figura.
Si reflexionamos un poco sobre estas tres posibilidades de los ejes de simetría, podemos concluir
que los tipos a) y c) sólo pueden aparecer en los polígonos con un número de lados y vértices
par, mientras el tipo b) sólo puede aparecer en polígonos con un número de vértices y lados
impar.
Las dos cuestiones que se van a tratar en este apartado son de pleno interés para la observación de las propiedades que se infieren -también con ayuda de sus representaciones poligonalesdel estudio de los modos de transposición limitada de Olivier Messiaen, estudiados en el apartado 5.2.1 en la página 72.
5.1.3.1.
Propiedades derivadas de la simetría
El identificar los ejes de simetría de una figura poligonal, representante de un grupo de
sonidos cualquiera, va a ser de extrema utilidad dado que nos va a proporcionar dos datos con
respecto a dicha agrupación:
el número de maneras diferentes que puede ordenarse ese grupo, que llamaremos ’subgrupos’ (ejemplo: con las siete notas diatónicas: do, re, mi, fa, sol, la y si, se dan siete
maneras diferentes -los siete modos- de ordenarse el grupo);
y el número de veces que una determinada manera de ordenarse -de dicho grupo- va a
aparecer -partiendo de diferentes sonidos-, que llamaremos ’versiones’ de esos subgrupos
(ejemplo: un acorde de séptima disminuida tiene una única manera de ordenarse que,
partiendo cada vez de uno de sus sonidos, va a aparecer cuatro veces).
Estos datos los vamos a obtener en función de estas dos relaciones con el número de ejes de
simetría, respectivamente:
sonidos
ejesdesimetrı́a
= nº subgrupos diferentes
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
59
nº ejes de simetría = versiones de cada subgrupo
Para que quede más claro este apartado, llevaremos a la práctica estas dos afirmaciones
trabajando con un grupo de cuatro sonidos con unas peculiares manifestaciones de simetría, el
acorde de Dominante con séptima con la quinta rebajada, que en segunda inversión llamaríamos
sexta aumentada Francesa (acorde estudiado en el apartado 5.4.3.2 en la página 96), cuya
representación responde a la forma de un rectángulo. Si buscamos los ejes de simetría de este
polígono, veremos que son dos (cf. fig. 5.1.3)
Figura 5.1.3: Representación del acorde de sexta aumentada Francesa con sus ejes de simetría
Así pues, nuestros resultados observando este acorde serían:
Dividiendo sus cuatro sonidos entre sus dos ejes de simetría, obtenemos que habría dos
maneras de ordenar diferentes (lógicamente, una empezando desde un lado pequeño y otra
desde un lado grande) que corresponderían con dos maneras de interpretar este grupo de
sonidos: como un acorde de Séptima de Dominante con la quinta rebajada o como un
acorde de séptima de sensible con la tercera elevada.
Dado que tiene dos ejes de simetría, cada uno de estas dos posibles maneras de ordenar los
sonidos, aparecerá dos veces; esto es, hay dos acordes de Dominante con séptima con la
quinta rebajada y dos de séptima de sensible con la tercera elevada, de cuatro tonalidades
diferentes.
Creo que es innecesario señalar lo ventajoso que resulta el poder deducir con tanta rapidez,
las propiedades enarmónicas de un grupo de sonidos, especialmente con fines modulatorios, y
cómo, una vez aprendido este sencillo método, se pueden obtener resultados con mucha mayor
brevedad que si lo hubiésemos intentado simplemente atendiendo a las notas constitutivas del
acorde.
Comparativamente, por otra parte, el conocer el número de ejes de simetría es una pista
importante para comparar superficies de polígonos dado que podemos afirmar sin dudarlo que,
con dos conjuntos con igual número de sonidos, tendrá mayor área el que posea mayor número
de ejes de simetría. El valorar el área de una representación poligonal tendrá cierta consecuencia
en su grado de consonancia que trataremos con detenimiento más adelante, en el apartado 5.1.4
en la página 62.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.1.3.2.
60
La inversión
Todo eje de simetría que aparezca en una figura poligonal cualesquiera, como resultado de la
representación de un conjunto de sonidos en el Espiropentagrama, va a implicar la posibilidad de
invertir el sentido de lectura (como las agujas del reloj o a la inversa) de los sonidos implicados -lo
cual a nivel musical respondería a la posibilidad de leer del mismo modo de forma ascendente
que descendente-, siempre que se lea desde cualquiera de los dos puntos de intersección de
cualquier eje de simetría con la figura poligonal que habíamos obtenido hasta dar una vuelta
completa llegando otra vez al punto de intersección de partida. Es decir, desde un punto de
intersección de un eje de simetría con la figura, hasta este mismo punto, podemos leer hacia
la derecha o hacia la izquierda, que encontraremos el mismo orden de intervalos, o sea, igual
secuencia en sentido ascendente que en el descendente, y consecuentemente, sin que cambie
ninguno de los sonidos que participan del mismo. Sería una especie de conjunto de sonidos con
palíndromo.
Para ilustrar nuestras palabras vamos a tomar una figura importante de nuestra cultura
musical: las siete notas diatónicas. Este conjunto está tratado, en lo que respecta a su representación y cualidades, en el apartado 5.3.1 en la página 79. Si observamos la fig. 5.1.4 de abajo,
podemos comprobar cómo el heptágono que representa la escala diatónica posee un único eje
de simetría. Sin embargo, esto le va a posibilitar ser invertible en un orden ascendente o descendente desde dos puntos: el sonido re, y entre el sonido sol y la -ya que está entre los dos-.
Esto no es otra cosa que la igualdad de intervalos en un sentido que en otro desde estos puntos,
o sea: re-mi-fa-sol-la-si-do-re tiene los mismos intervalos (2ª Mayor, 2ª menor, 2ª Mayor, 2ª
Mayor, 2ª Mayor, 2ª menor, 2ª Mayor) pero en sentido ascendente en lugar de descendente
que re-do-si-la-sol-fa-mi-re; del mismo modo que sucede con la-si-do-re-mi-fa-sol3 (2ª Mayor, 2ª
menor, 2ª Mayor, 2ª Mayor, 2ª menor, 2ª Mayor) y sol-fa-mi-re-do-si-la.
No alcanza la octava, como en el caso anterior de re, porque el punto de intersección del heptágono con el
eje de simetría está entre el sol y el la, por eso, tomará una de estas notas como punto de partida pero no podrá
llegar hasta esta nota de partida.
3
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
61
Figura 5.1.4: Heptágono diatónico con eje de simetría
5.1.3.3.
La transposición limitada
Igualmente, se puede conocer cuántas veces se puede disponer un conjunto de sonidos sobre
las doce alturas del sistema temperado, sin que éste se repita4 . Para ello, basta con dividir
el número de alturas posibles del sistema temperado, o sea, doce, entre el número de ejes de
simetría que posea el conjunto de sonidos con el que se está trabajando. Es decir, el número
de ocasiones que un conjunto de sonidos puede transportarse sin que se repitan sus sonidos
integrantes, responde a esta igualdad:
12
ejes de simetria
= transposiciones posibles
Veámoslo con un ejemplo, si tomamos el acorde tríada aumentado5 (cf. figura 5.1.5 adjunta)
podemos observar con facilidad que tiene tres ejes de simetría; de este modo, aplicando la
En este sentido, son especialmente notables los conocidos modos de transposición limitada de Messiaen,
modos que pueden transportarse -sin repetir los sonidos que en ellos participan-, sólo un número contado de
ocasiones. Se tratará con detenimiento de ellos en el apartado 5.2.1 en la página 72.
5
Que se analiza con mayor exhaustividad en el apartado 5.4.1.3 en la página 84.
4
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
62
fórmula con que sintetizábamos la explicación anterior, procederíamos de la siguiente forma:
12
= 4, ergo este acorde puede transportarse sólo cuatro veces, sin que sus sonidos se repitan6 .
3
Figura 5.1.5: Tríada aumentado con sus ejes de simetría
De nuevo, destaca la manera tan sencilla de conocer este dato respecto de los conjuntos
de sonidos, que de una manera habitual (que podríamos asimilar con “la cuenta de la vieja”)
nos llevaría una considerable mayor cantidad de tiempo. Quedan invitados a probarlo tomando
como objeto cualquiera de los modos de Messiaen que se explican y se representan, en sus
respectivos subapartados, desde la página 72.
5.1.4.
El área, un índice orientativo del grado de disonancia
Antes que nada, parece conveniente definir qué entendemos por disonancia; para hacerlo
hemos de conectar directamente con el concepto antónimo, el de ’consonancia’. Si tomamos
la definición de este último término aportada en el New Grove Dictionary, podemos leer que
“Acústicamente, se trata de la vibración simpática de ondas sonoras de diferentes frecuencias
relacionadas según la proporción de pequeños números enteros; psicológicamente, es una sonoridad armoniosa de un conjunto de dos o más notas, es decir, ’ausente de asperezas’, ’reposo
de una tensión tonal’ o el gusto”. En consecuencia, según se desarrolla en esta misma fuente,
’disonancia’ “es por lo tanto, el antónimo de consonancia, con correspondencia a los criterios
de ’aspereza’ y de ’tensión tonal’, y la dimensión consonancia-disonancia admite una gradación
relativa basada en cualquiera de estos criterios. El criterio de ’aspereza’, sin embargo, implica un juicio psicoacústico, mientras la noción de ’reposo de una tensión tonal’ depende de la
conexión con el ’lenguaje’ de la armonía tonal occidental. Hay un uso psicológico más amplio
Concretamente las cuatro transposiciones posibles del acorde tríada aumentado corresponderían con estos
cuatro grupos de sonidos: do-mi-sol# , reb -fa-la, re-fa# -la# y mib -sol-sib . Como podemos apreciar, ningún sonido
se repite entre las cuatro posibilidades y, si intentamos partir de cualquier nota posterior al mib , el resultado
sería un acorde enarmónico de los cuatro ya citados.
6
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
63
del término para referirse a preferencias estéticas, este criterio generalmente se aplica en función de lo placentero de una sonoridad”. Por otra parte, podríamos leer qué nos dice Zamacois
(1997) en su primer tomo del libro de Armonía, recogiendo las explicaciones de Pedrell: “La
consonancia es una combinación de reposo que podemos llamar estática, y la disonancia, una
combinación de movimiento o dinámica. La disonancia es una voz mantenida como con violencia fuera de la armonía. El oído desea que la disonancia se resuelva, esto es, que se mueva,
para que vuelva a su centro, que es la armonía”; una explicación, como podemos ver, basada
en criterios centrados en el ámbito psicológico.
Una vez observado el concepto, podemos deducir que se trata de algo subjetivo, que ha ido
variando a lo largo de la historia, así como entre las diferentes culturas musicales. Si añadimos
el hecho de que no sólo los criterios para la catalogación de las sonoridades han variado, sino que
también han cambiado los propios sistemas de afinación que los sustentaban, comprenderemos
que es muy difícil aportar unas coordenadas estables e indiscutibles, con que describir los
intervalos y su gradación de consonancia, siquiera restringiéndose a un único período de la
historia y en una sola tradición cultural musical. No obstante, tras un estudio detallado, se
podría deducir qué características y gradación puede atribuírsele a un determinado corpus
musical; con estas conclusiones, podría elaborarse las premisas que aplicar al Espiropentagrama
para utilizarlo como herramienta de ayuda con este fin.
En cualquier caso, como referencia fundamental para las ideas aquí expresadas, conectando
el valor del área de figuras poligonales que representen conjuntos de sonidos, con un análisis de
sus cualidades, es imprescindible citar los trabajos de D. Rappaport7 , que han sido de notable
influencia y han servido de punto de partida para esta parte del capítulo que nos ocupa.
5.1.5.
Aplicación a nuestro sistema tonal
5.1.5.1.
Consideraciones preliminares sobre intervalos consonantes y disonantes
En el caso que nos ocupa, la música tonal de lo que Piston llamaría “la práctica común”, y
tomando las palabras de S. Seguí (1987) en su tomo I de su Teoría Musical (pp. 89-90):
En la época actual es comunmente aceptada la siguiente clasificación de los intervalos armónicos en:
a) consonancias perfectas o invariales (los intervalos de cuarta, quinta y octava justas);
b) consonancias imperfectas o invariables (las terceras y sextas, mayores y menores);
c) disonancias absolutas o diatónicas (las segundas y séptimas, mayores y menores);
Es conveniente señalar que Rappaport, principalmente en un artículo de 2007) ya hizo un trabajo haciendo
ver cómo las escalas diatónicas, la escala hexátona y la escala octatónica o disminuida, representadas como
polígonos proyectados sobre un diagrama de reloj, tienen el mayor área posible que los grupos de 6, 7 u 8
sonidos (de entre 12), respectivamente, pueden tener.
7
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
64
d) disonancias condicionales o cromáticas, también denominadas aparentes o artificiales (las
que enarmonizando alguno de los sonidos que las forman quedan convertidas en una
consonancia);
e) intervalos armónicos neutros, también denominados semiconsonantes o mixtos y asimismo
conocidos como disonancias atractivas (la cuarta aumentada y la quinta disminuida, cuyas
características no hacen aconsejable su inclusión ni entre las consonancias ni entre las
disonancias8 ).
Por no restringirnos a un solo autor, aunque sea bastante representativo, veamos cómo Zamacois
(1997, pág. 21) lo resuelve de otro modo, si bien bastante próximo:
a) Consonancias perfectas: la 8ª justa (o su reducción, el unísono), la 4ª justa (o perfecta o
menor) y la 5ª justa (o perfecta o mayor);
b) Consonancias imperfectas: la 3ª y la 6ª mayores y menores;
c) Semiconsonancias: la 4ª aumentada (o tritono o mayor) y la 5ª disminuida (o falsa o menor);
d) Disonancias absolutas: la 2ª y la 7ª mayores y menores y todos sus enarmónicos;
e) Disonancias condicionales: los intervalos aumentados y disminuidos que resultan enarmónicos de un intervalo consonante.
Una vez repasadas estas dos catalogaciones, evidentemente próximas, de los intervalos en consonancias y disonancias, tan vigentes al menos, dentro del canon académico de nuestro país,
debemos señalar cómo, en ambos casos, el tritono queda un poco en suspenso y en una situación
intermedia entre las consonancias y las disonancias; este hecho será de especial importancia en
líneas posteriores.
5.1.5.2.
El parámetro inmensurable: la subjetividad de la tradición
Es difícil establecer un principio que responda a principios objetivos medibles, cuando se
trata de un asunto que implica tanta subjetividad. Baste citar un caso sencillo, para hacernos
reflexionar, ¿qué acorde es más disonante: el séptima de sensible o el séptima de Dominante?
Es probable que la mayoría respondiera que el primero de estos dos, es más disonante; tanto
es así, que las normas de la Armonía nos enseñan que se debe manejar con mucho más recelo
este acorde construido sobre el séptimo grado que ese otro que se construye sobre el quinto. Sin
embargo, si observamos los intervalos que los componen:
Continuando las palabras de S. Seguí: Sin embargo, dado su carácter de inestabilidad, que parece exigir una
resolución obligada, ha llevado a la común aceptación de considerarlos como disonancias atractivas.
8
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
Séptima de sensible
3ª Mayor
3ª menor
3ª menor
3ª menor
65
Séptima de Dominante
3ª menor
3ª menor
3ª menor
3ª Mayor
nos daremos cuenta de que se trata de los mismos intervalos, podríamos decir que son
acordes equivalentes en cuanto a su grado de disonancia -de hecho, esto se puede apreciar con
celeridad viendo las figuras 5.4.9 (en la página 89) y 5.4.7 (en la página 87) que los representan
y permiten observar que no son más que un reflejo el uno del otro-. Empero, la realidad acústica
es que en ningún caso se considera equivalente su nivel de disonancia, esto se debe a que el
peso de la tradición y el uso que han tenido estos dos acordes a lo largo de la misma, ejerce
un papel determinante en el juicio sobre los usos, las sugestiones y las normas, que estos dos
acordes poseen.
5.1.5.3.
En grupos con un mismo número de sonidos
Después de haberse señalado la drástica influencia de la tradición cultural, con el ejemplo del
apartado anterior, sobre dos acordes con el mismo número de sonidos, parece difícil argumentar
cómo va a racionalizarse o enunciarse cualquier tipo de norma que pueda ser válida. No obstante,
nos fijaremos en un hecho sencillo y éste es que, en su proyección sobre el Espiropentagrama,
los sonidos que forman intervalos disonantes (las segundas serían iguales que las séptimas9 ) se
encuentran muy próximos entre sí, por lo tanto, se representan con las cuerdas de menor longitud
que pueden aparecer, de forma que, obviamente, darán lugar a polígonos de menor superficie.
De este modo, podríamos afirmar que, siendo la representación de dos acordes distintos, dos
polígonos cualesquiera, tendrá mayor grado de disonancia, aquel que menor superficie de los
dos posea. Finalmente, aclararemos que, aunque los resultados no sean siempre acordes con
las consideraciones estéticas establecidas, la apreciación de qué superficie (entre dos acordes
representados por dos polígonos) es mayor10 , es bastante más sencilla e intuitiva de aplicar que
lo que pueda parecer desde el papel. Pongamos por ejemplo estos dos conjuntos a) y b) de tres
sonidos, sonidos que vemos en la figura 5.1.6 de a continuación.
Anotemos el hecho de que en el Espiropentagrama no existe un intervalo más grande que la 4ª aumentada,
ya que los intervalos mayores a este son idénticos en distancia a los resultantes de su inversión, o sea, una 5ª
Justa es igual que una 4ª Justa.
10
Ofrecíamos una ayuda a este respecto, que parece conveniente recordar aquí, en el apartado sobre las
propiedades derivadas de la simetría, en la página 58; ésta era que, a igualdad de número de sonidos, tendrá
mayor superficie el polígono que tenga mayor número de ejes de simetría.
9
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
a)
66
b)
Figura 5.1.6: Comparación de superficies
No parece difícil afirmar que el conjunto a) que vemos a la izquierda, es más pequeño y, por
tanto, según lo dicho, más disonante que el b) que vemos a la derecha. De hecho, observando
los lados de estos dos triángulos con detenimiento, podríamos incluso distinguir cómo dos de
ellos son iguales (concretamente el que les sirve de base y el que aparece a la derecha) y que
sólo difieren en el lado de la izquierda, que en el caso de a) debe representar un intervalo
claramente menor. Bien, todas estas observaciones son correctas ya que en el caso de a), los
intervalos constituyentes eran: 2ª Mayor, 3ª menor y 4ª justa (por ejemplo los sonidos do, re
y fa), mientras b) tenía los siguientes: 3ª menor, 3ª Mayor y 4ª Justa (en sonidos sería un
acorde Mayor, por ejemplo sib , re y fa). Hacemos ver pues, que no se trata de un complicado
proceso matemático en el que haya realizar medicción alguna o aplicar, lápiz en mano, las
diversas fórmulas para el cálculo de área correspondientes al polígono concreto con que se esté
trabajando. No obstante, para aquellos que busquen un mayor grado de precisión en casos
complicados de valorar a simple vista, se puede utilizar el coeficiente de consonancia, según
queda explicado más adelante, en el punto 5.1.5.5.
Para aclarar aún más la forma de aplicar esta orientativa inferencia que posibilita el Espiropentagrama, veámoslo con otro ejemplo con acordes cuatríadas, tomemos los dos acordes de
novena de dominante, el de novena Mayor y el de novena menor, en su representación sobre el
Espiropentagrama con la forma de dos pentágonos, como vemos en la figura 5.1.7.
Figura 5.1.7: Novenas de Dominante Mayor y menor
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
67
A simple vista parece evidente que la novena de Dominante Mayor, tiene mayor superficie
que la novena menor; si no, fijémonos en la parte del polígono que da lugar a la diferencia, el
b
triángulo descrito por un lado por las notas: sol-la-si, y por el otro: sol-la -si. La idea y utilidad
de la observación que hacemos en este apartado esta, que es fácil -en la inmensa mayoría de
casos y a pesar de lo que podría suponerse- distinguir qué figura tiene mayor área. Así pues,
la conclusión sería que el acorde más disonante, según las premisas que hemos enunciado, es el
de novena de Dominante menor.
5.1.5.4.
En grupos con diferente número de sonidos
Es fácil inferir que, por lo general, un polígono que posea mayor número de lados será
consecuentemente más grande; sin embargo, no parece coherente deducir en consecuencia que,
a mayor número de notas exista mayor grado de consonancia. De hecho, sería precisamente
lo contrario, lo que adoptaríamos como norma básica, esto es, ante dos acordes con diferente
número de sonidos, aquel que posea mayor número de sonidos será el que se considerará más
disonante.
Esto, obviamente, no atiende a infinidad de casos particulares y trata simplemente de resolver la cuestión en concordancia a la lógica de la inmensa mayoría de comparaciones posibles. Si
se busca un resultado más objetivo y cuantificable se puede hallar el coeficiente de consonancia
-a través del método que se explica en el próximo apartado- de las dos figuras y, entonces sí,
extraer consecuencias de su comparación.
5.1.5.5.
El coeficiente de consonancia
El coeficiente de consonancia sería un índice numérico que aportaría una cierta objetividad
a la hora de comparar acordes. Para hallarlo el proceso será sencillo, una vez calculada la
superficie11 de las figuras estudiadas, se divide el resultado obtenido para cada una de ellas
por el producto del cuadrado del número de lados que posee y el área del círculo en el que se
inscribe dicha figura. Es decir, el cálculo del coeficiente de disonancia respondería a la siguiente
fórmula:
coeficiente de consonancia =
superf icie f igura
superf icie cı́rculo (nº lados)2
Así pues, si por ejemplo tenemos un acorde tríada perfecto Mayor (exactamente igual en
cuanto a superficie que el perfecto menor) con un área determinada - en este ejemplo de 18234-,
dividiríamos esta cantidad entre el cuadrado de sus lados -o sea nueve- multiplicado por el área
del círculo -51806 en este caso-, y obtendríamos como resultado 0,039107439. Si quisiéramos
Para calcular la superficie de polígonos, además de los métodos de cálculo tradicionales ofrecidos por la
geometría, existe a día de hoy, diversos programas de software -normalmente pluggins de programas de edición
de imagen o de diseño- que permiten su cálculo con exactitud. Para los cálculos ofrecidos en este apartado
hemos utilizado una de estas herramientas informáticas, de forma que los números que aparecen se refieren al
número de píxeles que contenía cada figura.
11
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
68
saber si este acorde es, proporcionalmente, más o menos disonante que el de séptima de dominante, por ejemplo, haríamos la misma operación con la figura de dicho acorde y obtendríamos
un resultado de 0,036273549. De este modo, dado que el coeficiente de consonancia del tríada
perfecto mayor es una cantidad más grande, podemos concluir que se trata de un acorde más
consonante, teniendo en cuenta la proporcionalidad de que se trata de sonoridades (polígonos)
con diferente cantidad de sonidos (vértices o lados).
En el cuadro 5.1 podemos ver una tabla ordenada en función a su coeficiente de consonancia
(arriba los más consonantes, abajo los más disonantes), de los acordes tríadas y cuatríadas más
habituales en la música tonal de nuestra cultura occidental.
Acorde
Figura
Coeficiente de consonancia
Tríada aumentado
0,044130453
Séptima disminuida
0,039413871
Perfecto Mayor
0,039107439
Perfecto menor
0,039107439
Perfecto menor con 7ª menor
0,036516041
Perfecto Mayor con 7ª menor
0,036273549
Disminuido con 7ª menor
0,036273549
Tríada disminuido
0,033921425
Perfecto menor con 7ª Mayor
0,031172789
Aumentado con 7ª Mayor
0,031172789
Perfecto Mayor con 7ª Mayor
0,030883247
Cuadro 5.1: Coeficiente de consonancia de tríadas y cuatríadas
5.1.5.6.
Excepciones notorias
Dentro de las sonoridades habituales de las piezas tonales, encontramos dos casos que,
siendo casos muy particulares, se oponen, como consecuencia estética de nuestra tradición, a
la norma básica dada en este apartado (a mayor área, mayor consonancia)12 . Se trataría de los
dos acordes de mayor superficie de entre los de tres y cuatro sonidos y que, además, según el
cuadro comparativo de coeficientes de consonancia recogido en el apartado anterior, serían los
más consonantes de todos. Hablamos, evidentemente, del acorde tríada de quinta aumentada
12
En cualquier caso, creo que sus circunstancias resultan igualmente particulares dentro del ámbito de la
normativa tradicional, puesto que, estrictamente hablando, aunque ambos se traten como acordes disonantes,
las únicas disonancias que en ellos aparecen son, en terminología de Zamacois, disonancias condicionales, es
decir, que son equivalentes a intervalos consonantes.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
69
y el acorde de séptima disminuida. Ambos se tratan específicamente en los apartados 5.4.1.3
(página 84) y 5.4.2.7 (página 93), respectivamente.
Como argumentación en defensa de la clasificación que el coeficiente de consonancia les
atribuye, aparte del cómodo argumento de que su condición de disonantes deriva del peso de
la tradición, tenemos el hecho de que ninguno de los dos acordes, en realidad, posee ningún
intervalo disonante, todos sus intervalos constituyentes son consonantes o semiconsonantes. En
el séptima disminuida tenemos tres terceras menores, obviamente consonantes, dos quintas disminuidas (que según la taxonomía ofrecida en el punto 5.1.5.1 en la página 63, no serían más
que intervalos semiconsonantes, pero nunca disonantes) y una séptima disminuida, completamente enarmónica de una sexta mayor (equivalente a otra tercera menor), también consonante;
por otro lado, en el tríada de quinta aumentada tenemos dos terceras mayores, consideradas
consonancias, y una quinta aumentada que una enarmonía incuestionable de una sexta menor
(equivalente a otra tercera mayor), consecuentemente también consonante. De esta forma, su
regularidad, su simetría y su ausencia de disonancias, pueden considerarse un punto a favor para respetar su posición en el ranking de consonancia; al igual que esperamos pueda respetarse,
aunque no deje de ser discutible, la observación que aquí se propone como índice orientativo:
que el área de las representaciones poligonales -y en consecuencia lo que hemos denominado el
coeficiente de consonancia- puede servir para valorar su grado de consonancia como conjunto
de sonidos y servir para compararlo con otros.
5.1.5.7.
La propuesta de Hindemith
Tratando, como lo hemos hecho en este apartado, sobre una manera de clasificar los acordes
en función de su grado de consonancia y de disonancia, parece que sería un lamentable olvido
no recoger, y de alguna forma comparar, en estas líneas, la interesante aportación que hiciera
a este respecto, el compositor Paul Hindemith13 en su volumen I de Unterweisung im Tonsatz
(1937-70). En cualquier caso, parece conveniente recordar que las consideraciones que realizó
este destacado compositor alemán, fueron utilizando una afinación derivada de la serie armónica
y no del sistema de temperamento igual, como hacemos en nuestro caso.
Su clasificación de los acordes dependía directamente de su catalogación de los intervalos
-que situaba el tritono en una categoría aparte, ni consonante ni disonante-, de forma que los
dividía en dos tipos principales: las combinaciones sin tritono y las combinaciones con tritono.
Cada una de estas clases se subdividía a su vez en tres categorías:
acordes sin segundas ni séptimas,
acordes con segundas y séptimas,
y acordes indeterminados14 .
13
14
Para esta subsección, ha sido de especial interés el artículo, citado en la bibliografía, de Ortmann (1940).
Este último grupo incluye entre otros los tríadas normalmente llamados aumentado y disminuido.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
70
Básicamente, según nos dice este autor, la energía armónica existe en función del desplazamiento
del peso armónico y de las relaciones entre las clases de acordes que acabamos de enunciar.
Así pues, los acordes con segundas, séptimas y tritonos, tienen una mayor tendencia hacia la
progresión armónica que aquéllos también con segundas y séptimas, pero sin tritonos. Estos
últimos, por su parte, tienen una mayor energía armónica que aquellos sin segundas ni séptimas.
Como podemos apreciar fácilmente, esta clasificación difiere de la forma acostumbrada en
tres aspectos principales: los acordes no se construyen obligatoriamente por terceras, la idea
usual de inversión como factor trascendente no resulta suficientemente convincente y el significado múltiple (cambio de notación, simplemente) de una misma combinación de sonidos no se
contempla. No creo que sea necesario comentar que, así como hace Hindemith, sucede también
en la propuesta que se ofrecía por nuestra parte, en los apartados anteriores.
5.2.
Las divisiones simétricas regulares de la circunferencia
Si tenemos en cuenta que nuestro sistema de afinación temperado divide la octava en doce
sectores iguales, comprenderíamos que las posibles divisiones regulares, en definitiva, de la
octava, son las mismas que los divisores posibles del número 12; o sea: 1, 2, 3, 4, 6 y el propio
12. Cada uno de estos factores va a dar lugar a una escala o acorde típico, así la división de
cada sonido da lugar a la escala dodecafónica de 12 sonidos (podemos verla representada en la
figura 5.2.2 en la página 72), cada 2 da lugar a las dos escalas hexátonas o de tonos enteros 15
(así se ve en la figura 5.2.1 en la página siguiente), cada 3 da lugar a la escala trifónica 16 o a los
tres acordes disminuidos conocidos (véase figura 5.4.13 en la página 93), cada 4 obtendríamos la
escala tetrafónica o los cuatro acordes aumentados posibles (podemos verlos en la figura 5.4.4
en la página 84), cada 6 tendríamos grupos de dos notas que forman la escala bifónica o el
tritono (como se ve en la figura 5.1.1 en la página 56) y, por último, podríamos considerar
de cada doce sonidos, cada sonido aislado, o sea, sólo una nota, como veíamos en las figuras
4.0.4 (pág. 45) y 4.0.5 (pág. 46) que mostraban los 12 sonidos de nuestro sistema temperado
(incluyendo sus enarmonías más frecuentes).
Que se correspondería con el modo 1 de transposiciones limitadas de Messiaen.
La nomenclatura de estas escalas ha sido extraída de la página 9 de la publicación de M. A. Mateu (2006),
citada en la bibliografía.
15
16
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
Figura 5.2.1: La escala hexátona
71
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
72
Figura 5.2.2: La escala dodecafónica
Y ahora pasamos a estudiar, como caso especialmente notable, de divisiones simétricas de
la circunferencia, los modos de transposiciones limitadas de Messiaen.
5.2.1.
Modos de transposiciones limitadas de Messiaen
Se trata de siete modos que se caracterizan por tener un número determinado de transposiciones posibles, esto es, que se pueden transportar sólo un número limitado de veces17 , puesto
que tras ese número de veces se produce una repetición del mismo conjunto de sonidos, aunque
tomando otra nota de comienzo. Para estudiar con detenimiento estos modos se recomienda
tener presente lo que se comentó sobre los ejes de simetría en las representaciones poligonales
del Espiropentagrama, en el apartado 5.1.3 en la página 58, puesto que su pertinencia y utilidad
para el estudio de estas escalas sintéticas diseñadas por Messiaen son irrebatibles.
17
Ya lo veíamos en el subapartado 5.1.3.3 en la página 61 dedicado específicamente a esta cuestión.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.2.1.1.
73
Modo 1 de transposición limitada de Messiaen
Coincide con la escala hexátona, que veíamos en la figura 5.2.1 en la página 71 y tiene, por
lo tanto, una división regular de los sonidos y sólo dos posibles transposiciones.
5.2.1.2.
Modo 2 de transposición limitada de Messiaen
Esta escala correspondería con un conjunto de ocho sonidos que, alternadamente, se van
separando uno y dos semitonos. Aparece ya en Sadko de Rimsky-Korsakov, si bien, Scriabin lo
usa de forma más consciente y también aparece de forma pasajera en Ravel y Stravinsky. Tiene
únicamente tres transposiciones -al igual que el acorde de séptima disminuida-.
Figura 5.2.3: Modo 2 de Messiaen
5.2.1.3.
Modo 3 de transposición limitada de Messiaen
De forma similar a como se organizaba la escala anterior, dividida en segmentos alternantes
de intervalos fijos, ésta se divide con la secuencia: un tono, un semitono, un semitono, y así
selecciona los nueve sonidos que la componen. Es un modo que tiene cuatro transposiciones
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
74
-como sucede con el acorde aumentado-.
Figura 5.2.4: Escala 2-1-1 de Messiaen
5.2.1.4.
Modo 4 de transposición limitada de Messiaen
También con ocho sonidos, este modo parece tener dos tetracordos claramente diferenciados,
equidistantes a una tercera menor respectivamente y constituidos, cada uno, por cuatro sonidos
a distancia de semitono. Tiene en total seis transposiciones.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
75
Figura 5.2.5: Modo 4 de Messiaen
5.2.1.5.
Modo 5 de transposición limitada de Messiaen
Como si se tratara del hermano menor del modo 4, tiene la misma forma, sólo que únicamente
con seis sonidos en total, pero igualmente separado en dos tricordos (con tres sonidos separados
por un semitono cada uno) distantes entre sí una tercera mayor. Al igual que ocurría en el
modo 4 también tiene seis transposiciones.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
76
Figura 5.2.6: Modo 5 de Messiaen
5.2.1.6.
Modo 6 de transposición limitada de Messiaen
Este modo, también con seis transposiciones, está constituido por ocho sonidos y está muy
emparentado con el modo anterior. Los dos sonidos que diferencian el modo 5 y el 6 están
colocados acortando la distancia de tercera mayor que separaban los sonidos en el modo cinco,
de forma que son como dos puntos intermedios entre estos dos grupos de tres sonidos -entre sí
a medio tono cada uno- en el punto intermedio de la tercera mayor, o sea, a una segunda mayor
de cada uno de los dos grupos.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
77
Figura 5.2.7: Modo 6 de Messiaen
5.2.1.7.
Modo 7 de transposición limitada de Messiaen
El último de los modos de Messiaen tiene diez sonidos y viéndolo en su proyección sobre el
Espiropentagrama, podemos apreciar cómo está totalmente emparentado con los modos 4 y 5,
de los que parece simplemente, una ampliación en dos sonidos. Tal y como aquéllos con los que
lo relacionamos, tiene únicamente seis transposiciones.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
78
Figura 5.2.8: Modo 7 de Messiaen
5.2.2.
Otros casos
5.2.2.1.
El acorde de quinta aumentada
Se tratará más adelante, dentro del apartado de los acordes tríadas en el subpunto 5.4.1.3
en la página 84.
5.2.2.2.
El acorde de séptima disminuida
Podemos encontrarlo, en la página 93, en el subapartado 5.4.2.7.
5.2.2.3.
La sexta aumentada francesa.
Véase el subapartado 5.4.3.2 en la página 96.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.3.
79
Las divisiones simétricas irregulares de la circunferencia
Aquí incluiríamos otros grupos de sonidos que manifiestan simetría a la hora de dividir
la octava musical, pero no entre cada uno de sus elementos. Una parte importante de estas
manifestaciones sonoras son construcciones derivadas de la especulación del siglo XX, aunque
también podemos encontrar casos que existen con carta de naturaleza, dentro de la tonalidad,
desde mucho antes.
La escala Mayor mixta
5.3.1.
El heptágono diatónico
Como caso principal de divisiones regulares no periódicas tendríamos los diferentes tipos
de escalas diatónicas18 , entre las que se cuentan las escalas mayor y menor, así como todas las
escalas de los modos medievales; todas ellas formadas en base a diferentes rotaciones de una
formación cuya representación correspondería con un heptágono irregular, pero que cuenta sin
embargo, con un eje de simetría, como podemos ver más abajo, en la figura 5.3.1.
Figura 5.3.1: El heptágono diatónico
Si estudiamos esta figura nos daremos cuenta de que, sólo con observarla ya podemos deducir
muchas de las características que van compartir los diferentes modos y escalas diatónicas; todas
poseen sólo dos semitonos (dos puntos contiguos en el Espiropentagrama), un único tritono
(sólo podemos trazar un diámetro con los vértices que forman este heptágono), cinco sonidos
separados a distancia de un tono (los lados grandes del heptágono), cuatro terceras menores
(los lados que se formatían con estos vértices de un posible cuadrado imaginario inscrito en la
circunferencia del Espiropentagrama), etc. (véase el cuadro 5.2 en la página siguiente).
Recordemos que, según nos dice el New Grove Dictionary en su voz “Scale”, son escalas diatónicas aquellas
que contienen un conjunto de sonidos dentro de una octava, con la siguiente determinación de intervalos: cinco
tonos y dos semitonos.
18
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
Modo Dórico
Escala Mayor o modo Jónico
Modo Frigio
Modo Lidio
Modo Mixolidio
Escala menor o modo Eólico
Modo Locrio
Cuadro 5.2: Los siete modos diatónicos
80
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.3.2.
81
Escalas sintéticas
Son las escalas que no proceden de ninguna tradición, ni folklórica ni académica, sino que
aparecen como producto de la creación de escuelas o de compositores concretos, especialmente, del s. XX. Es incuestionable que también para la observación y estudio de cualquier escala
inventada, a la que normalmente no estaremos acostumbrados, será de una gran utilidad el Espiropentagrama, dado que su proyección servirá para percibir con mayor claridad sus propiedades
y características19 .
5.4.
Divisiones tradicionales de la circunferencia en conjuntos de tres y cuatro sonidos
En este punto estudiaremos los conjuntos de tres y cuatro sonidos; con esto nos referimos
principalmente a su uso simultáneo, es decir, a los acordes tríadas y cuatríadas.
5.4.1.
Acordes tríadas
Dentro de los acordes tríadas vamos a tratar los cuatro más importantes: a) el perfecto
mayor, b) el perfecto menor, c) el de 5ª aumentada y d) el de 5ª disminuida (puede verse la
respectiva representación de cada uno en la figura 5.4.1).
a)
b)
c)
d)
Figura 5.4.1: Principales acordes tríadas
De hecho, además de utilizar una proyección de la escala en el Espiropentagrama, sería altamente recomendable utilizar la simbología de las cabezas de nota que aplicábamos en los árboles ya que esto permitirá
sintetizar además sus jerarquías y tendencias melódicas
19
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.1.1.
82
El acorde perfecto mayor
Figura 5.4.2: El acorde Perfecto Mayor
El acorde perfecto mayor se representa sobre el círculo cromático (o el Espiropentagrama)
como un triángulo acutángulo20 escaleno21 ; sus lados tienen una proporción equivalente a los
semitonos que componen sus intervalos, es decir, 4:3:5 (así podemos verlo en la figura 5.4.2 de
arriba).
Según la configuración de sus ángulos, el Diccionario de la RAE nos dice que un triángulo acutángulo es el
que tiene los tres ángulos agudos.
21
Según nos define el Diccionario de la RAE, un triángulo escaleno es el que tiene los tres lados desiguales.
20
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.1.2.
83
El acorde perfecto menor
Figura 5.4.3: El acorde perfecto menor
El acorde perfecto menor responde a una representación más que muy similar, idéntica, al
triángulo que servía para estos fines en el apartado anterior, del acorde perfecto mayor. La
diferencia estribaría en que se trata de una reflexión del polígono, o sea, que estamos ante un
ejemplo de axisimetría o simetría axial22 . De este modo podemos afirmar que las propiedades
de ambos polígonos son las mismas, lo cual sobreentiende la proporción que guardan sus lados,
derivada de sus intervalos -musicalmente hablando- constituyentes.
Llegados a este punto, a colación de la aximetría observada entre los acordes perfecto mayor
y perfecto menor, parece muy conveniente recordar las teorías existentes desde Zarlino (Zarlino,
1558) (vol. III, cap. 31), que justificaban la consonancia del acorde menor a través de la división
armónica, y entendían que este acorde nacía de los armónicos negativos.
La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como
referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno
que en una imagen reflejada en el espejo (Girbau Badó, 1993).
22
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.1.3.
84
El acorde de 5ª aumentada
Figura 5.4.4: El acorde de 5ª aumentada
El acorde de 5ª aumentada está formado por dos terceras mayores, lo que resulta una
5ª aumentada (que enarmónicamente sería igual a una 6ª menor y, por tanto, al invertirla
resultaría ser otra tercera mayor), así que sus proporciones son 4:4:4 y tiene como representación
poligonal una de las figuras más destacadas: el triángulo equilátero. Su absoluta simetría y la
igualdad de sus lados le conceden un importante e inigualable valor entre los acordes tríadas y
lo emparentan, por sus propiedades, con un cuatríada: el acorde de séptima disminuida (véase
el apartado 5.4.2.7 en la página 93). Sólo posee cuatro versiones posibles23 y va a ser de extrema
utilidad dentro del campo de la modulación.
Este acorde tiene su manifestación más clásica en el III< de las escalas menores melódica o
armónica, si bien también puede aparecer como resultado de la alteración en más de la 5ª de
un acorde mayor (como el I+5 o el IV+5 de un modo Mayor).
Como veíamos al tomarlo como ejemplo en el subapartado 5.1.3.3 en la página 61 sobre la transposición
limitada, observada a partir de los ejes de simetría de las figuras.
23
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.1.4.
85
El acorde de 5ª disminuida
Figura 5.4.5: El acorde de 5ª disminuida
Se trata de un acorde formado por dos terceras menores, de lo que resulta la 5ª que da
nombre al acorde, la 5ª disminuida (enarmónicamente igual a una 4ª aumentada o sea, un
tritono), así que sus proporciones son 3:3:6 y tiene también una representación poligonal muy
particular: un triángulo rectángulo24 isósceles25 . Normalmente este tríada tendrá función de
D, sólo pudiendo entenderse como el VII del modo Mayor o el VII< de las escalas menores
melódica o armónica. Otra posibilidad, aunque menos habitual, es que se tratara de un II del
modo menor.
En palabras de la Real Academia “el que tiene recto uno de sus ángulos”.
Sobre el triángulo isósceles nuestro diccionario nos dice, diferenciándolo del equilátero, que es “el que tiene
iguales solamente dos ángulos y dos lados.”
24
25
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.
a)
86
Acordes cuatríadas
b)
c)
f)
d)
e)
g)
Figura 5.4.6: Las siete especies de cuatríadas diatónicos
Respecto a los acordes diatónicos de cuatro sonidos, sabemos que podemos agruparlos en
siete grupos o especies (así lo hacen autores como Chailley y Challan (1964) o Martínez-Oña
(1991)) que responderían al siguiente esquema:
a) 1ª especie: 3ª mayor, 3ª menor, 3ª menor, o sea, un acorde perfecto mayor con séptima
menor;
b) 2ª especie: 3ª menor, 3ª mayor, 3ª menor, o lo que es lo mismo, un acorde perfecto menor
con séptima menor;
c) 3ª especie: 3ª menor, 3ª menor, 3ª mayor, es decir, un acorde tríada disminuido con séptima
menor;
d) 4ª especie: 3ª mayor, 3ª menor, 3ª mayor, esto es un acorde perfecto mayor con séptima
mayor;
e) 5ª especie: 3ª menor, 3ª mayor, 3ª mayor, o sea, un acorde perfecto menor con séptima
mayor;
f) 6ª especie: 3ª mayor, 3ª mayor, 3ª menor, es decir, un acorde tríada aumentado con séptima
mayor;
g) 7ª especie: 3ª menor, 3ª menor, 3ª menor, o el acorde conocido también como acorde de 7ª
disminuida.
Como es obvio los acordes cuatríadas o tetradas, tendrán como representaciones cuadriláteros
de diversos tipos, que iremos estudiando en sus respectivos subapartados, pero simplemente
atendiendo a la figura 5.4.6, podemos observar cómo poseen notables muestras de simetría,
bien en sí mismos -casos b), d) y g)- o bien por comparación entre sí, por ser axisimétricos
(véase nota al pie 22 en la página 83) -casos a) y c), y e) y g), respectivamente-.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.1.
87
Acordes con 7ª de 1ª especie (P. M. con 7ª menor): 7ª natural
Figura 5.4.7: El acorde Dominante con séptima
Éste es el acorde con séptima por antonomasia, el más habitual y el que más presencia
tiene en la tradición armónica occidental; hablamos, evidentemente, del acorde que sonará a
Dominante con séptima y por tanto, será una piedra angular de la tonalidad y su práctica
común.
La forma de representación de este acorde es un trapezoide irregular
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.2.
88
Acordes con 7ª de 2ª especie (P. m. con 7ª menor): 7ª menor
Figura 5.4.8: El acode Perfecto menor con 7ª menor
Se trata del acorde más frecuente dentro de los diatónicos con séptima, es el que aparece
sobre los grados II, III y VI de cualquier tonalidad Mayor (sus correlatos en el modo menor
serían el I, IV, y V -dominante menor-).
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.3.
89
Acordes con 7ª de 3ª especie (disminuido con 7ª menor): 7ª Submenor
Figura 5.4.9: El acorde de Séptima de Sensible
Este acorde, también llamado semidisminuido -por poseer sólo una quinta disminuida, a
diferencia del de séptima disminuida que posee dos-, aparece de forma más habitual, en el
modo Mayor al construirse diatónicamente sobre su VII, con una clara función de Dominante.
No obstante, también tiene la posibilidad de aparecer como II de un modo menor, especialmente
en primera inversión.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.4.
90
Acordes con 7ª de 4ª especie (P. M. con 7ª Mayor): 7ª Mayor
Figura 5.4.10: El acorde Perfecto Mayor con 7ª Mayor
De forma diatónica, este acorde sólo aparece en el I y IV del modo Mayor (III y VI del modo
menor26 ) y, en la mayoría de los casos en que aparece se entenderá como un acorde con una
apoyatura inferior de la octava de la fundamental, más que como una séptima propiamente.
Aunque teóricamente posible, será bastante improbable que encontremos VII natural de una escala menor
dórica (que sólo elevara el sexto grado) que mostrara al mismo tiempo sobre sí, un sexto elevado; carece de la
lógica que la elevación del VI y VII grados melódicos poseen dentro de la estética tonal.
26
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.5.
91
Acordes con 7ª de 5ª especie (P. m. con 7ª Mayor): 7ª sobre menor
Figura 5.4.11: El acorde perfecto menor con 7ª Mayor
Su único exponente sería el I de un modo menor melódico o armónico. De forma similar a
como comentábamos en el caso anterior, la 4ª especie, en la mayoría de ocasiones se entendería
la séptima mas como una apoyatura inferior de la octava de la fundamental, que como una
séptima en sí.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.6.
92
Acordes con 7ª de 6ª especie (aumentado con 7ª Mayor): 7ª sobre aumentado
Figura 5.4.12: El acorde aumentado con 7ª Mayor
Se elabora sobre el III del modo menor melódico o armónico y al igual que en los dos casos
anteriores, relativos a acordes con séptima Mayor, repetiríamos que será más probablemente
entendida como una apoyatura inferior que como una disonancia de séptima propia del acorde.
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.2.7.
93
Acordes con 7ª de 7ª especie: 7ª disminuida
Figura 5.4.13: El acorde de séptima disminuida
Es el acorde más especial de los acordes de séptima ya que está constituido por intervalos
iguales de 3ª menor entre sus notas y demuestra unas condiciones de simetría que ningún otro
acorde podría tener (recordemos lo que veíamos en sobre las propiedades derivadas de la simetría
que veíamos en el apartado 5.1.3.1 en la página 58). Estas posibilidades de enarmonización,
valoradas y empleadas con numerosos ejemplos, desde los comienzos de la tonalidad, permiten
que este acorde sea el instrumento más sencillo y habitual, para la modulación enarmónica
entre tonalidades, incluso tonalidades muy lejanas.
Si lo estudiamos con detenimiento observaremos que incluye dos diámetros completos de la
circunferencia en que está inscrito (lo que supone dos intervalos de tritono o de 5ª disminuida),
de forma que cualquiera de sus notas puede ejercer el papel de sensible y, por lo tanto, esto
le permitirá ser interpretado como otra versión de sí mismo, para cuatro Tónicas diferentes,
que corresponderían con la nota adyacente a cualquiera de sus vértices. Añadiremos además
el hecho de que estas cuatro tónicas pueden ser tanto de un modo Mayor como de un modo
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
94
menor, con lo que sirve para modular entre ocho tonalidades diferentes, conservando siempre
su identidad y sin que resulte abrupto, en modo alguno, su uso.
5.4.3.
Los acordes de sexta aumentada
b)
a)
c)
d)
Figura 5.4.14: Los acordes de sexta aumentada
Los acordes de sexta aumentada son acordes alterados27 , que normalmente aparecen sobre el
VI prestado en el modo mayor y el natural en el modo menor, y que tiene función de Dominante
de la Dominante (lo que sería una variante de función de subdominante, por eso las marcas de
presencia que aparecen en el Espiropentagrama son de ese tipo). Su intervalo característico, la
sexta aumentada, que les da nombre, aparece como consecuencia de tener alterada en menos
la nota que aparece en el bajo; así, con respecto a la sensible de la dominante se produce el
citado intervalo aumentado. Cuatro son los más utilizados (cuyas representaciones poligonales
coincidirán con las mostradas en la fig. 5.4.14) y son los siguientes:
a) la sexta aumentada italiana;
b) la sexta aumentada francesa;
c) la sexta aumentada alemana; y
d) la sexta aumentada suiza (o de 4ª doble aumentada).
Pasamos a continuación, a describir sus características y propiedades individualmente, en las
siguientes secciones.
Tomando las palabras de Artaza Fano (2002), diríamos que: “Un acorde alterado es cualquier acorde afectado
por una alteración, lo que significa que una de sus notas no corresponde a su forma original establecida por la
armadura. Existen tres posibles razones para que estas alteraciones se produzcan: - Deficiencia del sistema de
armadura, que no permite la intercambiabilidad de modos. Por eso no se consideran alterados los acordes que
alteren de forma modal el III, VI ó VII grados. - El papel de las dominantes secundarias. Que no se consideran
alterados por pertenecer, en realidad, a otro tono (de ahí el nombre de Acordes de préstamo) y que son las
más habituales. [Y el 6ª Napolitana] - Las alteraciones que aparecen cuando la presencia de la nota o notas
cromáticas da lugar a que se constituya un acorde distinto de todos aquellos que pueden formarse con las notas
de las escalas básicas. Que sí son verdaderamente alterados. Podemos pues definir a los acordes alterados como
aquellos que contienen una o más notas cromáticas.”
27
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.3.1.
95
La sexta aumentada italiana
Figura 5.4.15: El acorde de sexta aumentada italiana (DDi de Sol M/m)
Se trata del único acorde tríada de los cuatro, con lo que es el menos disonante de ellos.
Su forma, tomada de manera sintética, correspondería a lo que sería un acorde disminuido
sobre la sensible de la Dominante, con la tercera rebajada y en primera inversión. Su resolución
habitual es sobre el acorde de Dominante o la tónica en sexta y cuarta cadencial. En cuanto a
su disposición, dado que sólo tiene tres notas, aún siendo todas tendenciales, lo normal sería
duplicar la quinta (en pro de no duplicar la sensible o la nota alterada).
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.3.2.
96
La sexta aumentada francesa
Figura 5.4.16: El acorde de sexta aumentada francesa (DDf de Sol M/m)
Es un acorde cuatríada muy especial; se trata de una Dominante de la Dominante con
séptima y con la quinta rebajada en el bajo, o sea, en segunda inversión. Su resolución habitual
es sobre el acorde de Dominante en estado fundamental, aunque también puede -como la italiana
y la alemana- resolver sobre el acorde de tónica en sexta y cuarta, es decir, el sexta y cuarta
cadencial.
Es un acorde muy especial porque (si observamos la figura geométrica que lo representa
en la fig. 5.4.16 de arriba, esto nos puede servir de ayuda) posee unas propiedades de simetría
únicas28 , muy próximas a las del séptima disminuida (fig. 5.4.13 en la página 93). Es enarmónico
de otro igual a él que tendría su fundamental en el vértice opuesto de la figura, así como de
otra variedad de acorde, la séptima de sensible con la tercera alterada ascendentemente, que
aparecería en dos veces también, partiendo respectivamente de cada uno de los otros dos vértices
Se puede entender con mayor facilidad si se tiene presente la explicación que se daba en el apartado 5.1.3.1
en la página 58, que trataba sobre la transposición limitada de conjuntos de sonidos, ya que se ilustraba haciendo
uso, precisamente, de esta misma sonoridad.
28
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
97
restantes; o sea, que posee cuatro interpretaciones diferentes: dos sextas francesas (o Dominantes
con séptima con la quinta rebajada) y dos séptimas de sensible con la tercera elevada.
5.4.3.3.
La sexta aumentada alemana
La sexta aumentada alemana es quizá el acorde de sexta aumentada más utilizado, la razón más probable es que se trata del que tiene una sonoridad ya conocida29 , puesto que es
enarmónico del acorde de séptima de Dominante (la forma de su trapezoide lo hace fácilmente
perceptible). De hecho, esta propiedad enarmónica le otorgará un papel notable en las modulaciones de este tipo. En el caso que mostramos en el ejemplo de la figura 5.4.17, una DDa de Sol
Mayor, la enarmonía que lo convertiría en una D7 la encontraríamos si transformáramos el do#
en reb , entonces leeríamos el acorde como una simple Dominante con séptima de Lab Mayor o
menor.
Si bien, no podemos olvidar que es enarmónico de la sexta aumentada suiza, que por tanto también tendría
la sonoridad de un acorde de séptima de dominante, y estaría de la misma forma, ya incluido en el ámbito de las
sonoridades más aceptables para los acordes de sexta aumentada; sin embargo, la suiza tiene unas propiedades
derivadas de su lectura que hacen mucho más compleja su comprensión dentro del discurso y por tanto, su
utilización.
29
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
Figura 5.4.17: El acorde de sexta aumentada alemana (DDa de Sol M/m)
98
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
5.4.3.4.
99
La sexta aumentada suiza (acorde de 4ª doble aumentada30 )
Figura 5.4.18: El acorde de sexta aumentada suiza (DDs de Sol M/m)
Como podemos apreciar en la ilustración de la figura 5.4.18, el polígono que representa
este acorde (y ya se veía con claridad comparando los apartados c) y d) de la figura 5.4.14 en
la página 94) tiene una forma exactamente igual que la de la sexta aumentada alemana (fig.
5.4.17). Es evidente que se trata de dos acordes enarmónicos en los que, según una de sus notas
(en este caso la# , que en la 6ª aumentada alemana aparecía como sib ) se interprete como una
cuarta doble aumentada respecto del bajo (caso de este acorde, la 6ª aumentada suiza), o como
una quinta justa (en el caso de la 6ª aumentada alemana), se entenderá y se comportará de
una u otra forma. Además, hemos de añadir para que no pase desapercibido, que tal y como
sucedía con el acorde de sexta aumentada alemana -siendo éste un acorde enarmónico, es lógico, este acorde es también enarmónico de un acorde de séptima de dominante (compárese con el
apartado a) de la figura 5.4.6 en la página 86); siendo entonces dos las notas enarmonizadas
El hecho de aparecer esta cuarta doble aumentada obliga a resolver sobre un acorde de tónica en sexta y
cuarta, o sea, el sexta y cuarta cadencial.
30
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
100
(en este caso la# por sib y do# por reb ).
5.5.
El color como marca funcional
A la hora de escoger la correlación de colores que aplicar a las diferentes sonoridades tipo,
hemos atendido a los vínculos con las emociones que los colores suscitan, según diversos estudios consultados. No obstante, hemos de anotar antes que nada, que también la psicología ha
demostrado que la fuerza con que estas correlaciones se dan, más que ser inherente y universal,
depende de la herencia y el contexto cultural en que el individuo esté sumergido31 . Teniendo en
cuenta este hecho, hemos actuado en consonancia con los patrones de la cultura occidental a la
que principalmente va dirigido este trabajo; de esta forma, hemos seguido las conclusiones expuestas en el artículo Scaling the Association between Colors and Mood-tones de Warner Schaie
(1961).
Siguiendo la correlación que en dicho estudio (Warner Schaie, 1961, pág. 271) se recoge,
traducimos sus resultados y obtenemos el siguiente cuadro:
A este respecto es muy ilustrativo observar el estudio comparativo entre las asociaciones del color con las
emociones que hacía un grupo de estadounidenses y un grupo de indígenas mejicano, en el artículo de D’Andrade
(1974) citado en la bibliografía.
31
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
Color
Asociación fuerte
ROJO
protector, defensor; poderoso,
fuerte, señorial; (excitante,
estimulante)*
excitante, estimulante
NARANJA
AMARILLO
excitante, estimulante; divertido,
jovial, alegre; placentero
VERDE
AZUL
MORADO
MARRÓN
placentero; seguro, cómodo;
tierno, tranquilizador; (calmado,
pacífico, sereno; excitante,
estimulante)
solemne, estable; (abatido,
desanimado, melancólico, triste)
(seguro, cómodo)
BLANCO
tierno, tranquilizador; (calmado,
pacífico, sereno)
GRIS
abatido, desanimado,
melancólico, triste; (calmado,
pacífico, sereno)
NEGRO
angustiado, molesto, enfadado;
desafiante, obstinado, hostil;
abatido, desanimado,
melancólico, triste; solemne,
estable; poderoso, fuerte,
señorial
101
Asociación débil o ausencia de
ella
Calmado, pacífico, sereno;
tierno, tranquilizador
calmado, pacífico, sereno; tierno,
tranquilizador; solemne, estable
solemne, estable; abatido,
desanimado, melancólico, triste;
protector, defensor; poderoso,
fuerte, señorial
solemne, estable; protector,
defensor; poderoso, fuerte,
señorial; abatido, desanimado,
melancólico, triste
angustiado, molesto, enfadado;
abatido, desanimado,
melancólico, triste; desafiante,
obstinado, hostil
excitante, estimulante; divertido,
jovial, alegre
divertido, jovial, alegre;
desafiante, obstinado, hostil;
excitante, estimulante; poderoso,
fuerte, señorial; placentero
excitante, estimulante; abatido,
desanimado, melancólico, triste;
desafiante, obstinado, hostil;
angustiado, molesto, enfadado;
poderoso, fuerte, señorial
excitante, estimulante;
desafiante, obstinado, hostil;
poderoso, fuerte, señorial;
divertido, jovial, alegre
excitante, estimulante; seguro,
cómodo; tierno, tranquilizador;
divertido, jovial, alegre;
calmado, pacífico, sereno;
placentero
Cuadro 5.3: Colores y emociones
Aplicando este estudio a las nociones que la tonalidad32 tiene asentadas sobre los diferentes
Escogemos el ámbito tonal porque es el que más claro puede servir -tanto por el grado de conocimiento
que puede tener el lector, como por la amplitud del corpus que supone- para ejemplificar la aplicación de este
método de conexión de una sonoridad con una variedad crómica; si bien, es perfectamente aplicable a cualquier
otro sistema de organización musical, especialmente aquellos en los que haya una jerarquía y unas polarizaciones
32
CAPÍTULO 5. REPRESENTACIONES POLIGONALES DE LAS SONORIDADES
102
acordes, tendríamos como resultado el cuadro 5.4, en el que representamos el acorde propio de
cada grado de un tono mayor, con su figura poligonal y color correspondiente:
Grado de la Escala
Figura poligonal y color
Tónica (I)
Triángulo escaleno creciente azul
Supertónica (II)
Triángulo escaleno decreciente amarillo
Mediante (III)
Triángulo escaleno decreciente marrón
Subdominante (IV)
Triángulo escaleno creciente verde
Dominante (V)
Triángulo escaleno creciente rojo
Submediante33 (VI)
Triángulo escaleno decreciente morado
Sensible (VII)
Triángulo rectángulo isósceles naranja
Representación gráfica
Cuadro 5.4: Acordes de la escala Mayor en polígonos y colores
establecidas.
Capítulo 6
Aplicaciones del Espiropentagrama
Las aplicaciones del Espiropentagrama son múltiples, probablemente infinitas, como las de
cualquier herramienta que sirve para analizar y mostrar las propiedades de otros elementos.
Además, se trata de una herramienta que apenas acaba de nacer, con lo que no es de extrañar
que nos dejemos fuera de este capítulo muchas utilidades que ustedes los lectores descubran y
pongan en práctica con extraordinario provecho.
En cualquier caso, en estas páginas vamos a tratar aplicaciones que van a colaborar no sólo
con la enseñanza de la Armonía, sino también con la práctica de disciplinas como la Acústica
y el Análisis, siempre buscando servir de catalizador, de acelerador del proceso de aprendizaje,
de forma que el alumno alcance una mayor comprensión y un mayor dominio para su práctica
musical, de los contenidos tratados.
6.1.
Sistemas de afinación
Como es fácil de deducir, el Espiropentagrama, tanto por el trazado de la espiral irregular
en la que se basa, como por la colocación que preve de los sonidos sobre dicha espiral, se basa
en la subdivisión de una circunferencia en doce partes iguales, consecuencia del sistema de
afinación de temperamento igual que se usa en la actualidad. Sin embargo, por lo general, las
diferentes tradiciones musicales, e incluso la nuestra, occidental, si nos remontamos un poco
en el tiempo, poseen diferentes sistemas de afinación. De este modo, siendo este instrumento
una herramienta de patente utilidad para la comparación de conjuntos, podríamos usarlo para
hacer más visibles las características de un sistema de afinación en particular, al tiempo que
las diferencias que pudieran existir entre varios distintos.
Si por ejemplo, observamos un sistema de afinación como el Pitagórico, y lo comparamos con
el de temperamento igual, podríamos apreciar sus diferencias con mayor claridad, al observarlas
sobre el Espiropentagrama. Pongamos por caso que proyectamos sobre este instrumento, la
escala de Do Mayor en los dos sistemas de afinación -véase la fig. 6.1.1 adjunta- y comprobemos
qué ventajas pueden obtenerse.
103
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
104
Figura 6.1.1: Comparación de la Escala Mayor en el sistema temperado (en negro) y en el
pitagórico (en rojo)
Lo primero que salta a la vista al ver esta superposición de escalas de Do Mayor, en los
dos sistemas de afinación, es observar cómo las notas re y la, y más aún, mi y si, poseen una
entonación bastante diferenciada; ya que aparecen en el sistema Pitagórico, perceptiblemente
más agudas. Además, prestando algo más de atención, podemos apreciar cómo los semitonos
del sistema Pitagórico son más pequeños que en el sistema temperado, así como sus tonos son
más grandes1 . Huelga decir que esta manifiesta asimetría del sistema Pitagórico, redunda en un
claro perjuicio a sus posibilidades de transposición y de enarmonía. Nótese, de todas formas, el
hecho de cómo ambos heptágonos (cf. fig. 6.1.2) poseen un único eje de simetría que, pasando
por su centro, atravesaría por sus respectivas notas re (esto lo comentábamos ya, precisamente
analizando el heptágono diatónico en el apartado 5.1.3 en la página 58, en que tratábamos la
utilidad de los ejes de simetría de los polígonos para deducir propiedades de los conjuntos de
Tomando como fuente el somero estudio de Bartlett (1998), como fuente, hemos elaborado esta comparación
tomando los tonos del sistema Pitagórico con una separación de 204 cents y sus semitonos a una distancia de
90 cents. El sistema de temperamento igual presenta siempre una distancia de 200 cents entre sus tonos y de
100 entre sus semitonos.
1
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
105
sonidos que representan).
Temperamento igual
Sistema Pitagórico
Figura 6.1.2: Escala de Do M en los dos sistemas de afinación
6.2.
Procesos contrapuntísticos
Quizá el factor más importante dentro del campo del contrapunto o de la polifonía contrapuntística, sea su carácter imitativo. Así, las imitaciones de un motivo pueden hacerse aplicando
principalmente tres procesos individuales o la combinación de varios o de los tres. Estos procesos serían: la transposición2 , la inversión3 y la retrogradación4 . Además, no hemos de obviar el
hecho de que estos procesos no son excluyentes entre sí y permiten por lo tanto la aplicación
de dos o incluso de los tres, sobre un mismo motivo.
Para ejemplificar estos tres procesos, vamos a tomar un motivo de cinco sonidos (como
puede verse a continuación, en la figura 6.2.1) que trasladaremos al Espiropentagrama (véase
fig. 6.2.3) mediante la confección de una plantilla (sobre una lámina transparente) en la que
recogeremos estos cinco sonidos y su secuencia de aparición colocando unos números como
marcas de presencia (Cf. fig. 6.2.2). Una vez realizada esta plantilla, la obtención de resultados
será muy sencilla, como ahora detallaremos en los siguientes apartados, puesto que únicamente
requerirá de aplicar movimientos en la misma de carácter puramente intuitivo.
Figura 6.2.1: Motivo sobre el pentagrama
La voz “transposition” del New Grove Dictionary define el proceso como: “La escritura o interpretación de
un motivo en un tono diferente del que fue concebido o anotado, ascendiendo o descendiendo todas las notas del
mismo, a un intervalo dado”. Éste será el proceso imprescindible para la imitación directa de cualquier motivo.
3
Sería alterar la dirección de los intervalos de la secuencia de sonidos del motivo, esto es, los intervalos que
eran ascendentes se convierten en descendentes y viceversa.
4
La retrogradación consiste en tomar la secuencia de sonidos en sentido cronológico inverso, de forma que se
empieza por el que aparecía último y se acaba en el que daba comienzo al motivo.
2
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Figura 6.2.2: Plantilla de motivo para la transposición
106
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
107
Figura 6.2.3: Motivo para los procesos
Aquí lo hemos realizado con un motivo únicamente de cinco sonidos, pero podríamos imaginar que la aplicación de estos procedimientos sobre un motivo dodecafónico (de doce sonidos)
sería exactamente igual de sencillo y cómodo.
6.2.1.
La transposición
El Espiropentagrama es, inequívocamente, un instrumento para la transposición de sonidos,
bien tomados individualmente o bien tomados en conjuntos, que dará lo mismo que estén creados
en base a su dimensión melódica o armónica. No obstante, no parece baladí recordar, aunque no
fuera exactamente del mismo modo, cómo especialmente John Clough en un artículo (Clough,
1998), ya analizó con bastante profundidad y rigor científico de índole matemática, la manera
en que una proyección del sistema musical de doce sonidos, sobre una circunferencia, ofrecía
inmensas posibilidades como medio de transposición. Podríamos decir que la idea estaba ya en
muchos autores teóricos desde las primeras reflexiones sobre el círculo de quintas, si bien ninguno
lo había hecho hasta esta propuesta aquí expresada, utilizando un pentagrama dispuesto con
la forma de una espiral irregular.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
108
Como ejemplo más elemental de cómo puede funcionar el Espiropentagrama en este sentido, debería bastar las figuras 4.0.4 (pág. 45) y 4.0.5 (pág. 46) en las que observábamos las
12 posiciones de un sonido cualquiera (y su enarmonía) al someterlo a la rotación que las 2
circunferencias externas ocultas (véase el apartado 4.0.6 en la página 47, que trata de esto)
permiten, tomando su centro como eje. De hecho, el colocar cada sonido a la altura de lo que
sería una hora en este reloj imaginario que sería el Espiropentagrama, parece una imagen que,
de asimilarse bien, puede colaborar para facilitar la tarea al alumnado como método didáctico,
el observar cuántos semitonos (horas), están separados -en este reloj imaginario- dos sonidos,
cuando se están aprendiendo los intervalos.
Ahora bien, utilizando el motivo de cinco sonidos que veíamos en el apartado anterior
(fig. 6.2.1 en la página 105), vamos a proceder a transportarlo una segunda mayor ascendente,
o sea, dos semitonos hacia el grave.
Figura 6.2.4: Motivo original y su versión transportada una 2ª mayor descendente
Para ello, lo único que habrá que hacer es mover la plantilla del motivo dos doceavas partes
de la circunferencia (siguiendo la analogía de antes, dos horas) a la izquierda y así obtendríamos
el siguiente resultado, recogido en la figura 6.2.5:
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
109
Figura 6.2.5: Motivo transportado una segunda mayor descendente
Si lo que quisiéramos fuera hacer una transposición ascendente, por ejemplo, una tercera
menor ascendente.
Figura 6.2.6: Motivo original y su versión transportada una 3ª menor ascendente
En este caso, lo que haríamos sería mover la plantilla hacia la derecha; así, una tercera
menor ascendente, que equivaldría a tres simitonos hacia el agudo, supondría un movimiento
de un cuarto de circunferencia hacia la derecha (o sea, tres horas). Podemos verlo en la siguiente
figura 6.2.7:
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
110
Figura 6.2.7: Motivo transportado una tercera menor ascendente
6.2.2.
La inversión
Este proceso lo que hace es tomar la secuencia de sonidos y alterar la dirección de los
intervalos que la componía, tomándolos en sentido inverso. Así pues, los intervalos que eran
ascendentes pasan a ser descendentes y, por el contrario, los que eran descendentes se convierten
en ascendentes.
Figura 6.2.8: Motivo original y su versión invertida
En el Espiropentagrama, la manera de aplicar la inversión es muy sencillo, dado que trabajamos con una lámina transparente, sólo tendremos que darle la vuelta de manera vertical y
verla al revés (como si le aplicáramos un espejo al eje vertical). Podemos observar el resultado5
5
El resultado en la práctica, como podemos deducir, tendría los números también invertidos respecto a su eje
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
111
en la figura 6.2.9.
Figura 6.2.9: Motivo invertido sobre el Espiropentagrama
6.2.3.
La retrogradación
La retrogradación de un motivo es un procedimiento muy sencillo, consiste en tomar los
sonidos en sentido inverso a la sucesión en como aparecían, de esta forma el último es el
primero, el penúltimo es el segundo, etc.
Figura 6.2.10: Motivo original y su versión retrogradada
Así, trabajando con el Espiropentagrama y este motivo de cinco sonidos, lo único que
vertical, como reflejados. Aquí en la figura ilustrativa 6.2.9, para facilitar la lectura hemos corregido esta ligera
dificultad. No obstante, una versión más fidedigna de cómo resultaría esta aplicación invertida de la lámina
transparente del motivo, podemos observarla en la fig. 6.1b en la página 114, en la que también se ha aplicado
el proceso de inversión a este motivo.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
112
habría que hacer sería tomar el 5 primero, luegro el 4, etc. De esta forma, podemos observar
que el único cambio respecto de la versión original del motivo sobre el Espiropentagrama que
presentábamos en la fig. 6.2.3 en la página 107, es el sentido inverso de la dirección de las flechas
que colocábamos para seguir mejor la secuenciación de sonidos indicada mediante los números
(véase fig. 6.2.11).
Figura 6.2.11: Motivo retrogradado
6.2.4.
La combinación de estos procesos
Como ya se indicaba al comienzo de esta sección, estos procesos no son excluyentes, de
forma que pueden requerirse y aplicarse de manera simultánea. Para ejemplificar este hecho,
vamos a utilizar el motivo y aplicarle las tres acciones a la vez: retrogradación, inversión y
transposición, en concreto, a una cuarta justa descendente -como vemos en la fig. 6.2.12, la
versión transformada empieza en do en lugar de en fa, que siendo una retrogradación, debería
ser su nota de comienzo-.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
113
Figura 6.2.12: Modelo original y su versión invertido-retrogradada transportada una 4ª justa
descendente
Para su obtención mediante el Espiropentagrama deberíamos aplicar los tres procesos, tal y
como se describía en cada uno de los apartados correspondientes, siendo indistinto el orden en
que los hagamos; este proceso está ilustrado en el cuadro 6.1 en la página siguiente. Por mantener
la misma disposición con que hemos ido explicándolos, aquí haremos primero la transposición a
la 4ª justa descendente, o sea, cinco semitonos (fig. 6.1a). Así, esto supondría girar la plantilla
en sentido contrario a las agujas del reloj, cinco doceavas partes de la circunferencia (cinco
horas, en la analogía que usábamos en el apartado de la transposición).
Después realizaríamos la inversión del motivo obtenido tras la transposición, eso supondría
darle la vuelta a la plantilla del motivo en sentido vertical (fig. 6.1b).
Finalmente invertiríamos el sentido de la lectura de los números, partiendo desde el sonido
5 hasta llegar al 1 (fig. 6.1c).
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
(a) Transposición del motivo una cuarta justa
descendente
114
(b) Inversión del motivo una vez transportado
una cuarta justa descendente
(c) Retrogradación del motivo previamente invertido y transportado
Cuadro 6.1: Combinación de los tres procesos: transposición, inversión y retrogradación
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
6.3.
115
La modulación
Sin lugar a dudas, ser un soporte para la modulación6 es la aplicación más importante de este
instrumento, ya que permite de modo sencillo y rápido, la comparación de dos o más conjuntos
cualesquiera de sonidos, atendiendo a sus diversas propiedades, y resolver de este modo con
facilidad, un medio de modulación mediante un método exhaustivo -puesto que contempla todas
las posibilidades-, sistemático -dado que permite la aplicación de criterios para organización y
clasificación del todo- e integral -en tanto que posibilita la observación de elementos desde todos
sus ámbitos-.
La idea básica sería hacer una clasificación de los elementos que tienen en común los dos
tonos que van a conectarse. De esta forma, elaborado todo el catálogo de opciones quedará
a discreción del músico escoger una u otra, según el contexto musical en que se inserte el
proceso modulatorio. Para organizar el conjunto de opciones, nos apoyaremos, obviamente en
el concepto de árbol armónico que vimos en el capítulo 3 en la página 31. De esta forma,
comparando sucesivamente los árboles que representan los dos aspectos más importantes de la
tonalidad, su tensión hacia una tónica (árbol de Dominante) y su confirmación de la misma
mediante su simple enunciación o mediante el respaldo de dicha tensión (árbol de SubdominanteTónica), podremos ordenar las posibilidades de una manera más sistemática.
Siguiendo lo expresado en la voz Modulation del diccionario New Grove observamos que
se nos habla de seis tipos o categorías para este proceso musical: por acorde o acordes pivote
-que es lo que habitualmente se reconoce en castellano como la modulación por acorde común-,
a través de una nota común, la modulación directa o de frase, la modulación cromática, la
modulación por secuencias y la modulación por enarmonía7 . De estos modos de modulación
citados, podríamos observar cómo la modulación directa o la modulación por secuencias, no
requieren de ningún plan armónico que exija conexión entre los tonos implicados, sino que se
Nos referimos a la modulación entre dos tonalidades cualesquiera, según los métodos estudiados por la
Armonía Tonal tradicional, utilizando el sistema de afinación con temperamento igual.
7
Extracto del término ’Modulation’ -realizado por Janna Saslaw- del New Grove Dictionary of Music and
Musicians:
“Techniques of modulation often involve pivot chords, that is, chords common to the original key and the
new key which can provide a transition between the two. Some authors have warned against the use of the
dominant of either key as a pivot chord: the dominant of the original key, on the one hand, is a strong function
and not readily reinterpreted; the dominant of the new key, on the other hand, may be ineffective, since a simple
dominant–tonic progression may be too abrupt to establish the new tonal centre with sufficient force.
The choice of a pivot chord or chords depends on the range of pitches and chords held in common between the
original key and the new key. The possibility of modulation by pivot chord therefore depends on the relationship
between the two keys. The closer two keys are on the Circle of fifths, the more pitches they have in common,
and the larger the repertoire of available pivot chords.
In the case of modulation to a more distant key, when the two keys have fewer pitches in common, it becomes
more difficult to find a pivot chord. Other techniques of modulation are therefore used in these circumstances,
including the use of a single pitch as a ‘pivot note’; ‘direct’ or ‘phrase’ modulation, in which there is a change
of key between phrases without the use of any pivot; ‘chromatic’ modulation, using chromatic alteration in the
middle of a phrase; ‘sequential’ modulation, or straightforward restatement of a phrase in a different key; and
enharmonic reinterpretation, often involving the German augmented 6th chord (which may be respelled as a
dominant 7th), or the diminished 7th chord (which has special qualities of symmetry).”
6
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
116
basa más bien en una conexión establecida en base a una relación puramente formal de los
fragmentos; así que ninguno de estos dos medios implicaría comparación entre los conjuntos de
sonidos. Por lo tanto, los métodos para los que el Espiropentagrama sería útil serían los otros
cuatro: la modulación a través de una nota común y por acorde común (que por su similitud
podríamos considerarlas como variantes de una misma práctica, sometidas a las limitaciones
de la construcción de acordes en el segundo caso), la modulación cromática y la modulación
enarmónica.
6.3.0.1.
Organización de las posibilidades
Con la finalidad de organizar el proceso de comparación entre dos tonalidades (compuestas
cada una por su árbol de Dominante y su árbol de Subdominante-Tónica, sintetizables en lo que
llamamos el Árbol Tonal), estipulamos cuatro casos8 de comparación de los árboles en función
de la relativa rápidez y suavidad, con que se produce el cambio de tónica. Para ejemplificar
el método tomaremos como tonalidad de partida lab menor y como tonalidad de llegada, Sol
Mayor (véase sus árboles tonales en la fig. 6.3.1).
Figura 6.3.1: Árboles tonales de Lab menor y de Sol Mayor
Así pues los cuatro casos en que organizaremos el análisis sistemático de posibilidades serían
los siguientes:
1. Comparar el Árbol de Dominante del tono de partida con el de llegada. Si bien, todo
dependería del contexto y el pasaje concreto, podríamos afirmar que éste sería el proceso
más rápido y de mayor dramatismo; un acorde con función tendencial en la tonalidad de
partida se convierte o es en sí mismo (dependiendo del método de modulación que estemos
aplicando) un acorde tendencial para otro tono, el de llegada. Cabría la posibilidad de que
se entendiera simplemente como una resolución irregular de la Dominante de la tonalidad
de partida así que, muy probablemente, requerirá de una reafirmación de la nueva tónica
(cf. fig. 6.3.2 en la página siguiente).
Aclararemos que, para algunos autores, tal y como ya se recogía en el pie de página anterior, la modulación
que conecta directamente con un acorde de dominante de la tonalidad de llegada -esto sería lo que aquí hemos
contemplado como los casos 1 y 2-, sería excesivamente abrupto e insuficiente para establecer la tonalidad;
estamos de acuerdo en que en la mayoría de casos requeriría de un proceso posterior de reafirmación del tono de
8
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
117
Figura 6.3.2: Ejemplo de comparación del primer caso, D de la tonalidad de partida con D de
la de llegada
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
118
2. Comparar el Árbol de Subdominante-Tónica de la tonalidad de partida con el Árbol de
Dominante de la de llegada; éste sería el segundo caso y aunque igualmente veloz para
realizar el ingreso, supondría partir de un acorde no tendencial, con lo que resultará
llamativo el cambio de función y será algo más apreciable el cambio de tónica (como
ilustración, váyase a la fig. 6.3.3 en la página siguiente).
3. Comparar el Árbol de Dominante del tono de partida con el Árbol de SubdominanteTónica del tono de llegada. Este proceso modulatorio (ilustrado en la fig. 6.3.4 en la
página 120)será más progresivo que los dos anteriores, al necesitar de una posterior aparición de un acorde con función de Dominante para el asentamiento del nuevo tono. Al
igual que en el caso 1 se corre el riesgo de que la resolución de la Dominante de partida se
entienda más que ella misma como un acorde pivote, que el siguiente acorde -suponemos
que se trata de una Dominante del nuevo tono- es una resolución excepcional.
4. Comparar el Árbol de Subdominante-Tónica del tono de partida con el de la tonalidad
de llegada. Sería el proceso más pausado y más fácil de entender; además, es el que más
posibilidades ofrece, dada mayor amplitud de este tipo de árboles y su menor número de
restricciones, principalmente, destaca el hecho de que no exige la presencia de ninguna
nota en concreto, como sucede con la sensible en los Árboles de Dominante (véase la
fig. 6.3.5 en la página 121).
Según hemos ilustrado en las figuras y ejemplificaremos en las páginas siguientes, hemos utilizado los árboles armónicos contando también con sus posibilidades de notas alteradas y con la
subtónica, es decir en su estado más completo9 ; sin embargo, en la práctica va a ser muy improbable que utilicemos estas notas alteradas o la subtónica, dado que pertenecen a posibilidades
que ofrece el sistema tonal dentro del discurso de una tonalidad, pero que como acordes de
inflexión pueden no ser claros o determinantes. Así pues, lo más recomendable sería usar para
su comparación el estado intermedio de evolución de los árboles y no éste más completo; aquí,
empero, empleamos los árboles completos tanto por razones pedagógicas como por ofrecer de
forma más patente el grado de exhaustividad que se puede alcanzar con el proceso. En cualquier
caso, en los subapartados de más adelante en los que analizaremos detalladamente cada paso
en cada tipo de modulación, del proceso de comparación de árboles armónicos, a la hora de
aceptar el uso de los sonidos alterados, sólo tomaremos aquellos acordes que los utilicen como
quinta, que sería el modo de alteración más básico y descartaremos el resto de acordes posibles
que hayamos podido obtener alterando otros sonidos.
llegada, pero sería igualmente desestimable el obviar como método del proceso modulatorio, este uso, además,
tan habitual.
9
Explicábamos los diferentes estados o posibilidades de crecimiento de los árboles armónicos, de forma
específica, en el apartado 3.0.3 en la página 33.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
119
Figura 6.3.3: Ejemplo de la comparación del segundo caso, árbol subdominante-tónica de la
tonalidad de partida y de Dominante de la de llegada.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
120
Figura 6.3.4: Ejemplo de comparación del tercer caso, árbol de Dominante de la tonalidad de
partida y árbol de Subdominante-Tónica de la de llegada.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
121
Figura 6.3.5: Ejemplo de comparación del cuarto caso, entre árboles de Subdominante-Tónica
de las dos tonalidades
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
6.3.1.
122
Normas elementales para la comparación de árboles
La primera norma que debemos dar y que tal vez sea la más importante, se trata de que
cuando en la comparación participa (bien por parte de la tonalidad de llegada como de la de
partida) un árbol de Dominante, éste tendrá una sensible -simbolizada por un triángulo hacia
arriba sin rellenar, y teniendo como marca de referencia un cuadrado-, y siempre lo primero
habrá de ser comprobar que esta nota está presente (como nota común o como enarmonía10 ) o
si se puede obtener por cromatismo11 , ya que si no fuera así, la comparación del resto de notas
sería ociosa, puesto que la característica imprescindible para poder considerar un acorde con
función de Dominante es que posea la sensible, si esta no aparece, ningún acorde de Dominante
podrá entenderse como tal. Así sucede, por ejemplo, en el caso del apartado 6.3.3.1 en la página
siguiente y así podemos verlo en la figura (6.3.6) que lo acompaña.
A la hora de tomar notas y construir acordes, hemos de llevar cuidado y no tomar aquellas
notas que se encuentran a distancia de medio tono (salvo excepciones como los acordes con 9ª
menor o 7ª Mayor), es decir, hemos de entender su funcionamiento de la misma forma que lo
hacíamos al verlas representadas sobre los pentagramas, dentro de la forma esquemática normal
de los árboles, tal y como se explicaba en las diferentes secciones del apartado 3 en la página 31.
6.3.2.
La modulación por nota común
Para ello, bastaría comparar las notas que consideramos propias o atribuíbles a una tonalidad, con las de la otra. Para ello utilizaríamos simplemente las notas constituyentes del
árbol Tonal (Cf. apartado 3.3 en la página 37) de cada tonalidad, atribuyéndoles grafías mixtas cuando era conveniente, y compararlas sencillamente superponiendo ambas abstracciones
esquemáticas sobre el Espiropentagrama.
Como resultado de la comparación obtendríamos todo el conjunto de sonidos comunes,
tanto los que tienen el mismo nombre, luego pueden considerarse nota común, como los que se
obtienen por enarmonización o interpretación de un mismo sonido, con un nombre diferente.
6.3.3.
La modulación diatónica o por acorde común
Este tipo de modulación se basa en que un mismo acorde (con los mismos sonidos y nombres
de las notas, o sea, sonidos homónimos), que pertenece a dos tonalidades diferentes, sirve
para enlazar dos pasajes que tienen diferente tónica, o lo que es lo mismo, sirve como punto
En caso de que apareciera como nota enarmónica sólo podría modularse haciendo uso de este tipo de
modulación, y por tanto, hacer uso, únicamente, de las notas comunes y enarmónicas que aparecieran como
resultado de la comparación entre los dos árboles.
11
Siguiendo las pautas descritas en el apartado 6.3.5 en la página 140, ahora bien, sabiendo que sólo podrá
optarse por este tipo de modulación ya que al igual que explicábamos en la nota anterior, con relación a obtener
la sensible como enarmonía, se trata de un factor condicionante que singulariza drásticamente las posibilidades
modulatorias, en tanto en cuanto no se pueden mezclar, por ejemplo, notas obtenidas por cromatismo con notas
enarmónicas; recordemos pues que sólo las notas comunes estarán presentes y serán utilizables en todos los tipos
de modulación.
10
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
123
de inflexión. Veámos, en un caso concreto, que fuésemos desde Lab menor a Sol Mayor, qué
posibilidades de acordes comunes tendríamos; para ello compararemos de forma sucesiva los
árboles de Dominante y de Subdominante-Tónica de ambos tonos, proyectando estos esquemas
funcionales, llamados árboles, sobre el Espiropentagrama.
6.3.3.1.
Comparación de los árboles de Dominante entre sí (Caso 1: D1 =D2 )
La manera de obtener el resultado ofrecido en el Espiropentagrama, mediante la intersección
sobre el mismo de los árboles de Dominante correspondientes a cada tono, se explicaba en la
página 117
Sonidos comunes en el árbol de partida
eliminando los no homónimos.
Sonidos comunes en el árbol de llegada
eliminando los no homónimos.
Figura 6.3.6: Superposición de Árboles de Dominante y extracción de resultados
1. Ahora, atendiendo a la superposición de los dos árboles ofrecida en la figura 6.3.6 comprobamos si las dos sensibles (representadas por los dos triángulos: si y fa# ) están también,
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
124
cada una, en el otro de los árboles. Basta con que una sola de ellas no esté en el otro
árbol, para que no se pueda realizar la modulación que identifique dos dominantes, ya que
la sensible es la nota imprescindible de esta función. En este ejemplo podemos comprobar
que ninguna de las dos está en el otro; es cierto que podría parecer, atendiendo a las
marcas de referencia, que la sensible (la nota fa# ) del tono de llegada, Sol Mayor, sí está
en el árbol del tono de partida, Lab menor, pero sin embargo, no es así, ya que en entre las
posibles Dominantes de esta última tonalidad no aparece este sonido sino un enarmónico,
solb12 y esta forma de obtención del sonido no nos sirve para la modulación por acorde
común.
6.3.3.2.
Comparación del árbol de Subdominante-Tónica de la tonalidad de partida con el de Dominante de la de llegada (Caso 2: st1 =D2 )
Para obtener la figura resultado de la intersección de los dos árboles que ofrecemos en
la siguiente figura, hemos seguido el proceso que llevábamos a cabo en la figura 6.3.3 en la
página 119.
Además, en el caso de que se pudiera utilizar el sonido, como podemos ver atendiendo a su grafía, es una
subtónica, con lo que implica que tendríamos que entrar en el tono a través de su región subdominante, luego
no sería una verdadera Dominante y podría resultar complicada la afirmación tonal de la nueva tónica habiendo
hecho uso de su subtónica en el pasaje modulatorio.
12
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida
eliminando los no homónimos.
125
Sonidos comunes en el árbol de llegada
eliminando los no homónimos.
Figura 6.3.7: Superposición de Árboles de subdominante-tónica de la tonalidad de partida y de
Dominante de la de llegada y extracción de resultados
1. De forma similar a como sucedía en el caso descrito en el punto anterior, vemos en la figura
6.3.7 con la que trabajaremos ahora, si la sensible de la tonalidad de llegada (que es la que
usa Dominante en este caso de comparación) aparece como nota común. Según podemos
observar sí lo hace, el fa# en Lab menor puede actuar como nota alterada ascendente
(según leemos en la grafía). Además, si analizamos bien, nos daremos cuenta de que
esta nota alterada sólo puede escribirse y leerse como tal, dentro de las sonoridades de
Dominante de la Dominante, o sea, que para poder aparecer, únicamente podrá hacerlo
en solidaridad con la nota sensible de la Dominante, que es re.
2. Vemos qué acordes se pueden formar con el resto de sonidos que sean comunes y que
tengan el mismo nombre (o sea, no sean sonidos enarmónicos). La lista de sonidos sería
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
126
la siguiente: sib , re, fa, fa# , lab , la, do y mib ; porque el resto, que serían sibb , rebb , fab , dob
y mibb en Lab menor, no se interpretarían así en Sol Mayor, sino que serían enarmónicos
y se leerían la, do, mi, si y re, respectivamente, en la tonalidad de llegada.
3. Es el momento de confeccionar una lista de acordes posibles, construidos con los sonidos
homónimos comunes que hemos encontrado entre los dos tonos, si bien, siempre habrán
de contener la sensible del nuevo tono (fa# , o en su defecto y de forma cuestionable, la
subtónica -explicable en el área de la subdominante-, el fa natural)13 .
Sonidos que aparecen
sib , re, fa#
re, fa# , lab
sib , re, fa
re, fa, lab
fa, lab , do
re, fa# , lab , do
fa, lab , do, mib
Lab m
DD+5
VIIV +3
DD
VIIV
VI<
+5
T
DD7+3
VI<
7 +5
Sol M
D’v (= III’+5 )
D−5
III’
SSII 0 IV
SS’
D7−5
SS’7
Cuadro 6.2: Acordes comunes de la intersección del Árbol de subdominante-tónica de partida
y el de Dominante de llegada
4. Ahora tomamos de entre los acordes que hemos encontrado, aquellos que puedan no ser
del todo inteligibles en alguna de las dos tonalidades. De esta forma, el primer acorde que
deberíamos desestimar sería la Dominante de la Dominante tríada que sería equiparable
al III prestado del menor en Sol Mayor; éste, quizá siendo en apariencia la igualdad más
sencilla, introduce la nueva tonalidad a través de un acorde que aunque pueda ser identificable, más que conducir el oído hacia ella, cuando tiene lugar en el discurso, lo que suele
producir es lo contrario, apuntar hacia otras tónicas. Del mismo modo, resultará difícil de
entender y obligará a hacerlo a través del área de la subdominante, en general cualquiera
de los tres acordes que leíamos como Subdominante de la Subdominante prestada, en Sol
Mayor; pero especialmente complejo de entre ellos, es el que identifica el acorde del sexto
grado elevado con una subdominante de la subdominante representada por un segundo
prestado del modo menor, así que sería conveniente prescindir también de su utilización
en un sentido más realista y menos teórico.
6.3.3.3.
Comparación del árbol de Dominante de la tonalidad de partida con el
de Subdominante-Tónica de la de llegada (Caso 3: D1 =ST2 )
Disponemos de la imagen que nos ofrece la intersección de, respectivamente, el árbol de
Dominante de la tonalidad de particda, Lab menor, con el de Subdominante-Tónica de la de
llegada, Sol Mayor, siguiendo el proceso que ya veíamos en la figura 6.3.4 en la página 120.
Dado lo que observábamos en el punto 1, sobre que la aparición del sonido fa# en Lab menor, implicaba
que apareciera también la nota re, debiéramos buscar acordes que tengan estas dos notas.
13
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida
eliminando los no homónimos.
127
Sonidos comunes en el árbol de llegada
eliminando los no homónimos.
Figura 6.3.8: Superposición de Árboles de Dominante de tonalidad de partida y de
Subdominante-Tónica de llegada y extracción de resultados
1. Atendiendo ahora a la figura 6.3.8 de arriba, podemos observar cómo sí es sonido común la
sensible de la tonalidad de partida, Lab menor, con los sonidos posibles de las sonoridades
de Subdominante y Tónica del tono de llegada, Sol Mayor. Además, comprobamos que no
sólo es que el sonido esté presente en ambos árboles, sino que tiene el mismo nombre14 , y
por fin, podemos continuar el proceso.
2. Comprobamos todos los sonidos comunes posibles tomando sólo aquellos que son la misma
nota (tienen igual nombre), y resulta la siguiente lista: reb , mib , sol y sib . Los sonidos
Este detalle será un factor determinante, ya que si tuviera diferente nombre y por tanto, fuese común
sólo por enarmonía, sólo podría llevarse a cabo este tipo de modulación (descrito en el apartado 6.3.4 en la
página 130) y no cabría pensar en la modulación por acorde común.
14
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
128
que en Lab menor leemos como sibb , dob y fab resultan no tener el mismo nombre en
Sol Mayor, sino que se llaman la, si y mi, respectivamente. Por otra parte, en el árbol
de Subdominante-Tónica de Sol Mayor, encontramos también las notas la# y do# , que
igualmente no podemos considerar porque aún siendo sonidos comunes, en realidad son
enarmonías de notas que sí tomaremos, pero con otro nombre: sib y reb .
3. fab , sibb y dob no podrían utilizarse porque, aunque podrían confundirse con sonidos
comunes, se leen con otro nombre en la tonalidad de partida (reb -que sí emplearemos
como tal, ya que también aparece con esta nomenclatura-, mi natural, la natural y si
natural, respectivamente) y por tanto, requieren del proceso de la enarmonía para su
identificación.
4. Elaboramos la lista de acordes posibles con los sonidos antes descubiertos, teniendo en
cuenta que el sonido sol (sensible de la tonalidad de partida) es imprescindible; teniendo
en cuenta esta premisa, la relación de acordes posibles quedaría en:
Sonidos que aparecen
mib , sol, sib
sol, sib , reb
mib , sol, sib , reb
Lab m
V
VIIº
V7
Sol M
VI’
I’-5
VI’-7
Cuadro 6.3: Acordes comunes de la intersección del Árbol de Dominante de partida y el
Subdominante-Tónica de llegada
5. Seleccionamos de los acordes obtenidos, dado que no todos van a ser válidos, aquéllos que
son realmente susceptibles de entenderse en el discurso tonal de ambos tonos, de forma
que de los tres que hemos obtenido sería inevitable prescindir del V7 de la tonalidad
de partida, dado que en la tonalidad de llegada daría como resultado un acorde con
la 7ª alterada y eso no es posible, dentro de las normas de los sonidos alterados. Algo
menos grave sería tomar el I’-5 que resulta de utilizar el VIIº en la tonalidad de partida,
aunque, eso sí, algo difícil de entender (dependería mucho del contexto armónico en el
que se enmarcara el uso del acorde), pero aún así, sería conveniente eliminarlo de las
posibilidades, de forma que nos quedaría únicamente la primera opción: V = VI’.
6.3.3.4.
Comparación de los árboles de Subdominante-Tónica entre sí (Caso 4:
st1 =ST2 )
La imagen que a continuación se ofrece, como resultado de la superposición de los dos árboles
de Subdominante-Tónica de las dos tonalidades implicadas, Lab menor y Sol Mayor, se obtiene
siguiendo el proceso que ya veíamos en la página 121, en la figura 121.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida
eliminando los no homónimos.
129
Sonidos comunes en el árbol de llegada
eliminando los no homónimos.
Figura 6.3.9: Superposición de Árboles de Subdominante-Tónica y extracción de resultados
1. En este caso ya no tenemos que buscar la sensible de ningún árbol, dado que es el único
en que no participa ninguno de Dominante, con lo que haríamos directamente lo que
hacíamos en apartado en segundo término, esto es, comprobar y elaborar una lista con
los sonidos comunes con el mismo nombre de nota. Así, atendiendo a la figura 6.3.9 que
ilustra este caso, veríamos que serían notas comunes entre el tono de partida, Lab menor,
y Sol M, el tono de llegada, son: do, reb , re, mib , lab , la15 y sib . Asimismo, otras notas
aparentemente comunes (rebb -que tomaremos, pero como do-, reb -luego como do# -, mibb ,
El la aparece en la tonalidad de partida como una nota alterada ascendente, por este hecho, su utilización
ya sería harto complicada, pero al acontecer al mismo tiempo que no existe como nota común el fa, se hace
imposible considerarla como 5ª en más -que sería la manera más fácil de aceptarla y utilizarla- y sólo podría
usarse como fundamental en más del I, algo excesivamente lejano como para considerarse verdaderamente como
opción. Por eso, en el punto 3, se comprobará que no se ha utilizado en ningún acorde, aún siendo como es,
nota común.
15
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
130
fab , fa, sibb y dob , según se entienden en Lab menor) aparecen en Sol M, pero sólo tras un
proceso de enarmonía y no son, por lo tanto, válidas en este tipo de modulación.
2. No sería ocioso observar también, qué papel juegan las diferentes notas comunes que
pueden participar, ya que por ejemplo, el reb en Sol M sólo podrá justificarse como una
nota alterada en menos y, por lo tanto, no podrá ocupar cualquier puesto en la sucesión
de terceras del acorde. Algo similar sucede también con el sonido lab que en Sol M sólo
podrá entenderse -dentro de las sonoridades de Subdominante-Tónica- como parte del
acorde Napolitano, de forma que exigirá darse en solidaridad de otras (do y mib ) y muy
preferiblemente, con una disposición concreta: en primera inversión (por eso aparece en
el esquema entre paréntesis, porque no suele ser el bajo del acorde).
3. Ahora sería el momento de confeccionar una relación de acordes posibles utilizando las
notas comunes que hemos hallado en el punto anterior; como resultado obtendríamos los
siguientes:
Sonidos que aparecen
lab , do, mib
sib , re, (fa)
do, mib , (sol)
Lab m
Ds
DDx5
IIIx5
Sol M
Sn
III’x5
S’x5
Cuadro 6.4: Acordes comunes de la intersección de los Árboles de Subdominante de ambos
tonos
4. Es el momento de elegir entre los acordes obtenidos, si bien, como ya tuvimos en cuenta
en el punto 2 de este apartado, la correcta elección y disposición de las notas posibles, la
lista obtenida en el punto 3 es válida en su totalidad. Sin embargo, dado que nos resultan
dos acordes que habrían de aparecer sin quinta (simbolizado con el subíndice x5 ) con los
problemas de duplicaciones y de movimiento, así como con el empobrecimiento sonoro
que eso supondría, el preferido sería el primero de los que recogíamos, esto es, que la Ds
de lab menor es en Sol M su Sn (recordemos que, por lo tanto, deberá estar en primera
inversión y duplicando su tercera).
6.3.4.
La modulación enarmónica
La modulación enarmónica tiene mucho en común con la que acabamos de tratar, la modulación diatónica; en sí, el proceso es el mismo16 , se busca una sonoridad que, inteligible tanto
en el tono de partida como en el de llegada, sirva de nexo entre ellos; sólo hay una diferencia y
ésta es la diferente interpretación de alguno, varios o todos los sonidos que participan en dicha
Dada la semejanza del proceso, hemos decidido explicarlo después de la Modulación Diatónica, si bien,
normalmente, en las programaciones didácticas -quizá siguiendo un criterio de proximidad tonal- se suele explicar
después de la modulación cromática.
16
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
131
sonoridad, mediante la enarmonización de este, estos o de todos sonidos los sonidos participantes. Así, si bien en la modulación diatónica que explicábamos hasta aquí, debíamos evitar
tomar los sonidos que no eran homónimos, en este proceso modulatorio nos veremos obligados
a tomar al menos uno de esos sonidos que tenían diferente nombre según se interpretaran desde
el punto de vista de la tonalidad de partida (en nuestro caso, recordemos que era Lab menor,
como origen, y Sol Mayor, como destino).
6.3.4.1.
Comparación de los árboles de Dominante entre sí (Caso 1: D1 ≡D2 )
La forma de obtención de la intersección sobre el Espiropentagrama que aquí se ofrece,
siguió el proceso que se veía en la página 117.
Sonidos comunes en el árbol de partida,
recuadrando los sonidos enarmónicos.
Sonidos comunes en el árbol de llegada,
recuadrando los sonidos enarmónicos.
Figura 6.3.10: Superposición de Árboles de Dominante y extracción de resultados
1. Tal y como hacíamos en el primer caso de la modulación diatónica, lo primero que haremos
132
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
será buscar que las sensibles de cada uno de los dos tonos implicados en la comparación,
aparezcan (ahora ya no nos importa que tengan diferente nombre) en el árbol de la otra
tonalidad. Como podemos observar, la sensible de Sol Mayor, tonalidad de llegada, sí
aparece en el árbol de Dominante de la de partida, pero como enarmonía (fa# = solb ). Sin
embargo, el sonido sol, no está entre las notas comunes o enarmonizables. Es más, el hecho
de tener que utilizar el fa# que venía siendo solb en la tonalidad de partida, impediría
poder utilizar el sol, en el caso de que apareciese. Cuando, como sucede aquí, la sensible
no es común y sin embargo, sí lo es la subtónica, se elaboraría como opción -y ya quedaría
a criterio del alumno utilizarlos o no- la lista de acordes que utilizando este sonido de
subtónica (y por tanto, con una interpretación de subdominante de la subdominante)
pueden encontrarse. Eso es lo que haremos, teniendo en cuenta esta circunstancia de que
ya no es exactamente D≡D, sino más bien, ss≡D.
2. Los sonidos comunes con el mismo nombre que encontramos son únicamente dos, el mib y el
sib . El resto de sonidos se obtienen por enarmonía y son, respectivamente, los siguientes:
fab -luego leído mi-, solb -imprescindible por ser la sensible de la tonalidad de llegada,
o sea, fa# -, sibb -que será la- y dob -leido en Sol Mayor como si natural-. Los sonidos
sib y si -obtenido por enarmonía del dob -, aunque aparentemente a disposición para la
construcción de acordes, como no está presente la nota re como sonido común, no sería
fácil usarlos, ya que sólo servirían para crear acordes en las que funcionarían, uno u
otro, como apoyaturas no resueltas hacia el la y estos acordes habría que manejarlos con
especial cuidado y tendrían una poco concluyente definición de la tonalidad de llegada.
3. Una vez hecha esta relación de sonidos, podemos elaborar la lista de posibles acordes que
podemos utilizar.
Sonidos que aparecen (leídos en Sol M)
mib , *fa# , *la, (do)
*fa# , *la, (do), *mi
mib , *fa# , *la# , (do)
*fa# , *la# , (do), *mi
*fa# , *si, (do), *mi
mib , *fa# , sib , (do)
Lab m
ssii0IV
ss’7x5
ssiiIV
ss7x5
ss7x54
ssiiIV
Sol M
s
Dvx5
S
D7x5
s
Dvx5+3
S
D7x5+3
S
D7x54
s
Dvx54
Cuadro 6.5: Acordes comunes obtenidos con uso de *enarmonías, consecuencia de la superposición de los dos árboles de Dominante
Llama la atención, al estudiar este cuadro, cómo en varias ocasiones, una misma agrupación de sonidos idénticos, puede interpretarse, con diferentes lecturas, como acordes
diferentes.
4. Sería pertinente ahora, escoger cuáles de estos acordes pueden ser más comprensibles en
ambas tonalidades, y cuáles son más una elucubración teórica que una posibilidad real. De
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
133
esta forma, parece conveniente -aunque tal vez el contexto concreto del discurso armónico,
habiéndolo presentado ya, lo hiciera comprensible- eliminar los acordes de subdominante
de la subdominante que además vienen representados por un II de esta tonalidad, ya
que parece algo extremadamente lejano. Consecuentemente nos quedaríamos con los tres
subdominantes de la subdominante que parten de su cuarto grado (séptimo subtónica de
la tonalidad principal).
6.3.4.2.
Comparación del árbol de Subdominante-Tónica de la tonalidad de partida con el de Dominante de la de llegada (Caso 2: st1 ≡D2 )
El medio de alcanzar la imagen que aquí se ofrece, producto de la intersección del correspondiente árbol de subdominante-tónica de la tonalidad de partida con el de Dominante de
la tonalidad de llegada, sigue el proceso que ya llevábamos a cabo en la figura 6.3.3 en la
página 119.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida,
recuadrando los enarmónicos.
134
Sonidos comunes en el árbol de llegada,
recuadrando los enarmónicos.
Figura 6.3.11: Superposición de Árboles de subdominante-tónica y de Dominante y extracción
de resultados
1. En primer lugar, hay que comprobar que la sensible de la tonalidad de llegada, aparezca
en el árbol de subdominante-tónica de la tonalidad de partida, bien con el mismo nombre,
como nota común, o bien enarmonizado. En este caso, aparece como nota alterada -que
como ya decíamos en el análogo segundo caso, en la modulación diatónica- que únicamente
usaremos en las sonoridades de Dominante de la Dominante de Lab menor; eso implica
que esté simultáneamente a este fa# , la sensible de la Dominante de Lab menor, o sea, la
nota re. Como todas las demás veces, también es admisible aunque no sea exactamente
comparable el resultado, el tomar en lugar de la sensible del tono de llegada, la subtónica
y entrar en esta tonalidad a través del área de Subdominante; esto, obviamente, requeriría
de una posterior reafirmación de la tonalidad haciendo uso de una Dominante propia que
sí determinara su nuevo papel de tónica.
135
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
2. Los sonidos comunes son, en esta ocasión, numerosos. Las notas comunes serían: sib ,
re, fa, fa# , lab , la, do y mib . Añadiéndose a estos sonidos, aparecen tres más producto
de enarmonías y, recordemos que en este tipo de modulación que nos ocupa, debemos
utilizar al menos uno de estos sonidos: sibb17 (que en Sol Mayor será la, que también
teníamos como nota común), rebb (entendido como do en Sol Mayor, que también aparecía
como nota alterada ascendente), fab18 (único mi posible para la nueva tonalidad), dob (si
enarmonizado en la nueva tonalidad) y mibb (re en la tonalidad de llegada, que también
era nota común). Por otra parte, también tenemos un sonido que -como ya hemos visto
que pasaba con el la, con el do y con el re- es común y que también se puede obtener
por enarmonía, se trata del sib que es enarmonizable también por la quinta elevada de la
Dominante de Sol Mayor, o sea, la# .
3. Confeccionamos ahora la lista de acordes posibles que usen sonidos comunes, siendo al
menos uno de ellos, enarmónico.
Sonidos que aparecen (leídos en Sol M)
*la# , re, fa#
*la#, re, fa# , lab
re, fa# , (lab ), *dob
fa, lab , *rebb
re, fa, lab , *si
fa, lab , *si, *re#
Lab m
DD+5
DD+57
t
DDvx5+3
s< −f
t
DDv
svi<7
Sol M
D+5
D±5
Dv (= III)
SS’
s
DSv
s
DSv+3
Cuadro 6.6: Acordes comunes obtenidos con uso de *enarmonías, entre el árbol subdominantetónica de Lab menor y el de Dominante de Sol Mayor
4. Elegimos ahora de entre los acordes que hemos visto como posibles, los que verdaderamente tienen un papel con la suficiente importancia, como para servir a ambas tonalidades y
entenderse. De este modo, el t DDvx5+3 de Lab menor que no permitía la presencia de la 5ª
y llevaba una nota alterada, aunque enarmónico del fácilmente comprensible Dv de Sol
Mayor, parece algo alejado de la tonalidad de partida, aunque siempre todo depende del
contexto y qué y cómo se haya manejado la armonía antes y después. Del mimo modo, la
subdominante con la fundamental en más, que utiliza el sexto grado dórico, es también
un tanto inverosímil en un discurso tonal más o menos clásico. Respecto de los últimos
dos acordes, los que en Sol Mayor actuarían como séptimas disminuidas (la segunda, con
la tercera alterada ascendentemente), dependerían para su uso, de si es o no pertinente
Como este sonido en Lab menor sólo lo podemos explicar como fundamental del acorde napolitano, su
aparición exigirá que estén las otras dos notas que forman este acorde: el reb y el fab ; como podemos observar,
el reb no podremos usarlo porque no es sonido común, así que, simplificando el proceso, el sonido de sibb queda
eliminado en la práctica de este proceso.
18
Teniendo que usar la nota fa# , o en su defecto fa natural, y siendo ambas notas comunes (y no enarmónicas),
será imposible que aparezca este fab en ningún acorde en Lab menor, puesto que no puede aparecer si está una
de las otras dos; así, en conclusión, también esta nota, fab , queda eliminada del proceso.
17
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
136
entrar a través de la subdominante y mediante este proceso, cercano a la modulación
compuesta.
6.3.4.3.
Comparación del árbol de Dominante de la tonalidad de partida con el
de Subdominante-Tónica de la de llegada (Caso 3: D1 ≡ST2 )
Se logra el siguiente resultado que veremos en la próxima figura, tras superponer los árboles
implicados en esta comparación, tal y como se desglosaba en la figura 6.3.4 en la página 120.
Sonidos comunes en el árbol de partida,
recuadrando los enarmónicos.
Sonidos comunes en el árbol de llegada,
recuadrando los enarmónicos.
Figura 6.3.12: Superposición de Árboles de Dominante de tonalidad de partida y de
Subdominante-Tónica de llegada
1. Comprobamos que la sensible del árbol de partida de Lab menor, el sonido sol, está en el
árbol de Subdominante-Tónica de Sol Mayor, bien de forma homónima o por enarmonía.
137
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
2. Revisamos los sonidos comunes entre los dos árboles, conservando el mismo nombre están:
reb , mib , sol y sib ; mientras que como enarmónicos, estarían los siguientes que se leerían en
Lab menor: fab , sibb y dob y serían nombrados mi, la, y si en Sol Mayor, respectivamente.
Luego, podemos distinguir también, como sonidos que aparecen como comunes, pero
también pueden interpretarse como enarmónicos tendríamos en Sol Mayor: do# (reb en
Lab menor) y la#19 (que se entendía como sib en la tonalidad de partida).
3. Una vez conocidos los sonidos que pueden participar, es el momento de elaborar la lista de
acordes posibles20 , con sus respectivas interpretaciones en cada una de las dos tonalidades
implicadas en la modulación. Sólo debemos recordar que siempre debe estar presente la
nota sol -sensible de la Dominante de la tonalidad de partida- y al menos un sonido
enarmónico.
Sonidos que aparecen (leídos en Sol M)
sol, *si, reb
sol, *la, *do# , (mi)
sol, *la, *do# , *mi
mib , sol, *la, *do#
Lab m
VII4
VII−3
s
Dv−3
D7−5
Sol M
T−5
DD7x5
DD7
DD7−5
Cuadro 6.7: Acordes comunes con *enarmonías, entre el árbol de Dominante de Lab menor y el
de Subdominante-Tónica de Sol Mayor
4. Por último, como venimos haciendo hasta ahora en cada caso, seleccionamos de entre los
acordes que hemos visto como posibles, aquellos que puedan tener una inteligibilidad en
los dos tonos, además de ser posibles enlaces. De esta forma, el primer caso, siendo un
acorde disminuido con apoyatura para Lab menor y una tónica con la quinta alterada
en menos para Sol Mayor, no parece que tenga mucha utilidad ni sea representativo en
ninguno de los dos tonos. Del mismo modo, el segundo acorde de la lista, que vuelve a ser
un disminuido, pero ahora con la tercera en menos y que se equiparará a un acorde con
séptima de la Dominante de la Dominante sin quinta, vuelve a parecer ser más confuso
que clarificador para realizar el proceso. Los otros dos, por el contrario, los que tendrán
función de Dominante de la Dominante con séptima en Sol Mayor, el último con la quinta
en menos, serán perfectamente válidos, al menos a nuestro criterio.
Ahora bien, en tanto en cuanto este sonido es una nota alterada ascendente, sólo interpretable como la
fundamental en más del segundo grado, aunque posible va a ser algo complicado que pueda entenderse bien
como movimiento definitorio de la nueva tonalidad.
20
En el listado adjunto hay al menos conocido, un error importante, falta un acorde. Invitamos al lector a que
averigüe observando la figura 6.3.12 en la página anterior de cuál se trata y, para conocer la solución, atienda
a la figura 6.3.18 y al pie de página 28 de la página 151.
19
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
6.3.4.4.
138
Comparación de los árboles de Subdominante-Tónica entre sí (Caso 4:
st1 ≡ST2 )
La intersección que podemos observar en la imagen siguiente, deriva del proceso de superposición seguido en la figura 6.3.5 en la página 121.
Sonidos comunes en el árbol de partida,
recuadrando los enarmónicos.
Sonidos comunes en el árbol de llegada,
recuadrando los enarmónicos.
Figura 6.3.13: Superposición de Árboles de Subdominante-Tónica y extracción de resultados
1. Como en esta comparación sólo participan árboles de subdominante-tónica, no tenemos
que buscar la presencia imprescindible de ninguna nota en concreto, así que podemos
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
139
empezar a señalar qué notas son comunes: do, reb21 , re, mib , lab22 , la y sib . En cuanto a
sonidos exclusivamente enarmónicos que aparecen tendríamos: fab (luego leído mi) y dob
(que será si en Sol Mayor). Por otra parte, existe un conjunto de sonidos que según el
acorde en que participen podrían entenderse como notas comunes con el mismo nombre
en los dos tonos o no hacerlo, estos sonidos serían, según aparecen en Lab menor: rebb
(que se entenderá como otro modo de tener la nota do, que ya era nota común, en Sol
Mayor), reb (que es la nota común, interpretable como do# en Sol Mayor), mibb (que será
otra forma de re), fa (legible como mi# en la tonalidad de llegada, aparte de como fa),
lab (que es luego también interpretable como sol# ), sibb (equivalente a la, que ya existía
como nota común) y sib (que era nota común, pero que podría interpretarse en Sol Mayor,
como la nota la#23 ).
2. Podemos confeccionar ahora el listado de acordes posibles con que podría realizarse la
modulación enarmónica entre Lab menor y Sol Mayor, sin que por ninguna de las dos
partes participen sonoridades tendenciales hacia sus tónicas, es decir, de Dominante,
sino únicamente de Subdominante o de Tónica. Recordemos que, en tanto ya no hay
participación de tipos de Dominante alguno, no se requiere la presencia de ningún sonido
en especial, aunque, eso sí, deberá participar al menos, un sonido enarmónico en cada
uno de estos acordes posibles.
Sonidos que aparecen (leídos en Sol M)
*la, *do# , *mi
*do# , *mi# , la
*mi, *sol# , *si
sib , *do# , mi, (sol)
sib , *do# , *mi# , (sol)
*do# , *mi, (sol), *si
*do# , *mi# , (sol), *si
Lab m
sn
s< +5
svi
sii
sii<
sx57
s< x57
Sol M
DD
DD+5
VI+3 (= Dii )
t
DDvx5
t
DDv+3x5
T
DDx57
T
DD+3x57
Cuadro 6.8: Acordes comunes con uso de *enarmonías, producto de la comparación entre árboles
de Subdominante-Tónica
El reb como nota común sólo va a poder entenderse en Sol Mayor como nota alterada descendente, y dado
que el sol -para el que podría ser quinta alterada- no es sonido común, sus posibilidades se reducen a ser una
tercera en menos, algo que será bastante difícil de entender como método de entrada en el tono de llegada.
22
Tal y como apuntábamos ya anteriormente, el lab en Sol Mayor es el segundo grado rebajado y éste, en
contextos de subdominantes, sólo es explicable como un acorde Napolitano, así que para poder estar presente,
requiere de la presencia simultánea de otros dos sonidos: el do y el mib ; dado que ninguno de estos tres acordes
posee ningún sonido enarmónico, sino que son todos comunes entre las dos tonalidades, no podrá utilizarse este
acorde y por tanto, en la práctica, no habrá forma de contar con la nota lab , luego podemos eliminarlo de esta
lista. No obstante, otra posibilidad sería utilizarlo como nota alterada de un segundo grado con la fundamental
en menos, ahora ya, dejamos a criterio del alumnado si dentro del contexto de la pieza que estén realizando, es
o no pertinente una sonoridad alterada tan particular como medio de modulación.
23
Esta interpretación, sin embargo, será poco fructífera en general, porque su uso representaría una única
posibilidad, un segundo grado con la fundamental alterada ascendentemente y esto será bastante difícil de
aceptar como punto de inflexión y cambio hacia Sol Mayor.
21
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
140
3. Ahora, para finalizar, hacemos una criba entre los acordes posibles para elegir únicamente
aquellos que estimemos coherentes dentro de un discurso armónico, no forzado, en ambas
tonalidades. De esta forma, eliminaríamos rápidamente el tercero de los acordes ofrecido
en la lista, que suponía un acorde con la tercera como nota alterada y una aproximación
más bien hacia el área del segundo grado que hacia la tónica. Por otra parte, debería
observarse concienciudamente cómo ha transcurrido el discurso armónico, para valorar la
pertinencia o no del empleo de acordes de séptima disminuida o de séptima de sensible
(como los cuatro últimos acordes propuestos) sin quinta, algo bastante excepcional. En
conclusión, parece que los dos únicos acordes que sobrevivirían sin mayores reparos, serían
los dos primeros, el napolitano (que preferiblemente estaría en primera inversión) de Lab
menor que se entendería como Dominante de la Dominante de la tonalidad de llegada, Sol
Mayor, y la subdominante dórica con la quinta elevada de Lab menor que se convertiría
en una Dominante de la Dominante con quinta elevada en Sol Mayor.
6.3.5.
La modulación cromática
Aquí vamos a estudiar el proceso en su variante más suave, o sea, cromatizando parte
o todo el acorde, pero teniendo las demás notas comunes en el acorde que inicia la nueva
tonalidad. No obstante, para que el método modulatorio fuera válido no tendría por qué ser
así, bastaría con que una nota cromatizase, no sería necesario que las demás fueran comunes
entre los dos acordes que van a protagonizar el cambio de tono. Es obvio que si no se busca que
haya notas comunes, el proceso, aunque probablemente más abrupto y siendo menos evidente
el o los cormatismos que se hayan producido, será mucho más sencillo. Como observación que
pueda servir de ayuda, mencionaremos el hecho de que, por lo general, cuando se procede
de una tonalidad con alteraciones en menos (o sea con bemoles) -como es nuestro caso, Lab
menor, que tiene siete bemoles- o lo que sería lo mismo, de una tonalidad situada más a la
izquierda en el círculo de quintas hacia una que está más a la derecha del círculo de quintas,
con menos alteraciones en menos o incluso con alteraciones en más (o sea, con sostenidos) como nos pasa ahora, ya que recordemos que Sol Mayor tiene un sostenido-, proporcionalmente
a la distancia que las separe en el círculo de quintas, encontraremos más posibilidades de
cromatismos ascendentes que descendentes -en nuestro caso, siendo ocho las diferencias en más
(1 - (-7) = 8), no hay ninguna posibilidad de cromatismo descendente, como veremos, todos son
ascendentes-; sin embargo, si procediéramos al contrario, desde una tonalidad más a la derecha
hacia una que está más a la izquierda (con más alteraciones en menos o, lo que es igual, menos
en más), obtendríamos el caso contrario, una casuística mayor de posibilidades de cromatismo
descendente que ascendente, para efectuar la modulación, proporcional al grado de separación
que tuvieran las tonalidades entre sí.
Para comparar los árboles habría que observar que una nota que está en el árbol de partida
(ej. la b ) -que para aumentar el efecto sería preferible, pero no imprescindible- que no apareciera
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
141
en la tonalidad de llegada-, al cromatizar describiendo un intervalo de unísono aumentado (siguiendo el ej., a la natural) se convierta en una nota que, con ese nombre, sólo pueda explicarse
en la tonalidad de llegada; en el caso de que la nota resultante tras el cromatismo tuviera algún
sonido enarmónico en la tonalidad de partida (en nuestro ej. sería si bb ), habría que comprobar
que en el acorde en que apareciera no pudiera explicarse leyéndola con su nomenclatura enarmónica de la tonalidad de partida (continuando el ej., si el acorde en la tonalidad de llegada
estuviera constituido por fa# , la, do y mi; sería imposible reinterpretar el la como un si bb24 ). En
cualquier caso, esto se podrá ver con detenimiento en los siguientes apartados en los que se lleva
a la práctica, en sus cuatro casos de comparación, cómo podría realizarse una modulación por
cromatismo entre las dos tonalidades que hemos venido trabajando con los otros dos métodos:
Lab menor, como tono de partida, y Sol Mayor, como tonalidad de llegada.
Merece, asimismo, la pena comentar que para este tipo de modulación es -aún más claramente que podría serlo en los anteriores tipos de modulación- preferible usar los árboles,
no en su versión completa -que contaba con las notas alteradas- sino en el estado intermedio
(recordemos lo que explicábamos al respecto de los estados de los árboles armónicos en la página 33), ya que la aparición de las notas alteradas en los árboles, para los usos cromáticos
va a ser absolutamente innecesaria y va a dificultar bastante la lectura y comparación de los
mismos. No obstante, en las páginas siguientes utilizaremos los árboles completos para que se
tengan presentes todas las posibilidades y con una finalidad de continuidad con respecto a las
explicaciones dadas hasta ahora.
6.3.5.1.
Comparación de los árboles de Dominante entre sí (Caso 1: D1 ~D2 )
Para la obtención de la intersección de estos dos árboles se ha seguido el proceso que se
ilustraba en la página 117.
Aunque quedaría comprobar si leyendo enarmonizado -según las posibilidades de la tonalidad de partidauno o varios de los otros sonidos, sí fuera posible explicar el acorde, ya que entonces este cromatismo no sería
válido como medio modulatorio.
24
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida,
recuadrando los enarmónicos y señalando los
cromatizables.
142
Sonidos comunes en el árbol de llegada
eliminando los no homónimos y señalando los
cromatizados.
Figura 6.3.14: Superposición de Árboles de Dominante sin sensibles comunes
1. Nuestro primer movimiento ha de ser hacia la comprobación de que las sensibles de las
dos dominantes (o, en su defecto, las subtónicas) estén presentes como nota común o sean
alcanzables por cromatismo, en el árbol de la otra tonalidad. Consecuentemente, vemos
que el sol (sensible de Lab menor) no aparece en el árbol de Dominante de Sol Mayor y
que, en tanto no hay ningún sonido con el nombre sol en dicho árbol, porque es su nota
tónica, tampoco será factible conseguirlo mediante cromatismo. Atendemos entonces a la
posibilidad de contar con la subtónica de Lab menor en puesto de la sensible y formar
acordes del área de la subdominante, pero esto tampoco será posible dado que el sonido
solb es enarmónico y no es nota común25 , así que el resultado de esta primera comparación,
Como bien sabemos, en la modulación cromática podemos utilizar notas comunes y notas que cromaticen y
con este proceso, tengan sentido en la nueva tonalidad; no podemos en ningún caso utilizar sonidos enarmónicos,
25
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
143
dado que no se puede lograr la nota sensible del árbol de Dominante de la tonalidad de
partida, es que no existe ninguna posibilidad.
6.3.5.2.
Comparación del árbol de subdominante-tónica de la tonalidad de partida
con el de Dominante de la de llegada (Caso 2: st1 ~D2 )
El gráfico resultante de la superposición de los dos árboles sobre el Espiropentagrama, es
consecuencia del proceso que veíamos en la página 119.
Sonidos comunes en el árbol de partida
recuadrando los enarmónicos y señalando los
cromatizables.
Sonidos comunes en el árbol de llegada
eliminando los enarmónicos y selañando los
cromatizados.
Figura 6.3.15: Superposición de Árboles de subdominante-tónica y de Dominante y extracción
de resultados
1. La primera tarea será comprobar la posibilidad de contar con la sensible de la tonalidad
por eso es conveniente identificar cuáles son para evitar cualquier confunsión inconveniente.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
144
de llegada (la nota fa# ) partiendo del árbol de subdominante-tónica de Lab menor. Como podemos ver fa# puede entenderse como nota común en Lab menor, como una nota
alterada ascendente, sin embargo, dado que este sonido alterado no es en absoluto significativo dentro de la tonalidad, será más apropiado ver su acceso como cromatismo de la
nota fa natural. Así que sí, podemos contar con la sensible de Sol Mayor en el árbol de
la tonalidad de partida, como consecuencia de utilizar un cromatismo.
2. Vemos ahora el resto de sonidos comunes y cromatizables que vamos a poder utilizar,
distinguiendo especialmente aquellos que sean enarmónicos para proceder a su descuento.
Como sonidos comunes tendríamos, mayormente, tres notas: re, mib y sib . Aparte de
estos tres, vemos en los árboles de resultados que también habría otros tres sonidos que
también son comunes pero que eran notas alteradas en la tonalidad de partida, con lo
que difícilmente serán aceptables como comunes, éstos son las notas fa# -que de seguro
no usaremos-, la y do; sucede que, precisamente, como notas susceptibles de cromatizar
tenemos a estas tres, el lab que ascendiendo puede convertirse en la natural y el dob que,
aun siendo un sonido enarmonizable, también puede transformarse en do natural -que
como nota alterada ascendente no podemos considerar que impida la inteligibilidad del
cromatismo- y pertenecer a Sol Mayor; sin olvidar el caso del imprescindible cromatismo
de fa natural en Lab menor hacia fa# en Sol Mayor. Eliminamos de nuestra lista de
posibilidades por ser exclusivamente enarmónicos y no poderse tampoco utilizar para ser
cromatizados serían los sonidos nombrados en la tonalidad de partida como: rebb , mibb ,
fab y sibb ; mientras en la de llegada se eliminaría únicamente el la# . Por otra parte, no
podemos olvidar la posibilidad de mantener el fa natural como nota común y construir
acordes propios del área de la Subdominante de Sol Mayor (o sea, Do Mayor), aunque
ésta sea una posibilidad menos directa y definitoria.
3. A continuación, teniendo en cuenta que habría que usarse, como mínimo, una nota que
cromatizase para que sea posible adscribir el proceso modulatorio a la categoría de modulación por cromatismo -algo que en realidad será inevitable en este caso de comparación
dado que es mediante cromatismo como obtenemos la nota imprescindible para la Dominante de la tonalidad de llegada, fa# - y que en los acordes resultantes esté la nota sensible
de Sol Mayor, llegaríamos como conclusión a la siguiente lista de acordes:
145
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes y cromatizados que aparecen
re, fa # , la
re, fa# , lab
fa# , la, do
fa# , lab , do
sib , re, fa#
si, re, fa#
re, fa# , la, do
re, fa# , lab , do
fa# , la, do, mib
fa# , la, do, mi
fa, la, do
fa, lab , do
fa, la, do, mi
fa, lab , do, mib
si, re, fa, lab
si, re, fa, la
Lab m
VIIV
VIIV
VI<
VI<
II<
II<
t
DDv
t
DDv−3
VI<
7
VI<
7
VI<
VI<
VI<
7
VI<
7
II<
7
II<
7
Sol M
D
D−5
VII
VII−3
D’v (= III’)
Dv (= III)
D7
D7−5
s
Dv
T
D7
SS
SS’
SS7
SS’7
s
DSv
S
DS7
Cuadro 6.9: Acordes posibles para la modulación por cromatismo entre el árbol de subdominante
tónica de partida y el de Dominante de llegada
4. Por último, de entre la lista de acordes que hemos realizado, debemos chequear que todos
sean realmente válidos y no haya acordes que, por su lejanía o nivel de abstracción teórica,
supongan una imprudencia. De este modo, parece que los acordes que al cromatizar
alcanzan a ser Subdominantes de la Subdominante -y aún más los que son resultado de
préstamos de la subdominante menor- o Dominantes de la Subdominante, parece algo
bastante lejano, sobre todo teniendo una oferta de acordes tan amplia anterior, que sería
válida por completo, y que va a producir soluciones mucho más admisibles tanto por la
ortodoxia armónica, como para la coherencia del discurso.
6.3.5.3.
Comparación del árbol de Dominante de la tonalidad de partida con el
de Subdominante-Tónica de la de llegada (Caso 3: D1 ~ST2 )
La imagen del Espiropentagrama que nos muestra a continuación, la resulta de la superposición del árbol de Dominante de Lab menor y el de Subdominante-Tónica de Sol Mayor, estaba
desglosada en la figura 6.3.4 en la página 120.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida
recuadrando los enarmónicos y señalando los
cromatizables.
146
Sonidos comunes en el árbol de llegada
recuadrando los enarmónicos y señalando los
cromatizados.
Figura 6.3.16: Superposición de Árboles de Dominante y de Subdominante-Tónica y extracción
de resultados
1. Lo primero, como hemos hecho hasta ahora, sería comprobar si la sensible de Lab menor
(sol), tonalidad de partida, aparece en el árbol de Subdominante-Tónica de Sol Mayor.
Como se puede apreciar sí está y es una nota común.
2. Pasamos ahora a enumerar los sonidos que son comunes y los que se van a poder utilizar
en un cromatismo. Los sonidos comunes serían: mib , sol, sib y reb . Los que podrían cromatizar en la tonalidad de origen y sus respectivos resultados tras el cromatismo, serían los
siguientes: dob pasa a ser do natural -en Sol Mayor-, reb pasa a ser re natural, mib pasa a
mi natural, sol podría pasar a ser sol# -pero que siendo una nota alterada ascendente- y
sib que pasa a si natural. No podría utilizarse ninguno de los sonidos que únicamente son
147
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
enarmónicos, éstos son sibb y fab (en Lab menor) por una parte, y por otra (en Sol Mayor)
tendríamos la, la# y do# .
3. Una vez hecha la relación de sonidos participantes, sería el momento de hacer la lista de
acordes posibles que cumplan las condiciones de tener la nota sol (sensible del árbol de
Dominante de la tonalidad de partida), notas comunes y/o notas susceptibles de participar
del proceso de cromatismo.
Sonidos comunes y cromatizados que aparecen
sol, si, re
mi, sol, si
do, mi, sol
sol, sib , re
mi, sol, sib
do, mib , sol
mi, sol, si, re
mib , sol, sib , re
mi, sol, sib , re
do, mi, sol, si
do, mib , sol, sib
Lab m
VII
D
Dv (= III)
VII
D
Dv
D7
D7
D7
III7
III7
Sol M
T
VI
S
T’
VI’<
S’
VI7
VI’7
VI’< 7
S7
S’7
Cuadro 6.10: Acordes posibles para la modulación por cromatismo, entre el árbol de Dominante
de partida y el de Subdominante-Tónica del de llegada
4. Ahora seleccionamos dentro de ese corpus, aquellos que sí que son verdaderamente aceptables y válidos, distinguiéndolos de los que son apenas una entelequia teórica. Éste sería
el caso de, por ejemplo el III7 , que en Lab menor será harto improbable que se dé en un
discurso armónico normal, así que eliminaríamos las dos últimas opciones ofrecidas en
el cuadro. De forma similar, sucede con la tónica menor de Sol Mayor, que aunque es
posible que se dé circunstancialmente, a lo largo de un fragmento en esta tonalidad, no
es desde luego el método más oportuno para entrar en ella. Otro acorde que parece poco
recomendable, del elenco que hemos conseguido, sería el que en Sol Mayor veíamos como
VI’< , ya que es un acorde prestado del menor que presenta la tercera (el sib ) propia de
este modo y es contraproducente para realizar movimientos que apunten a la tonalidad
mayor; así también sucedería con el VI’7 , el VI’< 7 y el S’7 .
6.3.5.4.
Comparación de los árboles de Subdominante-Tónica entre sí (Caso 4:
st1 ~ST2 )
El proceso de superposición de la proyección de los árboles de Subdominante-Tónica de Lab
menor y Sol Mayor, sigue los pasos que se desarrollaban en la ilustración 6.3.5 en la página 121,
en la siguiente figura podemos observar su resultado.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Sonidos comunes en el árbol de partida,
recuadrando los enarmónicos y señalando los
cromatizables.
148
Sonidos comunes en el árbol de llegada,
recuadrando los enarmónicos y señalando los
cromatizados.
Figura 6.3.17: Superposición de Árboles de Subdominante-Tónica y extracción de resultados
1. Ya que sólo se están comparando árboles de subdominante y no hay que preocuparse
de la presencia de sensible alguna, comenzamos la catalogación de los sonidos que son
comunes: reb26 , re, mib , lab , la y sib , y la de aquellos que pueden obtenerse por cromatismo:
si (viniendo de un sib en la tonalidad de partida), do (procedente de un dob ), mi (antes
mib ) y la natural (que era lab en Lab menor). De esta forma, también quedaría descartar
los sonidos que son comunes pero no homónimos, o sea, los enarmónicos que leeríamos
como la# , mi# y sol# en la tonalidad de llegada; mientras que en la tonalidad de partida
De la misma forma que ya hemos observado en otros tipos de modulacion, comparando los árboles de
subdominante de estos dos tonos, volvemos a señalar cómo este sonido, el reb , al ser una nota que en Sol Mayor
será una nota alterada descendente y no existir el sonido sol, que le serviría para poder ejercer el papel de quinta
alterada, será muy difícil construir un acorde que lo use y que no sea un tanto complejo como para que sirva
para definir con solvencia una entrada en la nueva tonalidad.
26
149
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
tendríamos que anular los sonidos: rebb , fab , fa y mibb .
2. La lista de los acordes posibles, que como recordamos deberían contar con algún sonido
cromatizado o cromatizable, quedaría entonces de la siguiente forma:
Sonidos comunes y cromatizados que aparecen
lab , do, mib
la, do, mib
la, do, mi
do, mib , (sol)
do, mi, (sol)
do, mib , (sol), sib
do, mi, (sol), si
Lab m
t
t
t
IIIx5
IIIx5
IIIx57
IIIx57
Sol M
Sn
II’
II
S’x5
Sx5
S’x57
Sx57
Cuadro 6.11: Acordes posibles para la modulación por cromatismo, obtenidos de la intersección
de los árboles de Subdominante-Tónica
3. Finalmente, restringimos los acordes posibles únicamente a los verdaderamente comprensibles y con suficiente valor como para servir como punto de inflexión (especialmente, el
de llegada). Así, de modo similar a como hiciéramos en el caso comparativo de inmediatamente antes, parece conveniente no entrar en la tonalidad de Sol Mayor, utilizando un
acorde prestado que utilice la nota mediante del modo menor, dado que podría revertir en
confusión; con esto, dejaríamos de considerar la S’x57 que aparece. Igualmente complicada
sería la tarea de no realizar octavas cuando se trabaja a cuatro voces y en un acorde sin
quinta, las dos notas que aparecen, cromatizan, me estoy refiriendo a la Sx5 en Sol Mayor,
que sería imposible alcanzarla sin fallos, salvo que se silenciara dos de las cuatro voces.
6.3.6.
Utilización de los resultados y proceso de asimilación
Como hemos podido apreciar, el proceso de análisis de las posibilidades modulatorias entre
dos tonalidades haciendo uso del Espiropentagrama, es sin lugar a dudas, dinámico, sistemático
y exhaustivo27 , sin embargo, aunque familiarizados con este proceso, la comprobación de todas
las posibilidades -sobretodo si requieren su listado por escrito- será algo larga y tediosa. En
cualquier caso, con una finalidad eminentemente didáctica, sí es recomendable que un alumnado
que esté iniciándose en este tipo de procesos sea capaz de hallar todos los medios de modulación
con el máximo grado de detalle y, más que ninguna otra cosa, que pruebe cada uno de los
resultados que haya obtenido para ir asimilando (y memorizando) esa sonoridad en ese contexto
y poder elegir, de acuerdo al critetio acústico, la opción que se estime más conveniente.
Es dinámico porque permite adaptar los criterios de búsqueda de las posibilidades modulatorias en función
de lo que el observador requiera o crea conveniente; es sistemático porque de forma ordenada aporta toda una
organizada lista de resultados y es exhaustivo porque abarca completamente todas las posibilidades existentes
de acuerdo a las directrices que se hayan tomado de partida.
27
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
150
Ahora bien, todo este proceso no sería apenas gratificante si hubiese que hacerlo cada vez,
manualmente, aún contando con la ayuda del Espiropentagrama; por ello se está trabajando
ya, mientras se escriben estas líneas, en la elaboración de aplicaciones informáticas que puedan
resolver estos quehaceres algo anodinos (aunque de cuantioso valor para desarrollar el pensamiento y la lógica de la armonía en la mente del estudiante) de manera más cómoda y rápida. Y
más allá de esta muletilla -que esperemos pronto pueda estar acabada y ser de tanta utilidad como se desea- que la tecnología actual nos ofrece, en realidad, la vocación de todos estos procesos
es que cuando el alumno de enseñanzas artísticas musicales se enfrente a los procesos modulatorios -cuando menos en las Enseñanzas Profesionales de éstas y con mayor profundidad en las
Enseñanzas Superiores-, no necesite ningún utensilio más que el propio Espiropentagrama. Esto
es, no requiera transcribir para detallar los resultados de cada caso ni tampoco requiera de un
instrumento polifónico como el piano para tener clara su sonoridad. La idea es que el alumno,
con sólo ver el resultado de la superposición de los dos árboles que esté comparando, “vea” las
figuras de los acordes que son posibles e incluso, una vez viéndolas, sea capaz de imaginar su
sonoridad. Para ilustrar lo que intento decir, retomemos a modo de ejemplo el caso 3 (D1 ≡ST2 )
de modulación enarmónica que veíamos en el subapartado 6.3.4.3 en la página 136. Un alumno
formado en el código simbólico que aquí estamos explicando, cuando viera la imagen de superposición de los dos árboles, ayudado por las marcas de presencia, sería capaz de unir los
vértices comunes (teniendo en cuenta que siempre un vértice ha de ser el sonido sol, sensible de
la tonalidad de partida) e ir formando mentalmente las figuras poligonales que reconoce y por
tanto, elaborando una lista instantánea de las posibilidades que esa superposición le aporta; el
concepto de cómo procedería mentalmente queda ilustrado con los polígonos explicitados con
diferentes colores en la figura 6.3.18 que vemos a continuación.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
151
Figura 6.3.18: Superposición de dos árboles explicitando las figuras poligonales posibles
No creo que pueda contradecirse que es mucho más sencillo y casi lúdico, encontrar y
reconocer las figuras poligonales posibles utilizando los vértices comunes y que tengan un vértice
obligado, que ir viendo sonido por sonido, enarmonía por enarmonía. Además, no solamente
se le ha de reconocer la facilidad a este método visual, sino que también es más seguro y más
preciso28 , puesto que no supone confusión a la hora de interpretar sonidos o enarmonizarlos,
por eso, en definitiva, es hacia la que se ha de tender, por su practicidad y consistencia, de
educar a los alumnos de música en ella, desde sus etapas incipientes.
Hasta tal punto puedo afirmar que esta manera de resolución visual es útil, que concretamente elaborando
el ejemplo de la figura 6.3.18 he avistado un acorde que no había recogido en una primera redacción del
proceso escrito del subapartado 6.3.4.3 en la página 136; un acorde tan productivo como el séptima disminuida
(visualmente tan fácil de reconocer) que aparece entre las notas do# -mi-sol-sib , me había pasado desapercibido.
De esta forma decidí mantener el error para demostrar cómo la propuesta principal de este trabajo, consistente
en la adscripción de figuras geométricas a las sonoridades puede ser ya útil ahora para cualquiera y, sobre todo,
invitar a imaginar cuánto podría aportarle al alumnado si se consigue asimilar con un trabajo pedagógicamente
bien orientado, desde las etapas incipientes de la instrucción musical.
28
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
6.4.
152
La set-theory (teoría de conjuntos)
La set-theory no es lo mismo que el serialismo, pero ambos comparten muchos métodos e
ideas. La set-theory enlaza la noción de definir conjuntos de sonidos y de organizar la música
alrededor de estos conjuntos y sus varias manipulaciones. El análisis de las clases de conjuntos
(set classes) se refiere a los esfuerzos de los teóricos musicales por revelar los sistemas que
compositores como Schoenberg y sus seguidores usaron para organizar el contenido sonoro
de sus trabajos. Esto no debemos olvidarlo, los conjuntos y las clases de conjuntos determinan
únicamente un contenido de aturas, los compositores eran libres de establecer los demás aspectos
de la música de acuerdo a sus deseos artísticos (como mínimo hasta que el ultra-serialismo, una
filosofía que sometía todos los aspectos de la música a las técnicas seriales, alcanzara su máximo
explendor en torno a la década de 1950).
Un de conjunto de sonidos (pitch class set) es simplemete un grupo desordednado de alturas
sonoras. Los 12 sonidos del teclado, o clases de alturas, se numeran desde el 0 hasta el 11,
empezando en el do. Por ejemplo, un conjunto de sonidos (pitch class set) consistente en las
notas do, mi y sol se reescribiría como (0,4,7). Los compositores tratan los conjuntos con
cuantiosa y variada libertad, cuando aplican el método de los conjuntos de sonidos a su música
atonal. El conjunto (0,1,6) que fue tan popular entre Schoenberg y sus discípulos se ha acabado
llamando “el tríada vienés”.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
153
Figura 6.4.1: El tríada vienés
6.4.1.
La inversión de conjuntos de sonidos
El proceso y por tanto, sus resultados, son exactamente iguales a los ya descritos anteriormente en este mismo capítulo, en el apartado 6.2.2 en la página 110.
6.4.2.
La Forma Normal (Normal From)
Los conjuntos de sonidos se pueden sintetizar en su Forma Normal, que es una disposición
de los sonidos a una forma que podríamos llamar la más “compacta”. La disposición compacta
significa que el mayor de los intervalos entre dos sonidos consecutivos que aparece, se sitúa
como si estos dos sonidos fueran el primero y el último del conjunto. Así, si observáramos un
conjunto de sonidos representado sobre la esfera de un reloj, la forma normal sería la que leyendo
el conjunto en sentido de las agujas del reloj, recorriera la menor distancia de la circunferencia.
Por ejemplo, dado el conjunto (2,9,10), puede obserfarse en la figura 6.4.2 de más abajo,
para colocarlo en su Forma Normal, el intervalo entre 2 y 9 (7 semitonos de separación) que
es más grande que el que separa los sonidos 9 y 10 (1 solo semitono) y que entre 10 y 2 (4
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
154
semitonos), debería estar reflejado entre los sonidos primero y último nombrados, o sea, (9, 10,
2). Esta es la disposición en la que el intervalo mayor está “en la parte exterior”.
Figura 6.4.2: Conjunto (9,10,2)
Si no pudiera identificarse un intervalo como mayor, entonces la Forma Normal correspondería a la representación del conjunto que quede más “encajada a la izquerda”, es decir, aquella en
la que los intervalos más pequeños estén más próximos al principio del conjunto y los mayores
más cercanos a su final. Por ejemplo, el conjunto (0,2,3,7) está más ajustado a la izquierda que
(0,4,5,7) (Cf. fig. 6.4.3) porque su intervalo más grande está “en el interior” de (0,2,3,7) entre
los sonidos 3 y 7 (o “a la derecha”); mientras que el intervalo máyor de la parte interior de
(0,4,5,7) está entre el 0 y 4, más bien, cercano a la izquierda. Ambos conjuntos están en Forma
Normal, pero el primero está “más ajustado a la izquierda”.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
155
Figura 6.4.3: Conjuntos (0,2,3,7) y (0,4,5,7)
6.4.3.
La Forma Orignal (Prime Form)
Una vez hemos obtenido la Forma Normal de un conjunto y la de su inversión, la Forma
Original sería aquella de estas dos que esté más comprimida, transportada para empezar en
cero.
Por ejemplo, tomado un conjunto (7,8,2,5) que podríamos llamar A, vamos a ver cómo
podemos calcular su Forma Original.
1. La Forma Normal de A sería (2, 5, 7, 8)
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Figura 6.4.4: Acorde A (2, 5, 7, 8)
2. Su inversión sería (4, 5, 7, 10)
156
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Figura 6.4.5: Acorde A invertido (4, 5, 7, 10)
3. Su Forma Original (Prime Form) sería (0, 1, 3, 6)
157
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
158
Figura 6.4.6: El Acorde A en su Prime Form (0, 1, 3, 6)
6.4.3.1.
¿De qué sirve la Forma Original?
La Forma Original es una abstracción de conjuntos que nos da una representación única de
un grupo particular de notas. Si dos conjuntos tienen la misma Forma Original, podemos asegurar que sonarán similar el uno al otro. Los conjuntos con la misma Forma Original contienen
el mismo número de notas y los mismos intervalos entre ellas, por lo tanto son auditivamente
“equivalentes”, del mismo modo que todos los acordes mayores lo son entre sí, en el ámbito de
la música tonal.
Las representaciones de la Forma Original también reciben el nombre de “clases de conjuntos” (Set classes). Conjuntos que tienen idénticas formas originales se dice que pertenecen a la
misma clase. Por ejemplo, los conjuntos de sonidos (1,2,7), (8,2,3) y (0,11,6) pertenecen todos
a la clase (0,1,6).
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
6.5.
159
Los mapas armónicos
Esta aplicación del Espiropentagrama, que en realidad no atendería a su forma habitual,
sino que mostraría únicamente la circunferencia interior, habitualmente oculta, y sobre ella
las formas poligonales explícitas de determinados conjuntos de sonidos, indicaría segmentando
mediante diferentes colores29 la circunferencia -tal y como si fuera un gráfico de porcentajes en
forma de anillo-, la proporción de presencia que determinados conjuntos de sonidos -que estarían
representados como polígonos circunscritos con colores que los conectarían con dichos segmentos
de la circunferencia- tienen en un determinado pasaje o pieza. Ahora bien, aunque esto podría
concretarse de diferentes maneras según los intereses de cada estudio, aquí, en nuestros mapas
armónicos indicaremos los tres acordes que más aparecen y qué proporción del total del pasaje
o pieza, representan (en caso de haber una paridad entre varios acordes, si fuera en el índice de
mayor aparición o en el de segunda mayor aparición, lo repartiríamos de forma que estuvieran
los tres que más aparecen; y si fuera en el tercer lugar de nuestro ranking, escogeríamos el
de mayor trascendencia dentro de la pieza). Además, para completar la información aportada,
también se mostrará el acorde de mayor grado de disonancia30 que suena en el fragmento o
pieza (en caso de, por ejemplo, existir varios acordes de séptima disminuida, escogeríamos el
que apunte a un tono más lejano de la tonalidad principal).
Veamos este complicado proceso sobre un ejemplo práctico tomando el coral nº 20: “Ein
feste Burg ist unser Gott”, de J. S. Bach (fig. 6.5.1 en la página siguiente).
Según podemos apreciar, la partitura muestra ya un análisis de los grados que participan a
lo largo de la misma. Un desglose de los mismos respondería a la siguiente tabla:
Acorde
I
V
VI
IV
(V)V
III
VII6
II
(V)II
(VII)VI
(VII)II
Veces que aparece
11
8
6
5
4
4
2
2
2
1
1
Cuadro 6.12: Acordes presentes en el Coral nº 20 de J. S. Bach
Comprobamos de esta forma que hay 46 acordes en total, de los cuales el I aparece once
Estos colores, como es lógico, tendrán su correlación con lo explicado en este trabajo, en el apartado 5.5
titulado “El color como marca funcional” en la página 100.
30
Recordemos lo que comentábamos a este respecto, señalando el área de la representación poligonal de una
sonoridad como indicativo de su grado de disonancia, en el apartado 5.1.4 en la página 62.
29
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Figura 6.5.1: Coral nº 20: “Ein feste Burg ist unser Gott” de J. S. Bach
160
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
161
veces, el V sólo ocho y el VI seis. Así, a nivel estadístico podríamos decir que el I aparece casi
un 24 %, el V un 17 % y el VI un 13 %; si contamos los tres juntos vemos que suman casi el
54 % de los acordes de este coral. Al mismo tiempo, podemos comprobar Esta proporción es lo
que se indica con la segmentación de colores de la circunferencia en la siguiente figura 6.5.2:
Figura 6.5.2: Representación de las proporciones de aparición de acordes
Y finalmente, para simplificar y no requerir de leyenda alguna, así como para aportar al
observador el tipo y características (según se deducen de su morfología poligonal) de los acordes
más habituales de la pieza, se indican estos tres acordes encuadrados según correspondería a su
representación en el círculo cromático o la circunferencia interior del espiropentagrama -donde
do, si viéramos su posición como en un reloj, tendría la posición de las 12; si, a las 11; re,
las 2, etc.-. También, dibujado mediante una línea doble de puntos, se muestra el acorde más
disonante de la pieza, el (VII)II31 . De esta forma, podemos concluir que el mapa armónico de la
pieza quedaría expresado con la figura 6.5.3 que vemos a continuación en su forma policrómica
y en una versión en escala de grises32 :
Así como explicábamos al final del primer párrafo de este apartado, habiendo dos acordes disminuidos
ejerciendo su papel de dominantes secundarias, escogemos el del II (una alteración menos) por ser un tono más
lejano que el VI, que es el relativo menor y comparte las mismas alteraciones.
32
La idea es que, convertido el gráfico a escala de grises, sea más cómoda su distribución reprográfica y puedan
seguirse reconociendo las correspondencias entre los polígonos y su índice de participación, indicado como en la
versión en color, por cada segmento de circunferencia.
31
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
162
Figura 6.5.3: Mapa armónico del coral nº 20 de J. S. Bach (en color y en blanco y negro)
Finalmente, la idea sería adjuntar este esquema simbólico -probablemente, por comodidad,
en su versión en escala de grises- en las piezas revisadas, para así agilizar la comparación y la
deducción de sus características. De este modo podíamos observarlo en una versión monocrómica, en la esquina superior derecha de la partitura de este coral, que veíamos en la figura 6.5.1
en la página 160.
6.5.1.
Comparación de mapas armónicos
Es indudable que la finalidad principal de esta utilidad del Espiropentagrama es poder
comparar diversas piezas (o incluso autores o estilos, si estuvieran ya sintetizados) de forma
rápida y sencilla, para poder, de esta forma, obtener conclusiones de índole armónica sobre
la evolución de un autor, o el carácter contrastante de dos pasajes, sustentándose siempre en
hechos objetivos y estadísticos, y no en vagas apreciaciones con mayor o menor fundamento.
De esta forma, vamos a comparar el Coral nº 20 “Ein Feste Burg ist unser Gott” de J.
S. Bach, que tomamos como ejemplo en el apartado anterior, con el Walze op. 18 nº 2 de F.
Schubert. Podemos ver la partitura, con los grados ya indicados, en la figura 6.5.4 en la página
siguiente.
Así, obtenemos la tabla mostrada en el cuadro 6.13, en que se indica los acordes que aparecen
y el número de veces que lo hacen.
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Figura 6.5.4: Walze op. 18 nº 2 de F. Schubert
163
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
Acorde
I
V
IV
V7
II
III
VII6
VI
(V7)III
(V7)VI
(V7)V
(VIIº)II
164
Veces que aparece
9
3
2
2
2
2
2
1
1
1
1
1
Cuadro 6.13: Acordes presentes en el Walze op. 18 nº 2 de F. Schubert
Concluimos pues que, de 25 acordes en total que hay en este vals, nueve veces aparece el I,
tres el V y dos el IV, el V con 7ª, el II y el III -escogeremos el IV para nuestro mapa armónico
de esta pieza, por ser el de mayor trascendencia armónica-. De esta forma, si convirtiéramos
estos índices de aparición en porcentajes, nos encontraríamos con que el I tiene una presencia
de un 36 %, el V un 12 % y tanto IV como V con 7ª como II como III estarían igualados con un
8 %. Por otro lado, el acorde más disonante del conjunto, parece evidente que es una dominante
secundaria, el acorde de séptima disminuida del II, que aparece en el compás 21 (véase partitura
en la página anterior). El mapa armónico de esta pieza podemos verlo en la siguiente figura
6.5.5, en las dos versiones, la policrómica y la de escala de grises (que se mostraba ya en la
esquina superior derecha de la partitura ofrecida anteriormente).
Figura 6.5.5: Mapa armónico del Walze op. 18 nº 2 de F. Schubert (en color y en blanco y
negro)
Si ahora procedemos a comparar los dos mapas armónicos (el del Coral nº 20 de J. S. Bach
CAPÍTULO 6. APLICACIONES DEL ESPIROPENTAGRAMA
165
y el de este vals) como se muestra en la figura 6.5.6 que vemos a continuación, podemos obtener
varias conclusiones:
Coral nº 20 de J. S. Bach
Walze op. 18, nº 2 de F. Schubert
Figura 6.5.6: Comparación de dos mapas armónicos
Ambas son obras de marcada influencia tonal y de notable simplicidad armónica. En el
caso del segundo mapa, dada la presencia mayoritaria del I, IV y V, tríadas, podríamos
pensar que con probabilidad pertenece al Clasicismo33 .
Predominancia de acordes tríadas en ambos casos, si bien, observando el mapa de la
izquierda podemos deducir que no hay ningún cuatríada, ya que el acorde más disonante
es un tríada disminuido.
La pieza representada por el mapa de la izquierda es más tendente a la variedad de sonoridades, puesto que los tres acordes mayoritarios tienen una presencia bastante equiparada,
a diferencia de lo que sucede en el caso de la derecha, que la tónica ocupa más de un
tercio de la pieza (como ayuda a la rápida comprensión de este detalle, hago notar que
un tercio sería desde las 12 hasta las 4). Ésta es una de las características que singulariza
al Barroco frente al Clasicismo.
La pieza de la izquierda es menos disonante en general. Los tres acordes más frecuentes,
siendo tríadas, sólo ocupan 6 de los 9 vértices posibles; e incluso contando lo aportado
al esquema por el acorde más disonante, sólo suma un vértice más. Sin embargo, en el
caso de la derecha, también tres tríadas, ocupan 7 de los 9, y el cuatríada representado,
aporta dos vértices más. Así tenemso una figura global de 7 vértices frente a una de 9, que
obviamente tendrá un área mayor (recordemos lo dicho a este respecto en el apartado 5.1.4
en la página 62, sobre el área como indicativo del nivel de disonancia de una sonoridad).
33
mo.
Como sabemos, Schubert es para muchos teóricos un punto intermedio entre el Clasicismo y el Romanticis-
Capítulo 7
Propuesta de aplicación de esta
didáctica
En este capítulo vamos a plasmar lo que podría ser un plan de actuación con el que poner
en práctica la metodología aquí esbozada. La idea de estas páginas no es, en modo alguno,
ofrecer una detallada planificación sino apenas un apunte; sin lugar a dudas, tratar de llevar a la
realidad las directrices que aquí se proponen exigiría un estudio mucho más pormenorizado y un
replanteamiento de las programaciones didácticas, e incluso quizá también la propia legislación
vigente.
Esta propuesta de aplicación es sólo un boceto elaborado tras mucha reflexión e investigación
por una sola persona; no cabe la menor duda de que, pese a su mejor intención, un equipo de
personas especialistas en los diferentes niveles educativos, así como en pedagogía y psicología,
podrían -y ojalá así suceda- realizar muchas mejoras sobre este ambicioso diseño que abarca
todos los niveles educativos en que está presente la música1 .
7.1.
En la enseñanza general
El método aquí propuesto basa sus argumentaciones en establecer conexiones entre sonoridades y formas geométricas y colores. Así, estas conexiones pueden empezarse a plantear desde
un período incluso anterior a que el niño sea capaz de reconocer con precisión ambos apartados de la realidad, con el fin de que la asimilación de la solidaridad acústico-visual de estos
elementos, se produzca con total naturalidad más adelante.
En estas páginas se contempla tanto la enseñanza general, como las enseñanzas artísticas. Ha quedado sin
tratar, sin embargo, en parcelas en los que no es materia propiamente, como la danza; ahora bien, el método de
trabajo para estas secciones de la enseñanza que hemos omitido, pueden deducirse fácilmente a partir de este
capítulo según cuál sean los contenidos tratados y la finalidad de los mismos.
1
166
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
7.1.1.
167
En el ámbito de Preescolar
Este período educacional se dirige a los niños desde los 0 hasta los 6 años y va a ser de una
enorme trascendencia para los posteriores progresos educativos. Así pues, respecto de lo que
nos concierne podemos afirmar que según los estudios de la psicología evolutiva, desde los 2 a
los 3 años de edad, el niño ya es capaz de identificar y nombrar las formas geométricas básicas
y los colores primarios y algunos de los secundarios. Sería, por lo tanto, un buen momento para
trabajar la vinculación de figuras, colores y sonoridades. No obstante, aunque es probable que
apenas pueda aspirarse a la asimilación cognitiva del niño desde sólo la vertiente sonora, de las
equivalencias visuales, no sería descabellado empezar a trabajar también hacia ese objetivo y
evaluar la evolución.
Trabajaríamos únicamente con los tres colores básicos: azul, verde y rojo; y las tres formas
básicas: triángulo, cuadrado y círculo. Tal y como se describía en los apartados correspondientes2 , estos tres colores y estas tres figuras remitirían a diferentes realidades sonoras (véase
cuadro 7.1), que, para una mayor diferenciación por parte del niño, sería recomendable que
estuvieran practicadas por timbres lo menos semejantes posible. Una sugerencia sería que cada
figura estuviera interpretada por una familia de instrumentos diferente, por ejemplo, el círculo
(el glissando) por la cuerda, el triángulo (el acorde mayor) por el viento y el cuadrado (el acorde
disminuido) por la percusión.
Las vinculaciones propuestas de las sonoridades con los colores se explicaban en el apartado 5.5 en la
página 100 y de éstas con las figuras geométricas triangulares en el apartado 5.4.1 en la página 81 y con los
cuadriláteros en el 5.4.2 en la página 86.
2
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
168
Azul
Verde
Rojo
Cuadro 7.1: Tres colores, tres figuras, tres sonoridades
Una manera de trabajar con estas formas podría ser unirlas a movimientos, a modo de
juego. Por ejemplo, colocando estas figuras, con un tamaño grande, dibujadas en el suelo y que
al reproducirse la sonoridad propia a cada representación, los niños deban ir y colocarse sobre
la figura adecuada. Otra manera de vincular las sonoridades, figuras y movimiento, sería que,
al mismo tiempo que se reproduce la sonoridad y se muestra la figura, se deba colocar el cuerpo
de una manera concreta; por ejemplo, con el azul: sentado, con el verde: andando y con el rojo:
en cuclillas.
Como otra posible aplicación de esta vinculación, no sería difícil imaginar una especie de
teclado de tres teclas, que tuvieran la formas y colores que acabamos de describir, y que remitieran al ser pulsadas, a las sonoridades previstas (de forma similar a como pueden funcionar
los botones de la mano izquierda del acordeón). El teclado contaría con una pantalla electrónica
pequeña en la que se le indicaría al niño una serie de secuencias con estas figuras, graduadas
en dificultad creciente, para que el niño las fuera realizando pulsando las teclas. Este juguete
podría ser perfectamente apto desde los 18 hasta los 36 meses.
Una versión más desarrollada para niños desde los 3 años hasta los 6, contaría con más teclas
ampliando el número de colores y repitiendo figuras con diferentes colores, o una versión de
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
169
tipo xilófono3 . De hecho no es en absoluto imposible, imaginar su aplicación en acordeones de
juguete -como los que ya hay en el mercado- que permitiera acompañar una serie de canciones
pregrabadas en el aparato o incluso, para los niños más mayores (5 y 6 años) contemplar la
posibilidad de enseñarlos a tocar una melodía con la mano derecha y a acompañarse ellos
mismos con botones con estas figuras y colores, en la izquierda. También podría plantearse la
posibilidad de usar otros instrumentos de juguete, como guitarras o teclados elementales.
7.1.2.
En el ámbito de Primaria
En este período educativo, que en nuestro país abarca desde los 6 hasta los 12 años, la música
es una disciplina que se estudia académicamente a nivel general en las escuelas de enseñanza
básica. Cierto es que en la actualidad cuenta con un presupuesto temporal semanal muy bajo4 ,
que apenas permite una introducción somera del niño a la compleja teoría y práctica musical.
7.1.2.1.
Primer ciclo
Contemplando la posibilidad de que haya habido algún tipo de formación musical en el jardín
de infancia, según se propone aquí, la idea sería que durante los primeros cursos pudiera seguir
empleándose actividades similares a las que planteábamos antes en el apartado de preescolar (
en la página 167), para vincular las sonoridades con las figuras. Va a ser muy importante que
durante esta etapa inicial de la educación del niño, se le aporte un nexo y se le introduzca en el
mundo armónico, puesto que esta iniciación va a ser fundamental para las etapas posteriores.
Una manera de continuar creando esta conexión, y reelaborando propuestas que hacíamos
antes, podría tratarse de aprender canciones sencillas con coreografías elementales, que tengan
como localización espacial el colocarse en determinada postura sobre una parte de la clase en la
que estuviera esta forma geométrica o, mejor aún, formando en grupos, creando filas que serían
los lados, estas formas geométricas (triángulo, cuadrado, círculo).
7.1.2.2.
Segundo ciclo
Siguiendo con lo que se trabajaba en el ciclo anterior, se llevarían a cabo adaptaciones de
actividades, para ofrecer una mayor variedad y continuar asentando el reconocimiento de estas
sonoridades sencillas.
Podemos observar que ya existen xilófonos de juguete que utilizan láminas de colores para niños de corta
edad, sin embargo, los colores suelen ser diferentes a los que proponemos en este método, porque atienden
únicamente a sonidos individuales y no a sonoridades de varios sonidos. Así, los colores que podemos ver en
ellos son do: rojo, re: naranja, mi: amarillo, fa: verde, sol: azul o verde oscuro, la: azul oscuro o morado, y si: lila
o rosa. Se aprecia cómo esta relación se aproxima bastante a la secuenciación que hiciera Newton, que veíamos
en el apartado 2.2 en la página 27.
4
Dado que la estipulación de los currícula educativos ya no depende de la administración estatal, sino que
queda a discreción de las administraciones autonómicas, la situación que describimos es la que nos es conocida
en la región en la que nace este trabajo, la Región de Murcia. Aquí, en el nivel de Primaria, la asignatura de
Música sólo cuenta con una hora semanal.
3
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
170
Por otra parte, dado que en esta etapa ya se hará uso con toda probabilidad de los musicogramas, podría ser de especial utilidad el insertar los dibujitos (instrumentos musicales, que
normalmente se utilizan para ir marcando las partes y/o compases) en un marco poligonal que
corresponda con lo que se está trabajando (véase fig. 7.1.1 de abajo); de este modo se estaría
indicando, aunque no tenga por qué hacerse explícito para los alumnos, el tipo de acorde y la
función que tiene, y así ir contribuyendo al asentamiento de los conceptos.
Figura 7.1.1: Elemento de musicograma enmarcado
7.1.2.3.
Tercer ciclo
En este ciclo podríamos dar ya un paso más y tratar de que traten de reconocer los grados
tonales (I, IV y V) e identificarlos con los colores básicos (azul, verde y rojo, respectivamente).
Para ello podría utilizarse canciones básicas, a ser posible que les sean cercanas al alumnado5 ,
así se logrará interesarlos y hacerles ver que puede ser útil para entender cómo se estructura el
fraseo de la música, cómo se construye la tensión y la relajación dentro de la sintaxis musical.
7.1.3.
En el ámbito de Secundaria
Esta etapa abarca, de forma obligatoria, desde los 12 hasta los 16 años, con lo que se llama la
ESO (Enseñanza Secundaria Obligatoria). Terminada esta fase educativa, el estudiante puede
escoger si seguir cursando el Bachillerato (de los 17 a los 18 años) o comenzar las enseñanzas
de índole profesional. Ésta es por lo tanto, la última parte de la enseñanza que se ofrece a
todos los escolares de nuestro país, y ha de servir, en el ámbito de las enseñanzas musicales,
para consolidar los aprendizajes y para completar el desarrollo de las habilidades y destrezas
que se iniciaban en primaria. Es por esta razón que será relevante que se continúe con la labor
armónica que se venía haciendo e incluso se evolucione dentro del mismo.
7.1.3.1.
Primer ciclo
En el primer ciclo, al menos en el entorno desde el que nace este trabajo, sólo se imparte
música en uno de los dos niveles que lo componen, después de una leve cesura de un año, que
Secuencias basadas exclusivamente en estos tres acordes son muy populares dentro del pop y el rock, y
especialmente en el conocido punk rock, así que no será difícil encontrar una canción entre este género. Como
grupo emblemático de este tipo de música habría que señalar sin dudas a “Los Ramones”.
5
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
171
puede llegar a ser fatal para la asunción de todos los conceptos y destrezas, por parte de los
jóvenes. No obstante, en este curso lo más recomendable sería intentar recuperar el nivel que
se había alcanzado en el último ciclo de primaria y dotarlo de una base teórica más fuerte que
lo fundamentara y le sirviera para darle mayor consistencia.
Quizá, si el alumnado tuviera posibilidad y la destreza suficiente, se podría ampliar el
corpus de acordes con el que se trabaja con el acorde de séptima de dominante (cf. fig. 7.2.1 en
la página 175) y algún acorde menor, como el II y el VI, con sus respectivas formas y colores
(recordemos el cuadro 5.4 en la página 102).
7.1.3.2.
Segundo ciclo
En este período, además de existir un curso en el que la música se imparte como asignatura obligatoria, se ofrecen diversas posibilidades optativas, que permitirán hacer interesantes
progresos en la práctica interpretativa y auditiva armónica. En asignaturas como “El taller de
creatividad” en el que se potenciará la expresividad instrumental y vocal del alumno, podrá
avanzarse en el sentido que propone esta didáctica si se inicia al alumnado en instrumentos
polifónicos como los teclados o la guitarra. Esto, fuera de ser muy llamativo para los estudiantes de estas edades, servirá como extraordinario acicate para llevar a la práctica el trabajo de
conexión que hemos llevado a cabo desde las primeras etapas de la enseñanza. Como propuesta
presentamos el próximo párrafo que explica una forma de usar las formas poligonales a modo
de cifrado acórdico.
El cifrado poligonal. Desde bastante antiguo en nuestra tradición, se ha buscado medios
para representar sonoridades o acordes, de forma que fuera más rápido de escribirlas y además,
no requiriera de un conocimiento profundo a su receptor, del lenguaje musical, para su ejecución.
La mayoría de estos cifrados se basaban en principios conceptuales y no buscaban la solidaridad
del signo con su atribución6 ; como ejemplo sencillo y vigente, tendríamos el extendido cifrado
americano que recoge con letras y números el tipo de sonoridad con que se debe acompañar un
fragmento de una melodía, ésta sí, escrita sobre un pentagrama. La propuesta que se lanza en
este apartado de utilizar las figuras poligonales y colores con los que se venía trabajando, según
está recogido aquí el proyecto, desde prescolar, como método de cifrado para el acompañamiento
de piezas que, instrumentos polifónicos como el teclado o la guitarra, podrían leer y servirles,
también, como método facilitado de introducción al instrumento. Podemos ver una ilustración
que refleja cómo resultaría, llevada a un caso práctico, esta propuesta de cifrado, a continuación
en la figura 7.1.2.
Una excepción destacable es el cifrado de guitarra que en sí mismo, indica la posición de qué trastes hay
que pisar sobre el mástil para reproducir el acorde.
6
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
Figura 7.1.2: Imagine, de John Lennon, en cifrado americano y poligonal
172
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
7.2.
173
Dentro de las enseñanzas artísticas
Será éste el ámbito más apropiado y con mayores posibilidades de desarrollo para aplicar
por entero, el máximo potencial que este método didáctico ofrece. Al contar con un alumnado
que va a tener una formación específica y una continuidad, se puede trabajar con los medios
aquí propuestos desde una temprana edad y con la suficiente profundidad para alcanzar unos
resultados evidentes, en estadíos de estudio más avanzados.
7.2.1.
En las Enseñanzas Elementales
En este nivel, con alumnos de una corta edad, es fácil crear estímulos y conexiones que
puedan tener una resonancia útil posterior. De este modo, pudiendo haber trabajado o estarlo
haciendo, ya en la educación general de prescolar y de primaria, con los elementos básicos,
en la asignatura de Lenguaje Musical se profundizará en éstos y se buscará desarrollar una
integración de los mismos aún más consumada, dentro del corpus teórico-conceptual adquirido
por los niños.
7.2.1.1.
Primer curso de Lenguaje Musical
En el primero los cuatro cursos, se insistirá sobre la imbricación de símbolos poligonales y
policrómicos elementales7 ; mi propuesta sería incluir progresivamente una mayor cantidad de
figuras y colores, pero para empezar partir apenas de los 3 colores básicos de los tres grados
tonales (I = azul; IV = verde y V = rojo) y el triángulo escaleno creciente propio del acorde
perfecto mayor. Así, primeramente sería un trabajo exclusivamente con colores, con la finalidad
de asentar auditivamente los tres grados principales y las funciones básicas del lenguaje tonal. En
el segundo trimestre, si ha habido una buena evolución, se añadiría un color más correspondiente
a otro grado, la supertónica (II = amarillo), junto con la figura propia del acorde menor: el
triángulo escaleno decreciente; semanas más tarde se introduiría también la submediante o
superdominante (VI = lila), que tendría la misma forma pero otro color. En el último trimestre,
se incorporaría los dos grados que faltan, primero la mediante (III = marrón) que sólo sumaría
un color más al corpus conceptual; y por último, la sensible (VII = naranja) que supondría no
sólo un nuevo color, sino también una forma nueva: el triángulo rectángulo isósceles. Con esto
habríamos introducido al alumno a todas las sonoridades tríadas propias de la escala Mayor,
siempre en discursos armónicos breves y elementales (apenas tres acordes). Sería aconsejable
que, además de vincular puramente los acordes con las figuras y colores mencionados, a la
manera tradicional de dictado, se practicara de manera lúdica con movimientos en danzas
y juegos, que pudieran servir para redundar en las características funcionales de tensión y
distensión, propias de estas sonoridades según el contexto del discurso.
Recordamos que existe una tabla ilustrativa de la representación poligonal de los tríadas de la escala Mayor
en la página 102.
7
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
174
Es probable que para el mejor reconocimiento de los acordes, sea conveniente reproducir
los acordes arpegiándolos un poco, para facilitar la escucha de todas sus notas a estos alumnos
nóveles.
7.2.1.2.
Segundo curso de Lenguaje Musical
En segudo se repasaría y profundizaría en lo aprendido en primero haciendo uso de estructuras armónicas con mayor complejidad (utilizando más de tres acordes diferentes) y longitud
(alcanzando desde el segundo trimestre, la frase de ocho compases). Si fuera posible, se añadiría
al final, en el tercer trimestre, la sonoridad de un cuatríada con una representación y sonoridad
muy características: el acorde de séptima disminuida, que en este nivel inicial, mantendría el
color naranja8 de su tríada base, pero estaría representado por una figura nueva, el cuadrado
(tratábamos este acorde en el apartado 5.4.2.7 en la página 93).
Además, dado que se empieza a iniciar a los alumnos en este curso9 en los intervalos básicos
(mayores, menores y justos) y la escala de Do Mayor y de la menor, parece que sería un
buen momento para apoyar la explicación de estos elementos de la teoría musical mediante su
proyección sobre el Espiropentagrama (que recordemos se trató en el capítulo 4 en la página 41);
un utensilio de fácil fabricación que podrán hacerse ellos mismos (aportándoles las plantillas
para que únicamente tengan que recortar) y que, probablemente, será recibido como un juguete.
Con bastante certeza será más fácil para los niños contar los intervalos como si fueran horas del
reloj, y al mismo tiempo, este mecanismo servirá como cimiento nemotécnico que les ayudará
a retener y a realizar mentalmente una visualización de la escala y de los intervalos.
7.2.1.3.
Tercer curso de Lenguaje Musical
En el siguiente curso, el tercero de grado elemental, se partiría de frases de ocho compases
con al menos cuatro acordes diferentes, y se insistiría en el manejo de las sonoridades vistas
hasta el momento, incluyendo especialmente el acorde de séptima disminuida. Una evolución
respecto del curso anterior, sería empezar a trabajar el reconocimiento de la inversión en que
están los acordes; la manera de simbolizar esto, que colaboraría sería muy sencillo mediante la
rotación de las figuras poligonales que se venía usando hasta ahora.
Si fuera posible, se distinguiría entre dos naranjas diferentes, aunque sólo a nivel visual y sin ninguna
referencia explícita para el alumnado; el naranja del tríada sería más apagado y el del cuatríada disminuido,
más brillante (como si se mezclara el naranja propio del VII con el amarillo propio del II).
9
Según he podido constatar consultando las programaciones docentes de varios conservatorios.
8
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
Estado Fundamental
1ª inversión
175
2ª inversión
Acorde Perfecto Mayor
Acorde perfecto menor
Cuadro 7.2: Representación de las inversiones de los acordes perfectos Mayor y menor
A mediados del segundo trimestre, como novedad, se comenzaría a aplicar un dictado mixto que incluyera alturas melódicas sencillas con una rítmica elemental, junto al uso de estas
sonoridades. Y en el tercero, si todo se desarrollara con éxito, se podría incorporar un nuevo
acorde, el cuatríada principal de la tonalidad: el acorde de séptima de dominante, representado
por un trapezoide10 con un ángulo recto de color rojo11 (puede verse en la fig. 7.2.1).
Figura 7.2.1: Trapezoide que representa el acorde de Dominante con séptima
Por otra parte, sería recomendable que en este curso se empezara a usar timbres diferentes
al del piano, que presumimos sea el único que se haya utilizado hasta el momento, para no
restringir su capacidad a un solo timbre y para incorporarlo también al vasto mundo de la
identificación de otros instrumentos polifónicos o de conjuntos de instrumentos, a través de la
audición.
Asimismo, continuando con el uso del Espiropentagrama que comenzamos en el curso anterior, en éste añadiríamos su propuesta como soporte para la comprensión de la transposición
de las escalas Mayores y menores, próximas, así como de intervalos más complejos (incluyendo
los aumentados y disminuidos) y la inversión12 de todos ellos. Por otro lado, colaborará en la
explicación de los conceptos de unísono cromático y diatónico, y en el de enarmonía.
Recordemos que, según nos define el DRAE, un trapezoide sería un “cuadrilátero irregular que no tiene
ningún lado paralelo a otro”.
11
En caso de poder matizarse, el rojo de este cuadrilátero sería un rojo anaranjado cercano al conocido naranja
butano, consecuencia de una visión del mismo como suma del rojo del V grado y el naranja del VII.
12
La inversión de intervalos en el Espiropentagrama es tan sencilla como contar semitonos en el sentido de
las agujas del reloj o en el contrario.
10
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
7.2.1.4.
176
Cuarto curso de Lenguaje Musical
Por último, en cuarto, el alumno debería poder hacer frente a un dictado que contara con una
melodía y un acompañamiento básico con los acordes que conoce, añadiéndose el reconocimiento
de las cadencias básicas (suspensivas o finales). Si se ve el grupo con un progreso adecuado,
podría incluirse en el segundo o tercer trimestre dos sonoridades de cuatríada nuevas: el acorde
menor con séptima menor y el acorde mayor con séptima mayor, construidas sobre el II y el
IV con 7ª, respectivamente. Su representación poligonal sería la de dos trapecios13 , tal como se
muestra en la figura 7.2.2 de abajo, el II en un color amarillo (si es posible matizar, un amarillo
oscurecido casi verde, consecuencia de la mezcla de estos dos colores que simbolizaban el II y
el IV) y el IV en verde (de nuevo, de ser posible matizar sería un verde turquesa, producto de
la mezcla de los colores respectivos del IV y el VI, el verde y el morado). Primeramente sólo en
estos dos grados cada una de ellas y de estar perfectamente asumidas, podría ampliarse hasta
completar todos los cuatríadas posibles de la escala Mayor, en el tercer trimestre. O sea, tratar
y usar también la sonoridad de perfecto menor con séptima menor sobre el III y el VII, cuyos
polígonos representativos serían el mismo trapecio que servía para el II7 , pero con diferentes
colores, el III en su marrón (ahora, si se puede escoger gama, sería un marrón rojizo) y el VI
en su color morado (en caso de poderse graduar, sería un color malva cercano al azul).
Figura 7.2.2: Representación del II y IV con 7ª de una escala Mayor
En caso de introducir al alumnado en el campo de la armonía, sería un buen momento para
hacerlo explicando las tendencias, funciones y jerarquías de la tonalidad haciendo uso, a modo de
esquema y resumen, de los árboles armónicos (de ellos hablamos en el capítulo 3 en la página 31)
en una versión elemental, ya que las grafías con que se simbolizan los diferentes papeles de cada
sonido dentro de cada sonoridad pueden ser muy útiles para su mejor comprensión.
Se evidenciará en el Espiropentagrama la motivación de las representaciones de todos los
acordes aprendidos hasta este curso y se mostrará su inclusión dentro del heptágono diatónico
de diferentes tonalidades (hasta 5 alteraciones en más y en menos).
Atendiendo a la definición aportada por el Diccionario de la RAE, un trapecio en geometría es un “cuadrilátero irregular que tiene paralelos solamente dos de sus lados”.
13
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
7.2.2.
177
En las Enseñanzas Profesionales
Este nivel educativo14 conducirá a la obtención de un título profesional de música y requerirá
de la adquisición de unas destrezas y de todo un compendio de conceptos teóricos, que el alumno
deberá poder manejar con soltura. Entre ellos, se iniciará en esta etapa de las enseñanzas
artísticas, propiamente en el mundo de la Armonía, debiendo ser capaz de reconocer (tanto
teóricamente como en la práctica) y utilizar en ejercicios de diferentes tipos, las principales
sonoridades de la ortodoxia tonal. Desde luego, éste será el momento en el que se podrá empezar
a hacer uso, verdaderamente, del núcleo fundamental del material que aquí se aporta; para ello,
los usos propuestos para la enseñanza general y el nivel elemental de las enseñanzas artísticas,
han sido apenas un preludio, una preparación para que ahora no resulte brusca y, al mismo
tiempo, pueda aprovecharse con plenitud, al tener ya asimiladas la manera de esquematizar y
las analogías de representación.
7.2.2.1.
Lenguaje musical
Esta asignatura se daría en los dos primeros cursos de las Enseñanzas Profesionales, y
teniendo en cuenta lo trabajado en el último curso de las Enseñanzas Elementales, habría de
continuar afirmando y profundizando en los contenidos armónicos que, desde estas páginas,
se proponían para ese curso, en el apartado 7.2.1.4 en la página anterior. Es decir, trabajar
con todos los acordes tríadas (perfecto Mayor y menor, disminuido) y añadir el de quinta
aumentada -que estaría representado por un triángulo equilátero, de color marrón (que si se
pudiera matizar, sería más bien marrón rojizo)- que de manera natural se da sobre el III<
del menor melódico (fig. 7.2.3); así como con los acordes cuatríadas que se habían visto hasta
ahora (séptima disminuida, Mayor con séptima menor y mayor, menor con séptima menor) y
añadiéndose uno: el de séptima de sensible, propio del VII grado del mayor -simbolizado por
un trapezoide naranja (y de poder matizarse, amarillo huevo), como podemos ver también en
la figura 7.2.3 de abajo-.
Figura 7.2.3: III< de la escala menor melódica y el VII7 propio del modo Mayor
Del mismo modo que ya se comenzaba a hacer en el último curso de las Enseñanzas Elementales, estos polígonos se harán visibles partiendo de su fundamentación en el Espiropentagrama,
El currículo de las Enseñanzas Profesionales en el que se basa este apartado es el propio de la Región de
Murcia, acorde con lo publicado en el BORM de 7 de Mayo de 2008.
14
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
178
así como se trabajará en estos dos cursos sobre él, tanto en las explicaciones como en la resolución de ejercicios propuestos para el alumnado (un ejemplo de este tipo de ejercicios propuesto
lo tenemos en la figura 7.2.4 en la página siguiente), en los que haya que deducir sonidos o
construir representaciones geométricas a partir de unos sonidos dados que bien podría servir,
para trabajar y repasar armaduras, grados y funciones de tonalidades diferentes; alcanzando
ahora sí, todos los sostenidos y bemoles posibles e incluso, las alteraciones accidentales dobles de
sostenido y bemol. Este trabajo colaborará notablemente para la interiorización y comprensión
teórica de las sonoridades con enarmonías, que de manera aislada habíamos propuesto trabajar
ya desde el tercer curso de Elemental.
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
179
Figura 7.2.4: Trabajando con las figuras derivadas de la representación en el Espiropentagrama
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
7.2.2.2.
180
Armonía
Esta asignatura aparece en nuestro currículo en los dos cursos centrales de las Enseñanzas
Profesionales, una vez concluidos los dos cursos de Lenguaje Elemental de los dos primeros
años. Es evidente que será al alcanzar esta asignatura, donde mayor provecho podrá obtenerse
de las ideas aquí expuestas, especialmente si, como aquí se sugiere, se ha venido trabajando con
los árboles armónicos desde final de las Enseñanzas Elementales, en la asignatura de Lenguaje
Musical, y si las proyecciones de sonoridades sobre el Espiropentagrama, como analogías de su
esencia sonora, están no sólo entendidas sino perfectamente incorporadas a la realidad teórica
musical del alumno. Así pues, se podrá trabajar partiendo de un conocimiento sólido de las
propiedades de las sonoridades más habituales del lenguaje tonal, tanto en su dimensión teórica
como en la acústica, y esto permitirá que el alumno maneje las realidades sonoras en sus
ejercicios de Armonía siendo plenamente consciente de cómo suenan y de sus grados de tensión,
y escogiendo conscientemente las progresiones y enlaces que quiere realizar, en función de lo
que le es permitido y lo que tiene perfectamente asimilado como producto de su bagaje musical.
La asignatura, por lo tanto, a lo largo de los dos cursos que abarca, tratará de desarrollar el
oído interno sintáctico-armónico del alumno, haciéndole comprender y valorar las progresiones y
enlaces más aconsejables u ortodoxos de nuestro sistema musical occidental en su variante tonal
de la práctica común; además, no sería inoportuno completar esta enseñanza introduciéndolo
a otras posibilidades de otros períodos históricos y de otros sistemas diferentes al tonal. Para
ello, como es lógico, se haría uso de los árboles armónicos (que veíamos en el capítulo que
dedicábamos al respecto) y así se podría ir mostrando la evolución de la Armonía tonal y
su comparación con la Armonía modal o la atonal, por citar algún ejemplo. Como es lógico,
conforme el alumno vaya aumentando sus conocimientos, sus árboles armónicos irán creciendo,
así como la figura resultante de su proyección en el Espiropentagrama.
De este modo, como ejemplo práctico y significativo de la incidencia de este material en
esta asignatura, podríamos citar una aplicación del Espiropentagrama que se explicaba en
el capítulo anterior; hablamos pues de la modulación diatónica, una forma de modular que
suele estar incluida en los contenidos del segundo curso de este nivel, y que se explicaría en
este momento haciendo uso de unos árboles armónicos sin las notas alteradas -que es como lo
hicimos nosotros-, o sea, en su estado elemental o medio15 , pero siguiendo el proceso descrito
para este tipo de modulación en el apartado 6.3.3 en la página 122.
7.2.2.3.
Análisis
Análisis se estudiará en los dos últimos cursos de los seis que integran las Enseñanzas
Profesionales, si bien el alumnado tendrá que escoger entre esta materia o Fundamentos de
Composición. La aportación que los árboles armónicos pueden hacer dentro del campo del
En caso de no entender a qué forma de los árboles armónicos nos referimos, recomendamos acudir a la
página 33 en la que se explicaba este asunto.
15
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
181
análisis es más que notable ya que, siendo una manera de esquematizar jerarquías, funciones y
tendencias de unos sonidos dentro de un conjunto, van a servir fructíferamente para resumir las
características de autores o de obras y compararlas entre sí. Podría de esa manera apreciarse, en
apenas unos escasos centímetros de papel, las conclusiones armónicas de una pieza comparadas
con el resto de la obra de un autor, o simplemente esquematizarse las cualidades de índole
armónica que sobresalen en ella.
En cualquier caso, dentro de este campo, quizá la mayor aportación que estas páginas
pueden realizar serían las que ofrecen los mapas armónicos de los que hablábamos como una de
las aplicaciones del Espiropentagrama en el apartado 6.5 en la página 159; entonces poníamos
como ejemplo los resultados de su empleo en un coral de Bach y una pieza de Schubert.
7.2.2.4.
Fundamentos de Composición
Esta asignatura, como alternativa a Análisis, se estudiará en los últimos dos cursos de las
Enseñanzas Profesionales y tratará de iniciar a los estudiantes que la elijan, en métodos compositivos elementales. De esta forma, nuevamente, los árboles armónicos y los mapas armónicos
que mencionábamos como instrumentos de utilidad de Análisis, van a ser de un destacado provecho para esta otra asignatura. Van a aportar y proponer esquemas de modelos armónicos
de los que partir para realizar por ejemplo una sonatina a la manera de Beethoven, o unas
variaciones en el estilo de Mozart.
Entre los contenidos que suele incluir esta materia, se suele incorporar la modulación cromática, que bien podría hacerse (aunque trabajando con árboles simplificados, como ya decíamos
antes) siguiendo el método de comparación de la proyección de árboles sobre el Espiropentagrama, tal y como hacíamos en el apartado 6.3.3 en la página 122.
Por otra parte, el Espiropentagrama puede colaborar a realizar análisis o mostrar propiedades de los motivos melódicos o armónicos que se escojan o a crear otras formas de composición
a partir de otros principios.
7.2.3.
En las Enseñanzas Superiores
El currículo de las Enseñanzas Superiores de música de nuestra región está aún por conformarse mientras redactamos estas páginas, tras la implantación de un nuevo plan educativo de
enseñanzas superiores por este motivo cabe la posibilidad de que lo que aquí se recoja no sea
exactamente la manera en que se desarrolle en la práctica estas enseñanzas, una vez alcancen
las aulas.
7.2.3.1.
Análisis
La asignatura de Análisis en las Enseñanzas Superiores va a ser de una enorme importancia
y va a abarcar todos los períodos de la historia de la música occidental. De esta forma, los
métodos que se describían para esta asignatura en las Enseñanzas Profesionales, en el apartado
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
182
7.2.2.3 en la página 180. Obviamente, se tratará con mayor profundidad y se intentará enseñar
al alumno a elaborar y comparar los mapas y árboles armónicos, que representarán las piezas
analizadas y a sacar conclusiones de ellos.
Evidentemente estos métodos resultarán muy útiles para comparar y comprender mejor
diferentes estilos, sistemas compositivos de diferentes corrientes, etc.
7.2.3.2.
Armonía
De forma similar a como se proponía trabajar en las Enseñanzas Profesionales, en el apartado 7.2.2.2 en la página 180, se haría ahora en las Enseñanzas Superiores, pero obviamente,
trabajando con mayor exhaustividad y profundidad todas las posibilidades tanto del sistema
tonal, como de otros que puedan ser interesantes para completar su formación.
Continuando el ejemplo que citábamos antes, en el apartado que trataba el estudio de esta
asignatura en las Enseñanzas Profesionales, sería un buen momento para introducir al alumno
en los árboles con notas alteradas (progresivamente, según fueran incluyéndose a lo largo de
los dos cursos) y en los otros dos métodos de modulación que desarrollábamos, la modulación
enarmónica (en el apartado 6.3.4 en la página 130) y la modulación cromática (apartado 6.3.5
en la página 140).
7.2.3.3.
Contrapunto
Contrapunto va a ser una asignatura nueva para los estudiantes de música de este nivel, ya
que aunque hayan cursado los estudios profesionales, no se van a haber enfrentado a ninguna
materia que tratara estos contenidos; únicamente, aquéllos que hubieran elegido Fundamentos
de Composición, podrían haber tenido algún contacto con consideraciones melódicas que se
tratarán con mayor profundidad en esta asignatura de Grado Superior.
Respecto de las aportaciones que la propuesta didáctica que se ha desarrollado en estas
páginas, puede hacer a la enseñanza de Contrapunto, fuera de lo ya comentado que no dejaría
de ser útil, de las asignaturas de Armonía y de Análisis, estarían la elaboración de árboles que
tuvieran como finalidad explicar mejor el comportamiento melódico de determinados estilos y
autores, o de árboles que ayudaran al alumno a asimilar las posibilidades de realización melódica
que posee para un tipo de ejercicio en concreto (como el árbol que ofrecíamos en el apartado 3.4.1
en la página 39). Asimismo, haciendo uso del Espiropentagrama, podría analizarse la interválica
constituyente de un motivo cualquiera, o trabajarse los diferentes tipos de imitación como se
proponía en la sección 6.2 en la página 105, en el capítulo dedicado a las aplicaciones de esta
herramienta.
7.2.3.4.
Otras asignaturas que podrían beneficiarse
Sin lugar a duda, lograr que el alumno posea una mayor capacidad a la hora de analizar,
utilizar y reconocer sonoridades va a poder ser útil para todas las disciplinas del mundo mu-
CAPÍTULO 7. PROPUESTA DE APLICACIÓN DE ESTA DIDÁCTICA
183
sical; no obstante, por mencionar aquí otras que van a poder beneficiarse más directamente,
señalaremos aquí las que parecen más señaladas en este sentido.
Tal vez la asignatura que primero venga a la mente sea, inevitablemente, la de Educación
Auditiva. Una asignatura que suele causar bastantes quebraderos de cabeza entre el alumnado
que llega a este nivel, y que consequentemente al ingente incremento de la educación del oído
armónico que se propone en estas páginas, iniciándose desde el nivel de preescolar, encontraría
mucho menor fracaso y podría, sin lugar a dudas, afrontar niveles de enseñanza mucho más
altos si la propuesta realizada en estas páginas, se llevara a la práctica.
Quizá otra de las más destacadas, en cuanto a poder utilizar lo expuesto en este trabajo,
sería propia asignatura de Composición (o su variante de Composición aplicada), que va a
poder gozar de un sistema de esquemas y de análisis nuevo y extremadamente útil, al tiempo
que va a poder usar estas herramientas para proponerse nuevos métodos y nuevas organizaciones
sonoras.
Otro caso relevante sería el de Acústica, que va a contar con un clarificador medio para
mostrar las diferencias entre diversos sistemas de afinación y sus propiedades con el Espiropentagrama (así lo demostrábamos en la sección 6.1 en la página 103, que comparaba el sistema
de afinación temperado con el sistema pitagórico).
Conclusiones
La investigación que aquí se ha ofrecido perseguía contribuir a la teorética y a la enseñanza general de la música de diversas maneras. La primera sería incentivar la ampliación de los
marcos de aprendizaje de la Armonía mucho más allá de lo que hasta ahora han tenido, al
menos dentro de nuestra región y por extensión, de nuestro país. La ampliación propuesta en
estas páginas tiene dos sentidos, en un primer término, extender la posibilidad de educar a
todo el conjunto de la sociedad, en el reconocimiento de sonoridades, en su valoración y en
su disfrute. Y en segundo, hacerlo desde el mismo comienzo de su educación, no esperando
a que puedan poseer los complejos conocimientos teóricos que el manejo de los conjuntos de
sonidos implica, que requeriría desde luego (y así se venía haciendo hasta ahora) una enseñanza específica continuada, sino simplemente ofreciéndole instrumentos para distinguir estas
sonoridades y someterlas a una taxonomía elemental; especialmente iniciándose en el período
infantil que es cuando mayor capacidad de aprendizaje existe en la persona. Éste sería, por
lo tanto, el doble marco de actuación, abarcar las enseñanzas generales y disminuir la edad
de iniciación, en consecuencia también en las enseñanzas artísticas específicas, de los alumnos
a las posibilidades expresivas y artísticas de las combinaciones de sonidos. Al respecto de los
medios que van a usarse para alcanzar este fin, tal y como enunciábamos líneas más arriba, la
propuesta que realizamos estribaría en utilizar como signo de las realidades sonoras armónicas,
figuras poligonales policrómicas. Unos signos gráficos que son perfectamente accesibles para los
niños desde las edades más tempranas y que permitirán dejar sembradas las semillas de una
prometedora educación musical futura, sobre todo apuntando a considerable mayor evolución
de su capacidad auditiva musical.
Al respecto de cómo se ha hecho para elaborar estas figuras policrómicas, apuntaremos
que éstas son producto en cuanto a su dimensión policrómica, de los estudios psicológicos que
vinculan ciertos colores con ciertas emociones y en cuanto a su dimensión geométrica, a la proyección de los sonidos posibles dentro de un ámbito de octava sobre un soporte gráfico circular.
Esta manera de representar los sonidos sobre lo que normalmente se llamaba diagrama de reloj
musical, en este trabajo se ha tomado como base para construir una nueva herramienta en la
que los puntos representativos de los sonidos sobre la circunferencia no se indican haciendo uso
de sus nombres sino de su representación musical sobre un pentagrama que, con una particular
forma de espiral irregular, lo permite; a esta herramienta se le ha llamado “Espiropentagrama”.
La segunda de las contribuciones que vamos a señalar es su búsqueda de una explicación
184
CONCLUSIONES
185
más completa, más profunda y más exhaustiva de cualquier sistema musical, pero dado el
contexto en que ha nacido, especialmente del occidental tonal. Para ello, esta propuesta observa,
analiza y clasifica los comportamientos de determinados sonidos y/o conjuntos de sonidos, y
se propone sintetizarlos en esquemas que reflejen lo observado con la suficiente precisión en
todas sus dimensiones, como para permitir un más fácil acercamiento de otras personas, o su
uso para la comparación con otros conjuntos o la práctica de cualesquiera estudios ulteriores.
La consecución de este objetivo se intenta llevar a cabo mediante un sistema de grafías y una
organización que, una vez explicadas y entendidas, permiten a sus usuarios acceder, profundizar
y contrastar las características de un determinado orden sonoro. A este tipo de esquemas, no
sólo por su aspecto sino también por su conexión con la Graph Theory de la Matemática actual,
le hemos llamado “árboles”.
Asimismo, otra aportación que debemos reconocer a la propuesta que resulta del estudio que
pergeñábamos a lo largo de nuestro discurso, sería la coherencia que posee en su totalidad y la
capacidad de adaptación a diferentes grados de conocimiento; este hecho le permite tener una
proyección que no se restringe a un único nivel educativo y que no experimenta contradicción
alguna en todas sus extensiones, desde su versión simplificada con que se ofrecerá a los más
noveles, hasta su pormenorizada expansión en los niveles más superiores. Al mismo tiempo,
estas mismas cualidades la hacen posible y conveniente en otras disciplinas prácticas y teóricas
del arte musical, y no la confinan exclusivamente dentro de las parcelas de la Armonía, o por
extensión, de la teoría compositiva. Respecto de cómo se ha logrado esto, es sencillo; el punto
de partida fueron analogías que servían de ayuda en los niveles más avanzados de la instrucción
musical, de esta forma, estas analogías pronto se vieron que eran muy sencillas de simplificar
para explicar cuestiones de niveles inferiores, hasta llegar finalmente a comprobarse, tras un
meditado examen, su extraordinaria utilidad incluso en los niveles más básicos, puesto que
permitía alcanzar un alumnado mucho más joven. De esta forma nació la idea de que si se
lograba asociar estas analogías en este alumnado desde corta edad, se lograría que el sistema
fuera aún más productivo, puesto que estaría mucho más asimilado y requeriría mucho menor
esfuerzo para la abstracción y el análisis de las mismas.
Por último, parece imprescindible reparar en las manifiestas conexiones que esta propuesta
esboza e incita a desarrollar, entre la música y otras tantas disciplinas como la psicología de la
percepción, la geometría o la pintura. Disciplinas que en este trabajo han encontrado un lugar
elevado al servir como fuentes de recursos para construir un método pedagógico que sirviera
para poder explicar y entender mejor el arte más abstracto de todos, quizá por eso el más
extraordinario, la música.
Bibliografía
Apel, W. (ed). 1969. Harvard dictionary of music. 2nd edn. Cambridge, Massachusetts: The
Beiknap Press of Harvard University Press.
Artaza Fano, J. 2002. Evolución armónica y procedimientos compositivos. Murcia: Master
Ediciones.
Balzano, G. J. 1980. The group-theoretic description of 12-fold and microtonal pitch system.
Computer music journal, 4(4), 66–84.
Bancroft, J., Young G. y Sanderson M. 1993. Musi-tecture : Seeking Correlations and
Between Architecture Useful Music. Leonardo music journal, 3, 39–43.
Baroody, A. J. 1988. .el pensamiento matemático de los niños". un marco evolutivo para
maestros de prescolar, ciclo inicial y educación especial. Aprendizaje VISOR. MEC.
Bartlett, D. Acoustic, sound and music.
Bergstrom, T., Karahalios K. y Hart J. C. 2007. Isochords: Visualizing structure in
music. Acm international conference proceeding series, Proceedings of Graphics Interface(234), 297–304.
Chailley, J. y Challan, H. 1964. Teoría completa de la música. Vol. I y II. Paris: Leduc,
A.
Clough, J. y Myerson, G. 1986. Musical scales and the generalized circle of fifths. The
american mathematical monthly, 93(9), 695–701.
Clough, J. 1979. Aspects of diatonic sets. Journal of music theory, 23(No. 1), 45–61.
Clough, J. 1998. A rudimentary geometric model for contextual transposition and inversion.
Journal of music theory, 42(2), 297–306.
Cohn, R. 1998. Introduction to neo-riemannian theory: A survey and a historical perspective.
Journal of music theory, Vol. 42(No.2), 167–180.
Cutietta, R. A. y Kelly J. H. 1987. A comparative study of color association with music
at various age levels. Journal of research in music education, 35(2), 78–91.
186
BIBLIOGRAFÍA
187
Dalcroze, E. J. 1965. La rythme, la musique et l’education. Paris: Fostich.
D’Andrade, R. y Egan, M. 1974. The colors of emotion. American ethnologist, 1(1), 49–63.
Deliège, I. y Sloboda, J. 1997. Perception and cognition of music. Hove, England: Psychology Press.
Díaz, M. 2003. La educación musical en la etapa 0-6 años. Aula de infantil, NoviembreDiciembre.
Diestel, Reinhard. 2005. Graph theory. 3rd edn. Graduate Text in Mathematics, vol. 173.
New York: Springer-Verlag Heidelberg.
Douthett, J. y Steinbach, P. 1998. Parsimonious graphs: A study in parsimony, contextual
transformations, and modes of limited transposition. Journal of music theory, Vol. 42(No.
2), 241–263.
Downling, W. J. y Harwood, D. L. 1986. Music cognition. San Diego: Academic Press.
Forte, A. 1973. The structure of atonal music. New Haven: Yale.
Galeyev, B. M. 1975. Sound visualization techniques and light-music. Pages 187–190 of:
Materials on the 3d all-union conference light and music.
Gauldin, R. 2004. Harmonic practice in tonal music. 2ª edn. Nueva York: Norton.
Girbau Badó, J. 1993. Geometria diferencial i relativitat. Universitat Autònoma de Barcelona.
Goldáraz Gaínza, J. J. 2010. Afinación y temperamentos históricos. Alianza Música.
Madrid: Alianza Editorial.
Gollin, E. 1998. Some aspects of three-dimensional "tonnetze". Journal of music theory,
42(2), 195–206.
Hindemith, P. 1937-70. Unterweisung im tonsatz. Vol. 1. Mainz (Germany): Schott.
Holland, S. 1986. Design considerations for a human-computer interface using 12-tone three
dimensional harmony space to aid novices to learn aspects of harmony and composition. Cite
report - open university, milton keynes.
Holland, S. 1987. Direct manipulation tools for novices based on new cognitive theories of
harmony. Proceedings of 1987 international computer music conference, 182–189.
Hook, Julian. 2002. Uniform triadic transformations. Journal of music theory, 46(No. 1/2),
57–126.
BIBLIOGRAFÍA
188
Howard, P., Holland S. y Whitelock D. 1994. Sound investments. patricia howard
reviews the uses of computers in harmony teaching, plus a round-up of educational materials.
The musical times, 135(1817), 467–475.
Hunter, D. J. y von Hippel, P. T. 2003. How rare is symmetry in musical 12-tone rows?
The american mathematical monthly, Vol. 110(No. 2), 124–132.
Hutchison, N. 2010. Colour music: Music for measure 1.
Krumhansl, C. L. 1990. Cognitive foundations of musical pitch. Oxford Psychology Series,
no. 17. New York: Oxford University Press.
Longuet-Higgins, H. C. 1962. Letter to a musical friend. Music review, August, 244–248.
Martínez-Oña, J. 1991. Cerca de la armonía. Cartagena: Madrigal todo en Música.
Mateu, M. A. 2006. Armonía práctica. Vol. 1 y 2. Valencia: Ab Ediciones Musicales.
McCabe, V. J. y Balzano G. J. (ed). 1986. Event cognition: An ecological perspective.
Hillsdale, New Jersey: Lawrence Erlbaum Associates.
McCartin, Brian J. 1998. Prelude to musical geometry. The college mathematics journal,
Vol. 29(No. 5), 354–370.
Messiaen, O. 1944. Technique de mon langage musical. Paris: Leduc, A.
Morris, R. O. 1968. Figured harmony at the keyboard. Vol. 1 y 2. Oxford University Press.
Motte, D. de la. 1989. Armonía. Barcelona: Ed. Labor.
Newton, I. 1704. Opticks. 1st edn. Vol. I y II. London: Royal Society.
Nuño, L. 2007. La rueda armónica.
Nuño, L. 2008. La rueda armónica: un nuevo recurso docente. Eufonía, didáctica de la música,
Abril, 101–111.
Ortmann, O. 1940. An analysis of paul hindemith’s ünterweisung im tonsatz". Bulletin of
the american musical society, September, 26–28.
Parncutt, R. 1989. Harmony: A psychoacoustical approach. Information Sciences. Berlin:
Springer-Verlag Heidelberg.
Pascual Mejía, P. 2002. Didáctica de la música. Pearson Education. Madrid: Prentice Hall.
Persichetti, V. 1961. Twentieth-century harmony: Creative aspects and practice. New York:
Norton.
BIBLIOGRAFÍA
189
Peters, G. D. y Miller, R. F. 1982. Music teaching and learning. Longman Music. New
York, London: Longman.
Piston, W. 1991. Armonía. Barcelona: Labor.
Rameau, J. P. 1971. Treatise on harmony. Nueva York: Dover.
Randel, D. (ed). 1997. Diccionario harvard de música. Alianza Diccionarios. Madrid: Alianza
Editorial.
Rappaport, D. 2007. Maximal area sets and harmony. Graphs and combinatorics, 321–329.
Rappaport, D. July 31 - August 3 2005. Geometry and harmony. 8th annual international
conference of bridges: Mathematical connections in art, music, and science banff, alberta,
67–72.
Raso del Molino, J. Compendio de armonía razonada. Vol. I, II, III. Ed. Si bemol.
Riemann, H. 1895. Harmony simplified or the theory of tonal functions of chords. London:
Augener and Co.
Rockstro, W. S. 1881. Practical harmony: A manual for the use of young students. London:
Robert Cocks y Co.
Rueda, E. 1998. Armonía. Madrid: Real Musical.
Sánchez Navarro, I. Apuntes y ejercicios de armonía.
Schoenberg, A. 1979. Armonía. Madrid: Real Musical.
Schoenberg, A. 1990. Funciones estructurales de la armonía. Barcelona: Labor.
Schoenberg, A. 1994. Fundamentos de composición. Madrid: Real Musical.
Seguí, S. 1987. Teoría musical. Vol. I. Madrid: Unión Musical Española.
Sloboda, J. A. 1985. The musical mind: The cognitive psychology of music. Oxford: Oxford
University Press.
Smaligo, M. A. 1998. Resources for Helping Blind Music Students. Music educators journal,
85(2), 23 – 26.
Solomon, L. J. 1997. Solomon’s music resources.
Spiegel, M. R. y Abellanas, L. 1992. Fórmulas y tablas de matemática aplicada. Aravaca
(Madrid): McGraw-Hill.
Steedman, M. 1972. The formal description of musical perception.
BIBLIOGRAFÍA
190
Thomson, W. 1965. Hindemith’s contribution to music theory. Journal of music theory, 9(1),
52–71.
Tomlin, J. All about set-theory.
Tucker, G. R. An introduction to pc set analysis.
Vanechkina, I. L. 1994. "musical graphics.as an instrument for musicologist and educators.
Leonardo music journal, 27(5), 437–439.
V.V.A.A. Grove music online.
V.V.A.A. 2010 (Abril). Diccionario de la real academia española.
Warner Schaie, K. 1961. Scaling the association between colors and mood-tones. The
american journal of psycology, 74(2), 266–273.
Zamacois, J. 1997. Tratado de armonía. Vol. 3 vols. Span Press.
Zarlino, G. 1558. Le istitutioni harmoniche.