Calculos formulas ejercicio 4.5

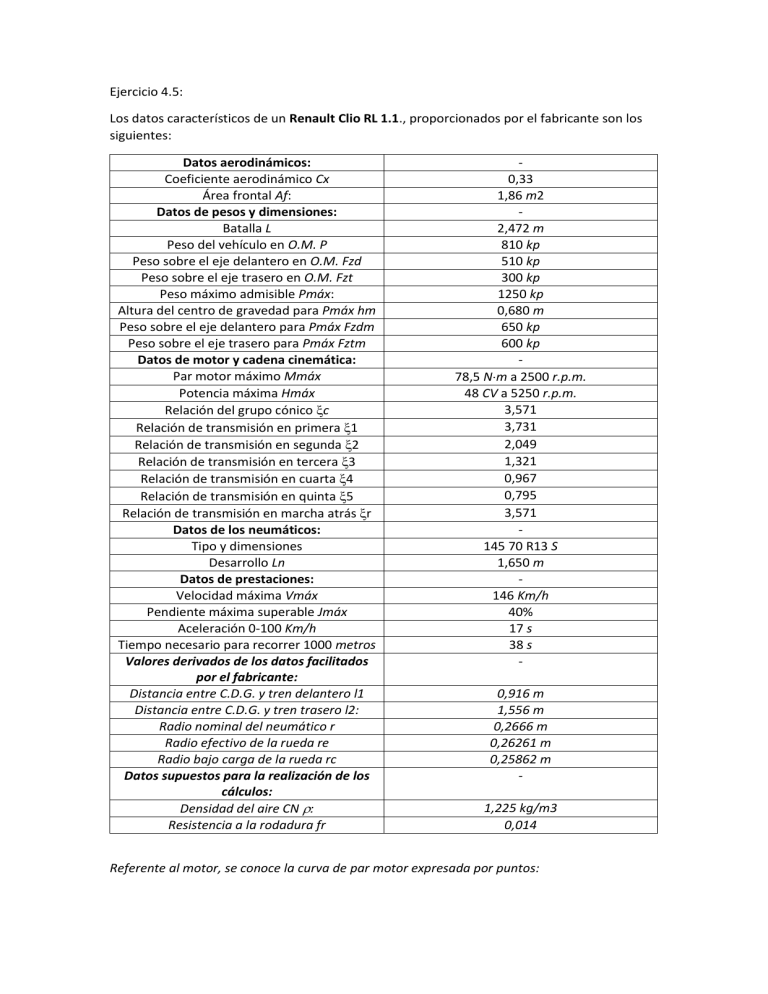
Ejercicio 4.5:
Los datos característicos de un Renault Clio RL 1.1., proporcionados por el fabricante son los
siguientes:
Datos aerodinámicos:
Coeficiente aerodinámico Cx
Área frontal Af:
Datos de pesos y dimensiones:
Batalla L
Peso del vehículo en O.M. P
Peso sobre el eje delantero en O.M. Fzd
Peso sobre el eje trasero en O.M. Fzt
Peso máximo admisible Pmáx:
Altura del centro de gravedad para Pmáx hm
Peso sobre el eje delantero para Pmáx Fzdm
Peso sobre el eje trasero para Pmáx Fztm
Datos de motor y cadena cinemática:
Par motor máximo Mmáx
Potencia máxima Hmáx
Relación del grupo cónico c
Relación de transmisión en primera 1
Relación de transmisión en segunda 2
Relación de transmisión en tercera 3
Relación de transmisión en cuarta 4
Relación de transmisión en quinta 5
Relación de transmisión en marcha atrás r
Datos de los neumáticos:
Tipo y dimensiones
Desarrollo Ln
Datos de prestaciones:
Velocidad máxima Vmáx
Pendiente máxima superable Jmáx
Aceleración 0-100 Km/h
Tiempo necesario para recorrer 1000 metros
Valores derivados de los datos facilitados
por el fabricante:
Distancia entre C.D.G. y tren delantero l1
Distancia entre C.D.G. y tren trasero l2:
Radio nominal del neumático r
Radio efectivo de la rueda re
Radio bajo carga de la rueda rc
Datos supuestos para la realización de los
cálculos:
Densidad del aire CN :
Resistencia a la rodadura fr
0,33
1,86 m2
2,472 m
810 kp
510 kp
300 kp
1250 kp
0,680 m
650 kp
600 kp
78,5 Nm a 2500 r.p.m.
48 CV a 5250 r.p.m.
3,571
3,731
2,049
1,321
0,967
0,795
3,571
145 70 R13 S
1,650 m
146 Km/h
40%
17 s
38 s
0,916 m
1,556 m
0,2666 m
0,26261 m
0,25862 m
1,225 kg/m3
0,014
Referente al motor, se conoce la curva de par motor expresada por puntos:
Error
Marcador no
definido.
(rpm)
PAR (N.m)
1650
2000
2500
4500
6000
61,8
72,6
78,5
64,75
48,07
Se pide:
1) Obtención de la curva de par motor.
2) Curvas de resistencia al avance-velocidad. Curvas de potencia-velocidad.
3) Fuerza tractora máxima limitada por la adherencia.
4) Relaciones de transmisión.
5) Análisis comparativo de las relaciones de transmisión calculadas y las proporcionadas por el
fabricante.
6) Esfuerzo tractor en llanta y esfuerzo resistente en función de la velocidad de circulación del
vehículo.
7) Determinar la rampa máxima y la velocidad de circulación para cada relación de
transmisión.
8) Aceleraciones: máxima en el arranque y media hasta alcanzar una cierta velocidad.
9) Tiempo de aceleración de 0 a 100 Km/h. Tiempo necesario para recorrer 1000 m con el
vehículo inicialmente parado.
1. OBTENCIÓN DE LA CURVA DE PAR MOTOR
Para una correcta evaluación de las prestaciones del vehículo, se ha aproximado la
curva de par motor en función del número de revoluciones del motor expresado en r.p.s.,
mediante un polinomio de 4º grado de la forma siguiente:
𝑀 𝑎 = 𝑀 𝑎𝑜 + 𝐾 1 𝑤𝑚 + 𝐾 2 𝑤2 𝑚 + 𝐾 3 𝑤3𝑚 + 𝐾 4 𝑤4𝑚
Para la obtención de los coeficientes del polinomio se emplean los cinco puntos de
funcionamiento del motor con par máximo de la tabla dada en el enunciado.
Una vez calculados los coeficientes del polinomio se obtienen los siguientes
resultados:
𝑀𝑎𝑜 = − 140,8613105 𝑁𝑚
𝐾1 = 14,19198867 𝑁𝑚/(𝑟. 𝑝. 𝑠. )
𝐾2 = − 0,326732154 𝑁𝑚/(𝑟. 𝑝. 𝑠. )2
𝐾3 = 3,17193716510 − 3 𝑁𝑚/(𝑟. 𝑝. 𝑠. )3
𝐾4 = − 1,13488411310 − 5 𝑁𝑚/(𝑟. 𝑝. 𝑠. )4
2. CURVAS DE RESISTENCIA AL AVANCE-VELOCIDAD Y CURVAS DE POTENCIAVELOCIDAD.
Para el cálculo de las curvas de resistencia al avance-velocidad, se han empleado las siguientes
expresiones:
𝑅 = 𝑅𝑟 + 𝐹 𝑥𝑎 + 𝑅𝑔
Donde:
𝑅𝑟 = 𝑓𝑟 𝑃 cos 𝜃 = 0,014 𝑚 𝑔 𝑐𝑜𝑠𝜃𝜃 = 𝑎𝑟𝑐𝑡𝑔
𝐽
100
𝐹 𝑥𝑎 = 𝜌 𝐶𝑥 𝐴𝑓 𝑉 2
𝑅𝑔 = 𝑃 𝑠𝑒𝑛 = 𝑚 𝑔 𝑠𝑒𝑛 = 𝑚 𝑔 𝑠𝑒𝑛 [𝑎𝑟𝑐𝑡𝑔
𝐽
]
100
 = 1,225 kg/m3
Se ha empleado el valor exacto del ángulo de la pendiente, en lugar de su aproximación,
debido a que para pendientes del 50% la aproximación del ángulo de la pendiente por su
tangente tiene menor exactitud.
La suma de las tres últimas ecuaciones conduce a una expresión cuadrática que se ha
representado en la figura 4.31.
3. FUERZA TRACTORA MÁXIMA LIMITADA POR LA ADHERENCIA.
𝐹𝑇𝑑𝑚 𝑥 = µ 𝑃 cos ɵ
Error Marcador no definido.
Pendiente (%)
0
10
20
30
40
50
𝑙2 + ℎ 𝑓𝑟
𝐿+µℎ
µ
1833,5
1824,4
1797,9
1756,1
1702,3
1639,9
µ
3368,8
3352,1
3303,4
3226,7
3127,9
3013,1