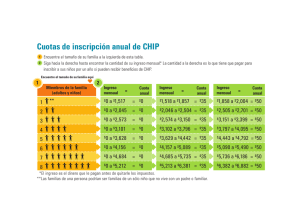
CAPITULO VIII: MATEMATICA FINANCIERA
2.1
Definiciones de matemática financiera
Según Hernán B. Garrafa Aragón en su texto MATEMATICA FINANCIERA,
nos dice “Matemática Financiera está considerada en el campo de la
matemática aplicada que estudia el valor del dinero en el tiempo,
teniendo en cuenta varios factores, como: La tasa, el capital y el tiempo
para obtener un monto o interés que permiten tomar decisiones de
inversión.
Jhonny de Jesús Meza Orozco en la contraportada de su texto
MATEMÁTICAS FINANCIERAS APLICADAS nos dice “Las Matemáticas
financieras aportan procedimientos matemáticos a la luz del principio del
valor del dinero en el tiempo, que resuelven diversas operaciones
financieras y comerciales cotidianas (préstamos bancarios, créditos
comerciales y de vivienda, valoración de activos financieros, cálculo de
indicadores de rentabilidad, equivalencia de tasas de interés, etc.)
VARIABLES EN UN FLUJO DE EFECTIVO
FLUJO REGULAR
Futuro
Anualidad
A
0 1 2 3 4
Tiempo
i% Tasa
P
Presente
Actual
Hoy
Inicial
2.2
5
FLUJO IRREGULAR
Futuro
R2 R3 R4
R1
n Tiempo
0
1
2
3
4
5n
i% Tasa
P
El dinero
Al analizar esta relación del Sector Industrial de la Intermediación
Financiera con su entorno surge la pregunta ¿cuál es el producto que
maneja este SI? y la respuesta se encuentra en el dinero.
El dinero tiene dos presentaciones y son:
1°.- La moneda conocida también como dinero del Banco Central de
Reserva “BCR” del Perú y el cual tiene las siguientes características:
.- Un patrón monetario que viene hacer el sol, es una moneda referencial
para determinar su equivalente en el contenido de metal precioso que la
garantiza (oro monetario).
1
2.3
El sistema financiero peruano
ORGANISMO RECTOR DEL SISTEMA FINANCIERO
MINISTERIO DE ECONOMIA Y
FINANZAS
MEF
BCR
SUPERINTENDENCIA
DEL MERCADO DE
VALORES (SMV)
SBS
BOLSA DE
VALORES
SISTEMA NO BANCARIO
SISTEMA BANCARIO
FIGURA N° 01
Observando la figura N° 01 se desprende que el sistema financiero peruano tiene
un organismo rector que es el Ministerio de Economía y Finanzas (MEF), quien
tiene a su cargo el diseño e implantación de la política económica monetaria y
tiene tres organismo autónomos que la ejecutan, así, el Banco Central de Reserva
del Perú (BCR) que se encarga de controlar y fiscalizar todas las operaciones
financieras que realizan las EIF en relación directa con el control de la oferta
monetaria, por esta razón interviene directamente en la Banca Comercial quienes
2
están autorizadas a recibir depósitos a la vista o Cuenta Corriente.
2.4
El interés.
Es la manifestación del valor del dinero en el tiempo.
Es una cuota que se carga por el uso del dinero de otra persona y
dependerá del tiempo que dure el préstamo.
Constituye una medida del incremento entre la suma original ya sea
tomada en préstamo o invertida y el monto final pagado o acumulado.
La fórmula es:
INTERES = CANTIDAD ACUMULADA – MONTO ORIGINAL
El monto original tiene como fuente un recurso propio o un préstamo y su
destino puede ser el consumo o la inversión, en este último caso puede ser
para la producción de bienes o prestación de servicios o para la
especulación, en el primer caso es generadora de riqueza aspecto que se
ocupa la ingeniera económica y tanto el primer caso como el segundo (la
especulación) se ocupa las finanzas entre ellas las finanzas corporativas,
en este último caso no se genera riqueza sino renta.
Uno de los recursos escasos que maneja la Ingeniería Económica es el
dinero, recurso que tiene las siguientes presentaciones:
MONEDA
Dinero del BCR
MONEDA METALICA
BILLETES
DINERO
DINERO BANCARIO
Cheques, Letras de cambio, Pagares, Bonos, Acciones,
etc
Clases de interés.- El interés en función al tiempo y su acumulación
puede ser:
1.-Interés simple donde no se acumulan los intereses en el vector tiempo.
2.-Interes al rebatir, que se da acumulando intereses en cada saldo
determinado por el vector tiempo, obedece al algebra financiera bancaria
3.-Interés compuesto donde sí se acumulan los intereses en el vector
tiempo dado en cada periodo de capitalización
Surge la pregunta ¿Con qué se mide el interés? Con la tasa de interés (i)
Esta variable se debe ubicar en el diagrama de flujo de efectivo como
sigue:
Anualidad
A
Futuro
F
0 1 2 3 4 5
P
i% Tasa
Presente
n Tiempo
3
Principal.
Actual
Hoy
Inicial
NOTA.- No se debe confundir la variable de flujo denominada anualidad
(A) con el relacionado al valor actual (VA) cuando se emplea Excel, en
este último caso
Periodo de capitalización.- El periodo de capitalización por ejemplo del
tiempo 2 se inicia al finalizar el tiempo 1 y concluye cuando se inicia el
tiempo 3, como se muestra en el siguiente flujo de efectivo; al periodo de
capitalización también se le conoce como periodo de interés.
Anualidad
A
Futuro
F
0 1 2 3 4 5
P
i% Tasa
Presente
n Tiempo
Fin del periodo de capitalización del tiempo 2
Inicio del periodo de capitalización del tiempo 2
Del flujo de efectivo se desprende que la variable “n” determina los periodos
de capitalización o frecuencia de capitalización.
2.5
Tasa de interés
La tasa de interés es la medida del interés, expresa porcentualmente la
suma de dinero que genera un valor inicial; esta tasa de interés al ingresar
a las formulas se expresa en tanto por uno y está en función de la variable
tiempo “n” y del principal, considerando este último caso, se determina la
siguiente relación:
Tasa de interés = Interés acumulado en el tiempo x 100%
Principal
Tasa de interés = Interés acumulado por unidad de tiempo x 100%
Suma original
Tomando los datos del ejemplo se tiene:
.i= 2080 x 100 = 10,4%
20000
Tasa de rendimiento = Interés acumulado por unidad de tiempo x 100%
Cantidad original
Estas relaciones de las tasas de interés son idénticas, solo expresadas de
distintas maneras.
4
EJEMPLO.- Una persona solicita un préstamos de S/. 5000 monto que
debe ser cancelado en un año cuyo valor final es de S/. 5200, se pide
determinar:
a.- El interés.
b.- La tasa de interés.
Para encontrar la solución al problema se emplea el siguiente
procedimiento:
Paso 1.- Se realiza el flujo de efectivo y se colocan las variables conocidas
y dadas seguidamente las variables incógnitas, en el ejemplo tendríamos.
F = 5200 Monto acumulado
----------------------------------P= 5000 i %?
n= 1 año I =?
Principal o monto original
Paso 2.- Se fórmula la pregunta ¿Qué se debe hallar? En este caso piden
hallar el interés y la tasa de interés.
Pasó 3.- Se emplean las fórmulas dadas, así para hallar el interés se tiene:
INTERES = CANTIDAD ACUMULADA – MONTO ORIGINAL
Para hallar la tasa de interés se tiene:
Tasa de interés = Interés acumulado en el tiempo x 100%
Principal
Paso 4.- Se aplica la parte matemática, como sigue:
Para Hallar el Interés se emplea la siguiente fórmula
INTERES = CANTIDAD ACUMULADA – MONTO ORIGINAL
INTERES = 5200 - 5000 = 200 (VALOR FINAL – VALOR INICIAL=
INTRES ACUMALADO)
Para hallar la tasa de interés se tiene:
Tasa de interés = Interés acumulado en el tiempo x 100%
Principal
Tasa de interés = 200 x 100%
5000
Tasa de interés = 4%
ORDEN DE LAS OPERACIONES:
PRIMEROS DIVIDI, MULT, SUMA Y RESTA
Paso 5.- Se describe la solución como sigue:
El interés acumulado fue de s/. 200 y la tasa que se cobra fue de 4% al
año
5
NOTA.- Ver el ejemplo 1.4 de Leland Black – Anthony Tarquin página 11
de la séptima edición.
Esta tasa de interés, para un prestamista o para un inversionista, el Interés
es una forma de obtener renta de una inversión o un préstamo, resulta de
la siguiente fórmula:
INTERES GENERADO = CANTIDAD FINAL – PRINCIPAL
La cantidad final viene o está constituida por el flujo de efectivo de
ingresos actualizados al momento que se da el desembolso inicial o valor
principal, se mide por la tasa de retorno (TR) o tasa de rentabilidad la cual
está en función al tiempo llamado PERIODO DE INTERES, también está
tasa de retorno se le conoce como RETORNO SOBRE LA INVERSIÓN
(RSI), su fórmula es:
Tasa de retorno =TR (i%)= Interés acumulado por unidad de tiempo x
100%
Principal
2.6
Interés simple
Es cuando los intereses se retiran quedando el capital constante,
ignorando cualquier interés que se haya acumulado en los periodos de
interés anteriores, las tasas de interés son en base anual (TEA).
Concepto poco utilizado en el cálculo financiero, es de fácil obtención,
pero con deficiencias por no capitalizar la inversión periodo a periodo.
El capital invertido es llevado directamente al final sin que se capitalice
periodo a periodo con los intereses ganados
El interés simple actúa cuando la tasa de interés es pequeña y se da en el
corto plazo, en finanzas solo existe el corto plazo que comprende un
tiempo de hasta un año y luego se tiene el largo plazo que comprende un
tiempo mayor a un año
-
VF = Monto acumulado (valor final)
VA = Inversión inicial (valor actual)
i = tasa de interés del periodo
n = número de períodos.
VF
=
VA* (1+i *n)
Se tiene los siguientes ejemplos:
PARA UN AÑO: se pide calcular el interés simple de un monto de s/. 1000
con una tasa del 20% anual en dos años
20% CONVERTIR EN NUMERO = 20/100=0.20
Aplicando la fórmula:
I = 1000 x 0.20 x 2
I = 400
6
Los textos de matemática financiera tienen la siguiente presentación:
I = 1000 x 20 x 2 = 1000 x 0.20 x 2 = 400
100
En esta presentación la tasa se divide entre 100 para expresarla en tanto
por uno.
PARA MESES: se pide calcular el interés simple de un monto de s/. 1000
con una tasa del 20% anual en 10 meses
Aplicando la fórmula: I = 1000 x 0.0166x 10
I = 166
PRIMERA (20/100) 0.20/12=0.0166
En este caso la tasa anual se expresa en tanto por uno y se convierte
mensualmente es decir 0.20 /12 = 0.01666
Los textos de matemática financiera tienen la siguiente presentación:
I = 1000 x 0.20 x 10 = 1000 x 0.0166 x 10= 166
12
En esta presentación la tasa anual es expresada en tanto por uno y se
divide entre 12 que es el número de meses al año, en otra presentación se
tiene
I = 1000 x
20 % x 10 = 1000 x 0.0166 x 10= 166
1200
CONVERTIR SEGÚN ESTE PROCEDIMIENTO (12*100)=1200
En esta presentación la tasa anual es expresada en tanto por uno y se
divide entre 1200 que es el número de meses al año multiplicado por 100.
PARA DIAS: se pide calcular el interés simple de un monto de s/. 1000 con
una tasa del 20% anual en 20 DIAS
Aplicando la fórmula: I = 1000 x 0.000555x 20
I = 11.10
(20/100= 0.20/360)=0.000555)
Los textos de matemática financiera tienen la siguiente presentación:
I = 1000 x 0.20 x 20 = 1000 x 0.000555 x 20 = 11.10
360
En esta presentación la tasa anual es expresada en tanto por uno y se
divide entre 360 que es el número de días que trae el año, en otra
presentación se tiene:
I = 1000 x 20
x 20 = 1000 x 0.000555 x 20= 11.10
7
36000
DIAS DEL AÑO 360*100=36000
En este último caso la tasa anual se divide entre 360 multiplicada por 100
El interés simple se caracteriza porque los intereses no se acumulan a
través de los periodos de capitalización o periodos de interés, por tanto su
función es lineal.
Se conceptúa como un porcentaje constante de un monto presente o un
principal que se multiplica por el tiempo de una vida de la operación, así se
tiene:
- Para un periodo
I=iP
Donde I es el interés generado, i es la tasa de interés simple y P es el
principal.
- Para n periodos I = n i P.
Por convenio cuando se aplica el interés simple los pagos se efectúan al
final del periodo de tiempo de un préstamo, por tanto el valor final (F)
incluye el pago del principal más los intereses acumulados, su fórmula es:
F = P + I = P + n i P, factorizando tenemos
F = P (1 + ni)
Para Black – Tarquín el interés simple se calcula a través de la siguiente
fórmula
Interés = (principal) (número de periodos) (tasa de interés)
I = Pni = Pin
Lectura: Leer las páginas de la 21 a la 22 del texto citado de Black –
tarquín que incluye el ejemplo1.14.
EJEMPLO.- Un estudiante pide prestado a un pariente s/. 5000 para
concluir sus estudios, el pariente acepta a una tasa de 5 ½ % de interés
simple anual, el estudiante debe pagar su deuda al cabo de dos años
¿Cuánto dinero tendrá que pagar?
½=0.50 +5 =5.50% CONVERTIR NRO 5.50/100 = 0.055
NOTA.- cuando se trata de cálculos financieros a interés simple se debe
mencionar este tipo de interés.
SOLUCIÓN:
Se pide hallar el monto a pagar con interés simple en los dos años:
F= P (1+in)
F= 5000 (1+ 0,055x2) SOBRE EL OREN DE LAS OPE MATE ()
F= 5 550
INTRES ACUMADO= VALOR FINAL – VALOR ACTUAL
El estudiante tendrá que pagar s/. 5 550, es decir s/. 5 000 por el principal
y s/. 550 de intereses.
Observación.- El interés simple es constante, no se capitaliza, así:
8
Pxi
Para el primer año se tiene s/. 5000 x 0,055 = s/. 275,00
Para el segundo año se tiene s/. 5000 x 0,055 = s/. 275,00
Suma total
s/. 550,00
Por tanto su gráfico es como sigue:
Monto
300
275,00
200
100
1
2
años.
GRAFICO
Tema de discusión.- ¿Qué pasa con el interés simple si la economía tiene
inflación y además paga impuestos?
0
Todo dependerá del rol de los sujetos activos en una operación de crédito; el
acreedor y el deudor, el acreedor pierde porque recibe menos en términos de
poder adquisitivo y el deudor gana porque paga menos en términos adquisitivos.
2.7
Interés compuesto
Según Jhonny De Jesús Meza Orozco en su texto Matemáticas
Financieras sobre el interés compuesto dice “El interés compuesto
(llamado también interés sobre el interés) es aquel que al final del periodo
capitaliza los intereses causados en el periodo inmediatamente anterior,
este autor también indica que el periodo de capitalización no siempre
coincide con el periodo de pago, por ejemplo el periodo de capitalización
es mensual y el pago es a los 60 días.
El autor citado hace referencia a las características del interés compuesto,
así dice:
“. El capital inicial cambia en cada periodo porque los intereses que se
causan se capitalizan, o sea, se convierten en capital.
. La tasa de interés siempre se aplica sobre un capital diferente,
. Los intereses periódicos siempre serán mayores.
Este mismo autor sobre las limitaciones de la fórmula de interés
compuesto manifiesta;
“. Los intereses que se causan periodo a periodo no se pagan sino se
capitalizan…
. Si los intereses se pagan al final de cada periodo, se reinvierten a la
misma tasa de interés. Esta es la interpretación del factor (1+ i)n
Contablemente, es la forma de calcular el interés, en la que cada período
de cálculo el interés se acumula al capital. Esta cifra sirve de base para
calcular los intereses en el siguiente período.
VF = Monto capitalizado (valor final)
VF = VA * (1+i) n
9
VA = Inversión inicial (valor actual)
i = tasa de interés del periodo
n = número de períodos
Interés flat
El monto de interés es el mismo para cada periodo y sobe la base del
monto total del préstamo; es decir no se toma en cuenta el saldo que
queda y sobre ello sacar el monto de interés
Mes
0
1
2
3
4
5
Saldo
1000
800
600
400
200
------
Amortización
Interés
Cuota
200
200
200
200
200
1000
60
60
60
60
60
300
260
260
260
260
260
1300
Interés al rebatir
El monto de interés es diferente para cada periodo y se calcula sobre la
base del saldo deudor en cada periodo. Cuanto mayor es el periodo de
pago, el interés es menor y cuanto menor sea el periodo de pago, el
interés es mayor
Mes
0
1
2
3
4
5
2.8
Saldo
1000
800
600
400
200
------
Amortización
Interés
Cuota
200
200
200
200
200
1000
60
48
36
24
12
180
260
248
236
224
212
1180
Tasas de interés en el sistema financiero
a) Tasa de interés nominal.- Se expresa anualmente, ignora el valor del
dinero en el tiempo al igual que el interés simple.
b) Tasa de interés efectiva.- Se toma en cuenta el periodo de
capitalización es decir se considera el valor del dinero en el tiempo.
c) Tasa de interés real.- Refleja el rendimiento del dinero en términos de
poder adquisitivo, pudiendo resultar en ganancia o en menoscabo real
del capital.
d) Tasa de interés moratorio.- Es el porcentaje que se cobra por no
pago de la deuda. Es el recargo del interés sobre las cuotas de la
obligación crediticia, cuando no se han cumplido con el pago dentro del
10
plazo establecido en el cronograma.
e) Interés compensatorio.- Los intereses compensatorios constituyen la
contraprestación por el uso del dinero o de cualquier otro bien. Tienen
carácter retributivo.
Mes comercial = 30 días
Año comercial = 360 días
2.9
Fórmulas utilizadas para el cálculo del interés para préstamos en
moneda nacional y extranjera
8.9.1 Calculo de la cuota fija
Para la generación de cronogramas de pago bajo esta modalidad, el
sistema utiliza las siguientes fórmulas:
8.9.2 Calculo de la tasa efectiva mensual
1
𝑇𝑒𝑚 = [1 + 𝑇𝑒𝑎]12 − 1
Tem : Tasa efectiva mensual.
Tea : Tasa de Interés Efectiva Anual
Si:
n=1 Capitalización anual
n=2 Capitalización Semestral 6
n=4 Capitalización Trimestral 3
n=12 Capitalización mensual.
n=360 Capitalización diaria
8.9.3 Calculo de la tasa efectiva diaria
CUOTA FIJA = Monto del crédito * Factor, Calculo de interés con
capitalización diaria
1
𝑇𝑒𝑑 = [1 + 𝑇𝑒𝑎]360 − 1.
26.82% (26.82/100=0.2682
(1+0.2682)*(0.0027778)-1
(1.2682)*(0.002778)-1
(1.0006602667)-1
TED=0.00066X100
TED= 0.066%
Ted
Tea
n
: Tasa efectiva diaria
: Tasa efectiva Anual
: Periodo de pago (30 días)
Interés = Capital * TED
8.9.4 Calculo de cuotas fijas mensuales
Calculo de las cuotas fijas mensuales
11
P∗i
𝐶=
1+
1
(1 + i)^n
Despejando
(1+𝑖)𝑛 ∗𝑖
𝐶 = 𝑃 [(1+i)n −1]
1.- (1.02)18= 1.4282*0.02 = RESULTADO = 0.02856
2.- (1+0.02)*18= 1.4282 -1= RESULATDO = 0.4282
3.- 0.02856 / 0.4282= 0.0666970
4.- 10,000*0.00666
CUOTA=667.07 + APORTE 10 = 677.07
2do ejercicio: La Coopac Los andes demesolsa un préstamo de 1000 soles
para 6 meses a una tasa de interes de 2% mensual. Pagadores de cuotas
fijas.
Datos:
VA=1000
N= 6
I=2%
Cuota = Fija
1.- (1+0.02)*6=1.126162*0.02=0.0225232484
2.- (1+0.02)*6=1.126162 – 1 = 0.126162
3.- 0.0225232484/ 0.126162 = 0.178525081
4.- 0.178525081*1000
5.- 178.53 cuota fija mensual
CUADRO DE PLAN PAGOS
Nro
saldos
cuotas
0
1,000
1
1000
2
841.47
3
679.77
4
514.83
5
346.60
6
175.00
total
Diferencia 0.03
amortización Interés
2%
cuota
aporte
Cuota
total
158.53
161.70
164.94
168.23
171.60
175.03
1,000.03
178.53
178.53
178.53
178.53
178.53
178.53
1,071.18
10
10
10
10
10
10
60
188.53
188.53
188.53
188.53
188.53
188.53
1,131.18
20
16.83
13.59
10.30
6.93
3.50
71.15
P= Capital inicial o monto del préstamo
i = Tasa de interés efectiva del periodo
n = Periodo de capitalización
c = Cuota fija del periodo
12
la COOPERATIVA LOS ANDES OTORGA UN PRESTAMO DE s/10,000.00
PARA 18 MESES A UNA TASA DE INTRES DE 2%, ¡HALLAR LA CUOTA
MENSUAL?
IDEMTIFICAR LOS VALORE:
Cuota=?
VA=10,000
I=2% mensual
N= 18 meses
C= 10,0000{(1+0.02)18*0.02/ (1+0.02)*18-1))
C=10000(1.02)*18*0.02 / (1.02)*18-1
C=10000(1.428246)*0.02 / (0.428246)
C=10,000(0.02856)/(0.428246)
C=10,000(0.066)
C=660.000
667.02
a. Calculo de anualidades deferidas
𝑃=
C
1
[1 −
]
𝑖 ∗ (1 + 𝑖)^𝑡
(1 + i)^n
Despejando
𝐶= 𝑃 [
(1+𝑖)𝑡 ∗ (1+𝑖)𝑛 ∗𝑖
]
(1+i)n −1
P= Capital inicial o monto del préstamo
i = Tasa de interés efectiva del periodo
n = Periodo de capitalización
c = Cuota fija del periodo
t = Periodo de gracia
8.9.5 Valor actual y futuro de una anualidad
Va =
𝑉𝑓
Vf
Vf
+
+⋯
(1 + 𝑖) (1 + 𝑖)^2
(1 + 𝑖)^𝑛
1
1
1
Va = Vf (1+𝑖) + (1+𝑖)^2 + ⋯ (1+𝑖)^𝑛
𝑉𝑓 = Va ∗ (1 + i)^n
Va =
Vf
(1 + i)^n
13
Va= Valor actual
Vf = Valor final
8.9.6 Interpolación
Dada la ecuación de equivalencia financiera, donde la incógnita es X1 ó
X2 su valor puede encontrarse por tanteo, asignando arbitrariamente sus
valores hasta lograr que se verifique la igualdad, el valor de la incógnita
puede reducirse notablemente aplicando la interpolación.
X − X1
=
X2 − X1
Y − Y1
Y2 − Y1
a. Calculo de interés
Factor
( 1 + i) n * i
------------------(1 + i ) n - 1
1 =
Interés = Capital * Factor
b. Calculo del interés moratorio
IM = TEA/360 * DA*KA
IM Interés moratorio
TEA Tasa efectiva anual
DA Días atrasados
KA Capital de la cuota atrasada
c. Calculo de interés compensatorio
TED = (((1+TEA) ^ (N/360)) – 1)
TED Tasa efectiva diaria
TEA Tasa efectiva Anual
N
Número de días de atraso
Interés Compensatorio = Capital vencido de la Cuota * TED
2.10 Ejemplo de aplicación
2.10.1 Para la elaboración del cronograma de pagos
Supongamos que deseamos generar un cronograma de pagos de
cuotas fijas bajo los siguientes supuestos: Monto a Prestar: 5,000Tasa
de Interés (T.E.A.): 26.82
14
Número de Cuotas: 12 Período de Pagos: Cada 30 días.
1
𝑇𝑒𝑚 = [1 + 𝑇𝑒𝑎]12 − 1
Tem =
Tem =
Tem =
(1+ 26.82%) ^ (1/12) - 1
0.0199
i = 2.00%
Remplazando
F =
F=
F=
VA *
( 1 + i) n * i
------------------(1 + i ) n - 1
( 1 + 2%) 12 * 2%
------------------(1 + 2%) 12 - 1
5000
472.798
Calculo de interés de la primera cuota, para ello empleamos la fórmula
TED:
TED = (((1+TEA) ^ (N/360)) – 1)
TED = (((1+ 0.26824179) ^ (30/360)-1)
TED = 0.02
Interés = capital *TED = 5000*0.02 = 100
Capital amortizado del capital = primera cuota – primer interés
Capital amortizado = 472.798 - 100 = 372.80
Calculo de interés de la segunda cuota, para ello empleamos la fórmula
TED:
Repetimos el proceso para la segunda cuota:
Saldo capital = 5000 – 372.80 = 4627.20
Interés = Capital * TED = 4627.20 * 0.02
Interés = 92.544 = 92.54
Se sigue el procedimiento para las siguientes cuotas.
F 472.798
Cronograma de pagos cuota fija
TEM 2.00%
N°
1
2
3
4
5
6
Saldo de capital
5,000.00
4,627.20
4,246.95
3,859.09
3,463.47
3,059.94
Amortización K
372.80
380.25
387.86
395.62
403.53
411.60
Intereses
Total Cuota
100.00
472.80
92.54
472.80
84.94
472.80
77.18
472.80
69.27
472.80
61.20
472.80
Aporte
10
10
10
10
10
10
Total cuota
482.80
482.80
482.80
482.80
482.80
482.80
15
7
8
9
10
11
12
2,648.35
2,228.51
1,800.29
1,363.49
917.97
463.53
Total Pagado
419.83
428.23
436.79
445.53
454.44
463.53
5,000.00
52.97
44.57
36.01
27.27
18.36
9.27
0.00
472.80
472.80
472.80
472.80
472.80
472.80
5,673.58
10
10
10
10
10
10
120.00
482.80
482.80
482.80
482.80
482.80
482.80
5,793.58
Para el cálculo del de la cuota decreciente se divide el saldo del capital inicial
entre el plazo del crédito.
Amortización fija = Capital inicial/ N = 5000/12 = 416.67
Calculo de la primera cuota
Calculo de interés = 5000 * 2% = 100
Calculo de la cuota = amortización fija + interés = 416.67 + 100 = 516.67
Calculo de la segunda cuota
Saldo capital = 5000 – 416.67 = 4583.33
Calculo de interés = 4583.33 *2% = 91.67
Calculo de la cuota = amortización fija más interés = 416.67 + 91.67 = 508.33
Cronograma de pagos cuota decreciente
N° cuota
1
2
3
4
5
6
7
8
9
10
11
12
Saldo de capital Amortización K Intereses Total Cuota Aporte Total cuota
5,000.00
516.67
416.67
100.00
10
526.67
508.33
4,583.33
416.67
91.67
10
518.33
500.00
4,166.67
416.67
83.33
10
510.00
491.67
3,750.00
416.67
75.00
10
501.67
483.33
3,333.33
416.67
66.67
10
493.33
475.00
2,916.67
416.67
58.33
10
485.00
466.67
2,500.00
416.67
50.00
10
476.67
458.33
2,083.33
416.67
41.67
10
468.33
450.00
1,666.67
416.67
33.33
10
460.00
441.67
1,250.00
416.67
25.00
10
451.67
433.33
833.33
416.67
16.67
10
443.33
425.00
416.67
416.67
8.33
10
435.00
Total Pagado
5,000.00
650.00
5,650.00 120.00
5,770.00
16
2.11 Calculo del interés moratorio
Vamos a calcular el interés moratorio del préstamo de 6900 nuevos
soles para 126 días de atraso en la primera cuota 165.90 con una tasa
de interés moratoria anual de 79.5856%.
Para ello vamos a utilizar la fórmula de tasa de interés
nominal anual:
Interés moratorio = Tasa Moratoria / 360*N*k
N
días de atraso
K
Capital de la primera cuota
Interés moratorio = 79.5856%./360 * 126 * 165.90
Interés moratorio = 46.21
2.12 Calculo del interés compensatorio
Ahora vamos a calcular el interés compensatorio del préstamo anterior
(sección 3.2), para 126 días de atraso en la primera cuota, con una
tasa de interés compensatorio anual de 42.5800
Para ello empleamos la misma fórmula de cálculo de interés con
capitalización diaria:
TED = (((1+TEA) ^ (N/360)) – 1)
TED = ((42.5800) ^ (126/360)-1)
Tasa de interés compensatorio = TED*Capital de la cuota atrasada =
0.13219313 * 165.9
Tasa de interés compensatorio = 21.9308
2.13 Formulas usadas en el cálculo
de interés para préstamos
agricultura
El interés simple
La tasa de interés simple se calcula sobre el capital inicial que
permanece invariable. Por lo tanto, el interés obtenido en cada intervalo
de tiempo (cada 30 días) es el mismo, la tasa de interés simple ignora el
valor del dinero en el tiempo
El interés que produce un capital es directamente proporcional al capital
inicial C, al tiempo T, y a la tasa de interés I.
I=C·I·T
I Interés simple
C Monto del capital desembolsado
I Tasa de interés
T Tiempo
Calculando El interés
Vamos a calcular el interés compensatorio del préstamo de 3000
nuevos soles con una tasa de interés mensual de 2% para 12
meses.
I = 3000* 2%*1= El interés para un mes es = 60.00
17
N° cuota
1
2
3
4
5
6
7
8
9
10
11
12
Total Pagado
Saldo de capital
3000
3000
3000
3000
3000
3000
3000
3000
3000
3000
3000
3000
Amortización K
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Intereses
Total Cuota
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
60.00
720.00
720.00
18