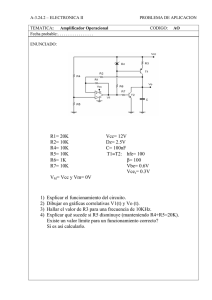
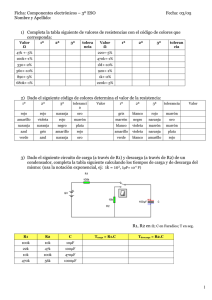
Ejercicio 1 Encontrar el rango de valores K para asegurar estabilidad, para los polinomios que no tiene k solo aplicar el criterio de Routh para justificar estabilidad. 1. Se tiene la forma desarrollada del polinomio: P (s) = s3 + 13s 2 + 55s + 75 Ante la presencia de al menos un coeficiente positivo, entonces existe una o más raíces con parte real positiva . Como todos los coeficientes son positivos, se construye el arreglo: s3 1 s2 13 s1 55 s0 75 Esbozo de la tabla de Routh Se procede con el resto de los términos: sn a0 a2 a4 ⠒ s3 1 55 sn−1 a1 a3 a5 ⠒ s2 13 0 sn−2 b1 b2 b3 ⠒ s1 640 13 0 ⠇ ⠇ ⠇ s0 75 0 s2 e1 e2 s1 f1 s0 e2 Tabla de Routh P (s) = s3 + 13s 2 + 55s + 75 Donde: b1 = a1 a2 −a0 a3 a1 = 13(55)−1(75) 13 = 640 13 a1 a4 −a0 a5 a1 b1 a3 −a1 b2 b1 b2 = c1 = 13(0)−1(0) =0 13 (640/13)(75)−13(0) (640/13) = = = 75 Se verifica si todos los coeficientes presentan el mismo signo y ni sin cero: s3 +1 55 s2 +13 0 s1 + s0 640 13 0 + 75 0 Como se cumple esta condición, se dice que el sistema es estable en sentido asintótico. 2. Se tiene la forma desarrollada del polinomio: P (s) = s4 + (k + 5)s3 + 35s2 + 10ks + 24 s4 1 35 24 s3 k+5 10k 0 s2 25k+175 k+5 24 0 0 0 0 0 s1 10k − s0 2 (k+5) 24 35k+140 24 P (s) = s4 + (k + 5)s3 + 35s2 + 10ks + 24 b1 = b2 = a1 a2 −a0 a3 a1 a1 a4 −a0 a5 a1 c2 = b1 a3 −a1 b2 b1 b1 a5 −a1 b3 b1 d1 = c1 b2 −b1 c2 c1 c1 = = = = (k+5)(35)−1(10k) = 25k+175 k+5 k+5 (k+5)(24)−1(0) = 24 k+5 ( 25k+175 k+5 )(10k)−(k+5)(24) ( 25k+175 k+5 ) = 10k − =0 = (10k− Condiciones de estabilidad (k+5)2 24 25k+175 24−0 (k+5)2 24 ) 10k− 25k+175 = 24 2 (k+5) 24 25k+175 ● k+5>0 ⇒ k >− 5 ● 25k+175 k+5 >0 25k + 175 > 0 ⇒ k >− 7 ● 10k − 2 (k+5) 24 25k+175 2 (k+5) 24 25k+175 10k < 250k 2 + 1750k < (k + 5)2 24 ⇒− 7.05758 < k < 0.37617 Entonces: ⇒ − 5 < k < 0.37617 3. Se tiene la forma desarrollada del polinomio: P (s) = s5 + 6s4 + 12s3 + 12s2 + 11s + 6 s5 1 12 11 s4 6 12 6 s3 10 10 0 s2 6 6 0 s1 ε 0 0 s0 6 0 0 P (s) = s5 + 6s4 + 12s3 + 12s2 + 11s + 6 b1 = b2 = b3 = c1 = c2 = c3 = d1 = a1 a2 −a0 a3 a1 a1 a4 −a0 a5 a1 a1 a6 −a0 a7 a1 b1 a3 −a1 b2 b1 b1 a5 −a1 b3 b1 b1 a7 −a1 b4 b1 c1 b2 −b1 c2 c1 = = (6)(12)−1(12) = 10 6 (6)(11)−1(6) = 10 6 =0 = (10)(12)−(6)(10) 10 = (10)(6)−6(0) 10 =6 = (10)(0)−6(0) 10 =0 = (6)(10)−(10)(6) 6 =6 =0 d2 = e1 = c1 b3 −b1 c3 c1 d1 c2 −c1 d2 d1 = = (6)(0)−(10)(0) = 6 (0)(6)−(6)(ε) → ε 0 6 Puesto que aparece un cero, y los demás coeficientes son de mismo signo, entonces el sistema presenta al menos un polo sobre el eje imaginario, siendo entonces, marginalmente estable. 4. Se tiene la forma desarrollada del polinomio: P (s) = s5 + 3s4 + 2s3 + 6s2 + 3s + 3 s5 1 2 3 s4 3 6 3 s3 s2 c1 s1 2 0 0 s0 3 0 0 c1 = d1 = b1 a3 −a1 b2 b1 c1 b2 −b1 c2 c1 = (ε)(6)−(3)(2) ε = (6(1−1/ε))(2)−(ε)(3) 6(1−1/ε) = 6 ε−1 ε = 6(1 − 1/ε) →− ∞ ε = 2(1 − ε ε−1 )→2 En este caso especial, el sistema es inestable. 5. Se tiene la forma desarrollada del polinomio: P (s) = s3 + 5s2 + (k − 6)s + k s3 1 k-6 s2 5 k s1 b1 0 s0 b1 = k a1 a2 −a0 a3 a1 0 = (k−6)(5)−1(k) 6 = 2k−15 3 Las condiciones de estabilidad son: ● k>0 ● 2k − 15 > 0 ⇒ k > 15/2 ⇒ k > 7.5 Ejercicio 2 Consideremos la siguiente planta nominal y el controlador: G(s) = 100 (s−0.5)(s+4) k (s) = k(s+3) s2 +4s+5 Encontrar el rango de valores de k para asegurar estabilidad para el polinomio característico [1 + k (s)G(s)] Fig. 1. Sistema de lazo cerrado La función de transferencia de lazo cerrado, donde la ganancia K se supone implícita en la función de transferencia, es: Y (s) F (s) = K(s)G(s) 1+K(s)G(s)H(s) En este caso H (s) = 1 . La ecuación de lazo cerrado se obtiene haciendo que el denominador del lado derecho de la ecuación sea cero, es decir: 1 + K (s)G(s) = 0 O bien: K (s)G(s) = − 1 Que es: k(s+3)•100 (s2 +4s+5)(s−0.5)(s+4) =− 1 La ecuación característica tiene la forma B (s) + K A(s) , es decir: (s2 + 4s + 5)(s − 0.5)(s + 4) + 100k(s + 3) Por lo tanto q (s) = s4 + 7.5s3 + 17s2 + 9.5s − 10 + 100ks + 300k ⇒ q (s) = s4 + 7.5s3 + 17s2 + (9.5 + 100k)s + 300k − 10 Estableciendo la tabla de Routh se tiene que: s5 1 17 300k-10 s4 7.5 9.5+100k 0 s3 b1 s2 c1 0 s1 s0 0 b1 = a1 a2 −a0 a3 a1 c1 = b1 a3 −a1 b2 b1 = = (7.5)(17)−1(9.5+100k) 7.5 = 0 0 0 0 118−100k 7.5 ( 118−100k 7.5 )(9.5+100k)−(7.5)(300k−10) 118−100k 7.5 = 9.5 + 100k − 16875k−562.5 118−100k Puesto que hay un cero, el sistema puede ser marginalmente estable siempre que se cumplan las condiciones de estabilidad: ● 118−100k 7.5 >0 ⇒ k > 1.18 ● 9.5 + 100k − 16875k−5625 118−100k >0 9.5 + 100k > ● 16875k−5625 118−100k (9.5 + 100k)(118 − 100k) > 16875k − 5625 − 10, 000k 2 + 10850k + 1121 > 16875k − 562.5 10, 000k 2 − 6025k + 1683.5 > 0 ⇒− 0.81027 < k < 0.20777 300k − 10 > 0 ⇒ k > 0.033 Puesto que no hay intersecciones para los valores aceptables de k, sistema resulta inestable para cualquier valor. En este sentido, se encuentra una raíz en el semiplano derecho, como se aprecia en el mapa de posición de raíces. Fig. 2. (izquierda) RLP (derecha) Respuesta al escalón unitario.