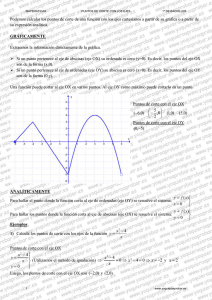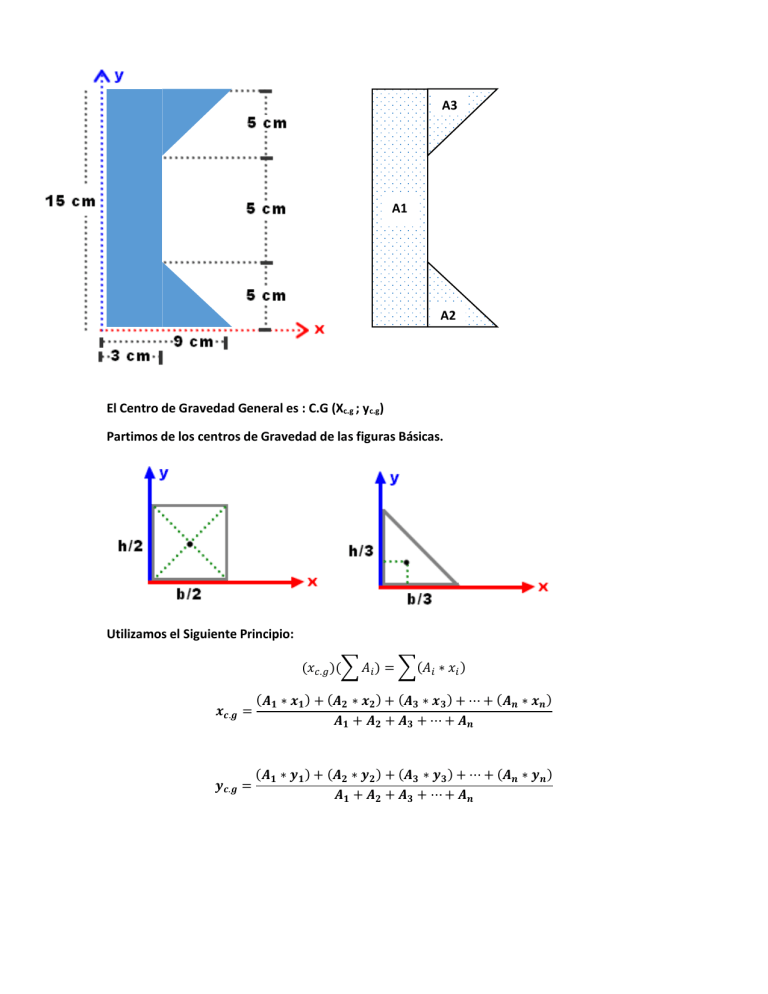
A3 A1 A1 A2 El Centro de Gravedad General es : C.G (Xc.g ; yc.g) Partimos de los centros de Gravedad de las figuras Básicas. Utilizamos el Siguiente Principio: (𝑥𝑐.𝑔 )(∑ 𝐴𝑖 ) = ∑(𝐴𝑖 ∗ 𝑥𝑖 ) 𝒙𝒄.𝒈 = (𝑨𝟏 ∗ 𝒙𝟏 ) + (𝑨𝟐 ∗ 𝒙𝟐 ) + (𝑨𝟑 ∗ 𝒙𝟑 ) + ⋯ + (𝑨𝒏 ∗ 𝒙𝒏 ) 𝑨𝟏 + 𝑨𝟐 + 𝑨𝟑 + ⋯ + 𝑨𝒏 𝒚𝒄.𝒈 = (𝑨𝟏 ∗ 𝒚𝟏 ) + (𝑨𝟐 ∗ 𝒚𝟐 ) + (𝑨𝟑 ∗ 𝒚𝟑 ) + ⋯ + (𝑨𝒏 ∗ 𝒚𝒏 ) 𝑨𝟏 + 𝑨𝟐 + 𝑨𝟑 + ⋯ + 𝑨𝒏 Calculamos las Áreas y los xi y yi Para el Área 1 (A1): 𝑨𝟏 = 𝒃 ∗ 𝒉 → 𝑨𝟏 = 𝟑𝒄𝒎 ∗ 𝟏𝟓𝒄𝒎 → 𝑨𝟏 = 𝟒𝟓𝒄𝒎𝟐 𝒙𝟏 = 𝒚𝟏 = 𝟑𝒄𝒎 𝟐 → 𝒙𝟏 = 𝟏, 𝟓 𝒄𝒎 𝟏𝟓𝒄𝒎 𝟐 → 𝒚𝟏 = 𝟕, 𝟓 𝒄𝒎 Para el Área 1 (A2): 𝑨𝟐 = 𝒃∗𝒉 𝟔𝒄𝒎 ∗ 𝟓𝒄𝒎 → 𝑨𝟐 = → 𝑨𝟐 = 𝟏𝟓𝒄𝒎𝟐 𝟐 𝟐 𝒙𝟐 = 𝟑𝒄𝒎 + 𝒚𝟐 = 𝟓𝒄𝒎 𝟑 𝟔𝒄𝒎 𝟑 → 𝒙𝟐 = 𝟓 𝒄𝒎 → 𝒚𝟐 = 𝟓/𝟑 𝒄𝒎 Para el Área 1 (A3): 𝑨𝟑 = 𝒃∗𝒉 𝟔𝒄𝒎 ∗ 𝟓𝒄𝒎 → 𝑨𝟑 = → 𝑨𝟑 = 𝟏𝟓𝒄𝒎𝟐 𝟐 𝟐 𝒙𝟑 = 𝟑𝒄𝒎 + 𝟔𝒄𝒎 𝟑 → 𝒙𝟑 = 𝟓 𝒄𝒎 𝒚𝟑 = 𝟏𝟎𝒄𝒎 + 𝟓𝒄𝒎 𝟑 → 𝒚𝟑 = 𝟑𝟓/𝟑 𝒄𝒎 Reemplazamos en la Fórmula 𝒙𝒄.𝒈 = 𝒚𝒄.𝒈 = (𝟒𝟓 ∗ 𝟏. 𝟓) + (𝟏𝟓 ∗ 𝟓) + (𝟏𝟓 ∗ 𝟓) → 𝒙𝒄.𝒈 = 𝟐. 𝟗 𝟒𝟓 + 𝟏𝟓 + 𝟏𝟓 𝟓 𝟑𝟓 (𝟒𝟓 ∗ 𝟕. 𝟓) + (𝟏𝟓 ∗ ) + (𝟏𝟓 ∗ ) 𝟑 𝟑 𝟒𝟓 + 𝟏𝟓 + 𝟏𝟓 → 𝒚𝒄.𝒈 = 𝟒𝟑 → 𝒚𝒄.𝒈 = 𝟕. 𝟏𝟔𝟔𝟔 𝟔 Para encontrar el Momento de Inercia con Respecto al Eje x Utilizamos la Siguiente: