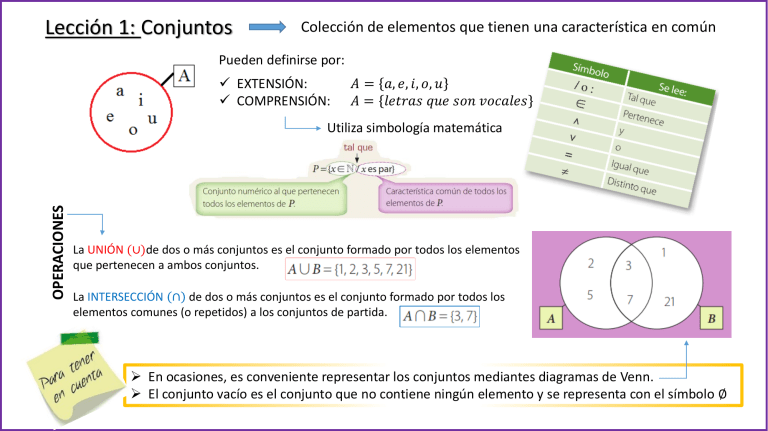
Lección 1: Conjuntos Colección de elementos que tienen una característica en común Pueden definirse por: EXTENSIÓN: COMPRENSIÓN: 𝐴 = 𝑎, 𝑒, 𝑖, 𝑜, 𝑢 𝐴 = 𝑙𝑒𝑡𝑟𝑎𝑠 𝑞𝑢𝑒 𝑠𝑜𝑛 𝑣𝑜𝑐𝑎𝑙𝑒𝑠 OPERACIONES Utiliza simbología matemática La UNIÓN (∪)de dos o más conjuntos es el conjunto formado por todos los elementos que pertenecen a ambos conjuntos. La INTERSECCIÓN ∩ de dos o más conjuntos es el conjunto formado por todos los elementos comunes (o repetidos) a los conjuntos de partida. En ocasiones, es conveniente representar los conjuntos mediantes diagramas de Venn. El conjunto vacío es el conjunto que no contiene ningún elemento y se representa con el símbolo ∅ Lección 2: Desigualdades Lección 3: Intervalos de números Reales Sería imposible escribir por extensión todos los números reales que cumplan la condición − 3 ≤ 𝑥 < 5, porque hay infinitos números. Existe una manera de representar este tipo de conjuntos: usando intervalos de números reales En este caso: INTERVALO SEMIABIERTO −3,5 Cerrado en el −3 , porque el conjunto incluye ese número. Abierto en el 5, porque no lo incluye. GRÁFICA Dibuja un círculo pintado en el −3, porque el intervalo incluye este valor. Dibuja un círculo en blanco en el 5, porque el intervalo no incluye este valor. Si tenemos los intervalos 𝐴 = −1,10 𝑦 𝐵 = 5, +∞ , podemos determinar la unión 𝐴 ∪ 𝐵 y la intersección 𝐴 ∩ 𝐵. Observa la representación gráfica de ambos conjuntos (en verde el conjunto A y en celeste el conjunto B) Para determinar la unión entre A y B, debemos incluir todos los valores de la recta que hayan quedado pintados, en este caso: 𝐴 ∪ 𝐵 = −1, +∞ Para determinar la intersección entre A y B, debemos considerar sólo los valores que hayan quedado pintados con ambos colores (verde y celeste), en este caso: 𝐴 ∩ 𝐵 = 5,10 OTRO EJEMPLO! Considera los intervalos 𝐶 = 1,5 𝑦 𝐷 = 7, +∞ . Observa su representación gráfica: Para determinar el conjunto unión, observamos que no es posible expresar la unión de ellos como un único intervalo, porque no tienen elementos en común. Cuando sucede esto, sólo lo representamos como: 𝐶 ∪ 𝐷 = 1,5 ∪ 7, +∞ Para determinar el conjunto intersección, observamos que, en este caso, los conjuntos no tienen elementos en común, luego, no hay intersección y decimos que: 𝐶∩𝐷 = ∅ EJEMPLO! Lección 4: Propiedades de las desigualdades. OBSERVA!








