OPTIMAL CONTROL OF A BALL MILL GRINDING
CIRCUIT-I.
GRINDING CIRCUIT MODELING AND
DYNAMIC SIMULATION
Utah Generic
Center
Control
m Comminution,
International
RAJ K. RAJAMANI
115 EMRO, University
of Utah, Salt Lake City, UT X4112, U.S.A.
JOHN
A. HERBST
Inc., 419 Wakara Way, Suite 101, Salt Lake City, UT 84108, U.S.A.
(Firsr received 28 April 1988; acrepled in
revisedform 29 June 1990)
Abstract-Mineral
grinding circuits can be controlled with a set of proportional-integral (PI) controllers or
alternatively
by specialized controllers which make use of optimal control theory. The latter control
strategy is superior in the sense that feed solid and water addition rates are manipulated
in concert to
achieve a specitied control objective. A dynamic model is needed for optimal control, and for PI control the
model can be used for ofi-line tuning. Off-line tuning circumvents
the problem of on-line tuning, during
which transients persist for a long time, resulting in lost production.
The key elements of the full dynamic
model are the population
balance model of the ball mill and an empirical model of the hydrocyclone.
The
model development
and its verification for both steady- and unsteady-state
responses are shown. On-line
computations
with the full dynamic
model require the solution of 37 differential
equations
at every
sampling
instant.
In addition,
optimal control calculations may overburden the control computer.
Therefore,
a slmplltied model usmg Just three state variables 1s shown to be adequate
for dynamic
predictions.
In Part 11 the full dynamic model is used in off-line tuning and the simplified model is used in
the optimal controller.
Both
model predictions and pilot scale ball mill circuit responses are shown.
INl’KODUCTION
Ball mill grinding circuits constitute
the primary unit
operation in the production
of metal from mined ore.
In a typical mineral processing plant for copper ore,
crushers are used to break large lumps of mined ore to
pieces of 2.5 cm size which are further reduced to a
fineness of 100 pm in ball milling circuits. After the
grinding stage, the ore is subjected to a concentration
operation
such as flotation.
The metal is extracted
from the concentrate
by leaching, solvent extraction,
electrowinning
or smelting operations.
Grinding is an inherently energy-intensive
process
in which less than 10% of the total electrical energy
input is utilized in the size reduction of ore particles.
Considering
the fact that thousands
of tonnes of ore
are processed every day in a typical plant, the cost of
operation
of the grinding plant often dictates the
overall cost of metal production.
Hence, it is essential
that such circuits be run as efficiently as possible. A
ball mill draws a certain level of power just to keep the
ball charge in motion and a fraction thereof to grind
the ore. Therefore, the cost of operation is minimized
by maintaining
the ore feed rate to the mill at the
maximum design capacity at all times. But, at the
same time, the product
from the circuit-the
fine
stream from the hydrocyclone
classifier-must
meet
the size specification for metal extraction efficiency in
subsequent processing.
During operation
the grinding circuit experiences
many
disturbances:
ore hardness
variations,
ore feed
rate changes and feed size variations. Ore feed rate
and feed size disturbances
can be easily countered by
adjusting the water additions to the circuit, but ore
hardness variations can cause drastic reduction in mill
throughput.
Hardness of the ore varies considerably,
depending on the location from which it was mined.
Owing to ore hardness disturbances,
the mass rate of
recycled stream and the fineness of the circuit product
tend to fluctuate and so the objective of computer
control strategy is to counteract these disturbances
in
the optimum sense.
Grinding circuits can be controlled with a series of
proportional-integral
controllers.
By their very own
nature
these controllers
gradually
vary process
streams until setpoint is reached. In other words, the
controllers hunt for steady-state
conditions.
As a result, circuit transients
persist for a very long time,
especially due to interaction
between controllers.
To
avoid these problems, some control strategies employ
a mathematical
model of the circuit to predict the
output of the process one sampling step ahead and
apply control actions accordingly. The optimal control discussed in this manuscript
uses a result known
as “Pontryagin’s Maximum Principle” which provides
a mathematical
solution to the dynamic optimization
problem.
In Part I of this paper models of the subunits in the
grinding circuit are developed.
Then experimental
verification
of the dynamic model is shown. The use of
dynamic models in control strategies is described in
Part II.
861
862
RAJ K.
RAJAMANI
CIRCUIT MODELS
Grinding
circuit models have been used for the
evaluation
(Herbst and Mular, 1980) of alternative
circuit configuration
and also for the evaluation
of
alternative
control strategies (Stewart, 1970, Herbst
and Rajamani,
1979) and to obtain a quantitative
measure of transients
of the circuits under control.
However, dynamic modeIs of the nature described
here are nonexistent
in the literature.
In the following, mathematical
models of the mill,
sump and hydrocyclone
are developed in detail. These
models form the basis of dynamic simulations and an
on-line simplified model.
Ball mill model
The application
of the population
balance concept
to particle breakage processes occurring in a ball mill
results in an integro-differential
equation in which the
particle size distribution
is expressed as a function of
time and particle size. A more convenient
model expression results when the continuous size range d,-d,
is divided into a set of n discrete intervals.
The linear, size-discretized
model for breakage kinetics is obtained by dividing the particulate assembly
being ground into n narrow size intervals with a
maximum size d, and a minimum size d,. The ith size
interval is bound by di above and di+ , below, and the
mass fraction of material in this size interval at time t
is denoted by mi. Then, for a continuous mill, a mass
balance for the material in the ith size interval at time
t yields
accumulation
dH(t)m,MP,i(f)
= input - output
=
dt
- S;N(t)m~,,Atl
M
Mf
m
MF.i -M
i-L
+ C b,SjH(t)
j=l
+ generation
MPm MP.i(t)
m,,,,(t)
JOHN
A.
HERBS
“concentration”
is the solids concentration,
C,, MP,
defined as the mass of solids per unit volume of slurry.
Then, the hold-up mass within the mill is given by
H(C) = V,C,,,P.
Then the variation
is described by
(2)
in solids concentration
dCs MP
Vnrk
=
dt
in the mill
QMFG,MF - QMPCS,MP
(3)
where VM is the volume of slurry in the mill, and Q is
the volumetric flow rate of slurry. The subscripts MF
and MP denote mill feed and mill discharge streams,
respectively.
Since for overflow ball mills V, is a
constant the volumetric feed rate to the mill equals the
volumetric discharge rate at all times. Utilizing this
fact in eq. (3) yields
dC S.MP
___
= +%s.
dt
M
MF - C,, hfp).
(4)
A total of n + 1 differential equations, i.e. n equations
for size distribution
and one equation for solids concentration
in the mill slurry is to be solved for complete dynamic description
of the ball mill.
Sump model
The slurry in the sump is kept suspended
by an
impeller and hence the sump behaves as a single
perfect mixer. Under the assumption that size changes
do not occur in the sump, i.e. negligible attrition due
to impeller blades, the following equations provide a
complete description
of sump behavior in a circuit
employing post classification:
dm,,
L=M
dt
(11
where H(t) is the total mass hold-up in the mill, and
are the mass rate of solids flow into
and discharge from the mill, respectively. In eq. (1) Si,
the size-discretized
selection function for the ith size
interval, denotes the fractional rate at which material
is broken out of the ith size interval, and bij, the sizediscretized breakage function, represents the fraction
of the primary breakage product material in the jth
size interval. The perfect mixing assumption is implied
in eq. (1). For the case in which the mill residence time
distribution
(RTD) corresponds
to an N mixers-inseries model, eq. (1) applies to each of the N perfect
mixers. Physically the N mixers-in-series
model may
be considered as N smaller mills connected in series
such that the discharge from one mill becomes the
feed to the next mill in the series. A description
of
holdup mass, H(t), as a function of time, t, is needed to
solve eq. (I). For overflow mlHs of the type used in this
study, the volume of slurry present in the mill is
reasonably
constant over a wide range of operating
conditions,
hence the slurry “concentration”
must be
solved to compute holdup. A convenient definition for
M MF and M,,
and
i
MPm MP.i -
Mspwp,,
(5)
z=Q+%-Q,,
; ( YS’~CS.SP)
= QM&S.MP - QS&S.SP
where M,, is the mass rate of solids discharge from
discharge
rate of
the sump, QSP is the volumetric
slurry, W,, is the mass rate of water added to the
sump, msp.( is the fraction of solids in the ith size
interval present in the sump, and C,.,, is the mass of
solids per unit volume of slurry in the sump.
Hydrocyclone
model
In general terms, the centrifugal force within the
hydrocyclone
carries the coarser and heavier particles
to the outside wall, which results in the discharge
through the spigot. Simultaneously,
an inner spiral of
fluid carries the finer particles to the vortex finder. A
dynamic model is unnecessary because the response of
the hydrocyclone
is virtually instantaneous.
Cohen
rt ul. (1966) experimentally
measured the residence
time of mineral particles in a 15-cm cyclone and
showed that the mean residence time is less than 5 s
Optimal
control
of a ball mill grinding
hd4,)
K = 1 - exp[
R, = ~1, + a8 WOFf
E;=
(9)
(10)
- 0.693(d,/d,,)a,]
WF
(11)
Y,(l-RR,)+R,
(12)
where WOF is the water flow rate in the overflow, WF
is the feed water rate, d,, is the size at which 50% of
the solids report to overflow and 50% reports to
underflow, Qc is the volumetric rate of pulp ked,f, is
the volume fraction of solids in the pulp feed, and R,
is the fraction of fines reporting to underflow. Ei is the
fraction of particles (in size class “i”) in the feed which
is classified to the underflow, and Yi is equal to Ei
corrected for particles carried off by water reporting
to the underflow.
The model uses eight empirical
constants,
a,, a2
. as, which must be determined
experimentally.
0
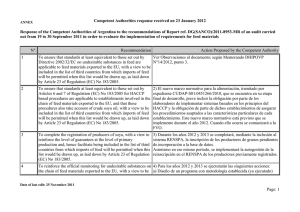
GRINDING CIRCUIT
A schematic of the major pieces of process equipment and instrumentation
is shown in Fig. 1. The ball
mill is a standard
Denver
mill, 76 cm in internal
diameter and 46 cm long. In all of the tests reported a
ball load of 345 kg, which corresponds
to 40% millfilling, was used. The classifier is a Krebs 7.5cm
hydrocyclone
and the sump is 30 cm in diameter and
80 cm in height. The objective of this work is to study
the behavior of industrial size mills using the pilot
circuit described. This would entail using ore samples
typically processed in a copper ore grinding circuit.
Since the quality of the metal-ore sample, in terms of
its grindability,
varies within a batch of sample, a
clean material such as limestone is used to validate
models. The feed material processed is - 1680~pm
limestone. For the range of flows encountered
in the
study a flow meter and a density gauge installed on
the cyclone-overflow
line would severely restrict the
flow. To avoid this problem, the cyclone overflow was
piped to a sump-pump
assembly as shown in Fig. 1.
The Microtrac particle size analyzer which operates in
the range of 2-176 nrn was used. A pneumatically
operated
sampling device supplied samples to the
analyzer every 2 min. Though the analyzer is capable
of providing
13 size fractions, the percent passing
44 pm was used in the size control experiments.
A
Hewlett-Packard
2100 A minicomputer
system consisting
of mass storage
disc, plotter,
monitor,
analog-digital
converter and printer served as the online computer control system. A specialized on-line
control software enabled configuring
control loops
(8)
a.,Qc + asf,
= a3 +
863
I
EXPERIMENTAL
for all sizes of particles at widely different operating
conditions.
This study conclusively
proves that the
dynamics associated with the cyclone are negligible
compared to the mill or the sump.
Hydrocyclone
modeling has not matured to fully
fluid flow based models. A number of papers have
made advances into the description
of swirling fluid
flow in this device, but a complete description of size
classification
is yet to emerge. Hence, we use the
empirical modeling approach proposed by Lynch and
Rao (1975) with a slight modification.
The model equations are
WOF=a,WF+a,
circuit-
_“II.Ic.I*C
,,:
......................
..............
......................
......................
level
PensOr
,e
I! PA
.....
......................
......................
::::,:::1
.........................
. . . . . . . . .
::::::::::::::::::::::
4mn
nm
...........
..
................................
.........
mo~ne+ic
13mm
................................
......................
:::
......................
.......
-,
..............
::::::
....
......................
......................
. ..
flomlcter
.: ;-
........................
..................................
... .
......................
.....................
.....................
.........................
.....
......................
......................
..........................
................
...............
75mm
........dlmrtnthl
..........
...............
........
\ :::::::: / C.”
cymnd
.
.
........................
......................
..................
......................
&ty
[“-‘“be
>
:.:
......
y=J==J
.
gucqe
micro rot
par*ic,e size OnOiyLBl
.,:
,.>:.yg:z :y.{.c..-
..........
..........
_.....
_...
..
.............
.......................
.........
............
Stream
: ..:
..........
-
b,”
PrmoCt
:
.....
.....
o,e
...........................
_, .
......
:;j:
q
.
PROCESS
EQ”lPMENT
...... .
1 /
750x450mm
boll mill
Fig. 1. Schematic
of the pilot scale grinding
circuit.
a
CONTROL
RAJ K. RAJAMANIand JOHN A. HERBSI
864
reported here. A total of 10 instrument
readings were
taken every 2 s and averaged over 12 s. Five final
control elements were controlled
by the computer
during control experiments.
DYNAMIC
MODEL
PARAMETERIZATION
AND
VERIFICATION
Ball
mill parameters
The parameters
of the mill model depend both on
the material consist within the mill and the mill operating condition.
This dependence,
although
highly
complex, has been well investigated.
The dependence
of selection and breakage functions on mill dimensions and operating
conditions
including
critical
speed, ball loading, particle loading and lifter geometry has been investigated
systematically
(Herbst
and Fuerstenau,
1973; Kim, 1974; Malghan
and
Fuerstenau,
1977; Herbst er al., 1983). Herbst and
Fuerstenau
(1973) proposed that all of the influences
on selection function can be equated as the corresponding influence of energy input to the mill on rate
of breakage. This single fact is extremely useful for
simplifying the modeling effort. Milling tests done on
a 25, a 3% and the 76-cm mill by Herbst et al. (1977)
confirmed the following hypotheses:
(9 Selection
proportional
mill, i.e.
functions
for a given material are
to the specific power draft of the
Si = S:(P/H)
i = 1,2,3
..n
(13)
where SF is the specific se!ection
function
values, P is the power drawn by the mill, and H
is the hold-up mass in the mill.
(ii) Breakage functions
for a given material are
approximately
invariant.
(iii) In wet ball milling, the linear model is applicable in the neighborhood
for which parameters
were estimated, i.e. a linear model is applicable
for the narrow range of mill discharge fineness
from which parameters
were estimated.
According to the first hypothesis, the selection function estimated at some feed rate can be used to predict
mill performance
at any other feed rate by normalizing the selection function as shown in eq. (13). This
fact combined with the last hypothesis enables calculation of mill dynamics with the linear model. The
selection and breakage function parameters
of the
linear
model
were estimated
with a computer
program
called ESTIMILL
(Herbst
et al., 1977;
Rajamani and Herbst, 1984).
The breakage function of the limestone feed material used here was determined
experimentally
in three
mills-a
25 and a 3%cm laboratory scale mill and the
76-cm pilot scale mill. To a good approximation,
the
breakage functions are the same in the three mills. The
cumulative form of the breakage function is given as
Bij = 0.31(di/dj+,)0.4s
The cumulative
breakage
+ 0.69(d,/dj+,)Z
function
R. (14)
BZiis the fraction
of
the material in size interval i that reports to all size
intervals below and including the interval i upon
breakage.
Circulating load refers to the ratio of mill feed rate
to the fresh feed rate. Mills are operated
at high
circulating loads so that overgrinding
does not occur
in the mill.
A description of the transient response of the mifl is
needed for dynamic model calculations.
For all practical purposes the RTD determined
with a suitabIe
tracer is adequate. It is assumed that the transport
characteristic
of particles of all sizes is identical. Detailed investigations
of the hold-up variations
and
RTDs on the 70-cm mill for various feed rates using a
liquid tracer (lithium chloride solution) yielded the
dimensionless
RTD of the form (Kinneberg
and
Herbst, 1984)
E(o)
=
ev( - O/&J)2+
evi -
@/I - 4)
1
(15)
where 8 = r/T,, = dimensionless
time, T, = mean retention time, and Q = fractlonal volume of the first
mixer. This expression corresponds
to two mixers of
unequal volume in series. Further studies with a solid
tracer (quartz particles) yielded identical RTD confirming that water and particles behaved identically
within the mill. In the dynamic model calculation the
RTD was taken to be a single perfect mixer since the
value of 4 was small (0.01-0.07) for most feed rates.
From a mathematical
point of view, the feed size
distribution
is linearly transformed
to mill discharge
size distribution.
The transformation
involves selection or breakage rate functions, a breakage distribution function and the RTD. Therefore if the breakage
distribution
function and RTD are known, the selection function can be estimated (Rajamani and Herbst,
1984). Accordingly,
steady-state
experimental
data
were gathered in the feed rate range of 9(X205 kg/h.
As stated earlier, the selection functions depend on the
fineness of the product in the mill. However, in the
feed rate range of 90-136 kg/h, the operating range for
both feedback and optimal control tests, a single set of
selection functions given by
S”(tonne/kWh)
= 10.6(Jd,d,,l/a)‘.4z7
(16)
was sufficient to predict all the data.
Figure 2 shows the model prediction during selection function estimation
at a feed rate of 159 kg/h.
Close agreement
is seen between model prediction
and experimental
distribution.
The
measurement
of the mill discharge
root mean squared error between
values and the experimental data is
the fitted model
0.0057, which is well below 0.0100, the standard norm
established for such estimation. The close fit assures
that the selection functions stated in eq. (16) would be
good enough for dynamic model calculations.
Hydrocyclone
A separate
taken
model parametrization
experimental
to determine
cyclone
test program
model
was under-
parameters.
The
Optimal
control
of a ball mill grinding
circuit-1
TEST NO. 5
IS9 UG./HR.
0
-
865
FRESH
EXPERIMENTAL
LINEdR
MODEL
FEED
FIT
Fig. 2. Linear model fit to the closed-circuit steady-state data.
75-mm
cyclone was mounted on an experimental
test
stand consisting of a sump, pump and return pipes. A
density gauge and a flow meter mounted
on the
cyclone feed line gave mass rate measurements
of
solids and water. The cyclone feed flow was varied
over the range 15 to 30 l/min and the feed solids
percentage was varied in the range 3C50. Samples of
feed, underflow and overflow were collected and their
size distributions
determined
by sieving. The parameters of the cyclone model eqs (8)-(12) were determined as follows:
Water split equation.
Multiple
linear
methods were used in correlating
cyclone
WF-WOF
relationship
was expressed as
one for higher feed rates and one for lower
given as
WOF (kg/min)
= 1.363WF (kg/min)
regression
data. The
two lines,
feed rates,
- 10.75
for WF < 21.4
WOF (kg/min)
= 0.837WF
(kg/min)
+ 0.35
for WF > 21.4.
The d,,
(17)
(18)
The dependence
of d,, on volumetric feed flow rate and percent solids in the feed is
given by the regression relationship
log,d,,(pm)
equation.
= 3.616 - 15.006
x 10-2Qc(1/min)
+ 2.3S,.
(19)
The sign of the coefficients of Q, andf, are in agreement with the expected performance
characteristics
of
the cyclone: as flow rate increases the cyclone produces a finer split and a coarser split is produced as
percent solids in the feed increases.
Short circuiting. The fraction
of fine material reporting to the underflow
is proportional
to the frac-
tion of feed water reporting to underflow. The regression relationship
between R, and fractional
water
split (to underflow)
WS is given as
R, = 0.818 - 0.7932 WS.
(20)
Corrected
ejiciency
curve.
This functional
form is
given as
x = 1 - exp[ - 0.6931(dJd,,)“].
The value
be 1.6.
of the parameter
MODEL
Steady-state
m was determined
(21)
to
VERIFICATION
response
The steady-state
predlctions
using rate parameters
given by eqs (14) and (16) for 170 kg/h feed rate
conditions are shown in Fig. 3. It should be noted that
the steady-state
predictions
made with the dynamic
simulator
involve both the mill and hydrocyclone
models. The circulating
load, defined as the ratio
(expressed as percent) of mass feed rate of solids in the
mill feed (includes recycle) to the mass feed rate of
fresh feed entering the circuit, is also closely predicted.
The excellent quality of predictions
confirms the appropriateness
of the models chosen for the mill and
cyclone and the accuracy of the parameter estimates.
Dynamic
response
The dynamic models incorporated in the simulator
can be checked for predictive accuracy only by comparing the transient
responses
of the circuit with
model computed responses. The transient response of
the circuit to changes in sump water addition rate is
well suited since to this disturbance
both the circulating load and product particle size react rapidly.
Control
loop tuning done with the simulator
for
feedback control relies on the ability of the simulator
to predict particle size responses to changes in sump
water addition rate. For these reasons, step changes in
sump water addition
rates were studied
experimentally and compared with model predictions.
Millfeedbox
delay model. Dynamic modeling studies indicated that there was a lag associated with the
mill to changes in feed flow. This lag was traced to the
mill feedbox which surrounded
the scoop-feeder.
Although the slurry volume in the mill is constant, it
and JOHN A. HERBST
RAJ K. RAJAMANI
866
PARTICLE
SIZE ( MESH )
IO
iub
TEST NO 5
FP,ZD ,WTE: 17,
0
-
EXPERIMENTAL
PREDICTED
CIRCVLATING
EXPERIMENT&‘
PREDICTED
I
20
Fig. 3. Modet
PL?&LE’“&E
predicrion
of closed-circuit
was detected that the mill feedbox tends to accumulate some slurry whenever transients occurred in the
circuit. The transient response of the mill was determined by introducing
a step change of 3.8 I/min in the
feed to the mill and measuring
the mill discharge
volumetric rate. The mill discharge flow response was
modeled
as a second-order
lag. The resulting
input-output
relationship
expressed in the Laplace
transfer function form is given as
1
m
Dynamic
= (0.45s + 1)(0.41s + 1)’
circuit
(22)
simulation
The computation
embodied in the models for the
mill, hydrocyclone
and sump are done in a simulation
program called DYNAMILL.
The program simulates
the transient
response of the circuit, and with the
proportional-integral
controller
subroutine
it can
also simulate the response of the circuit under control.
Dynamic
prediction
A unique feature of the product particle size response obtained under step changes in sump water
addition rate is that, upon a step increase (decrease),
the product particle size rapidly gets finer (coarser)
Pig.
4.
/“R
326
x
WAD
354 %
1
0
QdS)
KG
%?CRCJNS 500
I
1000
2000
steady state at 170 kg/h fresh feed.
and then slowly gets coarser (finer) until it reaches a
steady-state value that is finer (coarser) than the product size at start. Under a step increase in sump water
addition rate, the cyclone feed slurry becomes dilute
and also the volumetric rate to the cyclone increases
as a result of sump level control. Then, the cyclone cut
size decreases producing
a finer product, and simultaneously the amount of coarse solids returned to the
mill increases. Due to the increase in solids feed to the
mill, the mill discharge
stream gets coarser. The
coarse material now begins to appear in the cyclone
feed, resulting in a coarser product. Clearly then, the
initial part of the response is due to the dynamic
elements sump and cyclone, and the final part is due
to the mill. Similar reasoning applies for the inverse
response in percent solids in the sump slurry, observed experimentally.
The particle size response observed experimentally
and the dynamic model prediction for step changes of
2.3 kg/min in the sump water rate at feed solids rates
of 136 kg/h are shown in Fig. 4. For these step tests
the only active control loop is the sump level control
loop. The dynamic prediction is excellent both in the
time response and magnitude.
Such a dynamic predictive capability is imperative for classical feedback
control loop tuning.
Model prediction of product particle size transients for step changes in sump waler addition at
136 kg/h fresh feed.
Optimal
SIMPLIFIED
control
of a ball mill grinding
MODEL
The optimal control approach described in Part II
requires a state space model of the grinding circuit.
The state space model couId be linear or nonlinear
and in either case Pontryagin’s
Maximum
Principle
used in this study could be applied. Recourse
to
linearization
and model simplification
is taken owing
to the slow speed of the HP 2100 operating system.
One approach
to the development
of simplified dynamic models for control is to use “black box” models, i.e. a form of the model is assumed and the
parameters
are determined by forcing the model to fit
plant data. For example, the linear difference equation
form used by Borrison and Syding (1976) for crushers
and the Laplace
transform
blocks determined
by
Hulbert (1977) for ball mills takes the “black box”
approach. The principal drawback is that the model is
not physically meaningful and hence it may not extrapolate well. On the other hand, control schemes developed with phenomenological
models can be much
more easily extended
to a different system, i.e. an
industrial installation.
An alternative approach
is to
simplify the general phenomenological
models of the
subsystems
by suitable assumptions
while retaining
the accuracy of predictions.
Fortunately,
such simplifications are readily available for the grinding circuit
case. The parameters
of this model are then readily
obtained from steady-state
data.
Simplified model formulation
The use of the detailed model for control would
entail the solution of 37 nonlinear differential equations and 38 algebraic equations to provide a simulation of the grinding circuit at every control interval.
Such a detailed model is not appropriate
for real-time
calculations
on a minicomputer
owing to the large
number of arithmetic
operations
involved and the
storage required. Added to this burden would be the
additional
real-time computations
involved in optimal control problem solution and on-line model parameter estimation.
However, in recent years on-line
computing power has grown exponentially,
and so the
accuracy of predictions
possible with the full set of
model equations
can be taken advantage
of with a
powerful on-line computer. In this work models had
to be simplified due to the slower CPU speed of the
HP 2100 computer. The models described below are
simple enough for on-line use while retaining a reasonable level of predictive accuracy.
867
circui!--I
hold-up mass, R,,,,
is the fraction of solids retained
above the size interval k, and Bkj is the cumulative
breakage function given by
k-l
R MP,k =
c
mhfp, j
(24)
j=l
(25)
Equation (23) is equivalent to eq. (1) algebraically
but
as the independent
variable.
uses R,,,,
Under the assumption,
BkjSj = F,, where Fk is a
constant with respect to the parent size j, eq. (23) can
be written as
d”R,,
p1
k
dt
= MMMFRMMF.~
- F,“R.w,,
This assumption
was identified empirically
in conjunction with a study of the zero-order
production
of
fines (Herbst and Fuerstenau,
1968) and has been
exploited to estimate breakage function values from
batch bail mill data. In the present study the form of
eq. (26) for closed-circuit
operation becomes
HM%
= M,,R,,
-CM,,
+ M,,R,,
- k,HR,,.,
+ Mu,)&,,
Sump. The sump is considered
to be perfectly mixed.
The level control of the sump is assumed to involve a
well-tuned controller which maintains the sump level
steady at all times and so the slurry volume in the
sump is taken to be a constant. Then, the following
two mass balance equations
are applicable
for the
sump:
V,~=(M,,+M,,)-(Q,+~)C,
Ball mill model. A form of the simplified model can
be deduced from the more general population balance
model as follows. Consider a ball mill operating
in
open circuit at a feed rate of M,,,
then the size
reduction occurring in the mill is described by
d”R,,
L=M
kL
dt
MF
R
M~,lr
-
1
,Fl &SjHmj
- MMFRMF,, (23)
where M,,
is the fresh solids feed rate, H is the mill
(27)
where R, is defined as the fraction of material above
44 pm in the mill, M is the solids feed rate, and H,
mill hold-up mass. The subscript M refers to mill, FF
refers to fresh feed, and CJF refers to underflow. The
hold-up of solids in the mill was determined
experimentally to be approximately
constant
for all feed
rates.
(29)
where Vs is the volume of slurry in the sump, W,, is
the rate of addition of water to the sump, QM is the
total volume of slurry discharging from the mill, C, is
the concentration
of solids in the sump expressed as
mass of solids per unit volume of slurry, and Rs is the
fraction of solids above 44 pm in the sump.
Hydrocyclone
model. The size description
in the
circuit has now been reduced to two parts: the fraction
of material
retained
above
44 pm and
the fraction
868
RAJ K. RAJAMANIand JOHN A. HERBST
passing 44 pm size. Accordingly,
the classification
action of the cyclone must be represented
by two constants C, and C,, where C, is the fraction of plus
44 pm material in the cyclone feed that reports to
underflow,
and C, is the fraction of minus 44 pm
material in the cyclone feed that reports to underflow.
The variations in C, and C, with cyclone feed conditions are expressed through d,,. Owing to the widespread use of the variable d,,, both in design and
modeling of cyclones, it was decided in this study to
use d,, as a basis to specify classification.
It is apparent from the detailed model that C, and
C, are really a function of cyclone operating conditions and the size distribution
of the cyclone feed
stream. Several values of C, and C, were computed
with the detailed dynamic model simulation program
for fresh feed conditions
ranging from 90 to 160 kg/h
and sump water addition rates of 11.4-16 kg/mitt. C,
and C, each show a linear dependence
on d,, in the
range of interest. Therefore the dependence of both C,
and C, on d,, were expressed as
c, = Ul,&
+ a12
(30)
C, = a,,&,
+ ~22.
(31)
+
where Qc is the volumetric
k2Qc + k&b
MM
(kg/h)
MU,
Wmin)
159
136
125
496.3
449.4
450.3
113
355.2
model
(33)
C, = O.OO%d,,
k, in
data.
parameters
determined
R.U
RO,
0.883
0.888
0.880
0.832
0.790
0.768
0.760
0.715
0.42
0.32
0.30
0.28
40
Simplified
model prediction
of particle
(35)
from
experimental data
55
50
46
42
SlMPLlFlED
0.0345
0.0354
0.0344
0.0343
[MI
size response
136 kg/h.
C,
C*
0.8727
4.903 I
0.9205
0.905 1
0.2975
0.3184
0.4130
0.3894
MODEL
60
TIME
Fig. 5.
(34)
C’, = O.Wl(Od,, - 2.029.
k,
(min-‘)
R MF
20
+ 1.181
The excellent dynamic model prediction
obtained
with eqs (34) and (35) for sump water addition tests at
a fresh feed rate of 136 kg/h is shown in Fig. 5. A
similar procedure resulted in excellent prediction for
the 114-kg/h experimental
data but the numerical
coefticients in the classifier expression were different.
Two different sets of classifier description
equations
are expected because in such a simplified model the
classification constants C, and C, represent the combined effect of the size distribution
of solids in the feed
aud the classifier performance,
i.e. C, and C, are
determined
by both the mass of material and the
classification
occurring in each of the size intervals.
Variations in fresh solids feed rate cause variations in
cyclone feed size distribution.
Therefore, regression
feed rate to the cyclone.
Table 1. Simplified
MM, RM, - &
H,
R,
Similarly the values of the cyclone classification parameters C, and C, can be obtained from steady-state
relations. Table 1 gives the steady-state
experimental
data and model parameters.
From the steady-state
predictions made previously, the values of C,, C, and
predictions,
are
d 50, which give rise to accurate
known, The unknown coefficients aI 1, aI2 and azz in
eqs (30) and (31) were estimated by linear regression.
The resulting classification model equations that gave
the best fit are
(32)
Model parameters. The kinetic rate parameter
eq. (27) can be determined
from steady-state
k,, is given by
k, = ~
The dependence of d,, on the cyclone feed volumetric
rate and percent solids was assumed to be of the form
d,, = exp(k,
From the steady state the mass balance,
loo
NUT&o
for
step changes
in sump water addition
rate at
Optimal
Table 2. Comparison
control
of a ball mill
grinding
of simplified model prediction and experimental
Mill feed
Fresh
(mic&s)
(W-4
(kg/h)
Experimental
Predicted
136
136
136
125
117
113
113
113
684
816
954
684
816
684
816
954
585.6
592.7
610.9
636.6
484.3
457.3
412.1
415.9
426.8
563.8
468.5
equations
including
these two variables
were developed. The simplified cyclone model equation applicable in the entire feed rate range of 114-136 kg/h is
given by
C, = 0.0042M,,d,o
- O.O704M,,
C, = O.O502M,,d,,
-
2.9354M,,
- 0.01546,,
+ 1.3412
50.0
46.0
43.5
Predicted
Experimental
Predicted
48.8
46.7
45.0
46.1
40.9
43.6
41.6
40.2
68.0
70.0
71.0
70.0
75.0
72.0
74.0
76.0
67.75
69.75
71.24
70.55
74.97
72.33
74.48
76.09
a2 . .
a8
(37)
Bij
bij
C
CONCLUSIONS
Dynamic modeling of the grinding circuit involves
modeling the mill, sump, hydrocyclone
and mill feedbox, and suitably linking the models together. The
population
balance model of the milling process is
most convenient
for this purpose. In the mill model,
the rate parameter
dependence
on operating conditions can be accounted for using the specific selection
function hypothesis.
The sump model involves a description of the concentration
solids and size distribution in the discharge of the sump. A set of empirical
algebraic
equations
is sufficient
to model the hydrocyclone since the action of this device is instantaneous. The predictive capability of the dynamic model
was demonstrated
by predicting the response of the
circuit to changes in sump water addition rate.
A simplified dynamic model is needed especially if
the CPU speed of the on-line computer
cannot accommodate
both model and control calculations
at
each sampling instant. Therefore, a model of the circuit using three state variables was developed. The mill
model is a limiting case of the population
balance
model. Correspondingly,
models of the sump and
hydrocyclone
were simplified. In spite of these drastic
simplifications,
the predictive capability of the simplified model is adequate and so it can be employed in
control algorithms. In Part II of this paper computer
control of the grinding circuit using these dynamic
data
NOTATION
a,,
The comparison
of steady-state
simplified model predictions
and experimental
data are tabulated
in
Table 2. The predictions
are accurate enough for the
simplified dynamic model to be used in the synthesis
of an optimal control strategy.
steady-state
models is discussed. In particular, the detailed model
is used in the off-line tuning of proportional-integral
controllers
and the simplified model is used in the
optimal control algorithm.
Both model predictions
and experimental
responses are shown.
(34)
- 0.0660d,,
+ 4.642.
Experimental
869
Overflow
produce size
% passing 44 pm
d
(Wmin)
Sump water
feed
circuit-I
E(o)
Fk
H(t),
H
ko
4, k,, k,
M
4
n
P
Q
R MP.k
Rls
si, s;E
t
vhf, VF
WF
WOF
ws
Y,
cyclone model constants
cumulative breakage function
individual breakage function
concentration
of solids (units = mass of
solids per unit volume of slurry)
defined in eqs (30) and (31), respectively
mesh opening of size interval 2
cut size
fraction of solids (in the feed) reporting
to underflow in size interval i
residence time distribution
a constant ( Bkj Sj)
total mass hold-up in the mill
kinetic rate parameter
for milling [see
eq. (33)l
simplified cyclone model constants
mass rate of solids flow
mass fraction of material in size interval i
number of size intervals
net mill power draft
volumetric flow rate of slurry
fraction of solids retained above size interval k in mill product
fraction of fines (in the feed) reporting to
cyclone underflow
Laplace variable
selection function and specific selection
function, respectively
time
volume of mill and sump, respectively
water flow rate in the cyclone feed stream
water flow rate in the cyclone overflow
fractional water split to underflow
fraction of solids (in the feed) reporting
to cyclone underflow after correcting for
entrainment
RAJ K. RAJAMANI and JOIIN A. HERBST
870
Greek
letters
0
PW
4
dimensionless
retention time
density of water
fractional volume of the first mixer
Subscripts
C
FF
M
MF
MP
OF
S
SF
SP
WF
cyclone
fresh feed stream
mill
mill feed stream
mill discharge stream
cyclone overflow stream
sump
sump feed stream
sump discharge stream
underflow stream
REFERENCES
Borrison,
V. and
Syding, R., 1976, Self-tuning control of an
ore crusher. Automatica 12, l-7.
Cohen, H. E., Mizrahi, J., Reaven, C. H. J. and Fern, N., 1966,
The Residence Time of Mineral Particles in Hydrocyclones.
Institute of Mining and Metallurgy.
Herbst, I. A. and Fuerstenau,
D. W., 1968, The zero order
production
of fine sizes in comminution and its implications in simulation. ~rans. AiME 241, 538-548.
Herbst, J. A. and Fuerstenau,
D. W., 1973, Mathematical
simulation
of dry ball milhng using specific power information.
Trans. AIME 254, 343.
Herbst, J. A. and Mular, A. L., 1980, Analysis and control of
mineral processing,
in Computer
Methods for the 80’s
Society of Mining Engineers (Edited by A. Weiss), Section 5.
Herbst. J. A. and Rajamani,
K., 1979, Evaluation
of optimizing control strategies
of closed circuit grinding.
Proceedings of the 13th International
Mineral
Processing
Congress, Warsaw.
Herbst, J. A., Rajamani,
K. and Kinneberg,
D. J., 1977,
ESTIMILL--a
Program forGrinding Simulation
and
Parameter Estzmalion with Linear Models. Metallurgical
Engineering
Department,
University
of Utah. Salt Lake
City, UT.
Herbst, J. A., Siddique, M., Rajamam, K. and Sanchez, E.,
1983, Population
balance approach
to ball mill scale-up:
bench and pilot scale investigations.
Trans. A/ME 272,
194551954.
Huibert, D. G., 1977. Multivariable
control of a wet grinding
circuit. PhD dissertation,
IJniversity of Natal.
Kim, J. H., 1974, A normalized
model for wet batch milling.
PhD dissertation,
University of Utah, Salt Lake City, UT.
Kinneberg,
D. J. and Herbs& J. A., 1984, Comparison
of
models
for the simulation
of open circuit
ball mill
grinding. Int. J. Miner. Processing.
Lynch, A. J. and Rao, T. C., 1975, Modeling and scale-up of
hydrocyclone
classifiers. Proceedings
of the 1 lth International Mineral Processing congress, Cagliari, pp. 245-269.
Malghan, S. G. and Fuerstenau,
D. W., 1976, The scale-up of
ball mills using population
balance models and specific
power input. Symposium
Zerkleinern,
Dechema-Monographien, 79, Part II, No. 1586, 613.
Rajamani,
K. and Herbst, J. A., 1984, Simultaneous
estimation of selectton and breakage functions from batch and
continuous
grinding data. Trans. Instn Min. Merall. C 93,
c74-C85.
Stewart, P. S. B.. 1970, The control of wet grinding circuits.
Aust. them. Process Enyng 22-23.