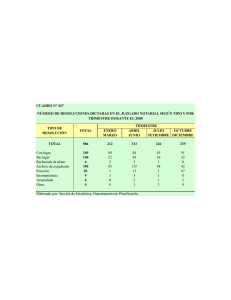
INSTITUTO TECNOLÓGICO DE TIJUANA INGENIERÍA INDUSTRIAL INGENIERÍA ECONÓMICA TÍTULO TASA DE INTERÉS Y TASA DE RENDIMIENTO MAESTRO: STEPHENS SANTIAGO EDUARDO PRESENTA: #17211206 JIMÉNEZ FLORES FERNANDO DE JESUS GRUPO: “7 Y” Tijuana, Baja California a de febrero de 2020 Tasa de interés y tasa de rendimiento 1.9 La compañía Trucking Giant Yellow Corp acordó comprar a la empresa rival Roadwaw en $966 millones a fin de reducir los costos denominados indirectos de oficinas, por ejemplo los costos por nómina y seguros que tienen un monto de $45 millones al año. Si los ahorros fueran los que se planearon, ¿Cuál sería la tasa de rendimiento de la inversión? SOLUCIÓN: COSTOS POR NÓMINA Y SEGUROS = $45 millones INVERSIÓN = $966 millones 𝑻𝑨𝑺𝑨 𝑫𝑬 𝑹𝑬𝑵𝑫𝑰𝑴𝑰𝑬𝑵𝑻𝑶 = $𝟒𝟓 𝑴𝒊𝒍𝒍𝒐𝒏𝒆𝒔 𝒙𝟏𝟎𝟎% = 𝟒, 𝟔𝟓% $𝟗𝟔𝟔 𝑴𝒊𝒍𝒍𝒐𝒏𝒆𝒔 1.10 Si las utilidades por cada acción de Ford Motor Company se incrementaron de 22 a 29 centavos en el trimestre entre abril y junio en comparación con el trimestre anterior, ¿Cuál fue la tasa de incremento en las utilidades de dicho trimestre? SOLUCIÓN: UTILIDAD ANTIGUA = 22 Centavos UTILIDAD ACTUAL = 29 Centavos 𝑻𝑨𝑺𝑨 𝑫𝑬 𝑰𝑵𝑪𝑹𝑬𝑴𝑬𝑵𝑻𝑶 = (𝟐𝟗 − 𝟐𝟐) 𝑿𝟏𝟎𝟎% = 𝟑𝟏, 𝟖𝟐% 𝟐𝟐 1.15 Una compañía química que comienza a operar se fijó la meta de obtener una tasa de rendimiento de al menos 35% anual sobre su inversión. Si la empresa adquirió $50 millones como capital de riesgo, ¿Cuánto debe percibir en el primer año? SOLUCIÓN TASA DE RENDIMIENTO = 35% CAPITAL DE RIESGO = $50 Millones 𝑰𝑵𝑻𝑬𝑹𝑬𝑺 𝑬𝑵 𝑬𝑳 𝑷𝑹𝑰𝑴𝑬𝑹 𝑨Ñ𝑶 = $𝟓𝟎 𝒎𝒊𝒍𝒍𝒐𝒏𝒆𝒔 ∗ (𝟎. 𝟑𝟓) = $𝟏𝟕 𝟓𝟎𝟎 𝟎𝟎𝟎 EQUIVALENCIA 1.16 Con una tasa de interés de 8% por año, ¿a cuánto equivalen $10000 de hoy, a) dentro de un año y b) hace un año? SOLUCIÓN a) Dentro de un año TASA DE INTERÉS = 8% PRESENTE = $10000 𝑭 = 𝑷 ∗ (𝟏 + 𝑰%)𝒏 𝑭 = 𝟏𝟎𝟎𝟎𝟎 ∗ (𝟏. 𝟎𝟖)𝟏 𝑭 = $𝟏𝟎𝟖𝟎𝟎 b) Hace un año TASA DE INTERÉS = 8% FUTURO = $10000 𝑷= 𝑷= 𝑭 (𝟏 + 𝑰%)𝒏 𝟏𝟎𝟎𝟎𝟎 = $𝟗𝟐𝟓𝟗, 𝟐𝟔 (𝟏. 𝟎𝟖)𝟏 1.18 ¿Con que tasa de interés son equivalentes una inversión de $40000 hace un año y otra de $50000 hoy? SOLUCIÓN PRESENTE = $40000 FUTURO = $50000 𝟓𝟎𝟎𝟎𝟎 = 𝟒𝟎𝟎𝟎𝟎 ∗ (𝟏 + 𝑰%)𝟏 𝑰% = 𝟏. 𝟐𝟓 − 𝟏 𝑰 = 𝟐𝟓% 1.19 ¿Con qué tasa de interés equivalen $100000 de ahora a $80000 de hace un año? SOLUCIÓN PRESENTE = $80000 FUTUTRO = $100000 𝑭 = 𝑷 ∗ (𝟏 + 𝑰%)𝒏 𝟏𝟎𝟎𝟎𝟎𝟎 = 𝟖𝟎𝟎𝟎𝟎 ∗ (𝟏 + 𝑰%)𝟏 𝑰% = 𝟏𝟎 −𝟏 𝟖 𝑰 = 𝟐𝟓% INTERÉS SIMPLE E INTERÉS COMPUESTO 1.20 Ciertos certificados de depósito acumulan un interés simple de 10% anual. Si una compañía invierte ahora $240000 en dichos certificados para la adquisición dentro de tres años de una máquina nueva, ¿Cuánto tendrá la empresa al final de ese periodo de tiempo? SOLUCIÓN TASA DE INTERÉS = 10% PRESENTE = $240000 PERIODO (n) = 3 Años FUTURO =? 𝑭 = 𝑷 + 𝑷 ∗ 𝒊% ∗ 𝒏 𝑭 = 𝟐𝟒𝟎𝟎𝟎𝟎 + 𝟐𝟒𝟎𝟎𝟎𝟎 ∗ 𝟎. 𝟏𝟎 ∗ 𝟑 𝑭 = 𝟐𝟒𝟎𝟎𝟎𝟎 + 𝟕𝟐𝟎𝟎𝟎 𝑭 = $𝟑𝟏𝟐𝟎𝟎𝟎 1.21 Un banco local ofrece pagar un interés compuesto de 7% anual sobre las cuentas de ahorro nuevas. Un banco electrónico ofrece 7.5% de interés simple anual por un certificado de depósito a cinco años. ¿Cuál oferta resulta más atractiva para una empresa que desea invertir ahora $1000000 para la expansión dentro de 5 años de una planta? SOLUCIÓN BANCO LOCAL TASA DE INTERÉS = 7% 𝑭 = 𝟏𝟎𝟎𝟎𝟎𝟎𝟎 ∗ (𝟏. 𝟎𝟕)𝟓 𝑭 = $𝟏𝟒𝟎𝟐𝟓𝟓𝟏. 𝟕𝟑𝟏 BANCO ELECTRÓNICO TASA DE INTERÉS =7.5% 𝑭 = 𝟏𝟎𝟎𝟎𝟎𝟎𝟎 + 𝟏𝟎𝟎𝟎𝟎𝟎𝟎 ∗ 𝟎. 𝟎𝟕𝟓 ∗ 𝟓 𝑭 = $𝟏𝟑𝟕𝟓𝟎𝟎𝟎 CONCLUSIÓN: la oferta más atractiva es la del banco electrónico, porque el pago que hará la empresa durante los 5 años es menor a la que ofrece el banco local. 1.22 Badger Pump Company invirtió $500000 hace cinco años en una nueva línea de productos que ahora reditúa $1000000. ¿Qué tasa de rendimiento percibió la empresa sobre la base de a) interés simple, y b) interés compuesto? SOLUCIÓN a) INTERÉS SIMPLE PRESENTE = $500000 FUTURO = $1000000 PERIODO (n) = 5 Años 𝟏𝟎𝟎𝟎𝟎𝟎𝟎 = 𝟓𝟎𝟎𝟎𝟎𝟎 + 𝟓𝟎𝟎𝟎𝟎𝟎 ∗ 𝑰% ∗ 𝟓 𝟓𝟎𝟎𝟎𝟎𝟎 = 𝟐𝟓𝟎𝟎𝟎𝟎𝟎 ∗ 𝑰% 𝟏 𝑰% = = 𝟎. 𝟐 𝟓 𝑰 = 𝟐𝟎% b) INTERÉS COMPUESTO PRESENTE = $500000 FUTURO = $1000000 PERIODO (n) = 5 Años 𝟏𝟎𝟎𝟎𝟎𝟎𝟎 = 𝟓𝟎𝟎𝟎𝟎𝟎 ∗ (𝟏 + 𝑰%)𝟓 𝟓 √𝟐 = 𝟏 + 𝑰% 𝟏. 𝟏𝟒𝟖𝟕 = 𝟏 + 𝑰% 𝑰% = 𝟎. 𝟏𝟒𝟖𝟕 𝑰 = 𝟏𝟒. 𝟖𝟕% 1.23 ¿Cuánto tiempo tomará para que una inversión se duplique con 5% por año, con a) interés simple, y b) interés compuesto? SOLUCIÓN PRESENTE = P FUTURO = 2P TASA DE INTERÉS = 5% a) INTERÉS SIMPLE 𝟐𝑷 = 𝑷 + 𝑷 ∗ 𝟎. 𝟎𝟓 ∗ 𝒏 𝟐 = 𝟏 + 𝟎. 𝟎𝟓 ∗ 𝒏 𝟏 𝒏= = 𝟐𝟎 𝒂ñ𝒐𝒔 𝟎. 𝟎𝟓 COMENTARIO: para que la inversión se duplique necesitará 20 años b) INTERÉS COMPUESTO 𝟐𝑷 = 𝑷 ∗ (𝟏. 𝟎𝟓)𝒏 𝟐 = (𝟏. 𝟎𝟓)𝒏 n = 14 años = 1.98 n = 15 años = 2.08 INTERPOLANDO 14 n 15 1.98 2 2.08 𝒏 − 𝟏𝟒 𝟎. 𝟎𝟐 = 𝟏 𝟎. 𝟏 𝟎. 𝟏𝒏 − 𝟏. 𝟒 = 𝟎. 𝟎𝟐 𝒏= 𝟏. 𝟒𝟐 𝟎. 𝟏 𝒏 = 𝟏𝟒. 𝟐 𝒂ñ𝒐𝒔 COMENTARIO: para que la inversión se duplique necesitará de 14.2 años